Oscillation Criteria for Nonlinear Third-Order Delay Dynamic Equations on Time Scales Involving a Super-Linear Neutral Term

Abstract

In the sense of an arbitrary time scale, some new sufficient conditions on oscillation are presented in this paper for a class of nonlinear third-order delay dynamic equations involving a local fractional derivative with a super-linear neutral term. The established oscillation results include known Kamenev and Philos-type oscillation criteria and are new oscillation results so far in the literature. Some inequalities, the Riccati transformation, the integral technique, and the theory of time scale are used in the establishment of these oscillation criteria. The proposed results unify continuous and discrete analysis, and the process of deduction is further extended to another class of nonlinear third-order delay dynamic equations involving a local fractional derivative with a super-linear neutral term and a damping term. As applications for the established oscillation criteria, some examples are given.

1. Introduction

In the qualitative analysis of solutions of differential and difference equations, oscillation is a hot topic. An equation is oscillatory if all its solutions are neither positive nor negative eventually. The oscillatory theory of differential and difference equations has extensive applications in control, ecology, economics, biology, life sciences, engineering, and many other fields. In the last few decades, there have been rich research results on oscillation in the literature. The main approaches for studying oscillation are the Riccati transformation and the integral average technique. In the early research, the studied differential equations were mainly of low order with simple forms (for example, see [1,2], and the references therein). Later, the research of oscillation was extended to other differential equations with complex forms, such as differential equations with a neutral form [3,4], or with distributed deviating arguments [5], or with a delay term [6], or with a damping term [7]. At the same time, research into oscillation was extended to various difference equations by many authors, for example, difference equations with retarded arguments [8], linear and half-linear difference equations [9], advanced difference equations [10], and so on.

With the increasing application of fractional derivatives and fractional differential equations in various fields, recently, many authors have paid much attention to the research into the oscillation of fractional differential equations [11], fractional difference equations [12], and q-fractional difference equations [13].

In [14], Hilger proposed the concept of time scale, which is desired to unify continuous and discrete analysis. Since then, the oscillation of dynamic equations on time scales has been given much attention by many authors, and a lot of valuable oscillation criteria have been established for various dynamic equations on time scales. The main approaches for studying oscillation for dynamic equations on time scales in most research are still the Riccati transformation and the integral average technique together with the theory of time scale, and the research contents are roughly divided into two directions. One is that the orders of a dynamic equation were from a lower order [15,16,17] to higher order [18,19,20,21,22]. The other is that the forms of dynamic equations appear different, for example, superlinear and sublinear dynamic equations [16], functional dynamic equations [18,19], and dynamic equations with a neutral term [20,23].

Delay dynamics is a theory that studies the delay effect in dynamical systems. The application of delayed dynamics is very extensive. For example, studying the delayed effects of signal transmission between neurons in neuroscience can help us better understand the function of the nervous system and disease control. Studying the delayed effects in the food chain in ecology can help us better protect the stability of ecosystems. In the current research on the oscillation of delay dynamic equations on time scales, most of the existing results are related to linear, half-linear, and quasi-linear delay dynamic equations, while little research is related to super-linear delay dynamic equations due to the complexity of the analysis process. In [24], Grace et al. researched a class of delay second-order dynamic equations on time scales with a super-linear neutral term, and based on some certain inequalities, Riccati functions, and the $\Delta$ integral technique, they established some new oscillation criteria, including Kamenev and Philos-type oscillation criteria for the equation. In this research, we notice that very few authors have paid attention to delay dynamic equations on time scales involving local fractional derivative with a super-linear neutral term so far in the literature.

Motivated by the above analysis, in this paper, we research the oscillation of a class of nonlinear third-order delay dynamic equations on time scales involving a local fractional derivative with a super-linear neutral term denoted as follows:

$$\begin{array}{cc}\hfill & D^{\theta }\left[s_1\left(x\right)D^{\theta }\left(s_2\left(x\right)D^{\theta }[w\left(x\right)+m\left(x\right)w^{\alpha }\left(l_1\left(x\right)\right)]\right)\right]+s_3\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)=0,\hfill \\ \hfill & x\in {\mathbb{T}}_0,0<\theta \le 1,\hfill \end{array}$$

(1)

and another class of nonlinear third-order delay dynamic equations involving a local fractional derivative with a super-linear neutral term and a damping term as follows:

$$\begin{array}{cc}\hfill & D^{\theta }\left[s_1\left(x\right)D^{\theta }\left(s_2\left(x\right)D^{\theta }[w\left(x\right)+m\left(x\right)w^{\alpha }\left(l_1\left(x\right)\right)]\right)\right]+v\left(x\right)D^{\theta }\left(s_2\left(x\right)D^{\theta }[w\left(x\right)+m\left(x\right)w^{\alpha }\left(x\right)]\right)\hfill \\ \hfill & +s_3\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)=0,x\in {\mathbb{T}}_0,0<\theta \le 1,\hfill \end{array}$$

(2)

where $\mathbb{T}$ is an arbitrary time scale, $D^{\theta }$ is the local fractional operator of $\theta$ order, w is the unknown function, $\alpha ,\beta$ are the ratios of two positive odd integers satisfying $\beta \ge \alpha \ge 1$, and ${\mathbb{T}}_0=[x_0,\infty )\bigcap \mathbb{T}$, $x_0>0$, $s_1,s_2,s_3,m,v\in C_{rd}({\mathbb{T}}_0,{\mathbb{R}}_{+})$. Assume $l_1,l_2$ are increasing delay functions, and $l_1\left(x\right)\le x,l_2\left(x\right)\le x$, $l_1^{-1}\left(l_2\left(x\right)\right)\ge x$.

The delay dynamic equations denoted by (1) and (2) have a wide range of applications in the fields of dynamics and thermodynamics in physics research. They can fully consider the historical changes of the research object and the impact of the current state on future state changes. By studying its qualitative properties such as oscillation and stability, they can more deeply and accurately grasp and control the current state of the physics research object.

Definition 1. 

A function $u\in (\mathbb{T},\mathbb{R})$ is regressive provided $1+\mu \left(x\right)u\left(x\right)\ne 0$, where $\mu \left(x\right)=\sigma \left(x\right)-x$, $\sigma \left(x\right)=inf\{t\in \mathbb{T},t>x\}$. The set of rd-continuous functions is denoted by $C_{rd}$, and the set of all regressive and rd-continuous functions is denoted by $\mathfrak{R}$, while ${\mathfrak{R}}^{+}=\left\{u\right|u\in \mathfrak{R},1+\mu \left(x\right)u\left(x\right)>0,\forall x\in \mathbb{T}\}$.

For more details on the theory of time scales, we refer the readers to [25,26].

Definition 2 

([27]). For $x\in \mathbb{T}$, $0<\theta \le 1$, the local fractional derivative of θ order for a function $f\in (\mathbb{T},\mathbb{R})$ is defined by $D^{\theta }f\left(x\right)$ satisfying

$$|[f\left(\sigma \left(x\right)\right)-f\left(s\right)]x^{1-\alpha }-D^{\theta }f\left(x\right)(\sigma \left(x\right)-s)|\le \epsilon |\sigma \left(x\right)-s|forallx\in \mathfrak{U},$$

where $\mathfrak{U}$ is a neighborhood of x.

Remark 1. 

The local fractional derivative defined on an arbitrary time scale $\mathbb{T}$ in Definition 2 unifies the continuous and discrete case; that is, if $\mathbb{T}=\mathbb{R}$ or $\mathbb{T}=\mathbb{Z}$, then $D^{\theta }f\left(x\right)$ becomes the fractional derivative on the set of real numbers and the set of integers, respectively. The latter can be denoted by the fractional difference operator ${\Delta }^{\theta }$.

According to Definition 2, if x is right-scattered, then one has $D^{\theta }f\left(x\right)=\frac{{\displaystyle f\left(\sigma \right(x\left)\right)-f\left(x\right)}}{{\displaystyle \sigma \left(x\right)-x}}$$x^{1-\theta }$, while $D^{\theta }f\left(x\right)=\underset{s\to x}{lim}\frac{{\displaystyle f\left(s\right)-f\left(x\right)}}{{\displaystyle s-x}}{x}^{1-\theta }$ if x is right-dense. So, $D^{\theta }f\left(x\right)=f^{\Delta }\left(x\right)x^{1-\theta }$. By use of this relationship, (1) and (2) can be diverted to the following equations:

$${\left[b_1\left(x\right){\left(b_2\left(x\right){[w\left(x\right)+m\left(x\right)w^{\alpha }\left(l_1\left(x\right)\right)]}^{\Delta }\right)}^{\Delta }\right]}^{\Delta }+n\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)=0,x\in {\mathbb{T}}_0,$$

(3)

and

$$\begin{array}{cc}\hfill & {\left[b_1\left(x\right){\left(b_2\left(x\right){[w\left(x\right)+m\left(x\right)w^{\alpha }\left(l_1\left(x\right)\right)]}^{\Delta }\right)}^{\Delta }\right]}^{\Delta }+v\left(x\right){\left(b_2\left(x\right){[w\left(x\right)+m\left(x\right)w^{\alpha }\left(x\right)]}^{\Delta }\right)}^{\Delta }\hfill \\ \hfill & +n\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)=0,x\in {\mathbb{T}}_0,\hfill \end{array}$$

(4)

where $b_1\left(x\right)=x^{1-\theta }{s}_1\left(x\right),b_2\left(x\right)=x^{1-\theta }{s}_2\left(x\right)$, and $b_3\left(x\right)=x^{\theta -1}{s}_3\left(x\right)$.

Define $A_1(x,x^{*})={\int }_{x^{*}}^x\frac{{\displaystyle 1}}{{\displaystyle b_1\left(t\right)}}\Delta t$, and$A_2(x,x^{*})={\int }_{x^{*}}^x\frac{{\displaystyle 1}}{{\displaystyle b_2\left(t\right)}}\Delta t$. In the following analysis, we always assume m is nondecreasing, and

$$\left\{\begin{array}{c}\underset{x\to \infty }{lim}m\left(x\right)=\infty ,\hfill \\ \\ \underset{x\to \infty }{lim}\frac{{\displaystyle A_1(x,x^{*})A_2(x,x^{*})}}{{\displaystyle m^{\frac{1}{\alpha }}\left(x\right)}}=0.\hfill \end{array}\right.$$

(5)

Set $y\left(x\right)=w\left(x\right)+m\left(x\right)w^{\alpha }\left(l_1\left(x\right)\right)$. Then, (4) and (5) can be converted into the following forms

$${\left(b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\right)}^{\Delta }+n\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)=0,x\in {\mathbb{T}}_0,$$

(6)

$${\left(b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\right)}^{\Delta }+v\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }+n\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)=0,x\in {\mathbb{T}}_0.$$

(7)

The rest of this paper is organized as follows. In Section 1, we present some new oscillation results for Equation (1) (or its equivalent form Equation (3)). Then, in Section 2, we extend the deduction process and establish some new oscillation criteria to Equation (2) (or its equivalent form Equation (4)). Some examples are presented in Section 3 for applying the established oscillation criteria. At last, we give some concluding comments. Throughout the paper, ${[x,\infty )}_{\mathbb{T}}=[x,\infty )\bigcap \mathbb{T}$.

2. Oscillation Results for Equation (1)

In this section, as Equation (1) is equivalent to (3), we only need to research the oscillation of Equation (3). First, we give some lemmas.

Lemma 1. 

Assume Equation (3) has an eventually positive solution $w\left(x\right)$, satisfying $w\left(x\right)>0,w\left(l_1\left(x\right)\right)>0,w\left(l_2\left(x\right)\right)>0$ on ${[x_1,\infty )}_{\mathbb{T}}$, where $x_1\in {[x_0,\infty )}_{\mathbb{T}}$ and $x_1>x_0$. If

$$\underset{x\to \infty }{lim}{A}_1(x,x_0)=\infty ,$$

(8)

$$\underset{x\to \infty }{lim}{A}_2(x,x_0)=\infty ,$$

(9)

then it holds that

$\left(a\right)$. There exists $x_2\in {[x_1,\infty )}_{\mathbb{T}}$ such that ${\left(b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\right)}^{\Delta }<0,{\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }>0$ on ${[x_2,\infty )}_{\mathbb{T}}$.

$\left(b\right)$. We suppose an arbitrary $\overline{x}$ such that $B_1(x,c)>0$ on $x\in {[\overline{x},\infty )}_{\mathbb{T}}$, where $B_1(x,c)=\frac{{\displaystyle 1}}{{\displaystyle m\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}[1-\frac{{\displaystyle c^{\frac{1}{\alpha }-1}}}{{\displaystyle m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\right)}}]$, and c is an arbitrary positive constant. If it further satisfies that

$$\underset{x\to \infty }{lim}sup{\int }_{\overline{x}}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{\rho }^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,c)\Delta t)\Delta \xi ]\Delta \rho =\infty ,$$

(10)

then either $y^{\Delta }\left(x\right)>0$ on ${[x^{*},\infty )}_{\mathbb{T}}$ or $\underset{x\to \infty }{lim}w\left(x\right)=0$, where $x^{*}$ is sufficiently large.

Proof. $\left(a\right)$: As $w\left(x\right)$ is positive on ${[x_1,\infty )}_{\mathbb{T}}$, one has $y\left(x\right)>0,x\in {[x_1,\infty )}_{\mathbb{T}}$, and

$$b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }{)}^{\Delta }=-n\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)<0.$$

(11)

So, $b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }$ is strictly decreasing on ${[x_1,\infty )}_{\mathbb{T}}$, which implies the sign of ${\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }$ does not change eventually. Here, we conclude ${\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }>0$ on ${[x_2,\infty )}_{\mathbb{T}}$ for some sufficiently $x_2\in {[x_1,\infty )}_{\mathbb{T}}$. If not, we can find $x_3\in {[x_2,\infty )}_{\mathbb{T}}$ satisfying ${\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }<0,x\in {[x_3,\infty )}_{\mathbb{T}}$. So, $b_2\left(x\right)y^{\Delta }\left(x\right)$ is strictly decreasing on ${[x_3,\infty )}_{\mathbb{T}}$, and

$$\begin{array}{cc}\hfill & b_2\left(x\right)y^{\Delta }\left(x\right)-b_2\left(x_3\right)y^{\Delta }\left(x_3\right)={\int }_{x_3}^x\frac{{\displaystyle b_1\left(t\right){\left[b_2\left(t\right)y^{\Delta }\left(t\right)\right]}^{\Delta }}}{{\displaystyle b_1\left(t\right)}}\Delta t\hfill \\ \hfill & \le b_1\left(x_3\right){\left[b_2\left(x_3\right)y^{\Delta }\left(x_3\right)\right]}^{\Delta }{\int }_{x_3}^x\frac{{\displaystyle 1}}{{\displaystyle b_1\left(t\right)}}\Delta t.\hfill \end{array}$$

(12)

By (8), one can deduce that $\underset{x\to \infty }{lim}{b}_2\left(x\right)y^{\Delta }\left(x\right)=-\infty$. So, we can find $x_4\in {[x_3,\infty )}_{\mathbb{T}}$ such that $b_2\left(x\right)y^{\Delta }\left(x\right)<0$ on ${[x_4,\infty )}_{\mathbb{T}}$, and

$$y\left(x\right)-y\left(x_4\right)={\int }_{x_4}^x\frac{{\displaystyle b_2\left(t\right)y^{\Delta }\left(t\right)}}{{\displaystyle b_2\left(t\right)}}\Delta t\le b_2\left(x_4\right)y^{\Delta }\left(x_4\right){\int }_{x_4}^x\frac{{\displaystyle 1}}{{\displaystyle b_2\left(t\right)}}\Delta t.$$

By (9), we can obtain $\underset{x\to \infty }{lim}y\left(x\right)=-\infty$, which is a contradiction. So, ${\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }>0$ on ${[x_2,\infty )}_{\mathbb{T}}$. The proof is complete.

$\left(b\right)$: By $y\left(x\right)=w\left(x\right)+m\left(x\right)w^{\alpha }\left(l_1\left(x\right)\right)$, one has $w^{\alpha }\left(l_1\left(x\right)\right)=\frac{{\displaystyle y\left(x\right)-w\left(x\right)}}{{\displaystyle m\left(x\right)}}\le \frac{{\displaystyle y\left(x\right)}}{{\displaystyle m\left(x\right)}}$. So

$$w^{\alpha }\left(x\right)=\frac{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)-w\left(l_1^{-1}\left(x\right)\right)}}{{\displaystyle m\left(l_1^{-1}\left(x\right)\right)}}\ge \frac{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)-{\left[\frac{{\displaystyle y\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}{{\displaystyle m\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}\right]}^{\frac{1}{\alpha }}}}{{\displaystyle m\left(l_1^{-1}\left(x\right)\right)}}$$

$$=\frac{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)}}{{\displaystyle m\left(l_1^{-1}\left(x\right)\right)}}[1-\frac{{\displaystyle y^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}].$$

According to $\left(a\right)$, as ${\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }>0$ on ${[x_2,\infty )}_{\mathbb{T}}$, one can conclude the sign of $y^{\Delta }\left(x\right)$ does not change eventually. Thus, we can find $x_5\in {[x_2,\infty )}_{\mathbb{T}}$ satisfying either $y^{\Delta }\left(x\right)>0$ or $y^{\Delta }\left(x\right)<0$ for $x\in {[x_5,\infty )}_{\mathbb{T}}$.

If $y^{\Delta }\left(x\right)<0$, then $y\left(x\right)$ is strictly decreasing. Since $y\left(x\right)>0,x\in {[x_1,\infty )}_{\mathbb{T}}$, we deduce that $\underset{x\to \infty }{lim}y\left(x\right)={\epsilon }_1\ge 0$ and $\underset{x\to \infty }{lim}{b}_2\left(x\right)y^{\Delta }\left(x\right)={\epsilon }_2\le 0$. Here, we conclude ${\epsilon }_1=0$. If not, we can find $x_6\in {[x_5,\infty )}_{\mathbb{T}}$ satisfying $y\left(x\right)\ge {\epsilon }_1>0,y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\ge {\epsilon }_1>0$ for $x\in {[x_6,\infty )}_{\mathbb{T}}$, and

$$w^{\alpha }\left(x\right)\ge \frac{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)}}{{\displaystyle m\left(l_1^{-1}\left(x\right)\right)}}[1-\frac{{\displaystyle y^{\frac{1}{\alpha }}\left(l_1^{-1}\left(x\right)\right)}}{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}]$$

$$\ge \frac{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)}}{{\displaystyle m\left(l_1^{-1}\left(x\right)\right)}}[1-\frac{{\displaystyle {\epsilon }_1^{\frac{1}{\alpha }-1}}}{{\displaystyle m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}]>0,x\in {[x_6,\infty )}_{\mathbb{T}},$$

where the first equality of (5) is used in the last inequality. So,

$$w^{\alpha }\left(l_2\left(x\right)\right)\ge \frac{{\displaystyle y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}{{\displaystyle m\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}[1-\frac{{\displaystyle {\epsilon }_1^{\frac{1}{\alpha }-1}}}{{\displaystyle m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\right)}}]=B_1(x,{\epsilon }_1)y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)>0.$$

From (3) and (6), one has

$${\left(b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\right)}^{\Delta }\le -n\left(x\right)B_1^{\frac{\beta }{\alpha }}(x,{\epsilon }_1)y^{\frac{\beta }{\alpha }}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right).$$

(13)

After taking the $\Delta$ integral on both sides of (13), from x to ∞, one can deduce that

$$-b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }$$

$$=-\underset{x\to \infty }{lim}{b}_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }+{\int }_x^{\infty }-n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)y^{\frac{\beta }{\alpha }}\left(l_1^{-1}\left(l_2\left(t\right)\right)\right)\Delta t$$

$$\le -{\int }_x^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)y^{\frac{\beta }{\alpha }}\left(l_1^{-1}\left(l_2\left(t\right)\right)\right)\Delta t\le -{\epsilon }_1^{\frac{\beta }{\alpha }}{\int }_x^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)\Delta t,$$

which implies

$$-{\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\le -\frac{{\displaystyle {\epsilon }_1^{\frac{\beta }{\alpha }}}}{{\displaystyle b_1\left(x\right)}}{\int }_x^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)\Delta t.$$

(14)

Replacing x with $\xi$ in (14), taking the $\Delta$ integral on both sides of (14) yields

$$b_2\left(x\right)y^{\Delta }\left(x\right)\le \underset{x\to \infty }{lim}{b}_2\left(x\right)y^{\Delta }\left(x\right)-{\epsilon }_1^{\frac{\beta }{\alpha }}{\int }_x^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)\Delta t)\Delta \xi$$

$$={\epsilon }_2-{\epsilon }_1^{\frac{\beta }{\alpha }}{\int }_x^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)\Delta t)\Delta \xi$$

$$\le -{\epsilon }_1^{\frac{\beta }{\alpha }}{\int }_x^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)\Delta t)\Delta \xi ,$$

which is followed by

$$y^{\Delta }\left(x\right)\le -{\epsilon }_1^{\frac{\beta }{\alpha }}[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(x\right)}}{\int }_x^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)\Delta t)\Delta \xi ].$$

(15)

Replacing x with $\rho$ in (15), taking the $\Delta$ integral on both sides of (15) yields

$$y\left(x\right)-y\left(x_6\right)\le -{\epsilon }_1^{\frac{\beta }{\alpha }}{\int }_{x_6}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{\rho }^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,{\epsilon }_1)\Delta t)\Delta \xi ]\Delta \rho .$$

(16)

Due to (10), one has $\underset{x\to \infty }{lim}y\left(x\right)=-\infty ,$ which is a contradiction. So, it holds that $\underset{x\to \infty }{lim}y\left(x\right)=0,$ and $\underset{x\to \infty }{lim}w\left(x\right)=0$. We have finished the proof. □

Lemma 2. 

If $w\left(x\right)$ is an eventually positive solution of Equation (3) satisfying

$${\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }>0,y^{\Delta }\left(x\right)>0 on {[x^{*},\infty )}_{\mathbb{T}},$$

then it holds that

$$\frac{{\displaystyle A_1(x,x^{*})b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }}}{{\displaystyle b_2\left(x\right)}}\le y^{\Delta }\left(x\right)$$

$$\le \frac{{\displaystyle b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)+b_1\left(x^{*}\right){\left[b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)\right]}^{\Delta }{A}_1(x,x^{*})}}{{\displaystyle b_2\left(x\right)}},x\in {[x^{*},\infty )}_{\mathbb{T}},$$

(17)

and

$$\begin{array}{cc}\hfill & y\left(x\right)\le y\left(x^{*}\right)+b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)A_2(x,x^{*})+b_1\left(x^{*}\right){\left[b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)\right]}^{\Delta }{A}_1(x,x^{*})A_2(x,x^{*}),\hfill \\ \hfill & x\in {[x^{*},\infty )}_{\mathbb{T}}.\hfill \end{array}$$

(18)

Proof. 

According to Lemma 1, there exists $x^{*}$ such that $b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }>0$ and decreasing on $[x^{*},\infty )$, $b_2\left(x\right)y^{\Delta }\left(x\right)>0$ and increasing on $[x^{*},\infty )$. So, one has

$$b_2\left(x\right)y^{\Delta }\left(x\right)=b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)+{\int }_{x^{*}}^x\frac{{\displaystyle b_1\left(t\right){\left[b_2\left(t\right)y^{\Delta }\left(t\right)\right]}^{\Delta }}}{{\displaystyle b_1\left(t\right)}}\Delta t$$

$$\ge b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }{\int }_{x^{*}}^x\frac{{\displaystyle 1}}{{\displaystyle b_1\left(t\right)}}\Delta t=A_1(x,x^{*})b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }$$

and

$$b_2\left(x\right)y^{\Delta }\left(x\right)\le b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)+b_1\left(x^{*}\right){\left[b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)\right]}^{\Delta }{A}_1(x,x^{*}).$$

Furthermore,

$$y\left(x\right)=y\left(x^{*}\right)+{\int }_{x^{*}}^x\frac{{\displaystyle b_2\left(t\right)y^{\Delta }\left(t\right)}}{{\displaystyle b_2\left(t\right)}}\Delta t\le y\left(x^{*}\right)+b_2\left(x\right)y^{\Delta }\left(x\right){\int }_{x^{*}}^x\frac{{\displaystyle 1}}{{\displaystyle b_2\left(t\right)}}\Delta t.$$

From above, the desired results can be obtained. □

Theorem 1. 

Under the conditions of (8)–(10), if, for an arbitrary $x^{*}\in {\mathbb{T}}_0$, it holds that

$$\underset{x\to \infty }{lim}sup{\int }_{x_0}^x\{c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x^{*})}}\}\Delta t=\infty ,$$

(19)

where η is one known nonnegative function,

$$B_2(x,x^{*},c)=$$

$$\frac{{\displaystyle 1}}{{\displaystyle m\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}\{1-\frac{{\displaystyle c^{\frac{1}{\alpha }-2}}}{{\displaystyle m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\right)}}[y\left(x^{*}\right)+b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)A_2(l_1^{-1}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right),x^{*})$$

$$+b_1\left(x^{*}\right){\left[b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)\right]}^{\Delta }{A}_1(l_1^{-1}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right),x^{*})A_2\left(l_1^{-1}(l_1^{-1}\left(l_2\left(x\right)\right),x^{*})\right]\},$$

and c is an arbitrary positive constant, then the solution $w\left(x\right)$ of Equation (3) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Proof. 

Suppose $w\left(x\right),x\in {[x_0,\infty )}_{\mathbb{T}}$ is a non-oscillatory solution of Equation (3). We may assume $w\left(x\right)>0,w\left(l_1\left(x\right)\right)>0,w\left(l_2\left(x\right)\right)>0$ on ${[x_1,\infty )}_{\mathbb{T}}$ without loss of generality, where $x_1\in {[x_0,\infty )}_{\mathbb{T}}$. According to Lemma 1, we can find a sufficiently large $x_2\in {[x_1,\infty )}_{\mathbb{T}}$ such that $b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }$ is positive and decreasing on $[x_2,\infty )$, and either $y^{\Delta }\left(x\right)>0,x\in {[x_2,\infty )}_{\mathbb{T}}$ or $\underset{x\to \infty }{lim}w\left(x\right)=0$.

It is enough to consider the case $y^{\Delta }\left(x\right)>0,x\in {[x_2,\infty )}_{\mathbb{T}}$. In this case, $y\left(x\right)$ is increasing on ${[x_2,\infty )}_{\mathbb{T}}$. Then, there exists a positive constant $c_1$ such that $y\left(x\right)\ge c_1,y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\ge c_1$ on ${[x_2,\infty )}_{\mathbb{T}}$.

On the other hand, $w^{\alpha }\left(x\right)\ge \frac{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)}}{{\displaystyle m\left(l_1^{-1}\left(x\right)\right)}}\{1-\frac{{\displaystyle y^{\frac{1}{\alpha }-1}\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}{{\displaystyle m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}\left[\frac{{\displaystyle y\left(l_1^{-1}\left(l_1^{-1}\left(x\right)\right)\right)}}{{\displaystyle y\left(l_1^{-1}\left(x\right)\right)}}\right]\}.$

Combining with (18) and the second equality of (5), one can deduce that for some sufficiently large $x_3\in {[x_2,\infty )}_{\mathbb{T}}$, it holds that

$$w^{\alpha }\left(l_2\left(x\right)\right)\ge B_2(x,x_2,c_1)y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)>0,x\in {[x_3,\infty )}_{\mathbb{T}}.$$

By the use of (3) and (6), combined with $\alpha \le \beta$, one can deduce that

$$\begin{array}{cc}\hfill & {\left(b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\right)}^{\Delta }\le -n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)y^{\frac{\beta }{\alpha }}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\hfill \\ \hfill & \le -c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right),x\in {[x_3,\infty )}_{\mathbb{T}}.\hfill \end{array}$$

(20)

Now, we construct a Riccati function with definition $\zeta \left(x\right)=\frac{{\displaystyle \eta \left(x\right)}}{{\displaystyle y\left(x\right)}}\left[b_1\left(x\right){\left(b_2\left(x\right)y^{\Delta }\left(x\right)\right)}^{\Delta }\right].$ Then, $\zeta \left(x\right)\ge 0,x\in {[x_2,\infty )}_{\mathbb{T}}$ according to Lemma 1 $\left(a\right)$, and

$${\zeta }^{\Delta }\left(x\right)=\frac{{\displaystyle \eta \left(x\right)}}{{\displaystyle y\left(x\right)}}{\left[b_1\left(x\right){\left(b_2\left(x\right)y^{\Delta }\left(x\right)\right)}^{\Delta }\right]}^{\Delta }+{\left[\frac{{\displaystyle \eta \left(x\right)}}{{\displaystyle y\left(x\right)}}\right]}^{\Delta }{b}_1\left(\sigma \left(x\right)\right){\left(b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right)}^{\Delta }$$

$$=\frac{{\displaystyle \eta \left(x\right)}}{{\displaystyle y\left(x\right)}}{\left[b_1\left(x\right){\left(b_2\left(x\right)y^{\Delta }\left(x\right)\right)}^{\Delta }\right]}^{\Delta }+\left[\frac{{\displaystyle y\left(x\right){\eta }^{\Delta }\left(x\right)-y^{\Delta }\left(x\right)\eta \left(x\right)}}{{\displaystyle y\left(x\right)y\left(\sigma \right(x\left)\right)}}\right]b_1\left(\sigma \left(x\right)\right){\left(b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right)}^{\Delta }$$

$$=\frac{{\displaystyle \eta \left(x\right)}}{{\displaystyle y\left(x\right)}}{\left[b_1\left(x\right){\left(b_2\left(x\right)y^{\Delta }\left(x\right)\right)}^{\Delta }\right]}^{\Delta }+\frac{{\displaystyle {\eta }^{\Delta }\left(x\right)}}{{\displaystyle \eta \left(\sigma \right(x\left)\right)}}\zeta \left(\sigma \left(x\right)\right)$$

$$-\left[\frac{{\displaystyle \eta \left(x\right)y^{\Delta }\left(x\right)}}{{\displaystyle y\left(x\right)}}\right]\frac{{\displaystyle b_1\left(\sigma \left(x\right)\right){\left(b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right)}^{\Delta }}}{{\displaystyle y\left(\sigma \right(x\left)\right)}}$$

$$\le -\frac{{\displaystyle c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}{{\displaystyle y\left(x\right)}}+\frac{{\displaystyle {\eta }^{\Delta }\left(x\right)}}{{\displaystyle \eta \left(\sigma \right(x\left)\right)}}\zeta \left(\sigma \left(x\right)\right)$$

$$-\left[\frac{{\displaystyle \eta \left(x\right)y^{\Delta }\left(x\right)}}{{\displaystyle y\left(x\right)}}\right]\frac{{\displaystyle b_1\left(\sigma \left(x\right)\right){\left(b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right)}^{\Delta }}}{{\displaystyle y\left(\sigma \right(x\left)\right)}}$$

$$\le -c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)+\frac{{\displaystyle {\eta }^{\Delta }\left(x\right)}}{{\displaystyle \eta \left(\sigma \right(x\left)\right)}}\zeta \left(\sigma \left(x\right)\right)$$

$$-\left[\frac{{\displaystyle \eta \left(x\right)y^{\Delta }\left(x\right)}}{{\displaystyle y\left(x\right)}}\right]\frac{{\displaystyle b_1\left(\sigma \left(x\right)\right){\left(b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right)}^{\Delta }}}{{\displaystyle y\left(\sigma \right(x\left)\right)}},$$

where $y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\ge y\left(x\right)$ and $l_1^{-1}\left(l_2\left(x\right)\right)\ge x$ are used in the last step.

By (17) in Lemma 2, one has

$$y^{\Delta }\left(x\right)\ge \frac{{\displaystyle A_1(x,x_2)b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }}}{{\displaystyle b_2\left(x\right)}},x\in {[x_2,\infty )}_{\mathbb{T}}.$$

So, we can deduce that

$$\begin{array}{cc}\hfill & {\zeta }^{\Delta }\left(x\right)\le -c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)+\frac{{\displaystyle {\eta }^{\Delta }\left(x\right)}}{{\displaystyle \eta \left(\sigma \right(x\left)\right)}}\zeta \left(\sigma \left(x\right)\right)\hfill \\ \hfill & -\left(\frac{{\displaystyle \eta \left(x\right)}}{{\displaystyle y\left(x\right)}}\right)\left[\frac{{\displaystyle A_1(x,x_2)b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }}}{{\displaystyle b_2\left(x\right)}}\right]\frac{{\displaystyle b_1\left(\sigma \left(x\right)\right){\left(b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right)}^{\Delta }}}{{\displaystyle y\left(\sigma \right(x\left)\right)}}\hfill \\ \hfill & \le -c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)+\frac{{\displaystyle {\eta }^{\Delta }\left(x\right)}}{{\displaystyle \eta \left(\sigma \right(x\left)\right)}}\zeta \left(\sigma \left(x\right)\right)\hfill \\ \hfill & -\left(\frac{{\displaystyle \eta \left(x\right)}}{{\displaystyle y\left(\sigma \right(x\left)\right)}}\right)\frac{{\displaystyle A_1(x,x_2)}}{{\displaystyle b_2\left(x\right)}}\left\{b_1\left(\sigma \left(x\right)\right){\left[b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right]}^{\Delta }\right\}\frac{{\displaystyle b_1\left(\sigma \left(x\right)\right){\left(b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right)}^{\Delta }}}{{\displaystyle y\left(\sigma \right(x\left)\right)}}\hfill \\ \hfill & =-c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)+\frac{{\displaystyle {\eta }^{\Delta }\left(x\right)}}{{\displaystyle \eta \left(\sigma \right(x\left)\right)}}\zeta \left(\sigma \left(x\right)\right)\hfill \\ \hfill & -\left[\frac{{\displaystyle \eta \left(x\right)A_1(x,x_2)}}{{\displaystyle b_2\left(x\right)}}\right]{\left[\frac{{\displaystyle b_1\left(\sigma \left(x\right)\right){\left(b_2\left(\sigma \left(x\right)\right)y^{\Delta }\left(\sigma \left(x\right)\right)\right)}^{\Delta }}}{{\displaystyle y\left(\sigma \right(x\left)\right)}}\right]}^2\hfill \\ \hfill & =-c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)+\frac{{\displaystyle {\eta }^{\Delta }\left(x\right)}}{{\displaystyle \eta \left(\sigma \right(x\left)\right)}}\zeta \left(\sigma \left(x\right)\right)\hfill \\ \hfill & -\left[\frac{{\displaystyle \eta \left(x\right)A_1(x,x_2)}}{{\displaystyle b_2\left(x\right)}}\right]{\left[\frac{{\displaystyle \zeta \left(\sigma \right(x\left)\right)}}{{\displaystyle \eta \left(\sigma \right(x\left)\right)}}\right]}^2\hfill \\ \hfill & \le -c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)+\frac{{\displaystyle b_2\left(x\right){\left[{\eta }^{\Delta }\left(x\right)\right]}^2}}{{\displaystyle 4\eta \left(x\right)A_1(x,x_2)}},x\in {[x_3,\infty )}_{\mathbb{T}}.\hfill \end{array}$$

(21)

Replacing x with t in (21), taking the $\Delta$ integral on both sides of (21) yields

$${\int }_{x_3}^x\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}\}\Delta t\le \zeta \left(x_3\right)-\zeta \left(x\right)\le \zeta \left(x_3\right).$$

So,

$${\int }_{x_0}^x\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}\}\Delta t$$

$$\le \zeta \left(x_3\right)+{\int }_{x_0}^{x_3}\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}\}\Delta t<\infty ,$$

which contradicts (19). We have finished the proof. □

Theorem 2. 

Under the conditions of (8)–(10), furthermore, suppose for an arbitrary $x_2$ and $x_3\in {[x_2,\infty )}_{\mathbb{T}}$, it holds that $B_2(x,x_2,c)>0,x\in {[x_3,\infty )}_{\mathbb{T}}$, where c is an arbitrary constant, and $B_2$ is defined as in Theorem 1. If

$$\underset{x\to \infty }{lim}sup\left\{\frac{{\displaystyle {\int }_{x_3}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{x_3}^{\rho }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c)\Delta t)\Delta \xi ]\Delta \rho }}{{\displaystyle A_1(x,x_2)A_2(x,x_2)}}\right\}=\infty ,$$

(22)

then the solution $w\left(x\right)$ of Equation (3) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Proof. 

Suppose $w\left(x\right)$ is a non-oscillatory solution of Equation (3). Similar to the first two paragraphs in Theorem 1, all that is left is to consider the case $y^{\Delta }\left(x\right)>0,x\in {[x_2,\infty )}_{\mathbb{T}}$, and one can further obtain that

$${\left(b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\right)}^{\Delta }\le -c_1^{\frac{\beta }{\alpha }}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1),x\in {[x_3,\infty )}_{\mathbb{T}},$$

(23)

where $x_3\in {[x_2,\infty )}_{\mathbb{T}}$ is sufficiently large.

By taking the $\Delta$ integral on both sides of (23), one can deduce that

$$-b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }=-\underset{x\to \infty }{lim}{b}_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }+{\int }_x^{\infty }-c_1^{\frac{\beta }{\alpha }}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\Delta t$$

$$\le -c_1^{\frac{\beta }{\alpha }}{\int }_x^{\infty }n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\Delta t,$$

which implies

$$-{\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\le -\frac{{\displaystyle c_1^{\frac{\beta }{\alpha }}}}{{\displaystyle b_1\left(x\right)}}{\int }_x^{\infty }n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\Delta t.$$

(24)

Furthermore,

$$b_2\left(x\right)y^{\Delta }\left(x\right)\ge b_2\left(x_3\right)y^{\Delta }\left(x_3\right)+c_1^{\frac{\beta }{\alpha }}{\int }_{x_3}^x(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\Delta t)\Delta \xi$$

$$\ge c_1^{\frac{\beta }{\alpha }}{\int }_{x_3}^x(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\Delta t)\Delta \xi ,$$

which is followed by

$$y^{\Delta }\left(x\right)\ge c_1^{\frac{\beta }{\alpha }}[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(x\right)}}{\int }_{x_3}^x(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{x_3}^{\tau }n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\Delta t)\Delta \xi ].$$

(25)

Moreover,

$$y\left(x\right)\ge y\left(x_3\right)+c_1^{\frac{\beta }{\alpha }}{\int }_{x_3}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{x_3}^{\rho }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\Delta t)\Delta \xi ]\Delta \rho .$$

(26)

On the other hand, by (18) in Lemma 2, one has

$$\begin{array}{cc}\hfill & y\left(x\right)\le y\left(x_2\right)+b_2\left(x_2\right)y^{\Delta }\left(x_2\right)A_2(x,x_2)+b_1\left(x_2\right){\left[b_2\left(x_2\right)y^{\Delta }\left(x_2\right)\right]}^{\Delta }{A}_1(x,x_2)A_2(x,x_2),\hfill \\ \hfill & x\in {[x_2,\infty )}_{\mathbb{T}}.\hfill \end{array}$$

(27)

Equations (26) and (27) lead to a contradiction with (22). So, the proof is complete. □

Next we establish the Kamenev and Philos-type oscillation criteria for Equation (3). To this end, define $\mathbb{D}=\left\{(x,t)\right|x\ge t\ge x_0\}$, and $\mathcal{H}\in C_{rd}(\mathbb{D},\mathbb{R})$ satisfying

$$\left\{\begin{array}{c}\mathcal{H}(x,x)=0,x\ge x_0,\hfill \\ \mathcal{H}(x,t)>0,x>t\ge x_0,\hfill \\ {\mathcal{H}}_t^{\Delta }(x,t)\le 0.\hfill \end{array}\right.$$

(28)

Theorem 3. 

Under the conditions of (8)–(10), if, for an arbitrary $x^{*}$, it holds that

$$\underset{x\to \infty }{lim}sup\frac{{\displaystyle 1}}{{\displaystyle \mathcal{H}(x,x_0)}}\{{\int }_{x_0}^x\mathcal{H}(x,t)\{c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x^{*})}}\}\Delta t\}=\infty ,$$

(29)

where $\eta ,B_2(x,x^{*},c)$ are defined as in Theorem 1; then, the solution $w\left(x\right)$ of Equation (3) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Proof. 

Suppose $w\left(x\right)$ is a non-oscillatory solution of Equation (3). Similar to Theorem 1, all that is left is to consider the case $y^{\Delta }\left(x\right)>0,x\in {[x_2,\infty )}_{\mathbb{T}}$.

Let $\zeta \left(x\right)$ be defined as in Theorem 1. Due to (21), one has

$$c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)-\frac{{\displaystyle b_2\left(x\right){\left[{\eta }^{\Delta }\left(x\right)\right]}^2}}{{\displaystyle 4\eta \left(x\right)A_1(x,x_2)}}\le -{\zeta }^{\Delta }\left(x\right),x\in {[x_3,\infty )}_{\mathbb{T}}.$$

(30)

So, one has

$${\int }_{x_3}^x\mathcal{H}(x,t)\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}\}\Delta t$$

$$\le -{\int }_{x_3}^x\mathcal{H}(x,t){\zeta }^{\Delta }\left(t\right)\Delta s=\mathcal{H}(x,x_3)\zeta \left(x_3\right)+{\int }_{x_3}^x{H}_t^{\Delta }(x,t)\zeta \left(\sigma \left(t\right)\right)\Delta s$$

$$\le \mathcal{H}(x,x_3)\zeta \left(x_3\right)\le \mathcal{H}(x,x_0)\zeta \left(x_3\right),$$

where the deduction (28) is used. Then,

$${\int }_{x_0}^x\mathcal{H}(x,t)\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}\}\Delta t$$

$$={\int }_{x_0}^{x_3}\mathcal{H}(x,t)\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}\}\Delta t$$

$$+{\int }_{x_3}^x\mathcal{H}(x,t)\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}\}\Delta t$$

$$\le \mathcal{H}(x,x_0)\zeta \left(x_3\right)+\mathcal{H}(x,x_0){\int }_{x_0}^{x_3}|c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}|\Delta t.$$

Moreover,

$$\underset{x\to \infty }{lim}sup\frac{{\displaystyle 1}}{{\displaystyle \mathcal{H}(x,x_0)}}\{{\int }_{x_0}^x\mathcal{H}(x,t)\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}\}\Delta t$$

$$\le \zeta \left(x_3\right)+{\int }_{x_0}^{x_3}|c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x_2)}}|\Delta t<\infty ,$$

which leads to a contradiction with (29). By taking $x^{*}=x_2$, we have finished the proof. □

In Theorem 3, if we select $\mathcal{H}(x,t)={(x-t)}^l,l\ge 1$, or $\mathcal{H}(x,t)=ln\frac{{\displaystyle x}}{{\displaystyle t}}$, then we can obtain the following corollary.

Corollary 1. 

Under the conditions of (8)–(10), if, for an arbitrary $x^{*}$, either of the following two conditions holds:

$\left(a\right)$.

$$\begin{array}{cc}\hfill & \underset{x\to \infty }{lim}sup\frac{{\displaystyle 1}}{{\displaystyle {(x-x_0)}^l}}\{{\int }_{x_0}^x{(x-t)}^l\{c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x^{*})}}\}\Delta t\}\hfill \\ \hfill & =\infty ,l\ge 1,\hfill \end{array}$$

(31)

$\left(b\right)$.

$$\begin{array}{cc}\hfill & \underset{x\to \infty }{lim}sup\frac{{\displaystyle 1}}{{\displaystyle (lnx-ln{x}_0)}}\{{\int }_{x_0}^x(lnx-lnt)\{c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x^{*})}}\}\Delta t\}\hfill \\ \hfill & =\infty ,\hfill \end{array}$$

(32)

then the solution $w\left(x\right)$ of Equation (3) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

3. Oscillation Results for Equation (2)

In this section, we research the oscillation of Equation (2) and extend the main results established in the last section for Equations (3) and (4), as Equation (2) is equivalent to (4). For the sake of convenience, define ${\tilde{A}}_1(x,x^{*})={\int }_{x^{*}}^x\frac{{\displaystyle e_{-\frac{v}{b_1}}(t,x_0)}}{{\displaystyle b_1\left(t\right)}}\Delta s$.

For $v\in \mathfrak{R}$, the exponential function is denoted by $e_v(x,t)$. According to ([25], Theorems 5.1 and 5.2), it holds that $e_v(x,t)>0$ for $v\in {\mathfrak{R}}^{+}$, and

$$\left\{\begin{array}{c}{\left[e_v(x,x_0)\right]}^{\Delta }=v\left(x\right)e_v(x,x_0),\hfill \\ \\ e_v(x_0,x_0)=1.\hfill \end{array}\right.$$

For $-\frac{{\displaystyle v}}{{\displaystyle b_1}}\in {\mathfrak{R}}_{+}$, one has $e_{-\frac{v}{b_1}}(x,x_0)>0$, and one has the following observation

$${\left(\frac{{\displaystyle b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }}}{{\displaystyle e_{-\frac{v}{b_1}}(x,x_0)}}\right)}^{\Delta }$$

$$=\frac{{\displaystyle e_{-\frac{v}{b_1}}(x,x_0){\left(b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\right)}^{\Delta }-{\left(e_{-\frac{v}{b_1}}(x,x_0)\right)}^{\Delta }{b}_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }}}{{\displaystyle e_{-\frac{v}{b_1}}(x,x_0)e_{-\frac{v}{b_1}}(\sigma \left(x\right),x_0)}}$$

$$=\frac{{\displaystyle b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }{)}^{\Delta }+v\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(x\right),x_0)}}=\frac{{\displaystyle -n\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(x\right),x_0)}}.$$

Furthermore, we have the following two lemmas.

Lemma 3. 

Assume Equation (4) has an eventually positive solution $w\left(x\right)$ satisfying $w\left(x\right)>0,w\left(l_1\left(x\right)\right)>0,w\left(l_2\left(x\right)\right)>0$ on ${[x_1,\infty )}_{\mathbb{T}}$, where $x_1\in {[x_0,\infty )}_{\mathbb{T}}$, and $x_1>x_0$. If $-\frac{{\displaystyle v}}{{\displaystyle b_1}}\in {\mathfrak{R}}_{+}$, and

$$\underset{x\to \infty }{lim}{\tilde{A}}_1(x,x_0)=\infty ,$$

(33)

$$\underset{x\to \infty }{lim}{A}_2(x,x_0)=\infty ,$$

(34)

then

$\left(a\right)$. There exists $x_2\in {[x_1,\infty )}_{\mathbb{T}}$ such that $\frac{{\displaystyle {\left(b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }\right)}^{\Delta }}}{{\displaystyle e_{-\frac{v}{b_1}}(x,x_0)}}<0,{\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }>0$ on ${[x_2,\infty )}_{\mathbb{T}}$.

$\left(b\right)$. If, furthermore,

$$\underset{x\to \infty }{lim}sup{\int }_{\overline{x}}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{\rho }^{\infty }(\frac{{\displaystyle e_{-\frac{v}{b_1}}(\xi ,x_0)}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }\frac{{\displaystyle n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,c)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}\Delta t)\Delta \xi ]\Delta \rho =\infty ,$$

(35)

where $B_1$ is defined as in Lemma 1 satisfying $B_1(x,c)>0,x\in {[\overline{x},\infty )}_{\mathbb{T}}$, then either $y^{\Delta }\left(x\right)>0$ on ${[x^{*},\infty )}_{\mathbb{T}}$ or $\underset{x\to \infty }{lim}w\left(x\right)=0$, where $x^{*}$ is sufficiently large.

Lemma 4. 

If $-\frac{{\displaystyle v}}{{\displaystyle b_1}}\in {\mathfrak{R}}_{+}$, and $w\left(x\right)$ is an eventually positive solution to Equation (4) satisfying

$${\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }>0,y^{\Delta }\left(x\right)>0on{[x^{*},\infty )}_{\mathbb{T}},$$

then it holds that

$$\begin{array}{cc}\hfill & \frac{{\displaystyle {\tilde{A}}_1(x,x^{*})b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }}}{{\displaystyle b_2\left(x\right)e_{-\frac{v}{b_1}}(x,x_0)}}\le y^{\Delta }\left(x\right)\hfill \\ \hfill & \le \frac{{\displaystyle b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)+\frac{{\displaystyle b_1\left(x^{*}\right){\left[b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)\right]}^{\Delta }}}{{\displaystyle e_{-\frac{v}{b_1}}(x^{*},x_0)}}{\tilde{A}}_1(x,x^{*})}}{{\displaystyle b_2\left(x\right)}},x\in {[x^{*},\infty )}_{\mathbb{T}},\hfill \end{array}$$

(36)

and

$$\begin{array}{cc}\hfill & y\left(x\right)\le y\left(x^{*}\right)+b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)A_2(x,x^{*})+\frac{{\displaystyle b_1\left(x^{*}\right){\left[b_2\left(x^{*}\right)y^{\Delta }\left(x^{*}\right)\right]}^{\Delta }}}{{\displaystyle e_{-\frac{v}{b_1}}(x^{*},x_0)}}{\tilde{A}}_1(x,x^{*})A_2(x,x^{*}),\hfill \\ \hfill & x\in {[x^{*},\infty )}_{\mathbb{T}}.\hfill \end{array}$$

(37)

The proofs of Lemmas 3 and 4 are similar to those of Lemmas 1 and 2. So, we omitted them here.

Theorem 4. 

Under the conditions of (33)–(35), if $-\frac{{\displaystyle v}}{{\displaystyle b_1}}\in {\mathfrak{R}}_{+}$, and for an arbitrary $x^{*}$, it holds that

$$\underset{x\to \infty }{lim}sup{\int }_{x_0}^x\{\frac{{\displaystyle c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right){\tilde{A}}_1(t,x^{*})}}\}\Delta t=\infty ,$$

(38)

where $\eta ,B_2$ are defined as in Theorem 1, then the solution $w\left(x\right)$ of Equation (4) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Proof. 

Suppose $w\left(x\right)$ is a non-oscillatory solution of Equation (3), and assume $w\left(x\right)>0,w\left(l_1\left(x\right)\right)>0,w\left(l_2\left(x\right)\right)>0$ on ${[x_1,\infty )}_{\mathbb{T}}$ without loss of generality. Furthermore, there exists $x_2\in {[x_1,\infty )}_{\mathbb{T}}$ such that $b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }$ is positive and decreasing on $[x_2,\infty )$, and either $y^{\Delta }\left(x\right)>0,x\in {[x_2,\infty )}_{\mathbb{T}}$ or $\underset{x\to \infty }{lim}w\left(x\right)=0$.

If $y^{\Delta }\left(x\right)>0,x\in {[x_2,\infty )}_{\mathbb{T}}$, there exists $c_1>0$ such that $y\left(x\right)\ge c_1,y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\ge c_1$ on ${[x_2,\infty )}_{\mathbb{T}}$, and similar to Theorem 1, $w^{\alpha }\left(l_2\left(x\right)\right)\ge B_2(x,x_2,c_1)y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)>0,x\in {[x_3,\infty )}_{\mathbb{T}}$. Furthermore, one can deduce that

$$\begin{array}{cc}\hfill & {\left(\frac{{\displaystyle b_1\left(x\right){\left[b_2\left(x\right)y^{\Delta }\left(x\right)\right]}^{\Delta }}}{{\displaystyle e_{-\frac{v}{b_1}}(x,x_0)}}\right)}^{\Delta }=\frac{{\displaystyle -n\left(x\right)w^{\beta }\left(l_2\left(x\right)\right)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(x\right),x_0)}}\hfill \\ \hfill & \le \frac{{\displaystyle -n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)y^{\frac{\beta }{\alpha }}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(x\right),x_0)}}\le \frac{{\displaystyle -c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)y\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(x\right),x_0)}}.\hfill \end{array}$$

(39)

Let $\zeta \left(x\right)=\frac{{\displaystyle \eta \left(x\right)}}{{\displaystyle y\left(x\right)}}\left[\frac{{\displaystyle b_1\left(x\right){\left(b_2\left(x\right)y^{\Delta }\left(x\right)\right)}^{\Delta }}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(x\right),x_0)}}\right].$ Following a similar process to that of Theorem 1, one can obtain that

$$\begin{array}{c}\hfill {\zeta }^{\Delta }\left(x\right)\le \frac{{\displaystyle -c_1^{\frac{\beta }{\alpha }-1}n\left(x\right)B_2^{\frac{\beta }{\alpha }}(x,x_2,c_1)\eta \left(x\right)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(x\right),x_0)}}+\frac{{\displaystyle b_2\left(x\right){\left[{\eta }^{\Delta }\left(x\right)\right]}^2}}{{\displaystyle 4\eta \left(x\right){\tilde{A}}_1(x,x_2)}},x\in {[x_3,\infty )}_{\mathbb{T}}.\end{array}$$

(40)

Moreover,

$${\int }_{x_3}^x\{\frac{{\displaystyle c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c_1)\eta \left(t\right)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right){\tilde{A}}_1(t,x_2)}}\}\Delta t\le \zeta \left(x_3\right)-\zeta \left(x\right)\le \zeta \left(x_3\right),$$

which is a contradiction of (38). Then, the proof is complete. □

Similar to Theorems 2 and 3, we can obtain the following two theorems.

Theorem 5. 

Assume $-\frac{{\displaystyle v}}{{\displaystyle b_1}}\in {\mathfrak{R}}_{+}$. Under the conditions of (8)–(10), furthermore, suppose for an arbitrary $x_2$ and $x_3\in {[x_2,\infty )}_{\mathbb{T}}$, it holds that $B_2(x,x_2,c)>0,x\in {[x_3,\infty )}_{\mathbb{T}}$, where c is an arbitrary constant, and $B_2$ is defined as in Theorem 1. If

$$\underset{x\to \infty }{lim}sup\left\{\frac{{\displaystyle {\int }_{x_3}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{x_3}^{\rho }(\frac{{\displaystyle e_{-\frac{v}{b_1}}(\xi ,x_0)}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }\frac{{\displaystyle n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}\Delta t)\Delta \xi ]\Delta \rho }}{{\displaystyle A_1(x,x_2)A_2(x,x_2)}}\right\}=\infty ,$$

(41)

then the solution $w\left(x\right)$ of Equation (4) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Theorem 6. 

Under the conditions of (33)–(35), if $-\frac{{\displaystyle v}}{{\displaystyle b_1}}\in {\mathfrak{R}}_{+}$, and for an arbitrary $x^{*}$, it holds that

$$\underset{x\to \infty }{lim}sup\frac{{\displaystyle 1}}{{\displaystyle \mathcal{H}(x,x_0)}}\{{\int }_{x_0}^x\mathcal{H}(x,t)\{\frac{{\displaystyle c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right){\tilde{A}}_1(t,x^{*})}}\}\Delta t\}=\infty ,$$

(42)

where $\mathcal{H}$ is defined as in Theorem 3, then the solution $w\left(x\right)$ of Equation (4) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Remark 2. 

We will make a comparison between our results and the existing results. Firstly, the critically used Riccati transformation function denoted by $\zeta \left(x\right)$ in the last two sections is designed to be adapted to certain delay dynamic equations of fractional order, which is different from [15,16,17,18,19,20,21,22,23]. As a result, the oscillation criteria established above are essentially different from those existing results. Secondly, for the research into the oscillation of super-linear dynamic equations, in [24], the authors considered a non-fractional second-order delay dynamic equation on time scales with a super-linear term as follows:

$${\left(a\left(x\right){(z\left(x\right)+p\left(x\right)z^{\alpha }\left(x\right))}^{\Delta }\right)}^{\Delta }+q\left(x\right)z^{\beta }\left(\phi \left(x\right)\right)=0.$$

We note that the third-order dynamic equations with a super-linear term denoted by Equations (1)–(4) are different from above. In the establishment of Kamenev and Philos-type oscillation criteria in [24], a critic inequality is unsuitably used (see (4.13)–(4.14) in [24]), which leads to the invalidity of part of the oscillation results. In fact, after changing the form of the Riccati functions suitably, corresponding Kamenev and Philos-type oscillation criteria can also be obtained. Moreover, it is worthy of note that these provided results are not only an extension of those in [24] from a second-order case to a third-order case, as the proof processes for the third-order case here are essentially different from those for the second-order case in [24]. And the oscillation criteria described in the theorems above are new results in the literature to the best of our knowledge.

4. Applications

As applications for the oscillation criteria established above, we will propose some examples. For the examples with $\mathbb{T}=\mathbb{R}$, we also give the numerical computation results demonstrated in graphics under the given initial value condition. Comparison of the oscillatory behavior between the equation without the damping term and the equation with the damping term are also given in the first two examples.

First, we consider the following nonlinear third-order delay differential equation involving a local fractional derivative with a super-linear neutral term:

Example 1. 

$$D^{\frac{1}{2}}\left[x^{\frac{1}{6}}{D}^{\frac{1}{2}}\left(x^{\frac{7}{24}}{D}^{\frac{1}{2}}[w\left(x\right)+x^2{w}^3\left(\frac{{\displaystyle x}}{{\displaystyle 4}}\right)]\right)\right]+x^{\frac{29}{12}}{w}^5\left(\frac{{\displaystyle x}}{{\displaystyle 2}}\right)=0,x\in [1,\infty ).$$

(43)

Compared with (1) and (3), one has $\mathbb{T}=\mathbb{R},b_1\left(x\right)=x^{\frac{2}{3}},m\left(x\right)=x^2,n\left(x\right)=x^{\frac{23}{12}},b_2\left(x\right)=x^{\frac{19}{24}},l_1\left(x\right)=\frac{{\displaystyle x}}{{\displaystyle 4}},l_2\left(x\right)=\frac{{\displaystyle x}}{{\displaystyle 2}},\alpha =3,\beta =5,and{x}_0=1.$ Then, one can see (8) and (9) hold from the following analysis:

$$\underset{x\to \infty }{lim}{A}_1(x,x_0)={\int }_{x_0}^{\infty }\frac{{\displaystyle 1}}{{\displaystyle b_1\left(t\right)}}\Delta t={\int }_1^{\infty }\frac{{\displaystyle 1}}{{\displaystyle t^{\frac{2}{3}}}}dt=\infty ,$$

and

$$\underset{x\to \infty }{lim}{A}_2(x,x_0)={\int }_{x_0}^{\infty }\frac{{\displaystyle 1}}{{\displaystyle b_2\left(t\right)}}\Delta t={\int }_1^{\infty }\frac{{\displaystyle 1}}{{\displaystyle t^{\frac{19}{24}}}}dt=\infty .$$

Furthermore, as $B_1(x,c)=\frac{{\displaystyle 1}}{{\displaystyle m\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}[1-\frac{{\displaystyle c^{\frac{1}{\alpha }-1}}}{{\displaystyle m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\right)}}]=\frac{{\displaystyle 1}}{{\displaystyle 4x^2}}[1-\frac{{\displaystyle c^{-\frac{2}{3}}}}{{\displaystyle {\left(8x\right)}^{\frac{2}{3}}}}]$, one can find a sufficiently large $\overline{x}\in \mathbb{R}$ such that $B_1(x,c)\ge \frac{{\displaystyle 1}}{{\displaystyle 8x^2}},x\in [\overline{x},\infty )$. Then, one has

$${\int }_{\overline{x}}^{\infty }[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{\rho }^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,c)\Delta t)\Delta \xi ]\Delta \rho$$

$$={\int }_{\overline{x}}^{\infty }\left[\frac{{\displaystyle 1}}{{\displaystyle {\rho }^{\frac{19}{24}}}}{\int }_{\rho }^{\infty }\left(\frac{{\displaystyle 1}}{{\displaystyle {\xi }^{\frac{2}{3}}}}{\int }_{\xi }^{\infty }{t}^{\frac{23}{12}}{B}_1^{\frac{5}{3}}(t,c)dt\right)d\xi \right]d\rho$$

$$\ge \frac{{\displaystyle 1}}{{\displaystyle 8^{\frac{5}{3}}}}{\int }_{\overline{x}}^{\infty }\left[\frac{{\displaystyle 1}}{{\displaystyle {\rho }^{\frac{19}{24}}}}{\int }_{\rho }^{\infty }\left(\frac{{\displaystyle 1}}{{\displaystyle {\xi }^{\frac{2}{3}}}}{\int }_{\xi }^{\infty }{t}^{-\frac{17}{12}}dt\right)d\xi \right]d\rho$$

$$=\frac{{\displaystyle 12}}{{\displaystyle 8^{\frac{5}{3}}5}}{\int }_{\overline{x}}^{\infty }\left[\frac{{\displaystyle 1}}{{\displaystyle {\rho }^{\frac{19}{24}}}}{\int }_{\rho }^{\infty }{\xi }^{-\frac{13}{12}}d\xi \right]d\rho =\frac{{\displaystyle 144}}{{\displaystyle 8^{\frac{5}{3}}5}}{\int }_{\overline{x}}^{\infty }\frac{{\displaystyle 1}}{{\displaystyle {\rho }^{\frac{21}{24}}}}d\rho =\infty ,$$

which shows that (10) is satisfied.

Moreover, as $A_1(x,x^{*})=3[x^{\frac{1}{3}}-{\left(x^{*}\right)}^{\frac{1}{3}}],A_2(x,x^{*})=\frac{{\displaystyle 24}}{{\displaystyle 5}}[x^{\frac{5}{24}}-{\left(x^{*}\right)}^{\frac{5}{24}}]$, according to the definition of $B_2(x,x^{*},c)$ in Theorem 1, one has

$$B_2(x,x^{*},c)=\frac{{\displaystyle 1}}{{\displaystyle 4x^2}}[1-\frac{{\displaystyle k_1{x}^{\frac{13}{24}}+k_2{x}^{\frac{5}{24}}+k_3}}{{\displaystyle {\left(8x\right)}^{\frac{2}{3}}}}],$$

where $k_i,i=1,2,3$ are constants related to $x^{*}$. Then, we can find a sufficiently large $x_3\in [x^{*},\infty )$ satisfying $A_1(x,x^{*})\ge \frac{{\displaystyle 3}}{{\displaystyle 2}}{x}^{\frac{1}{3}}$ and $B_2(x,x^{*},c)\ge \frac{{\displaystyle 1}}{{\displaystyle 8x^2}}>0$ on $x\in [x_3,\infty )$.

Select $\eta \left(x\right)=x$, and then, one has

$${\int }_{x_3}^x[c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\prime }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x^{*})}}]dt$$

$$\ge {\int }_{x_3}^x[\frac{{\displaystyle c^{\frac{2}{3}}}}{{\displaystyle 8^{\frac{5}{3}}}}\left(\frac{{\displaystyle 1}}{{\displaystyle t^{\frac{5}{12}}}}\right)-\frac{{\displaystyle 1}}{{\displaystyle 6t^{\frac{13}{24}}}}]dt={\int }_{x_3}^x\left(\frac{{\displaystyle c^{\frac{2}{3}}}}{{\displaystyle 8^{\frac{5}{3}}}}\right)\frac{{\displaystyle 1}}{{\displaystyle t^{\frac{5}{12}}}}[1-\left(\frac{{\displaystyle 8^{\frac{5}{3}}}}{{\displaystyle 6c^{\frac{2}{3}}}}\right)\frac{{\displaystyle 1}}{{\displaystyle t^{\frac{3}{24}}}}]dt.$$

If $x_3$ is selected as sufficiently large, then one can see the above integral tends to infinity when x tends to infinity. So, (19) is also satisfied in the case of $\mathbb{T}=\mathbb{R}$. Due to Theorem 1, one can deduce that the solution $w\left(x\right)$ of Equation (43) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Now, we consider the numerical computation of (43). Denote the step by h, and $x_i=x_0+ih,i=0,1,2...$. $w^i$ denotes the numerical solution of the unknown function $w\left(x\right)$ at the point $x_i$. $b_1^i=b_1\left(x_i\right),b_2^i=b_2\left(x_i\right),m^i=m\left(x_i\right),n^i=n\left(x_i\right),i=0,1,2,...$.

For the general form of (43), one can consider (1) or its equivalent form (3). For the sake of a graphical demonstration, we perform a numerical computation by use of the simple forward Euler method, and one can obtain the following numerical scheme:

$$b_1^{i+1}\{b_2^{i+2}[(w^{i+3}+m^{i+3}{\left(w\left(\frac{{\displaystyle x_{i+3}}}{{\displaystyle 4}}\right)\right)}^3)-(w^{i+2}+m^{i+2}{\left(w\left(\frac{{\displaystyle x_{i+2}}}{{\displaystyle 4}}\right)\right)}^3)]$$

$$-b_2^{i+1}[(w^{i+2}+m^{i+2}{\left(w\left(\frac{{\displaystyle x_{i+2}}}{{\displaystyle 4}}\right)\right)}^3)-(w^{i+1}+m^{i+1}{\left(w\left(\frac{{\displaystyle x_{i+1}}}{{\displaystyle 4}}\right)\right)}^3)]\}$$

$$-b_1^i\{b_2^{i+1}[(w^{i+2}+m^{i+2}{\left(w\left(\frac{{\displaystyle x_{i+2}}}{{\displaystyle 4}}\right)\right)}^3)-(w^{i+1}+m^{i+1}{\left(w\left(\frac{{\displaystyle x_{i+1}}}{{\displaystyle 4}}\right)\right)}^3)]$$

$$-b_2^i[(w^{i+1}+m^{i+1}{\left(w\left(\frac{{\displaystyle x_{i+1}}}{{\displaystyle 4}}\right)\right)}^3)-(w^i+m^i{\left(w\left(\frac{{\displaystyle x_i}}{{\displaystyle 4}}\right)\right)}^3)]\}+n^i{\left(w\left(\frac{{\displaystyle x_i}}{{\displaystyle 2}}\right)\right)}^5=0.$$

As is known, the local truncating error of the scheme is $O\left(h\right)$. In order to fulfill the numerical computation, we select the node variable i such that $\frac{{\displaystyle x_i}}{{\displaystyle 4}}$ is equivalent to some $x_j,j=0,1,2,...$. So, one has $\frac{{\displaystyle 1+ih}}{{\displaystyle 4}}=1+jh$, which implies $i=\frac{{\displaystyle 3}}{{\displaystyle h}}+4j,j=0,1,2...$. For the convenience of computing, one can set $w\left(\frac{{\displaystyle x_{i+k}}}{{\displaystyle 4}}\right)=w\left(\frac{{\displaystyle x_i}}{{\displaystyle 4}}\right),k=1,2,3$, $w\left(\frac{{\displaystyle x_{i+1}}}{{\displaystyle 2}}\right)=w\left(\frac{{\displaystyle x_i}}{{\displaystyle 2}}\right)$, and $w\left(x\right)=w\left(x_0\right)$ for all $x<x_0$.

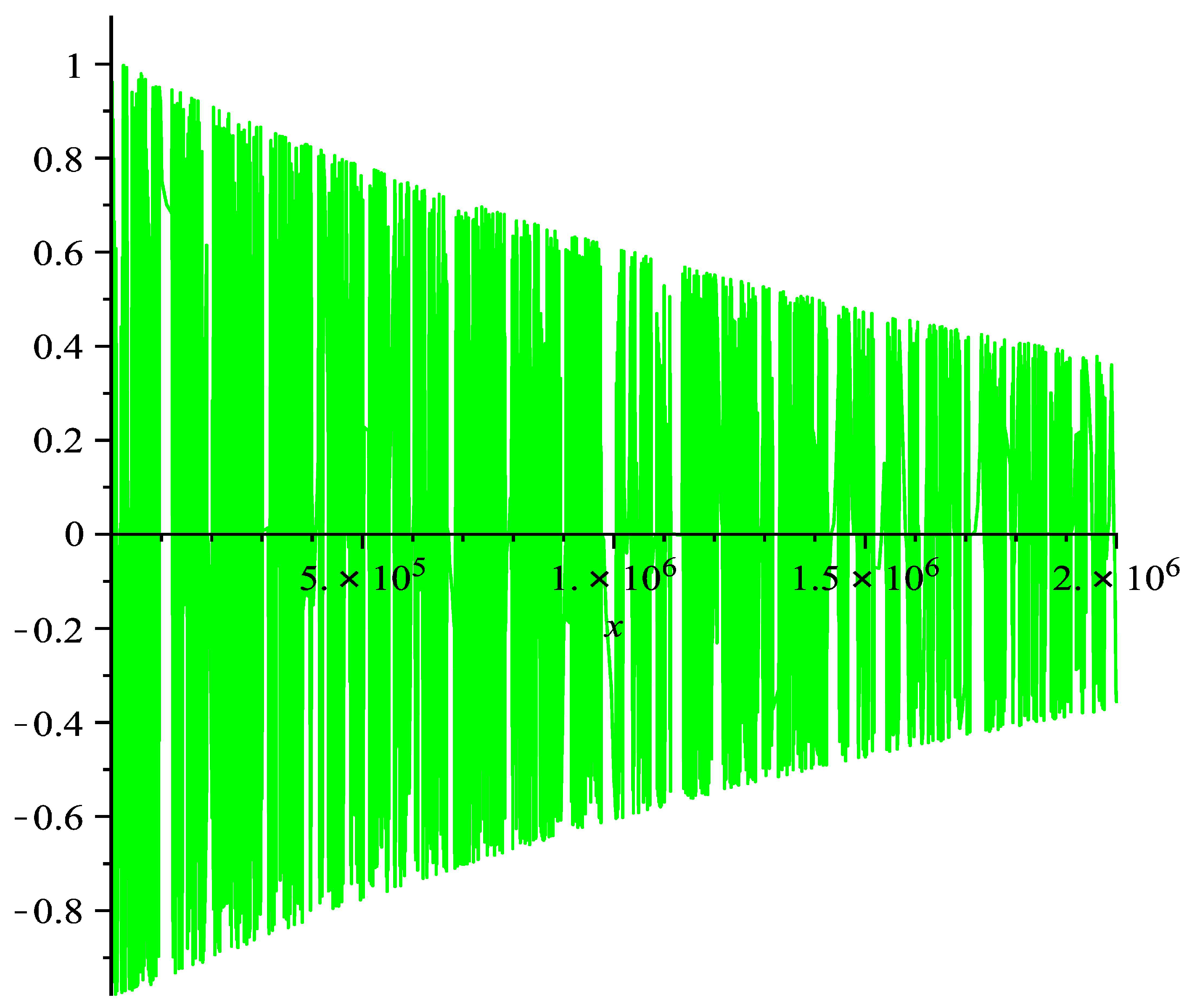
Selecting $h=0.1$ and the initial value condition $w\left(x_0\right)=0$, we obtain the numerical computation results, which are demonstrated in Figure 1.

From Figure 1, one can see that the solution of Equation (43) is oscillatory if x is large enough.

Next, we consider the following nonlinear third-order delay differential equation involving a local fractional derivative with a super-linear neutral term and a damping term.

Example 2. 

$$\begin{array}{cc}\hfill & D^{\frac{2}{3}}\left[x^{\frac{1}{6}}{D}^{\frac{2}{3}}\left(x^{-\frac{1}{3}}\left(D^{\frac{2}{3}}[w\left(x\right)+x^5{w}^3\left(\frac{{\displaystyle x}}{{\displaystyle 4}}\right)]\right)\right)\right]+x^{-\frac{3}{2}}{D}^{\frac{2}{3}}\left(x^{-\frac{1}{3}}\left(D^{\frac{2}{3}}[w\left(x\right)+x^5{w}^3\left(\frac{{\displaystyle x}}{{\displaystyle 4}}\right)]\right)\right)\hfill \\ \hfill & +x^{\frac{29}{3}}{w}^5\left(\frac{{\displaystyle x}}{{\displaystyle 2}}\right)=0,x\in [2,\infty ).\hfill \end{array}$$

(44)

Compared with (2) and (4), one has $\mathbb{T}=\mathbb{R},b_1\left(x\right)=\sqrt{x},m\left(x\right)=x^5,v\left(x\right)=x^{-\frac{3}{2}},n\left(x\right)=x^{\frac{28}{3}},b_2\left(x\right)=1,l_1\left(x\right)=\frac{{\displaystyle x}}{{\displaystyle 4}},l_2\left(x\right)=\frac{{\displaystyle x}}{{\displaystyle 2}},\alpha =3,\beta =5,and{x}_0=2.$ Then, $\mu \left(x\right)=0$, and $-\frac{{\displaystyle v}}{{\displaystyle b_1}}\in {\mathfrak{R}}_{+}$. Considering $e_{-\frac{v}{a}}(x,x_0)=e_{-\frac{v}{a}}(x,2)=exp(-{\int }_2^x\frac{{\displaystyle v\left(t\right)}}{{\displaystyle b_1\left(t\right)}}dt)$, one has

$$1>exp(-{\int }_2^x\frac{{\displaystyle v\left(t\right)}}{{\displaystyle b_1\left(t\right)}}dt)\ge 1-{\int }_2^x\frac{{\displaystyle v\left(t\right)}}{{\displaystyle b_1\left(t\right)}}dt=1-{\int }_2^x{t}^{-2}dt=1+[x^{-1}-2^{-1}]\ge \frac{{\displaystyle 1}}{{\displaystyle 2}}.$$

Obviously, $A_1(x,x^{*})=2[x^{\frac{1}{2}}-{\left(x^{*}\right)}^{\frac{1}{2}}],A_2(x,x^{*})=x-x^{*}$, which implies (33) and (34) hold. As

$$B_1(x,c)=\frac{{\displaystyle 1}}{{\displaystyle m\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}[1-\frac{{\displaystyle c^{\frac{1}{\alpha }-1}}}{{\displaystyle m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\right)}}]=\frac{{\displaystyle 1}}{{\displaystyle {\left(2x\right)}^5}}[1-\frac{{\displaystyle c^{-\frac{2}{3}}}}{{\displaystyle {\left(8x\right)}^{\frac{5}{3}}}}],$$

$$B_2(x,x_2,c)=\frac{{\displaystyle 1}}{{\displaystyle 32x^5}}[1-\frac{{\displaystyle k_1{x}^{\frac{3}{2}}+k_{2}x+k_3}}{{\displaystyle {\left(8x\right)}^{\frac{5}{3}}}}],$$

where $k_i,i=1,2,3$ are constants related to $x_2$, then we can find a sufficiently large $x_3\in \mathbb{R}$ such that $B_1(x,c)\ge \frac{{\displaystyle 1}}{{\displaystyle 64x^5}}$ and $B_2(x,x_2,c)\ge \frac{{\displaystyle 1}}{{\displaystyle 64x^5}}>0$ on $x\in [x_3,\infty )$.

For the sake of verifying (35), one can see that

$${\int }_{\overline{x}}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{\rho }^{\infty }(\frac{{\displaystyle e_{-\frac{v}{b_1}}(\xi ,x_0)}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }\frac{{\displaystyle n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,c)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}\Delta t)\Delta \xi ]\Delta \rho$$

$$\ge {\int }_{\overline{x}}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{\rho }^x(\frac{{\displaystyle e_{-\frac{v}{b_1}}(\xi ,x_0)}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^x\frac{{\displaystyle n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,c)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}\Delta t)\Delta \xi ]\Delta \rho$$

$$\ge \frac{{\displaystyle 1}}{{\displaystyle {\left(64\right)}^{\frac{5}{3}}2}}{\int }_{\overline{x}}^x\left[{\int }_{\rho }^x\left(\frac{{\displaystyle 1}}{{\displaystyle \sqrt{\xi }}}{\int }_{\xi }^{x}tdt\right)d\xi \right]d\rho$$

$$=\frac{{\displaystyle 1}}{{\displaystyle {\left(64\right)}^{\frac{5}{3}}2}}{\int }_{\overline{x}}^x\left[{\int }_{\rho }^x\left(\frac{{\displaystyle x^2-{\xi }^2}}{{\displaystyle 2\sqrt{\xi }}}\right)d\xi \right]d\rho$$

$$=\frac{{\displaystyle 1}}{{\displaystyle {\left(64\right)}^{\frac{5}{3}}2}}{\int }_{\overline{x}}^x[x^2(\sqrt{x}-\sqrt{\rho })-\frac{{\displaystyle 1}}{{\displaystyle 5}}(x^{\frac{5}{2}}-{\rho }^{\frac{5}{2}})]d\rho$$

$$=\frac{{\displaystyle 1}}{{\displaystyle {\left(64\right)}^{\frac{5}{3}}2}}[\frac{{\displaystyle 4}}{{\displaystyle 21}}{x}^{\frac{7}{2}}-\frac{{\displaystyle 4}}{{\displaystyle 5}}{x}^{\frac{5}{2}}\overline{x}+\frac{{\displaystyle 2}}{{\displaystyle 3}}{x}^2{\overline{x}}^{\frac{3}{2}}-\frac{{\displaystyle 2}}{{\displaystyle 35}}{\overline{x}}^{\frac{7}{2}}],$$

which tends to infinity when x tends to infinity. So (35) is satisfied. On the other hand, in order to verify (41), one has

$$\frac{{\displaystyle {\int }_{x_3}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{x_3}^{\rho }(\frac{{\displaystyle e_{-\frac{v}{b_1}}(\xi ,x_0)}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }\frac{{\displaystyle n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}\Delta t)\Delta \xi ]\Delta \rho }}{{\displaystyle A_1(x,x_2)A_2(x,x_2)}}$$

$$\ge \frac{{\displaystyle {\int }_{x_3}^x[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{x_3}^{\rho }(\frac{{\displaystyle e_{-\frac{v}{b_1}}(\xi ,x_0)}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^x\frac{{\displaystyle n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x_2,c)}}{{\displaystyle e_{-\frac{v}{b_1}}(\sigma \left(t\right),x_0)}}\Delta t)\Delta \xi ]\Delta \rho }}{{\displaystyle A_1(x,x_2)A_2(x,x_2)}}$$

$$\ge \frac{{\displaystyle 1}}{{\displaystyle {\left(64\right)}^{\frac{5}{3}}2}}\left\{\frac{{\displaystyle \frac{{\displaystyle 64}}{{\displaystyle 105}}{x}^{\frac{7}{2}}-x^3{\left(x_3\right)}^{\frac{1}{2}}+\frac{{\displaystyle 1}}{{\displaystyle 3}}{x}^2{\left(x_3\right)}^{\frac{3}{2}}+\frac{{\displaystyle 1}}{{\displaystyle 5}}x{\left(x_3\right)}^{\frac{5}{2}}-\frac{{\displaystyle 1}}{{\displaystyle 7}}{\left(x_3\right)}^{\frac{7}{2}}}}{{\displaystyle 2(\sqrt{x}-\sqrt{x_2})(x-x_2)}}\right\},$$

which tends to infinity when x tends to infinity. So, (41) holds. Due to Theorem 5, one can conclude that the solution $w\left(x\right)$ of Equation (44) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Similar to the numerical computation in Example 1, one can select the Euler method to construct a numerical scheme for (44), and the numerical computation results with the initial value condition $w\left(x_0\right)=1$ are demonstrated in Figure 2.

Comparing Figure 1 and Figure 2, one can see that the damping term can lead to an impact on the oscillatory behavior of the solutions.

Example 3. 

Next, we consider the following nonlinear third-order delay difference equation involving a local fractional difference with a super-linear neutral term:

$${\Delta }^{\frac{1}{3}}\left\{x^{\frac{1}{3}}{\Delta }^{\frac{1}{3}}\left(x^{-\frac{2}{3}}\left({\Delta }^{\frac{1}{3}}[w\left(x\right)+x^4{w}^3\left(\frac{{\displaystyle x}}{{\displaystyle 2}}\right)]\right)\right)\right\}+x^{\frac{8}{3}}{w}^3\left(x\right)=0,x\in {[2,\infty )}_{\mathbb{Z}},$$

(45)

where ${\Delta }^{\frac{1}{3}}$ is the fractional difference operator of $\frac{{\displaystyle 1}}{{\displaystyle 3}}$ order on $\mathbb{Z}$.

Compared with (1) and (3), one has $\mathbb{T}=\mathbb{Z},b_1\left(x\right)=x,m\left(x\right)=x^4,n\left(x\right)=x^2,b_2\left(x\right)=1,l_1\left(x\right)=\frac{{\displaystyle x}}{{\displaystyle 2}},l_2\left(x\right)=x,\alpha =\beta =3,and{x}_0=2.$ Then, for (8) and (9), one has

$$\underset{x\to \infty }{lim}{A}_1(x,x_0)={\int }_{x_0}^{\infty }\frac{{\displaystyle 1}}{{\displaystyle b_1\left(t\right)}}\Delta t=\sum _{t=2}^{\infty }\frac{{\displaystyle 1}}{{\displaystyle t}}=\infty ,$$

and

$$\underset{x\to \infty }{lim}{A}_2(x,x_0)={\int }_{x_0}^{\infty }\frac{{\displaystyle 1}}{{\displaystyle b_2\left(t\right)}}\Delta t=\sum _{t=2}^{\infty }1=\infty .$$

Furthermore, as $B_1(x,c)=\frac{{\displaystyle 1}}{{\displaystyle m\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)}}[1-\frac{{\displaystyle c^{\frac{1}{\alpha }-1}}}{{\displaystyle m^{\frac{1}{\alpha }}\left(l_1^{-1}\left(l_1^{-1}\left(l_2\left(x\right)\right)\right)\right)}}]=\frac{{\displaystyle 1}}{{\displaystyle {\left(2x\right)}^4}}[1-\frac{{\displaystyle c^{-\frac{2}{3}}}}{{\displaystyle {\left(4x\right)}^{\frac{4}{3}}}}]$, we can find a sufficiently large $\overline{x}\in \mathbb{Z}$ such that $B_1(x,c)\ge \frac{{\displaystyle 1}}{{\displaystyle 32x^4}},x\in {[\overline{x},\infty )}_{\mathbb{Z}}$. Then, it holds that

$${\int }_{\overline{x}}^{\infty }[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{\rho }^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,c)\Delta t)\Delta \xi ]\Delta \rho$$

$$=\sum _{\rho =\overline{x}}^{\infty }\left[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}\sum _{\xi =\rho }^{\infty }\left(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}\sum _{t=\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,c)\right)\right]$$

$$\ge \frac{{\displaystyle 1}}{{\displaystyle 32}}\sum _{\rho =\overline{x}}^{\infty }\left[\sum _{\xi =\rho }^{\infty }\left(\frac{{\displaystyle 1}}{{\displaystyle \xi }}\sum _{t=\xi }^{\infty }\frac{{\displaystyle 1}}{{\displaystyle t^2}}\right)\right]\ge \frac{{\displaystyle 1}}{{\displaystyle 32}}\sum _{\rho =\overline{x}}^{\infty }\left[\sum _{\xi =\rho }^{\infty }\left(\frac{{\displaystyle 1}}{{\displaystyle \xi }}\sum _{t=\xi }^{\infty }\frac{{\displaystyle 1}}{{\displaystyle t(t+1)}}\right)\right]=\frac{{\displaystyle 1}}{{\displaystyle 32}}\sum _{\rho =\overline{x}}^{\infty }\sum _{\xi =\rho }^{\infty }\frac{{\displaystyle 1}}{{\displaystyle {\xi }^2}}$$

$$\ge \frac{{\displaystyle 1}}{{\displaystyle 32}}\sum _{\rho =\overline{x}}^{\infty }\sum _{\xi =\rho }^{\infty }\frac{{\displaystyle 1}}{{\displaystyle \xi (\xi +1)}}=\frac{{\displaystyle 1}}{{\displaystyle 32}}\sum _{\rho =\overline{x}}^{\infty }\frac{{\displaystyle 1}}{{\displaystyle \rho }}=\infty .$$

So (8)–(10) are satisfied. Moreover, as

$$A_1(x,x^{*})={\int }_{x^{*}}^x\frac{{\displaystyle 1}}{{\displaystyle t}}\Delta t=\sum _{t=x^{*}}^{x-1}\frac{{\displaystyle 1}}{{\displaystyle t}}\ge {\int }_{x^{*}}^x\frac{{\displaystyle 1}}{{\displaystyle t}}dt=lnx-ln{x}^{*},$$

$$A_1(x,x^{*})\le {\int }_{x^{*}-1}^{x-1}\frac{{\displaystyle 1}}{{\displaystyle t}}dt=ln(x-1)-ln(x^{*}-1)<lnx,$$

$$A_2(x,x^{*})={\int }_{x^{*}}^{x}1\Delta t=\sum _{t=x^{*}}^{x-1}1=x-x^{*},$$

one can deduce that $B_2(x,x^{*},c)\ge \frac{{\displaystyle 1}}{{\displaystyle {\left(2x\right)}^4}}[1-\frac{{\displaystyle k_{1}xlnx+k_{2}x+k_3}}{{\displaystyle {\left(4x\right)}^{\frac{4}{3}}}}]$, where $k_i,i=1,2,3$ are constants related to $x^{*}$. Therefore, there exists $x_3\in {[x^{*},\infty )}_{\mathbb{Z}}$ such that $A_1(x,x^{*})\ge \frac{{\displaystyle 1}}{{\displaystyle 2}}lnx$ and $B_2(x,x^{*},c)\ge \frac{{\displaystyle 1}}{{\displaystyle 32x^4}}$ on $x\in {[x_3,\infty )}_{\mathbb{Z}}$.

Selecting $\eta \left(x\right)=x$, one has

$${\int }_{x_3}^x[c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x^{*})}}]\Delta t$$

$$=\sum _{t=x_3}^{x-1}[c^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x^{*})}}]$$

$$\ge \sum _{t=x_3}^{x-1}(\frac{{\displaystyle 1}}{{\displaystyle 32t}}-\frac{{\displaystyle 1}}{{\displaystyle 2tlnt}})=\sum _{t=x_3}^{x-1}\frac{{\displaystyle 1}}{{\displaystyle 32t}}(1-\frac{{\displaystyle 16}}{{\displaystyle lnt}}),$$

which tends to infinity when x tends to infinity as long as $x_3$ is sufficiently large. So, (19) satisfies in the case $\mathbb{T}=\mathbb{Z}$. It follows from Theorem 1 that the solution $w\left(x\right)$ of Equation (45) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

Example 4. 

Now, we research the oscillation of the following nonlinear third-order delay local fractional $\gamma -$difference equation with a super-linear neutral term:

$${\Delta }^{\frac{1}{2}}\left\{\sqrt{x}{\Delta }^{\frac{1}{2}}\left(x^{-\frac{1}{2}}\left({\Delta }^{\frac{1}{2}}[w\left(x\right)+x^4{w}^3\left(\frac{{\displaystyle x}}{{\displaystyle 2}}\right)]\right)\right)\right\}+x^{\frac{5}{2}}{w}^3\left(x\right)=0,x\in {[\gamma ,\infty )}_{{\gamma }^{\mathbb{Z}}},$$

(46)

where $\gamma \ge 2$, ${\Delta }^{\frac{1}{2}}$ is the fractional $\gamma -$ difference operator of $\frac{{\displaystyle 1}}{{\displaystyle 2}}$ order on ${\gamma }^{\mathbb{Z}}$.

Due to (1) and (3), one has $\mathbb{T}={\gamma }^{\mathbb{Z}},b_1\left(x\right)=x,m\left(x\right)=x^4,n\left(x\right)=x^2,b_2\left(x\right)=1,l_1\left(x\right)=\frac{{\displaystyle x}}{{\displaystyle 2}},l_2\left(x\right)=x,\alpha =\beta =3,and{x}_0=\gamma .$ Then, one can easily deduce that (8) and (9) hold. Similar to Example 3, there exists a sufficiently large $\overline{x}\in {\gamma }^{\mathbb{Z}}$ such that $B_1(x,c)\ge \frac{{\displaystyle 1}}{{\displaystyle 32x^4}}$ on $x\in {[\overline{x},\infty )}_{{\gamma }^{\mathbb{Z}}}$. So, (10) holds by the following observations:

$${\int }_{\overline{x}}^{\infty }[\frac{{\displaystyle 1}}{{\displaystyle b_2\left(\rho \right)}}{\int }_{\rho }^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle b_1\left(\xi \right)}}{\int }_{\xi }^{\infty }n\left(t\right)B_1^{\frac{\beta }{\alpha }}(t,c)\Delta t)\Delta \xi ]\Delta \rho$$

$$\ge \frac{{\displaystyle 1}}{{\displaystyle 32}}{\int }_{\overline{x}}^{\infty }[{\int }_{\rho }^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle \xi }}{\int }_{\xi }^{\infty }\frac{{\displaystyle 1}}{{\displaystyle t^2}}\Delta t)\Delta \xi ]\Delta \rho \ge \frac{{\displaystyle 1}}{{\displaystyle 32}}{\int }_{\overline{x}}^{\infty }[{\int }_{\rho }^{\infty }(\frac{{\displaystyle 1}}{{\displaystyle \xi }}{\int }_{\xi }^{\infty }\frac{{\displaystyle 1}}{{\displaystyle t\sigma \left(t\right)}}\Delta t)\Delta \xi ]\Delta \rho$$

$$=\frac{{\displaystyle 1}}{{\displaystyle 32}}{\int }_{\overline{x}}^{\infty }[{\int }_{\rho }^{\infty }\left(\frac{{\displaystyle 1}}{{\displaystyle \xi }}{[-\frac{{\displaystyle 1}}{{\displaystyle t}}]}_{\xi }^{\infty }\right)\Delta \xi ]\Delta \rho =\frac{{\displaystyle 1}}{{\displaystyle 32}}{\int }_{\overline{x}}^{\infty }[{\int }_{\rho }^{\infty }\frac{{\displaystyle 1}}{{\displaystyle {\xi }^2}}\Delta \xi ]\Delta \rho \ge \frac{{\displaystyle 1}}{{\displaystyle 32}}{\int }_{\overline{x}}^{\infty }[{\int }_{\rho }^{\infty }\frac{{\displaystyle 1}}{{\displaystyle \xi \sigma \left(\xi \right)}}\Delta \xi ]\Delta \rho$$

$$=\frac{{\displaystyle 1}}{{\displaystyle 32}}{\int }_{\overline{x}}^{\infty }\frac{{\displaystyle 1}}{{\displaystyle \rho }}\Delta \rho =\infty .$$

Furthermore, letting $F^{\Delta }\left(t\right)=f\left(t\right)$, one has

$${\int }_{x^{*}}^{x}f\left(t\right)\Delta t=F\left(x\right)-F\left(x^{*}\right)$$

$$=\sum _{k=1}^{{log}_{\gamma }^{\frac{x}{x^{*}}}}[F\left({\gamma }^k{x}^{*}\right)-F\left({\gamma }^{k-1}{x}^{*}\right)]=\sum _{k=1}^{{log}_{\gamma }^{\frac{x}{x^{*}}}}\left[({\gamma }^k{x}^{*}-{\gamma }^{k-1}{x}^{*})f\left({\gamma }^{k-1}{x}^{*}\right)\right].$$

So,

$$A_1(x,x^{*})={\int }_{x^{*}}^x\frac{{\displaystyle 1}}{{\displaystyle t}}\Delta t$$

$$=\sum _{k=1}^{{log}_{\gamma }^{\frac{x}{x^{*}}}}\left[({\gamma }^k{x}^{*}-{\gamma }^{k-1}{x}^{*})\frac{{\displaystyle 1}}{{\displaystyle {\gamma }^{k-1}{x}^{*}}}\right]=(\gamma -1){log}_{\gamma }^{\frac{x}{x^{*}}}=(\gamma -1)({log}_{\gamma }^x-{log}_{\gamma }^{x^{*}}),$$

$$A_2(x,x^{*})={\int }_{x^{*}}^{x}1\Delta t=x-x^{*},$$

$$B_2(x,x^{*},c)=\frac{{\displaystyle 1}}{{\displaystyle {\left(2x\right)}^4}}[1-\frac{{\displaystyle k_{1}x{log}_{\gamma }^x+k_{2}x+k_3}}{{\displaystyle {\left(4x\right)}^{\frac{4}{3}}}}].$$

Therefore, there exists $x_3\in {[x^{*},\infty )}_{{\gamma }^{\mathbb{Z}}}$ such that $A_1(x,x^{*})\ge \frac{{\displaystyle \gamma -1}}{{\displaystyle 2}}{log}_{\gamma }^x$ and $B_2(x,x^{*},c)\ge \frac{{\displaystyle 1}}{{\displaystyle 32x^4}}$ on $x\in {[x_3,\infty )}_{{\gamma }^{\mathbb{Z}}}$.

Under the selection $\eta \left(x\right)=x$, it holds that

$$\underset{x\to \infty }{lim}sup\frac{{\displaystyle 1}}{{\displaystyle (x-x_0)}}\{{\int }_{x_3}^x(x-t)\{c_1^{\frac{\beta }{\alpha }-1}n\left(t\right)B_2^{\frac{\beta }{\alpha }}(t,x^{*},c)\eta \left(t\right)-\frac{{\displaystyle b_2\left(t\right){\left[{\eta }^{\Delta }\left(t\right)\right]}^2}}{{\displaystyle 4\eta \left(t\right)A_1(t,x^{*})}}\}\Delta t\}$$

$$\ge \underset{x\to \infty }{lim}sup\frac{{\displaystyle 1}}{{\displaystyle (x-\gamma )}}{\int }_{x_3}^x(x-t)(\frac{{\displaystyle 1}}{{\displaystyle 32t}}-\frac{{\displaystyle 1}}{{\displaystyle 2(\gamma -1)t{log}_{\gamma }^t}})\Delta t$$

$$=\underset{x\to \infty }{lim}sup\frac{{\displaystyle 1}}{{\displaystyle (x-\gamma )}}{\int }_{x_3}^x\frac{{\displaystyle x-t}}{{\displaystyle 32t}}(1-\frac{{\displaystyle 16}}{{\displaystyle (\gamma -1){log}_{\gamma }^t}})\Delta t=\infty .$$

So, (31) is also satisfied with $l=1$. Due to Corollary 1, it can be seen that the solution $w\left(x\right)$ of Equation (46) is oscillatory or satisfies $\underset{x\to \infty }{lim}w\left(x\right)=0$.

5. Conclusions

By the use of some inequalities, the Riccati transformation, the integral technique, and the theory of time scale, we have deduced and proposed some new sufficient conditions on oscillation including some Kamenev and Philos-type oscillation criteria for a class of nonlinear third-order delay dynamic equations with a super-linear neutral term. Furthermore, these oscillation criteria are extended to another class of nonlinear third-order delay dynamic equations with a super-linear neutral term and a damping term. In order to apply the proposed oscillation results, some examples are given and analyzed. Finally, we note that the deduction process of the main results in this paper can be extended to other types of nonlinear high-order delay dynamic equations on time scales, and as $\alpha \le \beta$ here, the establishment of oscillation criteria in the case $\alpha >\beta$ is also worthy of further research.