Processing the Controllability of Control Systems with Distinct Fractional Derivatives via Kalman Filter and Gramian Matrix

Abstract

In this paper, we investigate the controllability conditions of linear control systems involving distinct local fractional derivatives. Sufficient conditions for controllability using Kalman rank conditions and the Gramian matrix are presented. We show that the controllability of the local fractional system can be determined by the invertibility of the Gramian matrix and the full rank of the Kalman matrix. We also show that the local fractional system involving distinct orders is controllable if and only if the Gramian matrix is invertible. Illustrative examples and an application are provided to demonstrate the validity of the theoretical findings.

1. Introduction

Fractional calculus is a field of mathematics that expands the notions of differentiation and integration to allow for non-whole number orders. It was pioneered in the 17th century by mathematicians Leibniz and l’Hopital. The idea behind fractional derivatives is to extend the concept of differentiation to fractional orders. Traditional calculus deals with integer order derivatives—the first derivative representing the rate of change, the second derivative relating to the acceleration, and so on. However, in many complex systems, especially those with irregular or fractal geometries, these integer-order derivatives are not sufficient to describe the system’s behavior accurately. This is where local fractional derivatives come into play, offering a more nuanced and precise tool for analysis [1,2]. Fractional calculus has an expansive range of applications in biology, engineering, mathematics, physics, and other fields. It can be used to model systems that exhibit memory or hereditary properties, such as viscoelastic materials and diffusion processes [3].

Fractional calculus matured through the original work of many mathematicians, including Euler, Riemann, Abel, Laplace, Liouville, and several other leading mathematicians [2]. In the last few decades, many researchers have devoted their research works to this modern area after they were captivated by its broad applicability, as it revealed itself as an excellent tool for describing countless dynamical phenomena occurring in nature and modeling various scientific fields [4,5].

Derivatives of arbitrary orders are named fractional derivatives (FD). Notably, researchers were able to introduce various definitions for fractional derivatives from several perspectives: Riemann–Liouville, Riesz, Hadamard, Caputo, conformable and Marchaud are just a few to name [6].

We present two of the most popular definitions of FD operators [2].

Definition 1.

The Riemann–Liouville FD of a function $\varphi :(0,\infty )\to R$ of order α is given as

$${}_n{D}_t^{\alpha }\varphi \left(t\right)=\frac{1}{\mathsf{\Gamma }(q-\alpha )}{\left(\frac{d}{dt}\right)}^q{\int }_n^t\varphi \left(\tau \right){(t-\tau )}^{(q-1)-\alpha }d\tau$$

with $q-1\le \alpha <q,q\in \mathbb{N},t>n,$ and $\alpha \in \mathbb{R}$.

Definition 2.

The Caputo FD of a function $\varphi :(0,\infty )\to R$ of order α is given as

$${}_c{D}_t^{\alpha }\varphi \left(t\right)=\frac{1}{\mathsf{\Gamma }(p-\alpha )}{\int }_c^t{\varphi }^{\left(p\right)}\left(\tau \right){(t-\tau )}^{(p-1)-\alpha }d\tau$$

with $p-1\le \alpha <p,p\in \mathbb{N},t>c,$ and $\alpha \in \mathbb{R}.$

The majority of FDs are defined using fractional integrals. Due to this reason, those fractional derivatives own some non-local behaviors. They do not satisfy many useful properties, for instance the chain rule, the product rule, and the quotient rule [7]. However, the local fractional derivative (LFD) takes a different approach. It directly extends classical derivatives to fractional orders, preserving the crucial properties of ordinary derivatives [8]. Several LFD definitions exist [9], but this work specifically utilizes the Gao–Yang–Kang LFD, which is given as

Definition 3

([9]). Let $\theta \in C_{\alpha }(a,b)$ and $0<\alpha \le 1$. The (Yang) LFD operator of θ with order α at $t=t_0$ is defined as

$$D_t^{\alpha }\theta \left(t_0\right)=\frac{d^{\alpha }\theta \left(t\right)}{d{t}^{\alpha }}{|}_{t=t_0}=\underset{t\to t_0}{lim}{\displaystyle \frac{{\Delta }^{\alpha }(\theta \left(t\right)-\theta \left(t_0\right))}{{(t-t_0)}^{\alpha }}},$$

(1)

where ${\Delta }^{\alpha }(\theta \left(t\right)-\theta \left(t_0\right))\cong \mathsf{\Gamma }(1+\alpha )((\theta \left(t\right)-\theta \left(t_0\right)),$ and the LFD of high order is represented as

$$D_t^{p\alpha }\theta \left(t\right)=\underset{ptimes}{\underbrace{D_t^{\alpha }\dots D_t^{\alpha }}}\theta \left(t\right).$$

A new type of fractional differential equation called the local fractional differential equation (LFDE) has emerged and shown great potential. Similar to regular fractional differential equations (FDEs), LFDEs have demonstrated an ability to model many scientific problems effectively, such as in viscoelastic materials [10], in electrochemistry [11], in fractal networks [12], and even in describing how to control dynamics of COVID-19 [13] and several other areas [14,15], and the references cited therein.

Lately, there has been growing interest in applying control theory to fractional dynamical systems. Controllability is an important concept in modern control theory, especially for fractional systems. Kalman introduced these concepts in 1960 in [16], with the objective of investigating the feasibility of transitioning the solution of a control system from its initial state to any desired state at terminal time. They significantly contribute in the analysis and design of control systems [17]. Recently, numerous researchers have investigated generalizing the fundamental controllability principles to the domain of fractional-order control systems, see [18,19,20], and the references cited therein.

Moreover, many techniques have been leveraged to analyze and design controllers for fractional-order control systems. For example, to control a vibratory system represented by a differential equation of non-integer order, linear quadratic regulator theory was employed in [21]. The necessary and sufficient rank conditions for controllability and observability of the discrete fractional system were obtained using Gramian and controllability matrices in [22]. Controllability of nonlinear systems of fractional order was studied using monotone operator theory and fixed point theorem in [23]. Jneid and Awadalla [24] investigated the controllability for conformable fractional semilinear finite dimensional control systems. Younus et al. [25] worked on the observability Gramian matrix and its rank criteria for the conformable linear system. Li et al. [26] studied the controllability of RL fractional delay differential equations. In [27], the authors explored the controllability and observability of fractional linear systems, described by the Caputo derivative with distinct orders. From our review of the literature, there appears to be a gap in studying the controllability for two types of different local fractional (LF) systems. Motivated by the previous research work using the Caputo derivative, we aim to obtain the sufficient and necessary conditions for the controllability of the linear control system involving local fractional derivatives with two distinct orders of the form:

$$\left[\begin{array}{c}{D}_t^{\alpha }{x}_1\left(t\right)\\ D_t^{2\alpha }{x}_2\left(t\right)\end{array}\right]=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]u\left(t\right)$$

(2)

where $D_t^{\alpha }$, $D_t^{2\alpha }$ are the local fractional derivative, $0<\alpha <1;$   $x_1\left(t\right)\in R^{n_1}$ and $x_2\left(t\right)\in R^{n_2}$ are the state vectors; $A_{ij}\in R^{n_i\times n_j}$, $B_i\in R^{n_i\times m}$, $i,j=1,2,$ $n_1+n_2=n$ are real matrices of sizes $n_i\times n_j$, $n_i\times m$, respectively; and $u\left(t\right)\in R^m$ is the state control.

The remaining sections of this paper are structured as follows. Section 2 provides helpful definitions, theorems, properties, and background results related to the local fractional derivative. In Section 3, we derive sufficient conditions for controllability of local fractional linear systems and give an example. In Section 4, we introduce the linear systems with distinct local fractional orders and establish the conditions of controllability for such systems. An application is given in Section 5. At the end, in Section 6, we deliver the key results in a short conclusion.

2. The Local Fractional Calculus

In 1996, Kolwankar and Gangal in [28] introduced the concept of the local fractional derivative (LFD) as a natural extension of classical derivatives to fractional orders while maintaining local behavior. Since then, several other LFD definitions have emerged. Yang’s LFD in [29,30] focuses on a specific type of fractional derivative calculation within a localized area. Jumarie’s fractal derivative in [31] leverages concepts from fractal geometry and advanced mathematical frameworks to capture the intricate nature of local derivatives. Parvate in [32] proposed a general LFD framework encompassing a wider range of possible derivative calculations, further elaborated on by Chen et al. in [33]. He’s LFD in [34] seems to be a specific implementation or application of an LFD, potentially using a unique formula or algorithm for local derivative calculations.

The main motivation for constructing the local fractional derivative was the need to express a local version of the fractional derivative that is needed in studying fractional differentiability. Hence, the construction of local fractional derivatives came as a generalization of the typical derivatives to fractional order maintaining the local characteristic of the derivative operator, unlike the other definitions of fractional derivatives that are mostly globally defined. The emergence of local fractional calculus as a convenient tool is due to its ability to address the local characteristics of non-differentiable functions defined on fractional sets. As a result, it has proved its efficiency in handling diverse phenomena across several domains of science and engineering.

By covering the essential findings of local fractional calculus, this section aims to provide the background needed to follow the original contributions presented later in the paper. We refer readers to the cited references [9,29,30] for rigorous definitions and proofs regarding local fractional calculus.

2.1. Main Properties

Definition 4.

A real valued map $\theta \left(t\right)$ on the interval $(a,b)$ is LF continuous at $t=t_0$ if, for each $\epsilon >0,$ there is a $\delta >0$ with

$$|\theta \left(t\right)-\theta \left(t_0\right)|<{\epsilon }^{\alpha },$$

(3)

whenever $|t-t_0|<\delta$, and $\epsilon ,\delta \in \mathbb{R}$.

It is written as

$$\underset{t\to t_0}{lim}\theta \left(t\right)=\theta \left(t_0\right).$$

(4)

A LF continuous map $\theta \left(t\right)$ on $(a,b)$, is represented by

$$\theta \left(t\right)\in C_{\alpha }(a,b).$$

(5)

Definition 5.

The Mittag-Leffler function is defined as

$$E_{\alpha }\left({\tau }^{\alpha }\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{\tau }^{k\alpha }}{\mathsf{\Gamma }(1+k\alpha )}},$$

(6)

with $0<\alpha <1,\tau \in \mathbb{R}.$

We have the following properties of the Mittag-Leffler function defined in fractal space:

(i)

$E_{\alpha }\left(t^{\alpha }\right)E_{\alpha }\left({\tau }^{\alpha }\right)=E_{\alpha }(t^{\alpha }+{\tau }^{\alpha });$

(ii)

$E_{\alpha }\left(t^{\alpha }\right)E_{\alpha }(-{\tau }^{\alpha })=E_{\alpha }(t^{\alpha }-{\tau }^{\alpha }).$

The hyperbolic functions defined through the Mittag-Leffler function in fractal space are given as:

$$\begin{array}{cc}\hfill {cosh}_{\alpha }\left(t^{\alpha }\right)& ={\displaystyle \frac{E_{\alpha }\left(t^{\alpha }\right)+E_{\alpha }(-t^{\alpha })}{2}}=\sum _{l=0}^{\infty }{\displaystyle \frac{t^{2l\alpha }}{\mathsf{\Gamma }(1+2l\alpha )}}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {sinh}_{\alpha }\left(t^{\alpha }\right)& ={\displaystyle \frac{E_{\alpha }\left(t^{\alpha }\right)-E_{\alpha }(-t^{\alpha })}{2}}=\sum _{l=0}^{\infty }{\displaystyle \frac{t^{(2l+1)\alpha }}{\mathsf{\Gamma }(1+(2l+1\left)\alpha \right)}}.\hfill \end{array}$$

(8)

2.1.1. Local Fractional Derivative

Theorem 1.

The fractional binomial theorem is given in the form

$${(\psi +\varphi )}^{p\alpha }=\sum _{j=0}^p\left({\displaystyle \genfrac{}{}{0pt}{}{p\alpha }{j\alpha }}\right){\psi }^{(p-j)\alpha }{\left(\varphi \right)}^{j\alpha }$$

(9)

where

$$\left({\displaystyle \genfrac{}{}{0pt}{}{p\alpha }{j\alpha }}\right)={\displaystyle \frac{\mathsf{\Gamma }(1+p\alpha )}{\mathsf{\Gamma }(1+i\alpha )\mathsf{\Gamma }(1+(p-i\left)\alpha \right)}}.$$

(10)

The basic properties of the LFD can be deduced from the previous definitions:

Lemma 1.

Suppose $\varphi ,\psi$ are non-differentiable functions and α is an order of the LF derivative. Then

(1) 

$D_t^{\alpha }\psi \left(t\right)=0$ for any constant functions ψ;

(2) 

$D_t^{\alpha }(r\varphi \left(t\right)+s\psi \left(t\right))=r\left(D_t^{\alpha }\varphi \left(t\right)\right)+s\left(D_t^{\alpha }\psi \left(t\right)\right)forr,s\in \mathbb{R}$;

(3) 

$D_t^{\alpha }\left(\varphi \left(t\right)\psi \left(t\right)\right)=\varphi \left(t\right)\left(D_t^{\alpha }\psi \left(t\right)\right)+\psi \left(t\right)\left(D_t^{\alpha }\varphi \left(t\right)\right)$;

(4) 

$D_t^{\alpha }\left[{\displaystyle \frac{\varphi \left(t\right)}{\psi \left(t\right)}}\right]={\displaystyle \frac{\psi \left(t\right)D_t^{\alpha }\varphi \left(t\right)-\varphi \left(t\right)D_t^{\alpha }\psi \left(t\right)}{{\psi }^2\left(t\right)}},$ given that $\psi \left(t\right)\ne 0$;

(5) 

$D_t^{\alpha }\left({\displaystyle \frac{t^{p\alpha }}{\mathsf{\Gamma }(1+p\alpha )}}\right)={\displaystyle \frac{t^{(p-1)\alpha }}{\mathsf{\Gamma }(1+(p-1\left)\alpha \right)}}$;

(6) 

$D_t^{\alpha }\left(E_{\alpha }\left(t^{\alpha }\right)\right)=E_{\alpha }\left(t^{\alpha }\right)$;

(7) 

$D_t^{\alpha }\left(E_{\alpha }\left(\beta t^{\alpha }\right)\right)=\beta E_{\alpha }\left(\beta t^{\alpha }\right)$.

2.1.2. Local Fractional Integral

Definition 6.

Suppose $\psi \left(t\right)\in C_{\alpha }[a,b]$. We define the LF integral of $\psi \left(t\right)$ of order α ( $0<\alpha \le 1$ ) by

$$\begin{array}{cc}\hfill {}_a{I}_b^{\left(\alpha \right)}\psi \left(t\right)& ={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_a^b\psi \left(t\right){\left(dt\right)}^{\alpha }\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}\underset{\Delta t_k\to 0}{lim}\sum _{k=0}^{N-1}\psi \left(t_k\right){(\Delta t_k)}^{\alpha },\hfill \end{array}$$

(12)

where $\Delta t_k=t_{k+1}-t_k$, $\Delta t=$ max $\{\Delta t_1,\Delta t_2,\Delta t_k,\dots \}$, and $[t_k,t_{k+1}]$ for $k=0,1,\dots ,N-1,$ $t_0=a<t_1<\dots <t_{N-1}<t_N=b$ is a partition of $[a,b]$.

Lemma 2.

Suppose $\varphi \left(t\right),\psi \left(t\right)$ and $\omega \left(t\right)$ $\in C_{\alpha }[a,b]$.

(1) 

${}_a{I}_b^{\left(\alpha \right)}\left[\varphi \left(t\right)\pm \psi \left(t\right)\right]={}_a{I}_b^{\left(\alpha \right)}\varphi \left(t\right)\pm {}_a{I}_b^{\left(\alpha \right)}\psi \left(t\right)$;

(2) 

${}_a{I}_b^{\left(\alpha \right)}\left[\beta \omega \left(t\right)\right]=\beta {}_a{I}_b^{\left(\alpha \right)}\omega \left(t\right),$ for any constant β;

(3) 

${}_a{I}_b^{\left(\alpha \right)}\psi \left(t\right)\ge 0,$ if $\psi \left(t\right)\ge 0$ $\forall t\in [a,b]$;

(4) 

${}_a{I}_b^{\left(\alpha \right)}\varphi \left(t\right)\ge {}_a{I}_b^{\left(\alpha \right)}\psi \left(t\right),$ provided that $\varphi \left(t\right)\ge \psi \left(t\right)$ for all $t\in [a,b]$;

(5) 

${}_a{I}_b^{\left(\alpha \right)}\psi \left(t\right)=-{}_b{I}_a^{\left(\alpha \right)}\psi \left(t\right)$;

(6) 

${}_a{I}_b^{\left(\alpha \right)}\psi \left(t\right){=}_a{I}_c^{\left(\alpha \right)}\psi \left(t\right){+}_c{I}_b^{\alpha }\psi \left(t\right)$;

(7) 

${}_a{I}_b^{\left(\alpha \right)}\lambda ={\displaystyle \frac{\lambda {(b-a)}^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}};$ for any constant function λ;

(8) 

${}_0{I}_t^{\left(\alpha \right)}{t}^{k\alpha }={\displaystyle \frac{\mathsf{\Gamma }(1+k\alpha )}{\mathsf{\Gamma }(1+(k+1\left)\alpha \right)}}{t}^{(k+1)\alpha }$;

(9) 

${}_a{I}_b^{\left(\alpha \right)}{E}_{\alpha }\left(t^{\alpha }\right)=E_{\alpha }\left(b^{\alpha }\right)-E_{\alpha }\left(a^{\alpha }\right);$

(10) 

${}_a{I}_b^{\left(\alpha \right)}{E}_{\alpha }\left(\lambda t^{\alpha }\right)={\displaystyle \frac{E_{\alpha }\left(\lambda b^{\alpha }\right)-E_{\alpha }\left(\lambda a^{\alpha }\right)}{\lambda }};$

(11) 

${}_0{I}_t^{\left(\alpha \right)}{sinh}^2\left(t^{\alpha }\right)=-\frac{1}{2}{\displaystyle \frac{t^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}+\frac{1}{8}\left[E_{\alpha }\left(2t^{\alpha }\right)-E_{\alpha }(-2t^{\alpha })\right];$

(12) 

${}_0{I}_t^{\left(\alpha \right)}{cosh}^2\left(t^{\alpha }\right)=\frac{1}{2}{\displaystyle \frac{t^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}+\frac{1}{8}\left[E_{\alpha }\left(2t^{\alpha }\right)+E_{\alpha }(-2t^{\alpha })\right].$

Theorem 2

(MVT for local fractional integrals). Assume $\varphi \left(t\right)\in C_{\alpha }[a,b]$. Then ∃ $\lambda \in (a,b)$ with

$${}_a{I}_b^{\left(\alpha \right)}\varphi \left(t\right)=\varphi \left(\lambda \right){\displaystyle \frac{{(b-a)}^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}.$$

(13)

Theorem 3.

Suppose that $\psi \left(t\right)\in C_{\alpha }[a,b]$. Then, for $t\in (a,b)$, ∃ $\mathsf{\Psi }\left(t\right)$ is given as

$$\mathsf{\Psi }\left(t\right)={}_a{I}_t^{\left(\alpha \right)}\psi \left(t\right)$$

(14)

and having the following local fractional derivative

$$D_t^{\alpha }\mathsf{\Psi }\left(t\right)=\psi \left(t\right).$$

(15)

Theorem 4.

Assume that $D_t^{\alpha }\mathsf{\Theta }\left(t\right)=\theta \left(t\right)$ $\in C_{\alpha }[a,b].$

Then,

$${}_a{I}_b^{\left(\alpha \right)}\theta \left(t\right)=\mathsf{\Theta }\left(b\right)-\mathsf{\Theta }\left(a\right).$$

(16)

Theorem 5.

Assume that $D_t^{k\alpha }\psi \left(t\right),D_t^{\left(\right(k+1\left)\alpha \right)}\psi \left(t\right)\in C_{\alpha }(a,b)$.

For $0<\alpha <1$, there exists a point $t_0\in (a,b)$, such that

$${}_{t_0}{I}_t^{\left(k\alpha \right)}\left[D_t^{k\alpha }\psi \left(t\right)\right]-{}_{t_0}{I}_t^{\left(\right(k+1\left)\alpha \right)}\left[D_t^{\left(\right(k+1\left)\alpha \right)}\psi \left(t\right)\right]=D_t^{k\alpha }\psi \left(t_0\right){\displaystyle \frac{{(t-t_0)}^{k\alpha }}{\mathsf{\Gamma }(1+k\alpha )}},$$

(17)

where $D_t^{k\alpha }\psi \left(t\right)=\underset{ktimes}{\underbrace{D_t^{\alpha }\dots D_t^{\alpha }}}\psi \left(t\right)$ and ${}_{t_0}{I}_t^{k\alpha }\psi \left(t\right)=\underset{ktimes}{\underbrace{{}_{t_0}{I}_t^{\alpha }\dots {}_{t_0}{I}_t^{\alpha }}}\psi \left(t\right)$.

Theorem 6.

Suppose that $\varphi \left(t\right),\psi \left(t\right)\in C_{\alpha }[a,b],$ and $\varphi \left(t\right),\psi \left(t\right)\in D_{\alpha }(a,b).$ Then,

$${}_a{I}_b^{\left(\alpha \right)}\left\{\left[D_t^{\alpha }\varphi \left(t\right)\right]\psi \left(t\right)\right\}={\left[\varphi \left(t\right)\psi \left(t\right)\right]}_a^b-{}_a{I}_b^{\alpha }\left\{\varphi \left(t\right)\left[D_t^{\alpha }\psi \left(t\right)\right]\right\}.$$

(18)

2.2. The Laplace Transform

The derivation of the local fractional Laplace’s transform is obtained using principles from local fractional calculus.

2.2.1. LF Laplace’s Transform

Definition 7.

The LF Laplace transform of a local fractional continuous function, $\psi \left(t\right)$, of order α is defined as

$$\begin{array}{cc}\hfill L_{\alpha }\left\{\psi \left(t\right)\right\}& ={\mathsf{\Psi }}_s^{L,\alpha }\left(s\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{+\infty }{E}_{\alpha }(-s^{\alpha }{t}^{\alpha })\psi \left(t\right){\left(dt\right)}^{\alpha },0<\alpha \le 1,\hfill \end{array}$$

(19)

with $E_{\alpha }\left(t\right)$, the Mittag-Leffler function.

Definition 8.

(Inverse Laplace transform). The inverse local fractional Laplace transform is denoted as

$$\begin{array}{cc}\hfill \psi \left(t\right)& =L_{\alpha }^{-1}\left\{{\mathsf{\Psi }}_s^{L,\alpha }\left(s\right)\right\}\hfill \\ \hfill & ={\displaystyle \frac{1}{{\left(2\pi \right)}^{\alpha }}}{\int }_{\beta -i\infty }^{\beta +i\infty }{E}_{\alpha }\left(s^{\alpha }{t}^{\alpha }\right){\mathsf{\Psi }}_s^{L,\alpha }\left(s\right){\left(ds\right)}^{\alpha },\hfill \end{array}$$

(20)

where $s^{\alpha }={\beta }^{\alpha }+i^{\alpha }{\infty }^{\alpha }$.

A sufficient condition for convergence is presented as follows:

$${\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{\infty }\left|\psi \left(t\right)\right|{\left(dt\right)}^{\alpha }<C<\infty .$$

2.2.2. Properties of LF Laplace’s Transform

Property 1.

Suppose that $f,g\in C_{\alpha }[a,b]$, then

$$L_{\alpha }[f\psi \left(t\right)\pm g\varphi \left(t\right)]=f{L}_{\alpha }\left\{\psi \left(t\right)\right\}\pm g{L}_{\alpha }\left\{\varphi \left(t\right)\right\}.$$

(21)

Property 2.

$$L_{\alpha }\left[1\right]=\frac{1}{s^{\alpha }}.$$

(22)

Property 3.

$$L_{\alpha }\left[{\displaystyle \frac{t^{n\alpha }}{\mathsf{\Gamma }(1+n\alpha )}}\right]={\displaystyle \frac{1}{s^{\alpha (n+1)}}}.$$

(23)

Property 4.

Consider the function $\psi \left(t\right)=E_{\alpha }\left(a^{\alpha }{t}^{\alpha }\right)$. The LF Laplace transform of $\psi \left(t\right)$ is given as

$$L_{\alpha }\left[E_{\alpha }\left(a^{\alpha }{t}^{\alpha }\right)\right]={\displaystyle \frac{1}{s^{\alpha }-a^{\alpha }}}$$

(24)

provided that $s^{\alpha }>a^{\alpha }$.

Theorem 7.

Suppose that $L_{\alpha }\left[\psi \left(t\right)\right]={\mathsf{\Psi }}^{L,\alpha }\left(s\right)$, and ${lim}_{t\to \infty }\psi \left(t\right)=0$, then

$$L_{\alpha }\left[D_t^{\alpha }\psi \left(t\right)\right]=s^{\alpha }{L}_{\alpha }\left[\psi \left(t\right)\right]-\psi \left(0\right).$$

(25)

We note that we also have

$$L_{\alpha }\left[D_t^{n\alpha }\psi \left(t\right)\right]=s^{k\alpha }{L}_{\alpha }\left[\psi \left(t\right)\right]-\sum _{k=1}^n{s}^{(k-1)\alpha }{D}_t^{(n-k)\alpha }\psi \left(0\right).$$

(26)

Definition 9.

The local fractional convolution of two functions, $\varphi \left(t\right)$ and $\psi \left(t\right)$, of order α, is defined as

$$\begin{array}{cc}\hfill {(\varphi \left(t\right)*\psi \left(t\right))}_{\alpha }& ={}_0{I}_{\infty }^{\left(\alpha \right)}\left[\varphi \left(t\right)\psi (\tau -t)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{\infty }\varphi \left(\tau \right)\psi (t-\tau ){\left(d\tau \right)}^{\alpha }.\hfill \end{array}$$

(27)

Theorem 8.

$$L_{\alpha }\left[\varphi \left(t\right)\ast \psi \left(t\right)\right]={\mathsf{\Phi }}^{L,\alpha }\left(s\right){\mathsf{\Psi }}^{L,\alpha }\left(s\right)$$

(28)

or

$$\mathsf{\Phi }\left(t\right)\ast \mathsf{\Psi }\left(t\right)=L_{\alpha }^{-1}\left[{\mathsf{\Phi }}^{L,\alpha }\left(s\right){\mathsf{\Psi }}^{L,\alpha }\left(s\right)\right].$$

(29)

3. The Local Fractional Linear System

3.1. Solution of the Linear System

The linear time-invariant LF non-homogeneous differential system is of the following form

$$D_t^{\alpha }x\left(t\right)=Ax\left(t\right)+f\left(t\right),x\left(0\right)=x_0\in {\mathbb{R}}^n,$$

(30)

where $D_t^{\alpha }$ is the local fractional derivative, with $0<\alpha \le 1$, $t\in I=[0,t_1]$, $A\in {\mathbb{R}}^{n\times n},$ $x\left(t\right)\in {\mathbb{R}}^n$ is the state function of the system, and $f\left(t\right)\in {\mathbb{R}}^m$ is a continuous function, for each $t\in I.$

Theorem 9.

The function

$$x\left(t\right)=E_{\alpha }\left(A{t}^{\alpha }\right)x_0+{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)f\left(\tau \right){\left(d\tau \right)}^{\alpha }$$

(31)

is the solution of (30), with $x\left(0\right)=x_0$.

Proof. 

Applying the LF Laplace transform on both sides of the system (30), we have

$$X^{L,\alpha }\left(s\right)=\frac{1}{I{s}^{\alpha }+A}[x_0-F^{L,\alpha }\left(s\right)].$$

Now, using the inverse LF Laplace transform with some quick calculations, we obtain

$$\begin{array}{cc}\hfill x\left(t\right)& =L_{\alpha }^{-1}\left[\frac{1}{I{s}^{\alpha }+A}[x_0+F^{L,\alpha }\left(s\right)]\right]\hfill \\ \hfill & =L_{\alpha }^{-1}\left[\frac{1}{I{s}^{\alpha }+A}{x}_0\right]+L_{\alpha }^{-1}\left[\frac{1}{I{s}^{\alpha }+A}{F}^{L,\alpha }\left(s\right)\right]\hfill \\ \hfill & =E_{\alpha }\left(A{t}^{\alpha }\right)x_0+{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)f\left(\tau \right){\left(d\tau \right)}^{\alpha }.\hfill \end{array}$$

(32)

□

3.2. Controllability

Now we consider the following local fractional linear time invariant system, obtained by rewriting (30) with a control function

$$D_t^{\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right),x\left(0\right)=x_0\in {\mathbb{R}}^n,$$

(33)

where $A\in {\mathbb{R}}^{m\times n}$, $B\in {\mathbb{R}}^{n\times m}$, $x\left(t\right)\in {\mathbb{R}}^n$ is a state vector and $u\left(t\right)\in {\mathbb{R}}^m$ is a control state.

Let $L^2(I,{\mathbb{R}}^m)$, the space of all square integrable ${\mathbb{R}}^m$ valued functions defined on $I=[0,t_1]$.

Definition 10

([35]). The system (33) is said to be controllable over I if, for every $x_0,x_1\in {\mathbb{R}}^n$, there exists a control, $u\left(t\right)\in L^2(I,{\mathbb{R}}^m)$, such that the solution $x\left(t\right)$ given by (31) satisfies $x\left(0\right)=x_0$ and $x\left(t_1\right)=x_1.$ We say that u steers the system from $x_0$ to $x_1$ during the interval $[0,t_1]$.

We define the control operator  $T_c:L^2(I,{\mathbb{R}}^m)\to {\mathbb{R}}^n$ by

$$T_{c}u:={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)Bu\left(\tau \right){\left(d\tau \right)}^{\alpha }.$$

(34)

It clear that $T_c$ is a bounded linear operator.

Theorem 10.

The system (33) is controllable on I if and only if the operator $T_c$ is onto.

Proof. 

The system (33) is controllable on I if and only if there exists a control, $u\left(t\right)\in L^2(I,{\mathbb{R}}^m)$, such that the solution $x\left(t\right)$ given by (31) satisfies $x\left(0\right)=x_0$ and $x\left(t_1\right)=x_1.$

Set $t=t_1$ in (31), we obtain

$$x_1-E_{\alpha }\left(A{t}_1^{\alpha }\right)x_0={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{t_1}{E}_{\alpha }\left(A{(t_1-\tau )}^{\alpha }\right)Bu\left(\tau \right){\left(d\tau \right)}^{\alpha }=T_c\left(u\right)$$

(35)

Since $x_0$ and $x_1$ are chosen randomly, consequently the system (33) is controllable on I if $T_c$ is onto. □

Now, define the adjoint of $T_c:L^2(J,{\mathbb{R}}^m)\to {\mathbb{R}}^n$ by $T_c^{*}$ from ${\mathbb{R}}^n$ into $L^2(J,{\mathbb{R}}^m)$ and find it as follows.

For $z\in {\mathbb{R}}^n,$ one can obtain

$$\begin{array}{cc}\hfill {〈T_{c}u,z〉}_{{\mathbb{R}}^n}& ={〈{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)Bu\left(\tau \right){\left(d\tau \right)}^{\alpha },z〉}_{{\mathbb{R}}^n}\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{〈E_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)Bu\left(\tau \right),z〉}_{{\mathbb{R}}^n}{\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{〈u\left(\tau \right),B^T{E}_{\alpha }\left(A^T{(t-\tau )}^{\alpha }\right)z〉}_{{\mathbb{R}}^n}{\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & ={\langle u,T_c^{*}z\rangle }_{L^2(J,{\mathbb{R}}^m)}\hfill \end{array}$$

(36)

which gives that

$$\left(T_c^{*}z\right)\left(t\right)=B^T{E}_{\alpha }\left(A^T{(t-\tau )}^{\alpha }\right)z.$$

(37)

Hence, we can express $T_c{T}_c^{*}$ as

$$T_c{T}_c^{*}z=\frac{1}{\mathsf{\Gamma }(1+\alpha )}{\int }_0^t{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)B{B}^{*}{E}_{\alpha }\left(A^{*}{(t-\tau )}^{\alpha }\right)z{\left(d\tau \right)}^{\alpha }.$$

We can see that $T_c{T}_c^{*}:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is a bounded linear operator between two finite dimensional vector spaces. Thus, $T_c{T}_c^{*}$ is an $n\times n$ matrix.

Definition 11.

The matrix $T_c{T}_c^{*}=M_c(0,t)$ is called the  controllability Gramian  of the system (33).

Theorem 11.

The system (33) is said to be controllable on I if and only if the controllability Gramian, $M_c(0,t_1)$, is nonsingular.

Proof. 

Let $M_c(0,t_1)$ be nonsingular. Then, $M_c(0,t_1)$ is an invertible matrix and, for any initial state $x\left(0\right)=x_0$ and arbitrary state $x_1$, one can define a control state, $u\left(t\right)$, as follows:

$$u\left(t\right)=B^T{E}_{\alpha }\left(A^T{(t_1-t)}^{\alpha }\right)M_c^{-1}(0,t)[x_1-x_0{E}_{\alpha }\left(A{t}_1^{\alpha }\right)].$$

(38)

Now, substitute (38) into the solution of (30) with $x\left(0\right)=x_0$ at time $t_1$, and using Fubini’s theorem we obtain

$$\begin{array}{cc}\hfill x\left(t_1\right)& =E_{\alpha }\left(A{t}_1^{\alpha }\right)x_0+{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{t_1}{E}_{\alpha }\left(A{(t_1-\tau )}^{\alpha }\right)Bu\left(\tau \right){\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & =E_{\alpha }\left(A{t}_1^{\alpha }\right)x_0+{\int }_0^{t_1}{E}_{\alpha }\left(A{(t_1-\tau )}^{\alpha }\right)B{B}^T{E}_{\alpha }\left(A^T{(t_1-\tau )}^{\alpha }\right)M_c^{-1}(0,\tau )\times \hfill \\ \hfill & [x_1-x_0{E}_{\alpha }\left(A{t}_1^{\alpha }\right)]{\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & =E_{\alpha }\left(A{t}_1^{\alpha }\right)x_0+M_c(0,t_1)M_c^{-1}(0,t_1)[x_1-x_0{E}_{\alpha }\left(A{t}_1^{\alpha }\right)]=x_1,\hfill \end{array}$$

(39)

which shows that the system (33) is controllable on $I.$

For the second direction of proof, we use proof by contradiction. Suppose that matrix $M_c(0,t)$ is singular and the system (3.6) is controllable on $I.$ Thus, there exists an nonzero vector, $x\in R^n$, so that $x^T{M}_c(0,t)x=0,$ which gives that

$${\int }_0^t{x}^T{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)B{B}^T{E}_{\alpha }\left(A^T{(t-\tau )}^{\alpha }\right)x{\left(d\tau \right)}^{\alpha }=0,$$

and, clearly, for every $0\le \tau \le t,$ we obtain

$$x^T{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)B=0.$$

Since the system (33) is controllable on $I,$ we can select a control state, u, that steers the solution from any initial state to a desired state, $0.$

Now, selecting $x_0=-E_{\alpha }(-A{t}^{\alpha })x$ and placing it in (30) at $t=t_1$, we acquire

$$x={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{t_1}{E}_{\alpha }\left(A{(t_1-\tau )}^{\alpha }\right)Bu\left(\tau \right){\left(d\tau \right)}^{\alpha }.$$

Multiplying x by $x^T$ we obtain:

$$x^{T}x={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{t_1}{x}^T{E}_{\alpha }\left(A{(t_1-\tau )}^{\alpha }\right)Bu\left(\tau \right){\left(d\tau \right)}^{\alpha }=0.$$

Hence, $x=0$, which contradicts the assumption that x is a nonzero vector. Therefore, $M_c(0,t_1)$ is nonsingular. □

Example 1.

Consider the LF control system

$$D_t^{\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right),$$

with

$$x\left(0\right)=\left[\begin{array}{c}{x}_{1,0}\\ x_{2,0}\end{array}\right]\in R^2,A=\left[\begin{array}{ccc}-1& & -1\\ 0& & -2\end{array}\right],B=\left[\begin{array}{c}0\\ 1\end{array}\right].$$

We want to compute the controllability Gramian matrix to check its invertibility. This requires the computation of $E_{\alpha }\left(A{(t-\tau )}^{\alpha }\right).$

$$\begin{array}{cc}\hfill {(s^{\alpha }I-A)}^{-1}& ={\left[\begin{array}{ccc}{s}^{\alpha }+1& & 1\\ 0& & s^{\alpha }+2\end{array}\right]}^{-1}=\left[\begin{array}{ccc}{\displaystyle \frac{1}{s^{\alpha }+1}}& & {\displaystyle \frac{1}{(s^{\alpha }+1)(s^{\alpha }+2)}}\\ 0& & {\displaystyle \frac{1}{s^{\alpha }+2}}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{ccc}{\displaystyle \frac{1}{s^{\alpha }+1}}& & {\displaystyle \frac{1}{s^{\alpha }+1}}-{\displaystyle \frac{1}{s^{\alpha }+2}}\\ 0& & {\displaystyle \frac{1}{s^{\alpha }+2}}\end{array}\right]\hfill \\ \hfill E_{\alpha }\left(A{t}^{\alpha }\right)=& L^{-1}\left({\displaystyle \frac{1}{s^{\alpha }I-A}}\right)=\left[\begin{array}{ccc}{E}_{\alpha }(-t^{\alpha })& & E_{\alpha }(-t^{\alpha })-E_{\alpha }(-2t^{\alpha })\\ 0& & E_{\alpha }(-2t^{\alpha })\end{array}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill M_c(0,t)& =\frac{1}{\mathsf{\Gamma }(1+\alpha )}{\int }_0^t{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)B{B}^T{E}_{\alpha }\left(A^T{(t-\tau )}^{\alpha }\right){\left(d\tau \right)}^{\alpha }\hfill \\ \hfill =& \frac{1}{\mathsf{\Gamma }(1+\alpha )}{\int }_0^t\left[\begin{array}{ccc}{E}_{\alpha }(-{(t-\tau )}^{\alpha })& & E_{\alpha }(-{(t-\tau )}^{\alpha })-E_{\alpha }(-2{(t-\tau )}^{\alpha })\\ 0& & E_{\alpha }(-2{(t-\tau )}^{\alpha })\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]\left[\begin{array}{ccc}0& & 1\end{array}\right]\hfill \\ \hfill & \times \left[\begin{array}{ccc}{E}_{\alpha }(-{(t-\tau )}^{\alpha })& & 0\\ E_{\alpha }(-{(t-\tau )}^{\alpha })-E_{\alpha }(-2{(t-\tau )}^{\alpha })& & E_{\alpha }(-2{(t-\tau )}^{\alpha })\end{array}\right]{\left(d\tau \right)}^{\alpha }\hfill \\ \hfill =& \frac{1}{\mathsf{\Gamma }(1+\alpha )}{\int }_0^t\left[\begin{array}{ccc}{E}_{\alpha }(-2{(t-\tau )}^{\alpha })+E_{\alpha }(-4{(t-\tau )}^{\alpha })-2E_{\alpha }(-3{(t-\tau )}^{\alpha })& & E_{\alpha }(-3{(t-\tau )}^{\alpha })-E_{\alpha }(-4{(t-\tau )}^{\alpha })\\ E_{\alpha }(-3{(t-\tau )}^{\alpha })-E_{\alpha }(-4{(t-\tau )}^{\alpha })& & E_{\alpha }(-4{(t-\tau )}^{\alpha })\end{array}\right]{\left(d\tau \right)}^{\alpha }\hfill \\ \hfill =& \left[\begin{array}{ccc}\frac{1}{2}(1-E_{\alpha }(-2t^{\alpha }))+\frac{1}{4}(1-E_{\alpha }(-4t^{\alpha }))-\frac{2}{3}(1-E_{\alpha }(-3t^{\alpha }))& & \frac{1}{3}(1-E_{\alpha }(-3t^{\alpha }))-\frac{1}{4}(1-E_{\alpha }(-4t^{\alpha }))\\ \\ \frac{1}{3}(1-E_{\alpha }(-3t^{\alpha }))-\frac{1}{4}(1-E_{\alpha }(-4t^{\alpha }))& & \frac{1}{4}(1-E_{\alpha }(-4t^{\alpha }))\end{array}\right].\hfill \end{array}$$

We now compute the determinant of the obtained controllability Gramian matrix. $det\left(M_c(0,t)\right)\ne 0,$ hence the system is controllable.

Theorem 12

(Kalman’s Rank Condition). Let

$$K=\left[\begin{array}{ccccc}B& AB& A^{2}B& \cdots & A^{n-1}B\end{array}\right].$$

(40)

Then, the system (33) is controllable on I if and only if rank(K) $=n$.

Proof. 

Let the system (33) be controllable on $I.$ Then, $Range\left(T_c\right)={\mathbb{R}}^n.$ That means, for any $x\in R^n,$ we can find $u\in L^2(I,{\mathbb{R}}^m)\to {\mathbb{R}}^n$, such that

$$x={\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)Bu\left(\tau \right){\left(d\tau \right)}^{\alpha }.$$

(41)

Using the definition of the Mittag function, we obtain this following equality

$$E_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(A(t-\tau )\right)}^{k\alpha }}{\mathsf{\Gamma }(1+k\alpha )}}=\sum _{k=0}^{\infty }{\displaystyle \frac{\left(A^k{(t-\tau )}^{\alpha }\right)}{\mathsf{\Gamma }(1+k\alpha )}}.$$

(42)

Applying Cayley Hamilton Theorem on the matrix, we can express $E_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)$ as

$$E_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)=q_0(t-\tau )I+q_1(t-\tau )A+\cdots +q_{n-1}(t-\tau )A^{n-1},$$

where $q_{i^{\prime }s}$ are polynomials of $t-\tau$ for every $1\le i\le n-1.$ By using this expression we can rewrite x as

$$x=\left[\begin{array}{ccccc}B& AB& A^{2}B& \cdots & A^{n-1}B\end{array}\right]\left[\begin{array}{c}{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{p}_0(t-\tau )u\left(\tau \right){\left(d\tau \right)}^{\alpha }\\ {\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{p}_1(t-\tau )u\left(\tau \right){\left(d\tau \right)}^{\alpha }\\ ⋮\\ {\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t{p}_{n-1}(t-\tau )u\left(\tau \right){\left(d\tau \right)}^{\alpha }\end{array}\right]$$

(43)

which proves that x is an element of the range of $K.$ As x is arbitrarily selected, the range $T_c$ is a subset of the range of $K.$ Therefore Rank(K) = n.

Conversely, use proof by contradiction. Assume that rank(K) = n and the system (3.6) is not controllable. So, $M_c(0,t)$ is singular. Thus, there exists a nonzero vector, $x\in R^n$, so that $x^T{M}_c(0,t)x=0,$ which gives that

$${\int }_0^t{x}^T{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)B{B}^T{E}_{\alpha }\left(A^T{(t-\tau )}^{\alpha }\right)x{\left(d\tau \right)}^{\alpha }=0,$$

and, clearly, for every $0\le \tau \le t,$ we obtain

$$x^T{E}_{\alpha }\left(A{(t-\tau )}^{\alpha }\right)B=0.$$

For $k=0,1,\dots ,n-1,$ carrying out the local fractional derivative k– times with respect to $\tau ,$ and setting $\tau =t,$ we acquire $x^{T}AB=x^T{A}^{2}B=x^T{A}^{3}B=\cdots =x^T{A}^{n-1}B=0$, which implies that [Range K] ${}^{\perp }\ne \left\{0\right\}.$ Therefore, Range K $\ne {\mathbb{R}}^n,$ and Rank K≠n, which contradicts the assumption. Hence, the system (33) is controllable on $I.$ □

Example 2.

Consider the LF control system

$$D_t^{\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right)$$

(44)

with

$$x\left(0\right)=\left[\begin{array}{c}{x}_{1,0}\\ x_{2,0}\end{array}\right]\in R^2,A=\left[\begin{array}{ccc}-1& & 0\\ 1& & -2\end{array}\right],B=\left[\begin{array}{c}1\\ 0\end{array}\right].$$

By simple computation, we have

$$\begin{array}{cc}\hfill K& =\left[\begin{array}{ccc}B& & AB\end{array}\right]=\left[\begin{array}{c}\left[\begin{array}{c}1\\ 0\end{array}\right]\left[\begin{array}{ccc}1& & -1\\ 0& & 1\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]\end{array}\right]=\left[\begin{array}{ccc}1& & -1\\ 0& & 1\end{array}\right].\hfill \end{array}$$

Then Rank(K) $=2$, and the system (44) is controllable.

Example 3.

Consider the following LF control system

$$D_t^{\alpha }x\left(t\right)=\left[\begin{array}{ccccc}-1& & 1& & 1\\ 5& & -3& & 1\\ 7& & -2& & -1\end{array}\right]x\left(t\right)+\left[\begin{array}{ccc}1& & 0\\ 0& & 1\\ 1& & 0\end{array}\right]u\left(t\right)$$

(45)

with

$$x\left(0\right)=\left[\begin{array}{c}{x}_{1,0}\\ x_{2,0}\\ x_{3,0}\end{array}\right]\in R^3$$

Using the Kalman controllability rank condition, we obtain the controllability matrix, K

$$\begin{array}{cc}\hfill AB& =\left[\begin{array}{ccccc}-1& & 1& & 1\\ 5& & -3& & 1\\ 7& & -2& & -1\end{array}\right]\left[\begin{array}{ccc}1& & 0\\ 0& & 1\\ 1& & 0\end{array}\right]=\left[\begin{array}{ccc}0& & 1\\ 6& & -3\\ 6& & -2\end{array}\right]\hfill \\ \\ \hfill A^{2}B& =\left[\begin{array}{ccc}0& & 1\\ 6& & -3\\ 6& & -2\end{array}\right]\left[\begin{array}{ccc}1& & 0\\ 0& & 1\\ 1& & 0\end{array}\right]=\left[\begin{array}{ccc}12& & -6\\ -12& & 12\\ -18& & 15\end{array}\right]\hfill \end{array}$$

$$K=\left[\begin{array}{ccccc}B& & AB& & A^{2}B\end{array}\right]=\left[\begin{array}{cccccc}1& 0& 0& 1& 12& -6\\ 0& 1& 6& -3& -12& 12\\ 1& 0& 6& -2& -18& 15\end{array}\right].$$

Evidently, Rank $\left(K\right)$ = 3 and hence the system (45) is controllable.

4. Linear Systems with Distinct Local Fractional Orders

Consider the following fractional linear system with two distinct orders:

$$\left[\begin{array}{c}{D}_t^{\alpha }{x}_1\left(t\right)\\ D_t^{2\alpha }{x}_2\left(t\right)\end{array}\right]=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]u\left(t\right)$$

(46)

with initial condition

$$x\left(0\right)=\left[\begin{array}{c}{x}_{1,0}\\ x_{2,0}\end{array}\right]\in R^n$$

where $D_t^{\alpha }$, $D_t^{2\alpha }$ are local fractional derivatives, $0<\alpha <1;$   $x_1\left(t\right)\in R^{n_1}$ and $x_2\left(t\right)\in R^{n_2}$ are the state vectors; $A_{ij}\in R^{n_i\times n_j}$ and $B_i\in R^{n_i\times m}$, $i,j=1,2,$ are matrices with real entries; $n_1+n_2=n$; and $u\left(t\right)\in R^m$ is the control vector.

4.1. Solution of the Linear System

Theorem 13.

The solution of system (46) can be presented as

$$\begin{array}{cc}\hfill x\left(t\right)& ={\mathsf{\Phi }}_1\left(t\right)x_0+{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t[{\mathsf{\Phi }}_1(t-\tau )B_{01}+{\mathsf{\Phi }}_2(t-\tau )B_{02}]u\left(\tau \right){\left(d\tau \right)}^{\alpha }\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & ={\mathsf{\Phi }}_1\left(t\right)x_0+{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t\mathsf{\Phi }(t-\tau )Bu\left(\tau \right){\left(d\tau \right)}^{\alpha }\hfill \end{array}$$

(48)

where

$$\mathsf{\Phi }(t-\tau )=\left[\begin{array}{c}{\mathsf{\Phi }}_1(t-\tau ){\mathsf{\Phi }}_2(t-\tau )\end{array}\right],$$

$$x\left(t\right)=\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right],x_0=\left[\begin{array}{c}{x}_{10}\\ x_{20}\end{array}\right],B=\left[\begin{array}{c}{B}_{01}\\ B_{02}\end{array}\right]$$

$$B_{01}=\left[\begin{array}{c}{B}_1\\ 0\end{array}\right],B_{02}=\left[\begin{array}{c}0\\ B_2\end{array}\right].$$

$$T_{kl}=\left\{\begin{array}{cc}{I}_n,\hfill & \mathrm{for}k=l=0\hfill \\ \left[\begin{array}{cc}{A}_{11}& A_{12}\\ 0& 0\end{array}\right],\hfill & \mathrm{for}k=1,l=0\hfill \\ \left[\begin{array}{cc}0& 0\\ A_{21}& A_{22}\end{array}\right],\hfill & \mathrm{for}k=0,l=1\hfill \\ T_{10}{T}_{k-1,l}+T_{01}{T}_{k,1-l},\hfill & \mathrm{for}k+l>0\hfill \end{array}\right.$$

(49)

$${\mathsf{\Phi }}_1\left(t\right)=\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}{\displaystyle \frac{t^{(2l+k)\alpha }}{\mathsf{\Gamma }(1+(2l+k\left)\alpha \right)}}$$

(50)

$${\mathsf{\Phi }}_2\left(t\right)=\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}{\displaystyle \frac{t^{(k+2l+1)\alpha }}{\mathsf{\Gamma }(1+(k+2l+1)\alpha )}}.$$

(51)

Proof. 

Applying the LF Laplace transform on both sides of (46), we acquire

$$\left[\begin{array}{c}{s}^{\alpha }{X}_1\left(s\right)\\ s^{2\alpha }{X}_2\left(s\right)\end{array}\right]=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{X}_1\left(s\right)\\ X_2\left(s\right)\end{array}\right]+\left[\begin{array}{c}{x}_{10}\\ s^{\alpha }{x}_{20}\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]U\left(s\right).$$

(52)

Since, by (26), we have

$$\begin{array}{cc}\hfill L_{\alpha }\left[D_t^{\alpha }{x}_1\left(t\right)\right]& =s^{\alpha }{X}_1\left(s\right)-x_{10}\hfill \\ \hfill L_{\alpha }\left[D_t^{2\alpha }{x}_2\left(t\right)\right]& =s^{2\alpha }{X}_2\left(s\right)-s^{\alpha }{x}_{20}\hfill \end{array}$$

where $X_i\left(s\right)=L_{\alpha }\left[x_i\left(t\right)\right]$ for $i=1,2$ and $U\left(s\right)=L_{\alpha }\left[u\left(t\right)\right].$

Then,

$$\left[\begin{array}{cc}{I}_{n_1}{s}^{\alpha }& 0\\ 0& I_{n_2}{s}^{2\alpha }\end{array}\right]\left[\begin{array}{c}{X}_1\left(s\right)\\ X_2\left(s\right)\end{array}\right]-\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{X}_1\left(s\right)\\ X_2\left(s\right)\end{array}\right]=\left[\begin{array}{c}{x}_{10}\\ s^{\alpha }{x}_{20}\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]U\left(s\right)$$

(53)

$$\left[\begin{array}{c}{X}_1\left(s\right)\\ X_2\left(s\right)\end{array}\right]={\left[\begin{array}{cc}{I}_{n_1}{s}^{\alpha }-A_{11}& -A_{12}\\ -A_{21}& I_{n_2}{s}^{2\alpha }-A_{22}\end{array}\right]}^{-1}\left\{\left[\begin{array}{c}{x}_{10}\\ s^{\alpha }{x}_{20}\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]U\left(s\right)\right\}.$$

(54)

We can prove by (49) that,

$$\left[\begin{array}{cc}{I}_{n_1}{s}^{\alpha }-A_{11}& -A_{12}\\ -A_{21}& I_{n_2}{s}^{2\alpha }-A_{22}\end{array}\right]\left[\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}{s}^{-\alpha (k+2l)}\right]=\left[\begin{array}{cc}{I}_{n_1}& 0\\ 0& I_{n_2}\end{array}\right]$$

(55)

where the matrices $T_{kl}$ are as given in (49).

By (55), we obtain

$$\begin{array}{cc}\hfill & {\left[\begin{array}{cc}{I}_{n_1}{s}^{\alpha }-A_{11}& -A_{12}\\ -A_{21}& I_{n_2}{s}^{2\alpha }-A_{22}\end{array}\right]}^{-1}\hfill \\ \hfill & ={\left\{\left[\begin{array}{cc}{I}_{n_1}{s}^{\alpha }& 0\\ 0& I_{n_2}{s}^{2\alpha }\end{array}\right]\left[\begin{array}{cc}{I}_{n_1}-A_{11}{s}^{-\alpha }& -A_{12}{s}^{-\alpha }\\ -A_{21}{s}^{-2\alpha }& I_{n_2}-A_{22}{s}^{-2\alpha }\end{array}\right]\right\}}^{-1}\hfill \\ \hfill & ={\left[\begin{array}{cc}{I}_{n_1}-A_{11}{s}^{-\alpha }& -A_{12}{s}^{-\alpha }\\ -A_{21}{s}^{-2\alpha }& I_{n_2}-A_{22}{s}^{-2\alpha }\end{array}\right]}^{-1}\left[\begin{array}{cc}{I}_{n_1}{s}^{-\alpha }& 0\\ 0& I_{n_2}{s}^{-2\alpha }\end{array}\right]\hfill \\ \hfill & =\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}{s}^{-\alpha (k+2l)}\left[\begin{array}{cc}{I}_{n_1}{s}^{-\alpha }& 0\\ 0& I_{n_2}{s}^{-2\alpha }\end{array}\right].\hfill \end{array}$$

(56)

Substituting (56) into (54) gives

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{X}_1\left(s\right)\\ X_2\left(s\right)\end{array}\right]& =\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}{s}^{-\alpha (k+2l)}\left[\begin{array}{cc}{I}_{n_1}{s}^{-\alpha }& 0\\ 0& I_{n_2}{s}^{-2\alpha }\end{array}\right]\left\{\left[\begin{array}{c}{x}_{10}\\ s^{\alpha }{x}_{20}\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]U\left(s\right)\right\}\hfill \\ \hfill & =\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}\left[x_0{s}^{-\alpha (k+2l+1)}+\left(B_{01}{s}^{-\alpha (k+2l+1)}+B_{02}{s}^{-\alpha (k+2l+2)}\right)U\left(s\right)\right].\hfill \end{array}$$

(57)

Using the inverse of the LF Laplace transform and the convolution Theorem 8, we obtain

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]& =L_{\alpha }^{-1}\left[\begin{array}{c}{X}_1\left(s\right)\\ X_2\left(s\right)\end{array}\right]\hfill \\ \hfill & =\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}{L}_{\alpha }^{-1}[x_0{s}^{-\alpha (k+2l+1)}+\hfill \\ \hfill & +\left(B_{01}{s}^{-\alpha (k+2l+1)}+B_{02}{s}^{-\alpha (k+2l+2)}\right)U\left(s\right)]\hfill \\ \hfill & =\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}[L_{\alpha }^{-1}\left\{{\displaystyle \frac{1}{s^{\alpha (k+2l+1)}}}\right\}{x}_0\hfill \\ \hfill & +B_{01}{L}_{\alpha }^{-1}\left\{{\displaystyle \frac{1}{s^{\alpha (k+2l+1)}}}\right\}\ast L_{\alpha }^{-1}\left\{U\left(s\right)\right\}+B_{02}{L}_{\alpha }^{-1}\left\{{\displaystyle \frac{1}{s^{\alpha (k+2l+2)}}}\right\}\ast L_{\alpha }^{-1}\left\{U\left(s\right)\right\}].\hfill \end{array}$$

(58)

Therefore, due to property (3), we obtain the desired solution

$$\begin{array}{c}\hfill \left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]={\mathsf{\Phi }}_1\left(t\right)x_0+{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^t[{\mathsf{\Phi }}_1(t-\tau )B_{01}+{\mathsf{\Phi }}_2(t-\tau )B_{02}]u\left(\tau \right){\left(d\tau \right)}^{\alpha }.\end{array}$$

(59)

□

4.2. Controllability

In this section, we derive the sufficient and necessary conditions of controllability for the local fractional linear system (46) with two distinct orders.

Theorem 14.

The system (46) is controllable on $[0,t_1]$ if the controllability matrix

$$M_c(0,t_1)={\int }_0^{t_1}\mathsf{\Phi }(t_1-\tau )B{B}^T{\mathsf{\Phi }}^T(t_1-\tau ){\left(d\tau \right)}^{\alpha }$$

(60)

is nonsingular.

Proof. 

Assume that the matrix $M_c(0,t_1)$ is nonsingular. Hence, $M_c(0,t_1)$ is invertible. For a given initial state $x\left(0\right)=x_0$, define the control, u, as

$$u\left(t\right)=\mathsf{\Gamma }(1+\alpha )B^T{\mathsf{\Phi }}^T(t_1-t)\times M_c^{-1}(0,t_1)[x_1-x_0{\mathsf{\Phi }}_1\left(t_1\right)].$$

(61)

It follows from the solution of system (46) with initial condition $x\left(0\right)=x_0$ that

$$x\left(t_1\right)={\mathsf{\Phi }}_1\left(t_1\right)x_0+{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{t_1}[{\mathsf{\Phi }}_1(t_1-\tau )B_{01}+{\mathsf{\Phi }}_2(t_1-\tau )B_{02}]u\left(\tau \right){\left(d\tau \right)}^{\alpha }.$$

(62)

From (61) we have,

$$\begin{array}{cc}\hfill x\left(t_1\right)& ={\mathsf{\Phi }}_1\left(t_1\right)x_0+{\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_0^{t_1}\mathsf{\Phi }(t_1-\tau )Bu\left(\tau \right){\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & =x_0{\mathsf{\Phi }}_1\left(t_1\right)+{\int }_0^{t_1}\mathsf{\Phi }(t_1-\tau )B{B}^T{\mathsf{\Phi }}^T(t_1-\tau )\hfill \\ \hfill & \times M_c^{-1}(0,t_1)[x_1-x_0{\mathsf{\Phi }}_1\left(t_1\right)]{\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & =x_0{\mathsf{\Phi }}_1\left(t_1\right)+M_c(0,t_1)M_c^{-1}(0,t_1)[x_1-x_0{\mathsf{\Phi }}_1\left(t_1\right)]\hfill \\ \hfill & =x_1.\hfill \end{array}$$

Therefore, the system (46) is controllable. □

Example 4.

Consider the following LF control system involving two distinct orders

$$\left[\begin{array}{c}{D}_t^{\alpha }{x}_1\left(t\right)\\ D_t^{2\alpha }{x}_2\left(t\right)\end{array}\right]=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]u\left(t\right)$$

(63)

where

$$A_{11}=\left[\begin{array}{ccc}1& & 0\\ 0& & -1\end{array}\right],A_{12}=\left[\begin{array}{c}0\\ 0\end{array}\right],A_{21}=A_{12}^T,A_{22}=\left[\begin{array}{c}1\end{array}\right]B_1=\left[\begin{array}{c}1\\ 1\end{array}\right]B_2=\left[\begin{array}{c}1\end{array}\right].$$

(64)

To test the controllability of this system over $[0,t_1],$ we need to compute the controllability Gramian matrix $M_c(0,t_1)$. Through simple calculations, $T_{kl}$ is reduced to the following form

$$T_{kl}=\left\{\begin{array}{cc}{I}_n,\hfill & \mathit{for}k=l=0,\hfill \\ T_{10}^k\hfill & \mathit{for}l=0,k=1,2,\cdots ,\hfill \\ T_{01}^l,\hfill & \mathit{for}k=0,l=1,2,\cdots ,\hfill \\ 0_n,\hfill & \mathit{others},\hfill \end{array}\right.$$

(65)

with

$$T_{10}=\left[\begin{array}{ccc}{A}_{11}& & 0\\ 0& & 0\end{array}\right],T_{01}=\left[\begin{array}{ccc}0& & 0\\ 0& & A_{22}\end{array}\right].$$

Now, we can calculate ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$:

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_1\left(t\right)& =\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}{\displaystyle \frac{t^{(2l+k)\alpha }}{\mathsf{\Gamma }(1+(2l+k\left)\alpha \right)}}\hfill \\ \hfill & =T_{00}+T_{01}{\displaystyle \frac{t^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}+T_{02}{\displaystyle \frac{t^{4\alpha }}{\mathsf{\Gamma }(1+4\alpha )}}+\cdots \hfill \\ \hfill & +T_{10}{\displaystyle \frac{t^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}+T_{11}{\displaystyle \frac{t^{3\alpha }}{\mathsf{\Gamma }(1+3\alpha )}}+T_{12}{\displaystyle \frac{t^{5\alpha }}{\mathsf{\Gamma }(1+5\alpha )}}+\cdots \hfill \\ \hfill & +T_{20}{\displaystyle \frac{t^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}+T_{21}{\displaystyle \frac{t^{4\alpha }}{\mathsf{\Gamma }(1+4\alpha )}}+T_{22}{\displaystyle \frac{6\alpha }{\mathsf{\Gamma }(1+6\alpha )}}+\cdots \hfill \\ \hfill & +\cdots \hfill \\ \hfill & =\left[\begin{array}{ccc}{I}_{n_1}& & 0\\ 0& & I_{n_2}\end{array}\right]+{\displaystyle \frac{t^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}\left[\begin{array}{ccc}0& & 0\\ 0& & A_{22}\end{array}\right]+{\displaystyle \frac{t^{4\alpha }}{\mathsf{\Gamma }(1+4\alpha )}}{\left[\begin{array}{ccc}0& & 0\\ 0& & A_{22}\end{array}\right]}^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +{\displaystyle \frac{t^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}\left[\begin{array}{ccc}{A}_{11}& & 0\\ 0& & 0\end{array}\right]+{\displaystyle \frac{t^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}{\left[\begin{array}{ccc}{A}_{11}& & 0\\ 0& & 0\end{array}\right]}^2+\cdots \hfill \\ \hfill & =\left[\begin{array}{ccc}\sum _{k=0}^{\infty }{\displaystyle \frac{t^{k\alpha }}{\mathsf{\Gamma }(1+k\alpha )}}{A}_{11}^k& & 0\\ 0& & \sum _{l=0}^{\infty }{\displaystyle \frac{t^{2l\alpha }}{\mathsf{\Gamma }(1+2l\alpha )}}{A}_{22}^l\end{array}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_2\left(t\right)& =\sum _{k=0}^{\infty }\sum _{l=0}^{\infty }{T}_{kl}{\displaystyle \frac{t^{(k+2l+1)\alpha }}{\mathsf{\Gamma }(1+(k+2l+1)\alpha )}}\hfill \\ \hfill & =T_{00}{\displaystyle \frac{t^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}+T_{01}{\displaystyle \frac{t^{3\alpha }}{\mathsf{\Gamma }(1+3\alpha )}}+T_{02}{\displaystyle \frac{t^{5\alpha }}{\mathsf{\Gamma }(1+5\alpha )}}+\cdots \hfill \\ \hfill & +T_{10}{\displaystyle \frac{t^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}+T_{11}{\displaystyle \frac{t^{4\alpha }}{\mathsf{\Gamma }(1+4\alpha )}}+T_{12}{\displaystyle \frac{t^{6\alpha }}{\mathsf{\Gamma }(1+6\alpha )}}+\cdots \hfill \\ \hfill & +T_{20}{\displaystyle \frac{t^{3\alpha }}{\mathsf{\Gamma }(1+3\alpha )}}+T_{21}{\displaystyle \frac{t^{5\alpha }}{\mathsf{\Gamma }(1+5\alpha )}}+T_{22}{\displaystyle \frac{t^{7\alpha }}{\mathsf{\Gamma }(1+7\alpha )}}+\cdots \hfill \\ \hfill & +\cdots \hfill \\ \hfill & ={\displaystyle \frac{t^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}\left[\begin{array}{ccc}{I}_{n_1}& & 0\\ 0& & I_{n_2}\end{array}\right]+{\displaystyle \frac{t^{3\alpha }}{\mathsf{\Gamma }(1+3\alpha )}}\left[\begin{array}{ccc}0& & 0\\ 0& & A_{22}\end{array}\right]+{\displaystyle \frac{t^{5\alpha }}{\mathsf{\Gamma }(1+5\alpha )}}{\left[\begin{array}{ccc}0& & 0\\ 0& & A_{22}\end{array}\right]}^2\hfill \\ \hfill & +{\displaystyle \frac{t^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}\left[\begin{array}{ccc}{A}_{11}& & 0\\ 0& & 0\end{array}\right]+{\displaystyle \frac{t^{3\alpha }}{\mathsf{\Gamma }(1+3\alpha )}}{\left[\begin{array}{ccc}{A}_{11}& & 0\\ 0& & 0\end{array}\right]}^2+\cdots \hfill \\ \hfill & =\left[\begin{array}{ccc}\sum _{k=0}^{\infty }{\displaystyle \frac{t^{(k+1)\alpha }}{\mathsf{\Gamma }(1+(k+1\left)\alpha \right)}}{A}_{11}^k& & 0\\ 0& & \sum _{l=0}^{\infty }{\displaystyle \frac{t^{(2l+1)\alpha }}{\mathsf{\Gamma }(1+(2l+1\left)\alpha \right)}}{A}_{22}^l\end{array}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \mathsf{\Phi }(t_1-\tau )B{B}^T{\mathsf{\Phi }}^T(t_1-\tau )\hfill \\ \hfill & =[{\mathsf{\Phi }}_1(t_1-\tau )B_{10}+{\mathsf{\Phi }}_2(t_1-\tau )B_{01}]B^T{\mathsf{\Phi }}^T(t_1-\tau )\hfill \\ \hfill & =\left[\begin{array}{c}\sum _{k=0}^{\infty }{\displaystyle \frac{{(t_1-\tau )}^{k\alpha }}{\mathsf{\Gamma }(1+k\alpha )}}{A}_{11}^k{B}_1\\ \sum _{l=0}^{\infty }{\displaystyle \frac{{(t_1-\tau )}^{(2l+1)\alpha }}{\mathsf{\Gamma }(1+(2l+1\left)\alpha \right)}}{A}_{22}^l{B}_2\end{array}\right]{\left[\begin{array}{c}\sum _{k=0}^{\infty }{\displaystyle \frac{{(t_1-\tau )}^{k\alpha }}{\mathsf{\Gamma }(1+k\alpha )}}{A}_{11}^k{B}_1\\ \sum _{l=0}^{\infty }{\displaystyle \frac{{(t_1-\tau )}^{(2l+1)\alpha }}{\mathsf{\Gamma }(1+(2l+1\left)\alpha \right)}}{A}_{22}^l{B}_2\end{array}\right]}^T\hfill \\ \hfill & =\left[\begin{array}{c}{E}_{\alpha }\left(A_{11}{(t_1-\tau )}^{\alpha }\right)B_1\\ {sinh}_{\alpha }\left(A_{22}{(t_1-\tau )}^{\alpha }\right)B_2\end{array}\right]{\left[\begin{array}{c}{E}_{\alpha }\left(A_{11}{(t_1-\tau )}^{\alpha }\right)B_1\\ {sinh}_{\alpha }\left(A_{22}{(t_1-\tau )}^{\alpha }\right)B_2\end{array}\right]}^T\hfill \\ \hfill & =\left[\begin{array}{c}{E}_{\alpha }\left(A_{11}{(t_1-\tau )}^{\alpha }\right)B_1\\ {sinh}_{\alpha }\left(A_{22}{(t_1-\tau )}^{\alpha }\right)B_2\end{array}\right]\left[\begin{array}{ccc}{\left(E_{\alpha }\left(A_{11}{(t_1-\tau )}^{\alpha }\right)B_1\right)}^T& & {\left({sinh}_{\alpha }\left(A_{22}{(t_1-\tau )}^{\alpha }\right)B_2\right)}^T\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{ccc}{E}_{\alpha }\left(A_{11}{(t_1-\tau )}^{\alpha }\right)B_1{\left(E_{\alpha }\left(A_{11}{(t_1-\tau )}^{\alpha }\right)B_1\right)}^T& & E_{\alpha }\left(A_{11}{(t_1-\tau )}^{\alpha }\right)B_1{B}_2^T{sinh}_{\alpha }\left({(t_1-\tau )}^{\alpha }\right)\\ {sinh}_{\alpha }\left({(t_1-\tau )}^{\alpha }\right)B_2{\left(E_{\alpha }\left(A_{11}{(t_1-\tau )}^{\alpha }\right)B_1\right)}^T& & {sinh}_{\alpha }\left({(t_1-\tau )}^{\alpha }\right)B_2{B}_2^T{sinh}_{\alpha }\left({(t_1-\tau )}^{\alpha }\right)\end{array}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\left[\begin{array}{ccccc}{E}_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)& & 1& & \frac{E_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)-1}{2}\\ 1& & E_{\alpha }(-2{(t_1-\tau )}^{\alpha })& & \frac{1-E_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)}{2}\\ \frac{E_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)-1}{2}& & \frac{1-E_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)}{2}& & {\left({sinh}_{\alpha }\left({(t_1-\tau )}^{\alpha }\right)\right)}^2\end{array}\right]\hfill \end{array}$$

The controllability Gramian matrix becomes

$$\begin{array}{cc}\hfill & M_c(0,t_1)\hfill \\ \hfill & ={\int }_0^{t_1}\mathsf{\Phi }(t_1-\tau )B{B}^T{\mathsf{\Phi }}^T(t_1-\tau ){\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & ={\int }_0^{t_1}\left[\begin{array}{ccccc}{E}_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)& & 1& & \frac{E_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)-1}{2}\\ 1& & E_{\alpha }(-2{(t_1-\tau )}^{\alpha })& & \frac{1-E_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)}{2}\\ \frac{E_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)-1}{2}& & \frac{1-E_{\alpha }\left(2{(t_1-\tau )}^{\alpha }\right)}{2}& & {\left({sinh}_{\alpha }\left({(t_1-\tau )}^{\alpha }\right)\right)}^2\end{array}\right]{\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & =\left[\begin{array}{ccccc}\frac{1-E_{\alpha }\left(2{\left(t_1\right)}^{\alpha }\right)}{2}& & \frac{t_1^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}& & \frac{1-E_{\alpha }\left(2{\left(t_1\right)}^{\alpha }\right)}{4}-\frac{t_1^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}\\ \frac{t_1^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}& & \frac{-1+E_{\alpha }(-2{\left(t_1\right)}^{\alpha })}{2}& & \frac{-1+E_{\alpha }\left(2{\left(t_1\right)}^{\alpha }\right)}{4}+\frac{t_1^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}\\ \frac{1-E_{\alpha }\left(2{\left(t_1\right)}^{\alpha }\right)}{4}-\frac{t_1^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}& & \frac{-1+E_{\alpha }\left(2{\left(t_1\right)}^{\alpha }\right)}{4}+\frac{t_1^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}& & {\displaystyle \frac{-t_1^{\alpha }}{2\mathsf{\Gamma }(1+\alpha )}}+{\displaystyle \frac{E_{\alpha }\left(2t_1^{\alpha }\right)-E_{\alpha }(-2t_1^{\alpha })}{8}}\end{array}\right]\hfill \end{array}$$

Computing the determinant of the obtained controllability matrix, we obtain that $det(M_c(0,t_1)\ne 0$, so it is invertible and hence the system (4) is controllable on $[0,t_1].$

5. Application

Let us examine linear electrical circuits that are comprised of resistors, capacitors, inductors, and voltage sources [36]. The voltages across the capacitors and the currents flowing through the inductors are typically selected to represent the state variables of the system.

Let $i_C\left(t\right)$ represent the current in a capacitor with capacitance $C,$ where $i_C\left(t\right)$ is defined as the fractional derivative of the charge, $q\left(t\right)$, stored in the capacitor over time. So,

$$i_C\left(t\right)=D_t^{\alpha }q\left(t\right),$$

(66)

where $0<\alpha <1$, and $D_t^{\alpha }$ is the local fractional derivative defined in Definition (3). Taking $q\left(t\right)=C{u}_C\left(t\right)$, we obtain

$$i_C\left(t\right)=C{D}_t^{\alpha }{u}_C\left(t\right)$$

(67)

where $u_C$ is the voltage on the condensator. In a similar manner, let $u_L\left(t\right)$ denote the voltage across an inductor with inductance $L,$ where $u_L\left(t\right)$ is defined as the double $\alpha$ th-order derivative of the magnetic flux, $\mathsf{\Psi }\left(t\right)$, linking the inductor over time.

$$u_L\left(t\right)=D_t^{2\alpha }\mathsf{\Psi }\left(t\right).$$

(68)

Knowing that $\mathsf{\Psi }\left(t\right)=L{i}_L\left(t\right),$ we have

$$u_L\left(t\right)=L{D}_t^{2\alpha }{i}_L\left(t\right)$$

(69)

where $i_L$ represents the current flowing through the inductor. Let us consider an electrical circuit composed of resistors, n capacitors, and m voltage sources. Through application of Equation (67) along with Kirchhoff’s circuit laws, we can derive a fractional-order differential equation capable of characterizing the transient responses within this circuit topology.

$$D_t^{\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right)$$

(70)

where $0<\alpha <1,$ $x\left(t\right)\in {\mathbb{R}}^n,u\left(t\right)\in {\mathbb{R}}^m,A\in {\mathbb{R}}^{n\times n},B\in {\mathbb{R}}^{n\times m}.$ Moreover, the state vector, $x\left(t\right)$, is comprised of the capacitor voltages, while the input vector, $u\left(t\right)$, contains the source voltage terms. Let us consider an electrical circuit consisting of resistors, n inductors, and m current sources. Similarly, through utilization of Equation (69) in conjunction with Kirchhoff’s circuit laws, we can characterize the transient responses within this circuit topology by means of a fractional-order differential equation.

$$D_t^{2\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right)$$

(71)

where $0<\alpha <1,$ $x\left(t\right)\in {\mathbb{R}}^n,u\left(t\right)\in {\mathbb{R}}^m,A\in {\mathbb{R}}^{n\times n},B\in {\mathbb{R}}^{n\times m}.$ For this circuit configuration, the state vector, $x\left(t\right)$, is comprised of the currents flowing through the inductors. Now consider an electrical circuit topology comprised of resistive, capacitive, and inductive elements, along with either voltage or current sources. We designate the capacitor voltages and inductor currents as the state variables for this system, constituting the entries of the state vector, $x\left(t\right)$. Through application of Equations (67) and (69), in conjunction with Kirchhoff’s circuit laws, we can obtain the state-space model describing the fractional-order transient responses of these linear circuits as

$$\left[\begin{array}{c}{D}_t^{\alpha }{x}_C\left(t\right)\\ D_t^{2\alpha }{x}_L\left(t\right)\end{array}\right]=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{x}_C\left(t\right)\\ x_L\left(t\right)\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]u\left(t\right)$$

(72)

with the initial conditions

$$x_0=\left[\begin{array}{c}{x}_C\left(0\right)\\ X_{L\left(0\right)}\end{array}\right]\in {\mathbb{R}}^{n_1+n_2}$$

(73)

where $x_C\left(t\right)\in {\mathbb{R}}^{n_1}$ represents the capacitor voltages, $x_L\left(t\right)\in {\mathbb{R}}^{n_2}$ represents the inductor currents, $u\left(t\right)\in {\mathbb{R}}^m$ contains the voltage or current source terms, $A_{ij}\in {\mathbb{R}}^{n_i\times n_j},B_i\in {\mathbb{R}}^{n_i\times m}$; for $i,j=1,2,$

Example 5.

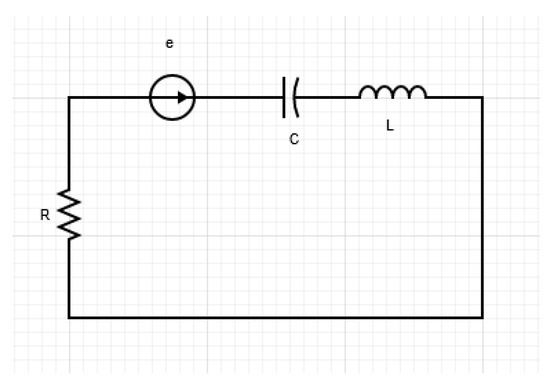
We examine the fractional linear circuit depicted in Figure 1 below, where we have a specified resistance, R, capacitance, C, inductance, L, and a voltage source, e [37]. Using (67), (69) and the second Kirchhoff’s law, the following state equation is derived

$$\left[\begin{array}{c}{D}_t^{\alpha }{u}_C\\ D_t^{2\alpha }i\end{array}\right]=A\left[\begin{array}{c}{u}_C\left(t\right)\\ i\end{array}\right]+Be$$

(74)

where $0<\alpha <1,$ and $0<t<1,$

$$A=\left[\begin{array}{cc}0& \frac{1}{C}\\ -\frac{1}{L}& -\frac{R}{L}\end{array}\right],B=\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{L}}\end{array}\right].$$

Here,

$$A_{11}=\left[\begin{array}{c}0\end{array}\right],A_{12}=\left[\begin{array}{c}\frac{1}{C}\end{array}\right],A_{21}=-\frac{1}{L},A_{22}=\left[\begin{array}{c}-\frac{R}{L}\end{array}\right]B_1=\left[\begin{array}{c}0\end{array}\right]B_2=\left[\begin{array}{c}{\displaystyle \frac{1}{L}}\end{array}\right].$$

(75)

Now, following the same procedure of Example 4, computing the controllability Gramian $M(0,1),$ we obtain

$$\begin{array}{cc}\hfill & M_c(0,1)\hfill \\ \hfill & ={\int }_0^1\mathsf{\Phi }(1-\tau )B{B}^T{\mathsf{\Phi }}^T(1-\tau ){\left(d\tau \right)}^{\alpha }\hfill \\ \hfill & ={\int }_0^1\left[\begin{array}{ccc}{E}_{\alpha }\left(A_{11}{(1-\tau )}^{\alpha }\right)B_1{\left(E_{\alpha }\left(A_{11}{(1-\tau )}^{\alpha }\right)B_1\right)}^T& & E_{\alpha }\left(A_{11}{(1-\tau )}^{\alpha }\right)B_1{B}_2^T{sinh}_{\alpha }\left({(1-\tau )}^{\alpha }\right)\\ {sinh}_{\alpha }\left({(1-\tau )}^{\alpha }\right)B_2{\left(E_{\alpha }\left(A_{11}{(1-\tau )}^{\alpha }\right)B_1\right)}^T& & {sinh}_{\alpha }\left({(1-\tau )}^{\alpha }\right)B_2{B}_2^T{sinh}_{\alpha }\left({(1-\tau )}^{\alpha }\right)\end{array}\right]d\tau \hfill \\ \hfill & =\frac{1}{L^2}\left[\begin{array}{ccc}0& & 0\\ 0& & {\displaystyle \frac{-1}{2\mathsf{\Gamma }(1+\alpha )}}+{\displaystyle \frac{E_{\alpha }\left(2\right)-E_{\alpha }(-2)}{8}}\end{array}\right]\hfill \end{array}$$

which clearly is singular, and consequently the system (74) is not controllable on the interval $[0,1]$.

6. Discussion and Conclusions

The concept of local fractional derivatives has gained significant attention in recent years due to their potential applications in various fields, including control systems. When we consider the broader implications of local fractional derivatives in the context of controllability for linear control systems, we find that they introduce a new dimension to control theory as we have seen in application on circuit electricals. Local fractional derivatives allow us to describe and manipulate systems with non-local memory effects, making them especially valuable in dealing with systems that exhibit fractal-like behavior or long-range dependencies. By incorporating local fractional derivatives into control theory, we may enhance our ability to control and regulate complex systems with a higher degree of precision and efficiency, ultimately opening up new avenues for control engineering research and practical applications. The application of the invertibility of the Gramian matrix and the full rank of the Kalman matrix play a pivotal role in determining the controllability of fractional linear systems.

In such systems, controllability is a key concept, referring to the ability to maneuver the system’s state to any desired position in a finite time using appropriate control inputs. The Gramian matrix, when invertible, indicates that the system can be driven from any initial state to any final state within a specified time frame. This is crucial in fractional systems where dynamics are often more complex due to the non-integer order of the systems’ differential equations. Similarly, the full rank condition of the Kalman matrix is another critical criterion. It ensures that a system’s states are sufficiently influenced by the control inputs, signifying complete controllability. These mathematical conditions are essential in designing and analyzing control strategies for fractional linear systems, ensuring that they respond predictably and effectively to control inputs. In this study, we have provided the necessary and sufficient criteria to determine controllability of the fractional systems, as well as fractional systems involving distinct orders, expressed as follows:

$$\begin{array}{cc}\hfill D_t^{\alpha }x\left(t\right)& =Ax\left(t\right)+Bu\left(t\right)\hfill \\ \hfill \left[\begin{array}{c}{D}_t^{\alpha }{x}_1\left(t\right)\\ D_t^{2\alpha }{x}_2\left(t\right)\end{array}\right]& =\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]u\left(t\right),\hfill \end{array}$$

where $\alpha$ is the local fractional derivative considered. Particularly, we proved that the local fractional linear system is controllable if and only if the Gramian matrix is invertible and if the Kalman matrix has full rank. We also showed that a local fractional linear system involving distinct orders is controllable if and only if the Gramian matrix is invertible. The conditions we obtained do not depend on the non-integer order derivative $\alpha$, which is similar to the results obtained in previous works for linear systems with the classical derivative. However, the tools we used to obtain these results are based solely on local fractional calculus theory. We also raised the following questions for future works. What are the necessary and sufficient conditions for which a linear time-variant local fractional system is controllable? Can we find a controllability Kalman rank matrix, K, for the local fractional linear system involving distinct orders?