Abstract
In this paper, we use two Fractional-Order Chaotic Systems (FOCS)—one for the sender and one for the receiver—to determine the optimal synchronisation for a secure communication technique. With the help of the Step-By-Step Sliding-Mode Observer (SBS-SMO), this synchronisation is accomplished. An innovative optimisation method, known as the artificial Harris hawks optimisation (HHO), was employed to enhance the observer’s performance. This method eliminates the random parameter selection process and instead selects the optimal values for the observer. In a short amount of time, the secret message that could have been in the receiver portion (signal, voice, etc.) was successfully recovered using the proposed scheme. The experimental validation of the numerical results was carried out with the assistance of an Arduino microcontroller and several electronic components. In addition, the findings of the experiments were compared with the theoretical calculations, revealing a satisfactory level of agreement.
1. Introduction
The field of fractional calculus is a subfield of mathematical analysis that has garnered the interest of a number of academics due to its intriguing potential as a one-of-a-kind modelling tool across a wide range of scientific and engineering fields. Fractional differential equations are utilised because it was discovered that simulating experimental dynamics using these equations delivers better performance and superior results, enabling the construction of powerful controllers. Out of the many advantages that this discipline offers, model generalisation and long-term memory stand out as particularly advantageous. Furthermore, fractional-order modelling is superior when it comes to attempting to build a connection between any two places. It is possible to collect data for the instance of interest at any time from a model that is of fractional order. When we use an integer-order model, however, we are only able to obtain information that is relevant to this particular circumstance. Based on the problem at hand and the information gathered, one would select the most appropriate operator for the model. The definition proposed by Caputo is one of the most widely accepted in current usage.
In addition to investigating the numerous possibilities beyond the peculiar behaviour of dynamical systems across a variety of domains such as electrochemistry [1], viscoelasticity [2], and biology [3], it is possible to observe a great number of practical applications of fractional calculus in contemporary theory [4,5,6,7]. As a challenging area of mathematics, chaos theory is characterised by unexpected and complex behaviour. It focuses on deterministic laws and underlying patterns that are hyper-sensitive to the initial conditions. Chaos theory is a subject that is tough to study. In the past three decades, chaotic systems have emerged as a subject of research. Some examples of chaotic systems include the Lorenz system, the unified chaotic system, the Rossler system, the Lu system, and the Chen system [8,9,10,11]. There are numerous applications of these highly effective systems that have benefited from their chaotic and unpredictable behaviour, including commerce, electricity, healthcare, mathematics, chemical and biological reactors, and security [8,9,10,11]. Additionally, these systems have been successfully applied in a wide variety of control fields, including secure communication. According to the findings of researchers, the combination of chaos theory and fractional calculus could produce superior outcomes in terms of secure communication. This is due to the fact that FOCS exhibit significantly more intricate behaviour [12,13,14,15,16].
It is guaranteed that a sliding-mode observer produces a set of state estimates directly proportional to the transmitter’s real output, which is one of the unique characteristics of the observer we employed in this study. Another powerful tool is the optimal SBS-SMO. Many studies, such as [17,18], have resulted from the development of methods for synchronising chaotic systems with fractional order employing a sliding mode observer; thus, it is clear that there has been a lot of work in this area. An innovative approach to communication security is suggested in this paper. It involves synchronising two fractional-order Chua oscillators with an ideal SBS-SMO. The third-state derivative of fractional order of the chaotic system contains the message in the emitter portion. It is believed that the receiving procedure is flawed; hence, an SBS-SMO is employed to verify that the master and slave are communicating and obtaining the secret data.
The importance of fractional-order chaotic systems lies in their applications in various areas and fields, such as fractional evolution hemivariational inequalities generated by non-instantaneous impulses, which was examined in [19]. In [20], an innovative approach to the encryption of colour images was proposed, where the algorithm was based on extended DNA coding, the Zig-Zag transform, and a fractional-order laser system [21]. Other notable works in this area include “Achieving Superior Multi-Image Encryption Through the Use of Recently Conceived Fractional-Order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map” [22] and “Fragmentary Fractional Order Systems: Modeling and Initialization Using the Infinite State Representation” [23].
To achieve a secure real-time communication scheme, this work makes the following contributions:
- -
- The computation of the fractional order in the microcontroller needs memory allocation to compute the cumulative integration; this limitation in the memory of the atmega328p microcontroller was solved by using the numerical approximation method, Rung Kutta 4.
- -
- The noise produced by the electronics components, which negatively affects the quality of the transmitted and received data, was solved in two ways: two capacitors were added to the circuit to enhance the NRF24LO1 module’s performance, and a stochastic filter was implemented to filter the estimated input (message) in the slave part.
- -
- The optimal SBS-SMO parameters were chosen using HHO.
This paper is structured as follows. Fractional calculus is described in Section 2. The transmitter model is explained along with the injection of secret information in Section 3. In Section 4, the SBS-SMO and the recovered message are carefully revealed. In Section 5, the receiver model is discussed in detail. The optimisation algorithm used with the sliding-mode observer is explained in Section 6. In Section 7, it is shown that the proposed secure communication method works successfully through real-time validation.
2. Fundamental on Fractional Calculus
The Grünwald–Letnikov definition, the Riemann–Liouville definition, and the Caputo definition are the three most common ways to describe the general fractional differintegral [24].
Definition 1
([25]). Caputo presented a novel definition of the derivative of fractional order, which is described as follows:
It is important to highlight Euler’s gamma function, which is the most powerful component in fractional calculus. It is defined as follows:
As a generalisation of a factorial, this function takes the following form:
Definition 2
([25]). In the case of and being a causal function of t, that is, for , the Riemann–Liouville integral is defined as:
Definition 3
([25]). The Grünwald–Letnikov fractional-order derivative is defined as:
is the time step used in the simulation.
3. The Transmitter System’s Configuration
Many electric and magnetic phenomena can be modelled using fractional calculus. Many chaotic systems have been extended using non-integer-order derivatives, drawing inspiration from Chua’s oscillator and other well-known chaotic systems. In this section, we outline the transmitter system [26]:
where and . represents the fractional-order differentiation vector operator . If all the orders of the derivative are equal, which is , , the system is said to be of equivalent fractional order (commensurate) if and only if the fractional orders are equal. Take the example of a commensurate fractional-order system, which is defined as
Table 1 presents the parameters used in the transmitter system, with the state variables’ initial conditions set at zero. Figure 1, Figure 2 and Figure 3 illustrate the time responses of the system’s states , and Figure 4 illustrates the three-dimensional space of the chaotic attractor in .

Table 1.
Parameter values of the model given in Equation (4).
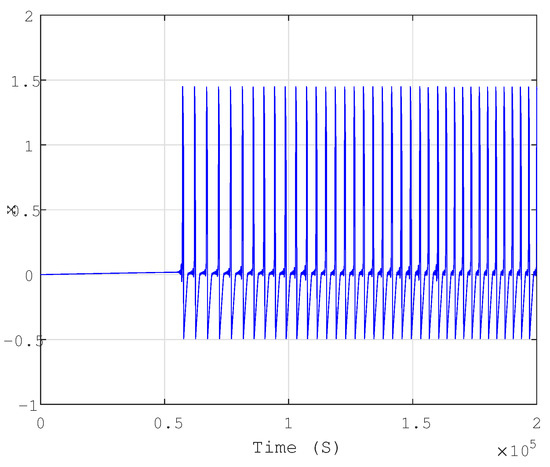
Figure 1.
Time response of state variable x for initial condition of zero.
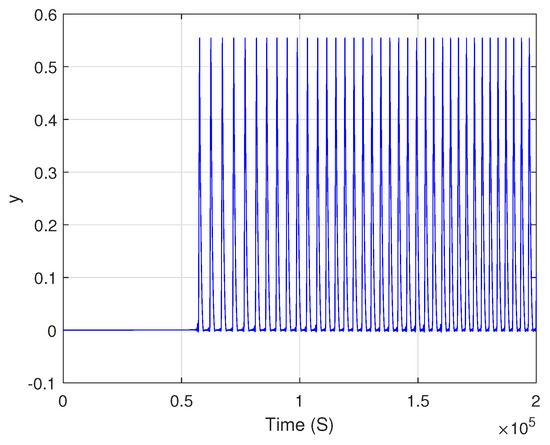
Figure 2.
Time response of state variable y for initial condition of zero.
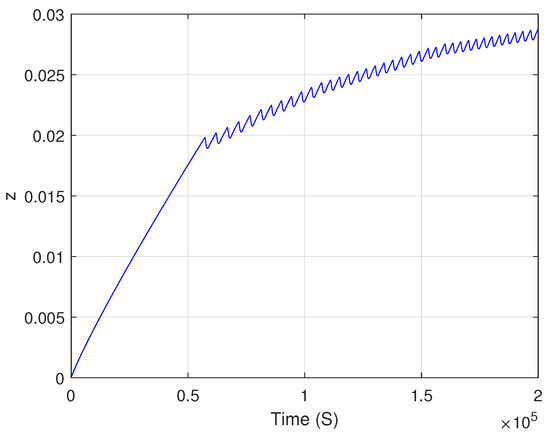
Figure 3.
Time response of state variable z for initial condition of zero.
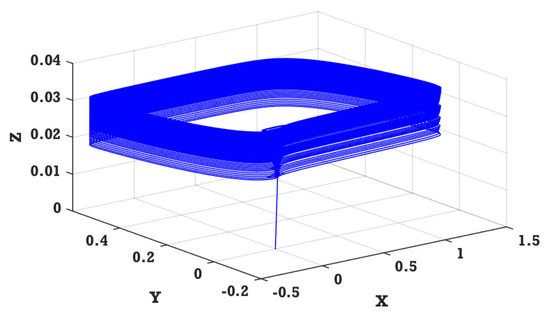
Figure 4.
Time responses of state variables for initial conditions of zero.
The Inclusion of Private Information
Equation (4) is modified by adding a new term (secret information), which is injected into the third derivative rather than in order to enhance the safety of the communication system. The model of the transmitter system can be expressed as follows:
Remark 1.
The secret message is considered as an unknown to be estimated and can represent a signal, voice, or image. In the simulation section, interactive examples are investigated.
4. SBS-SMO Theory
According to [27], designing the SBS-SMO for integer-order nonlinear systems usually involves a sequential method. This method involves injecting virtual inputs produced from the iterative first-order SBS-SMO. Accurately estimating and , is our objective.
The triangular representation of the commensurate fractional-order nonlinear system is given as follows:
where is the measured output, is the secret message, and the nonlinear functions are denoted by , , and . The parameters are all non-zero constants.
Consider that the system in Equation (7) is a bounded-input bounded-state system, and , , and are bounded, i.e.,
Assumption 1.
.
Assumption 2.
and for all .
The purpose is to use the step-by-step first-order siding observers to estimate the state variables and the unknown input . Following the same approach used with integer-order systems, the following equations characterise the suggested sliding-mode observer that injects the available observed output signal
The secret message estimation is defined as follows:
The terms in Equation (9) are parameters that are only positive and developed to guarantee the observer’s convergence.
The following are the definitions of the auxiliary variables :
The intermediate estimation errors are expressed as
where through construction. The estimation errors are expressed as
Remark 2.
To obtain the convergence condition, the rule of the switching logic must achieve:
Theorem 1.
Let us assume that Assumptions 1 and 2 are accurate. In this situation, given the existence of positive parameters , the observer states and the estimated input converge to and the secret message , respectively, within a finite period of time [26].
5. The Receiver System’s Configuration
In order to simplify the receiver design that relies on an SBS-SMO and ensure successful synchronisation, we present a reformulation of Equation (6):
where
The following sliding-mode observer describes the receiver:
The auxiliary variables are defined as
The recovered message is given by
6. Selection of the Observer’s Optimal Parameters via HHO
In this section, the objective is to determine the optimal settings for the receiver system through the utilisation of the novel HHO in order to accomplish synchronisation. HHO was selected from a range of optimisation strategies documented in the literature due to its superior performance across more than 50 benchmark optimisation issues in comparison to other meta-heuristic algorithms. The concept of HHO was first suggested by Heidari et al. in their study on artificial intelligence [28]. Our secure communication strategy is depicted in Figure 5, whereas the overall HHO framework is depicted in Figure 6. The HHO method is utilised to address the convex optimisation problem, formulated as an objective function (16), aimed at minimising the mean square error (MSE) between the states of the emitter and receiver.
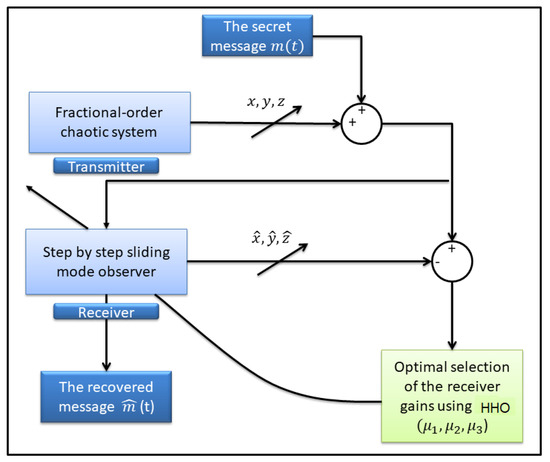
Figure 5.
The proposed secure data transmission scheme.
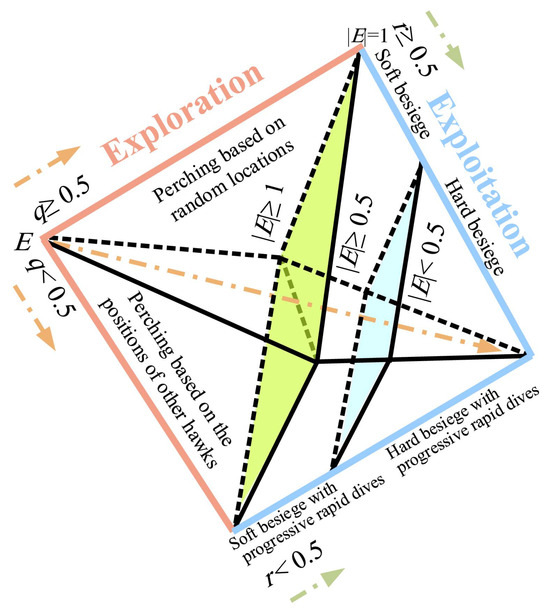
Figure 6.
Structure of HHO.
In this section, the effectiveness of the proposed strategy is demonstrated. When it comes to retrieving information in a short amount of time while maintaining high quality, it is essential to make use of specific settings for the sliding-mode observer. Some works in the literature, on the other hand, use parameters that are chosen at random. As shown in Figure 7 and Figure 8, the proper parameters for the SBS-SMO can be achieved by employing the described process. The simulation’s settings and values are presented in Table 2.
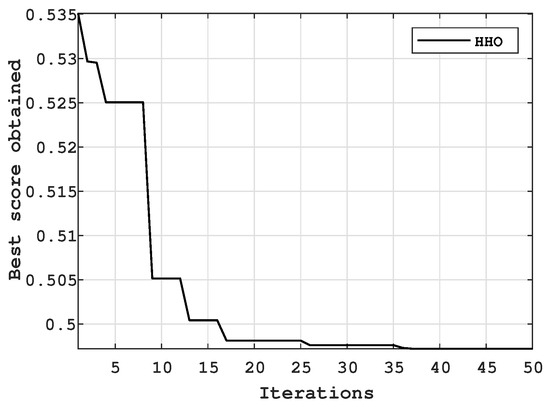
Figure 7.
The greatest possible HHO score attained during iterations.
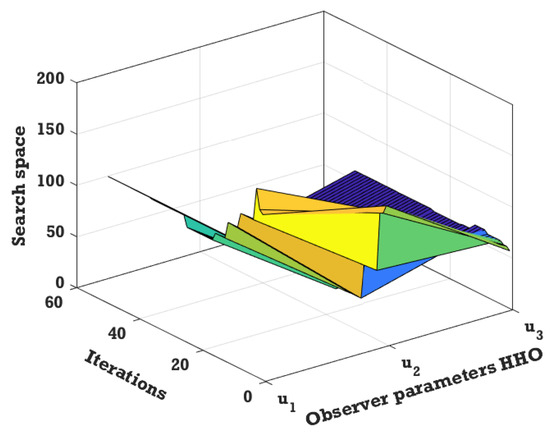
Figure 8.
The optimisation vector of the HHO algorithm and its dynamic changes.

Table 2.
Parameters and values used in simulations and in real time.
7. Results and Discussion
Figure 9, Figure 10 and Figure 11 show the responses of the states and their estimations . Figure 12 shows the collective estimation errors for the three state variables. This proves that the two FOCS can be synchronised optimally within a finite amount of time. The initial conditions are assumed to be , whereas the responding system’s initial conditions are all set to zero .
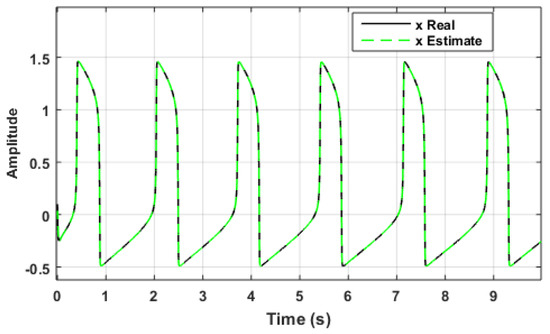
Figure 9.
Data set synchronisation of x and .
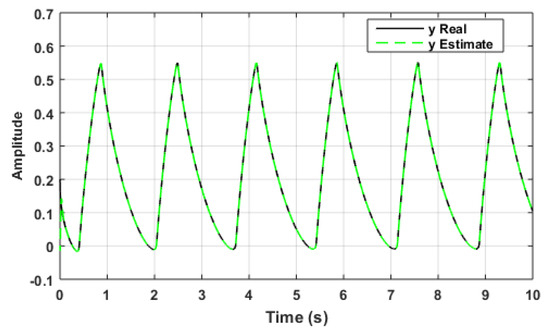
Figure 10.
Data set synchronisation of y and .
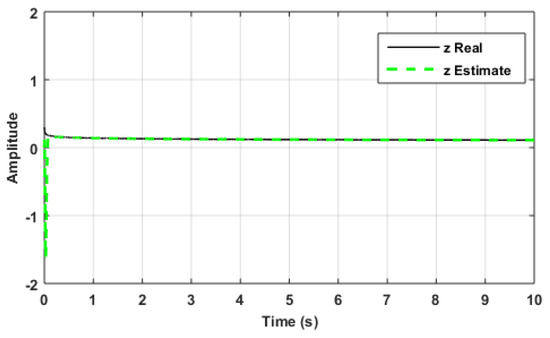
Figure 11.
Data set synchronisation of z and .
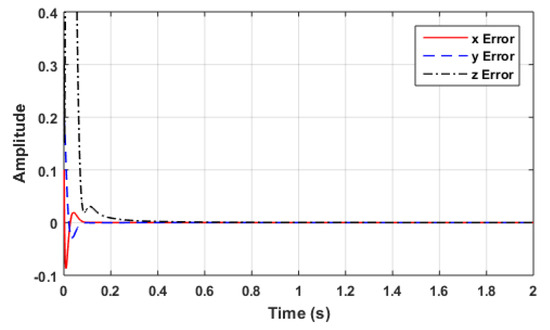
Figure 12.
The estimation errors: x error, y error, and z error.
7.1. Retrieving the Secret Message
The purpose of this section is to use the properties and characteristics of the SBS-SMO, specifically synchronisation and estimating the unknown inputs, for the information encryption process. First, we include the secret information, which we consider to be the sin, square, sawtooth, and voice signals. These signals are represented by the following formulations: , , and , respectively. As shown in Figure 13, Figure 14, Figure 15 and Figure 16, the recovered messages in the receiver system are similar to the original ones, with and . Additionally, Table 3 presents a comparison between the proposed work and the work in [26] across four distinct error messages: sin, square, sawtooth, and voice. Although [26] did not succeed in retrieving the voice message, we made an attempt to recover it for comparison with our own voice signal, revealing an MSE close to zero during the recovery process.
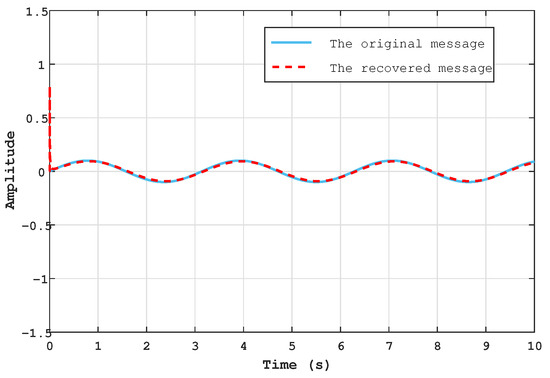
Figure 13.
The original message (sinusoidal wave ) and the recovered .
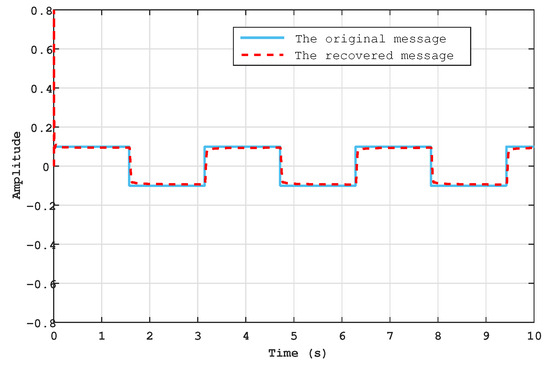
Figure 14.
The original message ( square(t)) and the recovered .
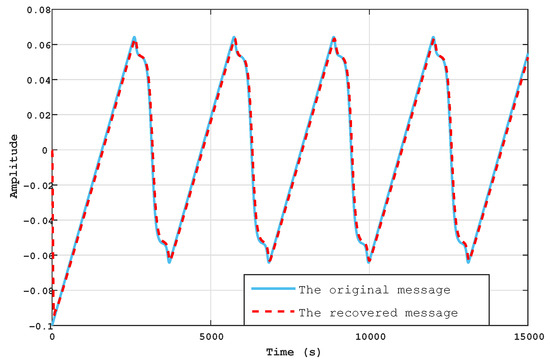
Figure 15.
The original message ( sawtooth(t)) and the recovered .
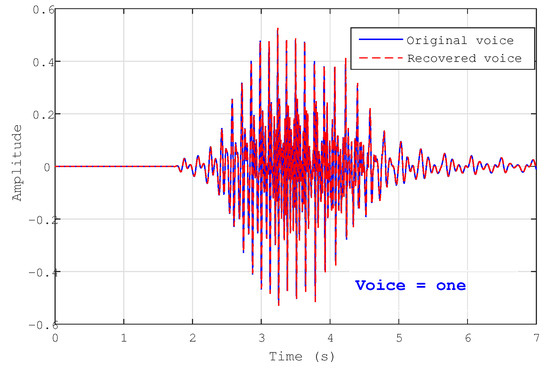
Figure 16.
The original message ( voice) and the recovered .

Table 3.
Comparison of different kinds of messages.
7.2. Security Analysis and Check
Two primary modifications were made in order to evaluate the level of security provided by the proposed secure transmission technique. These included alterations in the initial conditions and the sequence of transmissions between the transmitter and receiver. Due to the significance of the original voice message, it was selected from among the other messages that were received (Figure 17). We only made a tiny modification in the initial conditions of the transmitter system’s first state, which were , . As a result of our investigation, the message that was contained was completely lost by the receiver as well. The second check involved a small modification in the first state order of the transmitter system. As depicted in Figure 18, the value of was , the value of was , and the value of was . In addition, we discovered that the message that was inserted had been completely missed.
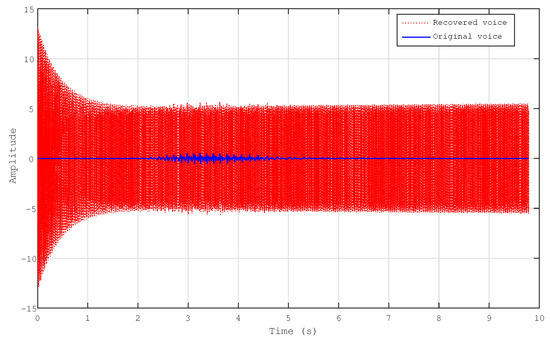
Figure 17.
The original message voice and the recovered with initial conditions , and . The order for both the transmitter and receiver is .
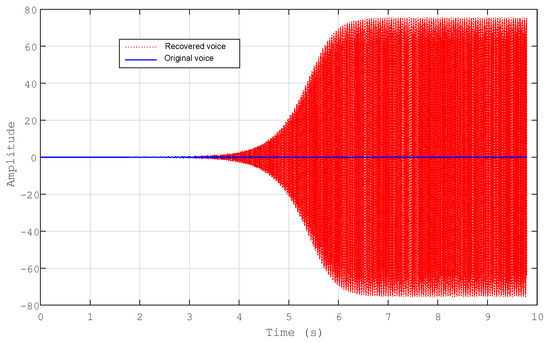
Figure 18.
The original message and the recovered with initial conditions and . The orders for the transmitter are , whereas those for the receiver are set to .
The fractional order of the chaotic system q was chosen randomly; the sensitivity of the chaotic system to this fractional order is advantageous. A small change in q was accompanied by a significant change in the behaviour of the system, which complicated the decoding of the proposed communication scheme’s encryption. Therefore, it was considered key to the decryption process. The same fractional order can be used on both sides, sender and receiver, with the same initial state conditions. Different values can be used as well, but for synchronisation to occur, the observer’s parameters must be chosen corresponding to this case.
7.3. Experimental Validation
Figure 19 shows the experimental validation of the proposed secure communication scheme. We implemented the FOCS and SBS-SMO in the two microcomputers in the transmitter and the receiver, respectively. The discrepancy between the theoretical and the experimental aspects has been minimised through mathematical tools such as Rung Kutta 4, approximation between fractional and integer transfer functions, and the Kalman filter. Wireless transmission was facilitated by the NRF24L01 module. The obtained results confirm the validity of the proposed idea from both mathematical and numerical aspects and its readiness for application in the experimental field.
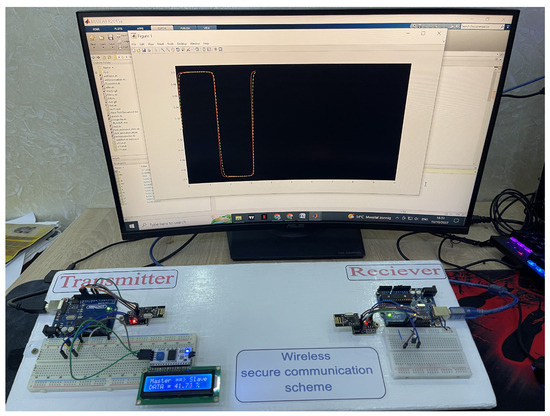
Figure 19.
Real-time investigation.
8. Conclusions
A novel approach to enhancing the security of encrypted communications is proposed in this article. The proposed method involves the utilisation of a novel optimisation algorithm in order to achieve the highest level of performance for the observer. To ensure synchronisation between the emitter and receiver, we established an ideal SBS-SMO device on the reception side.
In this work, we succeeded in transferring many pure mathematical concepts from digital simulations and incorporating them into electronic circuits and microcontrollers so that people could exploit them in their daily lives. Rung Kutta 4 was used to solve the limitation in the memory of the atmega328p microcontroller to compute the cumulative integration, as without it, we would need a memory allocation. We added capacitors to the circuit to enhance the NRF24L01 module’s performance, and a stochastic filter was implemented to denoise the recovered input (message) in the received part.
According to the obtained results, we have come to the conclusion that confidential information can only be recovered by outside individuals if the following details are provided:
- The type of chaotic system utilised, such as Lorenz, Rossler, Chua’s, and Chen, among others.
- The dynamic parameters of the chaotic system.
- The order and initial conditions of the system, as well as the state in which the message was embedded.
- The mechanism of the synchronisation process, such as a controller or observer, and the specific type of controller or observer.
- The characteristics of the encrypted and decrypted data, such as text, images, voice, and video.
On the other hand, assembling all of this equipment is an extraordinarily challenging task.
Future studies will include:
- Transmitting secure images instead of voice or signal data.
- Improving fractional Chua’s systems through real-time implementation of new 4D or 6D fractional chaotic systems.
- Replacing the synchronisation observer with advanced and more recent algorithms such as deep learning and machine learning approaches.
Author Contributions
Conceptualisation, B.N., I.E.T., M.A.A. and S.S.; methodology, B.N., I.E.T., M.A.A. and S.S.; software, I.E.T., M.A.A. and S.S.; validation, C.N. and B.N.; formal analysis, B.N. and C.N. investigation, I.E.T., M.A.A. and S.S.; resources, B.N. and C.N.; data curation, B.N., I.E.T., M.A.A. and S.S.; writing—original draft preparation, B.N., I.E.T., M.A.A. and S.S.; writing—review and editing, B.N. and C.N.; supervision, B.N., I.E.T., M.A.A., S.S. and C.N.; project administration, B.N. and C.N.; funding acquisition, C.N. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was partially supported by the Age-It: Ageing Well in an Ageing Society project, task 9.4.1, work package 4, spoke 9, within topic 8, extended partnership 8, under the National Recovery and Resilience Plan (PNRR), Mission 4 Component 2 Investment 1.3—Call for tender No. 1557 of 11/10/2022 of the Italian Ministry of University and Research funded by the European Union—NextGenerationEU, CUP B53C22004090006.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
This work has been developed at s.Lab() Intelligent Systems Laboratory at the Department of Computer, Control, and Management Engineering, Sapienza University of Rome (https://islab.diag.uniroma1.it).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Oldham, K.B. Fractional differential equations in electrochemistry. Adv. Eng. Softw. 2010, 41, 9–12. [Google Scholar] [CrossRef]
- Giona, M.; Cerbelli, S.; Roman, H.E. Fractional diffusion equation and relaxation in complex viscoelastic materials. Phys. A Stat. Mech. Its Appl. 1992, 91, 449–453. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Saad, K.M.; Khan, M.A.; Agarwal, P. Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: A fractional calculus approach. Phys. A Stat. Mech. Its Appl. 2019, 523, 48–65. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Agarwal, P. Numerical solution of multiterm variable-order fractional differential equations via shifted Legendre polynomials. Math. Methods Appl. Sci. 2019, 42, 3978–3991. [Google Scholar] [CrossRef]
- Rekhviashvili, S.; Pskhu, A.; Agarwal, P.; Jain, S. Application of the fractional oscillator model to describe damped vibrations. Turk. J. Phys. 2019, 43, 236–242. [Google Scholar] [CrossRef]
- Atoussi, M.A.; Saadi, S.; Nail, B. Design of an optimal step-by-step sliding mode observer for multiple fractional-order chaotic synchronisation with an application to secure communication. Int. J. Appl. Nonlinear Sci. 2023, 4, 58–71. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G.; Cheng, D.; Celikovsky, S. Bridge the gap between the Lorenz system and the Chen system. Int. J. Bifurc. Chaos 2002, 12, 2917–2926. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Pellicer-Lostao, C.; López-Ruiz, R. A chaotic gas-like model for trading markets. J. Comput. Sci. 2010, 1, 24–32. [Google Scholar] [CrossRef]
- Ditto, W.L. Applications of chaos in biology and medicine. AIP Conf. Proc. 1996, 376, 175–201. [Google Scholar]
- Bodnar, M.; Foryś, U. Three types of simple DDE’s describing tumor growth. J. Biol. Syst. 2007, 15, 453–471. [Google Scholar] [CrossRef]
- Lamba, P.; Hudson, J.L. Experiments on bifurcations to chaos in a forced chemical reactor. Chem. Eng. Sci. 1987, 42, 1–8. [Google Scholar] [CrossRef]
- Yang, T.; Chua, L.O. Secure communication via chaotic parameter modulation. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1996, 43, 817–819. [Google Scholar] [CrossRef]
- Delavari, H.; Mohadeszadeh, M. Robust finite-time synchronization of non-identical fractional-order hyperchaotic systems and its application in secure communication. IEEE/CAA J. Autom. Sin. 2016, 6, 228–235. [Google Scholar] [CrossRef]
- Tian, X.; Fei, S.; Chai, L. On modified second-order sliding mode synchronization of two different fractional order hyperchaotic systems. Int. J. Multimed. Ubiquitous Eng. 2015, 10, 387–398. [Google Scholar] [CrossRef]
- Durga, N.; Muthukumar, P.; Niezabitowski, M. Approximation and convergence analysis of optimal control for non-instantaneous impulsive fractional evolution hemivariational inequalities. Results Control Optim. 2022, 9, 1–20. [Google Scholar] [CrossRef]
- Meng, F.; Gu, Z. A Color Image-Encryption Algorithm Using Extended DNA Coding and Zig-Zag Transform Based on a Fractional-Order Laser System. Fractal Fract. 2023, 7, 795. [Google Scholar] [CrossRef]
- Roohi, M.; Zhang, C.; Taheri, M.; Basse-O’Connor, A. Synchronization of Fractional-Order Delayed Neural Networks Using Dynamic-Free Adaptive Sliding Mode Control. Fractal Fract. 2023, 7, 682. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting Newly Designed Fractional-Order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map for High-Performance Multi-Image Encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Trigeassou, J.-C.; Maamri, N. Modeling and Initialization of Nonlinear and Chaotic Fractional Order Systems Based on the Infinite State Representation. Fractal Fract. 2023, 7, 713. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Bettayeb, M.; Al–Saggaf, U.M.; Djennoune, S. Single channel secure communication scheme based on synchronization of fractional-order chaotic Chua’s systems. Trans. Inst. Meas. Control 2018, 40, 3651–3664. [Google Scholar] [CrossRef]
- Barbot, J.P.; Djemai, M.; Boukhobza, T. Sliding mode observers. Sliding Mode Control Eng. 2002, 11, 33. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).