A Hybrided Method for Temporal Variable-Order Fractional Partial Differential Equations with Fractional Laplace Operator
Abstract
1. Introduction
2. Preliminaries and Some Lemmas
- Case I: n = 1
- Case II: n ≥ 2
- whereandcorresponds to the variable coefficients at the point . It is verified that constitutes a monotonically decreasing sequence for each value of n with
2.1. Time-Discretization of the Present Scheme
2.2. Semi-Discretization in Space of the Present Scheme
2.3. Analysis of the Time–Space Discretization of the Present Scheme
3. Main Results
4. Numerical Experiments
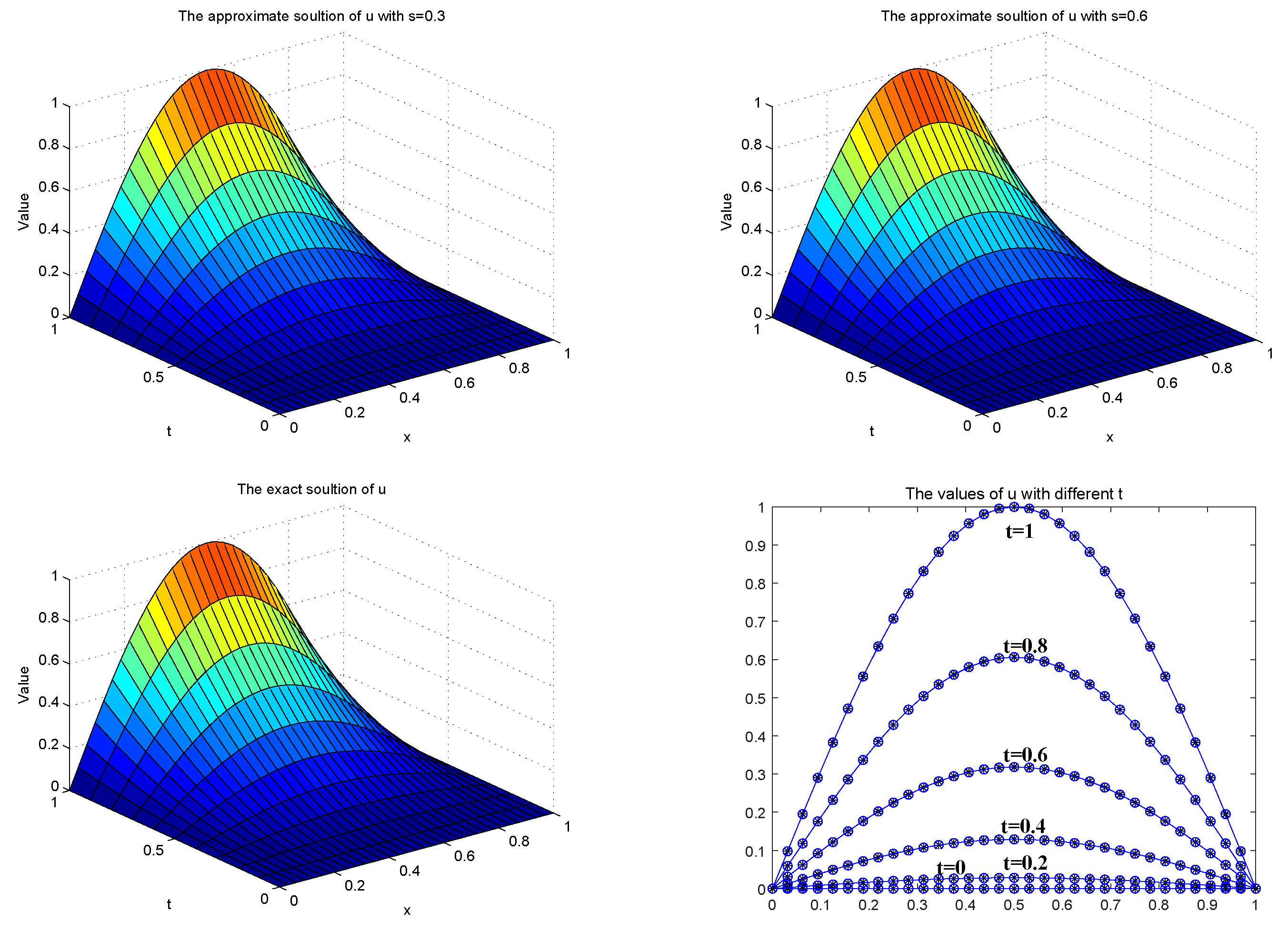
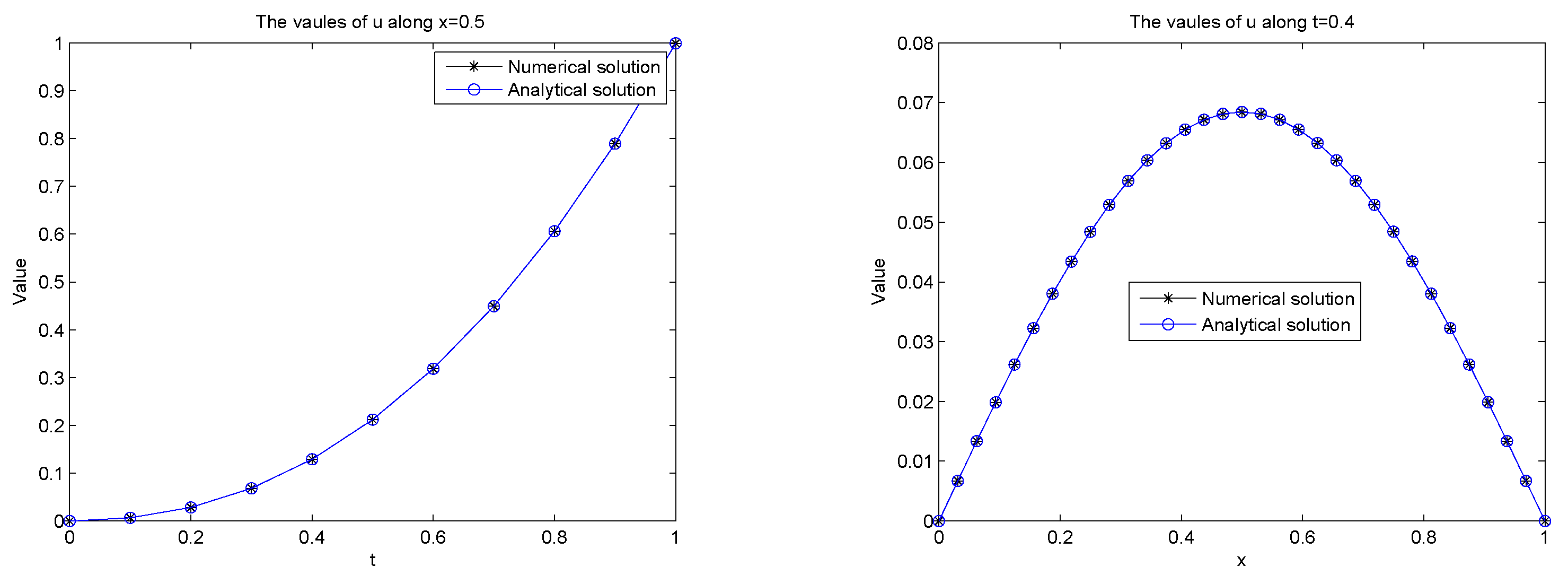
4.1. One-Dimensional Space-Fractional Laplace Case
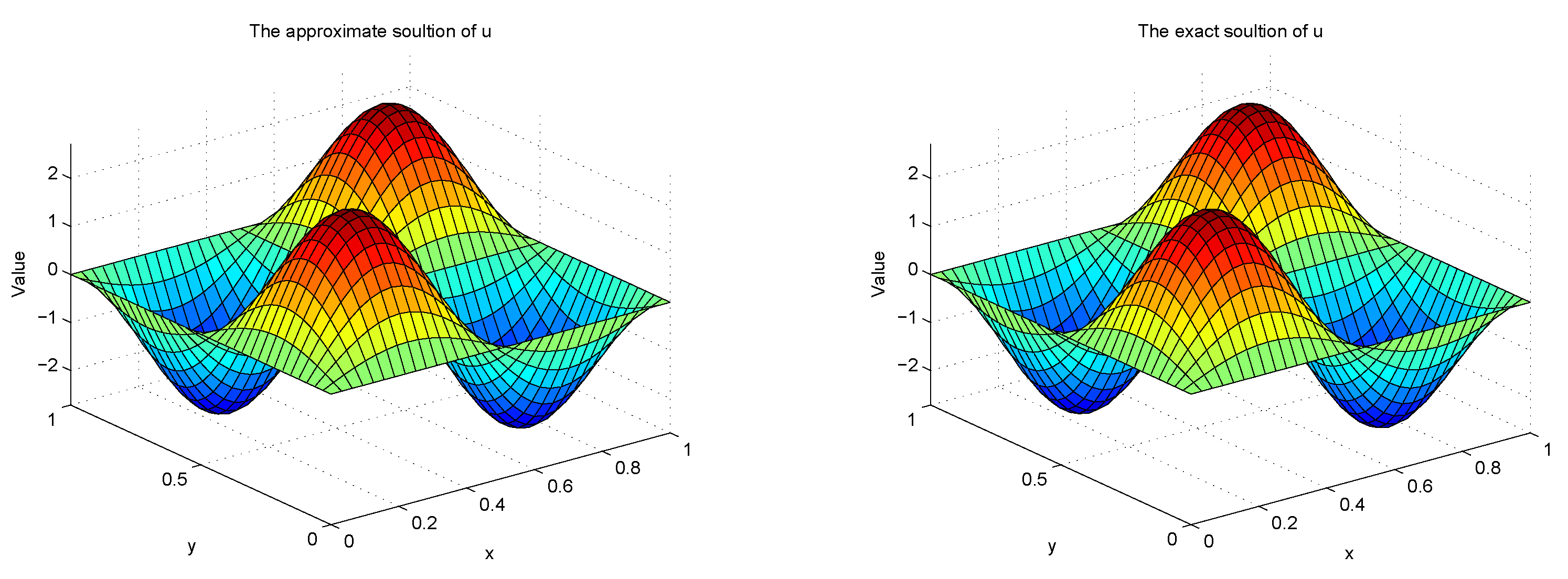
4.2. Two-Dimensional Space-Fractional Laplace Case
4.3. Three-Dimensional Space-Fractional Laplace Case
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland: New York, NY, USA, 2006. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods; Series on Complexity, Nonlinearity and Chaos; World Scientific: Boston, MA, USA, 2012. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Li, X.; Xu, C. A space–time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, J.; Xu, Y. Stability and convergence of an effective finite element method for multiterm fractional partial differential equations. Abstr. Appl. Anal. 2013, 2013, 857205. [Google Scholar] [CrossRef]
- Zhuang, P.; Gu, Y.T.; Liu, F.; Turner, I.; Yarlagadda, P.K.D.V. Time-dependent fractional advection–diffusion equations by an implicit MLS meshless method. Int. J. Numer. Methods Eng. 2011, 88, 1346–1362. [Google Scholar] [CrossRef]
- Li, C.; Zhao, Z.; Chen, Y. Numerical approximation of nonlinear fractional differential equations with subdiffusion and super diffusion. Comput. Math. Appl. 2011, 62, 855–875. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I. A fractional-order implicit difference approximation for the space time fractional diffusion equation. ANZIAM J. 2006, 47, 48–68. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, C. Fractional difference/finite element approximation for the time–space fractional telegraph equation. J. Appl. Math. Comput. 2012, 219, 2975–2988. [Google Scholar] [CrossRef]
- Yi, S.C.; Yao, L.Q. A steady barycentric lagrange interpolation method for the 2d higher order time-fractional telegraph equation with nonlocal boundary condition with error analysis. Numer. Methods Partial. Differ. Equ. 2019, 35, 1694–1716. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Zhang, X.; Korošakb, D. Anomalous diffusion modeling by fractal and fractional derivatives. J. Comput. Math. Appl. 2010, 59, 1754–1758. [Google Scholar] [CrossRef]
- Inc, M. The approximate and exact solutions of the space- and time-fractional Burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 2008, 345, 476–484. [Google Scholar] [CrossRef]
- Abdel-Rehim, E.A. Implicit difference scheme of the space–time fractional advection–diffusion equation. Fract. Calc. Appl. Anal. 2015, 59, 1452–1469. [Google Scholar] [CrossRef]
- Arshad, S.; Huang, J.F.; Khaliq, A.Q.M.; Tang, Y.F. Trapezoidal scheme for time–space fractional diffusion equation with Riesz derivative. J. Comput. Math. Phys. 2017, 390, 1–15. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. An improved collocation method for multi-dimensional space–time variable-order fractional Schrödinger equations. Appl. Numer. Math. 2010, 59, 1754–1758. [Google Scholar]
- Duo, S.W.; Ju, L.L.; Zhang, Y.Z. A fast algorithm for solving the space–time fractional diffusion equation. Comput. Math. Appl. 2018, 75, 1929–1941. [Google Scholar] [CrossRef]
- Nie, S.; Sun, H.; Zhang, Y.; Chen, D.; Chen, W.; Chen, L.; Schaefer, S. Vertical Distribution of Suspended Sediment under Steady Flow: Existing Theories and Fractional Derivative Model. Discret. Dyn. Nat. Soc. 2017, 2017, 5481531. [Google Scholar] [CrossRef]
- Gu, X.M.; Sun, H.W.; Zhao, Y.L.; Zheng, X. An implicit difference scheme for time-fractional diffusion equations with a time-invariant type variable order. Appl. Math. Lett. 2021, 120, 107270. [Google Scholar] [CrossRef]
- Gu, X.M.; Huang, T.Z.; Ji, C.C.; Carpentieri, B.; Alikhanov, A.A. Fast iterative method with a second order implicit difference scheme for time–space fractional convection-diffusion equations. J. Sci. Comput. 2016, 72, 957–985. [Google Scholar] [CrossRef]
- Li, M.; Gu, X.M.; Huang, C.; Fei, M.; Zhang, G. A fast linearized conservative finite element method for the strongly coupled nonlinear fractional Schrödinger equations. J. Comput. Phys. 2018, 358, 256–282. [Google Scholar] [CrossRef]
- Yi, S.C.; Sun, H.G. A Hybrided Trapezoidal-Difference Scheme for Nonlinear Time-Fractional Fourth-Order Advection-Dispersion Equation Based on Chebyshev Spectral Collocation Method. Adv. Appl. Math. Mech. 2019, 11, 197–215. [Google Scholar]

| h | 1/8 | 1/16 | 1/32 | 1/64 | 1/128 | 1/256 |
|---|---|---|---|---|---|---|
| k = 2, s = 0.65 | ||||||
| Error | ||||||
| Order | 2.0055 | 2.0018 | 2.0021 | 2.0070 | 2.0278 | |
| k = 3, s = 0.75 | ||||||
| Error | ||||||
| Order | 2.0065 | 2.0015 | 2.0000 | 1.9984 | 1.9931 |
| 1/8 | 1/16 | 1/32 | 1/64 | 1/128 | |
|---|---|---|---|---|---|
| s = 0.4 | |||||
| Error | |||||
| Order | 2.0195 | 2.0050 | 2.0018 | 2.0005 | |
| s = 0.7 | |||||
| Error | |||||
| Order | 2.0244 | 2.0061 | 2.0019 | 2.0005 |
| 1/5 | 1/10 | 1/15 | 1/20 | 1/30 | 1/40 | |
|---|---|---|---|---|---|---|
| s = 0.3 | ||||||
| Error | 0.0030 | |||||
| Order | 2.1033 | 2.1975 | 1.7781 | 2.0894 | −0.6296 | |
| s = 0.7 | ||||||
| Error | 0.0029 | |||||
| Order | 1.7810 | 2.1725 | 2.5511 | 2.2538 | −0.5653 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Yi, S. A Hybrided Method for Temporal Variable-Order Fractional Partial Differential Equations with Fractional Laplace Operator. Fractal Fract. 2024, 8, 105. https://doi.org/10.3390/fractalfract8020105
Wang C, Yi S. A Hybrided Method for Temporal Variable-Order Fractional Partial Differential Equations with Fractional Laplace Operator. Fractal and Fractional. 2024; 8(2):105. https://doi.org/10.3390/fractalfract8020105
Chicago/Turabian StyleWang, Chengyi, and Shichao Yi. 2024. "A Hybrided Method for Temporal Variable-Order Fractional Partial Differential Equations with Fractional Laplace Operator" Fractal and Fractional 8, no. 2: 105. https://doi.org/10.3390/fractalfract8020105
APA StyleWang, C., & Yi, S. (2024). A Hybrided Method for Temporal Variable-Order Fractional Partial Differential Equations with Fractional Laplace Operator. Fractal and Fractional, 8(2), 105. https://doi.org/10.3390/fractalfract8020105






