Inner Multifractal Dynamics in the Jumps of Cryptocurrency and Forex Markets
Abstract
1. Introduction
2. Literature Review
3. Data and Descriptive Statistics
3.1. Data
3.2. Descriptive Statistics
4. Methodology
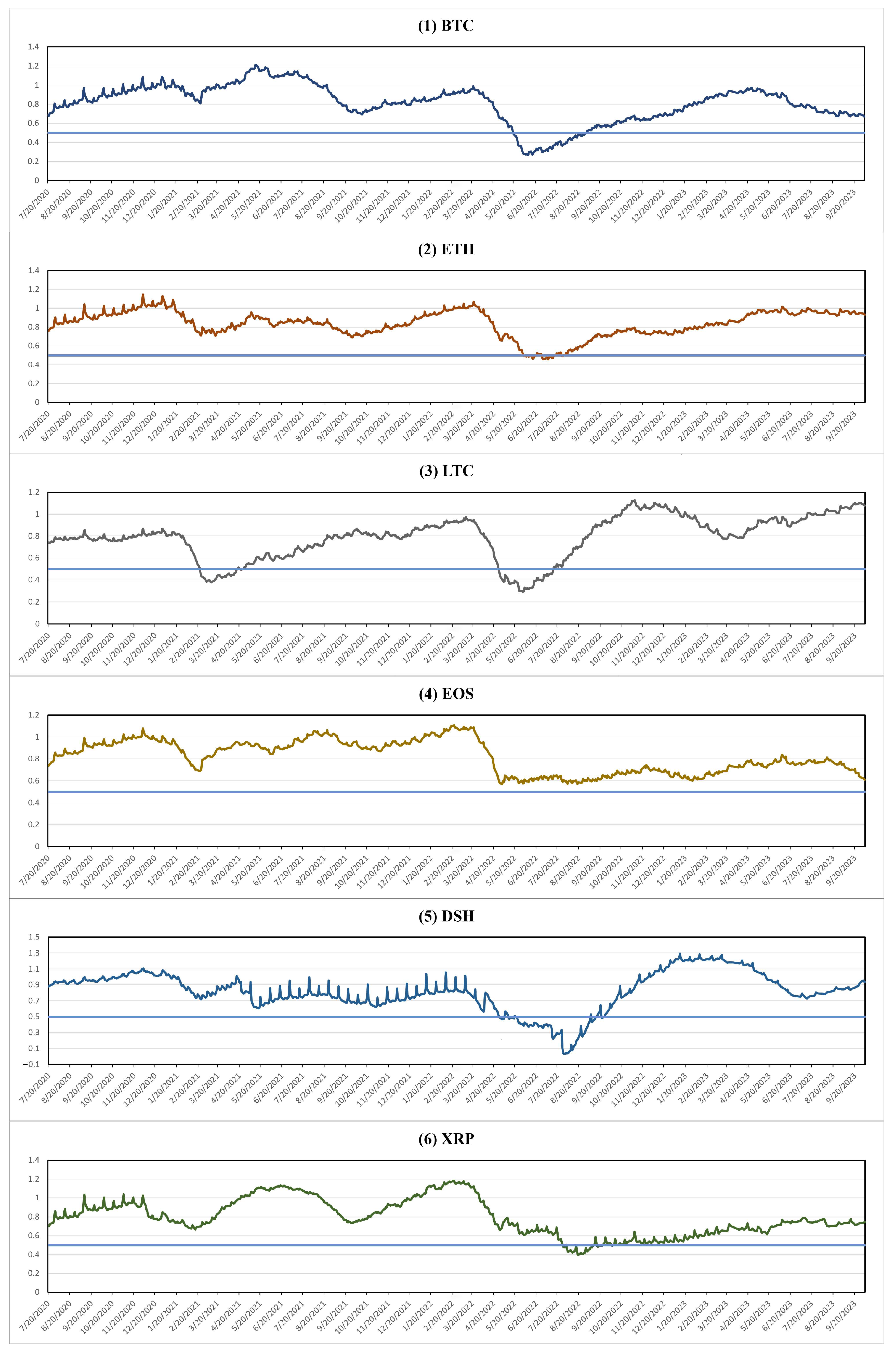
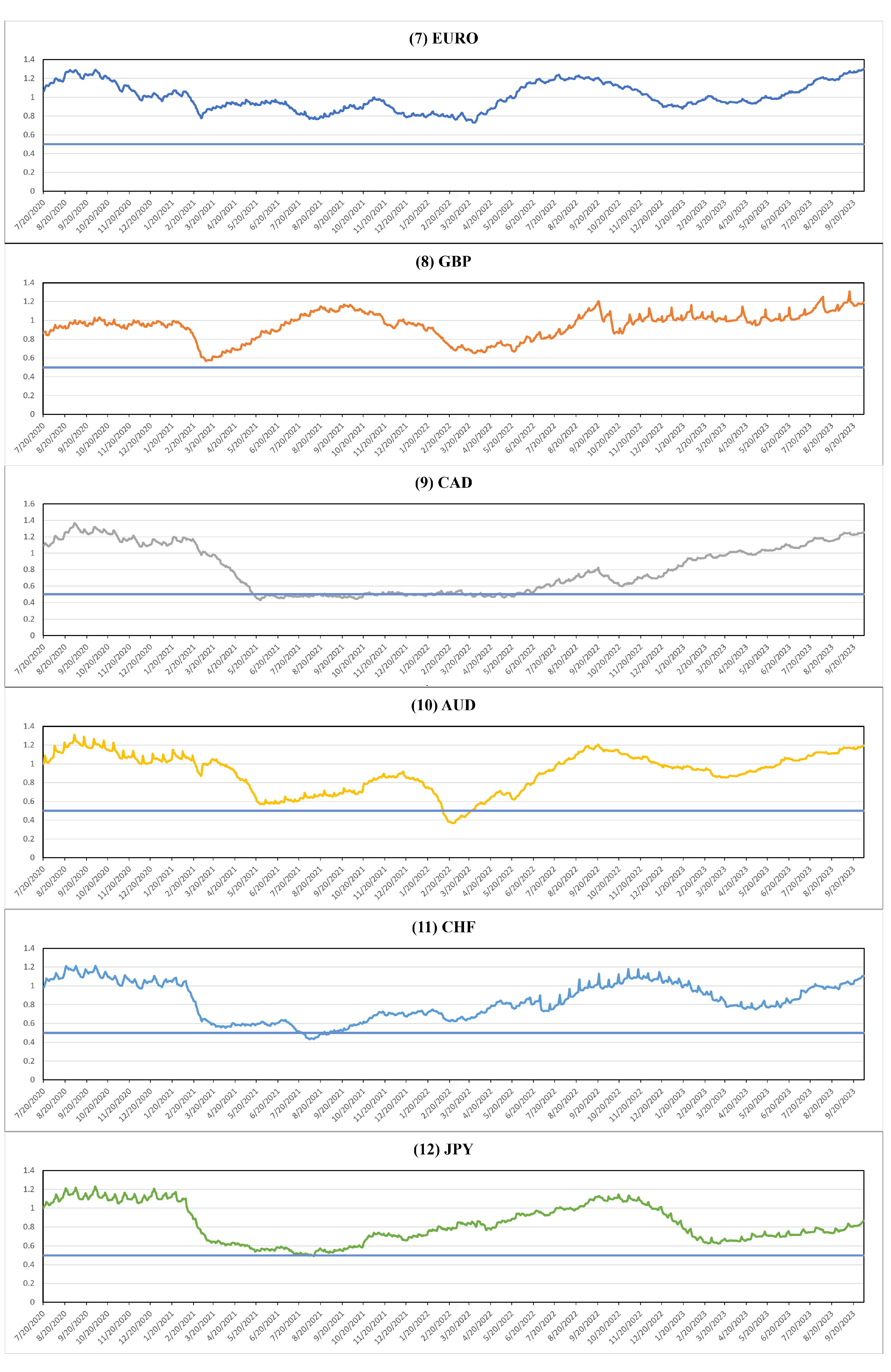
4.1. MinRV-Based Jump Detection Method
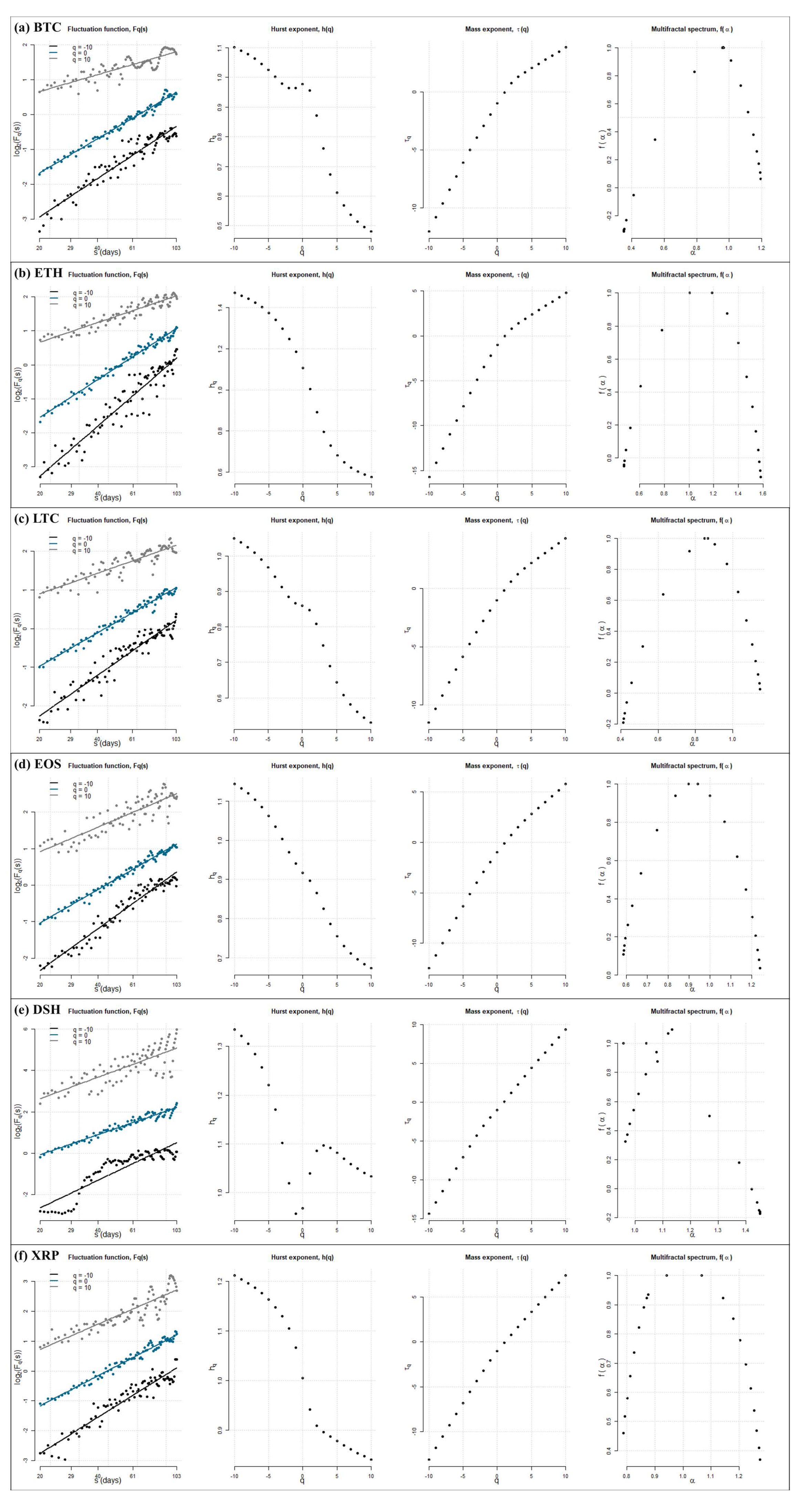
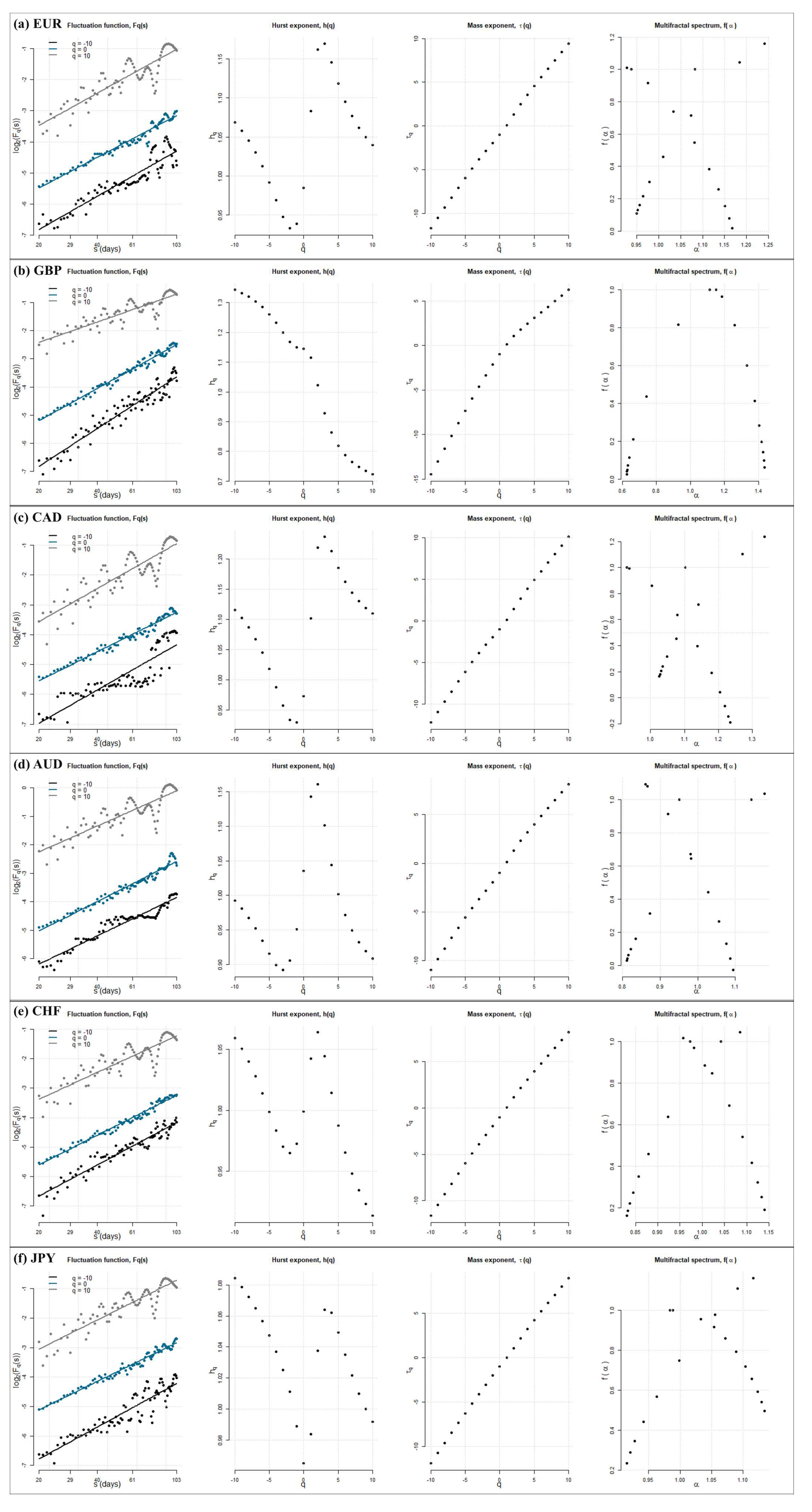
4.2. Multifractal Detrended Fluctuation Analysis—MFDFA
5. Results
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gkillas, K.; Gupta, R.; Wohar, M.E. Volatility Jumps: The Role of Geopolitical Risks. Financ. Res. Lett. 2018, 27, 247–258. [Google Scholar] [CrossRef]
- Caldara, D.; Iacoviell, M. Measuring Geopolitical Risk. Am. Econ. Rev. 2022, 112, 1194–1225. [Google Scholar] [CrossRef]
- Bissoondoyal-Bheenick, E.; Brooks, R.; Do, H.X. Jump Connectedness in the European Foreign Exchange Market. In Advances in Econometrics, Operational Research, Data Science and Actuarial Studies; Contributions to Economics; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Baker, S.R.; Bloom, N.; Davis, S.J.; Sammon, M. What Triggers Stock Market Jumps? SSRN Electron. J.; NBER working paper 28687. Available online: https://www.nber.org/papers/w28687 (accessed on 20 August 2024).
- Gao, Y.; Zhao, C.; Sun, B.; Zhao, W. Effects of Investor Sentiment on Stock Volatility: New Evidences from Multi-Source Data in China’s Green Stock Markets. Financ. Innov. 2022, 8, 77. [Google Scholar] [CrossRef] [PubMed]
- Alqahtani, A.; Selmi, R.; Hongbing, O. The Financial Impacts of Jump Processes in the Crude Oil Price: Evidence from G20 Countries in the Pre- and Post-COVID-19. Resour. Policy 2021, 72, 102075. [Google Scholar] [CrossRef]
- Conlon, T.; Corbet, S.; Hou, Y.G. Contagion Effects of Permissionless, Worthless Cryptocurrency Tokens: Evidence from the Collapse of FTX. J. Int. Financ. Mark. Inst. Money 2024, 91, 101940. [Google Scholar] [CrossRef]
- Tong, Y.; Wan, N.; Dai, X.; Bi, X.; Wang, Q. China’s Energy Stock Market Jumps: To What Extent Does the COVID-19 Pandemic Play a Part? Energy Econ. 2022, 109, 105937. [Google Scholar] [CrossRef]
- Diaconaşu, D.E.; Mehdian, S.M.; Stoica, O. The Reaction of Financial Markets to Russia’s Invasion of Ukraine: Evidence from Gold, Oil, Bitcoin, and Major Stock Markets. Appl. Econ. Lett. 2023, 30, 2792–2796. [Google Scholar] [CrossRef]
- Karkowska, R.; Urjasz, S. How Does the Russian-Ukrainian War Change Connectedness and Hedging Opportunities? Comparison between Dirty and Clean Energy Markets versus Global Stock Indices. J. Int. Financ. Mark. Inst. Money 2023, 85, 101768. [Google Scholar] [CrossRef]
- Akyildirim, E.; Conlon, T.; Corbet, S.; Goodell, J.W. Understanding the FTX Exchange Collapse: A Dynamic Connectedness Approach. Financ. Res. Lett. 2023, 53, 103643. [Google Scholar] [CrossRef]
- Jalan, A.; Matkovskyy, R. Systemic Risks in the Cryptocurrency Market: Evidence from the FTX Collapse. Financ. Res. Lett. 2023, 53, 103670. [Google Scholar] [CrossRef]
- Zhang, C. Testing for Self-Exciting Jumps in Bitcoin Returns. SSRN Electron. J. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3686237 (accessed on 20 August 2024).
- Choi, K.; Yu, W.C.; Zivot, E. Long Memory versus Structural Breaks in Modeling and Forecasting Realized Volatility. J. Int. Money Financ. 2010, 29, 857–875. [Google Scholar] [CrossRef]
- Degiannakis, S.; Floros, C. Intra-Day Realized Volatility for European and USA Stock Indices. Glob. Financ. J. 2016, 29, 24–41. [Google Scholar] [CrossRef]
- Oh, G.; Kim, S.; Eom, C. Long-Term Memory and Volatility Clustering in High-Frequency Price Changes. Phys. A Stat. Mech. Its Appl. 2008, 387, 1247–1254. [Google Scholar] [CrossRef]
- Maasoumi, E.; McAleer, M. Realized Volatility and Long Memory: An Overview. Econ. Rev. 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Tian, Y.; Shi, D.; Li, H. The Long Memory of the Jump Intensity of the Price Process. J. Math. Financ. 2021, 11, 176–189. [Google Scholar] [CrossRef]
- Corsi, F.; Ren, R. Volatility Forecasting: The Jumps Do Matter; Global COE Hi-Stat Discussion Paper Series gd08-036; Institute of Economic Research, Hitotsubashi University: Tokyo, Japan, 2008; pp. 1–35. [Google Scholar]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X. Roughing It up: Including Jump Components in the Measurement, Modeling, and Forecasting of Return Volatility. Rev. Econ. Stat. 2007, 89, 701–720. [Google Scholar] [CrossRef]
- Busch, T.; Christensen, B.J.; Nielsen, M.Ø. The Role of Implied Volatility in Forecasting Future Realized Volatility and Jumps in Foreign Exchange, Stock, and Bond Markets. J. Econom. 2011, 160, 48–57. [Google Scholar] [CrossRef]
- Forsberg, L.; Ghysels, E. Why Do Absolute Returns Predict Volatility so Well? J. Financ. Econom. 2007, 5, 31–67. [Google Scholar] [CrossRef]
- Giot, P.; Laurent, S. The Information Content of Implied Volatility in Light of the Jump/Continuous Decomposition of Realized Volatility. J. Futures Mark. 2007, 27, 337–359. [Google Scholar] [CrossRef]
- Shalen, C.T. Volume, Volatility, and the Dispersion of Beliefs. Rev. Financ. Stud. 1993, 6, 405–435. [Google Scholar] [CrossRef]
- Wang, J. A Model of Competitive Stock Trading Volume. J. Political Econ. 1994, 102, 127–168. [Google Scholar] [CrossRef]
- Hawkes, A.G. Spectra of Some Self-Exciting and Mutually Exciting Point Processes. Biometrika 1971, 58, 83–90. [Google Scholar] [CrossRef]
- Hawkes, A.G. Point Spectra of Some Mutually Exciting Point Processes. J. R. Stat. Soc. Ser. B Stat. Methodol. 1971, 33, 438–443. [Google Scholar] [CrossRef]
- Hawkes, A.G.; Oakes, D. A Cluster Process Representation of a Self-Exciting Process. J. Appl. Probab. 1974, 11, 493–503. [Google Scholar] [CrossRef]
- Aït-Sahalia, Y.; Cacho-Diaz, J.; Laeven, R.J.A. Modeling Financial Contagion Using Mutually Exciting Jump Processes. J. Financ. Econ. 2015, 117, 585–606. [Google Scholar] [CrossRef]
- Fulop, A.; Li, J.; Yu, J. Self-Exciting Jumps, Learning, and Asset Pricing Implications. Rev. Financ. Stud. 2015, 28, 876–912. [Google Scholar] [CrossRef]
- Carr, P.; Wu, L. Leverage Effect, Volatility Feedback, and Self-Exciting Market Disruptions. J. Financ. Quant. Anal. 2017, 52, 2119–2156. [Google Scholar] [CrossRef]
- Ali, H.; Aslam, F.; Ferreira, P. Modeling Dynamic Multifractal Efficiency of Us Electricity Market. Energies 2021, 14, 6145. [Google Scholar] [CrossRef]
- Fu, Z.; Niu, H.; Wang, W. Market Efficiency and Cross-Correlations of Chinese New Energy Market with Other Assets: Evidence from Multifractality Analysis. Comput. Econ. 2023, 62, 1287–1311. [Google Scholar] [CrossRef]
- Mensi, W.; Vo, X.V.; Kang, S.H. Upside-Downside Multifractality and Efficiency of Green Bonds: The Roles of Global Factors and COVID-19. Financ. Res. Lett. 2021, 43, 101995. [Google Scholar] [CrossRef]
- Barunik, J.; Aste, T.; Di Matteo, T.; Liu, R. Understanding the Source of Multifractality in Financial Markets. Phys. A Stat. Mech. Its Appl. 2012, 391, 4234–4251. [Google Scholar] [CrossRef]
- Fama, E.F. Efficient Market Hypothesis: A Review of Theory and Empirical Work. J. Financ. 1970, 25, 28–30. [Google Scholar] [CrossRef]
- Peters, E.E. Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility. J. Financ. 1993, 48, 2041–2044. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic Organization of DNA Nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series. Phys. A Stat. Mech. Appl. 2002, 316, 87–144. [Google Scholar] [CrossRef]
- da Silva Filho, A.C.; Maganini, N.D.; de Almeida, E.F. Multifractal Analysis of Bitcoin Market. Phys. A Stat. Mech. Appl. 2018, 512, 954–967. [Google Scholar] [CrossRef]
- Mnif, E.; Jarboui, A.; Mouakhar, K. How the Cryptocurrency Market Has Performed during COVID 19? A Multifractal Analysis. Financ. Res. Lett. 2020, 36, 101647. [Google Scholar] [CrossRef]
- Shao, Y.H.; Xu, H.A.N.; Liu, Y.L.; Xu, H.C. Multifractal Behavior of Cryptocurrencies before and during Covid-19. Fractals 2021, 29, 2150132. [Google Scholar] [CrossRef]
- Aslam, F.; Aziz, S.; Nguyen, D.K.; Mughal, K.S.; Khan, M. On the Efficiency of Foreign Exchange Markets in Times of the COVID-19 Pandemic. Technol. Forecast. Soc. Chang. 2020, 161, 120261. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.; Ning, Y. Comparative Analysis of the Multifractality and Efficiency of Exchange Markets: Evidence from Exchange Rates Dynamics of Major World Currencies. Phys. A Stat. Mech. Appl. 2019, 535, 122365. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Hernandez, J.A.; Hanif, W.; Kayani, G.M. Intraday Return Inefficiency and Long Memory in the Volatilities of Forex Markets and the Role of Trading Volume. Phys. A Stat. Mech. Appl. 2018, 506, 433–450. [Google Scholar] [CrossRef]
- Aslam, F.; Ferreira, P.; Ali, H.; Kauser, S. Herding Behavior during the Covid-19 Pandemic: A Comparison between Asian and European Stock Markets Based on Intraday Multifractality. Eurasian Econ. Rev. 2022, 12, 333–359. [Google Scholar] [CrossRef]
- Aslam, F.; Ferreira, P.; Mohti, W. Investigating Efficiency of Frontier Stock Markets Using Multifractal Detrended Fluctuation Analysis. Int. J. Emerg. Mark. 2023, 18, 1650–1676. [Google Scholar] [CrossRef]
- Aslam, F.; Ferreira, P.; Mughal, K.S.; Bashir, B. Intraday Volatility Spillovers among European Financial Markets during COVID-19. Int. J. Financ. Stud. 2021, 9, 5. [Google Scholar] [CrossRef]
- Stosic, T.; Nejad, S.A.; Stosic, B. Multifractal Analysis of Brazilian Agricultural Market. Fractals 2020, 28, 2050076. [Google Scholar] [CrossRef]
- Baumöhl, E. Are Cryptocurrencies Connected to Forex? A Quantile Cross-Spectral Approach. Financ. Res. Lett. 2019, 29, 363–372. [Google Scholar] [CrossRef]
- Böhme, R.; Christin, N.; Edelman, B.; Moore, T. Bitcoin: Economics, Technology, and Governance. J. Econ. Perspect. 2015, 29, 213–238. [Google Scholar] [CrossRef]
- Qureshi, S.; Aftab, M.; Bouri, E.; Saeed, T. Dynamic Interdependence of Cryptocurrency Markets: An Analysis across Time and Frequency. Phys. A Stat. Mech. Appl. 2020, 559, 125077. [Google Scholar] [CrossRef]
- Manavi, S.A.; Jafari, G.; Rouhani, S.; Ausloos, M. Demythifying the Belief in Cryptocurrencies Decentralized Aspects. A Study of Cryptocurrencies Time Cross-Correlations with Common Currencies, Commodities and Financial Indices. Phys. A Stat. Mech. Appl. 2020, 556, 124759. [Google Scholar] [CrossRef]
- Gnabo, J.Y.; Lahaye, J.; Laurent, S.; Lecourt, C. Do Jumps Mislead the FX Market? Quant Financ. 2012, 12, 1521–1532. [Google Scholar] [CrossRef]
- Ausloos, M. Statistical Physics in Foreign Exchange Currency and Stock Markets. Phys. A Stat. Mech. Appl. 2000, 285, 48–65. [Google Scholar] [CrossRef]
- Drozdz, S.; Kwapień, J.; Oświȩcimka, P.; Rak, R. The Foreign Exchange Market: Return Distributions, Multifractality, Anomalous Multifractality and the Epps Effect. New J. Phys. 2010, 12, 105003. [Google Scholar] [CrossRef]
- Xu, Z.; Gençay, R. Scaling, Self-Similarity and Multifractality in FX Markets. Phys. A Stat. Mech. Appl. 2003, 323, 578–590. [Google Scholar] [CrossRef]
- Berger, D.; Chaboud, A.; Hjalmarsson, E. What Drives Volatility Persistence in the Foreign Exchange Market? J. Financ. Econ. 2009, 94, 192–213. [Google Scholar] [CrossRef]
- Tabak, B.M.; Cajueiro, D.O. Assessing Inefficiency in Euro Bilateral Exchange Rates. Phys. A Stat. Mech. Appl. 2006, 367, 319–327. [Google Scholar] [CrossRef]
- Gębarowski, R.; Oświęcimka, P.; Wątorek, M.; Drożdż, S. Detecting Correlations and Triangular Arbitrage Opportunities in the Forex by Means of Multifractal Detrended Cross-Correlations Analysis. Nonlinear Dyn. 2019, 98, 2349–2364. [Google Scholar] [CrossRef]
- Oh, G.; Eom, C.; Havlin, S.; Jung, W.S.; Wang, F.; Stanley, H.E.; Kim, S. A Multifractal Analysis of Asian Foreign Exchange Markets. Eur. Phys. J. B 2012, 85, 214. [Google Scholar] [CrossRef]
- Bouri, E.; Roubaud, D.; Shahzad, S.J.H. Do Bitcoin and Other Cryptocurrencies Jump Together? Q. Rev. Econ. Financ. 2020, 76, 396–409. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T. The Volatility of Bitcoin and Its Role as a Medium of Exchange and a Store of Value. Empir. Econ. 2021, 61, 2662–2683. [Google Scholar] [CrossRef]
- Urquhart, A.; Zhang, H. Is Bitcoin a Hedge or Safe Haven for Currencies? An Intraday Analysis. Int. Rev. Financ. Anal. 2019, 63, 49–57. [Google Scholar] [CrossRef]
- Chemkha, R.; BenSaïda, A.; Ghorbel, A. Connectedness between Cryptocurrencies and Foreign Exchange Markets: Implication for Risk Management. J. Multinatl. Financ. Manag. 2021, 59, 100666. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Balli, F.; Naeem, M.A.; Hasan, M.; Arif, M. Do Conventional Currencies Hedge Cryptocurrencies? Q. Rev. Econ. Financ. 2022, 85, 223–228. [Google Scholar] [CrossRef]
- Corbet, S.; Meegan, A.; Larkin, C.; Lucey, B.; Yarovaya, L. Exploring the Dynamic Relationships between Cryptocurrencies and Other Financial Assets. Econ. Lett. 2018, 165, 28–34. [Google Scholar] [CrossRef]
- Dyhrberg, A.H. Bitcoin, Gold and the Dollar—A GARCH Volatility Analysis. Financ. Res. Lett. 2016, 16, 85–92. [Google Scholar] [CrossRef]
- Raza, S.A.; Ahmed, M.; Aloui, C. On the Asymmetrical Connectedness between Cryptocurrencies and Foreign Exchange Markets: Evidence from the Nonparametric Quantile on Quantile Approach. Res. Int. Bus. Financ. 2022, 61, 101627. [Google Scholar] [CrossRef]
- Drozdz, S.; Kwapień, J.; Oświecimka, P.; Stanisz, T.; Watorek, M. Complexity in Economic and Social Systems: Cryptocurrency Market at around COVID-19. Entropy 2020, 22, 1043. [Google Scholar] [CrossRef]
- Wątorek, M.; Drożdż, S.; Kwapień, J.; Minati, L.; Oświęcimka, P.; Stanuszek, M. Multiscale Characteristics of the Emerging Global Cryptocurrency Market. Phys. Rep. 2021, 901, 1–82. [Google Scholar] [CrossRef]
- Andersen, T.G.; Dobrev, D.; Schaumburg, E. Jump-Robust Volatility Estimation Using Nearest Neighbor Truncation. J. Econom. 2012, 169, 75–93. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E. Power and Bipower Variation with Stochastic Volatility and Jumps. J. Financ. Econom. 2004, 2, 1–37. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X.; Labys, P. The Distribution of Realized Exchange Rate Volatility. J. Am. Stat. Assoc. 2001, 96, 42–55. [Google Scholar] [CrossRef]
- Lee, S.S.; Hannig, J. Detecting Jumps from Lévy Jump Diffusion Processes. J. Financ. Econ. 2010, 96, 271–290. [Google Scholar] [CrossRef]
- Lee, S.S.; Mykland, P.A. Jumps in Financial Markets: A New Nonparametric Test and Jump Dynamics. Rev. Financ. Stud. 2008, 21, 2535–2563. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Shephard, N. Econometrics of Testing for Jumps in Financial Economics Using Bipower Variation. J. Financ. Econom. 2006, 4, 1–30. [Google Scholar] [CrossRef]
- Corsi, F.; Pirino, D.; Renò, R. Threshold Bipower Variation and the Impact of Jumps on Volatility Forecasting. J. Econ. 2010, 159, 276–288. [Google Scholar] [CrossRef]
- Huang, X.; Tauchen, G. The Relative Contribution of Jumps to Total Price Variance. J. Financ. Econom. 2005, 3, 456–499. [Google Scholar] [CrossRef]
- Aït-Sahalia, Y.; Jacod, J. Testing for Jumps in a Discretely Observed Process. Ann. Stat. 2009, 37, 184–222. [Google Scholar] [CrossRef]
- Podolskij, M.; Ziggel, D. New Tests for Jumps in Semimartingale Models. Stat. Inference Stoch. Process. 2010, 13, 15–41. [Google Scholar] [CrossRef]
- Jiang, G.J.; Oomen, R.C.A. Testing for Jumps When Asset Prices Are Observed with Noise-a “Swap Variance” Approach. J. Econ. 2008, 144, 352–370. [Google Scholar] [CrossRef]
- Maneesoonthorn, W.; Martin, G.M.; Forbes, C.S. High-Frequency Jump Tests: Which Test Should We Use? J. Econ. 2020, 219, 478–487. [Google Scholar] [CrossRef]
- Todorov, V.; Bollerslev, T. Jumps and Betas: A New Framework for Disentangling and Estimating Systematic Risks. J. Econ. 2010, 157, 220–235. [Google Scholar] [CrossRef]
- Lee, S.S.; Mykland, P.A. Jumps in Equilibrium Prices and Market Microstructure Noise. J. Econ. 2012, 168, 396–406. [Google Scholar] [CrossRef]
- Xue, Y.; Gençay, R.; Fagan, S. Jump Detection with Wavelets for High-Frequency Financial Time Series. Quant. Financ. 2014, 14, 1427–1444. [Google Scholar] [CrossRef]
- Peng, H.; Kitagawa, G.; Tamura, Y.; Xi, Y.; Qin, Y.; Chen, X. A Modeling Approach to Financial Time Series Based on Market Microstructure Model with Jumps. Appl. Soft Comput. J. 2015, 29, 40–51. [Google Scholar] [CrossRef]
- Yeung, J.F.K.A.; Wei, Z.-K.; Chan, K.Y.; Lau, H.Y.K.; Yiu, K.-F.C. Jump Detection in Financial Time Series Using Machine Learning Algorithms. Soft Comput. 2020, 24, 1789–1801. [Google Scholar] [CrossRef]
- Chaim, P.; Laurini, M.P. Volatility and Return Jumps in Bitcoin. Econ. Lett. 2018, 173, 158–163. [Google Scholar] [CrossRef]
- Gronwald, M. Is Bitcoin a Commodity? On Price Jumps, Demand Shocks, and Certainty of Supply. J. Int. Money Financ. 2019, 97, 86–92. [Google Scholar] [CrossRef]
- Hou, A.J.; Wang, W.; Chen, C.Y.H.; Härdle, W.K. Pricing Cryptocurrency Options. J. Financ. Econom. 2020, 18, 250–279. [Google Scholar] [CrossRef]
- Applebaum, D. Levy processes and infinitely divisible distributions, by Ken-iti Sato. Pp. 486.£ 50. 1999. ISBN 0 521 55302 4 (Cambridge University Press). Math. Gaz. 2001, 85, 568–569. [Google Scholar] [CrossRef][Green Version]
- Merton, R.C. Option Pricing When Underlying Stock Returns Are Discontinuous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef]
- Scaillet, O.; Treccani, A.; Trevisan, C. High-Frequency Jump Analysis of the Bitcoin Market. J. Financ. Econom. 2020, 18, 209–232. [Google Scholar] [CrossRef]
- Eyjolfsson, H.; Tjøstheim, D. Self-Exciting Jump Processes with Applications to Energy Markets. Ann. Inst. Stat. Math. 2018, 70, 373–393. [Google Scholar] [CrossRef]
- Callegaro, G.; Mazzoran, A.; Sgarra, C. A Self-Exciting Modeling Framework for forward Prices in Power Markets. Appl. Stoch. Model. Bus. Ind. 2022, 38, 27–48. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Z.; Xu, M.; Peng, Z. Good and Bad Self-Excitation: Asymmetric Self-Exciting Jumps in Bitcoin Returns. Econ. Model. 2023, 119, 106124. [Google Scholar] [CrossRef]
- Boswijk, H.P.; Laeven, R.J.A.; Yang, X. Testing for Self-Excitation in Jumps. J. Econ. 2018, 203, 256–266. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Bouri, E. Can a Self-Exciting Jump Structure Better Capture the Jump Behavior of Cryptocurrencies? A Comparative Analysis with the S&P 500. Res. Int. Bus. Financ. 2024, 69, 102277. [Google Scholar] [CrossRef]
- Shrestha, K. Multifractal Detrended Fluctuation Analysis of Return on Bitcoin. Int. Rev. Financ. 2021, 21, 312–323. [Google Scholar] [CrossRef]
- Takaishi, T. Statistical Properties and Multifractality of Bitcoin. Phys. A Stat. Mech. Appl. 2018, 506, 507–519. [Google Scholar] [CrossRef]
- Vaz, C.; Pascoal, R.; Sebastião, H. Price Appreciation and Roughness Duality in Bitcoin: A Multifractal Analysis. Mathematics 2021, 9, 2088. [Google Scholar] [CrossRef]
- Partida, A.; Gerassis, S.; Criado, R.; Romance, M.; Giráldez, E.; Taboada, J. The Chaotic, Self-Similar and Hierarchical Patterns in Bitcoin and Ethereum Price Series. Chaos Solitons Fractals 2022, 165, 112806. [Google Scholar] [CrossRef]
- Gunay, S.; Kaşkaloğlu, K. Seeking a Chaotic Order in the Cryptocurrency Market. Math. Comput. Appl. 2019, 24, 36. [Google Scholar] [CrossRef]
- Stosic, D.; Stosic, D.; Ludermir, T.B.; Stosic, T. Multifractal Behavior of Price and Volume Changes in the Cryptocurrency Market. Phys. A Stat. Mech. Appl. 2019, 520, 54–61. [Google Scholar] [CrossRef]
- Bariviera, A.F. One Model Is Not Enough: Heterogeneity in Cryptocurrencies’ Multifractal Profiles. Financ. Res. Lett. 2021, 39, 101649. [Google Scholar] [CrossRef]
- de Salis, E.A.V.; dos Santos Maciel, L. How Does Price (in)Efficiency Influence Cryptocurrency Portfolios Performance? The Role of Multifractality. Quant. Financ. 2023, 23, 1637–1658. [Google Scholar] [CrossRef]
- Stošić, D.; Stošić, D.; Stošić, T.; Stanley, H.E. Multifractal Analysis of Managed and Independent Float Exchange Rates. Phys. A Stat. Mech. Appl. 2015, 428, 13–18. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.; Xu, Y. Nonlinearity and Efficiency Dynamics of Foreign Exchange Markets: Evidence from Multifractality and Volatility of Major Exchange Rates. Econ. Res. Ekon. Istraz. 2020, 33, 731–751. [Google Scholar] [CrossRef]
- Czech, K.; Pietrych, Ł. The Efficiency of the Polish Zloty Exchange Rate Market: The Uncovered Interest Parity and Fractal Analysis Approaches. Risks 2021, 9, 142. [Google Scholar] [CrossRef]
- Grech, D.; Mazur, Z. Can One Make Any Crash Prediction in Finance Using the Local Hurst Exponent Idea? Phys. A Stat. Mech. Its Appl. 2004, 336, 133–145. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, P. Forecasting Volatility of SSEC in Chinese Stock Market Using Multifractal Analysis. Phys. A Stat. Mech. Appl. 2008, 387, 1585–1592. [Google Scholar] [CrossRef]
- Fernandes, L.H.S.; de Araújo, F.H.A.; Silva, I.E.M. The (in)Efficiency of NYMEX Energy Futures: A Multifractal Analysis. Phys. A Stat. Mech. Appl. 2020, 556, 124783. [Google Scholar] [CrossRef]
- Jia, Z.; Cui, M.; Li, H. Research on the Relationship between the Multifractality and Long Memory of Realized Volatility in the SSECI. Phys. A Stat. Mech. Appl. 2012, 391, 740–749. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Fu, J.; Wu, X. Multifractal Analysis of Realized Volatilities in Chinese Stock Market. Comput. Econ. 2020, 56, 319–336. [Google Scholar] [CrossRef]
- Pirino, D. Jump Detection and Long Range Dependence. Phys. A Stat. Mech. Appl. 2009, 388, 1150–1156. [Google Scholar] [CrossRef]
- Ben Omrane, W.; Guesmi, K.; Qianru, Q.; Saadi, S. The High-Frequency Impact of Macroeconomic News on Jumps and Co-Jumps in the Cryptocurrency Markets. Ann. Oper. Res. 2023, 330, 177–209. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A. Realized Variance and Market Microstructure Noise. J. Bus. Econ. Stat. 2006, 24, 127–161. [Google Scholar] [CrossRef]
- Liu, L.Y.; Patton, A.J.; Sheppard, K. Does Anything Beat 5-Minute RV? A Comparison of Realized Measures across Multiple Asset Classes. J. Econ. 2015, 187, 293–311. [Google Scholar] [CrossRef]
- Umar, Z.; Jareño, F.; González, M.; de la, O. The Impact of COVID-19-Related Media Coverage on the Return and Volatility Connectedness of Cryptocurrencies and Fiat Currencies. Technol. Forecast. Soc. Chang. 2021, 172, 121025. [Google Scholar] [CrossRef]
- Caferra, R.; Vidal-Tomás, D. Who Raised from the Abyss? A Comparison between Cryptocurrency and Stock Market Dynamics during the COVID-19 Pandemic. Financ. Res. Lett. 2021, 43, 101954. [Google Scholar] [CrossRef]
- Polat, O.; Kabakçı Günay, E. Cryptocurrency Connectedness Nexus the COVID-19 Pandemic: Evidence from Time-Frequency Domains. Stud. Econ. Financ. 2021, 38, 946–963. [Google Scholar] [CrossRef]
- Rubbaniy, G.; Polyzos, S.; Rizvi, S.K.A.; Tessema, A. COVID-19, Lockdowns and Herding towards a Cryptocurrency Market-Specific Implied Volatility Index. Econ. Lett. 2021, 207, 110017. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Anas, M.; Bouri, E. Price Explosiveness in Cryptocurrencies and Elon Musk’s Tweets. Financ. Res. Lett. 2022, 47, 102695. [Google Scholar] [CrossRef]
- Alvarez, F.; Argente, D.; Van Patten, D. Are Cryptocurrencies Currencies? Bitcoin as Legal Tender in El Salvador. Science 2023, 382, eadd2844. [Google Scholar] [CrossRef]
- Conlon, T.; Corbet, S.; Hu, Y. The Collapse of the FTX Exchange: The End of Cryptocurrency’s Age of Innocence. Br. Account. Rev. 2023, 101277. [Google Scholar] [CrossRef]
- Azzam, I.; El-Masry, A.A.; Yamani, E. Foreign Exchange Market Efficiency during COVID-19 Pandemic. Int. Rev. Econ. Financ. 2023, 86, 717–730. [Google Scholar] [CrossRef]
- Fasanya, I.O.; Oyewole, O.; Adekoya, O.B.; Odei-Mensah, J. Dynamic Spillovers and Connectedness between COVID-19 Pandemic and Global Foreign Exchange Markets. Econ. Res. Ekon. Istraz. 2021, 34, 2059–2084. [Google Scholar] [CrossRef]
- Hu, S.; Gu, Z.; Wang, Y.; Zhang, X. An Analysis of the Clustering Effect of a Jump Risk Complex Network in the Chinese Stock Market. Phys. A Stat. Mech. Appl. 2019, 523, 622–630. [Google Scholar] [CrossRef]
- Liu, L.; Wan, J. A Study of Correlations between Crude Oil Spot and Futures Markets: A Rolling Sample Test. Phys. A Stat. Mech. Appl. 2011, 390, 3754–3766. [Google Scholar] [CrossRef]
- Zhao, R.; Cui, Y. Dynamic Cross-Correlations Analysis on Economic Policy Uncertainty and US Dollar Exchange Rate: AMF-DCCA Perspective. Discret. Dyn. Nat. Soc. 2021, 2021, 6668912. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Kim, S.; Chang, W. Asymmetric Market Efficiency Using the Index-Based Asymmetric-MFDFA. Phys. A Stat. Mech. Appl. 2018, 512, 1278–1294. [Google Scholar] [CrossRef]
- Zhuang, X.; Wei, D. Asymmetric Multifractality, Comparative Efficiency Analysis of Green Finance Markets: A Dynamic Study by Index-Based Model. Phys. A Stat. Mech. Appl. 2022, 604, 127949. [Google Scholar] [CrossRef]
- Hanousek, J.; Novotný, J. Price Jumps in Visegrad-Country Stock Markets: An Empirical Analysis. Emerg. Mark. Rev. 2012, 13, 184–201. [Google Scholar] [CrossRef]
- Dungey, M.; Erdemlioglu, D.; Matei, M.; Yang, X. Testing for Mutually Exciting Jumps and Financial Flights in High Frequency Data. J. Econ. 2018, 202, 18–44. [Google Scholar] [CrossRef]
- Celeste, V.; Corbet, S.; Gurdgiev, C. Fractal Dynamics and Wavelet Analysis: Deep Volatility and Return Properties of Bitcoin, Ethereum and Ripple. Q. Rev. Econ. Financ. 2020, 76, 310–324. [Google Scholar] [CrossRef]
- Corbet, S.; Lucey, B.; Yarovaya, L. Datestamping the Bitcoin and Ethereum Bubbles. Financ. Res. Lett. 2018, 26, 81–88. [Google Scholar] [CrossRef]
- Gronwald, M. How Explosive Are Cryptocurrency Prices? Financ. Res. Lett. 2021, 38, 101603. [Google Scholar] [CrossRef]
- Zhang, L.; Bouri, E.; Chen, Y. Co-Jump Dynamicity in the Cryptocurrency Market: A Network Modelling Perspective. Financ. Res. Lett. 2023, 58, 104372. [Google Scholar] [CrossRef]
- Kang, H.J.; Lee, S.G.; Park, S.Y. Information Efficiency in the Cryptocurrency Market: The Efficient-Market Hypothesis. J. Comput. Inf. Syst. 2022, 62, 622–631. [Google Scholar] [CrossRef]
- Banerjee, A.K.; Akhtaruzzaman, M.; Dionisio, A.; Almeida, D.; Sensoy, A. Nonlinear Nexus between Cryptocurrency Returns and COVID-19 News Sentiment. J. Behav. Exp. Financ. 2022, 36, 100747. [Google Scholar] [CrossRef] [PubMed]
- Raimundo Júnior, G.D.; Palazzi, R.B.; Tavares, R.D.; Klotzle, M.C. Market Stress and Herding: A New Approach to the Cryptocurrency Market. J. Behav. Financ. 2022, 23, 43–57. [Google Scholar] [CrossRef]
- Almeida, J.; Gonçalves, T.C. A Systematic Literature Review of Investor Behavior in the Cryptocurrency Markets. J. Behav. Exp. Financ. 2023, 37, 100785. [Google Scholar] [CrossRef]
- Kakinaka, S.; Umeno, K. Asymmetric Volatility Dynamics in Cryptocurrency Markets on Multi-Time Scales. Res. Int. Bus. Financ. 2022, 62, 101754. [Google Scholar] [CrossRef]
- Phillip, A.; Chan, J.; Peiris, S. A New Look at Cryptocurrencies. Econ. Lett. 2018, 163, 6–9. [Google Scholar] [CrossRef]
- Kristoufek, L.; Vosvrda, M. Cryptocurrencies Market Efficiency Ranking: Not so Straightforward. Phys. A Stat. Mech. Appl. 2019, 531, 120853. [Google Scholar] [CrossRef]
- Lansiaux, E.; Tchagaspanian, N.; Forget, J. Community Impact on a Cryptocurrency: Twitter Comparison Example between Dogecoin and Litecoin. Front. Blockchain 2022, 5, 829865. [Google Scholar] [CrossRef]
- Katsiampa, P. An Empirical Investigation of Volatility Dynamics in the Cryptocurrency Market. Res. Int. Bus. Financ. 2019, 50, 322–335. [Google Scholar] [CrossRef]
- Al-Yahyaee, K.H.; Mensi, W.; Ko, H.U.; Yoon, S.M.; Kang, S.H. Why Cryptocurrency Markets Are Inefficient: The Impact of Liquidity and Volatility. North Am. J. Econ. Financ. 2020, 52, 101168. [Google Scholar] [CrossRef]
- Bariviera, A.F. The Inefficiency of Bitcoin Revisited: A Dynamic Approach. Econ. Lett. 2017, 161, 1–4. [Google Scholar] [CrossRef]
- Al-Yahyaee, K.H.; Mensi, W.; Yoon, S.M. Efficiency, Multifractality, and the Long-Memory Property of the Bitcoin Market: A Comparative Analysis with Stock, Currency, and Gold Markets. Financ. Res. Lett. 2018, 27, 228–234. [Google Scholar] [CrossRef]
- Caporale, G.M.; Gil-Alana, L.; Plastun, A. Persistence in the Cryptocurrency Market. Res. Int. Bus. Financ. 2018, 46, 141–148. [Google Scholar] [CrossRef]
- Bouri, E.; Azzi, G.; Dyhrberg, A.H. On the Return-Volatility Relationship in the Bitcoin Market around the Price Crash of 2013. Economics 2017, 11, 1–16. [Google Scholar] [CrossRef]
- Jiang, Y.; Nie, H.; Ruan, W. Time-Varying Long-Term Memory in Bitcoin Market. Financ. Res. Lett. 2018, 25, 280–284. [Google Scholar] [CrossRef]
- Aslam, F.; Memon, B.A.; Hunjra, A.I.; Bouri, E. The Dynamics of Market Efficiency of Major Cryptocurrencies. Glob. Financ. J. 2023, 58, 100899. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.; Lee, Y. Dissecting the Terra-LUNA Crash: Evidence from the Spillover Effect and Information Flow. Financ. Res. Lett. 2023, 53, 103590. [Google Scholar] [CrossRef]
- Vidal-Tomás, D.; Briola, A.; Aste, T. FTX’s Downfall and Binance’s Consolidation: The Fragility of Centralised Digital Finance. Phys. A Stat. Mech. Appl. 2023, 625, 129044. [Google Scholar] [CrossRef]
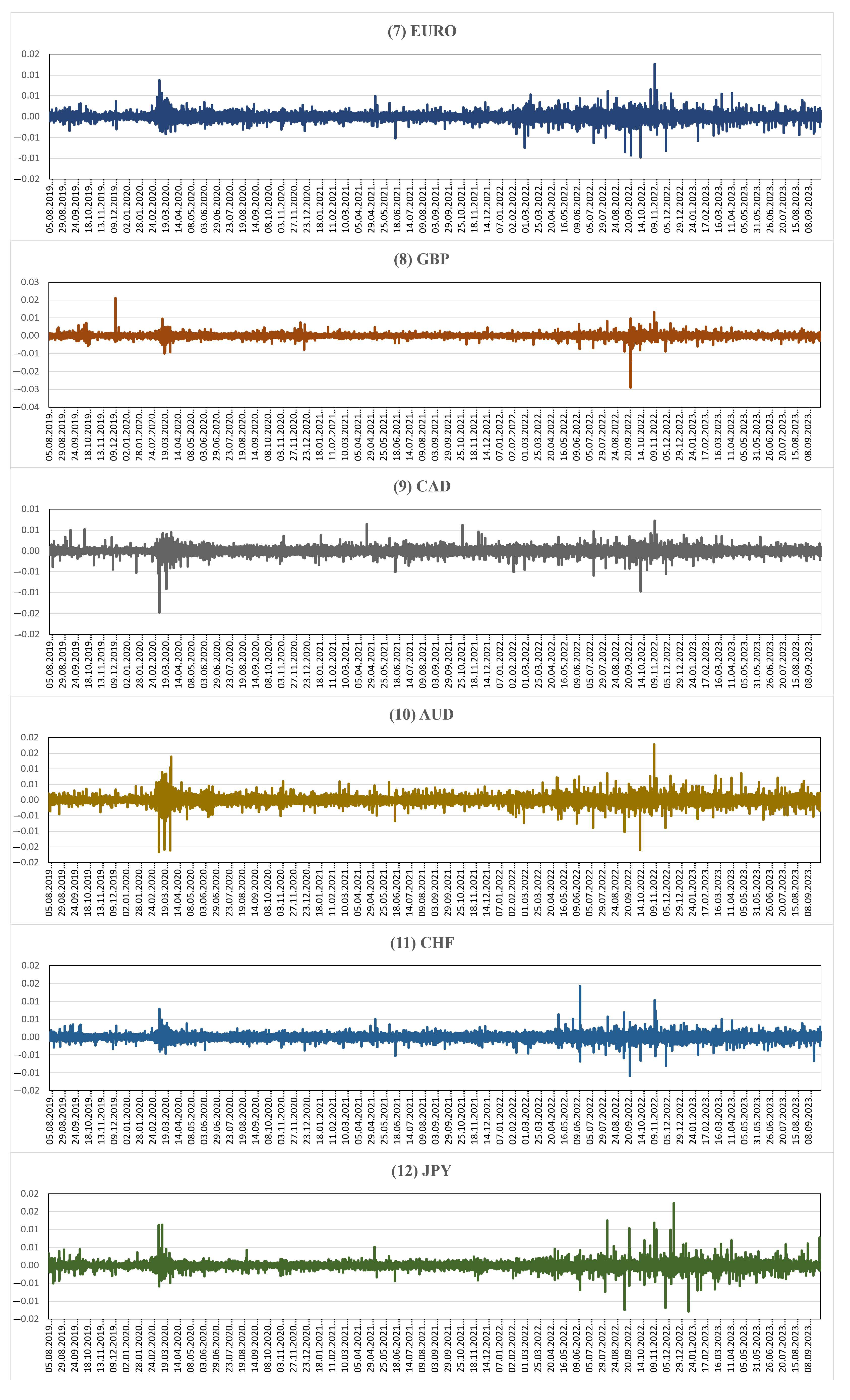
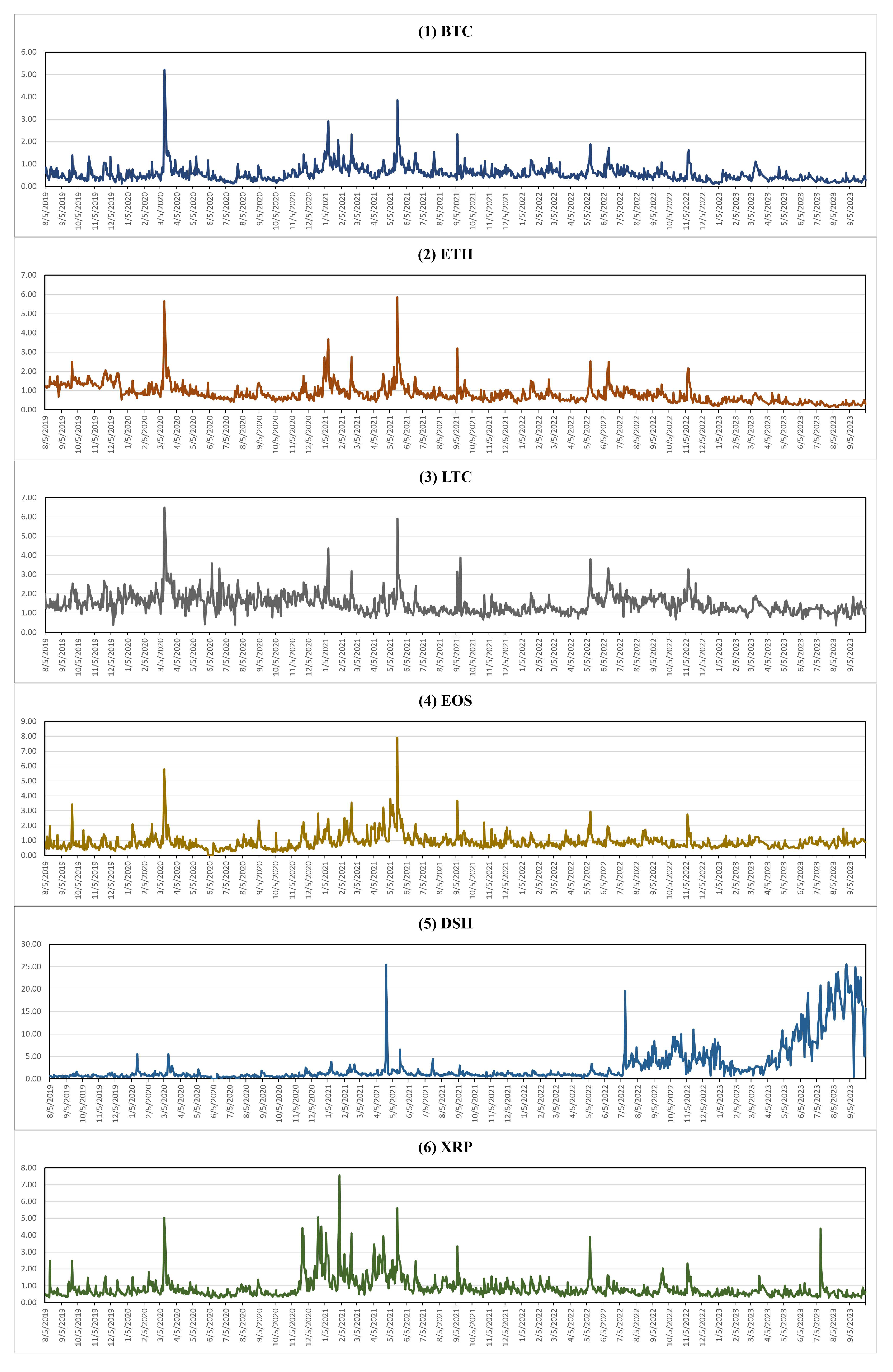
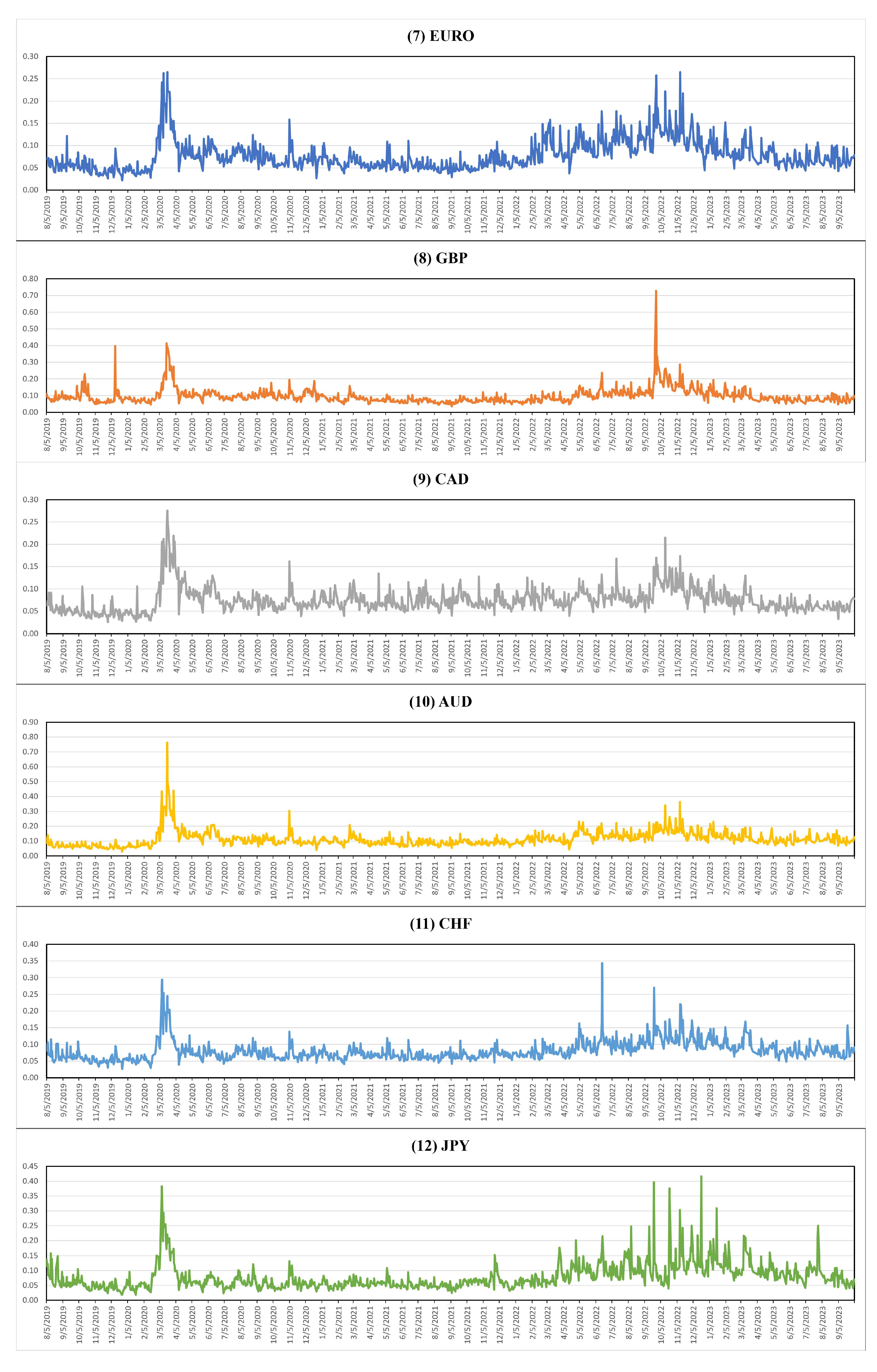
| BTC | ETH | LTC | EOS | DSH | XRP | |
|---|---|---|---|---|---|---|
| Minimum | −0.1334667 | −0.1541507 | −0.2231436 | −0.2568316 | −0.2407215 | −0.2274537 |
| Maximum | 0.1216104 | 0.3050206 | 0.2513144 | 0.2175317 | 0.3965783 | 0.5527772 |
| Mean | 0.0000021 | 0.0000055 | −0.0000018 | −0.0000073 | −0.0000048 | 0.0000016 |
| Standard Deviation | 0.0025901 | 0.0037046 | 0.0057694 | 0.0040466 | 0.0167969 | 0.0042855 |
| Kurtosis | 229.0234226 | 274.7694729 | 62.1027108 | 405.9822622 | 116.2893777 | 1242.2956452 |
| Skewness | −0.5426317 | 1.4953974 | −0.2512815 | −4.2124110 | 0.0780610 | 7.2159910 |
| Count | 298,943 | 298,943 | 298,943 | 298,943 | 298,943 | 298,943 |
| EURO | GBP | CAD | AUD | CHF | JPY | |
| Minimum | −0.0097635 | −0.0289145 | −0.0147172 | −0.0166296 | −0.0108653 | −0.0128702 |
| Maximum | 0.0126936 | 0.0211009 | 0.0072101 | 0.0177998 | 0.0142757 | 0.0173053 |
| Mean | −0.0000001 | 0.0000000 | −0.0000001 | −0.0000001 | 0.0000003 | −0.0000011 |
| Standard Deviation | 0.0002998 | 0.0003831 | 0.0002846 | 0.0004437 | 0.0003034 | 0.0003188 |
| Kurtosis | 46.0856627 | 180.2839098 | 52.3844694 | 60.8869285 | 50.1620370 | 128.0273178 |
| Skewness | 0.1686466 | −0.9621895 | −0.6799445 | −0.2011033 | 0.3431656 | 1.3942462 |
| Count | 298,943 | 298,943 | 298,943 | 298,943 | 298,943 | 298,943 |
| BTC | ETH | LTC | EOS | DSH | XRP | |
|---|---|---|---|---|---|---|
| Minimum | 0.0979 | 0.1493 | 0.3557 | 0.0000 | 0.0000 | 0.2623 |
| Maximum | 5.2125 | 5.8436 | 6.4878 | 7.9134 | 25.5424 | 7.5467 |
| Mean | 0.5813 | 0.8514 | 1.4960 | 0.9022 | 2.5563 | 0.8865 |
| Standard Deviation | 0.3781 | 0.4981 | 0.5579 | 0.5610 | 4.0132 | 0.6731 |
| Kurtosis | 36.0972 | 21.2925 | 15.1661 | 33.6345 | 12.1073 | 19.3090 |
| Skewness | 4.3281 | 3.1258 | 2.5592 | 4.1620 | 3.3372 | 3.6039 |
| Count | 1039 | 1039 | 1039 | 1039 | 1039 | 1039 |
| EURO | GBP | CAD | AUD | CHF | JPY | |
| Minimum | 0.0217 | 0.0357 | 0.0257 | 0.0293 | 0.0266 | 0.0180 |
| Maximum | 0.2649 | 0.7284 | 0.2757 | 0.7620 | 0.3434 | 0.4160 |
| Mean | 0.0785 | 0.0984 | 0.0755 | 0.1149 | 0.0811 | 0.0784 |
| Standard Deviation | 0.0339 | 0.0473 | 0.0280 | 0.0526 | 0.0299 | 0.0447 |
| Kurtosis | 4.6571 | 37.8015 | 8.1816 | 29.3221 | 12.5004 | 12.0677 |
| Skewness | 1.6924 | 4.3350 | 2.0683 | 3.6970 | 2.5341 | 2.7267 |
| Count | 1039 | 1039 | 1039 | 1039 | 1039 | 1039 |
| Order Q | BTC | ETH | LTC | EOS | DSH | XRP | EURO | GBP | CAD | AUD | CHF | JPY |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −10 | 1.1009 | 1.4712 | 1.0494 | 1.1431 | 1.3342 | 1.2119 | 1.0687 | 1.3426 | 1.1156 | 0.9921 | 1.0595 | 1.0843 |
| −9 | 1.0905 | 1.4588 | 1.0386 | 1.1324 | 1.3212 | 1.2049 | 1.0578 | 1.3322 | 1.1024 | 0.9807 | 1.0505 | 1.0787 |
| −8 | 1.0781 | 1.4438 | 1.0256 | 1.1196 | 1.305 | 1.1967 | 1.0450 | 1.3197 | 1.0865 | 0.9674 | 1.0401 | 1.0723 |
| −7 | 1.0633 | 1.4255 | 1.0099 | 1.1041 | 1.2843 | 1.1872 | 1.0299 | 1.3044 | 1.0675 | 0.9519 | 1.028 | 1.065 |
| −6 | 1.0457 | 1.4028 | 0.991 | 1.0852 | 1.257 | 1.1762 | 1.0122 | 1.2853 | 1.0447 | 0.9344 | 1.0141 | 1.0568 |
| −5 | 1.025 | 1.3748 | 0.9682 | 1.062 | 1.2205 | 1.1633 | 0.9916 | 1.2614 | 1.0177 | 0.9158 | 0.9988 | 1.0474 |
| −4 | 1.002 | 1.3402 | 0.9417 | 1.0344 | 1.1704 | 1.1481 | 0.9690 | 1.2321 | 0.9875 | 0.8994 | 0.9833 | 1.037 |
| −3 | 0.9795 | 1.2979 | 0.9129 | 1.0028 | 1.1019 | 1.1296 | 0.9473 | 1.1988 | 0.9571 | 0.8922 | 0.9704 | 1.0253 |
| −2 | 0.9643 | 1.2472 | 0.8857 | 0.9698 | 1.0188 | 1.105 | 0.9332 | 1.1678 | 0.9339 | 0.9056 | 0.965 | 1.011 |
| −1 | 0.9651 | 1.1858 | 0.8669 | 0.9401 | 0.9569 | 1.0665 | 0.9386 | 1.1496 | 0.9298 | 0.9508 | 0.9727 | 0.9887 |
| 0 | 0.9767 | 1.107 | 0.8597 | 0.9172 | 0.9674 | 1.0055 | 0.9847 | 1.1452 | 0.9732 | 1.0354 | 0.9991 | 0.9651 |
| 1 | 0.9568 | 1.004 | 0.8481 | 0.8963 | 1.0392 | 0.9417 | 1.0832 | 1.1143 | 1.1017 | 1.143 | 1.0426 | 0.9839 |
| 2 | 0.8709 | 0.8914 | 0.8083 | 0.8657 | 1.0858 | 0.9089 | 1.1621 | 1.0222 | 1.2191 | 1.1606 | 1.064 | 1.0376 |
| 3 | 0.7614 | 0.7971 | 0.7481 | 0.8254 | 1.0969 | 0.896 | 1.1694 | 0.9285 | 1.2366 | 1.1011 | 1.0447 | 1.064 |
| 4 | 0.6736 | 0.7289 | 0.6901 | 0.7865 | 1.0919 | 0.887 | 1.1456 | 0.8628 | 1.2128 | 1.0438 | 1.0144 | 1.062 |
| 5 | 0.612 | 0.6812 | 0.6435 | 0.7547 | 1.0813 | 0.8781 | 1.1186 | 0.8185 | 1.1854 | 1.0019 | 0.9873 | 1.0494 |
| 6 | 0.5689 | 0.6472 | 0.6082 | 0.7301 | 1.0697 | 0.8693 | 1.0954 | 0.7876 | 1.1626 | 0.9718 | 0.9656 | 1.035 |
| 7 | 0.5377 | 0.6223 | 0.5813 | 0.7109 | 1.0588 | 0.8611 | 1.0767 | 0.765 | 1.1445 | 0.9495 | 0.9483 | 1.0217 |
| 8 | 0.5143 | 0.6035 | 0.5605 | 0.6958 | 1.0489 | 0.8536 | 1.0617 | 0.7479 | 1.1303 | 0.9324 | 0.9344 | 1.01 |
| 9 | 0.4962 | 0.5889 | 0.544 | 0.6837 | 1.0402 | 0.8469 | 1.0496 | 0.7344 | 1.1189 | 0.9189 | 0.9231 | 1.0001 |
| 10 | 0.4817 | 0.5773 | 0.5308 | 0.6738 | 1.0327 | 0.8409 | 1.0397 | 0.7236 | 1.1096 | 0.9081 | 0.9138 | 0.9916 |
| Hurst Average | 0.8459 | 1.0427 | 0.8149 | 0.9111 | 1.1230 | 1.0180 | 1.0467 | 1.0592 | 1.0875 | 0.9789 | 0.9962 | 1.0327 |
| Delta H | 0.6192 | 1.0485 | 0.5802 | 0.8169 | 1.3669 | 1.0528 | 1.1084 | 1.0662 | 1.2252 | 0.9002 | 0.9733 | 1.0759 |
| Delta Alpha | 0.8440 | 1.1109 | 0.7346 | 0.6547 | 0.4943 | 0.488 | 0.3132 | 0.8098 | 0.4067 | 0.3673 | 0.3104 | 0.2196 |
| Fractal Dimension | 1.1541 | 0.9573 | 1.1851 | 1.0889 | 0.8770 | 0.9820 | 0.9533 | 0.9408 | 0.9125 | 1.0211 | 1.0038 | 0.9673 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, H.; Aftab, M.; Aslam, F.; Ferreira, P. Inner Multifractal Dynamics in the Jumps of Cryptocurrency and Forex Markets. Fractal Fract. 2024, 8, 571. https://doi.org/10.3390/fractalfract8100571
Ali H, Aftab M, Aslam F, Ferreira P. Inner Multifractal Dynamics in the Jumps of Cryptocurrency and Forex Markets. Fractal and Fractional. 2024; 8(10):571. https://doi.org/10.3390/fractalfract8100571
Chicago/Turabian StyleAli, Haider, Muhammad Aftab, Faheem Aslam, and Paulo Ferreira. 2024. "Inner Multifractal Dynamics in the Jumps of Cryptocurrency and Forex Markets" Fractal and Fractional 8, no. 10: 571. https://doi.org/10.3390/fractalfract8100571
APA StyleAli, H., Aftab, M., Aslam, F., & Ferreira, P. (2024). Inner Multifractal Dynamics in the Jumps of Cryptocurrency and Forex Markets. Fractal and Fractional, 8(10), 571. https://doi.org/10.3390/fractalfract8100571








