The Spatial Variation of Soil Structure Fractal Derived from Particle Size Distributions at the Basin Scale
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area Selection
2.2. Test Arrangement
2.3. Sample Testing and Fractal Dimension Theory
2.4. Theories and Methods of Spatial Variation Analysis
2.4.1. Spatial Autocorrelation
2.4.2. Normality Test
2.4.3. Spatial Heterogeneity
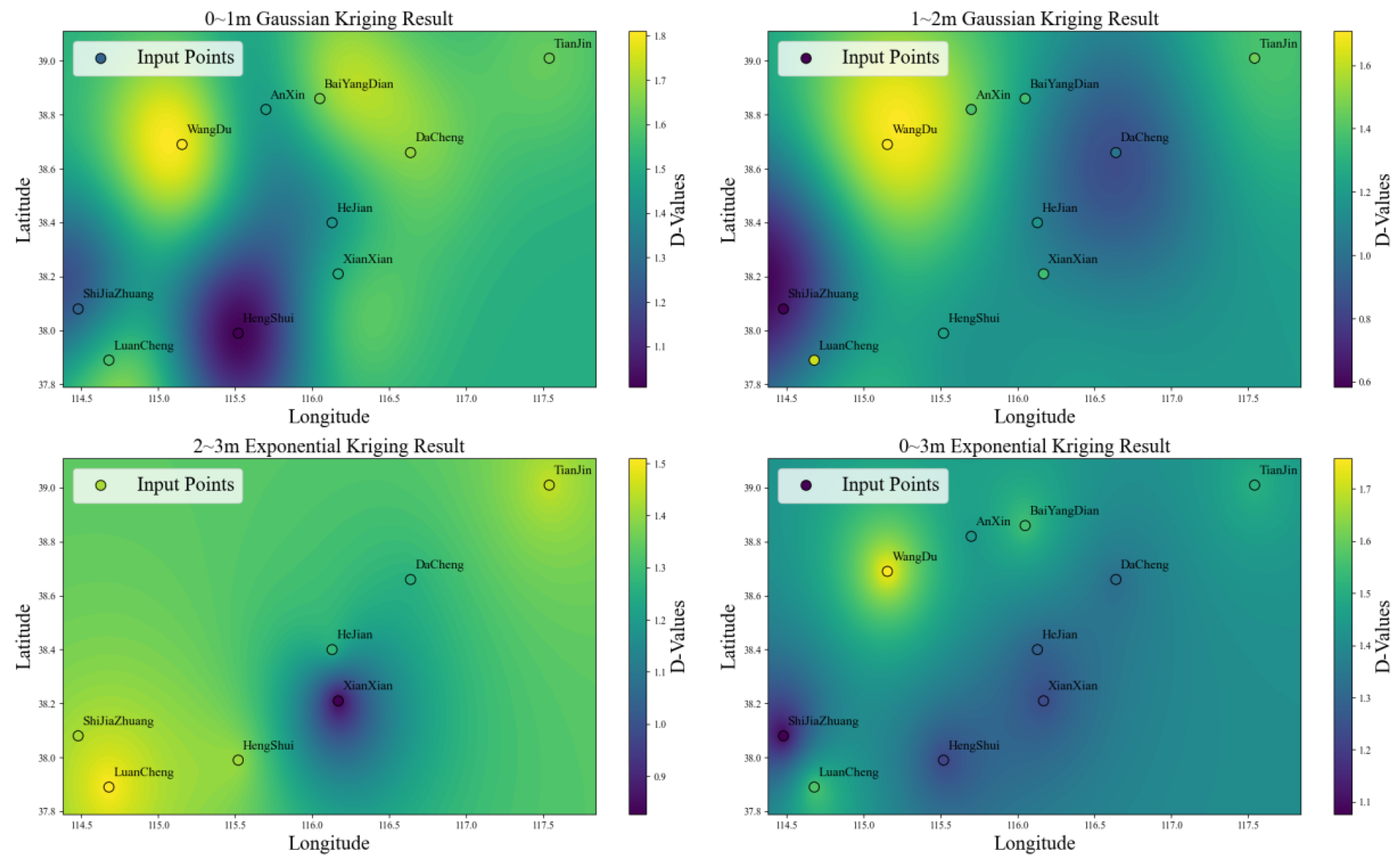
2.4.4. Kriging Interpolation
3. Results
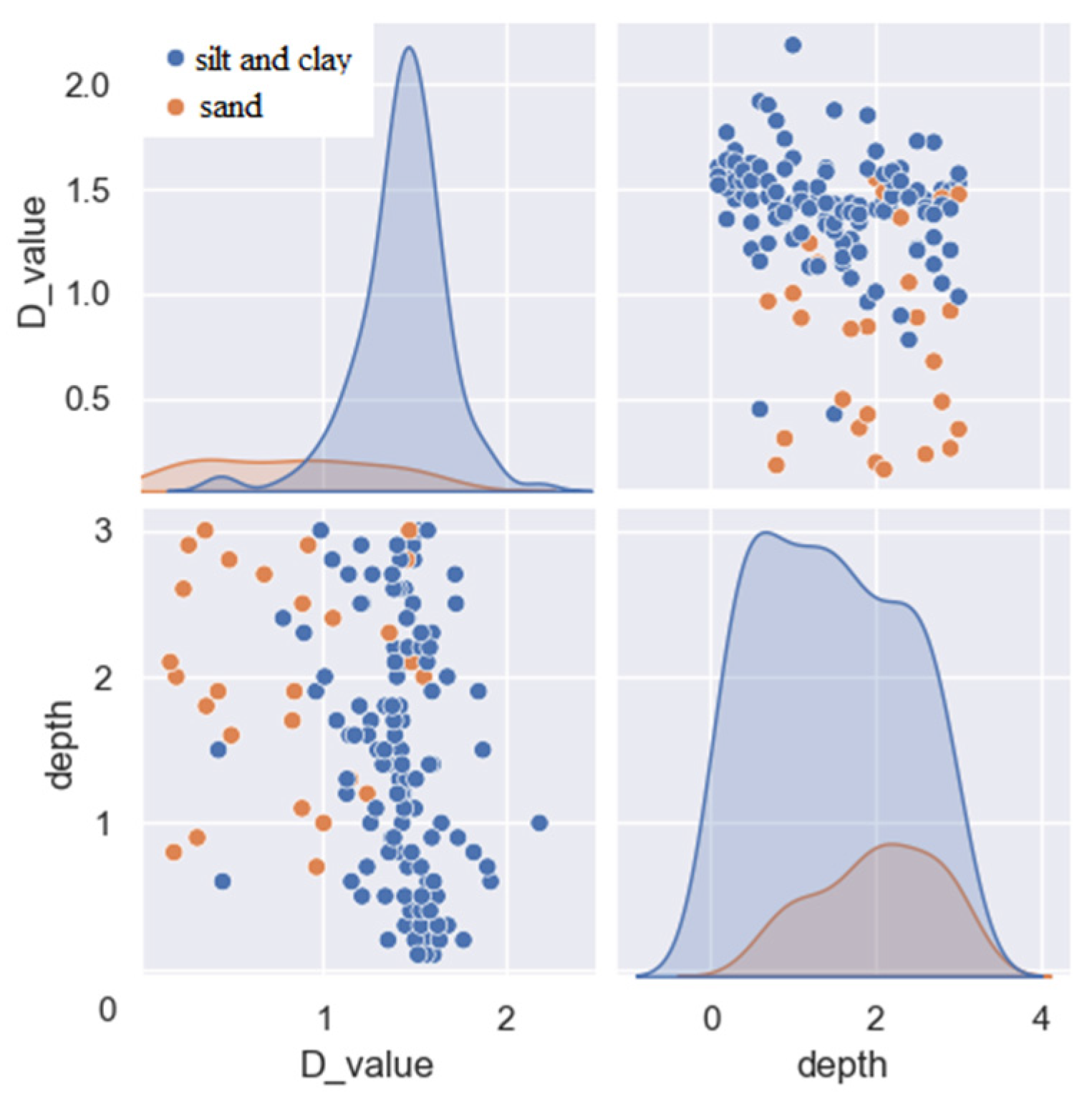
3.1. Soil Structure Profile Fractal Dimension (D-Value) Calculation
3.2. Spatial Variation of Soil Structure Fractal (D-Value) at the Basin Scale
3.2.1. Spatial Variation of D Values in Two River Basins
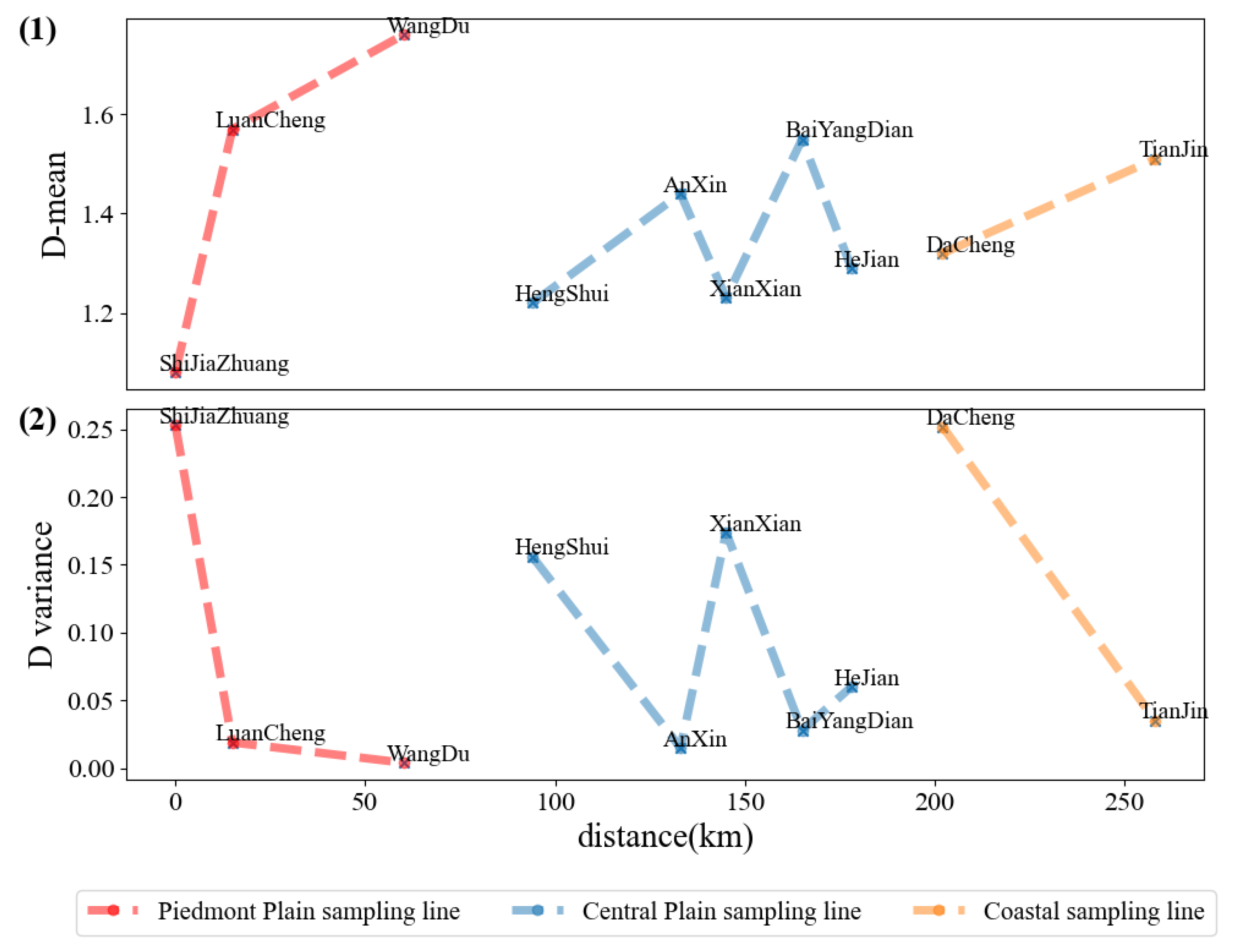
3.2.2. Spatial Variation of D Values in Piedmont Plain–Central Plain–Coastal Area
3.3. Spatial Variation Analysis
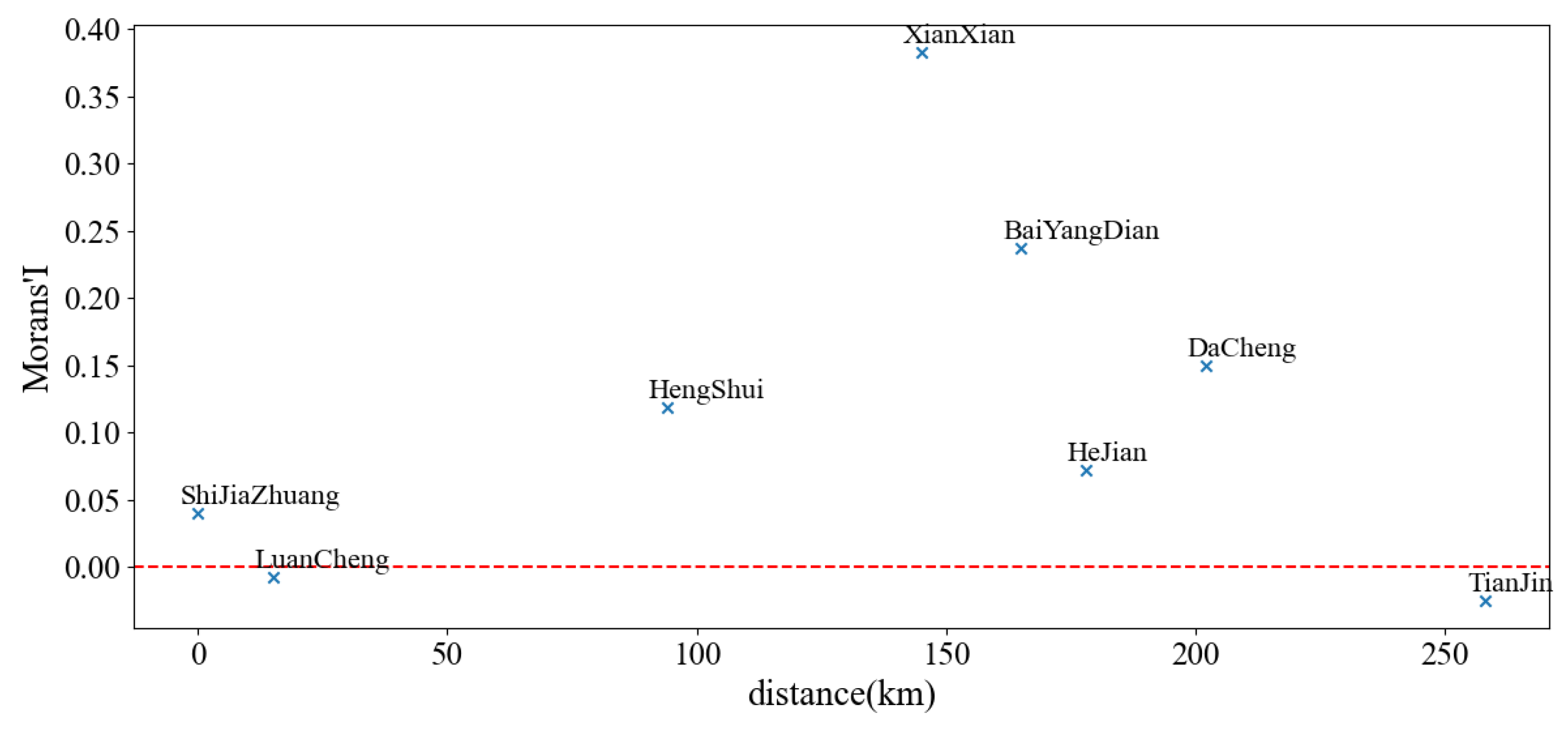
3.3.1. Spatial Autocorrelation Analysis of Profiles
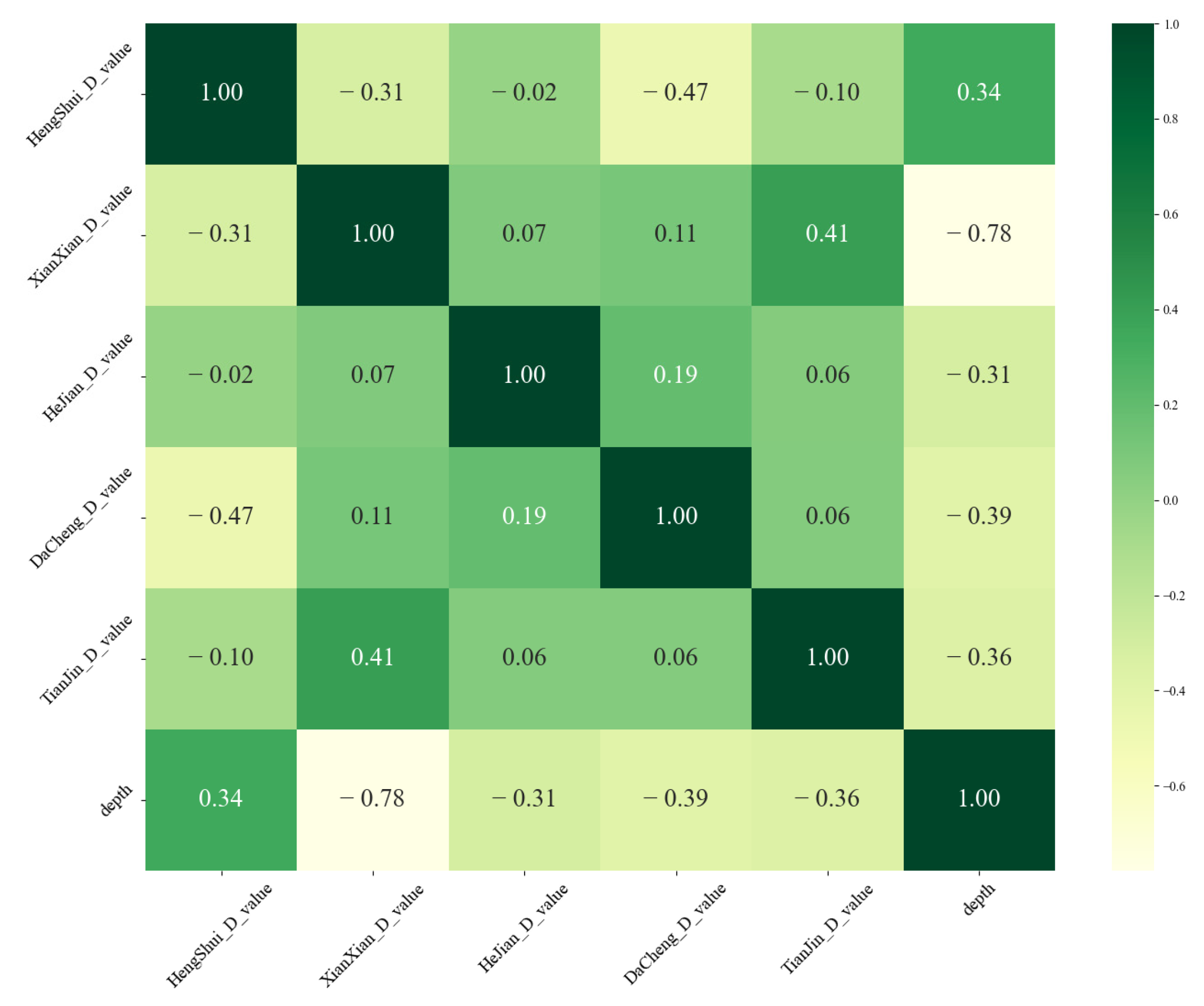
3.3.2. Spatial Correlation Analysis among Profiles
3.3.3. Spatial Analysis Models
4. Discussion
- (1)
- Physical Significance of Soil D Value and Its Role in Large-Scale Spatial Variation
- (2)
- Relationship between Soil D Value and Soil Particle Composition
- (3)
- Relationship between Soil D Value Spatial Variation and Climate, Regional Changes, and Human-Intensive Activity
5. Conclusions
- The mean, variance, and three-dimensional spatial distribution of soil D-values at the basin scale consistently showed that soil D-values tended to become more uniform from the piedmont to the coastal area. The closer one is to the coastal area, the smaller the differences in particle size, tending towards finer particles with less variation in depth. The maximum and minimum mean D-values were found in the piedmont profiles, and the variance in the D-values also exhibited their maximum and minimum values in the piedmont profiles. Coastal profiles show the smallest range of mean D-values (1.32–1.51). The mean variance of soil D-values in the Ziya River Basin was as high as 0.136, whereas it was 0.059 in the Daqing River Basin, indicating that the spatial variability of soil structural fractals in the Ziya River Basin was significantly larger than that in the Daqing River Basin.
- The results of the profile correlation analysis using the Moran’s I index method and heatmap analysis were consistent, showing that the Xian County profile had the highest degree of autocorrelation (Moran’s I index of 0.38) and the strongest correlation between the D-value and burial depth (−0.78). Inter-profile correlation analysis indicates that the Hengshui and Dacheng profiles have the strongest spatial correlation of soil D-values (−0.47), whereas the D-value correlations between other profiles are relatively low.
- Qualitative analysis, together with quantitative analysis results from the variogram and semivariance function models, consistently indicated that soil D-values exhibited the strongest spatial variability in the 1–2 m layer across all profiles in both basins. The coefficient of variation for the 1–2 m layer was 23.595%, which was significantly higher than those for the 0–1 m (14.569%) and 2–3 m (16.284%) layers. A Gaussian model was selected for the 0–1 and 1–2 m soil layers, whereas an exponential model was selected for the 2–3 and 0–3 m soil layers. In this study, the nugget-to-sill ratios for the 0–1, 1–2, and 0–3 m soil layers were all less than 0.25, indicating a strong spatial correlation across all layers.
- At the basin scale, soil structural fractals exhibited varying degrees of spatial variability in both the horizontal and vertical profiles. This variability results from the combined effects of internal and external factors, including the physical significance of soil D values, the relationship between soil D values and soil particle composition, climate change, geographic factors, and human activity. The specific contributions and mechanisms of these factors to the spatial variability of the soil structural fractals at different scales, ranges, and depths require further investigation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, Q.; Bai, H.; Liu, L.; Zhao, Y.; Zhao, Y. Model Representation and Quantitative Analysis of Pore Three-Dimensional Morphological Structure Based on Soil Computed Tomography Images. Eur. J. Soil Sci. 2020, 72, 1530–1542. [Google Scholar] [CrossRef]
- Mohammadi, M.; Shabanpour, M.; Mohammadi, M.H.; Davatgar, N. Characterizing Spatial Variability of Soil Textural Fractions and Fractal Parameters Derived from Particle Size Distributions. Pedosphere 2019, 29, 224–234. [Google Scholar] [CrossRef]
- Xie, J.; Liu, X.; Jasechko, S.; Berghuijs, W.R.; Wang, K.; Liu, C.; Reichstein, M.; Jung, M.; Koirala, S. Majority of Global River Flow Sustained by Groundwater. Nat. Geosci. 2024, 17, 770–777. [Google Scholar] [CrossRef]
- Yang, H.-F.; Meng, R.-F.; Bao, X.-L.; Cao, W.-G.; Li, Z.-Y.; Xu, B.-Y. Assessment of Water Level Threshold for Groundwater Restoration and Over-Exploitation Remediation the Beijing-Tianjin- Hebei Plain. J. Groundwater Sci. Eng. 2022, 10, 113–127. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, F.; Li, R.M.; Ma, Z.S.; Guo, H.Q.; Ma, H. Geologic and Geochemical Evolutive Feature of Topsoil in Northland of Haihe River Piedmont Plain to Coastal Plain, China. Geol. Bull. China 2010, 29, 1210–1214. [Google Scholar]
- Yuan, Y.; Zhang, T.L.; Zhang, C.; Ma, R. Spatial Variability of Vertical Permeability Coefficient from the Piedmont to the Coastal Area of Notrh China Plain. South-North Water Divers. Water Sci. Technol. 2020, 18, 184–190. [Google Scholar] [CrossRef]
- He, Y.P. Shallow Groundwater Hydrogeochemical Simulation Modeling from Piedmont Plain to Coastal Plain Shallow Area in the North Chian Plain. Master’s Thesis, China University of Geoscience, Beijing, China, 2012. [Google Scholar]
- Lee Peyton, R.; Gantzer, C.J.; Anderson, S.R.; Haeffner, B.; Pfeifer, P. Fractal Dimension to Describe Soil Macropore Structure Using X Ray Computed Tomography. Water Resour. Res. 1994, 30, 691–700. [Google Scholar] [CrossRef]
- Xia, Y.; Cai, J.; Wei, W.; Hu, X.; Wang, X.; Ge, X. A New Method for Calculating Fractal Dimensions of Porous Media Based on Pore Size Distribution. Fractals 2018, 26, 1850006. [Google Scholar] [CrossRef]
- Kong, B.; He, S.-H.; Tao, Y.; Xia, J. Pore Structure and Fractal Characteristics of Frozen–Thawed Soft Soil. Fractal Fract. 2022, 6, 183. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Chen, W.; Zhao, J.; Lv, J.; Song, J.; Cao, X. Influence of Groundwater Depth on Pile–Soil Mechanical Properties and Fractal Characteristics under Cyclic Loading. Fractal Fract. 2022, 6, 198. [Google Scholar] [CrossRef]
- Prosperini, N.; Perugini, D. Particle Size Distributions of Some Soils from the Umbria Region (Italy): Fractal Analysis and Numerical Modelling. Geoderma 2008, 145, 185–195. [Google Scholar] [CrossRef]
- Armstrong, A.C. On the Fractal Dimensions of Some Transient Soil Properties. J. Soil Sci. 1986, 37, 641–652. [Google Scholar] [CrossRef]
- Fu, X.; Ding, H.; Sheng, Q.; Zhang, Z.; Yin, D.; Chen, F. Fractal Analysis of Particle Distribution and Scale Effect in a Soil–Rock Mixture. Fractal Fract. 2022, 6, 120. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, Y.; Luo, W.; Deng, X. Mechanical Characterization and Parameter Identification of Rheological Deformation of Subgrade Compacted Soil. Chin. J. Rock Mech. Eng. 2011, 30, 208–216. [Google Scholar]
- Sun, Y.; Gao, Y.; Ju, W. Fractional Plasticity and Its Application in Constitutive Model for Sands. Chin. J. Geotech. Eng. 2018, 40, 1535–1541. [Google Scholar] [CrossRef]
- Anderson, A.N.; McBratney, A.B.; Crawford, J.W. Applications of Fractals to Soil Studies. Adv. Agron. 1997, 63, 1–76. [Google Scholar] [CrossRef]
- He, Y.; Lv, D. Fractal Expression of Soil Particle-Size Distribution at the Basin Scale. Open Geosci. 2022, 14, 70–78. [Google Scholar] [CrossRef]
- Westerholt, R. A Simulation Study to Explore Inference about Global Moran’s I with Random Spatial Indexes. Geogr. Anal. 2022, 55, 621–650. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Sun, X.; Guo, C.; Zhang, J.; Sun, J.; Cui, J.; Liu, M. Spatial-Temporal Difference between Nitrate in Groundwater and Nitrogen in Soil Based on Geostatistical Analysis. J. Groundwater Sci. Eng. 2023, 11, 37–46. [Google Scholar] [CrossRef]
- Ersahin, S. Comparing Ordinary Kriging and Cokriging to Estimate Infiltration Rate. Soil Sci. Soc. Am. J. 2003, 67, 1848–1855. [Google Scholar] [CrossRef]
- Ersahin, S.; Gunal, H.; Kutlu, T.; Yetgin, B.; Coban, S. Estimating Specific Surface Area and Cation Exchange Capacity in Soils Using Fractal Dimension of Particle-Size Distribution. Geoderma 2006, 136, 588–597. [Google Scholar] [CrossRef]
- He, Y.; Wang, G. Identifying the Soil Structure of the Piedmont–Plains by the Fractal Dimension of Particle Size. Soil Water Res. 2019, 14, 212–220. [Google Scholar] [CrossRef]
- Wang, C.; Song, J.; Tan, L.; Lv, M. Characteristics of Grain Size and Magnetic Susceptibility of Sediments and Their Environmental Significance in Piedmont Plain of Mt. Taihang since Early Pleistocene. J. Hebei Geo. Univ. 2023, 46, 14–20. [Google Scholar] [CrossRef]
- Xiong, Y.; Xi, C.F.; Zhang, T.L. Studies on the Soils of the Yellow River Valley II. Genesis and Evolution of the Soils of North China Greate Plain. Acta Pedol. Sin. 1958, 6, 25–43. [Google Scholar]
- Chang, X.L. Characteristics and Influencing Factors of Soil Saturated Water Conductivity under Different Land Use Modes in North China Plain. Water Sav. Irrig. 2023, 7, 28–33. [Google Scholar] [CrossRef]
- Huo, S.Y. Research on the Effect of Water Table Decline on Vertical Groundwater Recharge: A Case Study in the North China Plain. Ph.D. Thesis, China University of Geoscience, Wuhan, China, 2015. [Google Scholar]
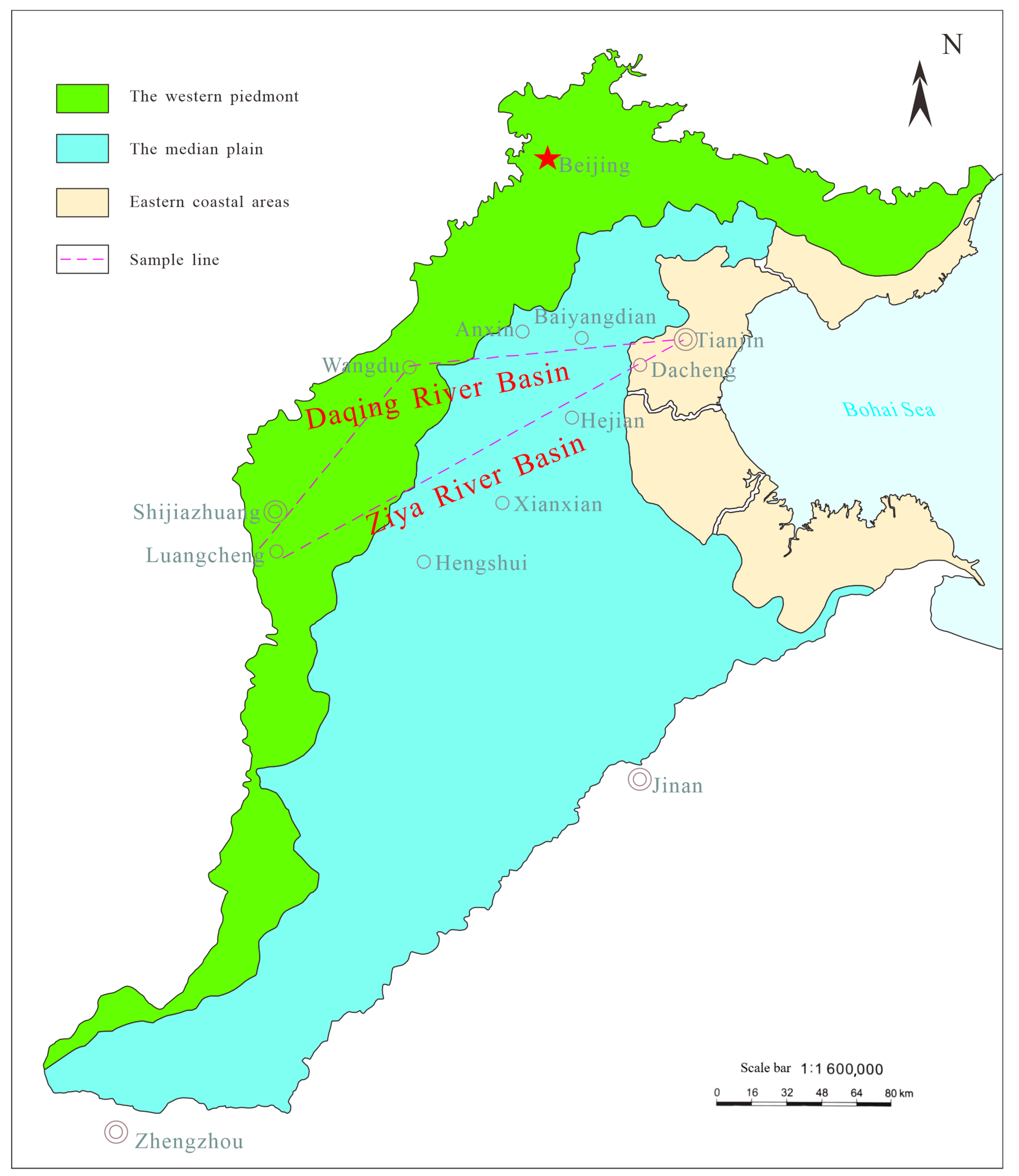
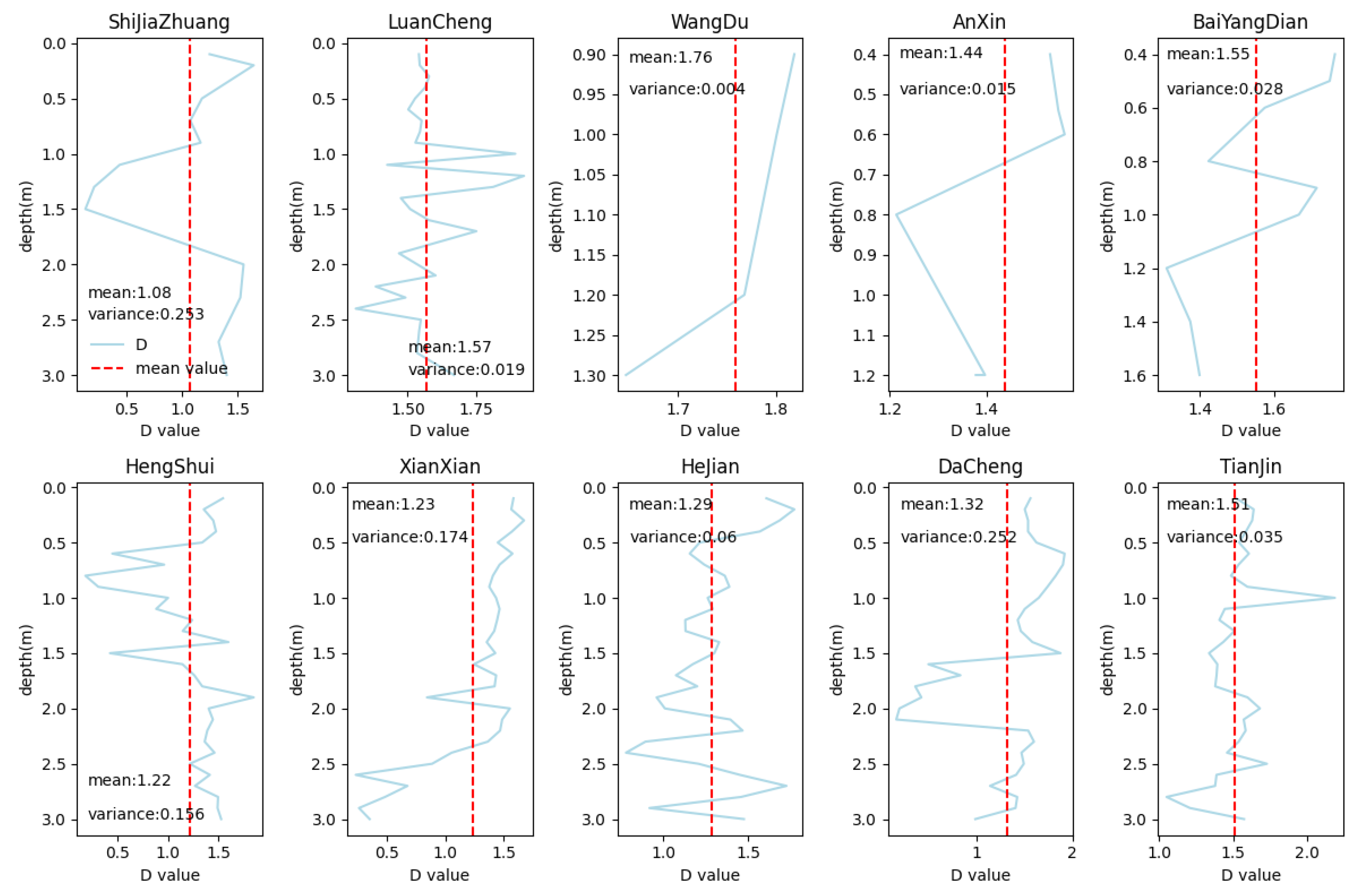
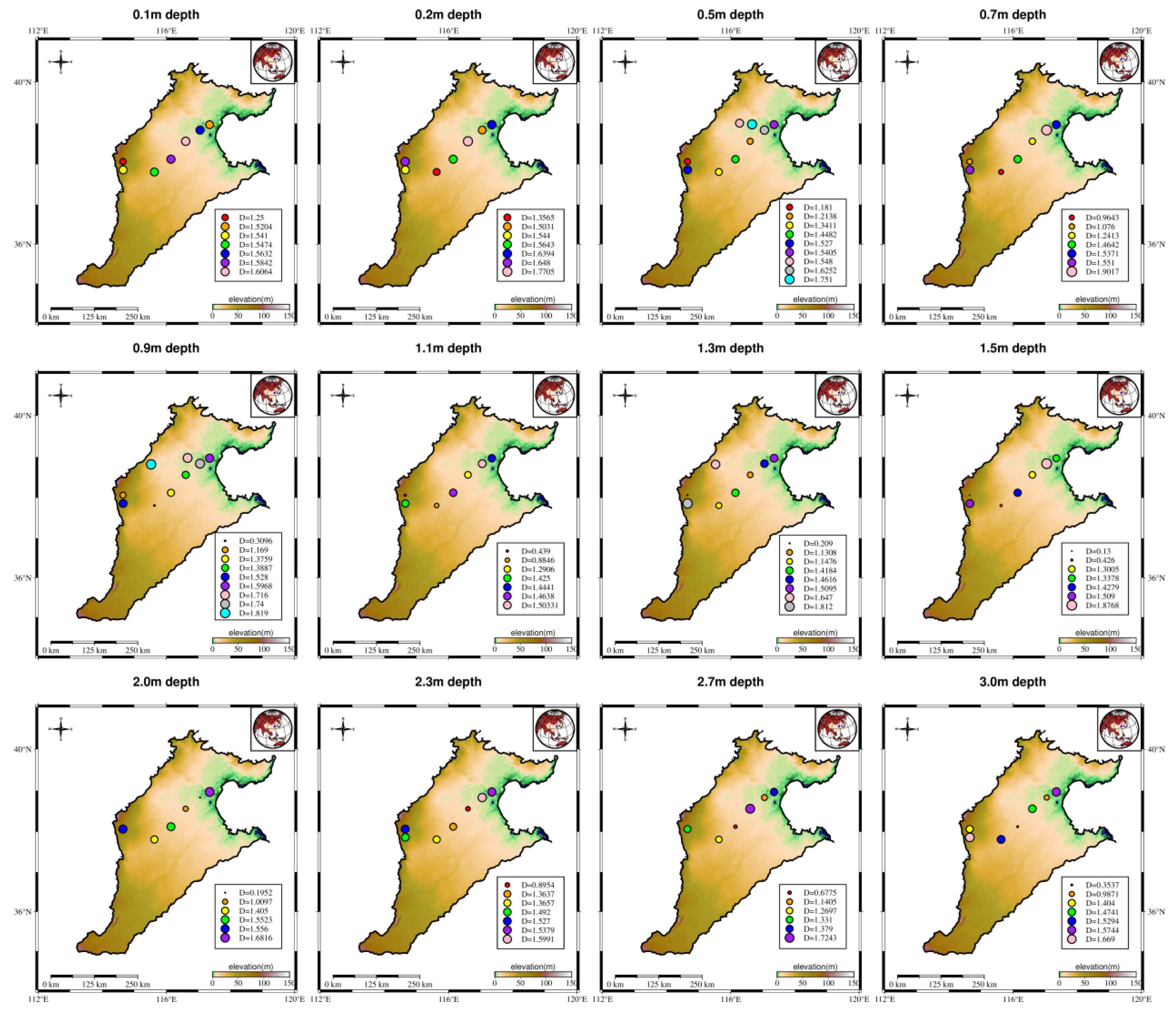
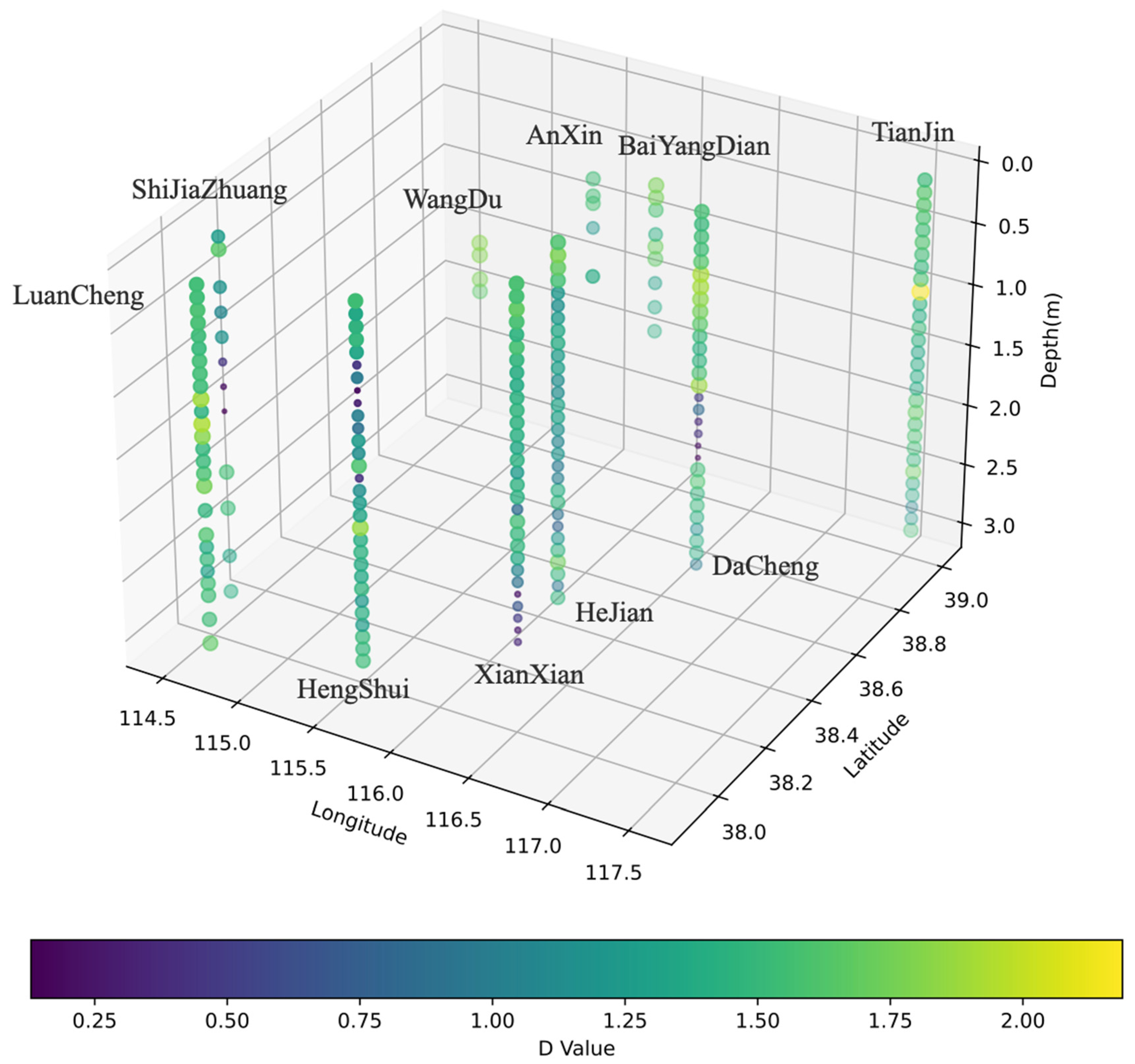


| Sample Num. | Depth (m) | Location | District | Geographical Coordinates | Elevation (m) | |
|---|---|---|---|---|---|---|
| ψ (N) | λ (E) | |||||
| SJZ01-30 | 0–3.0 | Shijiazhuang City | The western piedmont | 114°40′33″ | 37°53′16″ | 85 |
| LC01-26 | 0–3.0 | Luancheng County, Shijiazhuang City | 114°28′58″ | 38°04′59″ | 55 | |
| WD01-04 | 0.9–1.3 | Wangdu County, Baoding City | The median plain | 115°09′18″ | 38°24′40″ | 46 |
| AX01-06 | 0.4–1.2 | laohetou Town, Anxin County | 115°41′55″ | 38°30′24″ | 13 | |
| BYL01-09 | 0.4–1.6 | Baiyang Lake, Anxin County | 116°03′10″ | 38°35′52″ | 5 | |
| HS01-25 | 0–2.5 | Shenzhou County, Hengshui City | 115°30′58″ | 38°27′14″ | 30 | |
| XX01-19 | 0–1.9 | Xianxian County, Cangzhou City | 116°10′11″ | 38°29′29″ | 15 | |
| HJ01-23 | 0–2.3 | Hejian County, Cangzhou City | 116°07′55″ | 38°32′53″ | 14 | |
| DC01-30 | 0–3.0 | Dacheng County, Langfang City | Eastern coastal areas | 116°38′20″ | 38°39′37″ | 8 |
| BH01-11 | 0–1.1 | Binhai new-region, Tianjin City | 117°32′24″ | 39°00′48″ | 4 | |
| Soil Depth | Number of Samples | Mean | Median | Max | Min | Standard Deviation | CV(%) | Variance | Skewness | Kurtosis | K-S Test | p Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0–1 m | 10 | 1.502 | 1.543 | 1.81 | 1.008 | 0.219 | 14.569 | 0.048 | −0.894 | 0.206 | 0.162 | 0.918 |
| 1–2 m | 10 | 1.288 | 1.361 | 1.708 | 0.584 | 0.304 | 23.595 | 0.092 | −0.913 | 0.469 | 0.194 | 0.78 |
| 2–3 m | 7 | 1.308 | 1.409 | 1.51 | 0.827 | 0.213 | 16.284 | 0.045 | −1.444 | 0.867 | 0.274 | 0.577 |
| 0–3 m | 10 | 1.397 | 1.379 | 1.759 | 1.077 | 0.195 | 13.971 | 0.038 | 0.181 | −0.838 | 0.153 | 0.947 |
| Soil Depth | Fitting Model | Nugget C0 | Sill C0 + C | Nugget to Sill (C0/(C0 + C)) | Minimum Range (km−1) | Determination Coefficient (R2) | Residual Sum of Squares (RSS) |
|---|---|---|---|---|---|---|---|
| 0–1 m | Gaussian model | 0.03 | 0.246 | 0.122 | 152.4 | 0.21 | 0.0438 |
| 1–2 m | Gaussian model | 0.072 | 0.6138 | 0.117 | 588.9 | 0.27 | 0.297 |
| 2–3 m | Exponential model | 0.001 | 0.14 | 0.007 | 21.5 | 0.481 | 0.0156 |
| 0–3 m | Exponential model | 0.024 | 0.16845 | 0.142 | 481.1 | 0.159 | 0.0284 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Peng, B.; Dai, L.; Wang, Y.; Liu, Y.; Wang, G. The Spatial Variation of Soil Structure Fractal Derived from Particle Size Distributions at the Basin Scale. Fractal Fract. 2024, 8, 570. https://doi.org/10.3390/fractalfract8100570
He Y, Peng B, Dai L, Wang Y, Liu Y, Wang G. The Spatial Variation of Soil Structure Fractal Derived from Particle Size Distributions at the Basin Scale. Fractal and Fractional. 2024; 8(10):570. https://doi.org/10.3390/fractalfract8100570
Chicago/Turabian StyleHe, Yujiang, Borui Peng, Lei Dai, Yanyan Wang, Ying Liu, and Guiling Wang. 2024. "The Spatial Variation of Soil Structure Fractal Derived from Particle Size Distributions at the Basin Scale" Fractal and Fractional 8, no. 10: 570. https://doi.org/10.3390/fractalfract8100570
APA StyleHe, Y., Peng, B., Dai, L., Wang, Y., Liu, Y., & Wang, G. (2024). The Spatial Variation of Soil Structure Fractal Derived from Particle Size Distributions at the Basin Scale. Fractal and Fractional, 8(10), 570. https://doi.org/10.3390/fractalfract8100570






