Asymptotic Synchronization for Caputo Fractional-Order Time-Delayed Cellar Neural Networks with Multiple Fuzzy Operators and Partial Uncertainties via Mixed Impulsive Feedback Control

Abstract

To construct Caputo fractional-order time-delayed cellar neural networks (FOTDCNNs) that characterize real environments, this article introduces partial uncertainties, fuzzy operators, and nonlinear activation functions into the network models. Specifically, both the fuzzy AND operator and the fuzzy OR operator are contemplated in the master–slave systems. In response to the properties of the considered cellar neural networks (NNs), this article designs a new class of mixed control protocols that utilize both the error feedback information of systems and the sampling information of impulse moments to achieve network synchronization tasks. This approach overcomes the interference of time delays and uncertainties on network stability. By integrating the fractional-order comparison principle, fractional-order stability theory, and hybrid control schemes, readily verifiable asymptotic synchronization conditions for the studied fuzzy cellar NNs are established, and the range of system parameters is determined. Unlike previous results, the impulse gain spectrum considered in this study is no longer confined to a local interval (−2, 0) and can be extended to almost the entire real number domain. This spectrum extension relaxes the synchronization conditions, ensuring a broader applicability of the proposed control schemes.

1. Introduction

With the rapid development of smart computing and big data processing, artificial neural networks have received extensive attention from researchers due to their excellent learning capabilities, powerful nonlinear fitting capacity, and efficient parallel processing techniques [1,2,3,4,5]. Recently, the fundamental functions of neural networks have been widely investigated and applied in various areas such as machine learning [6], data sampling [7], system optimization [8], and stability analysis [9,10]. Among the different behaviors observed in neural networks, synchronization has become a popular research direction for many scientists and technicians [11,12]. In reality, numerous natural phenomena exhibit spontaneous synchronization, such as fireflies flickering in unison, schools of fish moving gracefully, crickets chirping together, and synchronized electrical signals from neurons in the brain.

A small number of network systems can rely on the evolution of their topologies to achieve network synchronization. For most NNs, external control inputs are required to bring the different neurons to a synchronization state [13,14]. In recent years, many scholars have begun to focus on various synchronization problems in NNs. To mention a few, Ding et al. [15] explored the quasi-synchronization of nonlinear NNs including mismatched parameters and distributed delays using the Lyapunov stability method and comparison principle. In [16], bipartite synchronization conditions for nonlinear memristive NNs were derived based on impulsive control protocols and parameter variation techniques. To reduce control burden and avoid the construction of complex Lyapunov–Krasovskii functions, Hua et al. [17] constructed a new impulsive controller for achieving the asymptotic synchronization of multi-layer coupled NNs with memristor characteristics. In [18], by introducing fuzzy operators and memristive units, a class of nonlinear fuzzy neural network models was established, and the corresponding synchronization task was converted to the stability problem of the error evolution network. In [19], Alsaedi et al. investigated the state synchronization of drive-response NNs with memristive features by utilizing a fuzzy adaptive control scheme. In [20], a fuzzy cellular neural network with signal delays was established by combining fuzzy theory and neural cell systems, with finite time synchronization criteria derived using discontinuous information feedback schemes.

Note that the neural network models and their synchronization theories discussed above mainly focused on integer-order calculus operators. The fractional-order calculus is used as an extension of the integer calculus with the addition of a freedom degree, which contains all the information from the initial state to the present moment [21]. Unlike integer-order calculus, fractional-order operators exhibit non-locality and memory, and more precisely characterize real-world phenomena such as nonlinear elasticity, fluid mechanics, and heat transfer [22]. With the continuous development of the theory of fractional-order calculus, researchers have attempted to apply this operator to model the dynamic properties of NNs [23]. In [24], with the help of the Riemann–Liouville fractional operator, the authors considered fractional-order memristive NNs containing uncertain network parameters, and practical synchronization results were obtained using adaptive control protocols. Similarly, research in [25] utilized the Caputo fractional derivative to construct fractional-order non-delayed NNs and derived asymptotic synchronization criteria for network systems under Filippov sense via error information feedback. In [26], Bao and Cao et al. deliberated the projective synchronization task of memristive network systems with Caputo fractional-order operators under mixed control schemes.

Each node in a neural network is represented by a fractional differential system to show its dynamic variation behavior. Because of measurement errors and environmental influences, it is generally difficult to obtain accurate parameters for most networks [27]. Studying the uncertainty factors in systems can enhance the applicability of networks in complex engineering applications. In [28], the authors constructed a class of real-world networks called fractional-order building structure vibration systems with uncertain structural parameters. In [29], Boulham et al. designed a control protocol based on sliding surfaces and radial basis function neural networks, which can be applied to the state estimation of uncertain fractional-order practical systems. In [30], uncertain factors were introduced to model fractional-order NNs with variable delays, and the real passive problem was successfully solved. In [31], Liu and Yu et al. discussed the Mittag–Leffler stability and robust synchronization for Caputo fractional-order NNs including parameter uncertainties using the closure arithmetic. In [32], Fan et al. handled the finite-time synchronization for fractional-order delayed NNs comprising uncertain connections on the basis of the double-layer error signal feedback. Using adaptive laws and pining control schemes, the authors in [33] solved the chaotic synchronization between the coupled drive networks and response networks with unknown parameters. Applying the differential inclusion technique and the Lyapunov stability mechanism, in [34], Yang et al. promoted the synchronization result of fractional-order nonlinear NNs with parameter perturbations from real fields to complex fields.

In practical engineering applications, mathematical modeling and reasoning rules are often fuzzy and inaccurate. Fuzzy logic theory, as an effective evaluation approach, can approximate various nonlinear functions and be applied to simulate different complex systems. In [35], by introducing fuzzy OR and fuzzy AND operators, Du et al. established Caputo-type fractional fuzzy cellular NNs with constant delays and derived the synchronization conditions by the Laplace transform and adaptive techniques. In [36], Peng et al. explored the asymptotic synchronization challenge of Caputo-type fractional coupled NNs with multiple fuzzy operators and impulses via an adaptive state feedback controller. In [37], Zhao et al. researched the asymptotic synchronization in finite time for fractional-order memristive NNs with two kinds of fuzzy operators and delays under adaptive information feedback. Utilizing error information feedback control, in [38], the authors explored the nonlocal synchronization challenge of fractional coupled NNs with fuzzy calculation rules. In [39], Li et al. derived the global synchronization criteria of Caputo fractional-order fuzzy NNs with changeable delays using a discontinuous adaptive controller. It should be noted that the synchronization control schemes of fractional-order fuzzy NNs in [35,36,37,38,39] rely on adaptive or error feedback techniques. However, to our knowledge, few works have addressed the asymptotic synchronization problem of fractional-order delayed cellar NNs with parameter uncertainties and multiple fuzzy operators by utilizing hybrid impulse and information feedback control techniques, which is the primary motivation of this research.

Inspired by the aforementioned works, this article investigates the asymptotic synchronization of uncertain FOTDCNNs with different fuzzy operators. The key contributions of this work include three aspects. First, we establish a generalized class of fractional-order nonlinear cellar NNs that incorporate partial uncertainties, fuzzy operators, and delays. Both the feedback link weights and the feedback templates consider uncertainties. Second, unlike the pure adaptive or information feedback techniques in [35,36,37,38,39], this article designs a mixed impulsive information feedback controller utilizing impulse sampling and the Dirac delta function. Finally, using the Laplace transform and comparison principle, we derive concise synchronization criteria for fuzzy FOTDCNNs with uncertainties under the proposed mixed control protocol. Different from [11,21], we extend the impulse gain from a local interval $(-2,0)$ to almost the entire real domain, significantly broadening the application scenarios for the proposed synchronization results.

2. Preparatory Knowledge and Methods

This part first presents some unsophisticated concepts related to fractional operators, involving mathematical definitions, lemmas, and assumptions. Afterward, two Caputo fractional-order time-delayed cellar NNs in complex environments will be established.

Definition 1. 

Define fractional integral for a known function $\mathcal{A}\left(t\right)$ as [40]

$$\begin{array}{c}\hfill {}_{t_0}I_t^{\mu }\mathcal{A}\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\mu \right)}}{\int }_{t_0}^t{(t-\xi )}^{\mu -1}\mathcal{A}\left(\xi \right)d\xi ,\end{array}$$

(1)

where $t\ge t_0$, $\mu >0$, and $\Gamma \left(\mu \right)={\int }_0^{+\infty }{\xi }^{\mu -1}{e}^{-\xi }d\xi$.

Definition 2. 

Define Caputo derivative for a known function $\mathcal{A}\left(t\right)$ as [40]

$$\begin{array}{c}\hfill {}_{t_0}{}^c\mathcal{D}_t^{\mu }\mathcal{A}\left(t\right)={\displaystyle \frac{1}{\Gamma (\kappa -\mu )}}{\int }_{t_0}^t{(t-\xi )}^{\kappa -\mu -1}{\mathcal{A}}^{\left(\kappa \right)}\left(\xi \right)d\xi ,\end{array}$$

(2)

where $t\ge t_0$, and $0\le \kappa -1<\mu <\kappa$. In addition, if $0<\mu <1$, ${}_{t_0}{}^c\mathcal{D}_t^{\mu }\mathcal{A}\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\mu )}}{\int }_{t_0}^t{(t-\xi )}^{-\mu }{\mathcal{A}}^{\prime }\left(\xi \right)d\xi$; if $\mu =1$, ${}_{t_0}{}^c\mathcal{D}_t^{\mu }\mathcal{A}\left(t\right)$ turns into the integer order operator.

Definition 3. 

For $z\in \mathbb{C}$, define the two-parameter Mittag–Leffler function as [40]

$$\begin{array}{c}\hfill {\mathbb{E}}_{u,v}\left(z\right)=\sum _{\xi =0}^{\infty }{\displaystyle \frac{z^{\xi }}{\Gamma (u\xi +v)}},\end{array}$$

(3)

where $u>0$ and $v>0$. Furthermore, if $v=1$, it becomes a simplified form as

$$\begin{array}{c}\hfill {\mathbb{E}}_u\left(z\right)=\sum _{\xi =0}^{\infty }{\displaystyle \frac{z^{\xi }}{\Gamma (u\xi +1)}}.\end{array}$$

(4)

Contemplate Caputo FOTDCNNs with partial uncertainties and two kinds of fuzzy operators as below:

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{v}_i\left(t\right)=-(p_i+\Delta p_i\left(t\right))v_i\left(t\right)+{\displaystyle \sum _{k=1}^m}(q_{ik}+\Delta q_{ik}\left(t\right)){\varphi }_k\left(v_k\left(t\right)\right)\hfill \\ +{\displaystyle \sum _{k=1}^m}{r}_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(v_k(t-\tau )\right)+{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(v_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\Phi }_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\Psi }_{ik}{x}_k+I_i,\hfill \\ v_i\left(t\right)={\beth }_i^v\left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(5)

where $0<\mu <1$, and $i\in {\mathbb{N}}_1^m=\{1,2,\cdots ,m\}$. $v_i\left(t\right)$ describes the state change of neuron i. Two functions ${\varphi }_k$ and ${\psi }_k$ characterize the activation behaviors. $\tau >0$ represents the time delay. $p_i$ denotes the self-feedback link weight. $x_i$ and $I_i$ represent the input and bias of neuron i. ⋁ and ⋀ stand for the fuzzy operators OR and AND, respectively. $q_{ik}$ and $r_{ik}$ denote elements of feedback and feed-forward templates. ${\beta }_{ik}$ and ${\gamma }_{ik}$ represent elements of fuzzy feedback MIN and MAX templates. ${\Phi }_{ik}$ and ${\Psi }_{ik}$ represent fuzzy feed-forward MIN and MAX templates. $\Delta p_i\left(t\right)$ and $\Delta q_{ik}\left(t\right)$ characterize bounded uncertainties, which satisfy $|\Delta p_i\left(t\right)|\le {\daleth }_i$ and $|\Delta q_{ik}\left(t\right)|\le {\gimel }_{ik}$.

In this article, we consider differential Equation (5) as the drive cellar networks and the response cellar networks are naturally characterized as

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{w}_i\left(t\right)=-(p_i+\Delta p_i\left(t\right))w_i\left(t\right)+{\displaystyle \sum _{k=1}^m}(q_{ik}+\Delta q_{ik}\left(t\right)){\varphi }_k\left(w_k\left(t\right)\right)\hfill \\ +{\displaystyle \sum _{k=1}^m}{r}_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(w_k(t-\tau )\right)+{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(w_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\Phi }_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\Psi }_{ik}{x}_k+I_i+U_i\left(t\right),\hfill \\ w_i\left(t\right)={\beth }_i^w\left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(6)

where $0<\mu <1$, and $i\in {\mathbb{N}}_1^m$. $w_i\left(t\right)$ characterizes the state change of neuron i of response networks and $U_i\left(t\right)$ represents the mixed control protocol to be devised. ${\beth }_i^w\left(t\right)$ represents the initial value of neuron i. The remaining network parameters have the same implications as cellar networks (5).

Define system synchronization error as ${\sigma }_i\left(t\right)=w_i\left(t\right)-v_i\left(t\right)$. Combining cellar NNs (5) and (6), one can acquire the Caputo derivative of error states as

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{\sigma }_i\left(t\right)=-(p_i+\Delta p_i\left(t\right)){\sigma }_i\left(t\right)+{\displaystyle \sum _{k=1}^m}(q_{ik}+\Delta q_{ik}\left(t\right))\left[{\varphi }_k\left(w_k\left(t\right)\right)-{\varphi }_k\left(v_k\left(t\right)\right)\right]\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(w_k(t-\tau )\right)-{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(v_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(w_k(t-\tau )\right)-{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(v_k(t-\tau )\right)+U_i\left(t\right),\hfill \\ {\sigma }_i\left(t\right)={\beth }_i^{\sigma }\left(t\right),t\in [-\tau ,0],i\in {\mathbb{N}}_1^m.\hfill \end{array}\right.$$

(7)

Based on the characteristics of the error equation mentioned above, an uncomplicated hybrid control protocol with impulsive sampling information and error feedback information is devised by

$$U_i\left(t\right)=-{\eta }_i{\sigma }_i\left(t\right)+{\displaystyle \sum _{ϵ=1}^{\infty }}\varpi {\sigma }_i\left(t\right)\delta (t-t_{ϵ}),$$

(8)

where ${\eta }_i$ represents the feedback gain, and $\varpi$ represents the impulsive gain at a certain impulse instant $t_{ϵ}$. $\delta (·)$ is the generalized Dirac delta function [41]. By time-varying evolution system (7) and control protocol (8), one can get

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{\sigma }_i\left(t\right)=-(p_i+\Delta p_i\left(t\right)+{\eta }_i){\sigma }_i\left(t\right)+{\displaystyle \sum _{k=1}^m}(q_{ik}+\Delta q_{ik}\left(t\right))\left[{\varphi }_k\left(w_k\left(t\right)\right)-{\varphi }_k\left(v_k\left(t\right)\right)\right]\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(w_k(t-\tau )\right)-{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(v_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(w_k(t-\tau )\right)-{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(v_k(t-\tau )\right),t\ne t_{ϵ},\hfill \\ {\sigma }_i\left(t_{ϵ}^{+}\right)-{\sigma }_i\left(t_{ϵ}^{-}\right)=\varpi {\sigma }_i\left(t_{ϵ}^{-}\right),t=t_{ϵ},\hfill \\ {\sigma }_i\left(t\right)={\beth }_i^{\sigma }\left(t\right),t\in [-\tau ,0],i\in {\mathbb{N}}_1^m.\hfill \end{array}\right.$$

(9)

Remark 1. 

Unlike the fractional Riemann–Liouville operator in [24,42], the fractional Caputo operator utilized in this article has an unequivocal physical meaning. Fractional-order NNs with the Caputo operator have similar starting values as integer-order NNs, making physical significance clear.

Remark 2. 

Compared with existing fractional-order fuzzy NNs in [35,36,37,38,39], this article’s nonlinear cellular network models contemplate multiple uncertainties, different types of fuzzy rules, and time delays, making the systems in this paper more universal and practical.

Lemma 1. 

Let $w_k$ and $v_k$ be two states of cellar neural networks (5) and (6), then we obtain [35]

$$|{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(w_k(t-\tau )\right)-{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(v_k(t-\tau )\right)|\le {\displaystyle \sum _{k=1}^m}{|\beta }_{ik}\left|\right|{\psi }_k\left(w_k(t-\tau )\right)-{\psi }_k\left(v_k(t-\tau )\right)|,$$

(10)

and

$$|{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(w_k(t-\tau )\right)-\underset{k=1}{\overset{m}{\bigvee }}{\gamma }_{ik}{\psi }_k\left(v_k(t-\tau )\right)|\le \sum _{k=1}^m{|\gamma }_{ik}\left|\right|{\psi }_k\left(w_k(t-\tau )\right)-{\psi }_k\left(v_k(t-\tau )\right)|,$$

(11)

where $i\in {\mathbb{N}}_1^m$.

Assumption 1. 

There are positive scalars ${\mathcal{L}}_k^{\varphi }$ and ${\mathcal{L}}_k^{\psi }$ fulfilling

$$\begin{array}{c}\hfill {|\varphi }_k\left(w\right)-{\varphi }_k\left(v\right)|\le {\mathcal{L}}_k^{\varphi }|w-v|,|{\psi }_k\left(w\right)-{\psi }_k\left(v\right)|\le {\mathcal{L}}_k^{\psi }|w-v|,\end{array}$$

(12)

for $\forall w,v\in \mathbb{R}$, $k\in {\mathbb{N}}_1^m$.

Lemma 2. 

Assume that $\mathcal{V}\left(t\right)\in {\mathbb{C}}^1([0,+\infty ),\mathbb{R})$ is differentiable, we get [43]

$${}_0{}^c\mathcal{D}_t^{\mu }\left|\mathcal{V}\left(t\right)\right|\le \mathrm{sign}{\left(\mathcal{V}\left(t\right)\right)}_0^c{\mathcal{D}}_t^{\mu }\mathcal{V}\left(t\right),0<\mu <1.$$

(13)

Lemma 3. 

Suppose that nonnegative functions $\tilde{v}\left(t\right)$ and $\overline{v}\left(t\right)$ meet [21]

$$\left\{\begin{array}{c}{}_{t_0}{}^c\mathcal{D}_t^{\mu }\tilde{v}\left(t\right)\le -b\tilde{v}\left(t\right)+c_1\tilde{v}(t-{\tau }_1\left(t\right))+c_2\tilde{v}(t-{\tau }_2\left(t\right)),t\ne t_{ϵ},\hfill \\ \tilde{v}\left(t_{ϵ}\right)\le {\chi }_k\tilde{v}\left(t_{ϵ}^{-}\right),t=t_{ϵ},ϵ\in {\mathbb{Z}}_{+},\hfill \\ \tilde{v}\left(t\right)=\tilde{F}\left(t\right),t\in [t_0-\tau ,t_0],\hfill \end{array}\right.$$

(14)

and

$$\left\{\begin{array}{c}{}_{t_0}{}^c\mathcal{D}_t^{\mu }\overline{v}\left(t\right)=-b\overline{v}\left(t\right)+c_1\overline{v}(t-{\tau }_1\left(t\right))+c_2\overline{v}(t-{\tau }_2\left(t\right)),t\ne t_{ϵ},\hfill \\ \overline{v}\left(t\right)=F\left(t\right),t\in [t_0-\tau ,t_0],\hfill \end{array}\right.$$

(15)

where $0<\mu <1,0\le {\tau }_1\left(t\right),{\tau }_2\left(t\right)\le \tau ,0<{\chi }_k\le 1$, $b\in \mathbb{R}$ and $c_1,c_2>0$, then $\tilde{F}\left(t\right)\le F\left(t\right)$ for $t_0-\tau \le t\le t_0$ yields that $\tilde{v}\left(t\right)\le \overline{v}\left(t\right)$ for $t\ge t_0$.

Remark 3. 

A large number of works paid attention to delayed cellar NNs based on conventional calculus operators, and useful network synchronization criteria have been obtained under external control, such as [18,19,20]. However, the traditional integer-order comparison inequality cannot be directly applied to the synchronization analysis of fractional cellar NNs, especially in this paper, the fractional-order networks are affected by multiple different factors. As a consequence, the theoretical analysis of this article must be completed with the help of Caputo fractional-order comparison inequalities.

Lemma 4. 

Contemplate the following Caputo fractional delayed system [6]

$$\begin{array}{c}\hfill {}_0{}^c\mathcal{D}_t^{\mu }X\left(t\right)=BX\left(t\right)+\overline{B}X(t-\tau ),0<\mu <1,\end{array}$$

(16)

where $X\left(t\right)={(X_1\left(t\right),X_2\left(t\right),\cdots ,X_n\left(t\right))}^T$, $X(t-\tau )={(X_1(t-{\tau }_1),X_2(t-{\tau }_2),\cdots ,X_n(t-{\tau }_n))}^T$, $B={\left(b_{kj}\right)}_{n\times n}$, and $\overline{B}={\left({\overline{b}}_{kj}\right)}_{n\times n}$. Providing the eigenvalues of system (16) tally with the circumstance $\left|\mathit{arg}\left(\lambda \right)\right|>{\displaystyle \frac{\pi }{2}}$ and $\mathit{det}(\Delta (s\left)\right)=0$ has no pure imaginary solutions for ∀${\tau }_j>0$, then the zero solution of (16) is globally asymptotically stable.

Lemma 5. 

Let function $\mathcal{V}\left(t\right)$ is continuous on $[t_0,+\infty )$, and fulfills [44]

$${}_{t_0}{}^c\mathcal{D}_t^{\mu }\mathcal{V}\left(t\right)\le \varsigma \mathcal{V}\left(t\right),$$

(17)

where $0<\mu <1$, and $\varsigma \in \mathbb{R}$, then we derive

$$\mathcal{V}\left(t\right)\le \mathcal{V}\left(t_0\right){\mathbb{E}}_{\mu }\left[\varsigma {(t-t_0)}^{\mu }\right].$$

(18)

Especially, one gets $\mathcal{V}\left(t\right)\le \mathcal{V}\left(0\right){\mathbb{E}}_{\mu }\left[\varsigma t^{\mu }\right]$ for $t_0=0$.

3. Main Results

For the convenience of subsequent theoretical analysis, this section first presents a noteworthy vector notation $\sigma \left(t\right)={({\sigma }_1\left(t\right),{\sigma }_2\left(t\right),\cdots ,{\sigma }_m\left(t\right))}^T$, then one can derive the below new sufficient conditions to ensure network synchronization.

Theorem 1. 

When $-2<\varpi <0$ and ${\eta }_i>0$, assume that Assumption 1 is satisfied and the below condition

$$\begin{array}{c}\hfill {\rho }_{\mathit{max}}<{\varrho }_{\mathit{min}}\mathit{sin}{\displaystyle \frac{\mu \pi }{2}}\end{array}$$

(19)

holds, where ${\rho }_{\mathit{max}}={\mathit{max}}_{1\le i\le m}\left[{\sum }_{k=1}^m\left(\right|{\beta }_{ki}|+|{\gamma }_{ki}\left|\right){\mathcal{L}}_i^{\psi }\right]>0$, ${\varrho }_{\mathit{min}}={\mathit{min}}_{1\le i\le m}\left[p_i-{\daleth }_i-{\sum }_{k=1}^m\left(\right|q_{ki}|+{\gimel }_{ki}){\mathcal{L}}_i^{\varphi }+{\eta }_i\right]>0$, and $0<\mu <1$. Then the asymptotic synchronization between fuzzy FOTDCNNs (5) and (6) can be finished via impulsive feedback control protocol (8).

Proof. 

Contemplate the below function

$$\begin{array}{c}\hfill \tilde{\mathbb{V}}\left(t\right)={\left|\right|\sigma \left(t\right)\left|\right|}_1=\sum _{i=1}^m\left|{\sigma }_i\left(t\right)\right|.\end{array}$$

(20)

Based on Lemmas 1 and 2, when $t\in [t_{ϵ-1},t_{ϵ})$, calculating the $\mu$-order derivative of $\tilde{\mathbb{V}}\left(t\right)$ yields that

$$\begin{array}{cc}\hfill {}_0{}^c\mathcal{D}_t^{\mu }\tilde{\mathbb{V}}\left(t\right)\le & \sum _{i=1}^m\mathrm{sign}{\left({\sigma }_i\left(t\right)\right)}_0^c{\mathcal{D}}_t^{\mu }{\sigma }_i\left(t\right)\hfill \\ \hfill =& \sum _{i=1}^m\mathrm{sign}\left({\sigma }_i\left(t\right)\right)[-(p_i+\Delta p_i\left(t\right)+{\eta }_i){\sigma }_i\left(t\right)+\sum _{k=1}^m(q_{ik}+\Delta q_{ik}\left(t\right))\hfill \\ \hfill & \times \left({\varphi }_k\left(w_k\left(t\right)\right)-{\varphi }_k\left(v_k\left(t\right)\right)\right)+\underset{k=1}{\overset{m}{\bigwedge }}{\beta }_{ik}{\psi }_k\left(w_k(t-\tau )\right)-\underset{k=1}{\overset{m}{\bigwedge }}{\beta }_{ik}{\psi }_k\left(v_k(t-\tau )\right)\hfill \\ \hfill & +\underset{k=1}{\overset{m}{\bigvee }}{\gamma }_{ik}{\psi }_k\left(w_k(t-\tau )\right)-\underset{k=1}{\overset{m}{\bigvee }}{\gamma }_{ik}{\psi }_k\left(v_k(t-\tau )\right)]\hfill \\ \hfill \le & \sum _{i=1}^m[(-p_i+{\daleth }_i-{\eta }_i){|\sigma }_i\left(t\right)|+\sum _{k=1}^m\left(\right|q_{ik}|+{\gimel }_{ik}){\mathcal{L}}_k^{\varphi }\left|{\sigma }_k\left(t\right)\right|\hfill \\ \hfill & +\sum _{k=1}^m\left(\right|{\beta }_{ik}|+|{\gamma }_{ik}\left|\right){\mathcal{L}}_k^{\psi }\left|{\sigma }_k(t-\tau )\right|]\hfill \\ \hfill =& \sum _{i=1}^m\left[-\left(p_i-{\daleth }_i-\sum _{k=1}^m\left(\right|q_{ki}|+{\gimel }_{ki}){\mathcal{L}}_i^{\varphi }+{\eta }_i\right)\right]\left|{\sigma }_i\left(t\right)\right|\hfill \\ \hfill & +\sum _{i=1}^m\left[\sum _{k=1}^m\left(\right|{\beta }_{ki}|+|{\gamma }_{ki}\left|\right){\mathcal{L}}_i^{\psi }\right]\left|{\sigma }_i(t-\tau )\right|.\hfill \end{array}$$

(21)

Note that ${\varrho }_{\min }={\min }_{1\le i\le m}\left[p_i-{\daleth }_i-{\sum }_{k=1}^m\left(\right|q_{ki}|+{\gimel }_{ki}){\mathcal{L}}_i^{\varphi }+{\eta }_i\right]>0$ and ${\rho }_{\max }={\max }_{1\le i\le m}\left[{\sum }_{k=1}^m\left(\right|{\beta }_{ki}|+|{\gamma }_{ki}\left|\right){\mathcal{L}}_i^{\psi }\right]>0$. From inequality (21), one can get

$$\begin{array}{c}\hfill {}_0{}^c\mathcal{D}_t^{\mu }\tilde{\mathbb{V}}\left(t\right)\le -{\varrho }_{\min }\tilde{\mathbb{V}}\left(t\right)+{\rho }_{\max }\tilde{\mathbb{V}}(t-\tau ).\end{array}$$

(22)

When $t=t_{ϵ}$, we derive

$$\begin{array}{cc}\hfill \tilde{\mathbb{V}}\left(t_{ϵ}^{+}\right)& =\sum _{i=1}^m{|\sigma }_i\left(t_{ϵ}^{+}\right)|=\sum _{i=1}^m|(1+\varpi ){\sigma }_i\left(t_{ϵ}^{-}\right)|\hfill \\ \hfill & \le \sum _{i=1}^m\left|(1+\varpi )\right||{\sigma }_i\left(t_{ϵ}^{-}\right)|\hfill \\ \hfill & \le {\gamma }_{\max }\tilde{\mathbb{V}}\left(t_{ϵ}^{-}\right),\hfill \end{array}$$

(23)

where $0<{\gamma }_{\max }=\left|(1+\varpi )\right|<1$.

By inequalities (22) and (23), one gets

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }\tilde{\mathbb{V}}\left(t\right)\le -{\varrho }_{\min }\tilde{\mathbb{V}}\left(t\right)+{\rho }_{\max }\tilde{\mathbb{V}}(t-\tau ),t\in [t_{ϵ-1},t_{ϵ}),\hfill \\ \tilde{\mathbb{V}}\left(t_{ϵ}^{+}\right)\le {\gamma }_{\max }\tilde{\mathbb{V}}\left(t_{ϵ}^{-}\right),t=t_{ϵ},ϵ\in {\mathbb{Z}}_{+}.\hfill \end{array}\right.$$

(24)

Deliberate the following $\mu$-order differential system

$${}_0{}^c\mathcal{D}_t^{\mu }\mathcal{N}\left(t\right)=-{\varrho }_{\min }\mathcal{N}\left(t\right)+{\rho }_{\max }\mathcal{N}(t-\tau ),$$

(25)

where $\mathcal{N}\left(t\right)$ is continuous on $[t_0-\tau ,\infty )$ and has identical initial value with $\tilde{\mathbb{V}}\left(t\right)$. Based on the limitation $0<{\gamma }_{\max }<1$ and using Lemma 3, one gets

$$\begin{array}{c}\hfill 0\le \tilde{\mathbb{V}}\left(t\right)\le \mathcal{N}\left(t\right).\end{array}$$

(26)

Utilizing the Laplace transform technique for fractional delayed Equation (25) derives that

$$\begin{array}{cc}\hfill s^{\mu }\mathcal{N}\left(s\right)-s^{\mu -1}\mathcal{N}\left(t_0\right)=& -{\varrho }_{\min }\mathcal{N}\left(s\right)+{\rho }_{\max }{\int }_{t_0}^{+\infty }{e}^{-st}\mathcal{N}(t-\tau )dt\hfill \\ \hfill =& -{\varrho }_{\min }\mathcal{N}\left(s\right)+{\rho }_{\max }{\int }_{t_0-\tau }^{+\infty }{e}^{-s(t+\tau )}\mathcal{N}\left(t\right)dt\hfill \\ \hfill =& -{\varrho }_{\min }\mathcal{N}\left(s\right)+{\rho }_{\max }{e}^{-s\tau }\left({\int }_{t_0-\tau }^{t_0}{e}^{-st}\mathcal{N}\left(t\right)dt+{\int }_{t_0}^{+\infty }{e}^{-st}\mathcal{N}\left(t\right)dt\right)\hfill \\ \hfill =& -{\varrho }_{\min }\mathcal{N}\left(s\right)+{\rho }_{\max }{e}^{-s\tau }\mathcal{N}\left(s\right)+{\rho }_{\max }{e}^{-s\tau }{\int }_{t_0-\tau }^{t_0}{e}^{-st}\mathcal{N}\left(t\right)dt.\hfill \end{array}$$

(27)

According to transformed Equation (27) and Lemma 4, one can get

$$\begin{array}{c}\hfill \det (\Delta \left(s\right))\mathcal{N}\left(s\right)=s^{\mu -1}\mathcal{N}\left(t_0\right)+{\rho }_{\max }{e}^{-s\tau }{\int }_{t_0-\tau }^{t_0}{e}^{-st}\mathcal{N}\left(t\right)dt,\end{array}$$

(28)

where $\det (\Delta \left(s\right))=s^{\mu }+{\varrho }_{\min }-{\rho }_{\max }{e}^{-s\tau }$. Next, utilize the reductio ad absurdum to show that $\det (\Delta (s\left)\right)=0$ has no pure imaginary solutions. Let $s=\mathcal{R}i=|\mathcal{R}|(cos{\displaystyle \frac{\pi }{2}}+isin(\pm {\displaystyle \frac{\pi }{2}}))$, where $\mathcal{R}\in \mathbb{R}$. If $\mathcal{R}>0$, consider $isin({\displaystyle \frac{\pi }{2}})$; $\mathcal{R}<0$, consider $isin(-{\displaystyle \frac{\pi }{2}})$. Bringing $s=\mathcal{R}i=|\mathcal{R}|(cos{\displaystyle \frac{\pi }{2}}+isin(\pm {\displaystyle \frac{\pi }{2}}))$ into $\det (\Delta (s))=0$ and applying the canonical Euler formula, one can derive

$$\begin{array}{c}\hfill {\left|\mathcal{R}\right|}^{\mu }\left(\cos {\displaystyle \frac{\mu \pi }{2}}+i\sin \left({\displaystyle \frac{\pm \mu \pi }{2}}\right)\right)+{\varrho }_{\min }-{\rho }_{\max }(\cos \mathcal{R}\tau -i\sin \mathcal{R}\tau )=0.\end{array}$$

(29)

By the definition of complex number equality, separately consider real and imaginary parts of (29) yields

$$\left\{\begin{array}{c}{\left|\mathcal{R}\right|}^{\mu }\cos {\displaystyle \frac{\mu \pi }{2}}+{\varrho }_{\min }-{\rho }_{\max }\cos \mathcal{R}\tau =0,\hfill \\ {\left|\mathcal{R}\right|}^{\mu }\sin {\displaystyle \frac{(\pm \mu \pi )}{2}}+{\rho }_{\max }\sin \mathcal{R}\tau =0,\hfill \end{array}\right.$$

(30)

which is equivalent to

$$\begin{array}{c}\hfill {\left({\left|\mathcal{R}\right|}^{\mu }\cos {\displaystyle \frac{\mu \pi }{2}}+{\varrho }_{\min }\right)}^2+{\left({\left|\mathcal{R}\right|}^{\mu }\sin {\displaystyle \frac{(\pm \mu \pi )}{2}}\right)}^2-{\rho }_{\max }^2=0.\end{array}$$

(31)

Simplifying and arranging Equation (31) gives

$$\begin{array}{c}\hfill {\left|\mathcal{R}\right|}^{2\mu }+2{\varrho }_{\min }cos{\displaystyle \frac{\mu \pi }{2}}{\left|\mathcal{R}\right|}^{\mu }+{\varrho }_{\min }^2-{\rho }_{\max }^2=0.\end{array}$$

(32)

Note that ${\left|\mathcal{R}\right|}^{\mu }>0$, $cos{\displaystyle \frac{\mu \pi }{2}}>0$, ${\varrho }_{\min }>0$. When ${\varrho }_{\min }\sin {\displaystyle \frac{\mu \pi }{2}}>{\rho }_{\max }$, one can derive ${\left|\mathcal{R}\right|}^{2\mu }+2{\varrho }_{\min }cos{\displaystyle \frac{\mu \pi }{2}}{\left|\mathcal{R}\right|}^{\mu }+{\varrho }_{\min }^2-{\rho }_{\max }^2>0$. Hence, absolute value Equation (32) has no real solutions, namely, $\det (\Delta (s\left)\right)=0$ does not have pure imaginary roots. Besides, when ${\varrho }_{\min }\sin {\displaystyle \frac{\mu \pi }{2}}>{\rho }_{\max }$, we derive $|\arg (-{\varrho }_{\min }+{\rho }_{\max })|>{\displaystyle \frac{\pi }{2}}$. Utilizing Lemma 4, the zero solution of (25) is asymptotically stable and ${lim}_{t\to +\infty }\mathcal{N}\left(t\right)=0$. By inequality $0\le \tilde{\mathbb{V}}\left(t\right)\le \mathcal{N}\left(t\right)$, we derive ${lim}_{t\to +\infty }\tilde{\mathbb{V}}\left(t\right)=0$, and the asymptotic synchronization of fuzzy cellar NNs (5) and (6) is finished. □

Remark 4. 

By combining the comparison principle of fractional order and the Laplace transform, we derive Equation (28) concerning characteristic polynomials. Based on the reductio ad absurdum and Euler’s formula, we obtained an indispensable Equation (32) that draws out contradictions, realizing the key proof of Theorem 1.

Remark 5. 

In this article, practical factors such as partial uncertainties, fuzzy operators, and time delay in complex nonlinear systems can increase the difficulty of reaching a stable state of the networks. Consequently, unlike existing feedback control or adaptive control methods in [35,36,37,38,39], we have designed a new mixed impulse feedback control strategy to ensure the implementation of network synchronization tasks.

Especially, when partial uncertainties are not taken into account for establishing cellar NNs, then fuzzy delayed systems (5) and (6) degenerate into

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{v}_i\left(t\right)=-p_i{v}_i\left(t\right)+{\displaystyle \sum _{k=1}^m}{q}_{ik}{\varphi }_k\left(v_k\left(t\right)\right)+{\displaystyle \sum _{k=1}^m}{r}_{ik}{x}_k\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(v_k(t-\tau )\right)+{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(v_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\Phi }_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\Psi }_{ik}{x}_k+I_i,\hfill \\ v_i\left(t\right)={\beth }_i^v\left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(33)

and

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{w}_i\left(t\right)=-p_i{w}_i\left(t\right)+{\displaystyle \sum _{k=1}^m}{q}_{ik}{\varphi }_k\left(w_k\left(t\right)\right)+{\displaystyle \sum _{k=1}^m}{r}_{ik}{x}_k\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(w_k(t-\tau )\right)+{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(w_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{m}{\bigwedge }}}{\Phi }_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{m}{\bigvee }}}{\Psi }_{ik}{x}_k+I_i+U_i\left(t\right),\hfill \\ w_i\left(t\right)={\beth }_i^w\left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(34)

where $0<\mu <1$, and $i\in {\mathbb{N}}_1^m=\{1,2,\cdots ,m\}$. Under mixed control protocol (8), applying the same analytical techniques for Theorem 1, we can derive a worthwhile synchronization result as follows.

Corollary 1. 

When $-2<\varpi <0$ and ${\eta }_i>0$, assume that Assumption 1 is satisfied and the below condition

$$\begin{array}{c}\hfill {\rho }_{\mathit{max}}<{\tilde{\varrho }}_{\mathit{min}}\mathit{sin}{\displaystyle \frac{\mu \pi }{2}}\end{array}$$

(35)

holds, where ${\tilde{\varrho }}_{\mathit{min}}={\mathit{min}}_{1\le i\le m}\left[p_i-{\sum }_{k=1}^m\left|q_{ki}\right|{\mathcal{L}}_i^{\varphi }+{\eta }_i\right]$, ${\rho }_{\mathit{max}}={\mathit{max}}_{1\le i\le m}\left[{\sum }_{k=1}^m\left(\right|{\beta }_{ki}|+|{\gamma }_{ki}\left|\right){\mathcal{L}}_i^{\psi }\right]$, and $0<\mu <1$. Then the asymptotic synchronization between fuzzy FOTDCNNs (33) and (34) can be finished via mixed impulsive control protocol (8).

Theorem 2. 

When $\varpi \in (-\infty ,-2)\cup (0,+\infty )$ and ${\eta }_i>0$, assume that Assumption 1 is satisfied and there exist parameters $\mathcal{G},\vartheta >1$ satisfying

$$\begin{array}{c}\hfill {\gamma }_{\mathit{max}}{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_{ϵ}-t_{ϵ-1})}^{\mu }\right]<{\vartheta }^{-1},\end{array}$$

(36)

where $\mathcal{Q}={\varrho }_{\mathit{min}}-{\rho }_{\mathit{max}}\mathcal{G}>0$, ${\rho }_{\mathit{max}}={\mathit{max}}_{1\le i\le m}\left[{\sum }_{k=1}^m\left(\right|{\beta }_{ki}|+|{\gamma }_{ki}\left|\right){\mathcal{L}}_i^{\psi }\right]$, ${\varrho }_{\mathit{min}}={\mathit{min}}_{1\le i\le m}\left[p_i-{\daleth }_i-{\sum }_{k=1}^m\left(\right|q_{ki}|+{\gimel }_{ki}){\mathcal{L}}_i^{\varphi }+{\eta }_i\right]$, ${\gamma }_{\mathit{max}}=\left|(1+\varpi )\right|>1$, and $0<\mu <1$. Then the asymptotic synchronization between fuzzy FOTDCNNs (5) and (6) can be achieved via mixed impulsive control protocol (8).

Proof. 

Consider a function as follows:

$$\begin{array}{c}\hfill \tilde{\mathbb{V}}\left(t\right)={\left|\right|\sigma \left(t\right)\left|\right|}_1={\displaystyle \sum _{i=1}^m}\left|{\sigma }_i\left(t\right)\right|.\end{array}$$

(37)

When $t\in [t_{ϵ-1},t_{ϵ})$, applying the similar analysis techniques of (21), one can get

$$\begin{array}{c}\hfill {}_0{}^c\mathcal{D}_t^{\mu }\tilde{\mathbb{V}}\left(t\right)\le -{\varrho }_{\min }\tilde{\mathbb{V}}\left(t\right)+{\rho }_{\max }\tilde{\mathbb{V}}(t-\tau ),\end{array}$$

(38)

whenever ${\sigma }_i\left(t\right)$ fulfills the below condition

$$\begin{array}{c}\hfill \tilde{\mathbb{V}}(t-\tau )\le \mathcal{G}\tilde{\mathbb{V}}\left(t\right),\end{array}$$

(39)

for $\mathcal{G}>1$. We can then obtain from inequalities (38) and (39) that

$$\begin{array}{c}\hfill {}_0{}^c\mathcal{D}_t^{\mu }\tilde{\mathbb{V}}\left(t\right)\le -\mathcal{Q}\tilde{\mathbb{V}}\left(t\right),\end{array}$$

(40)

where $\mathcal{Q}={\varrho }_{\min }-{\rho }_{\max }\mathcal{G}>0$. Using Lemma 5, we derive

$$\begin{array}{c}\hfill \tilde{\mathbb{V}}\left(t\right)\le \tilde{\mathbb{V}}\left(t_{ϵ-1}\right){\mathbb{E}}_{\mu }\left[-\mathcal{Q}{\left(t-t_{ϵ-1}\right)}^{\mu }\right],t\in \left[t_{ϵ-1},t_{ϵ}\right).\end{array}$$

(41)

When $t=t_{ϵ}$, we obtain

$$\begin{array}{cc}\hfill \tilde{\mathbb{V}}\left(t_{ϵ}^{+}\right)& ={\displaystyle \sum _{i=1}^m}{|\sigma }_i\left(t_{ϵ}^{+}\right)|={\displaystyle \sum _{i=1}^m}\left|(1+\varpi ){\sigma }_i\left(t_{ϵ}^{-}\right)\right|\hfill \\ \hfill & \le {\displaystyle \sum _{i=1}^m}\left|(1+\varpi )\right||{\sigma }_i\left(t_{ϵ}^{-}\right)|\hfill \\ \hfill & \le {\gamma }_{\max }\tilde{\mathbb{V}}\left(t_{ϵ}^{-}\right),\hfill \end{array}$$

(42)

where ${\gamma }_{\max }=\left|(1+\varpi )\right|>1$.

For $t\in \left[t_0,t_1\right)$, it is easy to obtain from inequality (41) that

$$\begin{array}{c}\hfill \tilde{\mathbb{V}}\left(t\right)\le \tilde{\mathbb{V}}\left(t_0\right){\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t-t_0)}^{\mu }\right].\end{array}$$

(43)

Combining inequalities (42) and (43) yields that

$$\begin{array}{c}\hfill \tilde{\mathbb{V}}\left(t_1\right)\le {\gamma }_{\max }\tilde{\mathbb{V}}\left(t_1^{-}\right)\le {\gamma }_{\max }\tilde{\mathbb{V}}\left(t_0\right){\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_1-t_0)}^{\mu }\right].\end{array}$$

(44)

For $t\in \left[t_1,t_2\right)$, we can similarly derive

$$\begin{array}{cc}\hfill \tilde{\mathbb{V}}\left(t\right)& \le \tilde{\mathbb{V}}\left(t_1\right){\mathbb{E}}_{\mu }\left[-\mathcal{Q}{\left(t-t_1\right)}^{\mu }\right]\hfill \\ \hfill & \le {\gamma }_{\max }\tilde{\mathbb{V}}\left(t_0\right){\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_1-t_0)}^{\mu }\right]{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t-t_1)}^{\mu }\right],\hfill \end{array}$$

(45)

and

$$\begin{array}{c}\hfill \tilde{\mathbb{V}}\left(t_2\right)\le {\gamma }_{\max }\tilde{\mathbb{V}}\left(t_2^{-}\right)\le \tilde{\mathbb{V}}\left(t_0\right)\left\{{\gamma }_{\max }{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{\left(t_1-t_0\right)}^{\mu }\right]\right\}\left\{{\gamma }_{\max }{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_2-t_1)}^{\mu }\right]\right\}.\end{array}$$

(46)

Iterating the preceding process, for $t\in \left[t_{ϵ-1},t_{ϵ}\right)$, we can obtain

$$\begin{array}{cc}\hfill \tilde{\mathbb{V}}\left(t\right)\le & \tilde{\mathbb{V}}\left(t_0\right)\left\{{\gamma }_{\max }{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_1-t_0)}^{\mu }\right]\right\}\left\{{\gamma }_{\max }{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_2-t_1)}^{\mu }\right]\right\}\left\{{\gamma }_{\max }{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_3-t_2)}^{\mu }\right]\right\}\hfill \\ \hfill & \times \cdots \times \left\{{\gamma }_{\max }{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_{ϵ-1}-t_{ϵ-2})}^{\mu }\right]\right\}\left\{{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t-t_{ϵ-1})}^{\mu }\right]\right\}\hfill \\ \hfill \le & \tilde{\mathbb{V}}\left(t_0\right){\displaystyle \frac{1}{{\vartheta }^{ϵ-1}}}\left\{{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t-t_{ϵ-1})}^{\mu }\right]\right\}.\hfill \end{array}$$

(47)

Note that $\vartheta >1$ and $\mathcal{Q}>0$, we have $\tilde{\mathbb{V}}\left(t\right)\to 0$ as $ϵ\to +\infty$, namely, the asymptotic synchronization of master–slave cellar neural networks (5) and (6) can be completed via our mixed control techniques. □

Based on the analytical idea of Theorem 2, an important result can be acquired as below.

Corollary 2. 

When $-2<\varpi <0$ and ${\eta }_i>0$, assume that Assumption 1 is satisfied and there exist parameters $\mathcal{G},\vartheta >1$ satisfying

$$\begin{array}{c}\hfill {\gamma }_{\mathit{max}}{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_{ϵ}-t_{ϵ-1})}^{\mu }\right]<{\vartheta }^{-1},\end{array}$$

(48)

where $\mathcal{Q}={\varrho }_{\mathit{min}}-{\rho }_{\mathit{max}}\mathcal{G}<0$, ${\rho }_{\mathit{max}}={\mathit{max}}_{1\le i\le m}\left[{\sum }_{k=1}^m\left(\right|{\beta }_{ki}|+|{\gamma }_{ki}\left|\right){\mathcal{L}}_i^{\psi }\right]$, ${\varrho }_{\mathit{min}}={\mathit{min}}_{1\le i\le m}$$\left[p_i-{\daleth }_i-{\sum }_{k=1}^m\left(\right|q_{ki}+{\gimel }_{ki}\left|\right){\mathcal{L}}_i^{\varphi }+{\eta }_i\right]$, $0<{\gamma }_{\mathit{max}}=\left|(1+\varpi )\right|<1$, and $0<\mu <1$. Then the asymptotic synchronization between fuzzy FOTDCNNs (5) and (6) can be achieved via mixed impulsive control protocol (8).

Remark 6. 

In [11,21], impulsive control gain of the controller is limited by a local interval $(-2,0)$. Unlike [11,21], the impulse gain spectrum can be extended from the interval $(-2,0)$ to almost the entire real field, making the control schemes more flexible and the synchronization results in this article more general.

Remark 7. 

The synchronization theorems and corollaries of FOTDCNNs derived in this article under the parameter limitation $0<\mu <1$. However, it is worth noting that these synchronization results still hold for integer-order cellar NNs.

Remark 8. 

Based on the derived Theorems and Corollaries, the algorithm steps of parameter design can be given in detail as follows:

• Step 1: Initialize network parameters $p_i,\Delta p_i\left(t\right),q_{ik},\Delta q_{ik}\left(t\right),r_{ik},{\beta }_{ik},\mu ,\tau ,{\gamma }_{ik},{\Phi }_{ik}$, and ${\Psi }_{ik}$.
• Step 2: Compute the Lipschitz parameters ${\mathcal{L}}_k^{\varphi }$ and ${\mathcal{L}}_k^{\psi }$ by Assumption 1.
• Step 3: Set impulsive gain ϖ and feedback gain ${\eta }_i$, and calculate the values of ${\varrho }_{\mathit{min}}$ and ${\rho }_{\mathit{max}}$.
• Step 4: Design impulsive intervals $t_{ϵ}-t_{ϵ-1}$ utilizing the following rules.

(i) 

When $-2<\varpi <0$ and condition (19) holds, impulsive intervals $t_{ϵ}-t_{ϵ-1}$ are not absolutely restricted.

(ii) 

When $-2<\varpi <0$, impulsive intervals are determined by ${\gamma }_{\mathit{max}}{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_{ϵ}-t_{ϵ-1})}^{\mu }\right]<{\vartheta }^{-1}$, where $\mathcal{Q}={\varrho }_{\mathit{min}}-{\rho }_{\mathit{max}}\mathcal{G}>0$, ${\gamma }_{\mathit{max}}=\left|(1+\varpi )\right|>1$, and $\vartheta >1$.

(iii) 

When $-2<\varpi <0$, impulsive intervals are determined by ${\gamma }_{\mathit{max}}{\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_{ϵ}-t_{ϵ-1})}^{\mu }\right]<{\vartheta }^{-1}$, where $\mathcal{Q}={\varrho }_{\mathit{min}}-{\rho }_{\mathit{max}}\mathcal{G}<0$, $0<{\gamma }_{\mathit{max}}=\left|(1+\varpi )\right|<1$, and $\vartheta >1$.

4. Discussion and Verification of Results

To show the applicability of the leading synchronization Theorems, different illustrative experiments are provided in this part.

Example 1. 

Contemplate the following 2-dimensional cellar NNs with fuzzy operators and partial uncertainties as the drive system.

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{v}_i\left(t\right)=-(p_i+\Delta p_i\left(t\right))v_i\left(t\right)+{\displaystyle \sum _{k=1}^2}(q_{ik}+\Delta q_{ik}\left(t\right)){\varphi }_k\left(v_k\left(t\right)\right)\hfill \\ +{\displaystyle \sum _{k=1}^2}{r}_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{2}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(v_k(t-\tau )\right)+{\displaystyle \underset{k=1}{\overset{2}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(v_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{2}{\bigwedge }}}{\Phi }_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{2}{\bigvee }}}{\Psi }_{ik}{x}_k+I_i,\hfill \\ v_i\left(t\right)={\beth }_i^v\left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(49)

where $\mu =0.92,p_1=0.2,p_2=0.1,\Delta p_1\left(t\right)=\Delta q_{1k}\left(t\right)=0.1\mathit{cos}t,\Delta p_2\left(t\right)=\Delta q_{2k}\left(t\right)=0.1\mathit{cos}t$, $\tau =0.2,I_i=0$, ${\left(q_{ik}\right)}_{2\times 2}=\left[\begin{array}{cc}-1.2& -2.0\\ 0.8& -1.4\end{array}\right]$, ${\left(r_{ik}\right)}_{2\times 2}=\left[\begin{array}{cc}0.2& 0.3\\ 0.1& 0.4\end{array}\right]$, ${\left({\Phi }_{ik}\right)}_{2\times 2}=\left[\begin{array}{cc}0.1& 0.3\\ 0.3& 0.1\end{array}\right]$, ${\left({\Psi }_{ik}\right)}_{2\times 2}=\left[\begin{array}{cc}0.3& 0.2\\ 0.4& 0.1\end{array}\right]$, ${\left({\beta }_{ik}\right)}_{2\times 2}=\left[\begin{array}{cc}-1.5& -0.1\\ -0.3& -2.5\end{array}\right]$, ${\left({\gamma }_{ik}\right)}_{2\times 2}=\left[\begin{array}{cc}-0.8& -0.1\\ -0.2& -1.5\end{array}\right]$, and ${\left(x_k\right)}_{2\times 1}=\left[\begin{array}{c}0.2\\ 0.2\end{array}\right]$. Choosing activation functions ${\varphi }_k\left(v\right)={\psi }_k\left(v\right)=\tan h\left(v\right)$, it is easy to validate Assumption 1 holds for ${\mathcal{L}}_k^{\varphi }=1$ and ${\mathcal{L}}_k^{\psi }=1$.

According to the above neural network parameters, we consider the following fuzzy NNs as the response system.

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{w}_i\left(t\right)=-(p_i+\Delta p_i\left(t\right))w_i\left(t\right)+{\displaystyle \sum _{k=1}^2}(q_{ik}+\Delta q_{ik}\left(t\right)){\varphi }_k\left(w_k\left(t\right)\right)\hfill \\ +{\displaystyle \sum _{k=1}^2}{r}_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{2}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(w_k(t-\tau )\right)+{\displaystyle \underset{k=1}{\overset{2}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(w_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{2}{\bigwedge }}}{\Phi }_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{2}{\bigvee }}}{\Psi }_{ik}{x}_k+I_i+U_i\left(t\right),\hfill \\ w_i\left(t\right)={\beth }_i^w\left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(50)

where the network parameters are the same as the drive system. Let impulsive interval $t_k-t_{k-1}=0.1$, feedback gain ${\eta }_i=8.1$ and impulsive gain $\varpi =-0.6$. Simple calculations indicate that ${\rho }_{\mathit{max}}=4.2,{\varrho }_{\mathit{min}}=4.6$, and ${\rho }_{\mathit{max}}-{\varrho }_{\mathit{min}}\mathit{sin}{\displaystyle \frac{\mu \pi }{2}}=-0.3637<0$, which shows the condition of Theorem 1 holds.

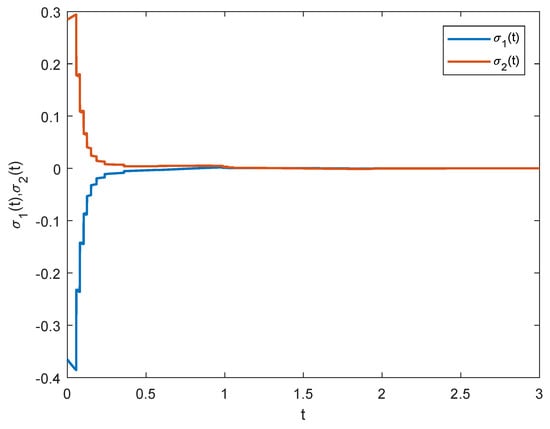
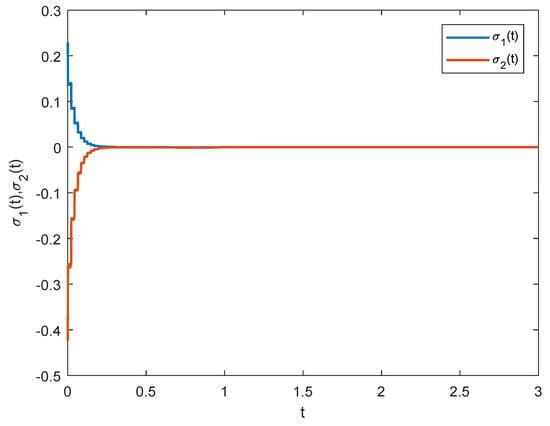
The initial values of fractional-order cellar NNs (49) and (50) are randomly produced from $[-0.5,0.5]$ and improved prediction correction schemes are applied to handle numerical simulations. Under impulsive controller with feedback gain ${\eta }_i=8.1$ and impulsive gain $\varpi =-0.6$, Figure 1 gives the synchronization errors between fractional-order cellar NNs (49) and (50) in Example 1. The blue and red error curves converge to zero with control time evolution indicating that master–slave NNs can achieve asymptotic synchronization. The control requirements of Theorem 1 also hold by slightly adjusting the control strengths as ${\eta }_i=7.9$ and $\varpi =-0.7$. Under this case, as shown in Figure 2, the fractional-order cellar NNs can still achieve asymptotic synchronization.

Example 2. 

Contemplate the following 3-dimensional fractional-order cellar NNs with fuzzy operators and uncertainties as the drive system.

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{v}_i\left(t\right)=-(p_i+\Delta p_i\left(t\right))v_i\left(t\right)+{\displaystyle \sum _{k=1}^3}(q_{ik}+\Delta q_{ik}\left(t\right)){\varphi }_k\left(v_k\left(t\right)\right)\hfill \\ +{\displaystyle \sum _{k=1}^3}{r}_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{3}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(v_k(t-\tau )\right)+{\displaystyle \underset{k=1}{\overset{3}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(v_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{3}{\bigwedge }}}{\Phi }_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{3}{\bigvee }}}{\Psi }_{ik}{x}_k+I_i,\hfill \\ v_i\left(t\right)={\beth }_i^v\left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(51)

where $\mu =0.95,p_1=1.5,p_2=1,p_3=1.2,\Delta p_1\left(t\right)=\Delta q_{1k}\left(t\right)=0.1\mathit{cos}t,\Delta p_2\left(t\right)=\Delta q_{2k}\left(t\right)=0.1\sin t,\Delta p_3\left(t\right)=\Delta q_{3k}\left(t\right)=0.1\mathit{cos}t$, ${\left(q_{ik}\right)}_{3\times 3}=\left[\begin{array}{ccc}1.8& -3.4& -3.1\\ -3.2& 1.5& 4.5\\ -4& -4.2& 1.3\end{array}\right]$, ${\left({\beta }_{ik}\right)}_{3\times 3}={\left({\gamma }_{ik}\right)}_{3\times 3}=\left[\begin{array}{ccc}-1.5& -1.2& -0.8\\ -2.2& -1.4& -2.5\\ -0.2& -1.4& -1.2\end{array}\right]$, ${\left(r_{ik}\right)}_{3\times 3}={\left({\Phi }_{ik}\right)}_{3\times 3}={\left({\Psi }_{ik}\right)}_{3\times 3}=\left[\begin{array}{ccc}0.1& 0& 0\\ 0& 0.2& 0\\ 0& 0& 0.5\end{array}\right]$, $\tau =0.2$, and $I_1=I_2=I_3=0.5$. Choosing activation functions ${\varphi }_k\left(v\right)={\psi }_k\left(v\right)=0.5\mathit{tan}h\left(v\right)$, it is readily validate Assumption 1 holds for ${\mathcal{L}}_k^{\varphi }=0.5$ and ${\mathcal{L}}_k^{\psi }=0.5$.

According to the above neural network parameters, we consider the following fuzzy NNs as the response system.

$$\left\{\begin{array}{c}{}_0{}^c\mathcal{D}_t^{\mu }{w}_i\left(t\right)=-(p_i+\Delta p_i\left(t\right))w_i\left(t\right)+{\displaystyle \sum _{k=1}^3}(q_{ik}+\Delta q_{ik}\left(t\right)){\varphi }_k\left(w_k\left(t\right)\right)\hfill \\ +{\displaystyle \sum _{k=1}^3}{r}_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{3}{\bigwedge }}}{\beta }_{ik}{\psi }_k\left(w_k(t-\tau )\right)+{\displaystyle \underset{k=1}{\overset{3}{\bigvee }}}{\gamma }_{ik}{\psi }_k\left(w_k(t-\tau )\right)\hfill \\ +{\displaystyle \underset{k=1}{\overset{3}{\bigwedge }}}{\Phi }_{ik}{x}_k+{\displaystyle \underset{k=1}{\overset{3}{\bigvee }}}{\Psi }_{ik}{x}_k+I_i+U_i\left(t\right),\hfill \\ w_i\left(t\right)={\beth }_i^w\left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(52)

where the network parameters are the same as drive system (51). Let impulsive interval $t_k-t_{k-1}=0.2$, feedback gain ${\eta }_i=16.4$, impulsive gain $\varpi =0.1$, and $\vartheta =1.5$, simple calculations show that ${\rho }_{\mathit{max}}=4.5,{\varrho }_{\mathit{min}}=8.6,\mathcal{Q}=3.6$, and ${\mathbb{E}}_{\mu }\left[-\mathcal{Q}{(t_{ϵ}-t_{ϵ-1})}^{\mu }\right]=0.4755$, which shows the conditions of Theorem 2 hold.

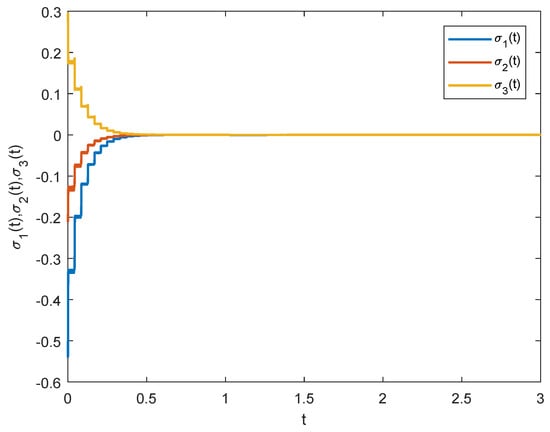
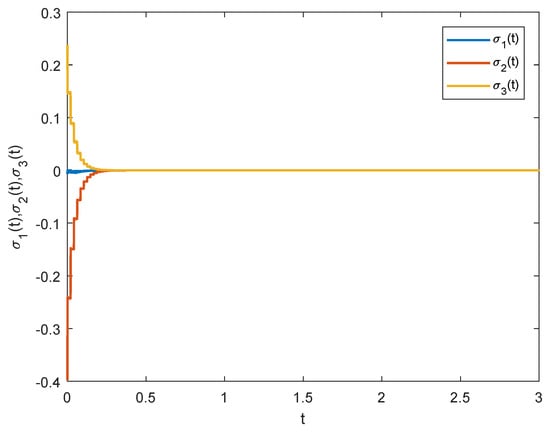
The starting values of fractional-order cellar NNs (51) and (52) are randomly selected from $[-1,1]$. To accomplish the asymptotic synchronization task, mixed impulsive control schemes (8) with feedback gain ${\eta }_i=16.4$ and impulsive gain $\varpi =0.1$ are utilized. As one can see in Figure 3, red curve, yellow curve, and blue curve stand for the time evolution of asymptotic synchronization errors of fractional-order master–slave NNs (51) and (52). We adjust the control gains as ${\eta }_i=16.2$ and $\varpi =0.2$ so that the sufficient conditions of Theorem 2 still hold. Figure 4. shows that the asymptotic synchronization errors of fractional-order fuzzy NNs also converge to zero, which implies that the asymptotic synchronization task can also be finished.

5. Conclusions

This article establishes a practical Caputo fractional-order network model by addressing uncertainties, fuzzy operators, and time delays in mathematical modeling. A mixed impulsive feedback control protocol is designed, integrating impulse sampling information at discrete intervals and error feedback at impulsive moments. Utilizing the fractional comparison principle and the Laplace transform, sufficient synchronization conditions for uncertain FOTDCNNs with two types of fuzzy operators are derived based on the proposed control techniques. The impulse gain of existing fractional-order controllers is limited to a local small interval. However, this study can adjust the impulse gain in almost the entire real range according to system control requirements, which ensures the generality of the control strategy and synchronization results. In the future, we will continue our research and apply the results obtained to the cooperative control of practical targets, such as the synchronized flight of small unmanned aircraft formations. In addition, we will design automatic event-triggering mechanisms for optimal decision-making in impulse control moments to reduce control costs and increase the security of information interactions.