Heavy Tail and Long-Range Dependence for Skewed Time Series Prediction Based on a Fractional Weibull Process
Abstract
:1. Introduction
1.1. Research Background
1.2. Literature Review for the Stochastic Time Series Prediction
1.3. Works and Contributions
1.4. Structure of the Paper
2. Statistical Properties of the fWp
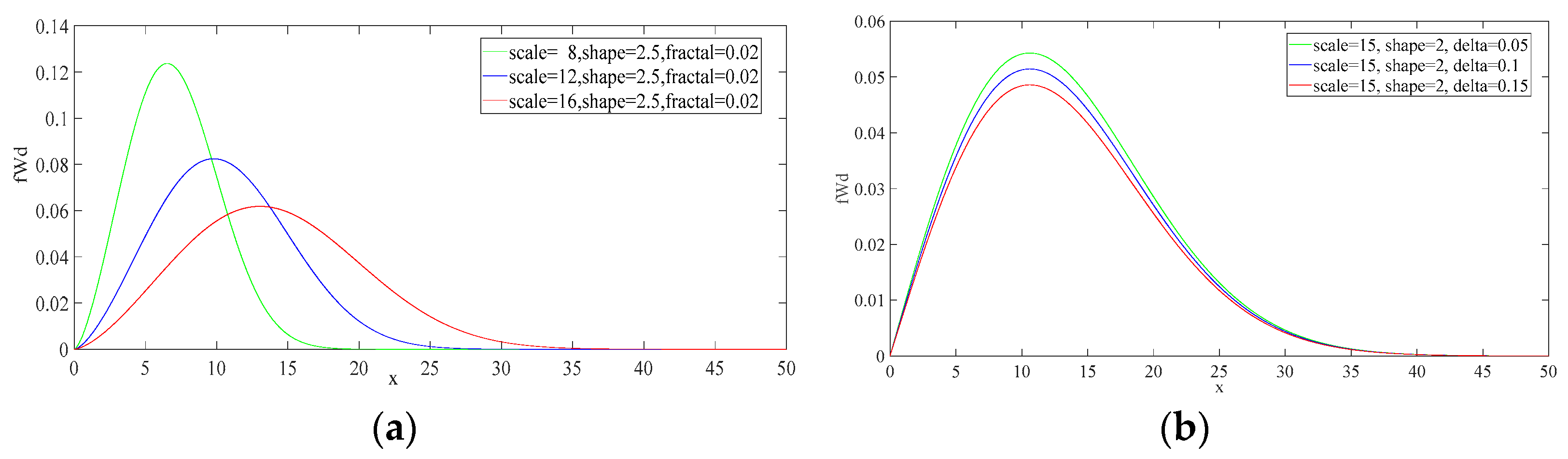
2.1. Skewness of the fWp
2.2. Heavy-Tailed Characteristics and Long-Range Dependence of the fWp
2.3. Random Walk Based on fWp
3. Difference Iterative Forecasting Model Based on the fWp
3.1. Black–Scholes Model with Long-Range Dependence and Non-Gaussian Characteristics
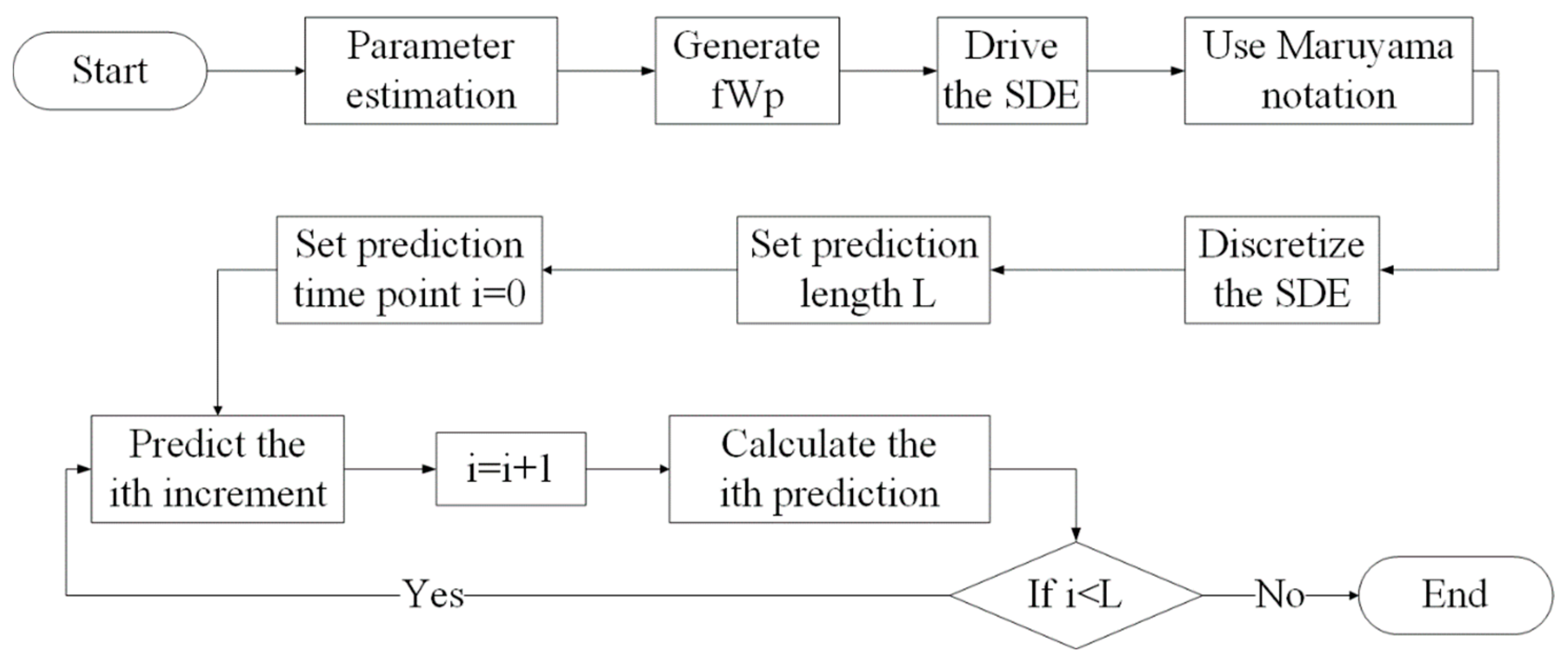
3.2. Stochastic Difference Scheme for the SDE-Based fWp Predictive Model
3.3. Parameter Estimation
4. Analysis of the Difference Scheme for the SDE Driven by the fWp
4.1. Consistency of the fWp Predictive Model
4.2. Stability of the fWp Predictive Model
4.3. Convergence of the fWp Predictive Model
4.4. Model Comparison for the Stochastic Time Series Prediction
5. Case Study of Wind Speed Forecasting
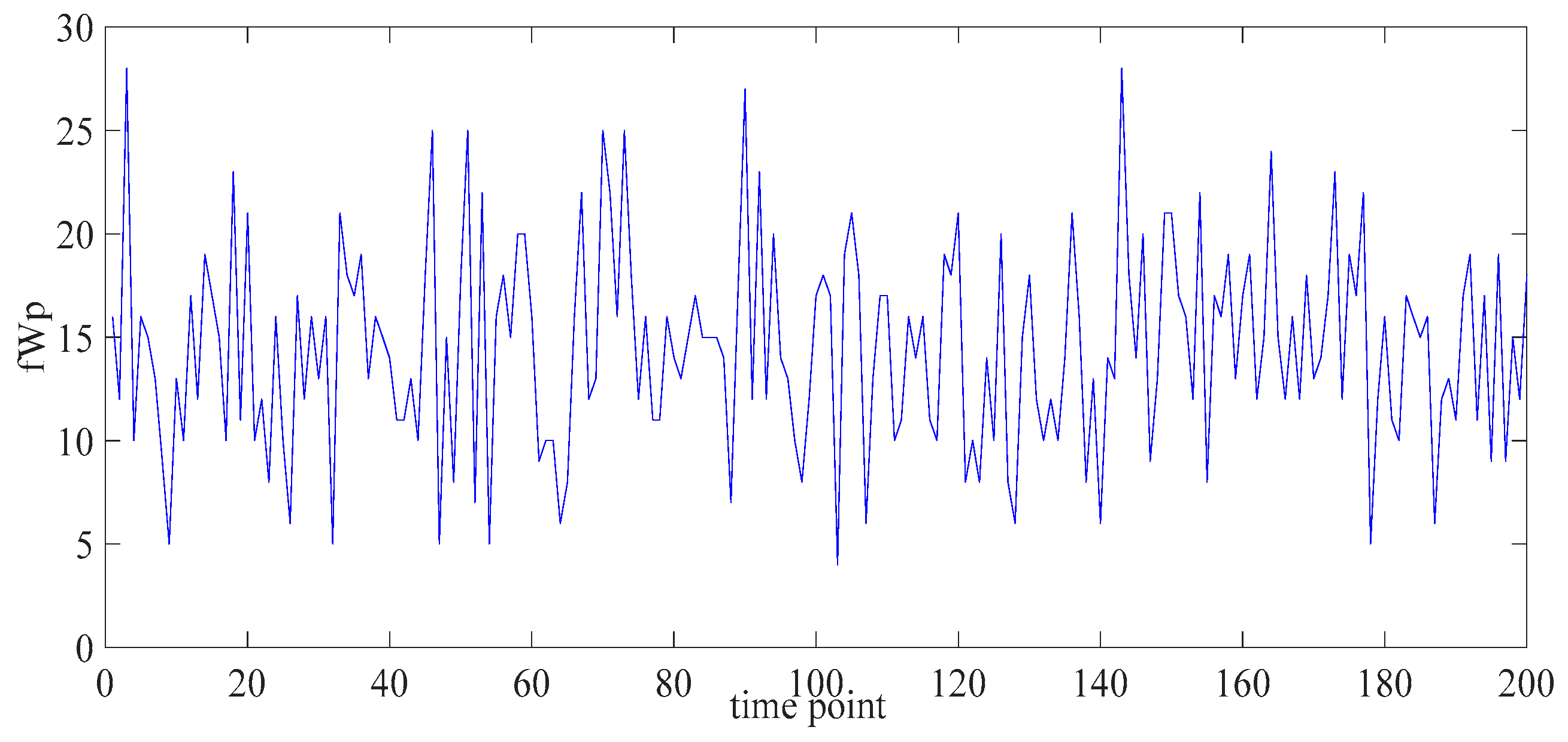
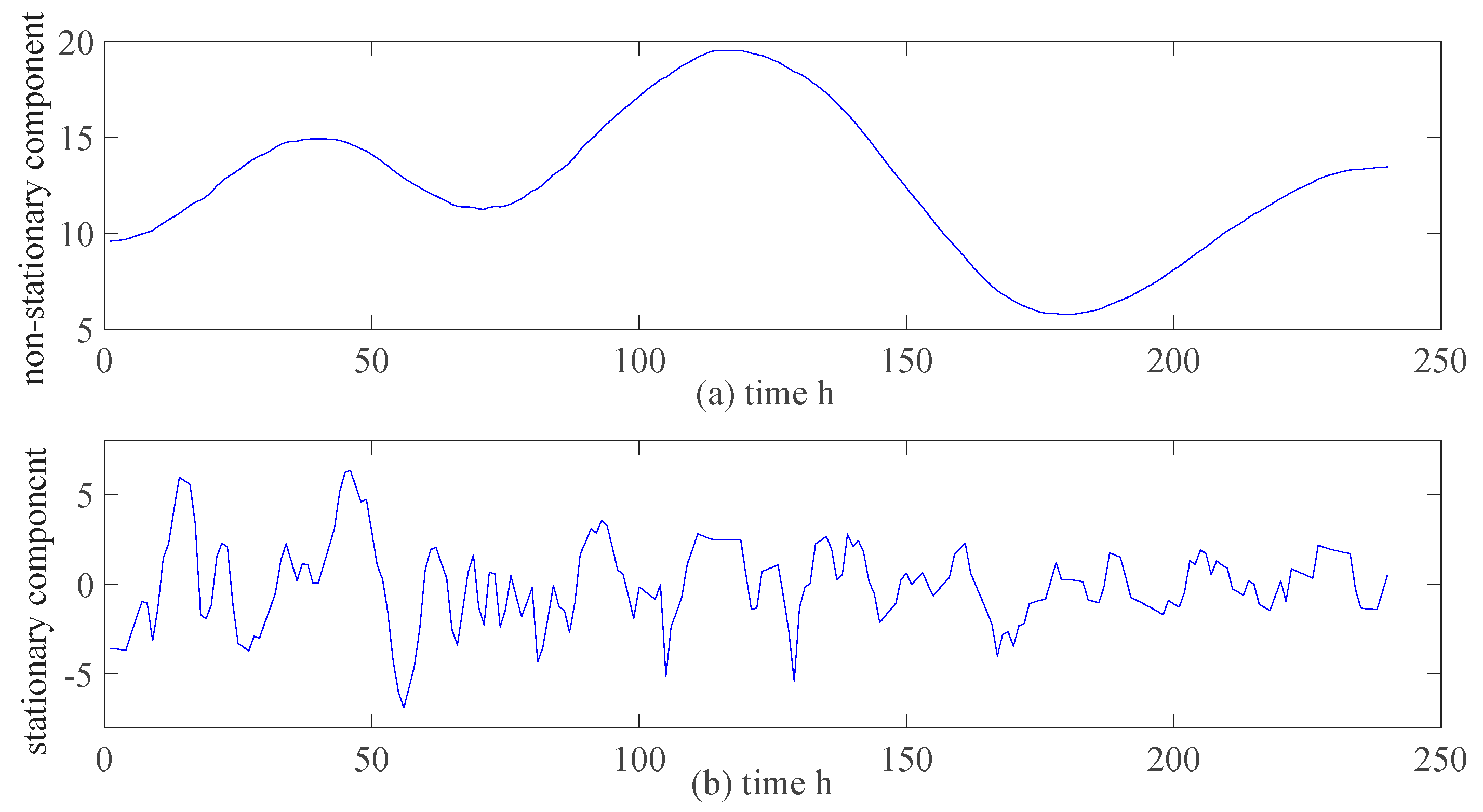
5.1. Data Preprocessing for the Wind Speed Training Dataset
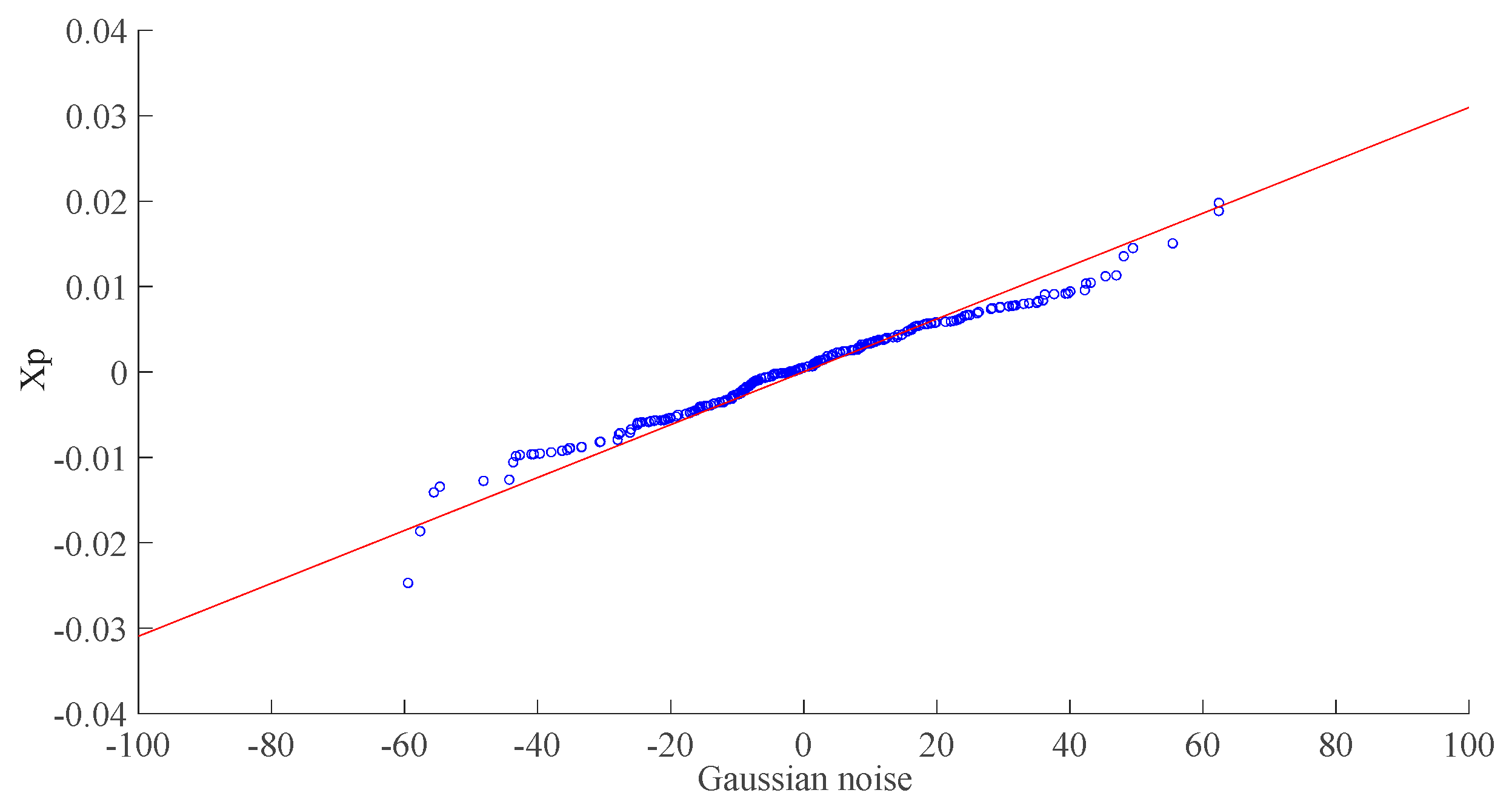
5.2. Statistical Properties of the Wind Speed Series
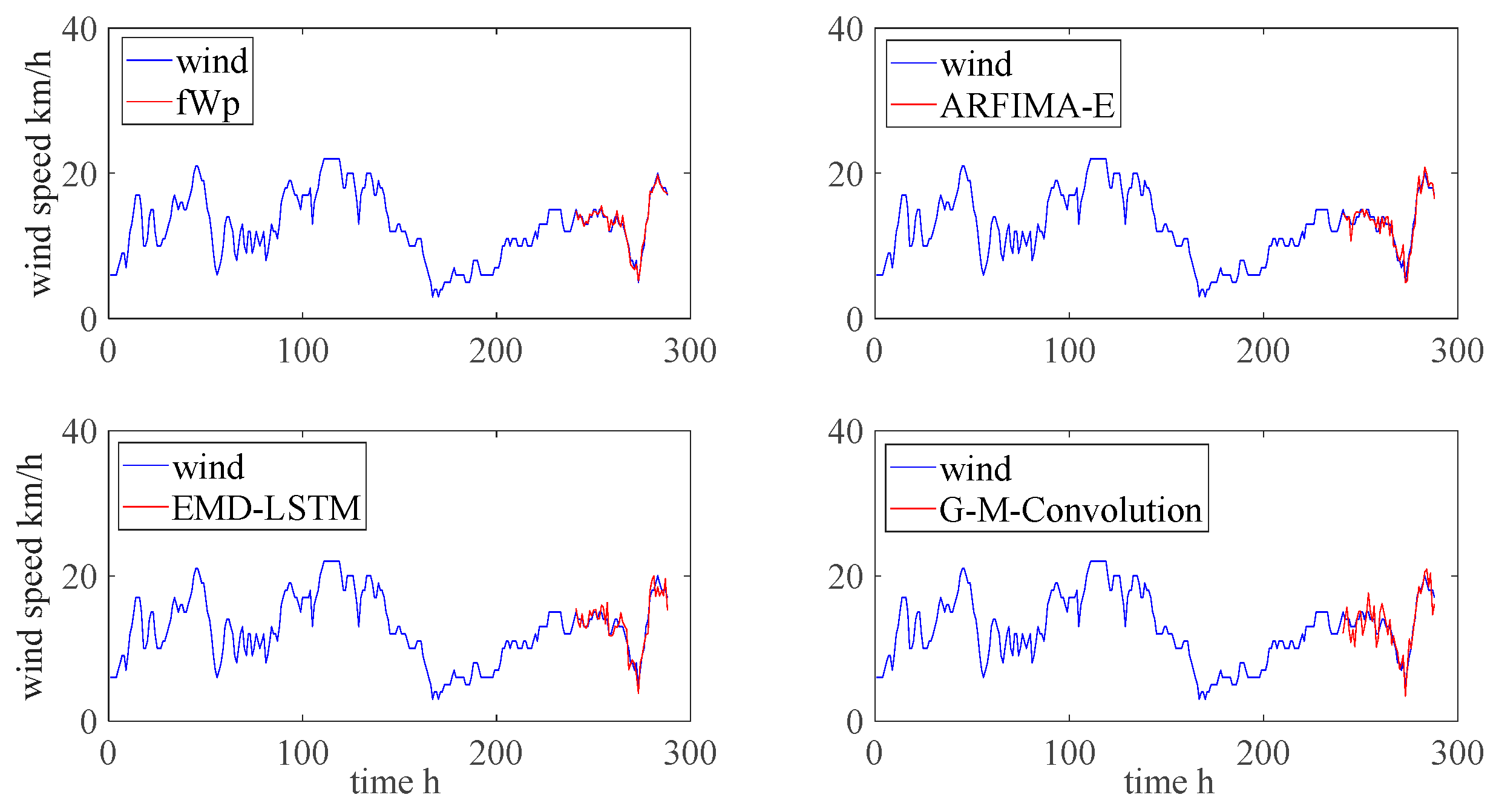
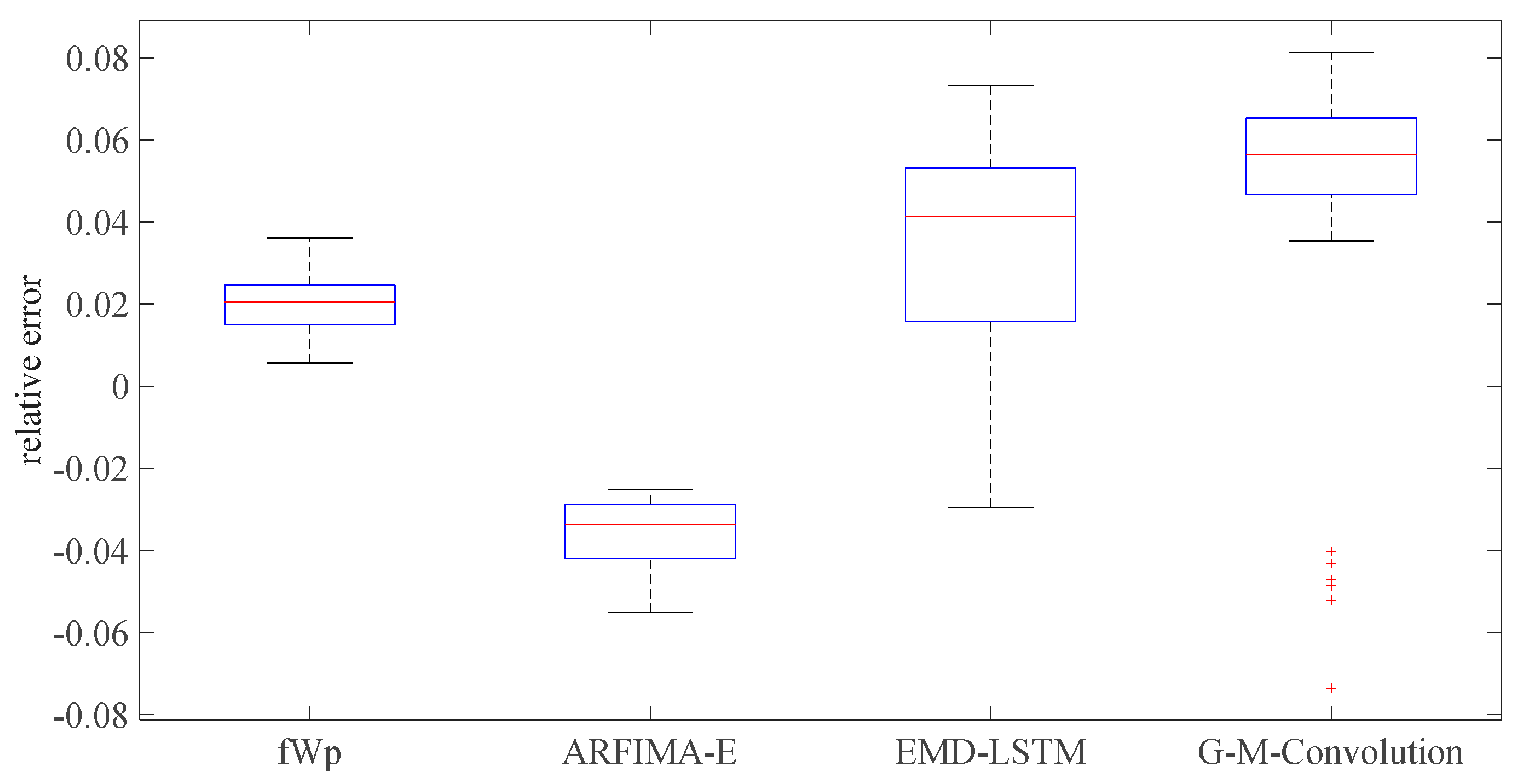
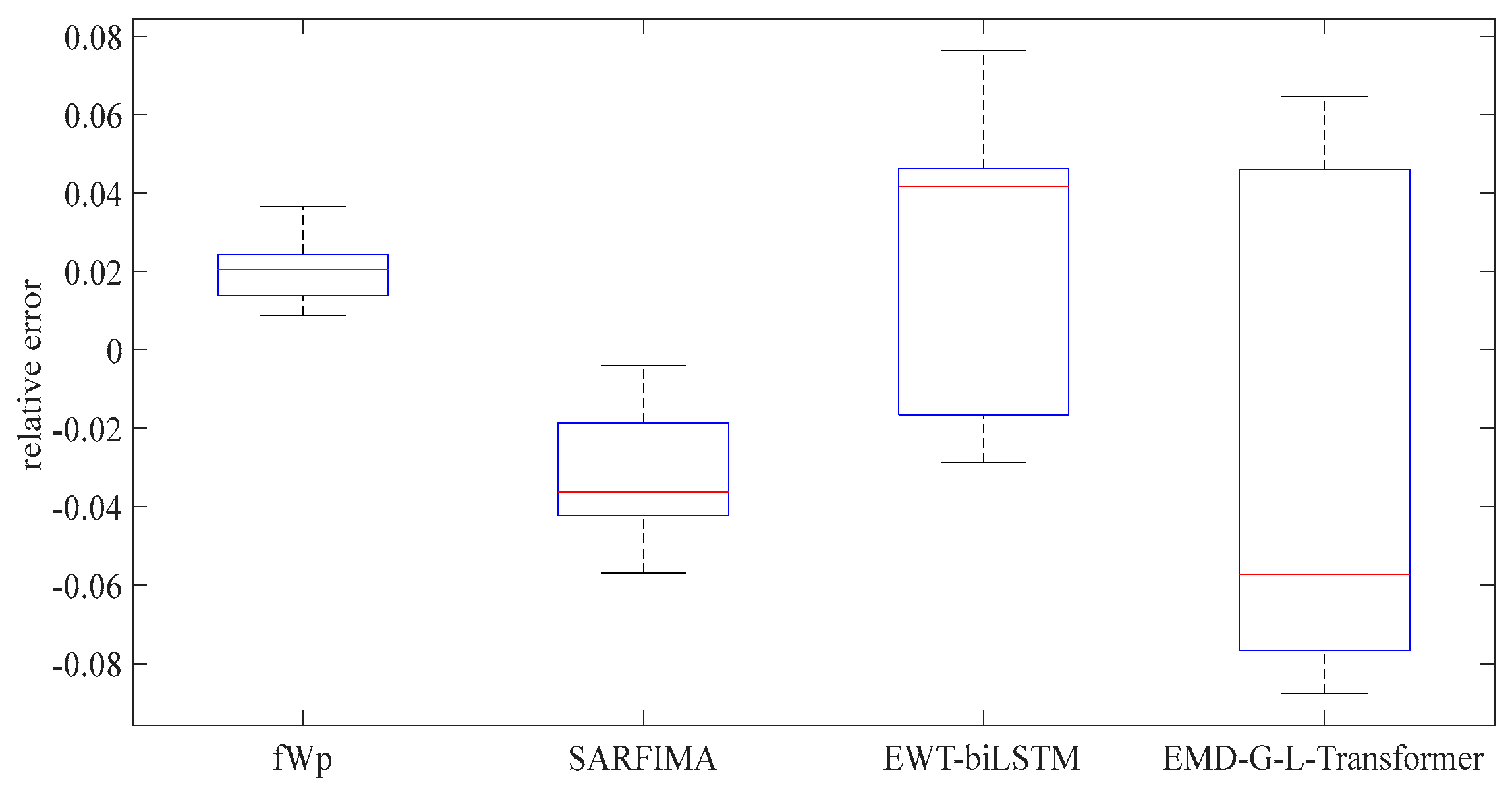
5.3. Performance Evaluation of the Wind Speed Prediction
6. Case Study of Stock Price Forecasting
6.1. Data Preprocessing for the Stock Price Training Dataset
6.2. Statistical Properties of the Stock Price Series
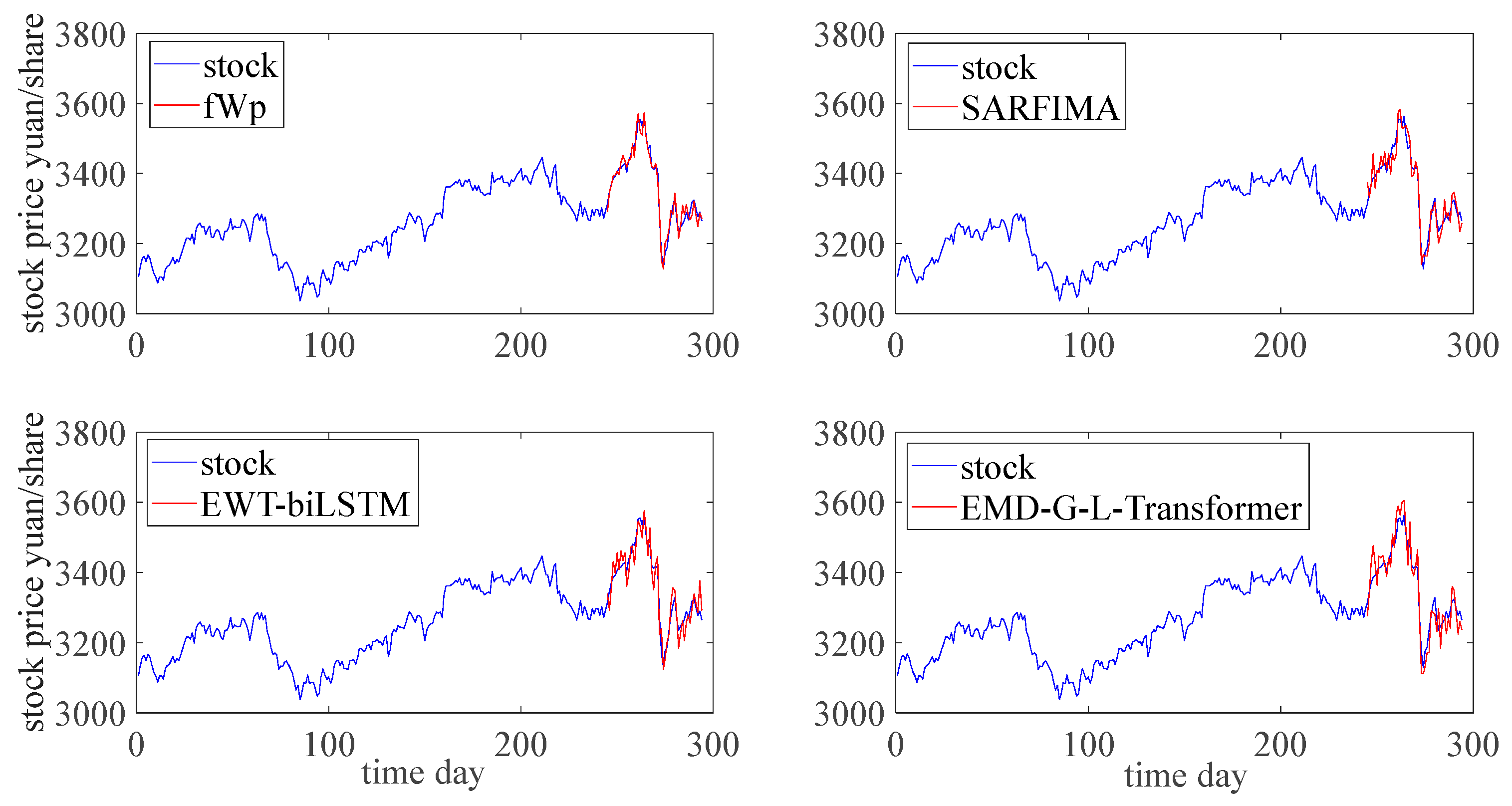
6.3. Performance Evaluation of the Stock Price Prediction
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GoF | goodness of fitting |
| fWd | fractional Weibull distribution |
| SSE | sum of squared error |
| RMSE | root mean square error |
| fWp | fractional Weibull process model |
| ARFIMA-E | autoregressive fractional integrated moving average ensemble learning model |
| EMD-LSTM | empirical mode decomposition–long short-term memory network |
| G-M-Convolution | graph-multiresolution convolution neural network |
| D-M | Diebold–Mariano test |
| FLOPs | floating-point operation params (number of parameters in the model) |
| SARFIMA | seasonal autoregressive fractional integrated moving average model |
| EWT-biLSTM | empirical wavelet transform–bidirectional long short-term memory network |
| EMD-G-L-Transformer | empirical mode decomposition–gated recurrent neural network–long short-term memory network–multi-head attention transformer |
References
- Muhammad, A. A study on skewness and kurtosis estimators of wind speed distribution under indeterminacy. Theor. Appl. Climatol. 2021, 143, 1227–1234. [Google Scholar]
- Park, Y.J. Skewness Versus Kurtosis: Implications for Pricing and Hedging Options. Asia-Pac. J. Financ. Stud. 2017, 46, 903–933. [Google Scholar]
- Yu, Z.W.; Tuzuzer, A. Fractional Weibull Wind Speed Modelling for Wind Power Production Estimation. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting (PES), Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Aslam, F.; Latif, S.; Ferreira, P. Investigating Long-Range Dependence of Emerging Asian Stock Markets Using Multifractal Detrended Fluctuation Analysis. Symmetry 2020, 12, 1157. [Google Scholar] [CrossRef]
- Katikas, L.; Dimitriadis, P.; Koutsoyiannis, D.; Kontos, T.; Kyriakidis, P. A stochastic simulation scheme for the long-term persistence, heavy-tailed and double periodic behavior of observational and reanalysis wind time-series. Appl. Energy 2021, 295, 116873. [Google Scholar] [CrossRef]
- Deng, W.J.; Song, W.Q.; Cattani, C.; Chen, J.X.; Chen, X.L. On the fractional Weibull process. Front. Phys. 2022, 10, 790791. [Google Scholar] [CrossRef]
- Bokde, N.; Feijoo, A.; Villanueva, D.; Kulat, K.A. Review on Hybrid Empirical Mode Decomposition Models for Wind Speed and Wind Power Prediction. Energies 2019, 12, 254. [Google Scholar] [CrossRef]
- Naik, J.; Satapathy, P.; Dash, P.K. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression. Appl. Soft Comput. 2018, 70, 1167–1188. [Google Scholar] [CrossRef]
- Dragomiretskig, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Wu, H.Y.; Lu, S.; Zhou, M. Ensemble FARIMA Prediction with Stable Infinite Variance Innovations for Supermarket Energy Consumption. Fractal Fract. 2022, 6, 276. [Google Scholar] [CrossRef]
- Hu, H.W.; Zhao, C.N.; Li, J.; Huang, Y.Q. Stock Prediction Model Based on Mixed Fractional Brownian Motion and Improved Fractional-Order Particle Swarm Optimization Algorithm. Fractal Fract. 2022, 6, 560. [Google Scholar] [CrossRef]
- Czapaj, R.; Kaminski, J.; Soltysik, M. A Review of Auto-Regressive Methods Applications to Short-Term Demand Forecasting in Power Systems. Energies 2022, 15, 6729. [Google Scholar] [CrossRef]
- Shang, T.; Li, W.Q.; Wu, L. Regional forecasting of wind speed in large scale wind plants. Int. J. Green Energy 2022, 20, 486–496. [Google Scholar] [CrossRef]
- Bayraktav, E.; Poor, V.H.; Rao, R. Prediction and tracking of long-range -dependent sequences. Syst. Control Lett. 2005, 54, 1083–1090. [Google Scholar] [CrossRef]
- Feng, S.; Wang, X.M.; Sun, H.W.; Zhang, Y.; Li, L. A better understanding of long range temporal dependence of traffic flow time series. Phys. A Stat. Mech. Appl. 2018, 492, 639–650. [Google Scholar] [CrossRef]
- Maria, C.M.; Md, A.M.B.; Osei, K.T.; Hector, G.H. Long memory effects and forecasting of earthquake and volcano seismic data. Phys. A Stat. Mech. Appl. 2020, 559, 125049. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Y.Q.; Zhang, X. An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs. Axioms 2017, 6, 16. [Google Scholar] [CrossRef]
- Wang, Y.S.; Fang, H.Z.; Jin, J.Y.; Ma, G.J.; He, X.; Dai, X.; Yue, Z.G.; Cheng, C.; Zhang, H.T.; Pu, D.L.; et al. Data-Driven Discovery of Stochastic Differential Equations. Engineering 2022, 17, 244–252. [Google Scholar] [CrossRef]
- Ali, S.; Abbas, Z.; Butt, M.M. A comparison of different weather forecasting models for the monthly forecast of Lahore city. Mausam 2021, 72, 749–780. [Google Scholar] [CrossRef]
- Sakthivel, R.; Joby, M.; Anthoni, S.M. Resilient dissipative based controller for stochastic systems with randomly occurring gain fluctuations. Inf. Sci. 2017, 218–419, 447–462. [Google Scholar] [CrossRef]
- Callado, A.; Kamienski, C.; Szabo, G.; Gero, B.P.; Kelner, J.; Fernandes, S.; Sadok, D. A Survey on Internet Traffic Identification. IEEE Commun. Surv. Tutor. 2009, 11, 37–52. [Google Scholar] [CrossRef]
- Song, W.Q.; Liu, H.; Enrico, Z. Long-range dependence and heavy tail characteristics for remaining useful life prediction in rolling bearing degradation. Appl. Math. Model. 2022, 102, 268–284. [Google Scholar] [CrossRef]
- Duan, S.; Song, W.Q.; Zio, E.; Cattani, C.; Li, M. Product technical life prediction based on multi-modes and fractional Lévy stable motion. Mech. Syst. Signal Process. 2021, 161, 107974. [Google Scholar] [CrossRef]
- Leland, W.E.; Taqqu, M.S.; Willinger, W.; Wilson, D.V. On the Self-Similar Nature of Ethernet Traffic. ACM Sigcomm Comput. Commun. Rev. 1993, 23, 183–193. [Google Scholar] [CrossRef]
- Shao, B.L.; Song, D.; Bian, G.Q.; Zhao, Y. Wind Speed Forecast Based on the LSTM Neural Network Optimized by the Firework Algorithm. Adv. Mater. Sci. Eng. 2021, 2021, 4874757. [Google Scholar] [CrossRef]
- Hao, W.; Sun, X.F.; Wang, C.Y.; Chen, H.Y.; Huang, L.M. A hybrid EMD-LSTM model for non-stationary wave prediction in offshore China. Ocean Eng. 2022, 246, 110566. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Kuenzel, S.; Colombo, N.; Watkins, C. Hybrid Short-term Load Forecasting Method Based on Empirical Wavelet Transform and Bidirectional Long Short-term Memory Neural Networks. J. Mod. Power Syst. Clean Energy 2022, 10, 1216–1228. [Google Scholar] [CrossRef]
- Song, Y.; Tang, D.Y.; Yu, J.S.; Yu, Z.T.; Li, X. Short-Term Forecasting Based on Graph Convolution Networks and Multiresolution Convolution Neural Network for Wind Power. IEEE Trans. Ind. Inform. 2023, 19, 1691–1702. [Google Scholar] [CrossRef]
- Li, C.Y.; Qian, G.Q. Stock Price Prediction Using a Frequency Decomposition Based GRU Transformer Neural Network. Appl. Sci. 2023, 13, 222. [Google Scholar] [CrossRef]
- Abderrahim, Q.; Ernesto, S.M. Generating data from improper distributions: Application to Cox proportional hazards models with cure. J. Stat. Comput. Simul. 2014, 84, 204–214. [Google Scholar]
- Applebaum, K.M.; Malloy, E.J.; Eisen, E.A. Left Truncation, Susceptibility, and Bias in Occupational Cohort Studies. Epidemiology 2011, 22, 599–606. [Google Scholar] [CrossRef]
- Sakthivel, R.; Sathishkumar, M.; Kaviarasan, B.; Anthoni, S.M. Synchronization and state estimation for stochastic complex networks with uncertain inner coupling. Neurocomputing 2017, 238, 44–45. [Google Scholar] [CrossRef]
- Downey, A.B. Lognormal and Pareto Distributions in the Internet. Comput. Commun. 2005, 28, 790–801. [Google Scholar] [CrossRef]
- Alghalith, M. Pricing the Americanoptions using the Black-Scholes pricing formula. Phys. A Stat. Mech. Appl. 2018, 507, 443–445. [Google Scholar] [CrossRef]
- Kwok, K.L.; Chiu, M.C.; Wong, H.Y. Demand for longevity securities under relative performance concerns: Stochastic differential games with cointegration. Insur. Math. Econ. 2017, 71, 353–366. [Google Scholar] [CrossRef]
- Roth, C.H. Difference Methods for Stochastic Partial Differential Equations. ZAMM-Z. Angew. Math. Mech. 2002, 82, 821–830. [Google Scholar] [CrossRef]
- Liu, L.; Li, M.L.; Deng, F. Stability equivalence between the neutral delayed stochastic differential equations and the Euler-Maruyama numerical Scheme. Appl. Numer. Math. 2008, 127, 370–386. [Google Scholar] [CrossRef]
- Lang, A. A Lax equivalence theorem for stochastic differential equations. J. Comput. Appl. Math. 2010, 234, 3387–3396. [Google Scholar] [CrossRef]
- Shi, H.Y.; Dong, Z.B.; Xiao, N.; Huang, Q.N. Wind Speed Distributions Used in Wind Energy Assessment: A Review. Front. Energy Res. 2021, 9, 769920. [Google Scholar] [CrossRef]
- Paparoditis, E.; Politis, D.N. The asymptotic size and power of the augmented Dickey-Fuller test for a unit root. Econom. Rev. 2018, 37, 955–973. [Google Scholar] [CrossRef]
- Hu, B.; Li, Y.D.; Yang, H.J.; Wang, H. Wind speed model based on kernel density estimation and its application in reliability assessment of generating systems. J. Mod. Power Syst. Clean Energy 2017, 5, 220–227. [Google Scholar] [CrossRef]
- Huang, G.Q.; Xia, L.L.; Liu, M.; Wang, D.H.; Zheng, H.T. Tail-Weighted Wind Speed Distribution by Mixture Model with Constrained Maximum Likelihood. Int. J. Struct. Stab. Dyn. 2022, 22, 2240016. [Google Scholar] [CrossRef]
- Xie, D.F.; Chen, K.S.; Yang, X.F. Effect of Bispectrum on Radar Backscattering From Non-Gaussian Sea Surface. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 12, 4367–4378. [Google Scholar] [CrossRef]
- Zheng, H.B.; Huang, W.F.; Zhao, J.H.; Liu, J.F.; Zhang, Y.Y.; Shi, Z.; Zhang, C.H. A normal falling model for wind speed probability distribution of wind farms. Renew. Energy 2022, 184, 91–99. [Google Scholar] [CrossRef]
- Serroukh, A.; Walden, A.T.; Percival, D.B. Statistical Properties and Uses of the Wavelet Variance Estimator for the Scale Analysis of Time Series. J. Am. Stat. Assoc. 2000, 95, 184–196. [Google Scholar] [CrossRef]
- Diebold, F.X. Comparing Predictive Accuracy, Twenty Years Later: A Personal Perspective on the Use and Abuse of Diebold-Mariano Tests. J. Bus. Econ. Stat. 2015, 33, 1. [Google Scholar] [CrossRef]
- Chen, H.; Wan, Q.L.; Wang, Y.R. Refined Diebold-Mariano Test Methods for the Evaluation of Wind Power Forecasting Models. Energies 2014, 7, 4185–4198. [Google Scholar] [CrossRef]
- Guo, Z.X.; Xiao, Y.F.; Liao, W.Z.; Veelaert, P.; Philips, W. FLOPs-efficient filter pruning via transfer scale for neural network acceleration. J. Comput. Sci. 2021, 55, 101459. [Google Scholar] [CrossRef]
- Lu, Y.; Lu, G.M.; Li, J.X.; Xu, Y.R.; Zheng, D. High-parameter-efficiency convolutional neural networks. Neural Comput. Appl. 2020, 32, 10633–10644. [Google Scholar] [CrossRef]





| Gaussian | Weibull | Rayleigh | fWd | |
|---|---|---|---|---|
| SSE | 0.0102 | 0.0102 | 0.8294 | 0.0098 |
| RMSE | 0.0101 | 0.0101 | 0.0911 | 0.0099 |
| fWp | ARFIMA-E | EMD-LSTM | G-M-Convolution | |
|---|---|---|---|---|
| D-M | 0 | −2.322 | −2.647 | −2.934 |
| FLOPs | 1923 | 2362 | 8.7 × 106 | 1.02 × 108 |
| params | 10 | 13 | 4.2 × 106 | 2.64 × 107 |
| Gamma | Inverse-Gamma | Weibull | fWd | |
|---|---|---|---|---|
| SSE | 0.0429 × 10−3 | 0.2078 × 10−3 | 0.0264 × 10−3 | 0.0240 × 10−3 |
| RMSE | 0.0007 | 0.0014 | 0.0005 | 0.0005 |
| fWp | SARFIMA | EWT-biLSTM | EMD-G-L-Transformer | |
|---|---|---|---|---|
| D-M | 0 | −2.368 | −2.734 | −2.976 |
| FLOPs | 2007 | 4447 | 9.6 × 106 | 3.301 × 1018 |
| params | 10 | 24 | 5.4 × 106 | 7.6 × 107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Chen, D.; Zio, E. Heavy Tail and Long-Range Dependence for Skewed Time Series Prediction Based on a Fractional Weibull Process. Fractal Fract. 2024, 8, 7. https://doi.org/10.3390/fractalfract8010007
Song W, Chen D, Zio E. Heavy Tail and Long-Range Dependence for Skewed Time Series Prediction Based on a Fractional Weibull Process. Fractal and Fractional. 2024; 8(1):7. https://doi.org/10.3390/fractalfract8010007
Chicago/Turabian StyleSong, Wanqing, Dongdong Chen, and Enrico Zio. 2024. "Heavy Tail and Long-Range Dependence for Skewed Time Series Prediction Based on a Fractional Weibull Process" Fractal and Fractional 8, no. 1: 7. https://doi.org/10.3390/fractalfract8010007
APA StyleSong, W., Chen, D., & Zio, E. (2024). Heavy Tail and Long-Range Dependence for Skewed Time Series Prediction Based on a Fractional Weibull Process. Fractal and Fractional, 8(1), 7. https://doi.org/10.3390/fractalfract8010007










