Geometric Properties and Hardy Spaces of Rabotnov Fractional Exponential Functions

Abstract

The aim of this study is to investigate a certain sufficiency criterion for uniform convexity, strong starlikeness, and strong convexity of Rabtonov fractional exponential functions. We also study the starlikeness and convexity of order $\gamma$. Moreover, we find conditions so that the Rabotnov functions belong to the class of bounded analytic functions and Hardy spaces. Various consequences of these results are also presented.

1. Introduction

Due to their significance in mathematical analysis, functional analysis, physics, and other subjects, special functions are those functions that have generally established names and notions. Although there is not a single formal definition for all these mathematical functions, the list includes several generally recognized as special. Elementary functions, particularly trigonometric functions, are considered special functions. With the help of Gauss, Jacobi, Klein, and many others, the theory was largely developed in the nineteenth century. Special functions have been employed for ages due to their extraordinary qualities. For instance, trigonometric functions have been used for over a thousand years due to their numerous astronomical applications. Since the beginning of the twentieth century, disciplines including topology, algebra, differential equations, real and functional analysis, and special functions have taken center stage. Nevertheless, a book written by G.N. Watson [1] was published then and is a crucial contribution to the theory, particularly in the context of asymptotic expansions of Bessel functions. As a classic today, special functions such as hypergeometric and Bessel functions are often utilized in statistics, probability, mathematical physics, and engineering disciplines due to their amazing features. Because of this, Paul Tur’an, a Hungarian mathematician, thought the term “special functions” was misleading and that the more accurate term would be useful functions.

A special function known as the Mittag-Leffler (ML) function arises naturally in the solution integral equations of fractional order and is acclaimed as the queen function of fractional calculus. The increased interest in this function over the past few years is mostly because of its strong connection to fractional calculus and, in particular, to fractional difficulties that arise in applications. In recent decades, the ML function and its various extensions have been used successfully to solve various problems in physics, engineering, chemistry, biology, and other practical disciplines, increasing its visibility among scientists. The study of these functions’ analytical features has generated a sizable body of literature; many authors have looked into these functions from a mathematical perspective [2].

The ML function ${\mathbb{E}}_{s,u}$ of two parameters, which can be regarded as a simple extension of the classical ML function, is provided as

$${\mathbb{E}}_{s,u}\left(\zeta \right)=\stackrel{\infty }{\sum _{n=0}}\frac{{\zeta }^n}{\Gamma \left(sn+u\right)},s,u\in \mathbb{C},\zeta \in \mathbb{C}.$$

(1)

The Mittag-Leffler functions described in (1) originally appeared in Wiman’s [3] work. These functions were later investigated by Agarwal [4].

In 1949, Russian researcher Yuriy Nicholaevich Rabotnov, who carried out work in solid mechanics consisting of a broad range of topics, including creep theory, plasticity, heredity mechanics, nonelastic stability, failure mechanics, shell theory, and composites, introduced a function by utilizing ${\mathbb{E}}_{s,u}$. Today, it is recognized in his name as the Rabotnov fractional exponential function [5] or simply Rabotnov function. It is provided as

$$R_{s,u}\left(\zeta \right)={\zeta }^s\stackrel{\infty }{\sum _{n=0}}\frac{u^n}{\Gamma \left(\left(n+1\right)\left(1+s\right)\right)}{\zeta }^{n\left(1+s\right)},s,u,\zeta \in \mathbb{C}.$$

It is clear that this series will converge at any argument value. Note that it becomes the typical exponential $exp\left(u\zeta \right)$ for $s=0$. The following is a possible way to express the relationship between $R_{s,u}$ and ${\mathbb{E}}_{s,u}$:

$$R_{s,u}\left(\zeta \right)={\zeta }^s{\mathbb{E}}_{1+s,1+s}\left(u{\zeta }^{1+s}\right),s,u,\zeta \in \mathbb{C}.$$

The fact that $R_{s,u}$ is a fractional extension of the fundamental functions is another significant and intriguing aspect of these functions. That is, $R_{0,1}(\pm \zeta )=e^{\pm \zeta }$, $R_{1,1}\left(\zeta \right)=sinh\left(\zeta \right)$, $R_{1,2}\left(\zeta \right)=sinh\left(2\sqrt{\zeta }\right)/\sqrt{2}$, $R_{1,1/2}\left(\zeta \right)=\sqrt{2}sinh\left(\frac{\zeta }{\sqrt{2}}\right).$

The Rabotnov fractional exponential function is utilized by Yang et al. [6] to introduce a fractional derivative with a nonsingular kernel.

Definition 1. 

The following represents the fractional derivative with Rabotnov exponential kernel of the function $f:\left[b,+\infty \right)\to \mathbb{R}$, of order s

$${\mathcal{D}}^{s,u}f\left(\zeta \right)=\stackrel{\zeta }{\underset{b}{\int }}{\Phi }_s\left(-u{\left(\zeta -t\right)}^s\right)f^{\prime }\left(t\right)dt,$$

with $\zeta >b,$ $s\in \left(0,1\right),$ $u,b\in {\mathbb{R}}^{+}$ and ${\Phi }_s\left(u{\zeta }^s\right)=R_{s,u}\left(\zeta \right).$

The following definition presents the integral representation of the fractional derivative with a Rabotnov exponential kernel.

Definition 2. 

The fractional integral with Rabotnov exponential kernel of the function $f:\left[b,+\infty \right)\to \mathbb{R}$, of order s is provided by

$${\mathcal{I}}^{s,u}f\left(\zeta \right)=\stackrel{\zeta }{\underset{b}{\int }}{\Phi }_s\left(-u{\left(\zeta -t\right)}^s\right)f\left(t\right)dt,$$

with $\zeta >b,$ $s\in \left(0,1\right),$ $u,b\in {\mathbb{R}}^{+}$ and ${\Phi }_s\left(u{\zeta }^s\right)=R_{s,u}\left(\zeta \right).$

Special functions like hypergeometric, Bessel, and Mittag-Leffler play a significant role in function theory. The solution of the classic Bieberbach conjecture may be the most well-known use of these functions in the theory. Due to the unexpected application of hypergeometric functions by L. de Branges, there has been much interest in the geometric characteristics of generalized, Kummer, and Gauss hypergeometric functions and certain other functions in recent years. Although the geometric characteristics of these functions are intriguing in and of themselves, they have proven useful in numerous other function theory problems.

The geometric characteristics and uses of the function ${\mathbb{E}}_{s,u}$ and some related functions have recently piqued scholars’ curiosity. It is natural to provide some recent developments on the geometric properties of ML functions as the function $R_{s,u}$ can be written in the form of ${\mathbb{E}}_{s,u}.$ Some geometrical characteristics of Mittag-Leffler functions were discussed by Bansal [7]. Partial sums of these functions were the focus of Raducanu’s [8] work. Noreen et al. [9,10,11] studied the geometric properties of this function extensively, whereas Das and Mehrez [12] improved the results of Noreen et al. Srivastava et al. [13] studied a three-parameter Mittag-Leffler function.

The upcoming sections are organized as follows: Section 2 starts with some basic definitions of concepts of geometric functions theory and Hardy spaces, followed by some important lemmas that are useful in our discussions in the next sections. Lastly, we provide brief discussions pertaining to the normalized form of Rabotnov functions and some recent work on the geometric properties of this function. In Section 3, we state and prove the main theorems related to the study of geometric properties of the Rabotnov function along with examples. In Section 4, Hardy spaces are demonstrated, along with final remarks.

2. Preliminaries

The following well-known definitions are required for our study.

Denote by $\mathcal{H}$, the class of analytic functions in $\mathbb{D}=\left\{\zeta :\left|\zeta \right|<1\right\}$ and $\mathcal{A}$ a subclass of $\mathcal{H}$, which contains functions f of the form

$$f\left(\zeta \right)=\zeta +\sum _{n=2}^{\infty }{a}_n{\zeta }^n,\zeta \in \mathbb{D}.$$

(2)

Let $\mathcal{S}$ stand for the class of all functions in $\mathcal{A}$ that contains univalent (one-to-one) functions in $\mathbb{D}$. Consider f, $g\in \mathcal{H}$. Then, f is subordinated by g and symbolically written as $f\left(\zeta \right)\prec g\left(\zeta \right)$ if there exists a function w known as Schwarz function that has the property that it is an analytic self map in $\mathbb{D}$ with $w\left(0\right)=0$ such that $f\left(\zeta \right)=g\left(w\right(\zeta \left)\right).$ Additionally, if g is one-to-one in $\mathbb{D}$, then the analogous relation shown below holds:

$$f\left(\zeta \right)\prec g\left(\zeta \right)⟺f\left(0\right)=g\left(0\right)\mathrm{and}f\left(\mathbb{D}\right)\subset g\left(\mathbb{D}\right).$$

Let $f$ be analytic in $\mathbb{D}$ and provided by (2) and

$$g\left(\zeta \right)=\zeta +\stackrel{\infty }{\sum _{n=2}}{b}_n{\zeta }^n,\zeta \in \mathbb{D},$$

is analytic in $\mathbb{D}$. Then, convolution (Hadamard product) of these functions is provided by

$$\left(f\ast g\right)\left(\zeta \right)=\zeta +\stackrel{\infty }{\sum _{n=0}}{a}_n{b}_n{\zeta }^n,\zeta \in \mathbb{D}.$$

Let $\stackrel{\sim }{{\mathcal{S}}^{\ast }}\left(\delta \right)$ and $\stackrel{\sim }{\mathcal{C}}\left(\delta \right)$ be subclasses of $\mathcal{A}$, which, respectively, represent strongly starlike and convex functions of order $\delta$.

Definition 3. 

A function $f\in \stackrel{\sim }{{\mathcal{S}}^{\ast }}\left(\delta \right)$, $\delta \in \left(0,1\right]$ if and only if

$$\left|arg\left(\frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}\right)\right|<\frac{\delta \pi }{2}.$$

Definition 4. 

A function $f\in \stackrel{\sim }{\mathcal{C}}\left(\delta \right)$ if and only if

$$\left|arg\left(1+\frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}\right)\right|<\frac{\delta \pi }{2},\delta \in \left(0,1\right].$$

It is noted that $\stackrel{\sim }{{\mathcal{S}}^{\ast }}\left(1\right)={\mathcal{S}}^{\ast }$ and $\stackrel{\sim }{\mathcal{C}}\left(1\right)=\mathcal{C},$ where ${\mathcal{S}}^{\ast }$ and $\mathcal{C}$ are familiar classes of starlike and convex functions, respectively. Similarly, ${\mathcal{S}}^{\ast }\left(\gamma \right)$ and $\mathcal{C}\left(\gamma \right)$ denote the classes of stalike and convex functions of order $\gamma \in \left[0,1\right).$ We define these as follows:

Definition 5. 

A function $f\in {\mathcal{S}}^{\ast }\left(\gamma \right)$ if and only if

$$Re\left(\frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}\right)>\gamma ,\gamma \in \left[0,1\right),\zeta \in \mathbb{D}.$$

Definition 6. 

A function $f\in \mathcal{C}\left(\gamma \right)$ if and only if and

$$Re\left(1+\frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}\right)>\gamma ,\gamma \in \left[0,1\right),\zeta \in \mathbb{D}.$$

Rosy et al. [14] introduced a subclass of $\mathcal{A}$. It is denoted by $\mathcal{USD}\left(\xi \right)$.

Definition 7. 

A function $f\in \mathcal{A}$ is in $\mathcal{USD}\left(\xi \right)$ if and only if

$$Re\left(f^{\prime }\left(\zeta \right)\right)\ge \xi \left|\zeta f^{″}\left(\zeta \right)\right|,\xi >0,\zeta \in \mathbb{D}.$$

We denote by $\mathcal{UCV}$ a class of uniformly convex functions in $\mathbb{D}$.

Definition 8. 

A function f is in $\mathcal{UCV}$ if and only if

$$Re\left(1+\frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}\right)\ge \left|\frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}\right|,\zeta \in \mathbb{D}.$$

Definition 9 

([15]). The classes $\mathcal{P}\left(\gamma \right)$ and $\mathcal{R}\left(\gamma \right)$ are defined as

$$\mathcal{P}\left(\gamma \right)=\left\{p:p\in \mathcal{H},p\left(0\right)=1andRe\left\{e^{i\theta }\left(p\left(\zeta \right)-\gamma \right)\right\}>0\right\}$$

and

$$\mathcal{R}\left(\gamma \right)=\left\{f:f\in \mathcal{A}andRe\left(\left\{e^{i\theta }\left(f^{\prime }\left(\zeta \right)-\gamma \right)\right\}\right)>0\right\},$$

where $\zeta \in \mathbb{D}$, $\gamma \in \left[0,1\right),\theta \in \mathbb{R}.$

For $\theta =0,$ the classes $\mathcal{P}\left(\gamma \right)$ and $\mathcal{R}\left(\gamma \right)$ are denoted by ${\mathcal{P}}_0\left(\gamma \right)$ and ${\mathcal{R}}_0\left(\gamma \right)$, respectively. Also, for $\theta =0$ and $\gamma =0,$ we have the classes $\mathcal{P}$ and $\mathcal{R}$.

Let ${\mathcal{H}}^{\infty }$ represent the space of functions on $\mathcal{H}$, which are bounded in $\mathbb{D}$. This set represents a Banach algebra with norm provided by

$${∥f∥}_{\infty }=\underset{\zeta \in \mathbb{D}}{sup}\left|f\left(\zeta \right)\right|.$$

The space of all those functions $f\in \mathcal{H}$ such that ${\left|f\right|}^p$ admits a harmonic majorant is denoted by ${\mathcal{H}}^p,p\in \left(0,\infty \right)$. If the norm of f is given to be p-th root of the least harmonic majorant of ${\left|f\right|}^p$ for some fixed $\zeta \in \mathbb{D}$, then it is a Banach space. Another definition of norm is provided as follows. Let $f\in \mathcal{H}$, set

$$M_p\left(r,f\right)=\left\{\begin{array}{c}{\left(\frac{1}{2\pi }\stackrel{2\pi }{\underset{0}{\int }}{\left|f\left(r{e}^{i\theta }\right)\right|}^{p}d\theta \right)}^{1/p},0<p<\infty ,\\ max\left\{\left|f\left(\zeta \right)\right|:\left|\zeta \right|\le r\right\},p=\infty .\end{array}\right.$$

Then, $f\in$ ${\mathcal{H}}^p,$ if $M_p\left(r,f\right)$ is bounded for all $r\in \left[0,1\right).$ We see that

$${\mathcal{H}}^{\infty }\subset {\mathcal{H}}^q\subset {\mathcal{H}}^p,0<q<p<\infty .$$

From [16], if $Re\left\{f^{\prime }\left(\zeta \right)\right\}>0$ in $\mathbb{D}$, then

$$\left\{\begin{array}{c}\hfill f^{\prime }\in {\mathcal{H}}^q,q<1,\hfill \\ \hfill f\in {\mathcal{H}}^{q/\left(1-q\right)},0<q<1.\hfill \end{array}\right.$$

(3)

Our aim in this study is to determine sufficiency criterion for Rabotnov function to be uniformly convex, strongly starlike, strongly convex, and demonstrate Hardy spaces of Rabotnov function.

The Rabotnov function $R_{s,u}$ is not in class $\mathcal{A}$; therefore, consider the transformation ${\mathbb{R}}_{s,u}$ such that ${\mathbb{R}}_{s,u}\left(0\right)={\mathbb{R}}_{s,u}^{\prime }\left(0\right)-1=0$ provided by

$${\mathbb{R}}_{s,u}\left(\zeta \right)={\zeta }^{1/\left(1+s\right)}\Gamma \left(1+s\right)R_{s,u}\left(\zeta \right)\left({\zeta }^{1/\left(1+s\right)}\right)=\zeta +\stackrel{\infty }{\sum _{n=2}}\frac{u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}{\zeta }^n,s,u\in \mathbb{C}.$$

The geometric properties of ${\mathbb{R}}_{s,u}$ have recently been discussed by Eker and Ece [17] and Eker et al. [18]. Partial sums of generalized function of ${\mathbb{R}}_{s,u}$ have been studied by Frasin [19]. Amourah et al. [20] have studied certain subclasses of bi-univalent functions involving the function ${\mathbb{R}}_{s,u}.$ Deniz and Kazimoglu [21] studied Hardy spaces by using a different technique for this function.

In this study, we restrict ourselves such that s and $u$ are real.

We require the following results for our study.

Lemma 1 

([22]). If $f\in \mathcal{USD}\left(\xi \right)$, $\xi >0$ and of the form (2), then

$$\underset{n=2}{\sum ^{\infty }}\left[n\left(1-\xi \right)+n^2\xi \right]\left|a_n\right|\le 1.$$

Lemma 2 

([17]). Let $s\ge 0$ and $u>0$. Then,

$$\left|{\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)-1\right|\le \left(1+\frac{u}{1+s}\right)e^{\frac{u}{1+s}}-1.$$

Lemma 3 

([23]). Let g and $f$ be analytic functions in $\mathbb{D}$ with $g\left(0\right)=f\left(0\right)=1.$ Let g be univalent and convex in $\mathbb{D}$ and $f\prec g$ in $\mathbb{D}$. Then,

$$(n+1){\zeta }^{-1-n}\underset{0}{\overset{\zeta }{\int }}{v}^{n}f\left(v\right)dv\prec (n+1){\zeta }^{-1-n}\underset{0}{\overset{\zeta }{\int }}{v}^{n}g\left(v\right)dv,\forall n\in \mathbb{N}\cup \left\{0\right\}.$$

Lemma 4 

([24]). If $f\in \mathcal{A}$ satisfies $\left|\frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}\right|<\frac{1}{2},$ then $f\in \mathcal{UCV}.$

Lemma 5 

([25]). ${\mathcal{P}}_0\left(\alpha \right)\ast {\mathcal{P}}_0\left(\beta \right)\subset {\mathcal{P}}_0\left(\gamma \right),$ where $\gamma =1-2\left(1-\alpha \right)\left(1-\beta \right)$ with $\alpha ,\beta <1$ and γ has the best possible value.

Lemma 6 

([26]). For $\alpha ,\beta <1$ and $\gamma =1-2\left(1-\alpha \right)\left(1-\beta \right),$ we have ${\mathcal{R}}_0\left(\alpha \right)\ast {\mathcal{R}}_0\left(\beta \right)\subset {\mathcal{R}}_0\left(\gamma \right)$ or equivalently $\mathcal{P}\left(\alpha \right)\ast {\mathcal{P}}_0\left(\beta \right)\subset {\mathcal{P}}_0\left(\gamma \right).$

Lemma 7 

([27]). If the function f, convex of order γ, where $\gamma \in \left[0,1\right),$ is not of the form

$$f\left(\zeta \right)=\left\{\begin{array}{c}m+l\zeta {\left(1-\zeta e^{i\theta }\right)}^{2\gamma -1},\gamma \ne \frac{1}{2},\hfill \\ m+llog\left(1-\zeta e^{i\theta }\right),\gamma =\frac{1}{2},\hfill \end{array}\right.$$

where m, $l\in \mathbb{C}$ and $\theta \in \mathbb{R},$ then the following claims are true:

(i) 

There exists $\rho =\rho \left(f\right)>0$ such that $f^{\prime }\in {\mathcal{H}}^{\rho +1/\left[2\left(1-\gamma \right)\right]};$

(ii) 

If $\gamma \in \left[0,1/2\right),$ then there exists $\tau =\nu \left(f\right)>0$ such that $f\in {\mathcal{H}}^{\nu +1/\left(1-2\gamma \right)};$

(iii) 

If $\gamma \ge 1/2,$ then $f\in {\mathcal{H}}^{\infty }.$

3. Main Results

Theorem 1. 

If $s\ge 0$ and $u>0$ and $0<\kappa \le 1,$ then ${\mathbb{R}}_{s,u}\in \stackrel{\sim }{{\mathcal{S}}^{\ast }}\left(\delta \right),$ where

$$\delta =\frac{2}{\pi }arcsin\left(\kappa \sqrt{1-\frac{{\kappa }^2}{4}}+\frac{\kappa }{2}\sqrt{1-{\kappa }^2}\right),$$

and $\kappa =\left(1+\frac{u}{1+s}\right)e^{\frac{u}{1+s}}-1.$

Proof. 

By using a result due to [17], we have

$$\left|{\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)-1\right|\le \left(1+\frac{u}{1+s}\right)e^{\frac{u}{1+s}}-1=\kappa .$$

(4)

For $0<\kappa \le 1$ and from (4) $,$ we concluded that

$${\mathbb{R}}_{s,u}^{\prime }\prec 1+\kappa \zeta \Rightarrow \left|arg\left({\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)\right|<arcsin\kappa .$$

(5)

For $n=0,$ by using Lemma 3, with $f\left(\zeta \right)={\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)$ and $g\left(\zeta \right)=1+\kappa \zeta ,$ we obtain

$$\frac{{\mathbb{R}}_{s,u}}{\zeta }\prec 1+\frac{\kappa }{2}\zeta .$$

(6)

As a result,

$$\left|arg\left(\frac{{\mathbb{R}}_{s,u}\left(\zeta \right)}{\zeta }\right)\right|<arcsin\frac{\kappa }{2}.$$

By using (5) and (6) $,$ we obtain

$$\begin{array}{ccc}\hfill \left|arg\left(\frac{\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)}{{\mathbb{R}}_{s,u}\left(\zeta \right)}\right)\right|& =& \left|arg\left(\frac{\zeta }{{\mathbb{R}}_{s,u}\left(\zeta \right)}\right)-arg\left({\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)\right|\hfill \\ & \le & \left|arg\left(\frac{\zeta }{{\mathbb{R}}_{s,u}\left(\zeta \right)}\right)\right|+\left|arg\left({\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)\right|\hfill \\ & <& arcsin\frac{\kappa }{2}+arcsin\kappa \hfill \\ & =& arcsin\left(\kappa \sqrt{1-\frac{{\kappa }^2}{4}}+\frac{\kappa }{2}\sqrt{1-{\kappa }^2}\right).\hfill \end{array}$$

Which implies that ${\mathbb{R}}_{s,u}\in \stackrel{\sim }{{\mathcal{S}}^{\ast }}\left(\delta \right)$ for $\delta =\frac{2}{\pi }arcsin\left(\kappa \sqrt{1-\frac{{\kappa }^2}{4}}+\frac{\kappa }{2}\sqrt{1-{\kappa }^2}\right).$ □

In the following, we provide a few examples by taking particular values of s and $u.$

Example 1. 

• The function ${\mathbb{R}}_{1,1/4}\left(\zeta \right)=2\sqrt{\zeta }sinh\left(\frac{\sqrt{\zeta }}{2}\right)\in \stackrel{\sim }{{\mathcal{S}}^{\ast }}\left({\delta }_1\right),$ where ${\delta }_1\approx 0.26486.$
• The function ${\mathbb{R}}_{1,1/2}\left(\zeta \right)=\sqrt{2\zeta }sinh\left(\sqrt{\frac{\zeta }{2}}\right)\in \stackrel{\sim }{{\mathcal{S}}^{\ast }}\left({\delta }_2\right),$ where ${\delta }_2\approx 0.609277.$
• The function ${\mathbb{R}}_{1/2,1/2}\left(\zeta \right)\in \stackrel{\sim }{{\mathcal{S}}^{\ast }}\left({\delta }_3\right),$ where ${\delta }_3\approx 0.94341.$
• The function ${\mathbb{R}}_{0,1/3}\left(\zeta \right)=\zeta e^{\zeta /3}\in \stackrel{\sim }{{\mathcal{S}}^{\ast }}\left({\delta }_4\right),$ where ${\delta }_4\approx 0.943354.$

Theorem 2. 

If $s\ge 0$ and $u>0$ and $0<\kappa \le 1,$ then ${\mathbb{R}}_{s,u}\in \stackrel{\sim }{\mathcal{C}}\left(\delta \right),$ where

$$\delta =\frac{2}{\pi }arcsin\left(\kappa \sqrt{1-\frac{{\kappa }^2}{4}}+\frac{\kappa }{2}\sqrt{1-{\kappa }^2}\right),$$

with $\kappa =\frac{(s^2+(2+3u)s+3u+u^2+1)}{{\left(1+s\right)}^2}{e}^{\frac{u}{1+s}}-1.$

Proof. 

Since

$$\left|{\zeta }_1+{\zeta }_2\right|\le \left|{\zeta }_1\right|+\left|{\zeta }_2\right|,$$

and

$$\frac{\Gamma \left(1+s\right)}{\Gamma \left(\left(1+s\right)n\right)}\le \frac{1}{{\left(1+s\right)}^{n-1}\left(n-1\right)!},\forall n\in \mathbb{N},$$

we obtain

$$\begin{array}{cc}\hfill \left|{\left(\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)}^{\prime }-1\right|& =\left|\sum _{n=2}^{\infty }\frac{n^2{u}^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(\left(1+s\right)n\right)}{\zeta }^{n-1}\right|\hfill \\ \hfill & \le \sum _{n=2}^{\infty }\frac{n^2{u}^{n-1}}{{\left(1+s\right)}^{n-1}\left(n-1\right)!}\hfill \\ \hfill & =\frac{s^2+(2+3u)s+3u+u^2+1}{{\left(1+s\right)}^2}{e}^{\frac{u}{1+s}}-1=\kappa .\hfill \end{array}$$

(7)

For $0<\kappa \le 1$ and from (7) $,$ we concluded that

$${\left(\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)}^{\prime }\prec 1+\kappa \zeta \Rightarrow \left|arg{\left(\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)}^{\prime }\right|<arcsin\kappa .$$

(8)

For $n=0,$ by using Lemma 3 with $f\left(\zeta \right)={\left(\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)}^{\prime }$ and $g\left(\zeta \right)=1+\kappa \zeta ,$ we obtain

$$\frac{\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)}{\zeta }\prec 1+\frac{\kappa }{2}\zeta .$$

This implies that

$${\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\prec 1+\frac{\kappa }{2}\zeta .$$

As a result,

$$\left|arg{\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right|<arcsin\frac{\kappa }{2}.$$

(9)

By using (8) and (9) $,$ we obtain

$$\begin{array}{ccc}\hfill \left|arg\left(\frac{{\left(\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)}^{\prime }}{{\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)}\right)\right|& =& \left|arg{\left(\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)}^{\prime }-arg{\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right|\hfill \\ & \le & \left|arg{\left(\zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)}^{\prime }\right|+\left|arg\left({\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)\right)\right|\hfill \\ & <& arcsin\frac{\kappa }{2}+arcsin\kappa \hfill \\ & =& arcsin\left(\kappa \sqrt{1-\frac{{\kappa }^2}{4}}+\frac{\kappa }{2}\sqrt{1-{\kappa }^2}\right).\hfill \end{array}$$

Which implies that ${\mathbb{R}}_{s,u}\in \stackrel{\sim }{\mathcal{C}}\left(\delta \right)$ for $\delta =\frac{2}{\pi }arcsin\left(\kappa \sqrt{1-\frac{{\kappa }^2}{4}}+\frac{\kappa }{2}\sqrt{1-{\kappa }^2}\right).$ □

Example 2. 

• The function ${\mathbb{R}}_{0,1/6}\left(\zeta \right)=\zeta e^{\zeta /6}\in \stackrel{\sim }{\mathcal{C}}\left({\delta }_1\right),$ where ${\delta }_1\approx 0.859182.$
• The function ${\mathbb{R}}_{1/3,1/4}\left(\zeta \right)\in \stackrel{\sim }{\mathcal{C}}\left({\delta }_2\right),$ where ${\delta }_2\approx 0.937653.$
• The function ${\mathbb{R}}_{1,1/4}\left(\zeta \right)=2\sqrt{\zeta }sinh\left(\frac{\sqrt{\zeta }}{2}\right)\in \stackrel{\sim }{\mathcal{C}}\left({\delta }_3\right),$ where ${\delta }_3\approx 0.576516$

Theorem 3. 

Let $s\ge 0$ and $u>0$ and $\frac{u}{1+s}<0.1399337508.$ Then ${\mathbb{R}}_{s,u}\in \mathcal{UCV}.$

Proof. 

By using the result

$$\left|\frac{\zeta {\mathbb{R}}_{s,u}^{″}\left(\zeta \right)}{{\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)}\right|\le \frac{\left(2+\frac{u}{1+s}\right)e^{\frac{u}{1+s}}}{2-\left(1+\frac{u}{1+s}\right)e^{\frac{u}{1+s}}}\frac{u}{1+s}.$$

due to [17] and by using Lemma 4, we have

$$\left|\frac{\zeta {\mathbb{R}}_{s,u}^{″}\left(\zeta \right)}{{\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)}\right|<\frac{1}{2},$$

if

$$\frac{\left(2+\frac{u}{1+s}\right)e^{\frac{u}{1+s}}}{2-\left(1+\frac{u}{1+s}\right)e^{\frac{u}{1+s}}}<\frac{1+s}{2u}.$$

which is equivalently $\frac{u}{1+s}<0.1399337508.$ Hence, the required result. □

Example 3. 

• The function ${\mathbb{R}}_{1,1/4}\left(\zeta \right)=2\sqrt{\zeta }sinh\left(\frac{\sqrt{\zeta }}{2}\right)\in \mathcal{UCV}$.
• The function ${\mathbb{R}}_{3,1/2}\left(\zeta \right)\in \mathcal{UCV}$.
• The function ${\mathbb{R}}_{1/2,1/5}\left(\zeta \right)\in \mathcal{UCV}$.

Theorem 4. 

Let $0\le \lambda \le 1,\xi >0.$ Then, $\left(1-\lambda \right){\mathbb{R}}_{s,u}\left(\zeta \right)+\lambda \zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)=h_{\lambda }\left(\zeta \right)\in \mathcal{USD}\left(\xi \right),$ if

$$\xi \lambda {\mathbb{R}}_{s,u}^{‴}\left(1\right)+\left(\xi +\lambda -5\xi \lambda \right){\mathbb{R}}_{s,u}^{″}\left(1\right)+\left(1+\lambda \right){\mathbb{R}}_{s,u}^{\prime }\left(1\right)-\lambda \le 2.$$

(10)

Proof. 

It is clear that

$$h_{\lambda }\left(\zeta \right)=\left(1-\lambda \right){\mathbb{R}}_{s,u}\left(\zeta \right)+\lambda \zeta {\mathbb{R}}_{s,u}^{\prime }\left(\zeta \right)=\zeta +\stackrel{\infty }{\sum _{n=2}}\frac{u^{n-1}\left(n+1\right)\left(1-\lambda \right)\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}{\zeta }^n,0\le \lambda \le 1.$$

Let

$${\mathbb{R}}_{s,u}\left(\zeta \right)=\zeta +\stackrel{\infty }{\sum _{n=2}}\frac{u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}{\zeta }^n.$$

Then,

$${\mathbb{R}}_{s,u}\left(1\right)-1=\stackrel{\infty }{\sum _{n=2}}\frac{u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}.$$

Now, differentiating ${\mathbb{R}}_{s,u}\left(\zeta \right)$ and putting $\zeta =1,$ we obtain

$${\mathbb{R}}_{s,u}^{\prime }\left(1\right)-1=\stackrel{\infty }{\sum _{n=2}}\frac{n{u}^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}.$$

(11)

Also, we obtain

$$\begin{array}{ccc}\hfill {\mathbb{R}}_{s,u}^{″}\left(1\right)& =& \stackrel{\infty }{\sum _{n=2}}\frac{n\left(n-1\right)u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)},\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\mathbb{R}}_{s,u}^{‴}\left(1\right)& =& \stackrel{\infty }{\sum _{n=2}}\frac{n\left(n-1\right)\left(n-2\right)u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}.\hfill \end{array}$$

(13)

For $h_{\lambda }\left(\zeta \right)\in \mathcal{USD}\left(\xi \right),$ by using Lemma 1, we show that

$$\underset{n=2}{\sum ^{\infty }}n\left(1-\xi +n\xi \right)\left(1+n\lambda -\lambda \right)\frac{u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}\le 1.$$

Now, let

$$\begin{array}{ccc}& & \underset{n=2}{\sum ^{\infty }}n\left(1-\xi +n\xi \right)\left(1+\lambda \xi -\lambda \right)\frac{u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}\hfill \\ & =& \xi \lambda \underset{n=2}{\sum ^{\infty }}\frac{n^3{u}^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}+\left(\xi +\lambda -2\xi \lambda \right)\underset{n=2}{\sum ^{\infty }}\frac{n^2{u}^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}\hfill \\ & & +\left(1+\xi \lambda -\xi \right)\underset{n=2}{\sum ^{\infty }}\frac{n{u}^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}.\hfill \end{array}$$

Then, writing $n^3=n\left(n-1\right)\left(n-2\right)-3n\left(n-1\right)+n$ and $n^2=n\left(n-1\right)+n,$ we have

$$\begin{array}{ccc}& & \underset{n=2}{\sum ^{\infty }}n\left(1-\xi +n\xi \right)\left(1+\lambda \xi -\lambda \right)\frac{u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}\hfill \\ & =& \xi \lambda \underset{n=2}{\sum ^{\infty }}\frac{n\left(n-1\right)\left(n-2\right)u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}+\left(\xi +\lambda -5\xi \lambda \right)\underset{n=2}{\sum ^{\infty }}\frac{n\left(n-1\right)u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}\hfill \\ & +& \left(1+\lambda \right)\underset{n=2}{\sum ^{\infty }}\frac{n{u}^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}.\hfill \end{array}$$

From (11)–(13), we obtain

$$\begin{array}{ccc}& & \underset{n=2}{\sum ^{\infty }}n\left(1-\xi +n\xi \right)\left(1+\lambda \xi -\lambda \right)\frac{u^{n-1}\Gamma \left(s+1\right)}{\Gamma \left(ns+n\right)}\hfill \\ & =& \xi \lambda {\mathbb{R}}_{s,u}^{‴}\left(1\right)+\left(\xi +\lambda -5\xi \lambda \right){\mathbb{R}}_{s,u}^{″}\left(1\right)\hfill \\ & & +\left(1+\lambda \right){\mathbb{R}}_{s,u}^{\prime }\left(1\right)-\left(1+\lambda \right).\hfill \end{array}$$

The above relation is bounded above by 1 if (10) is satisfied. This leads to the result. □

Theorem 5. 

Let $0\le \gamma <1,$ $s\ge 0,$ $u>0$ and $\frac{s}{1+u}{e}^{\frac{s}{1+u}}\le \left(1-\gamma \right)\left(2-e^{\frac{s}{1+u}}\right).$ Then, ${\mathbb{R}}_{s,u}\in {\mathcal{S}}^{\ast }\left(\gamma \right).$

Proof. 

It is a well-known result from [28] that $f\in \mathcal{A}$ is provided by (2) and satisfies ${\displaystyle \sum _{n=2}^{\infty }}\left(n-\gamma \right)\left|a_n\right|\le 1-\gamma ,$ $\gamma \in \left[0,1\right),$ and then $f\in {\mathcal{S}}^{\ast }\left(\gamma \right).$ To prove that ${\mathbb{R}}_{s,u}\in {\mathcal{S}}^{\ast }\left(\gamma \right),$ consider

$$R\left(s,u,\gamma \right)=\sum _{n=2}^{\infty }\frac{\left(n-\gamma \right)u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}.$$

Then, we have to show that $R\left(s,u,\gamma \right)\le 1-\gamma .$ By using the inequality $\frac{\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}\le \frac{1}{{\left(1+s\right)}^{n-1}\left(n-1\right)!},$ we may write

$$\begin{array}{ccc}\hfill R\left(s,u,\gamma \right)& =& \sum _{n=2}^{\infty }\frac{\left(n-1\right)u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}+\left(1-\gamma \right)\sum _{n=2}^{\infty }\frac{u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}\hfill \\ & \le & \sum _{n=2}^{\infty }\frac{1}{\left(n-2\right)!}{\left(\frac{u}{1+s}\right)}^{n-1}+\left(1-\gamma \right)\sum _{n=2}^{\infty }\frac{1}{\left(n-1\right)!}{\left(\frac{u}{1+s}\right)}^{n-1}\hfill \\ & =& \frac{u}{1+s}{e}^{\frac{u}{1+s}}+\left(1-\gamma \right)\left(e^{\frac{u}{1+s}}-1\right)\le \left(1-\gamma \right).\hfill \end{array}$$

This proves the result. □

Example 4. 

(i) 

${\mathbb{R}}_{1,1/2}\left(\zeta \right)=\sqrt{2\zeta }sinh\left(\sqrt{\frac{\zeta }{2}}\right)\in {\mathcal{S}}^{\ast }\left(\gamma \right),0\le \gamma <{\gamma }_0,{\gamma }_0\approx 0.55168.$

(ii) 

${\mathbb{R}}_{1,1/4}\left(\zeta \right)=2\sqrt{\zeta }sinh\left(\frac{\sqrt{\zeta }}{2}\right)\in {\mathcal{S}}^{\ast }\left(\gamma \right),0\le \gamma <{\gamma }_1,{\gamma }_1\approx 0.83666.$

(iii) 

${\mathbb{R}}_{1/2,1/4}\left(\zeta \right)\in {\mathcal{S}}^{\ast }\left(\gamma \right),0\le \gamma <{\gamma }_2,{\gamma }_2\approx 0.75947.$

(iv) 

${\mathbb{R}}_{2,1}\left(\zeta \right)\in {\mathcal{S}}^{\ast }\left(\gamma \right),0\le \gamma <{\gamma }_3,{\gamma }_3\approx 0.23031.$

In Figure 1, we provide the mappings of functions in $\mathbb{D}$ provided in Example 4.

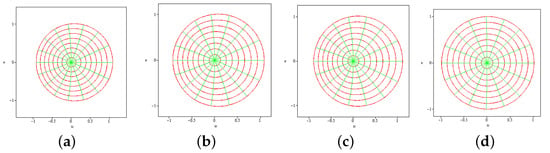
Figure 1. Mappings of ${\mathbb{R}}_{s,u}\left(\zeta \right)$ over $\mathbb{D}$. (a) Mapping of ${\mathbb{R}}_{1,\frac{1}{2}}\left(\zeta \right)$ over $\mathbb{D}$; (b) mapping of ${\mathbb{R}}_{1,\frac{1}{4}}\left(\zeta \right)$ over $\mathbb{D}$; (c) mapping of ${\mathbb{R}}_{\frac{1}{2},\frac{1}{4}}\left(\zeta \right)$ over $\mathbb{D}$; (d) mapping of ${\mathbb{R}}_{2,1}\left(\zeta \right)$ over $\mathbb{D}$.

Theorem 6. 

Let $0\le \gamma <1,$ $s\ge 0,$ $u>0.$

(a) 

If

$$\frac{u}{1+s}\left(\frac{u}{1+s}+1\right)e^{\frac{u}{1+s}}+\left(2-\gamma \right)\frac{u}{1+s}{e}^{\frac{u}{1+s}}\le \left(1-\gamma \right)\left(2-e^{\frac{u}{1+s}}\right),$$

then ${\mathbb{R}}_{s,u}\in \mathcal{C}\left(\gamma \right).$

(b) 

If $e^{\frac{u}{1+s}}<2-\gamma ,$ then $\frac{{\mathbb{R}}_{s,u}\left(\zeta \right)}{\zeta }\in \mathcal{P}\left(\gamma \right).$

Proof. 

(a)

It is a well-known result from [28] that function $f\in \mathcal{A}$ of the form (2) satisfies ${\displaystyle \sum _{n=2}^{\infty }}n\left(n-\gamma \right)\left|a_n\right|\le 1-\gamma ,$ $\gamma \in \left[0,1\right),$ and then $f\in \mathcal{C}\left(\gamma \right).$ To prove that ${\mathbb{R}}_{s,u}\in \mathcal{C}\left(\gamma \right),$ consider

$$G\left(s,u,\gamma \right)=\sum _{n=2}^{\infty }\frac{n\left(n-\gamma \right)u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}.$$

Then, we have to show that $G\left(s,u,\gamma \right)\le 1-\gamma .$ By using the inequality $\frac{\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}\le \frac{1}{{\left(1+s\right)}^{n-1}\left(n-1\right)!},$ we may write

$$\begin{array}{ccc}\hfill G\left(s,u,\gamma \right)& =& \sum _{n=2}^{\infty }\frac{{\left(n-1\right)}^2{u}^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}+\left(2-\gamma \right)\sum _{n=2}^{\infty }\frac{\left(n-1\right)u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}\hfill \\ & & +\left(1-\gamma \right)\sum _{n=2}^{\infty }\frac{u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}\hfill \\ & \le & \sum _{n=2}^{\infty }\frac{\left(n-1\right)}{\left(n-2\right)!}{\left(\frac{u}{1+s}\right)}^{n-1}+\left(2-\gamma \right)\sum _{n=2}^{\infty }\frac{1}{\left(n-2\right)!}{\left(\frac{u}{1+s}\right)}^{n-1}\hfill \\ & & +\left(1-\gamma \right)\sum _{n=2}^{\infty }\frac{1}{\left(n-1\right)!}{\left(\frac{u}{1+s}\right)}^{n-1}\hfill \\ & =& \frac{u}{1+s}\left(\frac{u}{1+s}+1\right)e^{\frac{u}{1+s}}+\left(2-\gamma \right)\frac{u}{1+s}{e}^{\frac{u}{1+s}}+\left(1-\gamma \right)\left(e^{\frac{u}{1+s}}-1\right)\le \left(1-\gamma \right).\hfill \end{array}$$

This proves the result.

(b)

To show that $\frac{{\mathbb{R}}_{s,u}\left(\zeta \right)}{\zeta }\in \mathcal{P}\left(\gamma \right),$ we consider the function $h\left(\zeta \right)=\frac{1}{1-\gamma }\left[\frac{{\mathbb{R}}_{s,u}\left(\zeta \right)}{\zeta }-\gamma \right].$ We prove that $\left|h\left(\zeta \right)-1\right|<1.$ Now,

$$\begin{array}{ccc}\hfill \left|h\left(\zeta \right)-1\right|& =& \frac{1}{1-\gamma }\left|\sum _{n=2}^{\infty }\frac{u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}{\zeta }^{n-1}\right|\hfill \\ & \le & \frac{1}{1-\gamma }\sum _{n=2}^{\infty }\frac{1}{\left(n-1\right)!}{\left(\frac{u}{1+s}\right)}^{n-1}\hfill \\ & =& \frac{1}{1-\gamma }\left(e^{\frac{u}{1+s}}-1\right)<1.\hfill \end{array}$$

This completes the result.

□

Corollary 1. 

Let $0\le \gamma <1,$ $s\ge 0,$ $u>0.$

(a) 

If

$$\frac{u}{1+s}\left(\frac{u}{1+s}+1\right)e^{\frac{u}{1+s}}+\frac{5u}{2(1+s)}{e}^{\frac{u}{1+s}}\le \frac{1}{2}\left(2-e^{\frac{u}{1+s}}\right),$$

then ${\mathbb{R}}_{s,u}\in \mathcal{C}\left(1/2\right).$

(b) 

If $2e^{\frac{u}{1+s}}<3,$ then $\frac{{\mathbb{R}}_{s,u}\left(\zeta \right)}{\zeta }\in \mathcal{P}\left(1/2\right).$

Corollary 2. 

Let $0\le \gamma <1,$ $s\ge 0,$ $u>0.$

(a) 

If

$$\frac{u}{1+s}\left(\frac{u}{1+s}+1\right)e^{\frac{u}{1+s}}+\frac{2u}{1+s}{e}^{\frac{u}{1+s}}\le 2-e^{\frac{u}{1+s}},$$

then ${\mathbb{R}}_{s,u}\in \mathcal{C}.$

(b) 

If $e^{\frac{u}{1+s}}<2,$ then $\frac{{\mathbb{R}}_{s,u}\left(\zeta \right)}{\zeta }\in \mathcal{P}.$

Example 5. 

(i) 

${\mathbb{R}}_{1/3,1/4}\left(\zeta \right)\in \mathcal{C}\left(\gamma \right)0\le \gamma <{\gamma }_0,{\gamma }_0\approx 0.12844.$

(ii) 

${\mathbb{R}}_{5,1}\left(\zeta \right)\in \mathcal{C}\left(\gamma \right),0\le \gamma <{\gamma }_1,{\gamma }_1\approx 0.31382.$

(iii) 

${\mathbb{R}}_{5/2,1/2}\left(\zeta \right)\in \mathcal{C}\left(\gamma \right),0\le \gamma <{\gamma }_2,{\gamma }_2\approx 0.48181.$

(iv) 

${\mathbb{R}}_{1/2,1/5}\left(\zeta \right)\in \mathcal{C}\left(\gamma \right),0\le \gamma <{\gamma }_3,{\gamma }_3\approx 0.53893.$

In Figure 2, we provide the mappings of functions in $\mathbb{D}$ provided in Example 5.

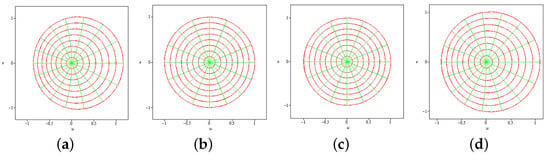
Figure 2. Mappings of ${\mathbb{R}}_{s,u}\left(\zeta \right)$ over $\mathbb{D}$ provided in Example 5. (a) Mapping of ${\mathbb{R}}_{\frac{1}{3},\frac{1}{4}}\left(\zeta \right)$ over $\mathbb{D}$; (b) mapping of ${\mathbb{R}}_{5,1}\left(\zeta \right)$ over $\mathbb{D}$; (c) mapping of ${\mathbb{R}}_{\frac{5}{2},\frac{1}{2}}\left(\zeta \right)$ over $\mathbb{D}$; (d) mapping of ${\mathbb{R}}_{\frac{1}{2},\frac{1}{5}}\left(\zeta \right)$ over $\mathbb{D}$.

Example 6. 

(i) 

$\frac{{\mathbb{R}}_{0,1/2}\left(\zeta \right)}{\zeta }=\zeta e^{\frac{\zeta }{2}}\in \mathcal{P}\left(\gamma \right),0\le \gamma <{\gamma }_4,{\gamma }_4\approx 0.3513.$

(ii) 

$\frac{{\mathbb{R}}_{1,1/2}\left(\zeta \right)}{\zeta }=\frac{\sqrt{2\zeta }sinh\left(\sqrt{\frac{\zeta }{2}}\right)}{\zeta }\in \mathcal{P}\left(\gamma \right),0\le \gamma <{\gamma }_5,{\gamma }_5\approx 0.7160.$

(iii) 

$\frac{{\mathbb{R}}_{2,1}\left(\zeta \right)}{\zeta }\in \mathcal{P}\left(\gamma \right),0\le \gamma <{\gamma }_6,{\gamma }_6\approx 0.6044.$

(iv) 

$\frac{{\mathbb{R}}_{1,1}\left(\zeta \right)}{\zeta }=\frac{\sqrt{\zeta }sinh\left(\sqrt{\zeta }\right)}{\zeta }\in \mathcal{P}\left(\gamma \right),0\le \gamma <{\gamma }_7,{\gamma }_7\approx 0.3513.$

In Figure 3, we provide the mappings of functions in $\mathbb{D}$ provided in Example 6.

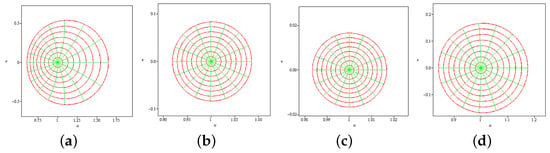
Figure 3. Mappings of ${\mathbb{R}}_{s,u}\left(\zeta \right)$ over $\mathbb{D}$ provided in Example 6. (a) Mapping of $\frac{{\mathbb{R}}_{0,1/2}\left(\zeta \right)}{\zeta }$ over $\mathbb{D}$; (b) mapping of $\frac{{\mathbb{R}}_{1,1/2}\left(\zeta \right)}{\zeta }$ over $\mathbb{D}$; (c) mapping of $\frac{{\mathbb{R}}_{2,1}\left(\zeta \right)}{\zeta }$ over $\mathbb{D}$; (d) mapping of $\frac{{\mathbb{R}}_{1,1}\left(\zeta \right)}{\zeta }$ over $\mathbb{D}$.

4. Hardy Spaces of Rabotnov Functions

Hardy spaces of certain special functions have been studied by various authors. For instance, Ponnusay [26] studied the problem for hypergeometric functions. The same problem by using the technique by Ponnusay for Bessel functions was used by Baricz [15]. Hardy spaces of generalized Struve functions were studied by Yagmur and Orhan [29]. The same problem for the case of Lommel functions was discussed by Yagmur [30]. Hardy spaces of ML functions are discussed in [9,31].

Theorem 7. 

Let $\gamma \in \left[0,1\right),$ $s\ge 0,$ $u>0$ and

$$\frac{u}{1+s}\left(\frac{u}{1+s}+1\right)e^{\frac{u}{1+s}}+\left(2-\gamma \right)\frac{u}{1+s}{e}^{\frac{u}{1+s}}\le \left(1-\gamma \right)\left(2-e^{\frac{u}{1+s}}\right).$$

Then,

(i) 

${\mathbb{R}}_{s,u}\in {\mathcal{H}}^{1/1-2\gamma }$ for $\gamma \in \left[0,1/2\right).$

(ii) 

${\mathbb{R}}_{s,u}\left(\zeta \right)\in {\mathcal{H}}^{\infty }$ for $\gamma \ge 1/2.$

Proof. 

Since

$${}_2{F}_1\left(a,b,c;\zeta \right)=\sum _{n=0}^{\infty }\frac{{\left(a\right)}_n{\left(b\right)}_n}{{\left(c\right)}_n}\frac{{\zeta }^n}{n!},$$

therefore,

$$\begin{array}{ccc}\hfill m+\frac{l}{{\left(1-\zeta e^{i\theta }\right)}^{1-2\gamma }}& =& m+l\zeta {}_2{F}_1\left(1,1-2\gamma ,1;\zeta e^{i\theta }\right)\hfill \\ & =& m+l\frac{{\left(1-2\gamma \right)}_n}{n!}{e}^{i\theta n}{\zeta }^{n+1},\hfill \end{array}$$

where $m,l\in \mathbb{C},$ $\gamma \ne 1/2$ and $\theta$ is any real number. Also, we have

$$\begin{array}{ccc}\hfill m+llog\left(1-\zeta e^{i\theta }\right)& =& m-l\zeta {}_2{F}_1\left(1,1,\zeta ;\zeta e^{i\theta }\right)\hfill \\ & =& m-l\sum _{n=0}^{\infty }\frac{1}{n+1}{e}^{i\theta n}{\zeta }^{n+1}.\hfill \end{array}$$

Hence, ${\mathbb{R}}_{s,u}$ cannot be written in the forms $m+l\zeta {\left(1-{\zeta }^{i\theta }\right)}^{2\gamma -1}$ for $\gamma \ne 1/2$ and $m+llog\left(1-\zeta e^{i\theta }\right)$ for $\gamma =1/2$, respectively $.$ By using Theorem 6 (a), ${\mathbb{R}}_{s,u}\in \mathcal{C}\left(\gamma \right);$ therefore, an application of Lemma 7 leads to the required result. □

Theorem 8. 

Let $s\ge 0,u>0,$ $e^{\frac{u}{1+s}}<2$ and $f\in \mathcal{R}$, and then $\left({\mathbb{R}}_{s,u}\ast f\right)$ ∈ ${\mathcal{H}}^{\infty }\cap \mathcal{R}.$

Proof. 

It is given that $f\in \mathcal{R}$, which implies that $f^{\prime }\in \mathcal{P}$. Let $h\left(\zeta \right)={\mathbb{R}}_{s,u}\left(\zeta \right)\ast f\left(\zeta \right).$ Now, using the definition of convolution

$$h^{\prime }\left(\zeta \right)=\frac{{\mathbb{R}}_{s,u}}{\zeta }\ast f^{\prime }\left(\zeta \right).$$

By applying Corollary 2 (b), it is evident that $\frac{{\mathbb{R}}_{s,u}}{\zeta }\in \mathcal{P}.$ Therefore, by using Lemma 5, $h^{\prime }\in \mathcal{P}.$ By using (3) $,$ it follows that $h^{\prime }\in {\mathcal{H}}^q$ for $q<1$ and $h\in {\mathcal{H}}^{q/\left(1-q\right)}$ for $0<q<1.$ This shows that $h\in {\mathcal{H}}^{\infty },q\in \left(0,\infty \right).$ Moreover, we see that

$$\begin{array}{ccc}\hfill \left|h\left(\zeta \right)\right|& \le & \left|\zeta \right|+\stackrel{\infty }{\sum _{n=2}}\frac{u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}\left|a_n\right|\left|{\zeta }^n\right|\hfill \\ & \le & 1+\stackrel{\infty }{\sum _{n=2}}\frac{u^{n-1}\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}\left|a_n\right|.\hfill \end{array}$$

Now, by using a result due to Macgregor [32] (p. 533, Theorem 1) on the coefficients for the class $\mathcal{R}$, $\left|a_n\right|\le 2/n,$ $n\ge 2,$ and the inequality $\frac{\Gamma \left(1+s\right)}{\Gamma \left(n\left(1+s\right)\right)}\le \frac{1}{{\left(1+s\right)}^{n-1}\left(n-1\right)!},$ we may write

$$\left|h\left(\zeta \right)\right|\le 1+\stackrel{\infty }{\sum _{n=2}}\frac{2u^{n-1}}{{\left(1+s\right)}^{n-1}n!}=1+\stackrel{\infty }{\sum _{n=1}}\frac{2u^n}{{\left(1+s\right)}^n\left(n+1\right)!}<\infty .$$

This shows that the series provided above absolutely converges in $\left|\zeta \right|=1$ for the given condition. Also, by using [16] (p. 42, Theorem 3.11), the result $h^{\prime }\in {\mathcal{H}}^q$ implies the continuity of h on closure of $\mathbb{D}$. Therefore, h is bounded. This completes the result. □

Theorem 9. 

Let $s\ge 0,u>0,e^{\frac{u}{1+s}}<2-\gamma ,\gamma \in \left[0,1\right)$ and $\zeta \in \mathbb{D}$. If $f\in \mathcal{R}\left(\eta \right),$ $\eta <1$, and then ${\mathbb{R}}_{s,u}\ast f\in \mathcal{R}\left(\delta \right),$ where $\delta =1-2\left(1-\gamma \right)\left(1-\eta \right).$

Proof. 

It is given that $f\in \mathcal{R}\left(\eta \right),$ which implies that $f^{\prime }\in \mathcal{P}\left(\eta \right).$ Let $h\left(\zeta \right)={\mathbb{R}}_{s,u}\left(\zeta \right)\ast f\left(\zeta \right)$. Then, it easy to see that

$$h^{\prime }\left(\zeta \right)=\frac{{\mathbb{R}}_{s,u}\left(\zeta \right)}{\zeta }\ast f^{\prime }\left(\zeta \right).$$

Now, by using Theorem 6 $\left(b\right),$ we have $\frac{{\mathbb{R}}_{s,u}\left(\zeta \right)}{\zeta }\in \mathcal{P}\left(\gamma \right).$ By using Lemma 6 and the given condition $f^{\prime }\in \mathcal{P}\left(\eta \right),$ we have $h^{\prime }\left(\zeta \right)\in \mathcal{P}\left(\delta \right),$ where $\delta =1-2\left(1-\gamma \right)\left(1-\eta \right)$. Hence, $h\in \mathcal{R}\left(\delta \right)$. □

Corollary 3. 

Let $s\ge 0,u>0,e^{\frac{u}{1+s}}<2-\gamma ,\gamma \in \left[0,1\right).$ If $f\in \mathcal{R}\left(\eta \right),$ $\eta =\left(1-2\gamma \right)/\left(2-2\gamma \right),$ then ${\mathbb{R}}_{s,u}\left(\zeta \right)\ast f\left(\zeta \right)\in \mathcal{R}\left(0\right).$

Corollary 4. 

Let $s\ge 0,u>0,2e^{\frac{u}{1+s}}<3.$ If $f\in \mathcal{R}\left(\frac{1}{2}\right),$ then ${\mathbb{R}}_{s,u}\left(\zeta \right)\ast f\left(\zeta \right)\in \mathcal{R}\left(0\right).$

Example 7. 

We see that the function

$$f\left(\zeta \right)=-\zeta -log(1-\zeta )=\zeta +\stackrel{\infty }{\sum _{n=2}}\frac{2}{n}{\zeta }^n$$

is in $\mathcal{R}$. We see that $f\notin {\mathcal{H}}^{\infty },$ (see Figure 4a). Also, for $s\ge 0,u>0,e^{\frac{u}{1+s}}<2,$ by using Theorem 8, ${\mathbb{R}}_{s,u}\ast f\in {\mathcal{H}}^{\infty }\cap \mathcal{R}$. Now, take $s=1,$ $u=\frac{1}{4}$ and, utilizing Theorem 8, consider

$$\begin{array}{ccc}\hfill h_0\left(\zeta \right)& =& {\mathbb{R}}_{1,1/4}\left(\zeta \right)\ast f\left(\zeta \right)=2\sqrt{\zeta }sinh\left(\frac{\sqrt{\zeta }}{2}\right)\ast f\left(\zeta \right)\hfill \\ & =& \zeta +\stackrel{\infty }{\sum _{n=2}}\frac{2}{2^{2n-3}n\Gamma \left(2n\right)}{\zeta }^n=-\zeta -16-16cosh\left(\frac{\sqrt{\zeta }}{2}\right).\hfill \end{array}$$

Here, Figure 4b shows that $h_0\left(\zeta \right)\in {\mathcal{H}}^{\infty }.$ Also, $Re\left(h_0^{\prime }\left(\zeta \right)\right)>0,$ (Figure 4c) for $\zeta \in \mathbb{D}$. This implies that $h_0\left(\zeta \right)\in \mathcal{R}$. Hence, ${\mathbb{R}}_{1,1/4}\left(\zeta \right)\ast f\left(\zeta \right)\in {\mathcal{H}}^{\infty }\cap \mathcal{R}$.

In Figure 4, we provide the mappings of functions in $\mathbb{D}$ provided in Example 7.

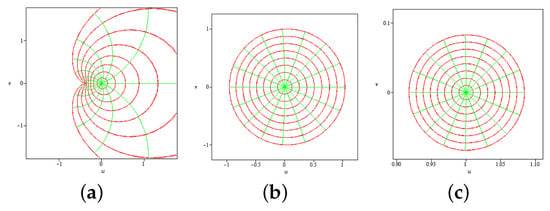
Figure 4. Mappings of functions over $\mathbb{D}$ provided in Example 7. (a) Mapping of $f\left(\zeta \right)$ over $\mathbb{D}$; (b) mapping of $h_0\left(\zeta \right)$ over $\mathbb{D}$; (c) mapping of $h_0^{\prime }\left(\zeta \right))$ over $\mathbb{D}$.

Example 8. 

Now, take $s=2,$ $u=1$ and, utilizing Theorem 8, consider

$$h_1\left(\zeta \right)={\mathbb{R}}_{2,1}\left(\zeta \right)\ast f\left(\zeta \right)=\zeta +\stackrel{\infty }{\sum _{n=2}}\frac{4}{n\Gamma \left(3n\right)}{\zeta }^n.$$

Here, Figure 5a shows that $h_1\left(\zeta \right)\in {\mathcal{H}}^{\infty }.$ Also, $Re\left(h_1^{\prime }\left(\zeta \right)\right)>0$ (Figure 5b) for $\zeta \in \mathbb{D}$. This implies that $h_1\left(\zeta \right)\in \mathcal{R}$. Hence, ${\mathbb{R}}_{2,1}\left(\zeta \right)\ast f\left(\zeta \right)\in {\mathcal{H}}^{\infty }\cap \mathcal{R}$.

Figure 5. Mappings of functions over $\mathbb{D}$ provided in Examples 8 and 9. (a) Mapping of $h_1\left(\zeta \right)$ over $\mathbb{D}$; (b) mapping of $h_1^{\prime }\left(\zeta \right))$ over $\mathbb{D}$; (c) mapping of $h_2^{\prime }\left(\zeta \right))$ over $\mathbb{D}$; (d) mapping of $h_2^{\prime }\left(\zeta \right))$ over $\mathbb{D}$.

Example 9. 

We take $s=1/2,$ $u=1/2$ and, utilizing Theorem 8, consider

$$h_2\left(\zeta \right)={\mathbb{R}}_{1/2,1/2}\left(\zeta \right)\ast f\left(\zeta \right)=\zeta +\stackrel{\infty }{\sum _{n=2}}\frac{\sqrt{\pi }{(1/2)}^{n-1}}{n\Gamma \left(\frac{3n}{2}\right)}{\zeta }^n.$$

Here, Figure 5c shows that $h_2\left(\zeta \right)\in {\mathcal{H}}^{\infty }.$ Also, $Re\left(h_2^{\prime }\left(\zeta \right)\right)>0$ (Figure 5d) for $\zeta \in \mathbb{D}$. This implies that $h_2\left(\zeta \right)\in \mathcal{R}$. Hence, ${\mathbb{R}}_{1/2,1/2}\left(\zeta \right)\ast f\left(\zeta \right)\in {\mathcal{H}}^{\infty }\cap \mathcal{R}$.

In Figure 5, we provide the mappings of the above-presented examples in $\mathbb{D}$.

5. Conclusions

We have studied various geometric properties of normalized Rabotnov functions in $\mathbb{D}$. In particular, we have found conditions on parameters so that the function ${\mathbb{R}}_{s,u}$ is uniformly convex, strongly starlike, and strongly convex. Furthermore, we have discussed the starlikeness and convexity of order $\gamma .$ We have also studied conditions so that the Rabotnov functions belong to the class of bounded analytic functions and Hardy spaces. Various consequences of these results are also presented by taking particular values of the parameters s and u. These examples are also illustrated by the figures. The results presented here provide a variety of particular examples.

By applying these techniques, similar kinds of results can be obtained for functions that can be represented by the Taylor series. Some other geometric properties such as close-to-convexity, prestarlikeness, and inclusions in some other subclasses of univalent functions can further be studied. Moreover, radii problems for various classes of analytic functions can be discussed.