Abstract
In this article, a considerably efficient predictor-corrector method (PCM) for solving Atangana–Baleanu Caputo (ABC) fractional differential equations (FDEs) is introduced. First, we propose a conventional PCM whose computational speed scales with quadratic time complexity as the number of time steps N grows. A fast algorithm to reduce the computational complexity of the memory term is investigated utilizing a sum-of-exponentials (SOEs) approximation. The conventional PCM is equipped with a fast algorithm, and it only requires linear time complexity . Truncation and global error analyses are provided, achieving a uniform accuracy order regardless of the fractional order for both the conventional and fast PCMs. We demonstrate numerical examples for nonlinear initial value problems and linear and nonlinear reaction-diffusion fractional-order partial differential equations (FPDEs) to numerically verify the efficiency and error estimates. Finally, the fast PCM is applied to the fractional-order Rössler dynamical system, and the numerical results prove that the computational cost consumed to obtain the bifurcation diagram is significantly reduced using the proposed fast algorithm.
1. Introduction
Fractional-order differential equations (FDEs) have been successfully applied in physics, biology, applied sciences, and engineering where memory effects are essential. FDEs are considered a novel mathematical model and are used to describe various phenomena in nature, such as anomalous transport [1,2,3], the flow in porous media [4], and so on. Some works [5,6,7,8,9] have demonstrated further applications, including in electrical circuits, chemistry, finance, chaos, control theory, heat transfer, gas dynamics, etc. The aforementioned applications adopted the Grünwald–Letnikov, Riemann–Liouville, or Liouville–Caputo fractional operators [5,6,8]. The definition of the Liouville–Caputo fractional operator is as follows:
Definition 1.
The Liouville–Caputo fractional derivative (Liouville–Caputo FD) of order , , for , which was introduced in [6,10], is defined by
Recently, new fractional differential operators with a nonlocal and non-singular kernel, e.g., Caputo–Fabrizio and Atangana–Baleanu, were proposed in [9,11]. Also, the more general Riemann–Liouville and Liuoville–Caputo fractional derivatives were introduced in [12,13].
In [14], Atangana and Baleanu suggested a new fractional differential operator involving the Mittag–Leffler kernel and applied it to a heat transfer model. This operator has been applied in many research areas [15,16,17]. In this paper, we aim to solve the nonlinear fractional differential equation of order ,
where is the Atangana–Baleanu fractional derivative of order in the Liouville–Caputo sense (ABC FD):
Definition 2.
The Atangana–Baleanu fractional derivative of order in the Caputo sense for , which was introduced in [14], is defined by
where is a normalization function with and , and is the one-parameter Mittag–Leffler function defined by
By taking the Laplace transform of (2) and then performing the inverse Laplace transform, we obtain the solution of the model problem (2) as the Volterra integral equation of the second kind [14], as follows:
where
Numerical methods for solving the ABC FDE (2) have been introduced by many researchers. The authors of [18] suggested utilizing the Crank–Nicholson schemes for solving the groundwater flow model with the ABC fractional derivative (3). The spectral collocation method, based on the Chebyshev approximations, was employed to handle a biological fractional model [19]. The authors of [20] developed the fractional Euler method and the predictor-corrector method (PCM), which is similar to the method in [21]. The PCM, using the product trapezoidal quadrature rule and the product rectangle rule for solving ABC fractional initial value problems, was introduced in [22]. The modified PCM was designed to be very accurate. Its performance stays the same regardless of the order of the fractional derivative, as explained in [23]. This method has worked well and has been used effectively in different research studies, for example, in [24,25].
Other numerical methods were suggested in [11,26,27,28,29,30,31,32,33,34].
This paper focuses on the following three topics:
- The development of a fast algorithm that can be applied to numerical methods for solving ABC FDEs.
- The development of a fast PCM and its application to ABC fractional-order PDEs (FPDEs) and fractional dynamical systems.
- Error estimates for both conventional and fast PCMs.
We introduce the fast algorithm regarding the computation of memory terms resulting from the non-local kernel in the ABC fractional derivative. The fast algorithm is integrated with the conventional PCM for solving the Volterra integral equation (4). To illustrate the idea of the proposed fast algorithm, we assume and discretize the uniform grid, as follows:
with . Equation (4) can be rewritten at time , as follows
where
In the numerical approximation of , the memory term (6) has to be computed from to for every n due to the non-local property of the kernel . Thus, it is easy to see that a computational cost of is incurred if linear interpolation of over is employed. To reduce the computational cost, we modify the sum-of-exponentials (SOEs) approximation for [35] and apply the algorithm to the memory term :
where and () are positive real numbers. Here, the integral term in (8) can be rewritten as the following recurrence relation:
It is worth noting that there exists a fixed number for all such that the error in (8) is given, where . Using the equation in (9), the integral term on the left-hand side can be evaluated recursively. Because of these facts, the computational cost to approximate the memory term is reduced by up to , even if the total number of time steps N is large. The highlights of this research, including the advantages of the proposed fast PCM, are as follows:
- The conventional PCM for solving ABC FDEs is suggested.
- The fast algorithm for the computation of the memory term is proposed, and the fast PCM only requires a computational cost of .
- Truncation and global error analyses for both conventional and fast PCMs are provided, achieving a uniform accuracy of order regardless of the fractional order .
- We apply the proposed fast PCM to sub-diffusion FPDEs to demonstrate the efficiency of the proposed method.
- The proposed fast PCM is implemented to handle the fractional Rössler dynamical system, and the performance of the fast algorithm is verified.
Our paper consists of the following sections. In Section 2, we succinctly describe a conventional PCM for solving FDEs with the ABC FD. We propose a modified SOE approximation of the power function based on [35]. We introduce a fast PCM for solving FDEs with the ABC FD. The error analyses for the suggested methods are provided in Section 3. In Section 4, numerical results are provided to support our theoretical results. Applications to reaction-diffusion FPDEs and the fractional Rössler dynamical system are also introduced. Finally, the conclusions are presented in Section 5.
2. Fast Predictor-Corrector Scheme
2.1. Description of Predictor-Corrector Scheme
First, let us define some notations. For each , we denote , . Let and be the predicted and corrected approximations of , respectively. Similarly, we also denote and . On each interval , we employ the Lagrange interpolating polynomial of , defined by
where
The value of ) can be expressed by using the linear interpolation of f on
where
Here, we employ the modified predictor-corrector method from [23] in order to obtain the second order of convergence. Specifically, referring to Lemma 1 [23], we have
2.2. Sum-of-Exponentials Approximation of the Power Function
In this section, we describe the modified version of the approximation of the kernel function based on [35]. First, we give a summary of the effective SOE approximation for ().
Lemma 1
([35]). For any ,
Lemma 2
([35]). For , there exists such that
In the original SOE approximation in [35], the upper limit of the definite integral p in (15) was . The interval was split into three dyadic intervals: , and . The Gauss–Jacobi and Gauss–Legendre quadrature rules were employed in the three intervals. Here, we normalize the interval into . That is,
Recalling and from Theorem 1 ([35]), we obtain following modified SOE approximation by setting :
Theorem 1
(Modified SOE approximation of the power function). thmmsoeapp Let be the desired error, and choose . Let ; ; and be n-point Gauss–Jacobi quadratures on the interval ; and and be n-point Gauss–Legendre quadrature points and weights on the intervals for . Then, for and ,
Remark 1.


We use Gauss–Legendre quadrature nodes and weights because all dyadic intervals are less than or equal to 1. Theorem 1 can be written as follows for some positive real numbers and
where is the number of exponentials to be determined later and .
As mentioned in [35], the number of exponentials is required to approximate because many nodes and weights are computed in each dyadic interval. Here, we apply the reduction method based on the balanced truncation method with singular-value decomposition instead of Cholesky factorization (see the details in Appendix A). Table 1 and Table 2 show comparisons between our method and the method in [35] regarding the number of exponentials for approximating for a fixed (Table 1) and for a fixed (Table 2). In most cases, the number of exponentials in our method is comparably smaller than the number of exponentials in [35]. For the comparisons, we set and used Gauss–Legendre nodes with corresponding weights.

Table 1.
Comparison of the number of exponentials for approximating with .

Table 2.
Comparison of the number of exponentials for approximating with .
2.3. Description of Fast Predictor-Corrector Scheme
In this section, we describe the fast PCM, which boosts the computational speed of the memory term . To do this, we use the SOE approximation of introduced in Section 2.2. For simplicity, let and be given. Then, we have the following: for ,
Since and
it is easy to determine that has the following recurrence relation:
Remark 2.
It is easy to see that is approximated by the sum of piecewise interpolations over n for each interval. That is, the computational cost for approximating is about . From the recurrence relation in (20), can be obtained by computing the interpolation over the interval combined with , which was computed at step n. Then, can be determined as the sum of for all i, . It costs to approximate using the recurrence relation. For , the computational cost for approximating is about .
3. Error Analysis
3.1. Truncation and Global Error Analyses for the Conventional PCM
In this section, we show that the proposed conventional PCM has a uniform convergence rate regardless of . First, we recall the error analysis of the second-order predictor-corrector scheme with linear interpolation for solving FDEs with the Liouville–Caputo FD in [23] and state the necessary lemmas for the error analysis. Herein, we denote by C a generic constant that is independent of all grid parameters and may change case by case.
Lemma 3
(Discrete Gronwall’s inequality [36]). Let , be non-negative sequences with monotonically increasing , satisfying
where is bounded and independent of h, and . Then,
Lemma 4.
For , and ,
It is worth noting that the Volterra integral equation for the model problem in (4) is similar to the form presented to (1.3) in [23], as is the PCM algorithm. Here, and . Therefore, it is straightforward to derive the following error analysis results.
Lemma 5
(Truncation error for the predictor [23]). Suppose that . Let the truncation error of the predictor at be
Then, there exists a constant C independent of all grid parameters such that
Lemma 6
(Global error for the predictor [23]). Suppose that satisfies the Lipschitz continuity condition in the second argument,
then, the global error for the predictor, , is given by
Lemma 7
(Truncation error for the corrector [23]). Under the same assumptions as those in Lemma 5, the truncation error of the corrector at time is given by
and can be expressed as
where .
Lemma 8
(Global error for the corrector [23]). Under the same assumptions as those in Lemma 6, the global error is given by
given that the starting error .
Now, using the aforementioned lemmas with the substitutions , , we prove the following truncation and global error analyses for the conventional PCM (14).
Theorem 2
(Truncation error for the predictor ). Let the truncation error of predictor be defined by
where . Under the same assumptions as those in Lemma 5, there exists a constant C independent of all grid parameters such that
Proof.
Let . Then, from (10) and Lemma 5, we have the following inequality:
□
Theorem 3
(Global error for the predictor ). Under the same assumptions as those in Lemma 6, the global error for the predictor, , can be estimated by
where .
Proof.
From (14) and the triangle inequality, we have
From the Lipschitz condition and Lemma 6 combined with the argument of (see in Theorem 2 [23]), we have
□
Theorem 4
(Truncation error for the corrector ). Under the same assumptions as those in Theorem 3, let the truncation error at time be
Then,
Proof.
From Lemma 7 and (14), we obtain the following:
□
Theorem 5
(Global error for the corrector ). Under the same assumptions as those in Theorem 3, the global error is
given that the starting error .
Proof.
From Lemma 4 and Theorem 4,
By applying a similar argument to in Theorem 3, we have
Using Theorem 3 and Equation (22) implies that
where
Then, the discrete Gronwall’s inequality yields
where
Since and in Theorem 2, it is clear that
This completes the proof. □
3.2. Global Error Analysis for the Fast PCM
Thus, we have the following:
Lemma 9.
For , suppose that Equation (18) is satisfied. Then,
Theorem 6
(Global error for the predictor ). Under the same assumptions as those in Theorem 3, the global error has the following inequality:
where .
Proof.
From Theorem 3 and Lemma 9 with , we obtain the following:
□
Theorem 7
(Global error for the corrector ). Under the same assumptions as those in Theorem 3, the global error is
given that the starting error .
Proof.
From Theorems 5 and 6 and Lemma 9, we have
Then, from the discrete Gronwall’s inequality, we have the following:
□
4. Numerical Results
In this section, we conduct numerical experiments to demonstrate the effectiveness of our proposed methods and numerically verify the error estimates. Let us define the following two errors over :
- Maximum norm error:
- Discrete norm error:
where is an approximate solution at time .
Throughout this section, ABC-PCM and ABC-FPCM are used to denote the conventional PCM (14) and the fast PCM (21), respectively. Several numerical demonstrations are performed to obtain approximate solutions of nonlinear ABC fractional-order initial value problems and nonlinear reaction-diffusion problems. Moreover, the efficiency of the fast algorithm is clearly demonstrated in its application to fractional dynamical systems. All numerical experiments are implemented using Matlab. For simplicity, in all our numerical experiments, we set the constant to a value of 1. In Section 4.1, we present the numerical results for the nonlinear ABC fractional differential equations in (2). These results validate our theoretical findings, including the convergence rate, and confirm the efficiency of our proposed fast algorithms compared to the conventional PCM. We discuss the extension of our proposed method to fractional partial differential equations. All pertinent numerical results supporting the efficacy and applicability of our method in this context are included in Section 4.2. Finally, the numerical efficiency of our fast algorithm is showcased through its application to various fractional dynamical systems in Section 4.3.
4.1. Nonlinear ABC Fractional-Order Initial Value Problems
Example 1.
Consider the following nonlinear problem with [20]:
where the solution is .
Example 2.
Consider the following nonlinear problem with [20]:
where the solution is .
In Examples 1 and 2, we fix , , and . From Table 3 and Table 4 and Figure 1, we can make the following observations:

Table 3.
Errors and rates of convergence versus h for Example 1 with , .

Table 4.
Errors and rates of convergence versus h for Example 2 with , .
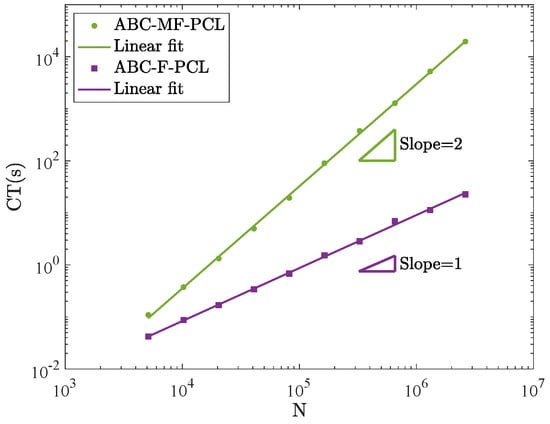
Figure 1.
Log-log plot of CPU time (CT(s)) versus the number of steps N with for Example 2.
- The numerical results obtained with the ABC-FPCM show little difference from those obtained with the ABC-PCM.
- The computational costs, obtained by measuring the CPU time (in seconds) executed by the conventional PCM and the fast PCM versus the total number of steps N on the log-log scale in Example 2, are depicted in Figure 1. The figure shows that the CPU consumption rate of the fast PCM is , whereas that of the conventional PCM is .
4.2. Application to Fractional Order PDEs
In this subsection, we discuss the ABC fractional-order reaction-diffusion equation. The general form of this equation is given by
where is of fractional order, is the diffusion coefficient, and g is the nonlinear source term. The approximated solution at time is denoted as follows:
with the space step size for , and the time step size for , and . We employ the second-order central difference quotient to approximate at :
By applying the conventional PCM (14) combined with the second-order central difference to the sub-diffusion Equation (23), we obtain the following numerical scheme:
where is an identity matrix, is the finite-difference matrix for the space derivative, and
Similarly, the fast PCM for the sub-diffusion equation can be expressed as follows:
where
Now, we apply the PCMs combined with the second-order central difference schemes (25) and (26) for solving ABC fractional order sub-diffusion PDEs to the following examples. Although our proposed method is capable of handling an arbitrary diffusion coefficient c, for simplicity in our simulation, we have chosen to set the diffusion constant to 1.
Example 3.
Consider the linear sub-diffusion problem with , which is given by
and the corresponding initial boundary conditions are as follows:
Then, is the exact solution.
Example 4.
Consider the nonlinear sub-diffusion problem with , which is given by
and the corresponding initial boundary conditions are as follows:
Then, is the exact solution.

Table 5.
Errors and rates of convergence versus h when and versus when for Example 3.

Table 6.
Errors and rates of convergence versus h when and versus when for Example 4.
- Theoretically, the rate of convergence for the second-order central difference quotient is , and the convergence rates for the proposed methods are shown to be 2. Thus, the global order of convergence for both (25) and (26) is expected to be 2 when either or h is fixed. In the tables, one can see that the rates of convergence computed by the ABC-FPCM and ABC-PCM are approximately 2 in both cases where is fixed and h is fixed. This verifies that the global estimates of our proposed methods are valid in solving sub-diffusion FPDEs.
- The gap between the CPU time executed by the ABC-PCM and that executed by the ABC-FPCM is evident in the tables. Particularly, the difference between them drastically increases as is fixed. This verifies that the proposed fast PCM is more efficient compared to the conventional PCM.
We apply the proposed methods to time-dependent PDEs in two dimensions. The authors of [37] discussed the finite-difference scheme for the predator–prey interaction in the two-dimensional space for the integer-order case. We aim to solve this model equipped with time-fractional derivatives, specifically the predator–prey reaction-diffusion systems with the Holling type functional response and logistic growth of the prey. These systems are described below.
Example 5.
Consider the two-component reaction-diffusion equation system [37]:
where , and the parameters , and c are strictly positive. denotes the Liouville–Caputo FD (1) or ABC FD. Its initial conditions are given by
where the stationary solution is , and zero-flux boundary conditions are applied.
The suggested methods (25) and (26) can be extended to solve this example through the following setting:
and the matrix and the parameters , , , and are defined in [37].
We measure the CPU times of the suggested methods and investigate the effects of the types of fractional derivatives and fractional orders. We make the following observations:
- Table 7 shows the CPU times for Scheme 2 in [37], the ABC-PCM, and the ABC-FPCM for Example 5. To measure the rate of the CPU time, the time T increases twice from T = 125 to 1000, and we can observe that the rate of the CPU time for Scheme 2 and the ABC-FPCM is , whereas for the ABC-PCM, it is .
 Table 7. CPU times of the fractional-order predator–prey interaction (5) with the parameters , , , , , , and .
Table 7. CPU times of the fractional-order predator–prey interaction (5) with the parameters , , , , , , and . - Furthermore, the ABC-FPCM is much more efficient in terms of memory management compared to the existing method because it requires storing all previous values (, , and ) to calculate by using the ABC-PCM efficiently. On the other hand, the APC-FPCM requires only local values.
- Figure 2 shows the effect of fractional order and types of fractional derivatives for , , , and . The first row depicts the evolution of the system for . We can see that the spiral pattern is broken when , and an irregular pattern appears when .
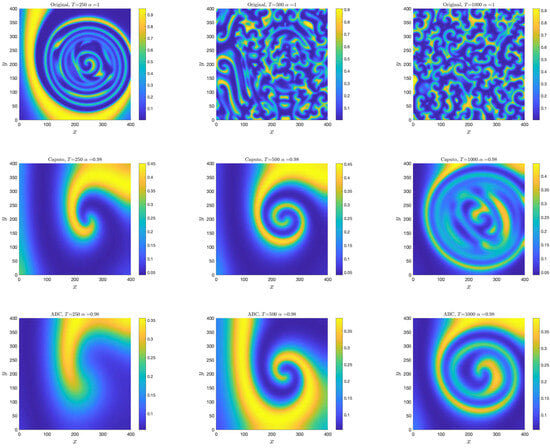 Figure 2. Comparison of numerical solution of Example 5 at with the parameters , , , , , , and . Each row represents , with the Liouville–Caputo FD, and with the ABC FD.
Figure 2. Comparison of numerical solution of Example 5 at with the parameters , , , , , , and . Each row represents , with the Liouville–Caputo FD, and with the ABC FD. - The second and third rows describe the evolution of the system for the ABC and Liouville–Caputo fractional derivatives of order , respectively. In the fractional-order system, similar to the case of , the spiral pattern is broken over time.
- In addition, in the fractional systems, a spiral pattern exists at , but the spiral pattern disappears at . This phenomenon is similar to the case where , , and has a wider pattern.
- It can be seen that the solution of the problem equipped with the ABC derivative is slower and wider than the solution of the problem equipped with the Liouville–Caputo derivative.
4.3. Application to Fractional Dynamical Systems
Here, we discuss the application to fractional dynamical systems. Recently, many researchers have studied fractional-order dynamical systems due to the memory effect. However, fractional-order dynamical systems consume excessive computational time compared to integer-order systems when drawing bifurcation diagrams with fixed points and extrema. We apply our fast PCM to plot bifurcation diagrams for the fractional-order Rössler dynamical system with the Liouville–Caputo FD and ABC FD. We aim to discuss the efficiency of the fast PCM and the influence of the definition of FD applied. First, we recall the fractional-order Rössler system:
Example 6.
The fractional-order Rössler system [38] is defined as
where is the fractional order; are the state variables; and are the parameters. denotes the Liouville–Caputo FD (1) or ABC FD. If , it becomes the integer-order Rössler system and is well known.
In this example, we show comparisons of the CPU times using the classical PCM and the fast PCM to obtain the bifurcation diagrams of the local maximum of y versus a for the Liouville–Caputo and ABC fractional Rössler systems, respectively. The parameters are set to , , , , and for the numerical simulations. The bifurcation diagrams for the Liouville–Caputo fractional Rössler system obtained by the ABC-FPCM (Figure 3a) and the ABC-PCM (Figure 3b) when parameter a varies from to are shown in Figure 3. Figure 4 shows the bifurcation diagrams for the ABC fractional system computed by the ABC-FPCM (Figure 4a) and the ABC-PCM (Figure 4b), as parameter a ranges from to , where the increment in parameter a in both systems is set to . It can be observed that the fast PCM significantly reduces the computational cost. For the Liouville–Caputo Rössler system, the CPU time for the ABC-FPCM is only 19 min, whereas that of the ABC-PCM is 2 days, 12 h, and 32 min. For the ABC system, the ABC-FPCM takes 1 h and 7 min, whereas the ABC-PCM takes four days, 21 h, and 2 min. This confirms that the proposed fast PCM has superior performance and efficiency compared to the conventional PCM.
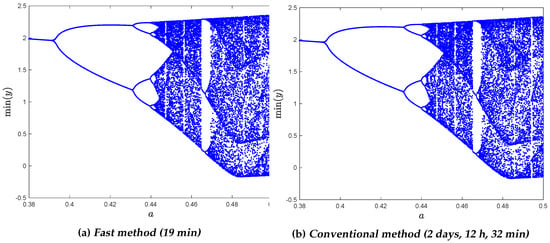
Figure 3.
Bifurcation diagrams for Rössler system with the Liouville–Caputo FD, .
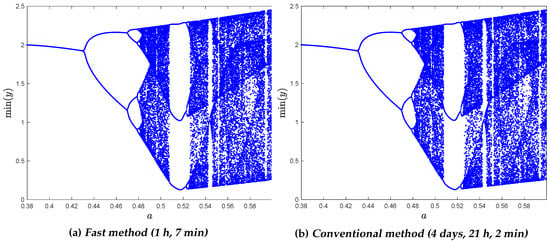
Figure 4.
Bifurcation diagrams for Rössler system with the ABC FD, .
5. Conclusions
In this paper, we have introduced two distinct predictor-corrector methods (PCMs) for solving ABC fractional differential equations: the conventional PCM, based on linear interpolation, and the fast PCM, enhanced by the sum-of-exponentials (SOEs) approximation of .
Our findings demonstrate that although the fast PCM achieves linear time complexity , the conventional PCM operates with quadratic time complexity , as illustrated numerically by the CPU time in Figure 1.
We have established truncation and global error estimates, and the uniform accuracy order of was empirically verified across Examples 1 through 4. Our methods were applied to a range of problems, including nonlinear ABC fractional-order differential problems, ABC fractional-order sub-diffusion PDEs, and the fractional-order Rössler dynamical system with both the ABC FD and Liouville–Caputo FD. Of particular note is the application to the fractional Rössler dynamical system, where the fast PCM demonstrated significant potential in reducing computational costs. This efficiency is especially valuable in the analysis of bifurcation diagrams for various values of in fractional dynamical systems, a topic we plan to explore further in subsequent work.
While our methods have shown promising results, we acknowledge certain limitations. The scope of comparison with the existing literature was constrained due to the unique nature of our methods, particularly in the context of ABC PDEs. In future research, we aim to extend our comparative analysis and explore the full potential of our methods in a broader range of applications. Additionally, we plan to address the practical implications and applications of our fast PCM in analyzing bifurcation diagrams in fractional dynamical systems in more depth, which could open new avenues in the study of complex dynamical behaviors.
In conclusion, our work represents a significant step forward in the computational handling of ABC fractional differential equations. We have achieved our initial objectives of developing efficient computational methods and have laid a foundation for future explorations that could further enhance the understanding and application of these methods in complex systems.
Author Contributions
Conceptualization, S.L and B.J.; methodology, S.L., H.K., and B.J.; software, S.L. and H.K.; validation, H.K. and B.J.; formal analysis, S.L and B.J.; investigation, H.K. and B.J.; writing—original draft preparation, S.L and B.J.; writing—review and editing, S.L., H.K., and B.J.; visualization, S.L. and H.K.; supervision, B.J. All authors have read and agreed to the published version of the manuscript.
Funding
S. Lee was supported by a National Institute for Mathematical Sciences (NIMS) grant, funded by the Korean government (MSIT) (No. B22810000). B. Jang and H. Kim acknowledge funding support from the National Research Foundation of Korea (NRF) grant, funded by the Korean government (MSIT) (2021R1A2C1011817, 2021R1A4A1032924 and 2022R1F1A1063605).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data used in this study are included in the article. Further inquiries can be directed to the author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Additional Information on the Sum-of-Exponentials Approximation
In this section, we describe the method for reducing the number of exponentials. Here, we introduce the balanced truncation method (BTM). It is one of the model reduction methods used for linear time-invariant (LTI) systems. First, we explain the motivation for using this method. Our objective is to create a reduced model of the LTI system:
where , and . The vectors , and are the state variables, input variables, and output variables, respectively. The transfer function is . We want to find the reduced system as , i.e.,
where , and . Before describing this method, let us intuitively observe why it can be used to reduce the number of quadratures. We set , , and , where ’s and ’s are the quadrature nodes and weights, respectively. The transfer function is given by
where . Note that this is the Laplace transform of our sum-of-exponentials approximation. So, we find the reduced form:
By applying the inverse Laplace transform, we obtain the reduced SOE approximation . Therefore, we can use this method to reduce the number of quadratures. Now, we state some important definitions and theorems.
Definition A1
([39]). When determining the specific situation of the system, we use Gramians. As an example, Gramians are used to determine whether a system is controllable or reachable. The reachability Gramian and the observability Gramian of the system (A1) are defined as follows:
- The reachability Gramian
- The observability Gramian
where is a fixed final time. Assume that A is asymptotically stable and . In this case, P and Q are the solutions of the following Lyapunov equations:
If the system (A1) is asymptotically stable and minimal, the two Lyapunov equations (A6) and (A7) have unique symmetric positive definite solutions.
Definition A2
([40]). The square roots of the eigenvalues (singular values) of the product are the so-called Hankel singular values of the system (A1):
There are some important properties of the Hankel singular values:
- are basis independent.
- In a lot of instances, not only the eigenvalues of P and Q but also the Hankel singular values decrease very quickly.
- Note that one of properties of the balanced basis is that hard-to-reach states are hard to observe. Therefore, we obtain the reduced model by using the Hankel singular values, except for the small ones.

Table A1.
The number of exponentials and relative errors for the approximation of with .
Table A1.
The number of exponentials and relative errors for the approximation of with .
| Theorem 1 | ||||||||
| 84 | 2.85 | 119 | 2.74 | 147 | 2.87 | 182 | 2.91 | |
| 182 | 5.29 | 238 | 6.15 | 308 | 7.97 | 378 | 9.39 | |
| 273 | 8.01 | 378 | 1.07 | 462 | 1.10 | 567 | 1.30 | |
| 15 | 1.01 | 19 | 9.18 | 23 | 1.11 | 27 | 1.14 | |
| 26 | 1.60 | 32 | 1.50 | 39 | 9.14 | 46 | 1.21 | |
| 37 | 1.10 | 47 | 8.56 | 54 | 7.89 | 64 | 1.16 | |
| 14 | 1.62 | 19 | 1.52 | 22 | 1.72 | 26 | 1.75 | |
| 25 | 3.23 | 31 | 2.99 | 38 | 1.57 | 45 | 2.20 | |
| 36 | 2.12 | 46 | 1.64 | 53 | 1.44 | 62 | 2.10 | |
| 14 | 3.19 | 18 | 2.96 | 21 | 3.35 | 25 | 3.41 | |
| 25 | 6.46 | 30 | 5.62 | 37 | 3.56 | 43 | 4.48 | |
| 35 | 5.44 | 44 | 4.22 | 52 | 4.47 | 61 | 4.31 | |

Table A2.
The number of exponentials and relative errors for the approximation of with .
Table A2.
The number of exponentials and relative errors for the approximation of with .
| T | 10 | |||||||
|---|---|---|---|---|---|---|---|---|
| Theorem 1 | ||||||||
| 98 | 2.85 | 119 | 2.74 | 133 | 2.74 | 147 | 2.74 | |
| 210 | 6.09 | 238 | 6.15 | 280 | 6.15 | 308 | 6.15 | |
| 336 | 8.84 | 378 | 1.07 | 420 | 1.07 | 462 | 1.07 | |
| 16 | 2.24 | 19 | 1.48 | 21 | 2.33 | 23 | 1.76 | |
| 29 | 1.15 | 32 | 2.78 | 36 | 2.51 | 39 | 1.89 | |
| 42 | 1.39 | 47 | 1.14 | 50 | 2.16 | 54 | 2.20 | |
| 16 | 3.89 | 19 | 3.37 | 20 | 6.79 | 22 | 5.16 | |
| 29 | 2.54 | 31 | 6.58 | 35 | 8.26 | 38 | 6.23 | |
| 41 | 2.77 | 46 | 2.56 | 49 | 5.90 | 53 | 7.82 | |
| 15 | 7.04 | 18 | 4.08 | 19 | 1.23 | 21 | 9.38 | |
| 28 | 5.32 | 30 | 1.05 | 34 | 1.66 | 37 | 1.27 | |
| 40 | 6.80 | 44 | 6.08 | 48 | 1.27 | 52 | 1.70 | |
In order to obtain the reduced system, the following theorem is crucial:
Theorem A1
([41]). Assume that the asymptotically stable, minimal realization of the full-order model transfer function, , is internally balanced, i.e.,
where , and are the Hankel singular values of the system. If we obtain the reduced model with the following transfer function
where , , and , the model reduction error is bounded
where is the norm for the transfer function.
We use the square-root method described in Algorithm A1. In our case, we use and instead of the Cholesky factors of P and Q because they are sometimes not positive-definite matrices in the numerical sense (i.e., they have some very small negative eigenvalues ). Moreover, the singular values of are also the Hankel singular values of the system (A1). Therefore, we can obtain the reduced system with the desired error using the balanced truncation method.
Table A1 and Table A2 show the number of exponentials and the relative error for the approximations of with some . To show the effectiveness of the balanced truncation method in Algorithm A1, we set and in Theorem 1. When the error bound becomes smaller, the number of exponentials also increases. It can be observed that the relative error is much smaller than the lowest value of using the method in Theorem 1. However, it is worth noting that the balanced truncation method in Algorithm A1 controls the number of exponentials with respect to the error bound . From the results in the tables, we can verify that the model reduction method significantly reduces the number of exponentials . It should be noted that the number of exponentials in Theorem 1 is almost independent of the value of in approximating .
| Algorithm A1: Balanced truncation method [42] |
Data: The desired error , quadrature points , and weights . Result: Reduced quadrature points and weights . Set , , and ; Solve two Lyapunov equations and ; Compute two singular-value decompositions of and ; Set and ; Compute a singular-value decomposition of , where ; Find k such that ; Form a matrix J, where , and otherwise; Set and ; Set , , and ; Compute the eigenvalue decomposition of ; Set ; Form and ; Set ; |
References
- Goychuk, I.; Heinsalu, E.; Patriarca, M.; Schmid, G.; Hänggi, P. Current and universal scaling in anomalous transport. Phys. Rev. E 2006, 73, 020101. [Google Scholar] [CrossRef]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport: Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar] [CrossRef]
- Caputo, M. Models of flux in porous media with memory. Water Resour. Res. 2000, 36, 693–705. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science & Business Media: Cham, Switzerland, 2010. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Cham, Switzerland, 2011. [Google Scholar]
- Giusti, A. A comment on some new definitions of fractional derivative. Nonlinear Dyn. 2018, 93, 1757–1763. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J. Fractional derivatives with no-index law property: Application to chaos and statistics. Chaos Solitons Fractals 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Srivastava, H.M. Some parametric and argument variations of the operators of fractional calculus and related special functions and integral transformations. J. Nonlinear Convex Anal. 2021, 22, 1501–1520. [Google Scholar]
- Srivastava, H.M. An introductory overview of fractional-calculus operators based upon the Fox-Wright and related higher transcendental functions. J. Adv. Eng. Comput. 2021, 5, 135–166. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Gómez, J.F. Fractional Derivatives with Mittag-Leffler Kernel: Trends and Applications in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Gómez-Aguilar, J.; Atangana, A. Fractional Derivatives with the Power-Law and the Mittag–Leffler Kernel Applied to the Nonlinear Baggs–Freedman Model. Fractal Fract. 2018, 2, 10. [Google Scholar] [CrossRef]
- Owolabi, K.M. Modelling and simulation of a dynamical system with the Atangana-Baleanu fractional derivative. Eur. Phys. J. Plus 2018, 133, 15. [Google Scholar] [CrossRef]
- Alqahtani, R.T. Atangana-Baleanu derivative with fractional order applied to the model of groundwater within an unconfined aquifer. J. Nonlinear Sci. Appl. 2016, 9, 3647–3654. [Google Scholar] [CrossRef]
- Saad, K.M.; Khader, M.; Gómez-Aguilar, J.; Baleanu, D. Numerical solutions of the fractional Fisher’s type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023116. [Google Scholar] [CrossRef] [PubMed]
- Baleanu, D.; Jajarmi, A.; Hajipour, M. On the nonlinear dynamical systems within the generalized fractional derivatives with Mittag–Leffler kernel. Nonlinear Dyn. 2018, 94, 397–414. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Djida, J.; Atangana, A.; Area, I. Numerical computation of a fractional derivative with non-local and non-singular kernel. Math. Model. Nat. Phenom. 2017, 12, 4–13. [Google Scholar] [CrossRef]
- Nguyen, T.B.; Jang, B. A high-order predictor-corrector method for solving nonlinear differential equations of fractional order. Fract. Calc. Appl. Anal. 2017, 20, 447–476. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Jang, B. An efficient numerical approach for solving two-point fractional order nonlinear boundary value problems with Robin boundary conditions. Adv. Differ. Equ. 2021, 193. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.; Kim, H.; Jang, B. A fast and high-order numerical method for nonlinear fractional-order differential equations with non-singular kernel. Appl. Numer. Math. 2021, 163, 57–76. [Google Scholar] [CrossRef]
- Sun, Z.z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
- Cui, M. Compact finite difference method for the fractional diffusion equation. J. Comput. Phys. 2009, 228, 7792–7804. [Google Scholar] [CrossRef]
- Brunner, H.; Hairer, E.; Nørsett, S. Runge-Kutta theory for Volterra integral equations of the second kind. Math. Comput. 1982, 39, 147–163. [Google Scholar] [CrossRef]
- Capobianco, G.; Conte, D.; Del Prete, I.; Russo, E. Fast Runge–Kutta methods for nonlinear convolution systems of Volterra integral equations. BIT Numer. Math. 2007, 47, 259–275. [Google Scholar] [CrossRef]
- Deng, J.; Zhao, L.; Wu, Y. Efficient algorithms for solving the fractional ordinary differential equations. Appl. Math. Comput. 2015, 269, 196–216. [Google Scholar] [CrossRef]
- Kumar, P.; Agrawal, O.P. An approximate method for numerical solution of fractional differential equations. Signal Process. 2006, 86, 2602–2610. [Google Scholar] [CrossRef]
- Li, C.; Chen, A.; Ye, J. Numerical approaches to fractional calculus and fractional ordinary differential equation. J. Comput. Phys. 2011, 230, 3352–3368. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. Chaotic behaviour in system of noninteger-order ordinary differential equations. Chaos Solitons Fractals 2018, 115, 362–370. [Google Scholar] [CrossRef]
- lknur Koca. Efficient numerical approach for solving fractional partial differential equations with non-singular kernel derivatives. Chaos Solitons Fractals 2018, 116, 278–286. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, J.; Zhang, Q.; Zhang, Z. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 2017, 21, 650–678. [Google Scholar] [CrossRef]
- Cao, J.; Xu, C. A high order schema for the numerical solution of the fractional ordinary differential equations. J. Comput. Phys. 2013, 238, 154–168. [Google Scholar] [CrossRef]
- Garvie, M.R. Finite-difference schemes for reaction–diffusion equations modeling predator–prey interactions in M ATLAB. Bull. Math. Biol. 2007, 69, 931–956. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Chen, D.; Ma, M.; Zhang, X.; Wu, Y. Feigenbaum’s constants in reverse bifurcation of fractional-order Rössler system. Chaos Solitons Fractals 2017, 99, 116–123. [Google Scholar] [CrossRef]
- Laub, A.; Heath, M.; Paige, C.; Ward, R. Computation of system balancing transformations and other applications of simultaneous diagonalization algorithms. IEEE Trans. Autom. Control 1987, 32, 115–122. [Google Scholar] [CrossRef]
- Gugercin, S.; Antoulas, A.C. A survey of model reduction by balanced truncation and some new results. Int. J. Control 2004, 77, 748–766. [Google Scholar] [CrossRef]
- Enns, D.F. Model reduction with balanced realizations: An error bound and a frequency weighted generalization. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 1984; IEEE: Manhattan, NY, USA,, 1984; pp. 127–132. [Google Scholar]
- Xu, K.; Jiang, S. A bootstrap method for sum-of-poles approximations. J. Sci. Comput. 2013, 55, 16–39. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).