Mandelbrot Set as a Particular Julia Set of Fractional Order, Equipotential Lines and External Rays of Mandelbrot and Julia Sets of Fractional Order
Abstract
1. Introduction
- •
- : Mandelbrot of IO;
- •
- : Filled Julia set of IO;
- •
- : Julia set of IO;
- •
- : Mandelbrot set of FO;
- •
- : Filled Julia set of FO;
- •
- FEL: Fractional equipotential line;
- •
- FER: Fractional external ray.
2. Mandelbrot Set and Julia Sets of FO
- P1.
- P2.
- sets are connected if the underlying c belongs to the interior of ; i.e., the set is the set of all parameters c for which is a connected set.
- P3.
3. Mandelbrot and Julia Maps of FO
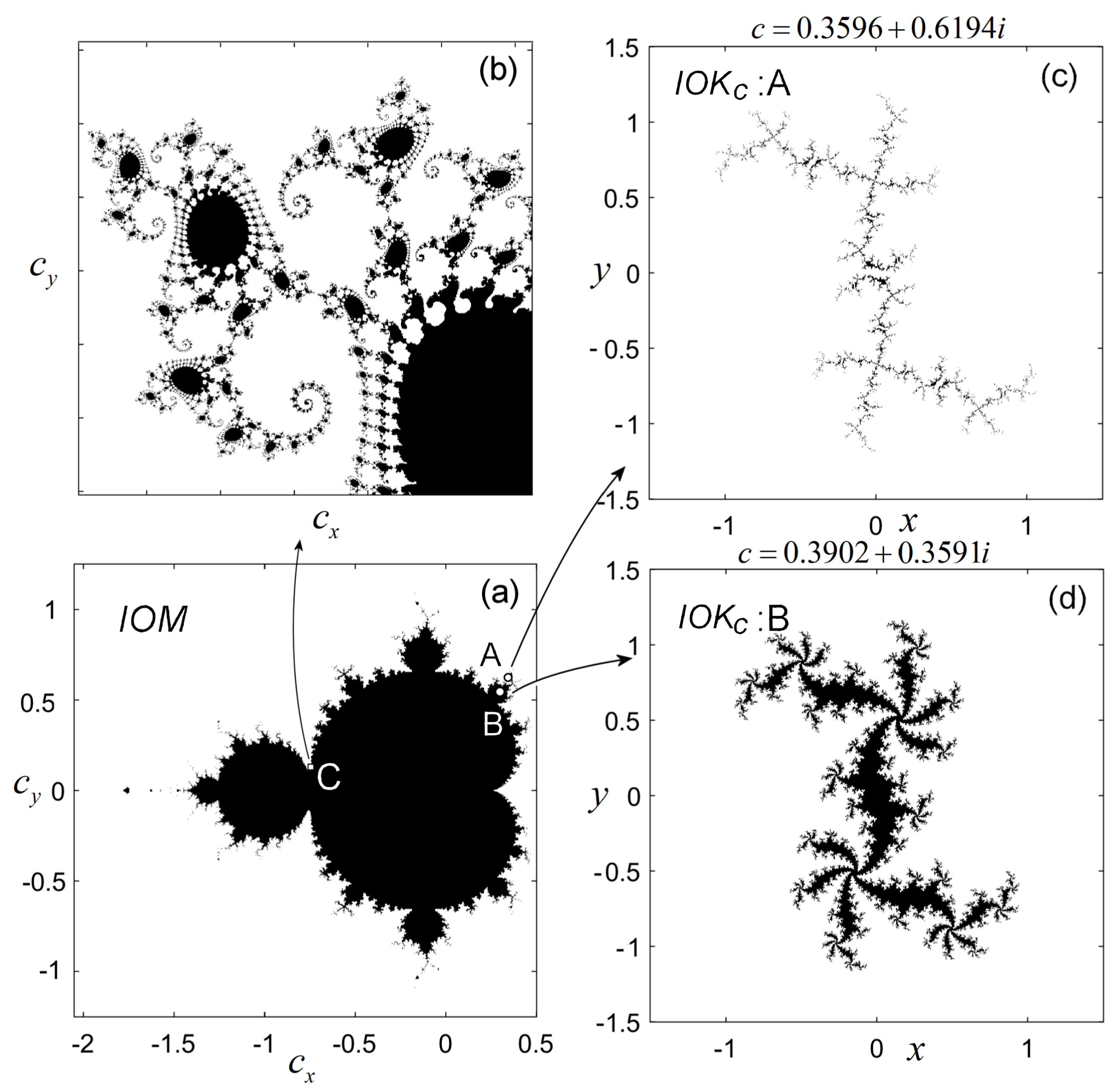
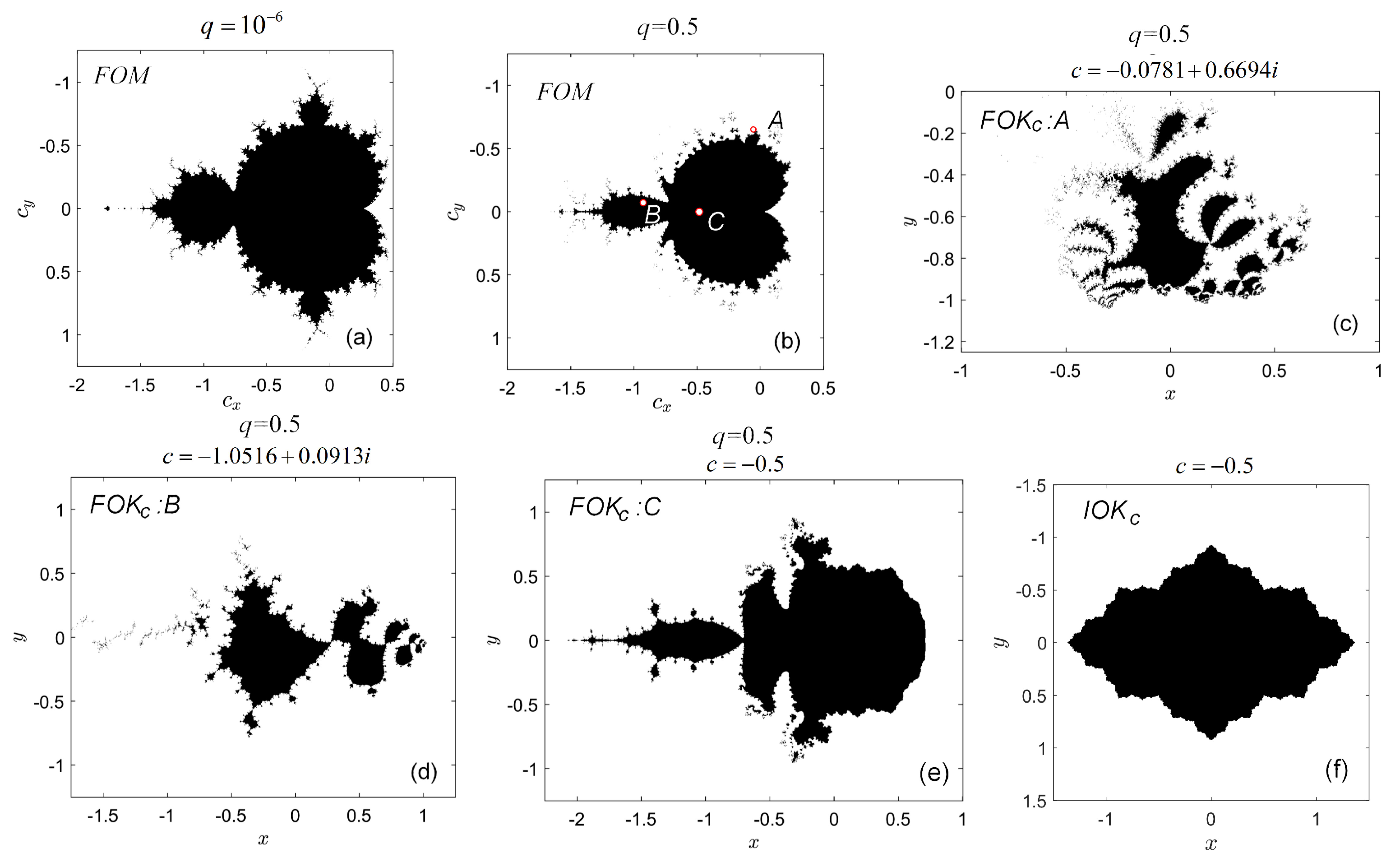
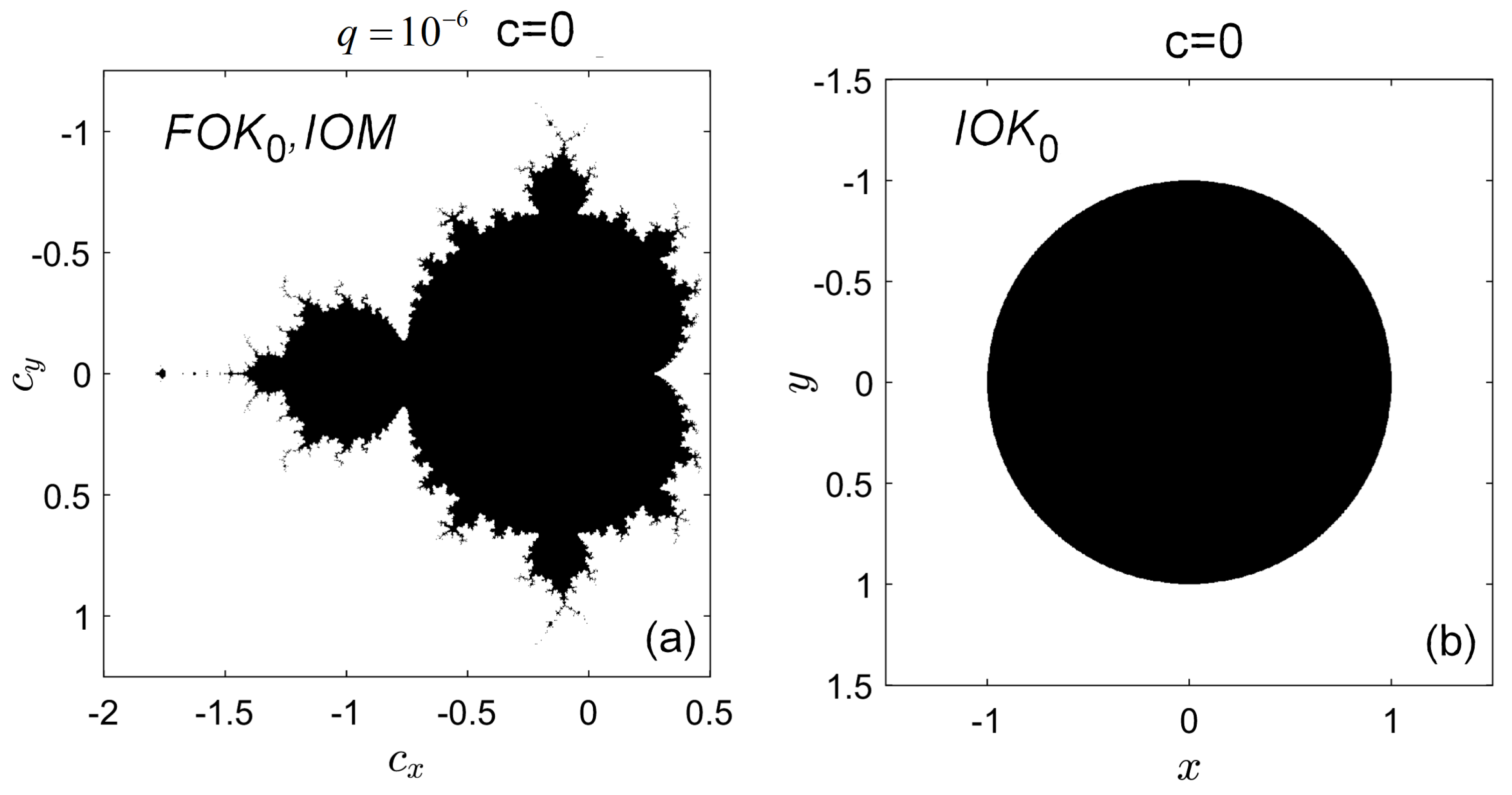
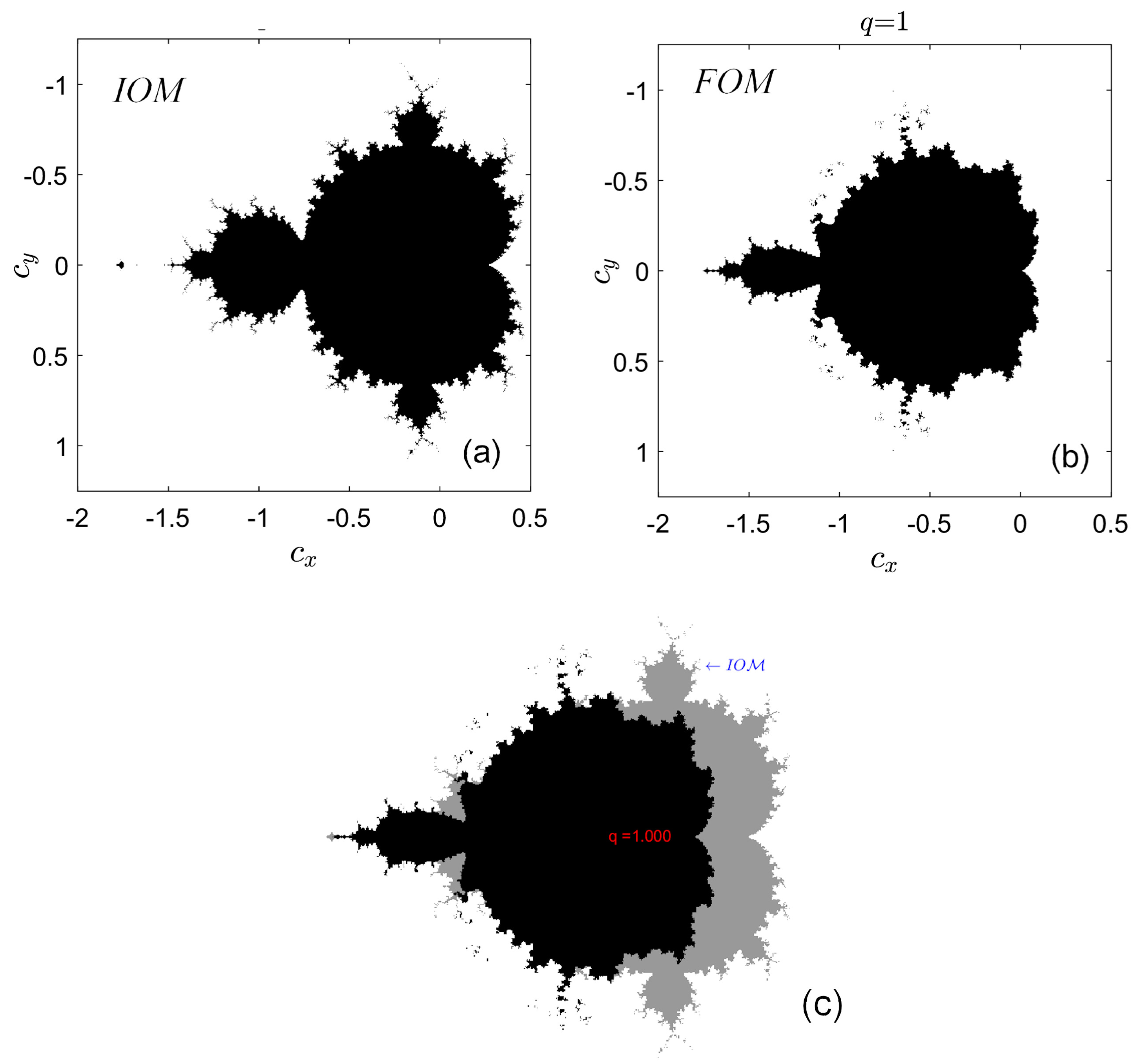
4. Properties of the Set
5. Equipotential Lines and External Rays
5.1. Basic Notions on Equipotential Lines and External Rays for and Sets
5.1.1. Approximations of Equipotential Lines and External Rays
- In [13], the potential is approximated by the value defined as follows: if , while is iterated, where M is, e.g., 10,000 [13], the potential can be approximated by ; otherwise, if remains smaller than M, the potential is set to 0. If, for a considered constant , is close or equal to , then c, or in the case of Julia sets, belongs to the equipotential line, and the point c, or , is plotted.An even simpler method is the level set method (LSM [13]), which, to a point c, or , within a complex lattice, attributes a color (e.g., black), depending on the number of iterations of for which remains bounded. Therefore, for each , one obtains a level set that is approximately identical to an equipotential line.
- On the other side, the external rays (9) can be approximated by the binary decomposition method (BDM [13]) with respect to the fixed angle . Thus, to a point c, or , within a complex lattice, one attributes a color (e.g., black or white) if the argument of , , belongs or does not belong to the intervals .
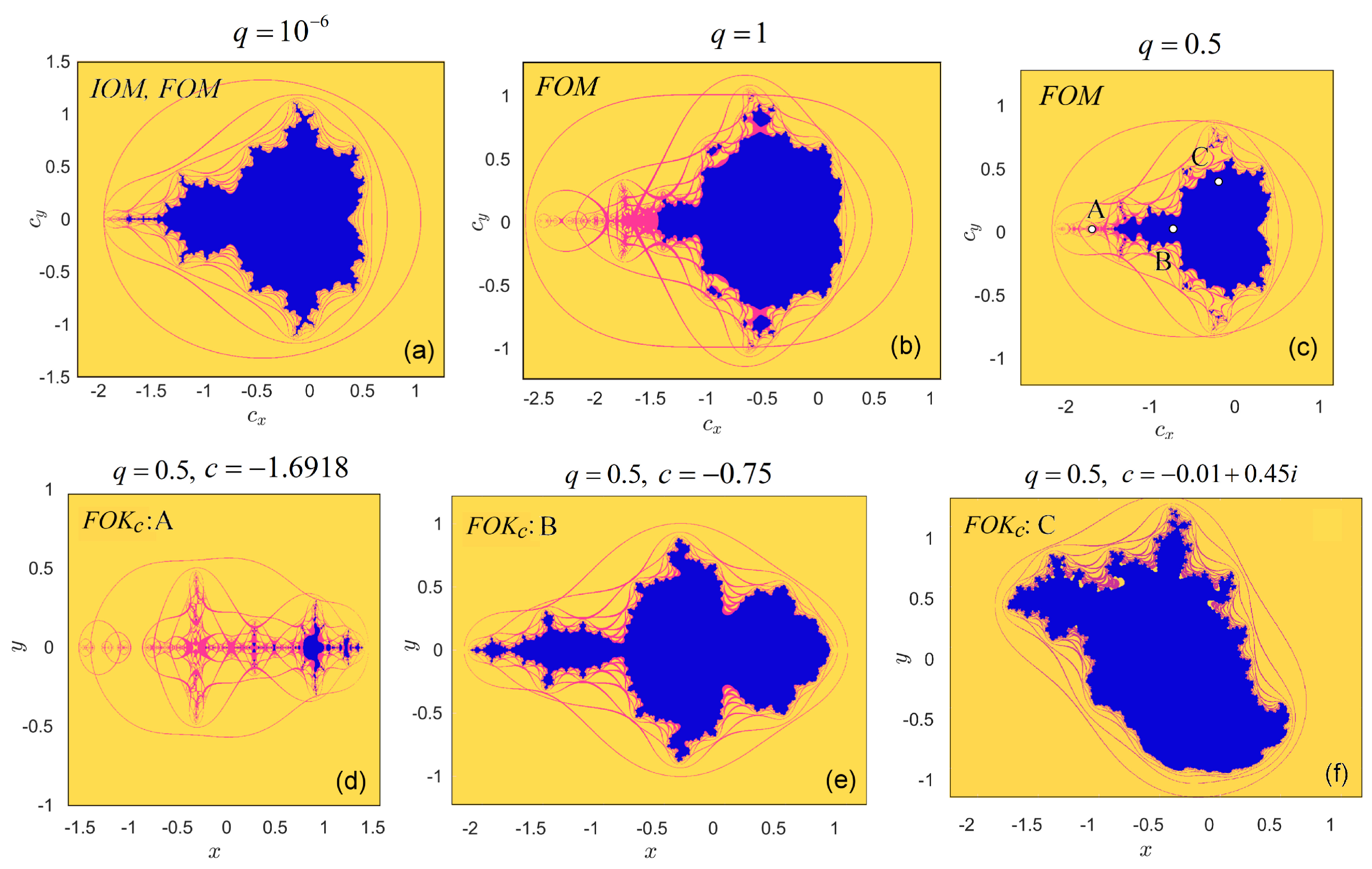
5.2. Equipotential Lines and External Rays of and Sets
6. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Danca, M.-F.; Fečkan, M. Mandelbrot set and Julia sets of fractional order, M. Nonlinear Dyn. 2023, 111, 9555–9570. [Google Scholar] [CrossRef]
- Elsadany, A.A.; Aldurayhim, A.; Agiza, H.N.; Elsonbaty, A. On the Fractional-Order Complex Cosine Map: Fractal Analysis, Julia Set Control and Synchronization. Mathematics 2023, 11, 727. [Google Scholar] [CrossRef]
- Fečkan, M.; Danca, M.-F. Non-Periodicity of Complex Caputo Like Fractional Differences. Fractal Fract. 2023, 7, 68. [Google Scholar] [CrossRef]
- Danca, M.-F. On the Stability Domain of a Class of Linear Systems of Fractional Order. Fractal Fract. 2023, 7, 49. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Wang, D.; Liu, S. A brief note on fractal dynamics of fractional Mandelbrot sets. Appl. Math. Comput. 2022, 432, 127353. [Google Scholar] [CrossRef]
- Brooks, R.; Matelski, P. Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference; The dynamics of 2-Generator Subgroups of PSL(2,C)Princeton University Press: Princeton, NJ, USA, 1981. [Google Scholar]
- Mandelbrot, B. Fractal Aspects of the Iteration of z↦z(1 − z) for Complex λ,z. Ann. New York Acad. Sci. 1980, 357, 249–259. [Google Scholar] [CrossRef]
- Li, J.; Pelliciari, J.; Mazzoli, C. Scale-invariant magnetic textures in the strongly correlated oxide NdNiO3. Nat. Commun. 2019, 10, 4568. [Google Scholar] [CrossRef]
- Gaston, J. Mémoire sur l’itération des fonctions rationnelles. J. Math. Pures Appl. 1918, 1, 47–245. (In French) [Google Scholar]
- Patou, P. Sur les substitutions rationnelles. Comptes Rendus Acad. Sci. Paris. 1917, 164, 806–808. [Google Scholar]
- Peitgen, H.-O.; Peter, H.R. The Beauty of Fractals Images of Complex Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Branner, B. The Mandelbrot Set. Devaney, R.L., Keen, L., Eds.; In Chaos and Fractals: The Mathematics Behind the Computer Graphics (Proceedings of Symposia in Applied Mathematics, 39); American Mathematical Society: Providence, RI, USA, 1989; Volume 39, pp. 75–105. [Google Scholar]
- Barnsley, M.F.; Devaney, R.L.; Mandelbrot, B.B.; Peitgen, H.O.; Saupe, D.; Voss, R.F. With Contributions by Yuval Fisher Michael McGuire: The Science of Fractal Image; Springer: New York, NY, USA, 1988. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; W. H. Freeman: New York, NY, USA, 1983. [Google Scholar]
- Douady, A.; Hubbard, J.H. Etude Dynamique des Polynômes Complexes. Prépublications mathémathiques d’Orsay; Université de Paris-Sud: Paris, France, 1984. [Google Scholar]
- Kahn, J. The Mandelbrot Set is Connected: A Topological Proof. 2001. Available online: http://www.math.brown.edu/~kahn/mconn.pdf (accessed on 14 January 2024).
- Devaney, R. The Mandelbrot Set and the Farey Tree, and the Fibonacci Sequence. Amer. Math. Mon. 1999, 106, 289–302. [Google Scholar] [CrossRef]
- Magin, R.L.; Ovadia, M. Modeling the cardiac tissue electrode interface using fractional calculus. Vibr. Control. 2008, 14, 1431–1442. [Google Scholar] [CrossRef]
- Heymans, N. Dynamic measurements in long-memory materials: Fractional calculus evaluation of approach to steady state. J. Vibr. Control. 2008, 14, 1587–1596. [Google Scholar] [CrossRef]
- Lima, M.F.M.; Machado, J.A.T.; Crisóstomo, M. Experimental signal analysis of robot impacts in a fractional calculus perspective. J. Adv. Comput. Intell. Intell. Informatics 2007, 11, 1079–1085. [Google Scholar] [CrossRef]
- Debnath, L. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 54, 3413–3442. [Google Scholar] [CrossRef]
- Huang, L.; Park, J.H.; Wu, G.C.; Mo, Z.W. Variable-order fractional discrete-time recurrent neural networks. J. Comput. App. Math. 2020, 370, 112633. [Google Scholar] [CrossRef]
- Wu, G.C. Baleanu; D. Lin, Z.X. Image encryption technique based on fractional chaotic time series. J. Vibr. Contr. 2016, 22, 2092–2099. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Banerjee, S.; Wu, G.C. Discrete tempered fractional calculus for new chaotic systems with short memory and image encryption. Optik 2020, 203, 163698. [Google Scholar] [CrossRef]
- Huang, C.; Wang, J.; Chen, X.; Cao, J. Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw. 2021, 141, 344–354. [Google Scholar] [CrossRef]
- Diaz, J.B.; Olser, T.J. Differences of Fractional Order. Math. Comput. 1974, 28, 185–202. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo Fractional Differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Fečkan, M.; Pospíšil, M.; Danca, M.-F.; Wang, J. Caputo Delta Weakly Fractional Difference Equations. Fract. Calc. Appl. Anal. 2022, 25, 2222–2240. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. Initial Value Problems in Discrete Fractional Calculus. Proc. Amer. Math. 2009, 137, 981–989. [Google Scholar] [CrossRef]
- Cermak, J.; Gyori, I.; Nechvatal, L. On Explicit Stability Conditions for a Linear Fractional Difference System. Fract. Calc. Appl. Anal. 2015, 18, 651–672. [Google Scholar] [CrossRef]
- Chen, F.L. A review of Existence and Stability Results for Discrete Fractional Equations. J. Comput. Complex Appl. 2015, 1, 22–53. [Google Scholar]
- Danca, M.-F. Fractional order logistic map: Numerical approach. Chaos, Solitons Fract. 2022, 157, 111851. [Google Scholar] [CrossRef]
- Diblík, J.; Fečkan, M.; Pospíšil, M. Nonexistence of Periodic Solutions and S-Asymptotically Periodic Solutions in Fractional Difference Equations. Appl. Math. Comp. 2015, 257, 230–240. [Google Scholar] [CrossRef]
- Mandelbrot Set. Available online: https://www.math.univ-toulouse.fr/~cheritat/wiki-draw/index.php/Mandelbrot_set (accessed on 12 January 2024).
- Milnor, J. Dynamics in One Complex Variable, 3rd ed.; Princeton University Press: Princeton, NJ, USA, 2006; AM-160. [Google Scholar]
- Anastassiou, G. Principles of Delta Fractional Calculus on Time Scales and Inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Bohner, M. Basic Calculus on Time Scales and Some of its Applications. Results Math. 1999, 35, 3–22. [Google Scholar] [CrossRef]
- FO_mandelbrot. Available online: https://www.mathworks.com/matlabcentral/fileexchange/121632-fo_mandelbrot (accessed on 1 January 2024).
- Danca, M.-F.; Kuznetsov, N. D3 Dihedral Logistic Map of Fractional Order. Mathematics 2022, 10, 213. [Google Scholar] [CrossRef]
- Douady, A.; Hubbard, J.H. Itération des Polynômes Quadratiques Complexes; Académie des Sciences: Paris, France, 1982; Volume 294, pp. 123–126, Comptes Rendus des Séances de l’Académie des Sciences: Série I. Mathématique; (accessed on 12 January 2024). [Google Scholar]
- Douady, A. Algorithms for computing angles in the Mandelbrot set. Barnsley, M., Demko, S.G., Eds.; In Chaotic Dynamics and Fractals; Academic Press: New York, NY, USA, 1986; Volume 2, pp. 155–168. [Google Scholar]
- Pastor, G.; Romera, M.; Álvarez, G.; Montoya, F. Operating with external arguments in the Mandelbrot set antenna. Physica D 2002, 171, 52–71. [Google Scholar] [CrossRef]
- Romera, M.; Pastor, G.; Orue, A.B.; Martin, A.; Danca, M.-F.; Montoya, F. A Method to Solve the Limitations in Drawing External Rays of the Mandelbrot Set. Math. Probl. Eng. 2013, 2013, 105283. [Google Scholar] [CrossRef]
- Carleson, L.; Gamelin, T.W. Complex Dynamics; Springer: New York, NY, USA, 1993; p. 139. [Google Scholar]
- Jung, W. Mandel: Software for Real and Complex Dynamics. 2012. Available online: http://www.mndynamics.com/indexp.html (accessed on 12 January 2024).
- De Jong, T.G. Dynamics of Chaotic Systems and Fractals. Bachelor’s Thesis, University of Groningen, Groningen, The Netherlands, 2009. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danca, M.-F. Mandelbrot Set as a Particular Julia Set of Fractional Order, Equipotential Lines and External Rays of Mandelbrot and Julia Sets of Fractional Order. Fractal Fract. 2024, 8, 69. https://doi.org/10.3390/fractalfract8010069
Danca M-F. Mandelbrot Set as a Particular Julia Set of Fractional Order, Equipotential Lines and External Rays of Mandelbrot and Julia Sets of Fractional Order. Fractal and Fractional. 2024; 8(1):69. https://doi.org/10.3390/fractalfract8010069
Chicago/Turabian StyleDanca, Marius-F. 2024. "Mandelbrot Set as a Particular Julia Set of Fractional Order, Equipotential Lines and External Rays of Mandelbrot and Julia Sets of Fractional Order" Fractal and Fractional 8, no. 1: 69. https://doi.org/10.3390/fractalfract8010069
APA StyleDanca, M.-F. (2024). Mandelbrot Set as a Particular Julia Set of Fractional Order, Equipotential Lines and External Rays of Mandelbrot and Julia Sets of Fractional Order. Fractal and Fractional, 8(1), 69. https://doi.org/10.3390/fractalfract8010069





