Fractional-Order Total Variation Geiger-Mode Avalanche Photodiode Lidar Range-Image Denoising Algorithm Based on Spatial Kernel Function and Range Kernel Function
Abstract
:1. Introduction
2. Algorithm Principle
2.1. Range-Image Extraction
2.2. Definition of Fractional Differential Operator and Its Effect on Image Signals
2.3. FOTV Denoising Model
2.4. Solution to the FOTV Denoising Model
| Algorithm 1 Range-Image Denoising Algorithm Based on G-L Fractional-Order Total Variation |
| 1. Initialize the system: , , , |
| 2. The value of the given parameter: 3. Calculation |
| 4. For If Else To step 4 End End |
2.5. Fractional-Order Total Variational Range-Image Denoising Algorithm Based on Spatial Kernel Function and Range Kernel Function
| Algorithm 2 FOTV Based on Spatial Kernel Function and Range Kernel Function |
| 1. Median filtering: |
| 2. Initialization: , , |
| 3. The value of the given parameter: 4. Calculation |
| 5. For If Else To step 5 End End |
3. Evaluation Index and Simulation Verification
3.1. Evaluation Index
3.2. Simulation Analysis
3.2.1. Fractional-Order Selection
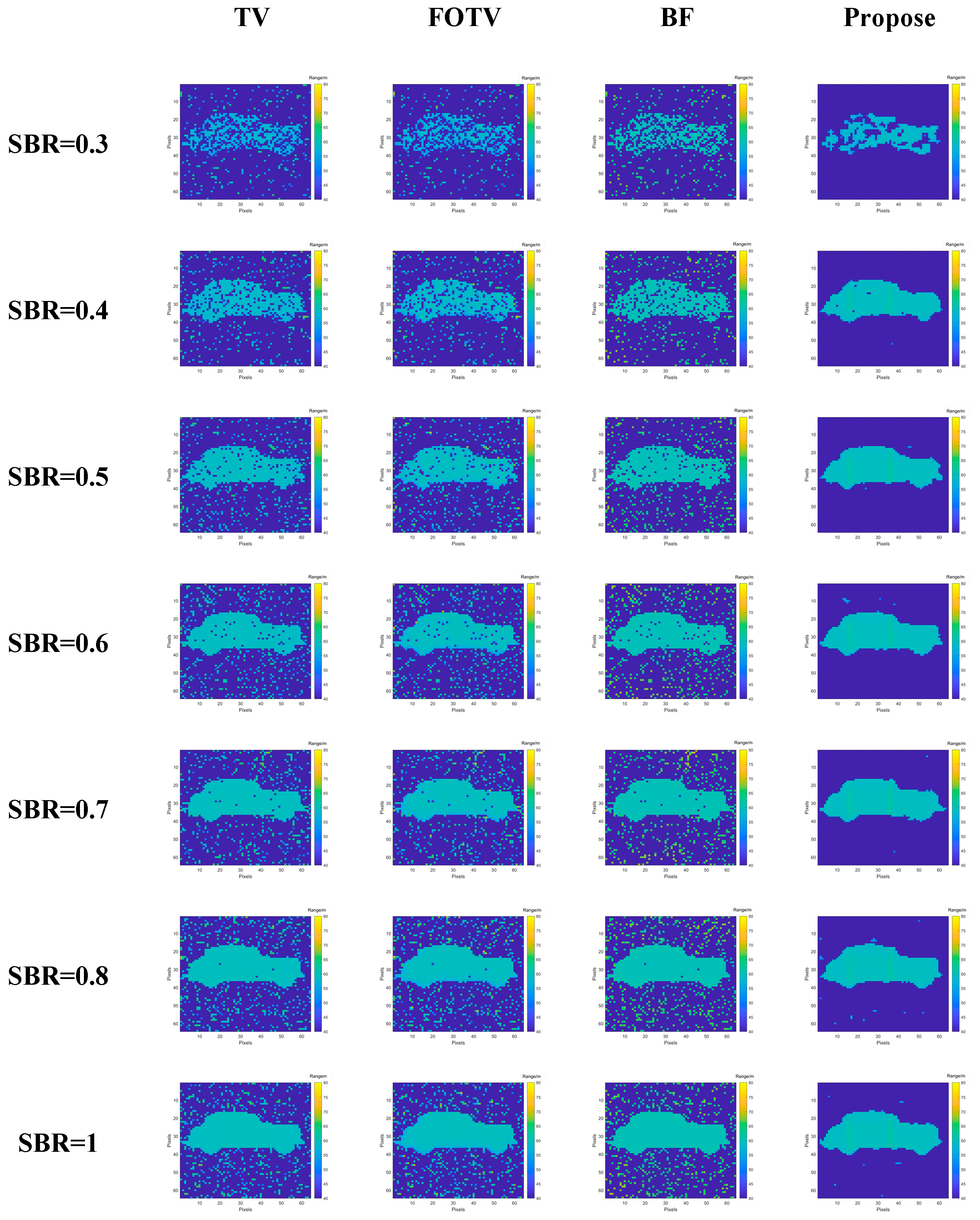
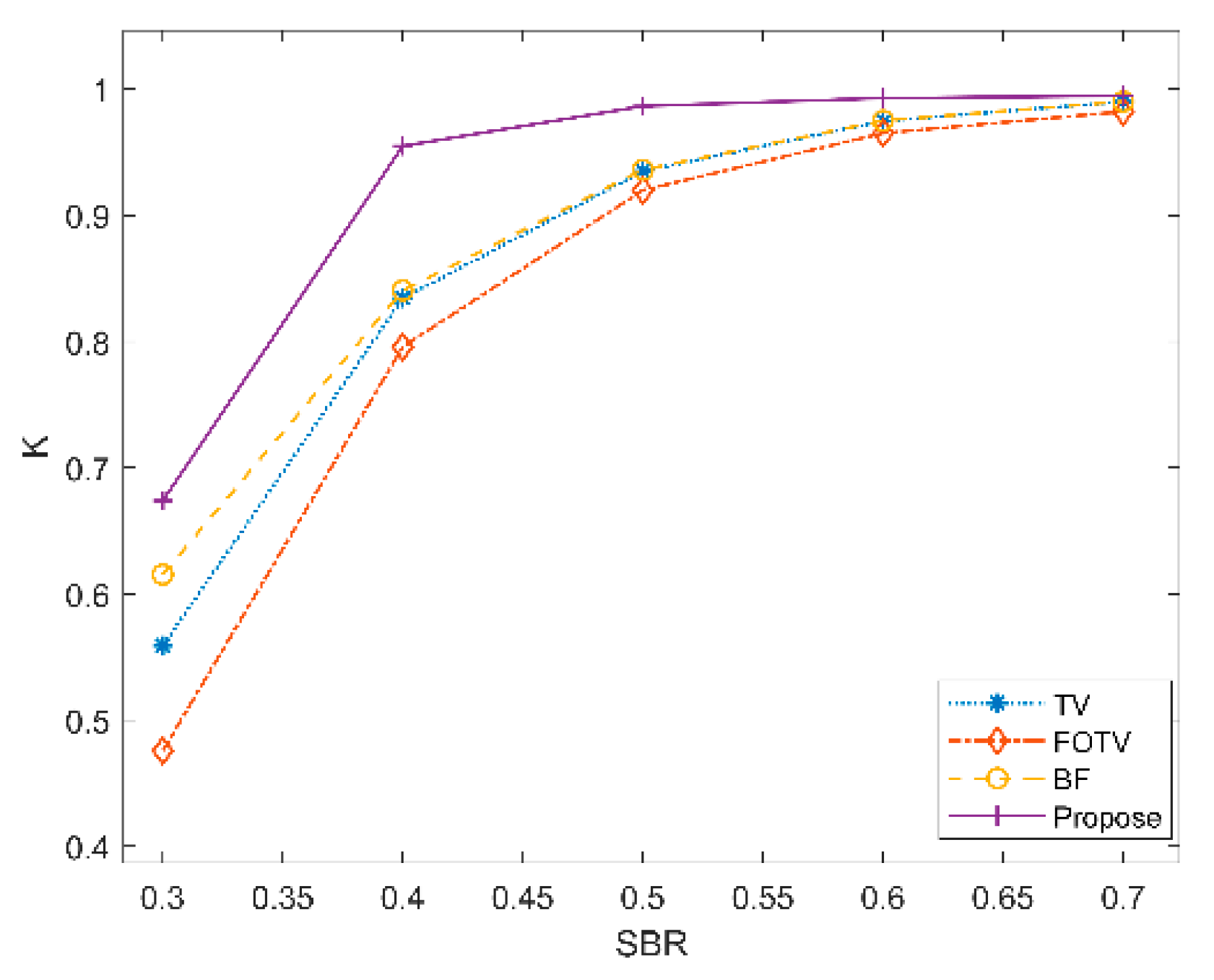
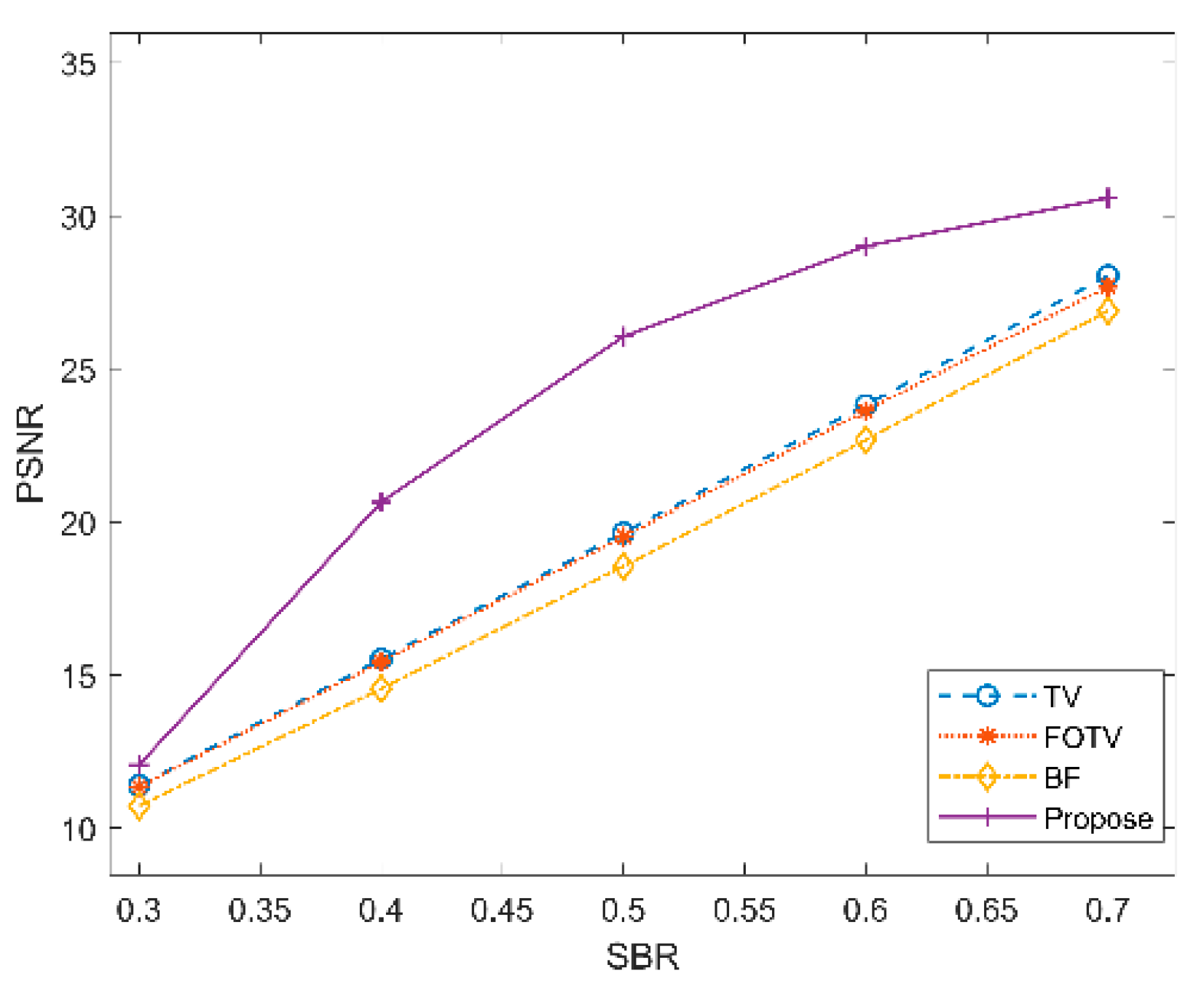
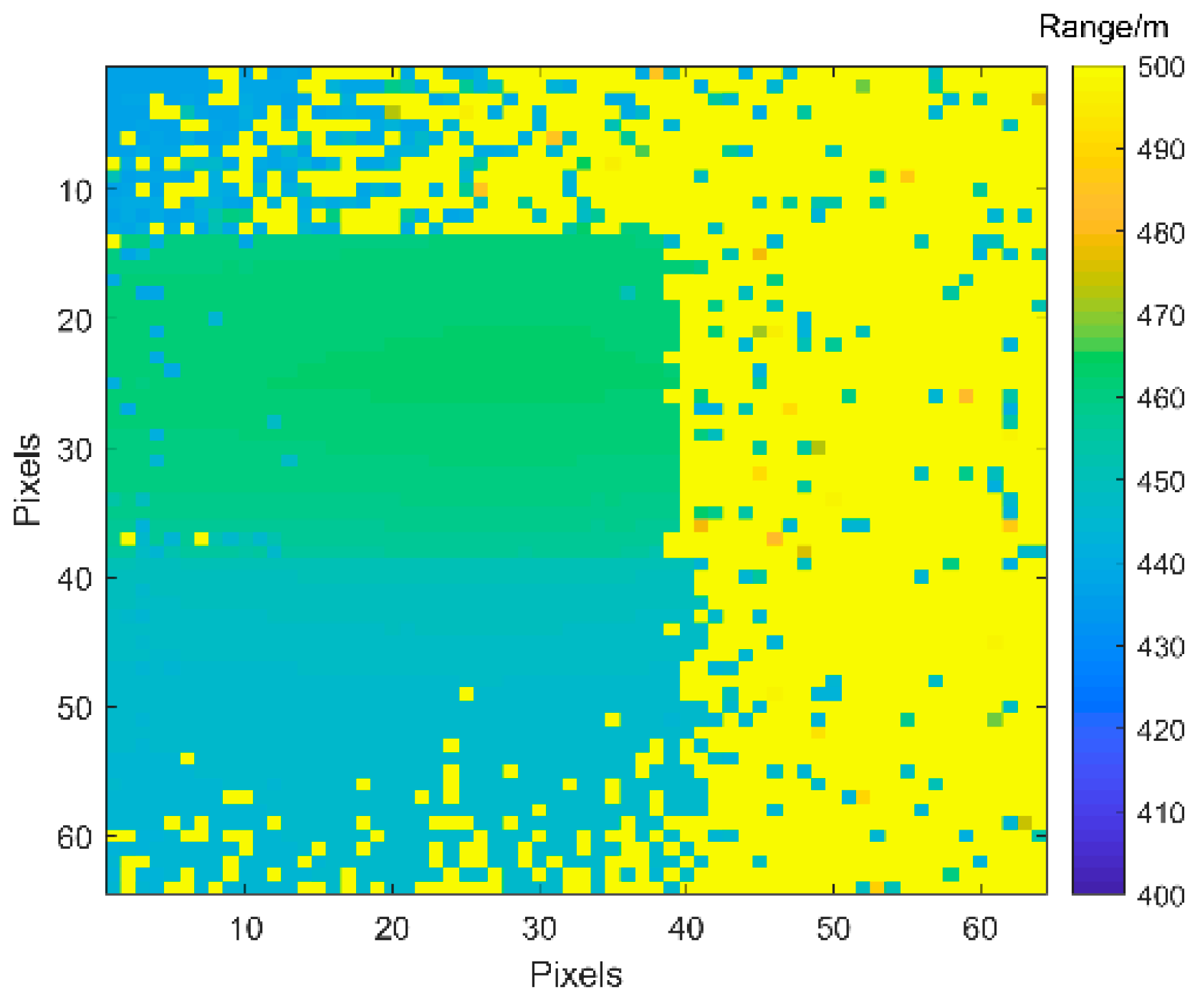
3.2.2. Simulation Analysis of Range Images with Different SBRs under 20 Frames
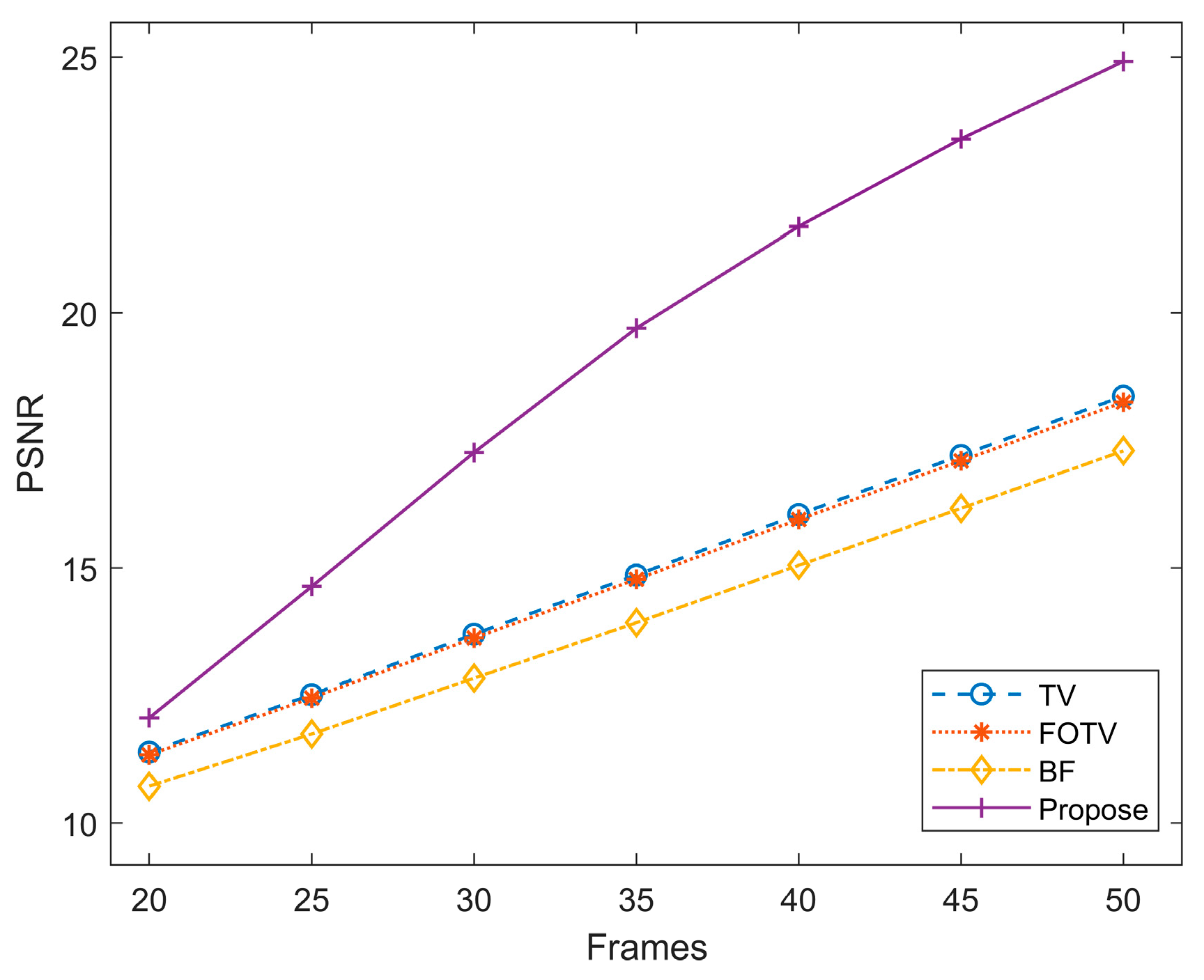
3.2.3. Simulation Analysis of Range Image with Different Frame Numbers When SBR Is 0.5
4. Experimental Verification
4.1. Experimental System Construction
4.2. Experimental Data Processing and Analysis
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, X.; Lu, W.; Sun, J.; Ge, W.; Zhang, H.; Li, S. Suppressing the influence of GM-APD coherent lidar saturation by signal modulation. Optik 2023, 275, 170619. [Google Scholar] [CrossRef]
- Liu, D.; Sun, J.; Lu, W.; Li, S.; Zhou, X. 3D reconstruction of the dynamic scene with high-speed targets for GM-APD LiDAR. Opt. Laser Technol. 2023, 161, 109114. [Google Scholar] [CrossRef]
- Wang, M.; Sun, J.; Li, S.; Lu, W.; Zhou, X.; Zhang, H. Research on infrared image guided GM-APD range image recovery algorithm under limited detections. Opt. Lasers Eng. 2023, 166, 107579. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, Z.; Cen, L.; Li, J.; Xie, J.; Zhao, Y. Prediction of the Number of Cumulative Pulses Based on the Photon Statistical Entropy Evaluation in Photon-Counting LiDAR. Entropy 2023, 25, 522. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Sun, J.; Zhang, X.; Zhou, X.; He, R.; Zhang, H. Three-dimensional imaging of ships in the foggy environment using a single-photon detector array. Optik 2023, 272, 170310. [Google Scholar] [CrossRef]
- Ding, Y.; Qu, Y.; Sun, J.; Du, D.; Jiang, Y.; Zhang, H. Long-distance multi-vehicle detection at night based on Gm-APD lidar. Remote Sens. 2022, 14, 3553. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Sun, J.; Liu, D.; Zhang, X.; Yang, X.; Zhou, X. Dual-parameter estimation algorithm for Gm-APD lidar depth imaging through smoke. Measurement 2022, 196, 111269. [Google Scholar] [CrossRef]
- Liu, D.; Sun, J.; Gao, S.; Ma, L.; Jiang, P.; Guo, S.; Zhou, X. Single-parameter estimation construction algorithm for Gm-APD lidar imaging through fog. Opt. Commun. 2021, 482, 126558. [Google Scholar] [CrossRef]
- Jiang, Y. Adaptive Suppression Method of LiDAR Background Noise Based on Threshold Detection. Appl. Sci. 2023, 13, 3772. [Google Scholar] [CrossRef]
- Green, T.J., Jr.; Shapiro, J.H. Detecting objects in three-dimensional laser radar range images. Opt. Eng. 1994, 33, 865–874. [Google Scholar] [CrossRef]
- Saban, I.; Faibish, S. Image processing techniques for laser images. In Proceedings of the 1996 Canadian Conference on Electrical and Computer Engineering, Calgary, AB, Canada, 26–29 May 1996; Volume 1, pp. 462–465. [Google Scholar] [CrossRef]
- Yu, J.; Yang, S.; Zhu, B. Noise suppression and the method evaluation for ladar range images. J. Optoelectron. Laser 2015, 26, 1215–1221. [Google Scholar] [CrossRef]
- Wang, M.; Sun, J.; Li, S.; Lu, W.; Zhou, X.; Zhang, H. A photon-number-based systematic algorithm for range image recovery of GM-APD lidar under few-frames detection. Infrared Phys. Technol. 2022, 125, 104267. [Google Scholar] [CrossRef]
- Xia, Z.W.; Li, Q.; Xiong, Z.P.; Wang, Q. Ladar range image denoising by a nonlocal probability statistics algorithm. Opt. Eng. 2013, 52, 017003. [Google Scholar] [CrossRef]
- Halimi, A.; Altmann, Y.; McCarthy, A.; Ren, X.; Tobin, R.; Buller, G.S.; McLaughlin, S. Restoration of intensity and depth images constructed using sparse single-photon data. In Proceedings of the 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; pp. 86–90. [Google Scholar] [CrossRef]
- Chen, S.; Halimi, A.; Ren, X.; McCarthy, A.; Su, X.; McLaughlin, S.; Buller, G.S. Learning Non-Local Spatial Correlations To Restore Sparse 3D Single-Photon Data. IEEE Trans. Image Process. 2020, 29, 3119–3131. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Lu, Y.; Li, H.; Mao, T.; Guan, Y.; Zhang, L.; He, W.; Wu, P.; Chen, Q. Intensity-guided depth image estimation in long-range lidar. Opt. Lasers Eng. 2022, 155, 107054. [Google Scholar] [CrossRef]
- Li, C.; He, C. Fractional-order diffusion coupled with integer-order diffusion for multiplicative noise removal. Comput. Math. Appl. 2023, 136, 34–43. [Google Scholar] [CrossRef]
- Huang, T.; Wang, C.; Liu, X. Depth Image Denoising Algorithm Based on Fractional Calculus. Electronics 2022, 11, 1910. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Xie, D.; Wei, X.; Huang, T.; Liu, X. A spatially correlated fractional integral-based method for denoising geiger-mode avalanche photodiode light detection and ranging depth images. Optik 2023, 288, 171244. [Google Scholar] [CrossRef]
- Xie, D.; Wang, X.; Wang, C.; Yuan, K.; Wei, X.; Liu, X.; Huang, T. A Fractional-Order Total Variation Regularization-Based Method for Recovering Geiger-Mode Avalanche Photodiode Light Detection and Ranging Depth Images. Fractal Fract. 2023, 7, 445. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, Y.; Zhang, Y.; Sun, X. Range accuracy limitation of pulse ranging systems based on Geiger mode single-photon detectors. Appl. Opt. 2010, 49, 5561–5566. [Google Scholar] [CrossRef]
- Chen, D.; Chen, Y.; Xue, D. Fractional-order total variation image denoising based on proximity algorithm. Appl. Math. Comput. 2015, 257, 537–545. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Y.; Guo, Z.; Wu, B.; Zhang, D. Multiplicative Noise Removal and Contrast Enhancement for SAR Images Based on a Total Fractional-Order Variation Model. Fractal Fract. 2023, 7, 329. [Google Scholar] [CrossRef]
- Parvaz, R. Image restoration with impulse noise based on fractional-order total variation and framelet transform. SIViP 2023, 17, 2455–2463. [Google Scholar] [CrossRef]
- Tom, G.; Stanley, O. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Micchelli, C.; Shen, L.; Xu, Y. Proximity algorithms for image models: Denoising. Inverse Probl. 2011, 27, 045009. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Q.; Ning, J. A region fusion based split Bregman method for TV denoising algorithm. Multimed. Tools Appl. 2021, 80, 15875–15900. [Google Scholar] [CrossRef]
- Cheng, S.W.; Lin, Y.T.; Peng, Y.T. A Fast Two-Stage Bilateral Filter Using Constant Time O(1) Histogram Generation. Sensors 2022, 22, 926. [Google Scholar] [CrossRef]
- Ma, L.; Sun, J.; Jiang, P.; Liu, D.; Zhou, X.; Wang, Q. Signal extraction algorithm of Gm-APD lidar with low SNR return. Optik 2020, 206, 164340. [Google Scholar] [CrossRef]
- Berginc, G.; Jouffroy, M. Simulation of 3D laser imaging. PIERS Online 2010, 6, 415–419. [Google Scholar] [CrossRef]






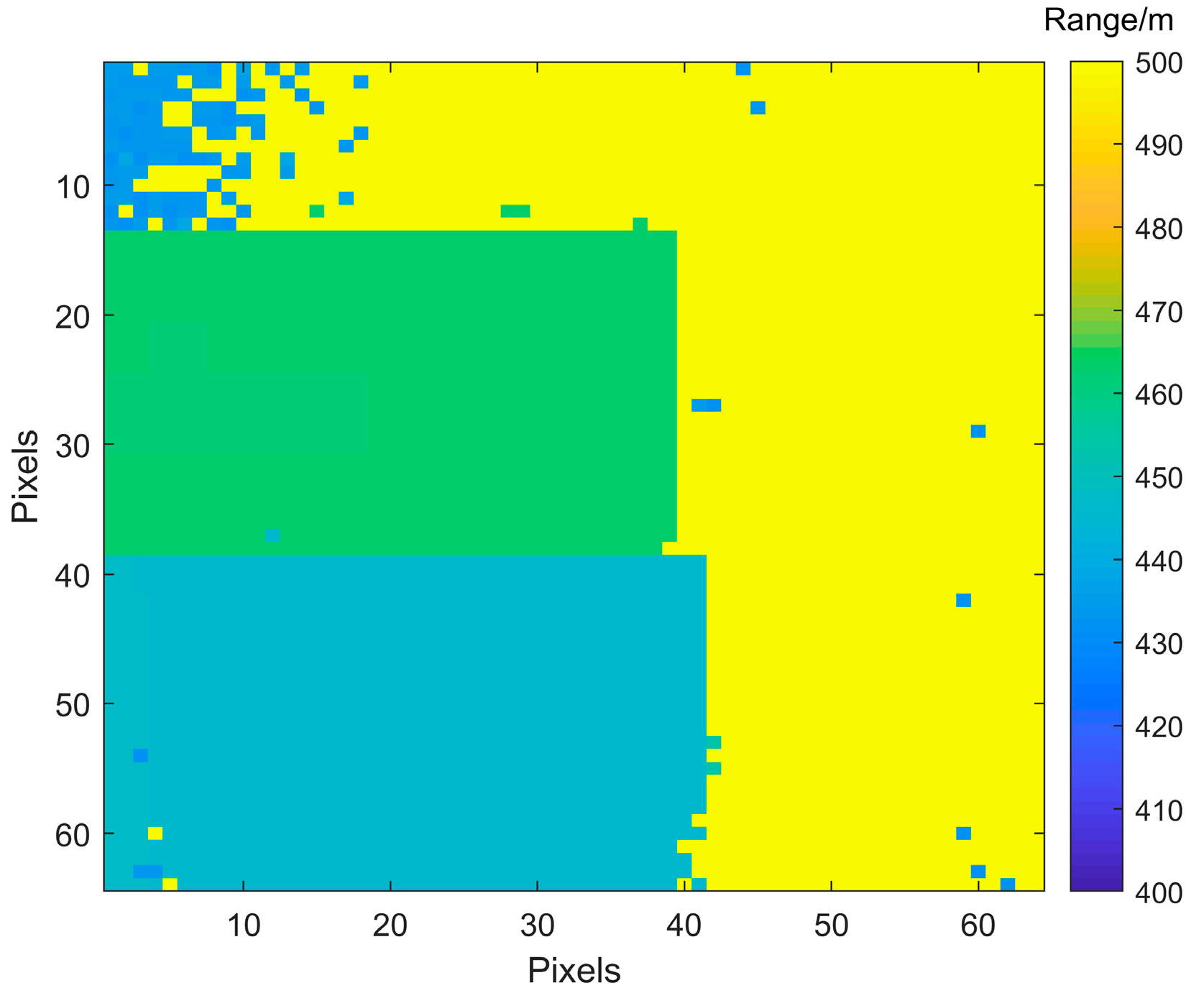
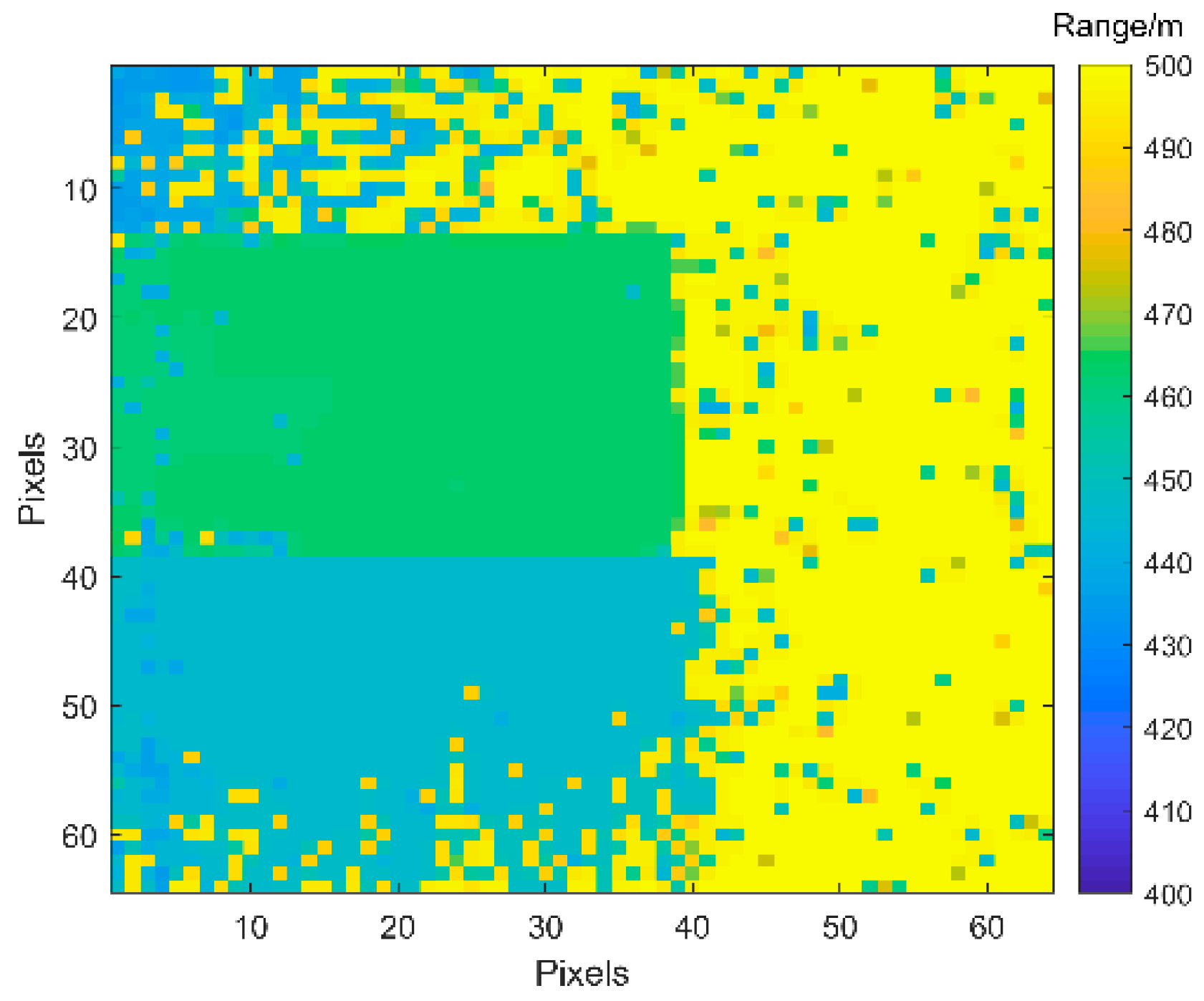
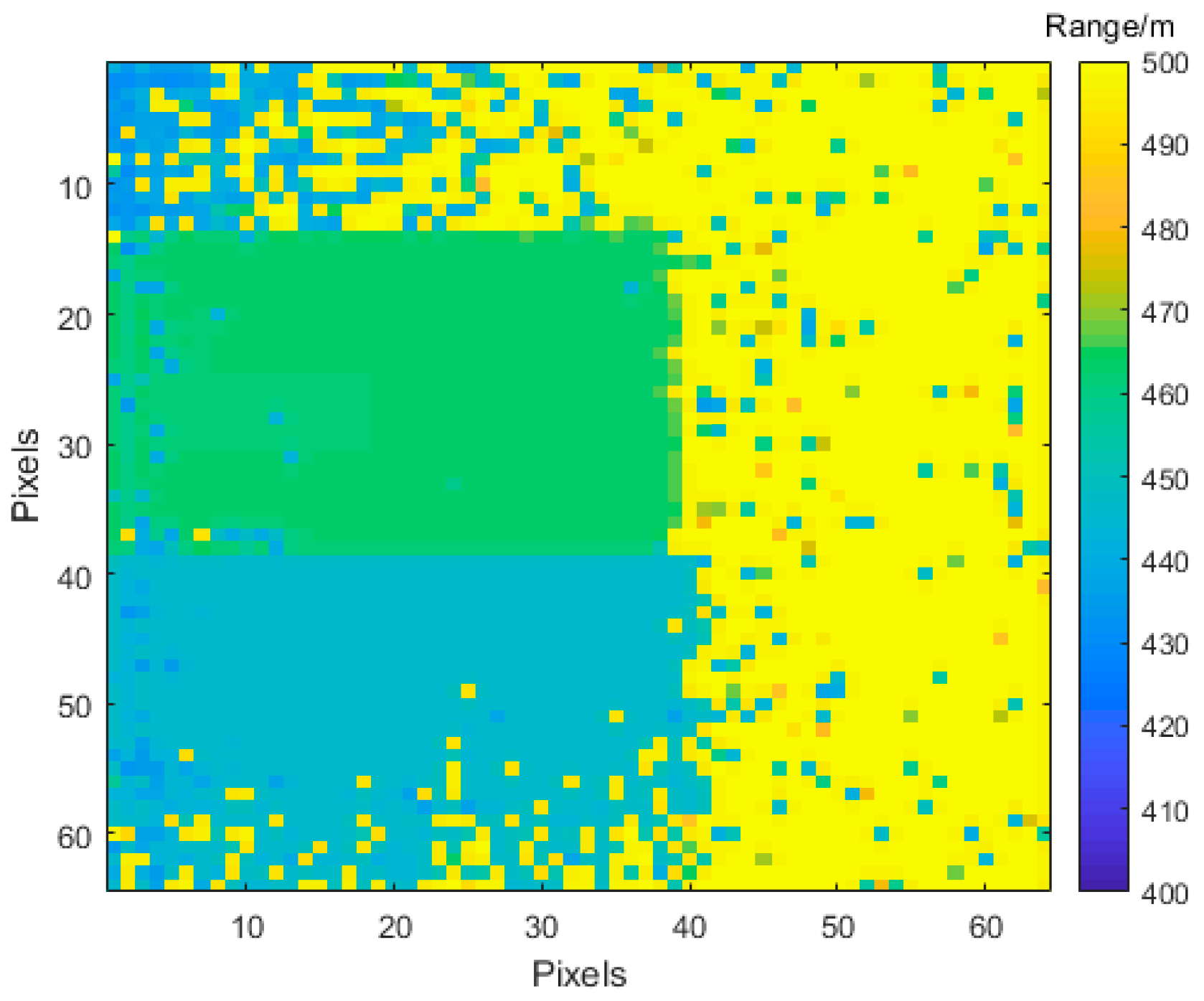

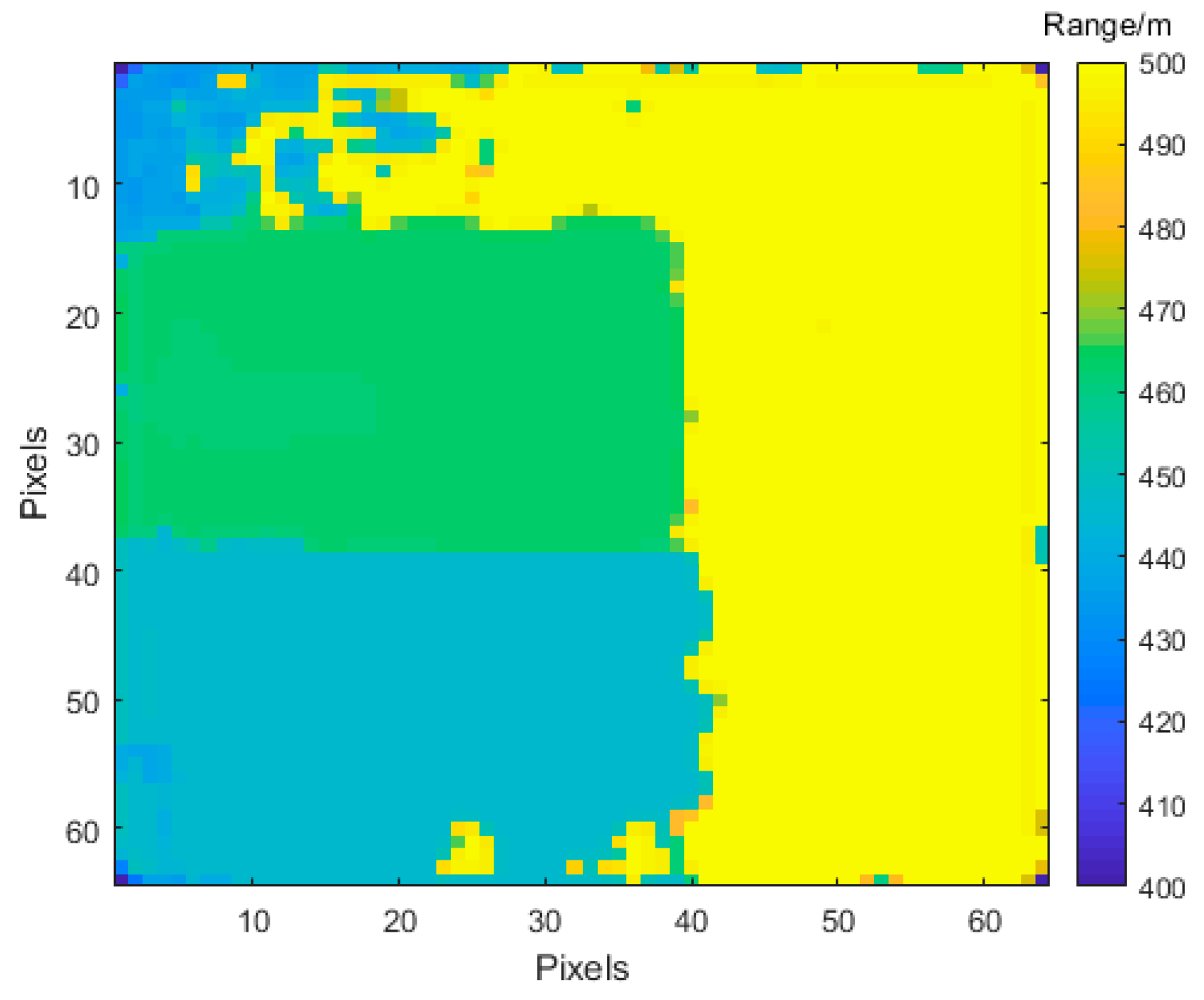
| Order | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 | 1 | 1.2 | 1.5 | 1.8 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|
| K | 0.6379 | 0.6592 | 0.6607 | 0.6738 | 0.6666 | 0.6700 | 0.6549 | 0.6527 | 0.6431 | 0.6388 |
| PSNR | 11.7418 | 11.9555 | 11.9501 | 12.063 | 11.9396 | 11.9394 | 11.4947 | 11.5250 | 11.5547 | 11.5779 |
| SBRS | TV | FOTV | BF | Proposed | ||||
|---|---|---|---|---|---|---|---|---|
| SBR = 0.3 | K | 0.5589 | K | 0.4757 | K | 0.6154 | K | 0.6738 |
| PSNR | 11.3933 | PSNR | 11.3409 | PSNR | 10.7250 | PSNR | 12.0630 | |
| SBR = 0.4 | K | 0.8342 | K | 0.7958 | K | 0.8405 | K | 0.9549 |
| PSNR | 15.5224 | PSNR | 15.4328 | PSNR | 14.5584 | PSNR | 20.6488 | |
| SBR = 0.5 | K | 0.9350 | K | 0.9199 | K | 0.9361 | K | 0.9865 |
| PSNR | 19.6460 | PSNR | 19.5210 | PSNR | 18.5497 | PSNR | 26.0541 | |
| SBR = 0.6 | K | 0.9747 | K | 0.9651 | K | 0.9750 | K | 0.9929 |
| PSNR | 23.8157 | PSNR | 23.6289 | PSNR | 22.6735 | PSNR | 29.0068 | |
| SBR = 0.7 | K | 0.9900 | K | 0.9822 | K | 0.9902 | K | 0.9947 |
| PSNR | 28.0463 | PSNR | 27.6851 | PSNR | 26.8942 | PSNR | 30.5839 | |
| Frames | TV | FOTV | BF | Proposed | ||||
|---|---|---|---|---|---|---|---|---|
| 20 | K | 0.5589 | K | 0.4757 | K | 0.6154 | K | 0.6738 |
| PSNR | 11.3933 | PSNR | 11.3409 | PSNR | 10.7250 | PSNR | 12.0630 | |
| 25 | K | 0.6648 | K | 0.5867 | K | 0.6958 | K | 0.8198 |
| PSNR | 12.5166 | PSNR | 12.4527 | PSNR | 11.7458 | PSNR | 14.6361 | |
| 30 | K | 0.7469 | K | 0.6841 | K | 0.7634 | K | 0.9018 |
| PSNR | 13.7025 | PSNR | 13.6282 | PSNR | 12.8409 | PSNR | 17.2648 | |
| 35 | K | 0.8067 | K | 0.7586 | K | 0.8157 | K | 0.9439 |
| PSNR | 14.8628 | PSNR | 14.7775 | PSNR | 13.9279 | PSNR | 19.6990 | |
| 40 | K | 0.8525 | K | 0.8179 | K | 0.8576 | K | 0.9645 |
| PSNR | 16.0490 | PSNR | 15.9514 | PSNR | 15.0531 | PSNR | 21.6841 | |
| 45 | K | 0.8864 | K | 0.8600 | K | 0.8897 | K | 0.9760 |
| PSNR | 17.2072 | PSNR | 17.1003 | PSNR | 16.1692 | PSNR | 23.3974 | |
| 50 | K | 0.9126 | K | 0.8921 | K | 0.9148 | K | 0.9827 |
| PSNR | 18.3680 | PSNR | 18.2520 | PSNR | 17.2977 | PSNR | 24.9162 | |
| Evaluation Metric | TV Denoising | FOTV Denoising | BF Denoising | Proposed |
|---|---|---|---|---|
| K | 0.8270 | 0.7828 | 0.8885 | 0.9283 |
| PSNR | 4.6869 | 4.6866 | 4.6871 | 4.6969 |
| Evaluation Metric | [21] | Proposed |
|---|---|---|
| K | 0.8965 | 0.9283 |
| PSNR | 4.4421 | 4.6969 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Wang, C.; Xie, D.; Yuan, K.; Liu, X.; Wang, Z.; Wang, X.; Huang, T. Fractional-Order Total Variation Geiger-Mode Avalanche Photodiode Lidar Range-Image Denoising Algorithm Based on Spatial Kernel Function and Range Kernel Function. Fractal Fract. 2023, 7, 674. https://doi.org/10.3390/fractalfract7090674
Wei X, Wang C, Xie D, Yuan K, Liu X, Wang Z, Wang X, Huang T. Fractional-Order Total Variation Geiger-Mode Avalanche Photodiode Lidar Range-Image Denoising Algorithm Based on Spatial Kernel Function and Range Kernel Function. Fractal and Fractional. 2023; 7(9):674. https://doi.org/10.3390/fractalfract7090674
Chicago/Turabian StyleWei, Xuyang, Chunyang Wang, Da Xie, Kai Yuan, Xuelian Liu, Zihao Wang, Xinjian Wang, and Tingsheng Huang. 2023. "Fractional-Order Total Variation Geiger-Mode Avalanche Photodiode Lidar Range-Image Denoising Algorithm Based on Spatial Kernel Function and Range Kernel Function" Fractal and Fractional 7, no. 9: 674. https://doi.org/10.3390/fractalfract7090674
APA StyleWei, X., Wang, C., Xie, D., Yuan, K., Liu, X., Wang, Z., Wang, X., & Huang, T. (2023). Fractional-Order Total Variation Geiger-Mode Avalanche Photodiode Lidar Range-Image Denoising Algorithm Based on Spatial Kernel Function and Range Kernel Function. Fractal and Fractional, 7(9), 674. https://doi.org/10.3390/fractalfract7090674










