Energy-Preserving AVF Methods for Riesz Space-Fractional Nonlinear KGZ and KGS Equations
Abstract
1. Introduction
2. Discretization of the Riesz Space Fractional Derivative
3. Energy Preserving Method of Fractional KGZ and KGS Equations
3.1. Energy Preserving Method of the Fractional KGZ Equation
3.2. Energy Preserving Method of the Fractional KGS Equation
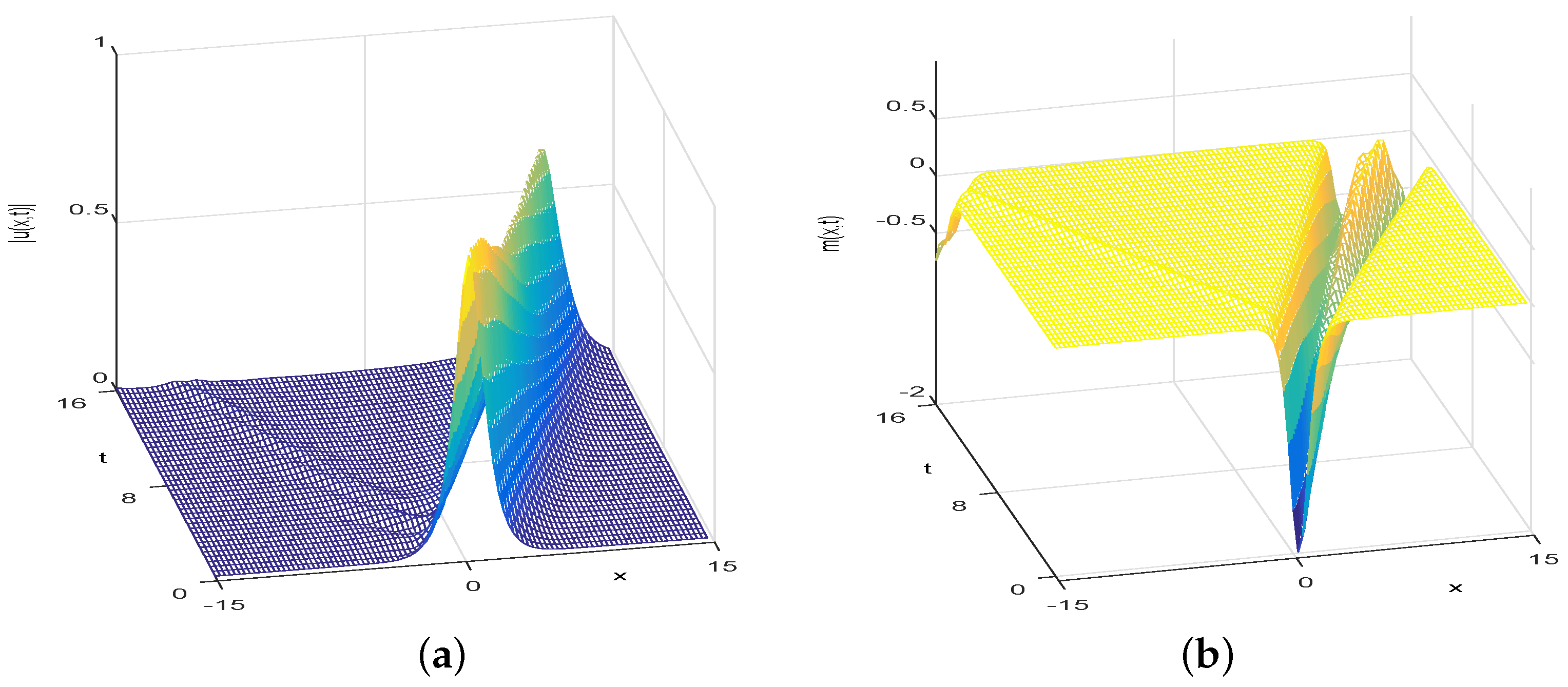
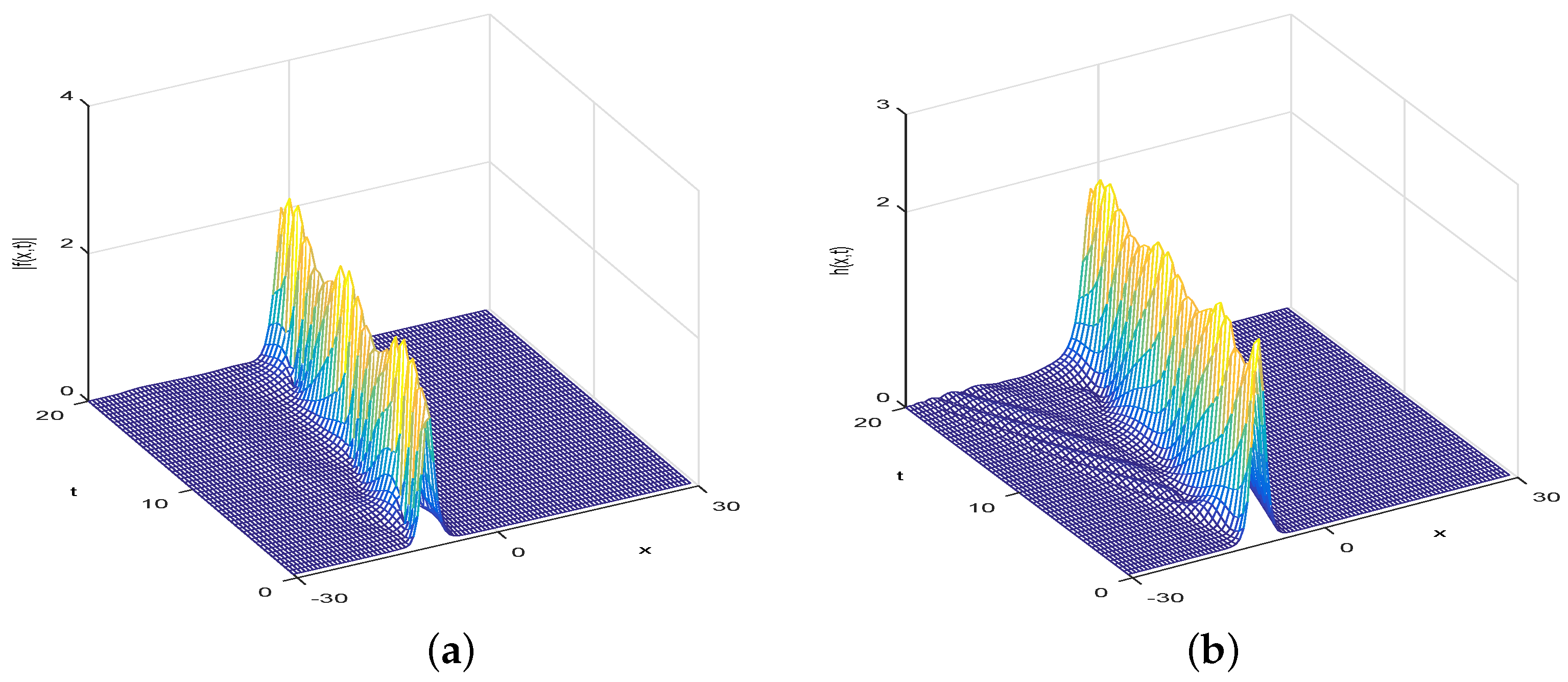
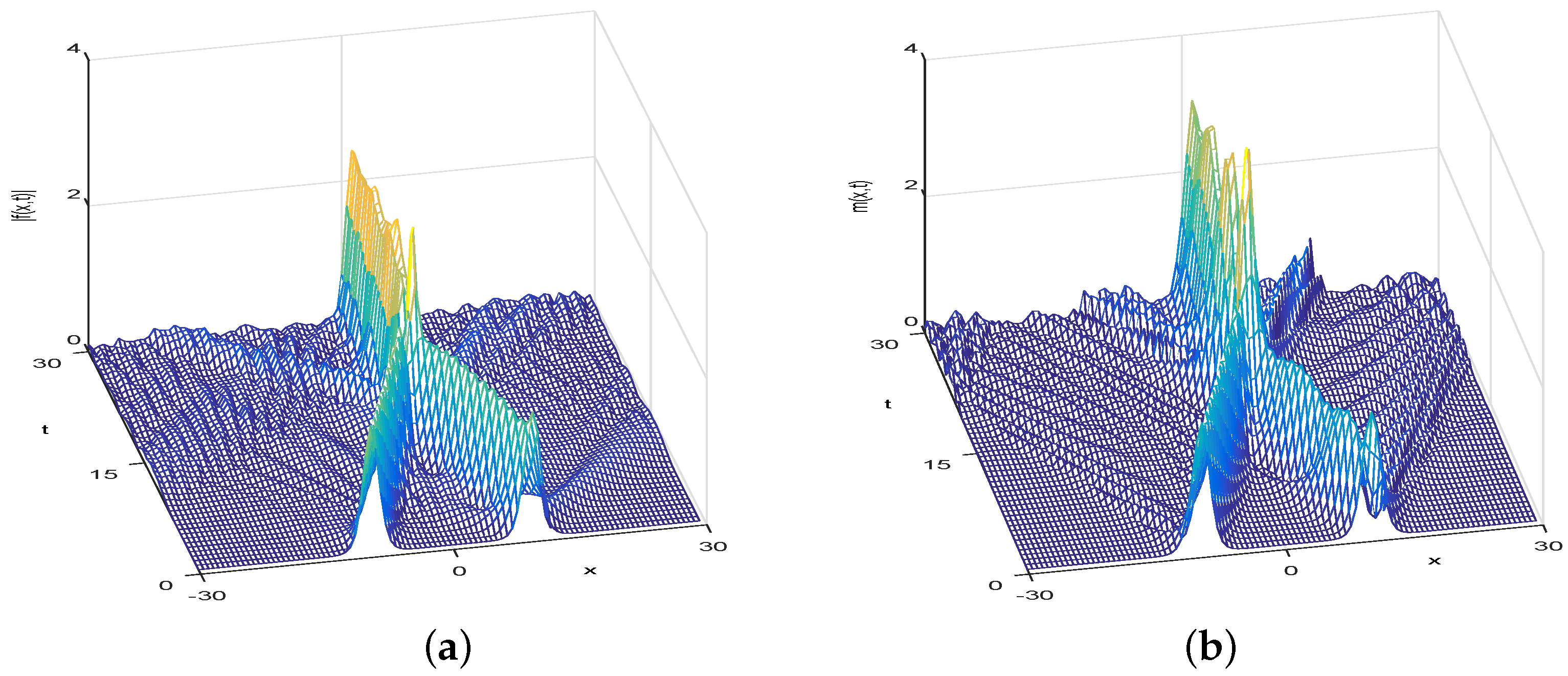
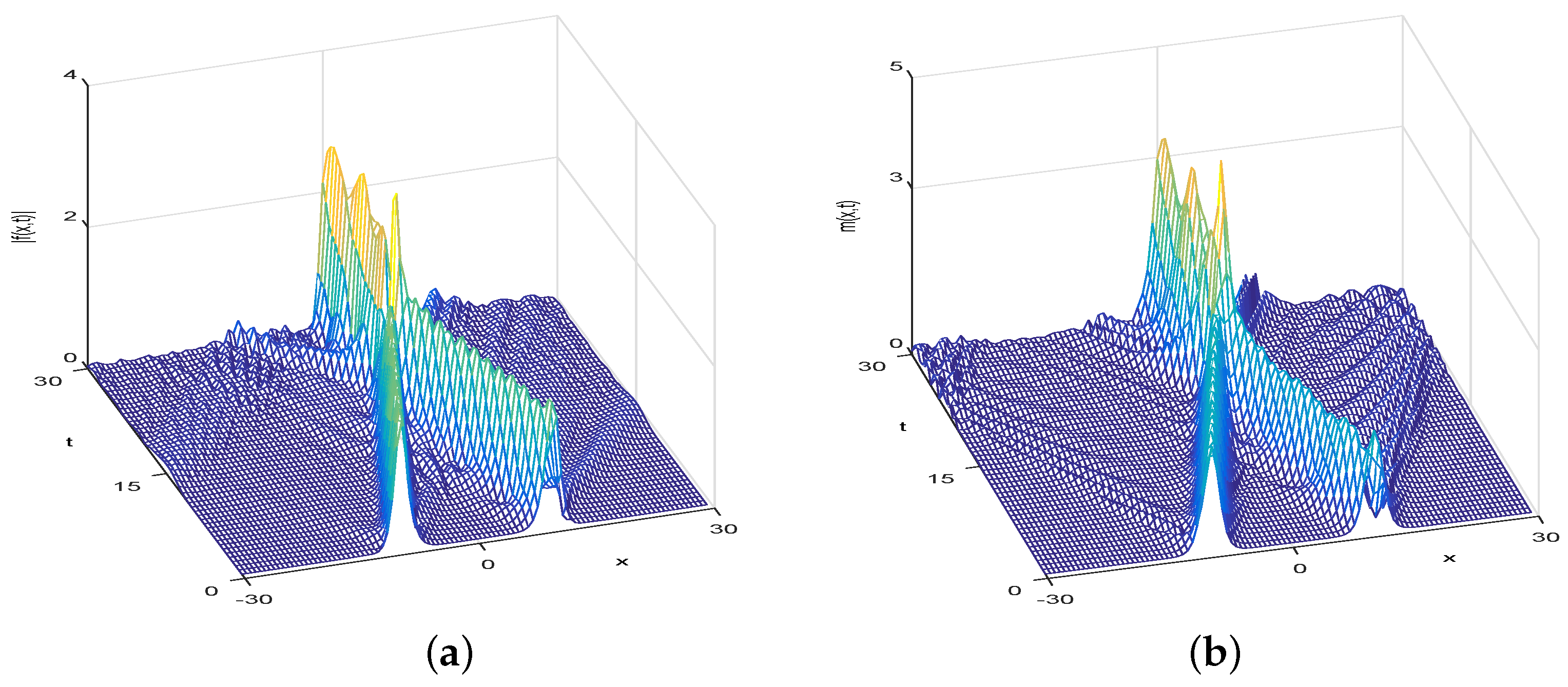
4. Numerical Simulation
4.1. Numerical Simulation of the Fractional KGZ Equation
4.2. Numerical Simulation of the Fractional KGS Equation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| KGS | Klein–Gordon–Schrödinger |
| KGZ | Klein–Gordon–Zakharov |
| AVF | average vector field |
| PDEs | partial differential equations |
| FPS | Fourier pseudo-spectral |
References
- Ray, S.S. A new analytical modelling for nonlocal generalized Riesz fractional sine-Gordon equation. J. King Saud Univ. Sci. 2016, 28, 48–54. [Google Scholar]
- Wang, P.D.; Huang, C.M. Structure-preserving numerical methods for the fractional Schrödinger equation. Appl. Numer. Math. 2018, 129, 137–158. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, G. Finite Difference Methods for Fractional Differential Equations; Science Press: Beijing, China, 2015. [Google Scholar]
- Li, C.P.; Zeng, F.H. Numerical Methods for Fractional Calculus; CRC Press: New York, NY, USA, 2015; pp. 1–17. [Google Scholar]
- Ding, H.; Li, C. Fractional-compact numerical algorithms for Riesz spatial fractional reaction-dispersion equations. Fract. Calc. Appl. Anal. 2017, 20, 722–764. [Google Scholar] [CrossRef][Green Version]
- Denghan, M.; Nikpour, A. The solitary wave solution of coupled Klein-Gordon-Zakharov equations via two different numerical methods. Comput. Phys. Commun. 2013, 184, 2145–2158. [Google Scholar] [CrossRef]
- Wang, J.J. Solitary wave propagation and interactions for the Klein-Gordon-Zakharov equations in plasma physics. J. Phys. A Math. Theory 2009, 42, 085205. [Google Scholar] [CrossRef]
- Macias-Diaz, J.E.; Hemdy, A.S.; Staelen, R.D. A compact fourth-order in space energy-preserving method for Riesz space-fractional nonlinear wave equations. Appl. Math. Comput. 2018, 325, 1–14. [Google Scholar] [CrossRef]
- Su, C.M.; Zhao, X.F. A uniformly first-order accurate method for Klein-Gordon-Zakharov system in simultaneous high-plasma-frequency and subsonic limit regime. J. Comput. Phys. 2021, 428, 110064. [Google Scholar] [CrossRef]
- Bao, W.; Su, C. Uniform error bounds of a finite difference method for the Klein-Gordon-Zakharov system in the subsonic limit regime. Math. Comput. 2018, 87, 2133–2158. [Google Scholar] [CrossRef]
- Akbulut, A.; Tascn, F. Application of conservation theorem and modified extended tanh-function method to (1+1) dimensional nonlinear coupled Klein-Gordon-Zakharov equation. Chaos Solitons Fractals 2017, 104, 33–40. [Google Scholar] [CrossRef]
- Ma, Y.; Su, C.M. A uniformly and optimally accurate multiscale time integrator method for the Klein-Gordon-Zakharov system in the subsonic limit regime. Comput. Math. Appl. 2018, 76, 602–619. [Google Scholar] [CrossRef]
- Wang, H.M. Numerical simulation for solitary wave of Klein-Gordon-Zakharov equation based on the lattice Boltzmann model. Comput. Math. Appl. 2019, 78, 3941–3955. [Google Scholar] [CrossRef]
- Gao, Y.L.; Mei, L.Q.; Li, R. Galerkin finite element methods for the generalized Klein-Gordon-Zakharov equations. Comput. Math. Appl. 2017, 74, 2466–2484. [Google Scholar] [CrossRef]
- Macias-Diaz, J.E.; Hendy, A.S.; Staelen, R.D. A pseudo energy-invariant method for relativistic wave equations with Riesz space fractional derivatives. Comput. Phys. Commun. 2017, 224, 98–107. [Google Scholar] [CrossRef]
- Hendy, A.S.; Macias-Diaz, J.E. A numerically efficient and conservative model for a Riesz space-fractional Klein-Gordon-Zakharov system. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 22–37. [Google Scholar] [CrossRef]
- Martinez, R.; Macias-Diaz, J.E.; Hendy, A.S. Theoretical analysis of an explicit energy-conserving scheme for a fractional Klein-Gordon-Zakharov system. Appl. Numer. Math. 2019, 146, 245–259. [Google Scholar] [CrossRef]
- Martinez, R.; Macias-Diaz, J.E. An energy-preserving and efficient scheme for a double-fractional conservative Klein-Gordon-Zakharov system. Appl. Numer. Math. 2020, 158, 292–313. [Google Scholar] [CrossRef]
- Macias-Diaz, J.E. Existence of solutions of an explicit energy-conserving scheme for a fractional Klein-Gordon-Zakharov system. Appl. Numer. Math. 2020, 151, 40–43. [Google Scholar] [CrossRef]
- Ohta, M. Stability of stationary states for coupled Klein-Gordon-Schrödinger equations. Nonlinear Anal. Theory, Methods Appl. 1996, 27, 455–461. [Google Scholar] [CrossRef]
- Huang, C.; Guo, B.; Huang, D.; Li, Q. Global well-posedness of the fractional Klein-Gordon-Schrödinger system with rough initial data. Sci. China Math. 2016, 59, 1345–1366. [Google Scholar] [CrossRef]
- Kong, L.H.; Chen, M.; Yin, X.L. A novel kind of efficient symplectic scheme for Klein-Gordon-Schrödinger equation. Appl. Numer. Math. 2019, 135, 481–496. [Google Scholar] [CrossRef]
- Wang, J.J.; Xiao, A.G. A efficient conservation difference scheme for fractional Klein-Gordon-Schrödinger equations. Appl. Math. Comput. 2018, 320, 691–709. [Google Scholar] [CrossRef]
- Wang, J.J.; Xiao, A.G. Conservative fourier spectral method and numerical investigation of space fractional Klein-Gordon-Schrödinger equations. Appl. Math. Comput. 2019, 350, 348–365. [Google Scholar] [CrossRef]
- McLachlan, R.I.; Quispel, G.R.W.; Robidoux, N. Geometric integration using discrete gradients. Philos. Trans. R Biol. Sci. 1999, 357, 1021–1045. [Google Scholar] [CrossRef]
- Quispel, G.R.W.; Mclaren, D.I. A new class of energy-preserving numerical integration methods. J. Phys. A Math. Theor. 2008, 41, 045206. [Google Scholar] [CrossRef]
- Furihata, D.; Matsuo, T. Discrete Variational Derivative Method, a Structure-Preserving Numerical Method for Partial Differential Equations; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Brugnano, L.; Iavernarivo, F.; Trigiante, D. Hamiltonian boundary value methods (Energy preserving discrete line integral methods). J. Numer. Anal. Appl. Math. 2010, 5, 17–37. [Google Scholar]
- Celledonia, E.; Grimmb, V.; McLachlanc, R.I.; McLarend, D.I.; O’Nealed, D.; Owrena, B.; Quispel, G.R.W. Preserving energy resp. dissipation in numerical PDEs using the “Average Vector Field” method. J. Comput. Phys. 2012, 231, 6770–6789. [Google Scholar] [CrossRef]
- Jiang, C.L.; Sun, J.Q.; He, X.F. High order energy-preserving method of the Good Boussinesq equation. Numer. Methods Appl. 2016, 9, 111–122. [Google Scholar] [CrossRef]
- Bridges, T.J. Multi-symplectic structures and wave propagation. Math. Proc. Camb. Phil. Soc. 1997, 121, 147–190. [Google Scholar] [CrossRef]
- Chen, J.B. Symplectic and multisymplectic Fourier pseudospectral discretizations for the Klein-Gordon equation. Lett. Math. Phys. 2006, 75, 293–305. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Yang, S.; Zhang, L. Energy-Preserving AVF Methods for Riesz Space-Fractional Nonlinear KGZ and KGS Equations. Fractal Fract. 2023, 7, 711. https://doi.org/10.3390/fractalfract7100711
Sun J, Yang S, Zhang L. Energy-Preserving AVF Methods for Riesz Space-Fractional Nonlinear KGZ and KGS Equations. Fractal and Fractional. 2023; 7(10):711. https://doi.org/10.3390/fractalfract7100711
Chicago/Turabian StyleSun, Jianqiang, Siqi Yang, and Lijuan Zhang. 2023. "Energy-Preserving AVF Methods for Riesz Space-Fractional Nonlinear KGZ and KGS Equations" Fractal and Fractional 7, no. 10: 711. https://doi.org/10.3390/fractalfract7100711
APA StyleSun, J., Yang, S., & Zhang, L. (2023). Energy-Preserving AVF Methods for Riesz Space-Fractional Nonlinear KGZ and KGS Equations. Fractal and Fractional, 7(10), 711. https://doi.org/10.3390/fractalfract7100711







