A New Hybrid Optimal Auxiliary Function Method for Approximate Solutions of Non-Linear Fractional Partial Differential Equations
Abstract
:1. Introduction
2. Preliminaries
3. The Basic Idea of the Optimal Auxiliary Function Method
4. Numerical Experiments and Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Non-Uniform System I: Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Cahn, J.W. On Spinodal Decomposition. Acta Metall. 1961, 9, 795–801. [Google Scholar] [CrossRef]
- Elliott, C.M. The Cahn-Hilliard Model for the Kinetics of Phase Separation, in Mathematical Models for Phase Change Problems; Rodrigues, J.F., Ed.; International Series of Numerical Mathematics; Birkhauser: Basel, Switzerland, 1989; Volume 88. [Google Scholar]
- Novick-Cohen, A. The Cahn-Hilliard Equation. In Handbook of Differential Equations, Evolutionary Partial Differential Equations; Dafermos, C.M., Pokorny, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 4, pp. 201–228. [Google Scholar]
- Baillie, R.T. Long Memory Processes and Fractional Integration in Econometrics. J. Econom. 1996, 72, 217–242. [Google Scholar] [CrossRef]
- Copetti, M.I.M.; Elliott, C.M. Kinetics of Phase Decomposition Processes: Numerical Solutions to the Cahn-Hilliard Equation. Mater. Sci. Technol. 1990, 6, 273–283. [Google Scholar] [CrossRef]
- Dhmani, Z.; Benbachir, M. Solutions of the Cahn-Hilliard Equation with Time- and Space-Fractional Derivatives. Int. J. Non-Linear Sci. 2009, 8, 19–26. [Google Scholar]
- De Mello, E.V.L.; Otto, T.; Da Silveira, F. Numerical Study of the Cahn-Hilliard Equation in One, Two and Three Dimensions. Physica A 2005, 347, 429–443. [Google Scholar] [CrossRef]
- Junseok, K. A Numerical Method for the Cahn-Hilliard Equation with a Variable Mobility. Commun. Non-Linear Sci. Numer. Simul. 2007, 12, 1560–1572. [Google Scholar]
- Rybka, P.; Hoffmann, K.H. Convergence of Solutions to Cahn-Hilliard Equation. Commun. Partial. Differ. Equ. 1999, 24, 1055–1077. [Google Scholar] [CrossRef]
- Ugurlu, Y.; Kaya, D. Solutions of the Cahn-Hilliard Equation. Comput. Math. Appl. 2008, 56, 3038–3045. [Google Scholar] [CrossRef]
- Fellnerand, K.; Schmeiser, C. Burgers-Poisson: A Nonlinear Dispersive Model Equation. SIAM J. Appl. Math. 2004, 64, 1509–1525. [Google Scholar]
- Kondo, C.I.; Webler, C.M. The Generalized BBM-Burgers Equations: Convergence Results for Conservation Law with Discontinuous Flux Function. Appl. Anal. 2016, 95, 503–523. [Google Scholar] [CrossRef]
- Tawfiq, L.N.M.; Yahya, Z.R. Using Cubic Trigonometric B-spline Method to Solve BBM-Burger Equation. In Proceedings of the MDSG Conference 2016 Conferences, Sintok, Kedah, 6–7 March 2016. [Google Scholar]
- Shakeel, M.; Ul-Hassan, Q.M.; Ahmad, J.; Naqvi, T. Exact Solutions of the Time Fractional BBM-Burger Equation by Novel (G’/G)-Expansion Method. Adv. Math. Phys. 2014, 2014, 181594. [Google Scholar] [CrossRef]
- Al-Refai, M. Maximum Principles for Non-linear Fractional Differential Equations in Reliable Space. Prog. Fract. Differ. Appl. 2020, 6, 95–99. [Google Scholar]
- Gao, W.; Baskonus, H.M.; Shi, L. New Investigation of Bat Hosts-Reservoir-People Coronavirus Model and Application to 2019-nCoV System. Adv. Differ. Equ. 2020, 2020, 391. [Google Scholar] [CrossRef] [PubMed]
- Atangana, A. Fractal-Fractional Differentiation and Integration: Connecting Fractal Calculus and Fractional Calculus to Predict Complex Systems. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Baleanu, D.; Ghanbari, B.; Asad, J.H.; Jajarmi, A.; Pirouz, H.M. Planar System-Masses in an Equilateral Triangle: Numerical Study within Fractional Calculus. CMES—Comput. Model. Eng. Sci. 2020, 124, 953–968. [Google Scholar] [CrossRef]
- Ghanim, F.; Bendak, S.; Al Hawarneh, A. Certain Implementations in Fractional Calculus Operators Involving Mittag-Leffler-Confluent Hypergeometric Functions. Proc. R. Soc. A 2022, 478, 20210839. [Google Scholar] [CrossRef]
- Ghanim, F.; Al-Janaby, H.F. Some Analytical Merits of Kummer-Type Function Associated with Mittag-Leffler Parameters. Arab. J. Basic Appl. Sci. 2021, 28, 255–263. [Google Scholar] [CrossRef]
- Ghanim, F.; Al-Janaby, H.F.; Bazighifan, O. Some New Extensions on Fractional Differential and Integral Properties for Mittag-Leffler Confluent Hypergeometric Function. Fractal Fract. 2021, 5, 143. [Google Scholar] [CrossRef]
- Almalahi, M.A.; Ghanim, F.; Botmart, T.; Bazighifan, O.; Askar, S. Qualitative Analysis of Langevin Integro-Fractional Differential Equation under Mittag–Leffler Functions Power Law. Fractal Fract. 2021, 5, 266. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D. A New Iterative Method for the Numerical Solution of High-Order Non-Linear Fractional Boundary Value Problems. Front. Phys. 2020, 8, 220. [Google Scholar] [CrossRef]
- Sajjadi, S.S.; Baleanu, D.; Jajarmi, A.; Pirouz, H.M. A New Adaptive Synchronization and Hyperchaos Control of a Biological Snap Oscillator. Chaos Solitons Fractals 2020, 138, 10991. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D. On the Fractional Optimal Control Problems with a General Derivative Operator. Asian J. Control 2019, 23, 1062–1071. [Google Scholar] [CrossRef]
- Mohammadi, F.; Moradi, L.; Baleanu, D.; Jajarmi, A. A Hybrid Functions Numerical Scheme for Fractional Optimal Control Problems: Application to Nonanalytic Dynamic Systems. J. Vib. Control 2018, 24, 5030–5043. [Google Scholar] [CrossRef]
- Tuan, N.H.; Ngoc, T.B.; Baleanu, D.; O’Regan, D. On Well-Posedness of the Sub-Diffusion Equation with Conformable Derivative Model. Commun. Non-Linear Sci. Numer. Simul. 2020, 89, 105332. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Ali Shaikh, A.; Inc, M.; Baleanu, D. Mathematical Modeling for Adsorption Process of Dye Removal Non-linear Equation Using Power Law and Exponentially Decaying Kernels. Chaos Interdiscip. J. Non-Linear Sci. 2020, 30, 043106. [Google Scholar] [CrossRef]
- Kumar, P.; Qureshi, S. Laplace-Carson Integral Transform for Exact Solutions of Non-Integer Order Initial Value Problems with Caputo Operator. J. Appl. Math. Comput. Mech. 2020, 19, 57–66. [Google Scholar] [CrossRef]
- Hadi, S.H.; Ali, A.H. Integrable Functions of Fuzzy Cone and ξ—Fuzzy Cone and Their Application in the Fixed Point Theorem. J. Interdiscip. Math. 2021, 25, 247–258. [Google Scholar] [CrossRef]
- Marinca, B.; Marinca, V. Approximate Analytical Solutions for Thin Film Flow of a Fourth-Grade Fluid down a Vertical Cylinder. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2018, 19, 69–71. [Google Scholar]
- Zada, L.; Nawaz, R.; Ayaz, M.; Ahmad, H.; Alrabaiah, H.; Chu, Y.M. New Algorithm for the Approximate Solution of Generalized Seventh Order Korteweg-Devries Equation Arising in Shallow Water Waves. Results Phys. 2020, 20, 103744. [Google Scholar] [CrossRef]
- Arshad, U.; Sultana, M.; Ali, A.H.; Bazighifan, O.; Al-moneef, A.A.; Nonlaopon, K. Numerical Solutions of Fractional-Order Electrical RLC Circuit Equations via Three Numerical Techniques. Mathematics 2022, 10, 3071. [Google Scholar] [CrossRef]
- Sultana, M.; Arshad, U.; Ali, A.H.; Bazighifan, O.; Al-Moneef, A.A.; Nonlaopon, K. New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations. Symmetry 2022, 14, 1653. [Google Scholar] [CrossRef]
- Khan, F.S.; Khalid, M.; Al-moneef, A.A.; Ali, A.H.; Bazighifan, O. Freelance Model with Atangana–Baleanu Caputo Fractional Derivative. Symmetry 2022, 14, 2424. [Google Scholar] [CrossRef]
- Raza, A.; Abed, A.M.; Almusawa, M.Y.; Seddek, L.F.; Ali, A.H. Prabhakar Fractional Simulation for Inspection of CMC-Based Nanofluid Flowing through a Poured Vertical Channel. Case Stud. Therm. Eng. 2023, 45, 102911. [Google Scholar] [CrossRef]
- de Oliveira, E.C.; Machado, J.A.T. A Review of Definitions for Fractional Derivatives and Integral. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S.; Akpan, U. Iterative Methods for Solving Fourth and Sixth Order Time-Fractional Cahn-Hillard Equation. arXiv 2019, arXiv:1903.10337v2 [math.AP]. [Google Scholar] [CrossRef]
- Zeng, C.; Yang, Q.; Zhang, B. Homotopy Perturbation Method for Fractional-Order Burgers-Poisson Equation. arXiv 2010, arXiv:1003.1828v1 [nlin.PS]. [Google Scholar]
- Zhang, J.; Wei, Z.; Yong, L.; Xiao, Y. Analytical Solution for the Time Fractional BBM-Burger Equation by Using Modified Residual Power Series Method. J. Hindawi 2018, 18, 11. [Google Scholar] [CrossRef]
- Jagdev, S.; Ram, S.; Devendra, K. A Computational Approach for Fractional Convection-Diffusion Equation via Integral Transforms. Ain Shams Eng. J. 2016, 9, 1019–1028. [Google Scholar]
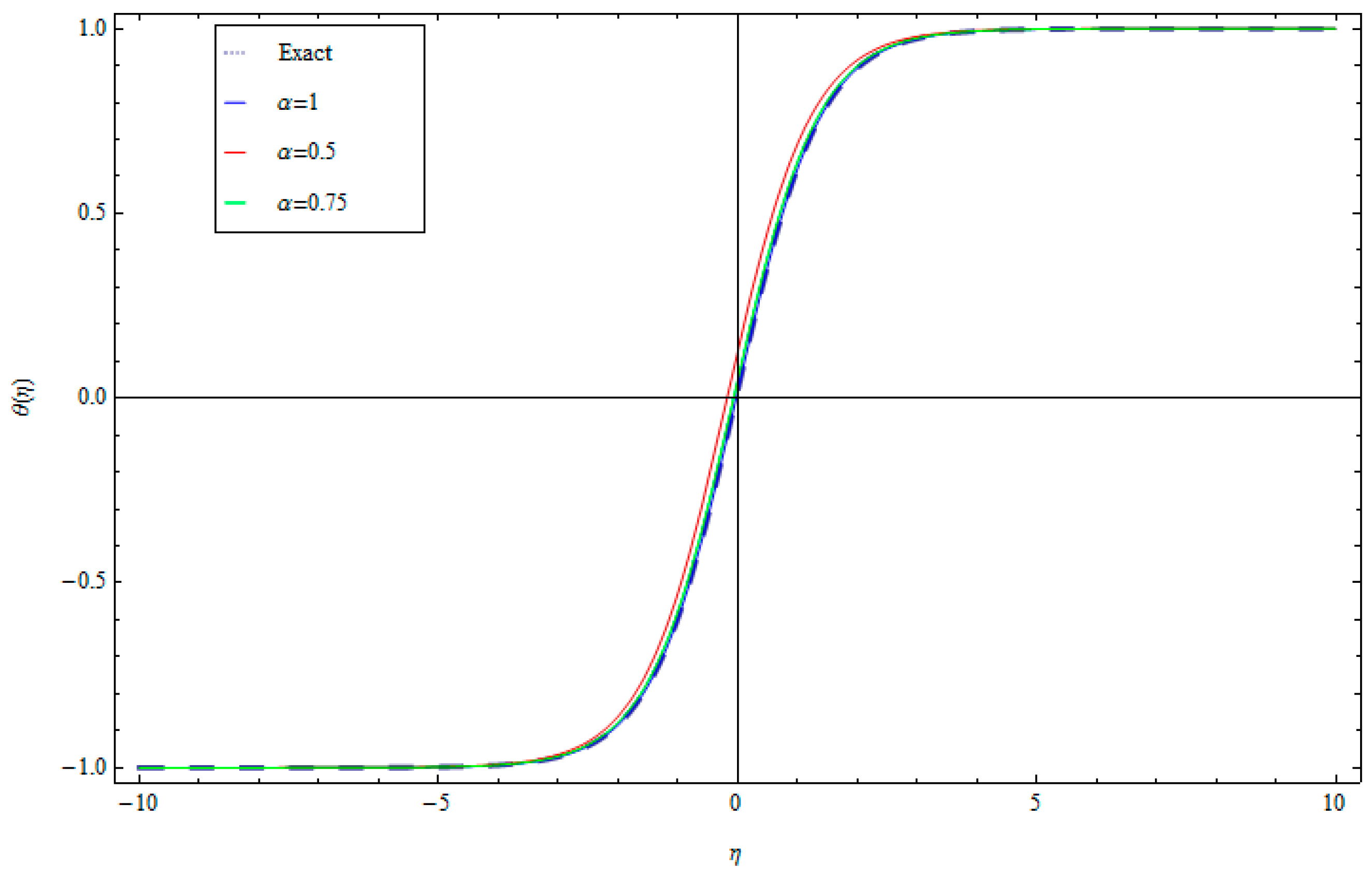
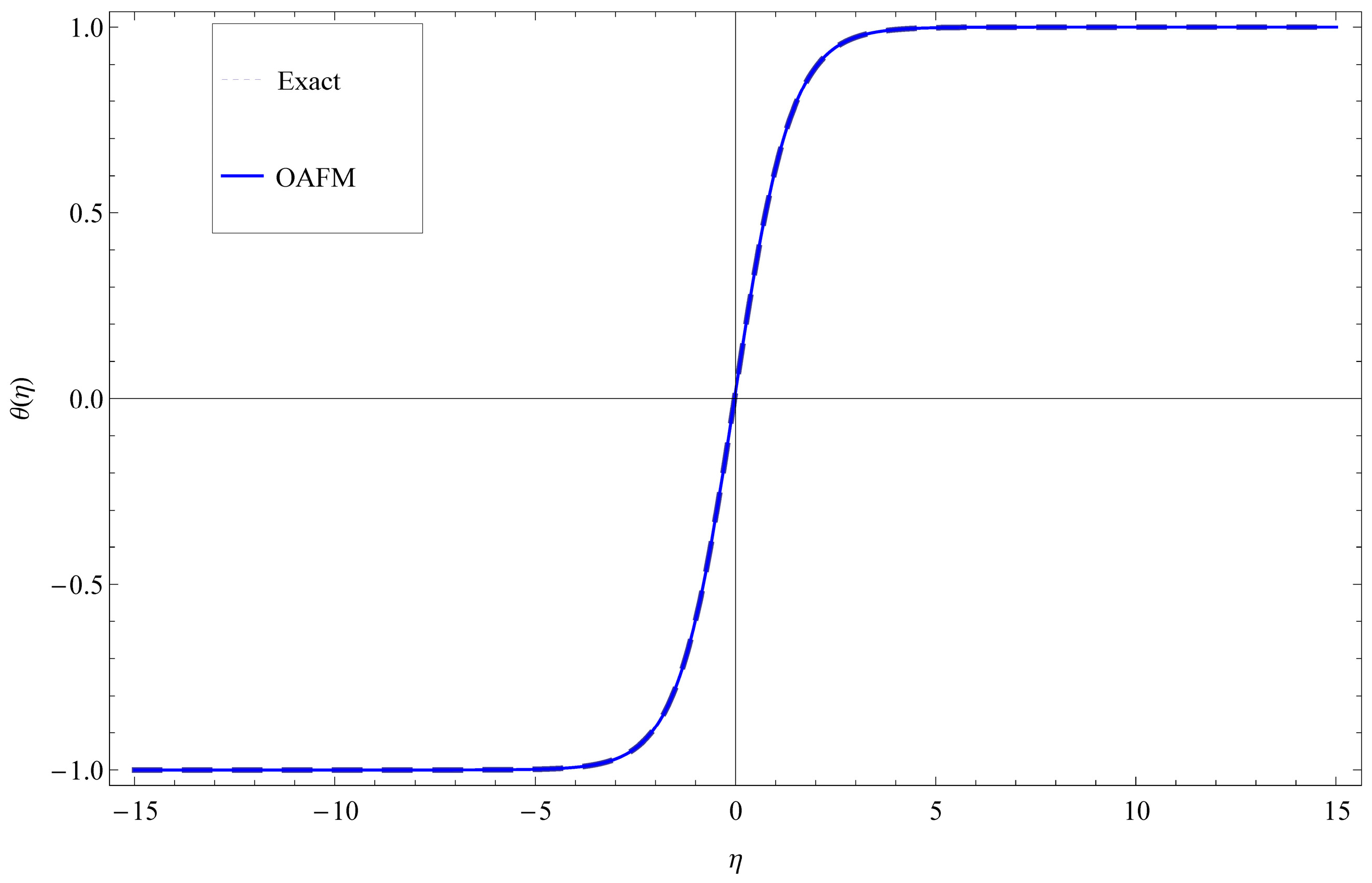



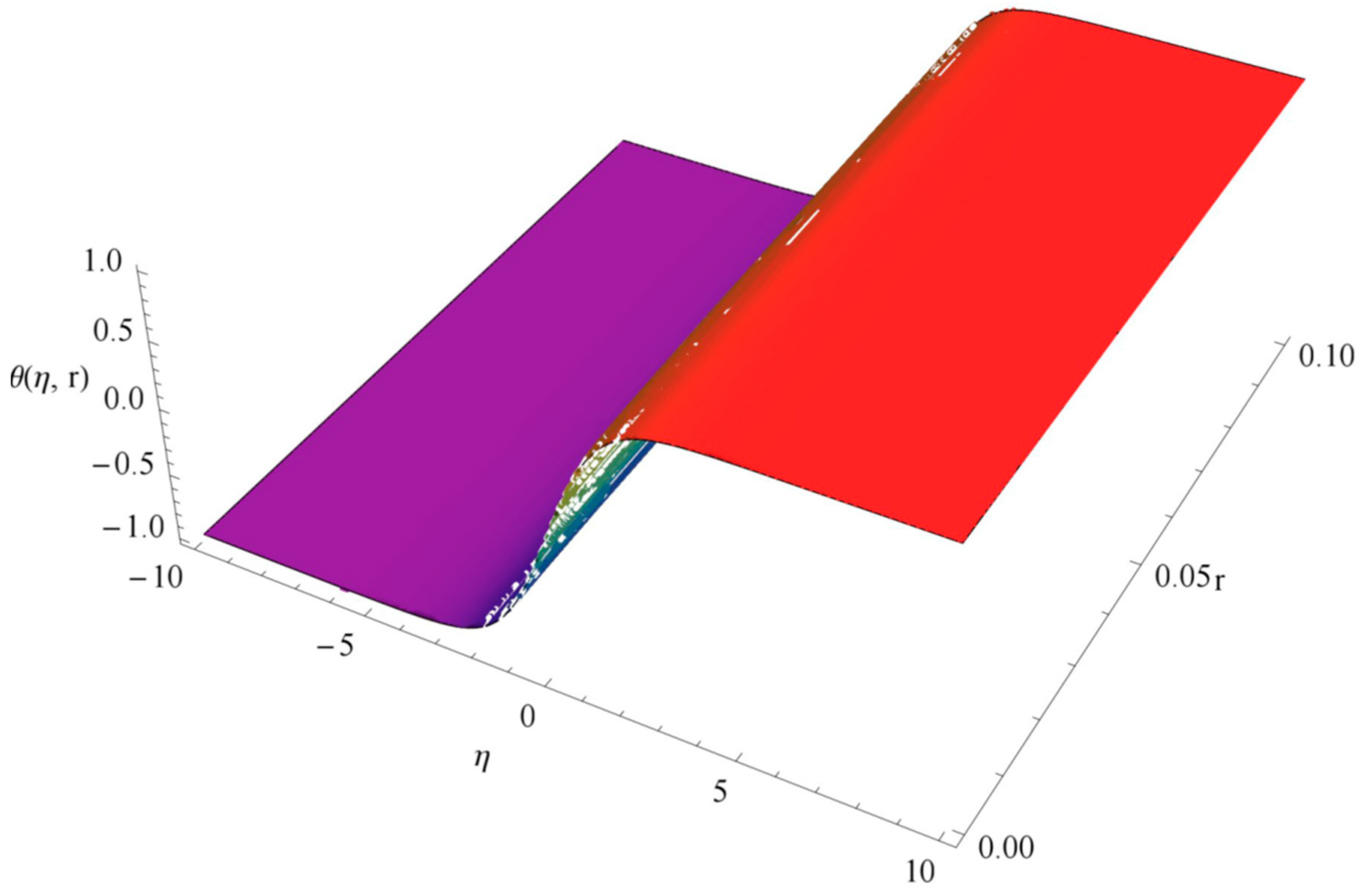
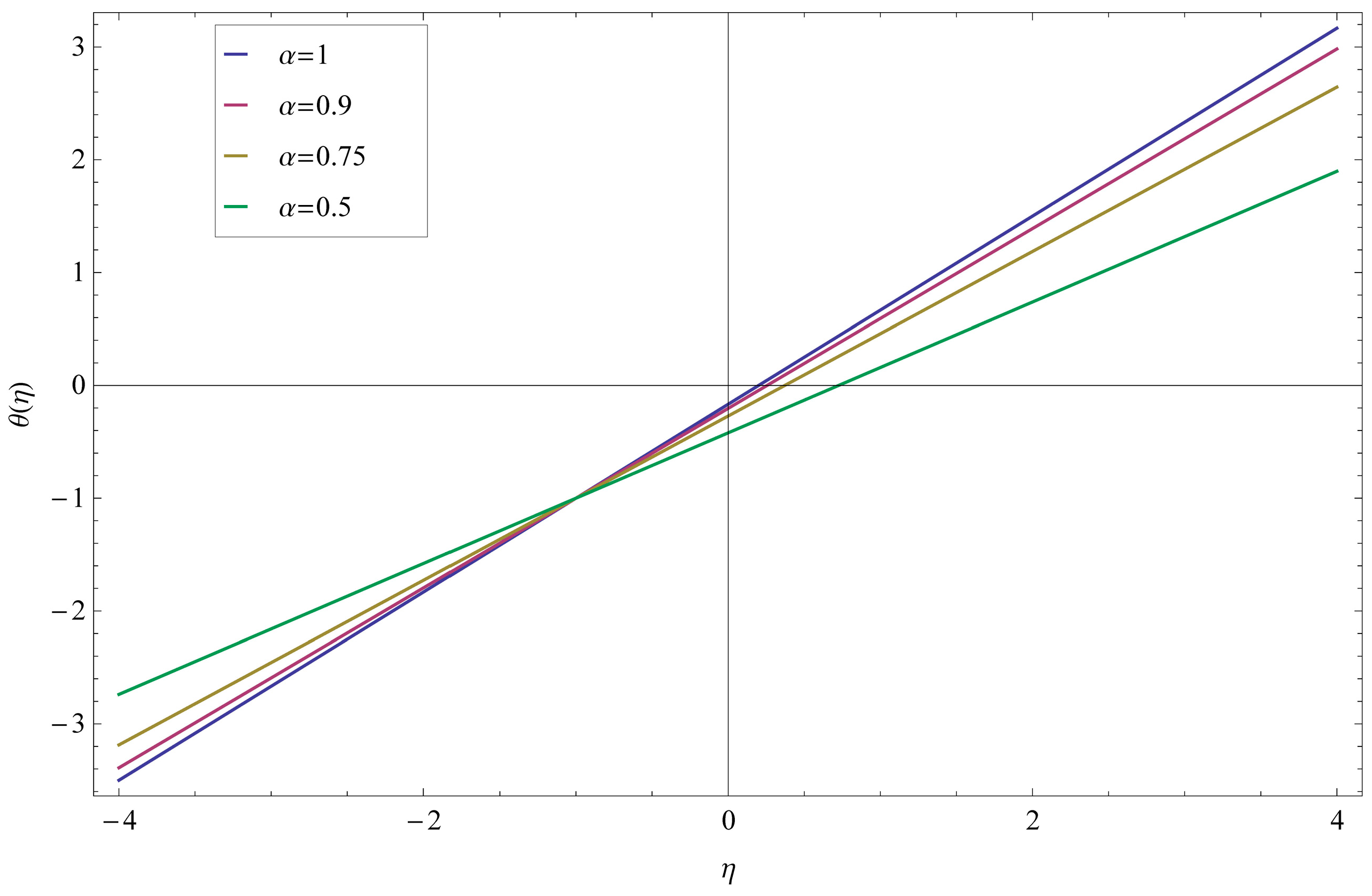

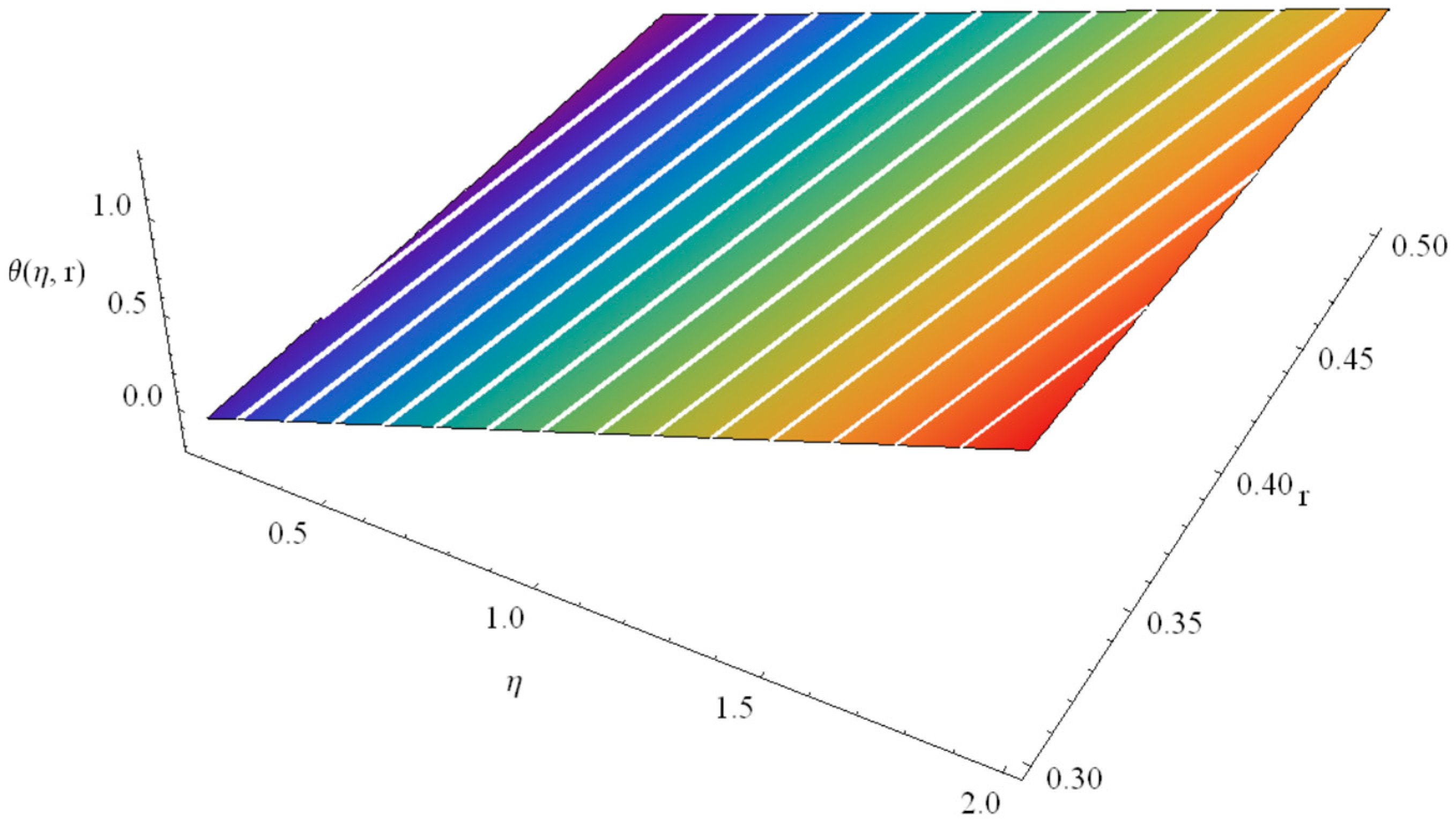
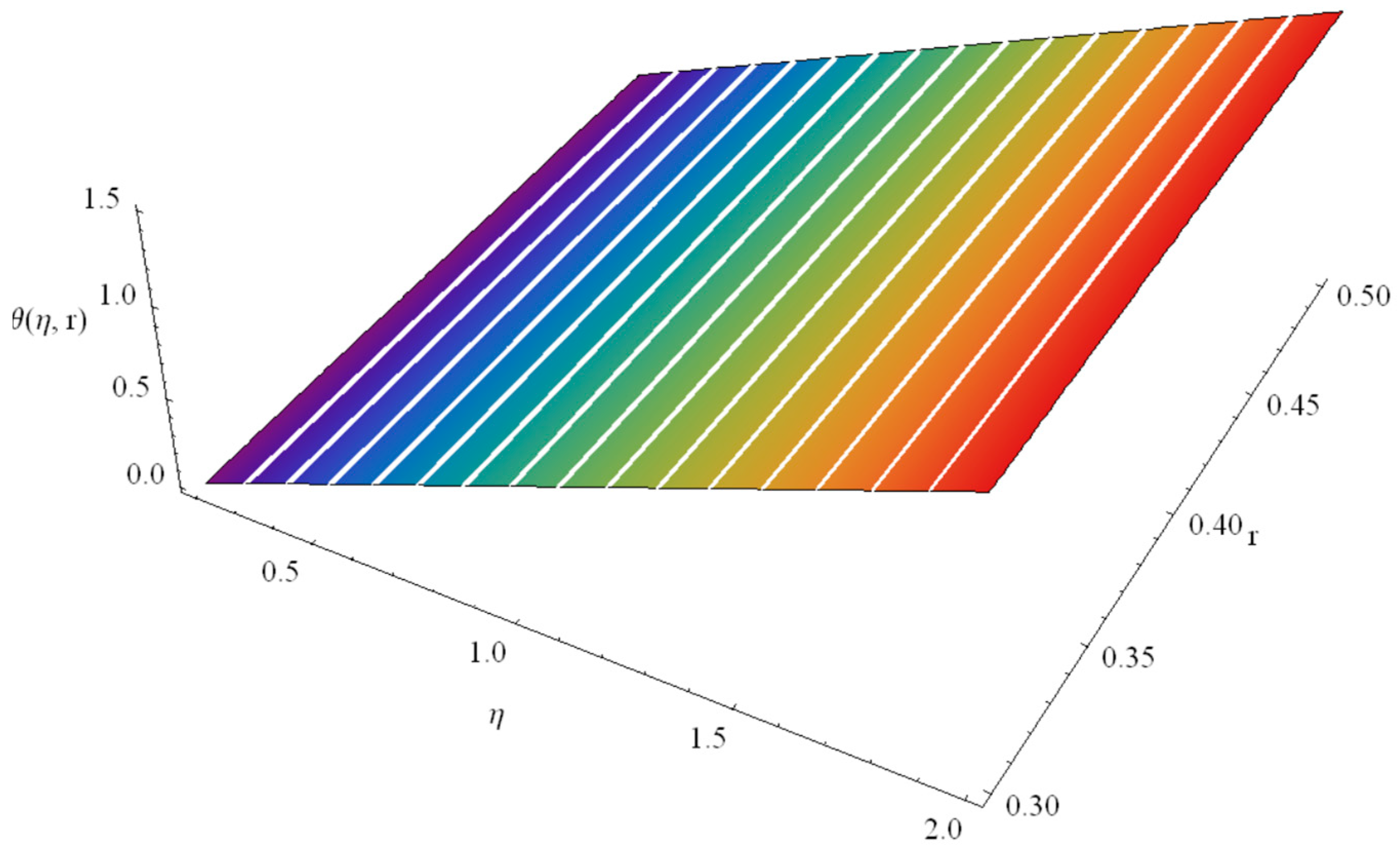

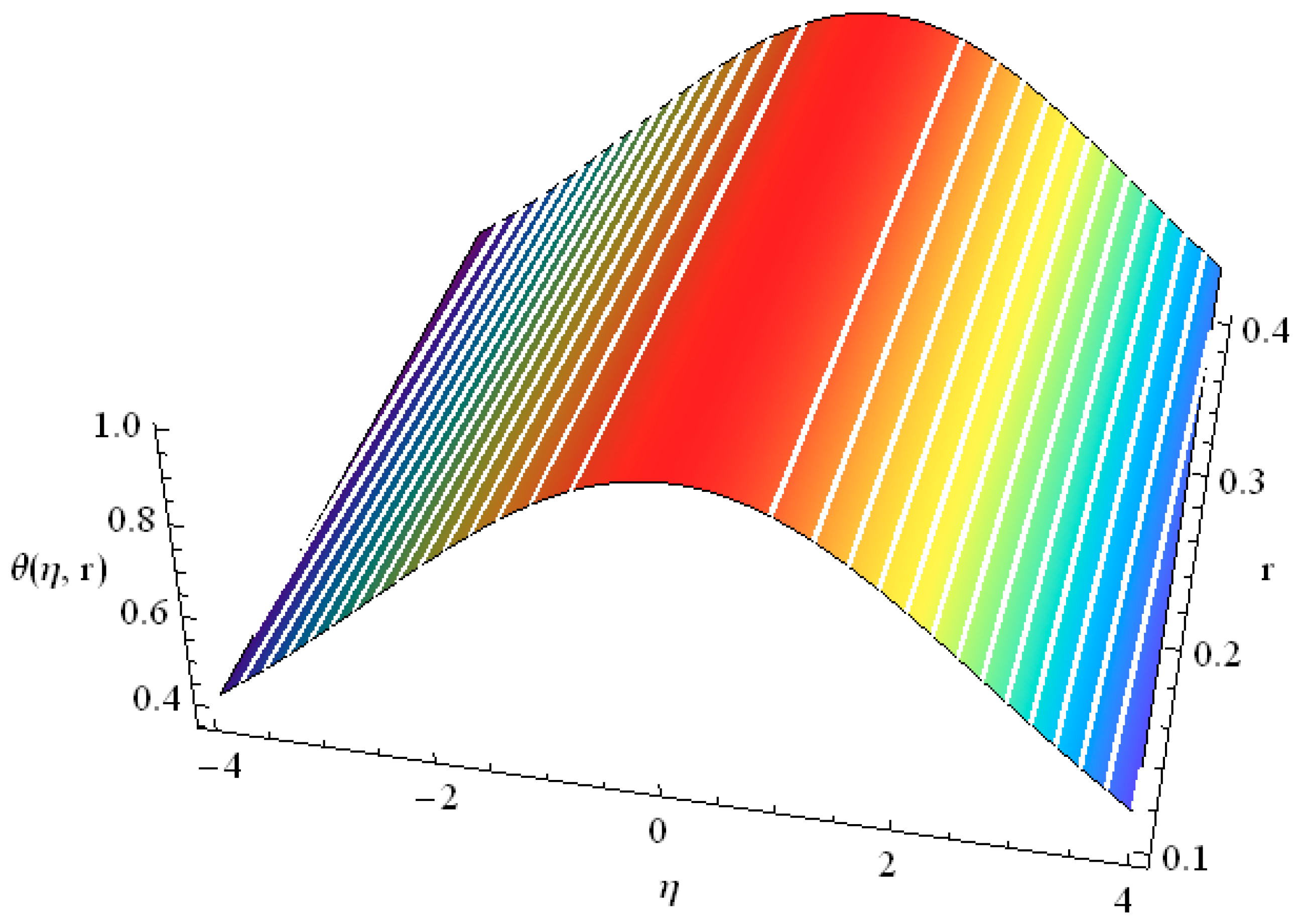
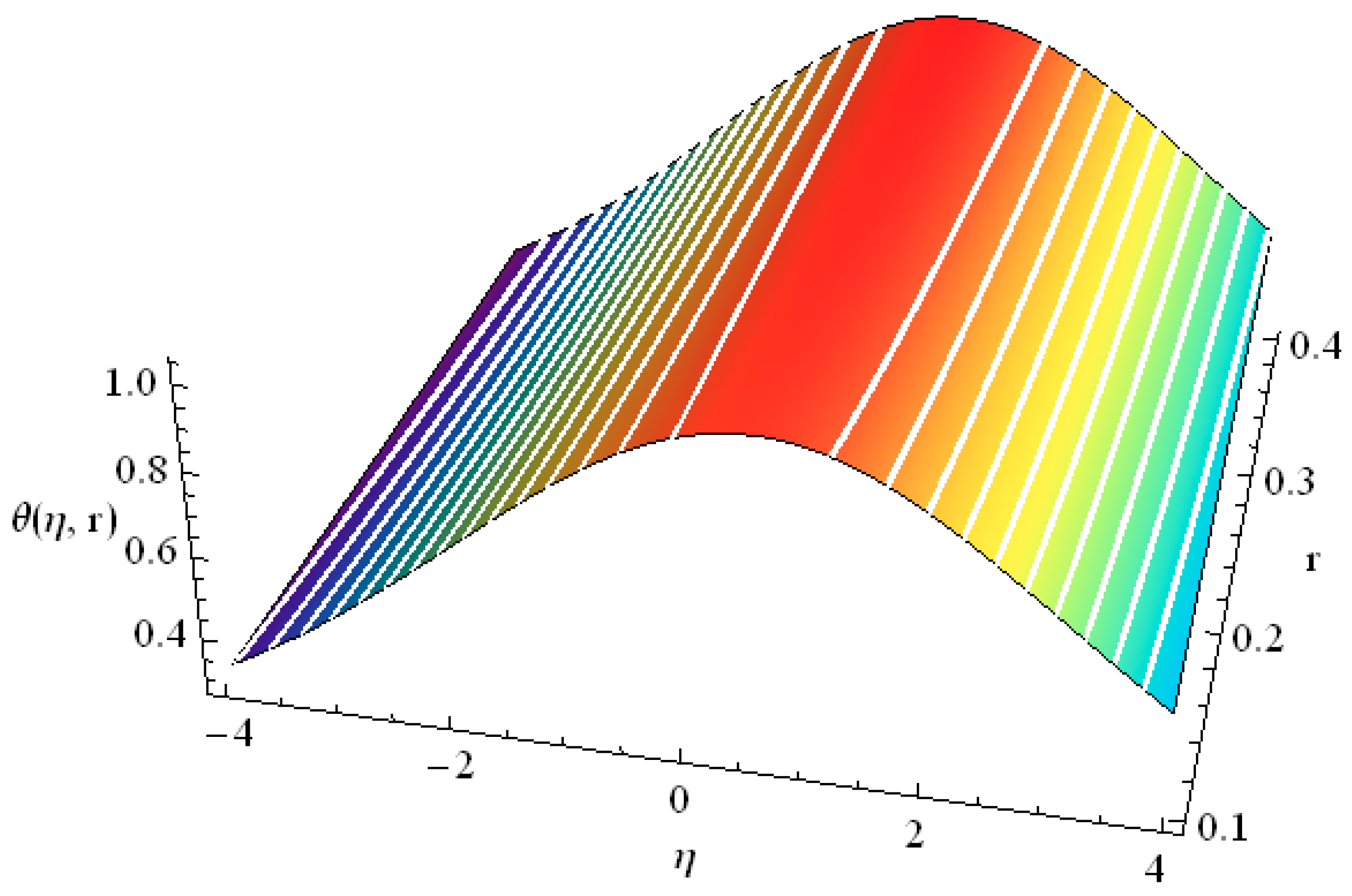

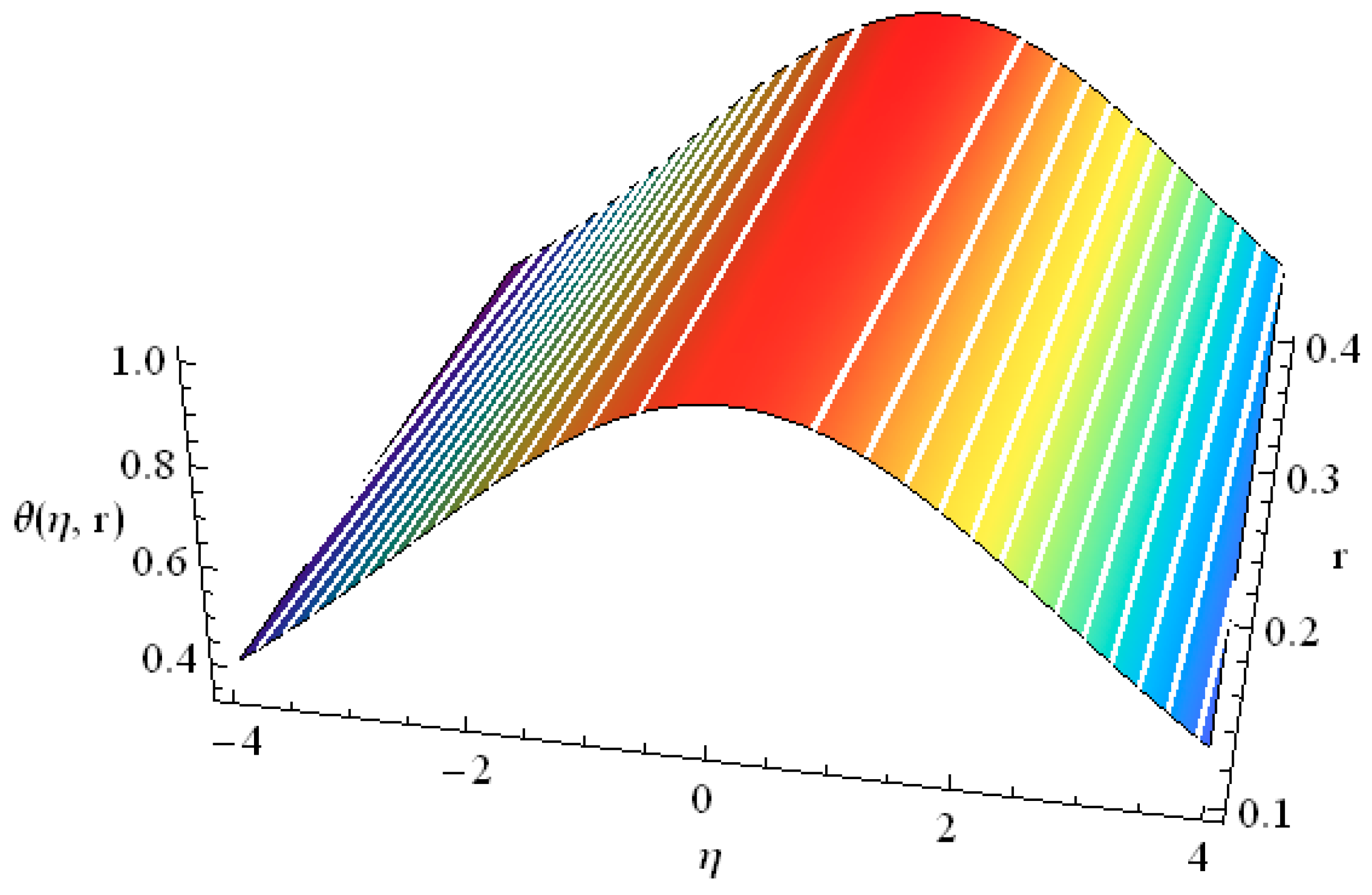
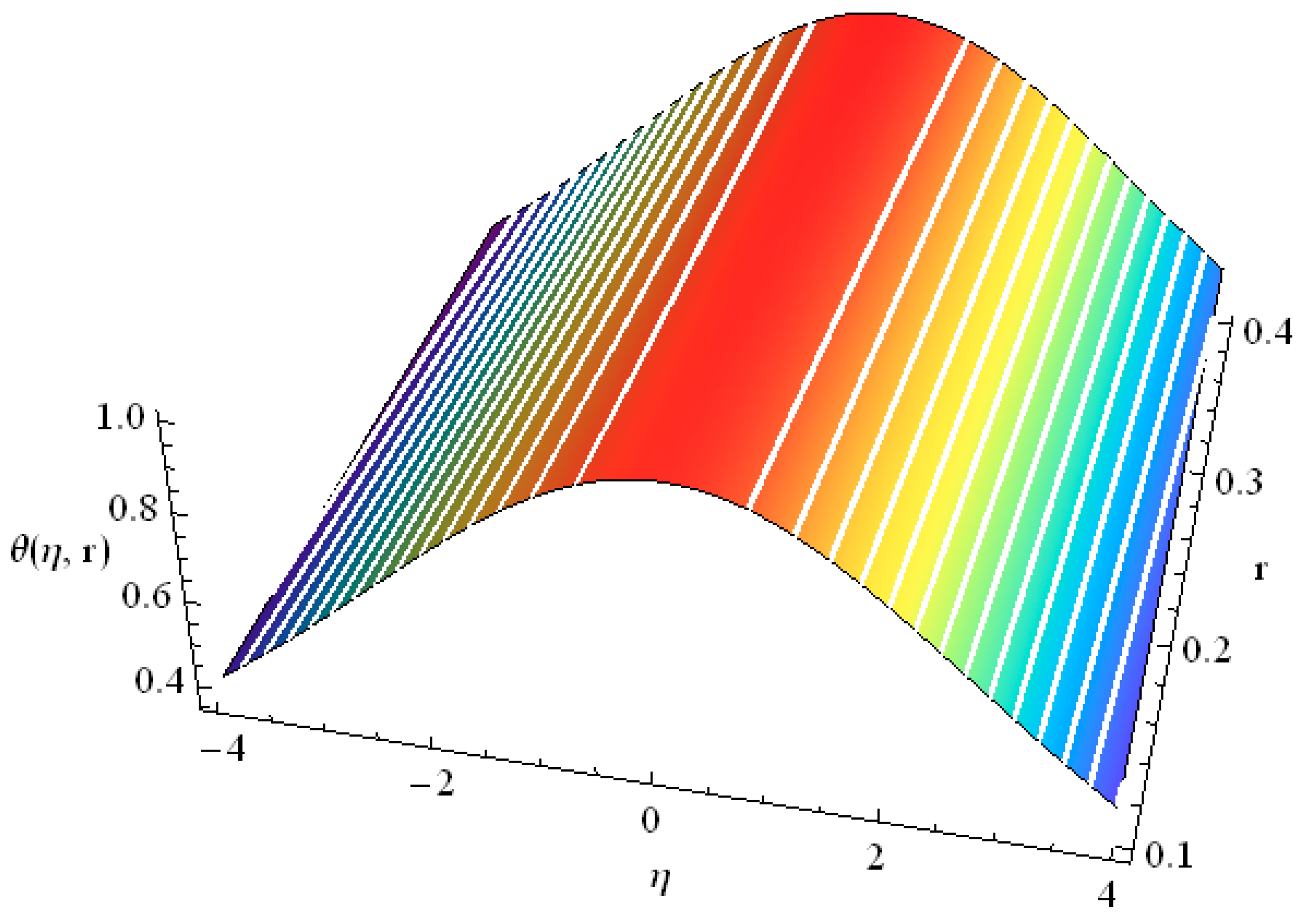
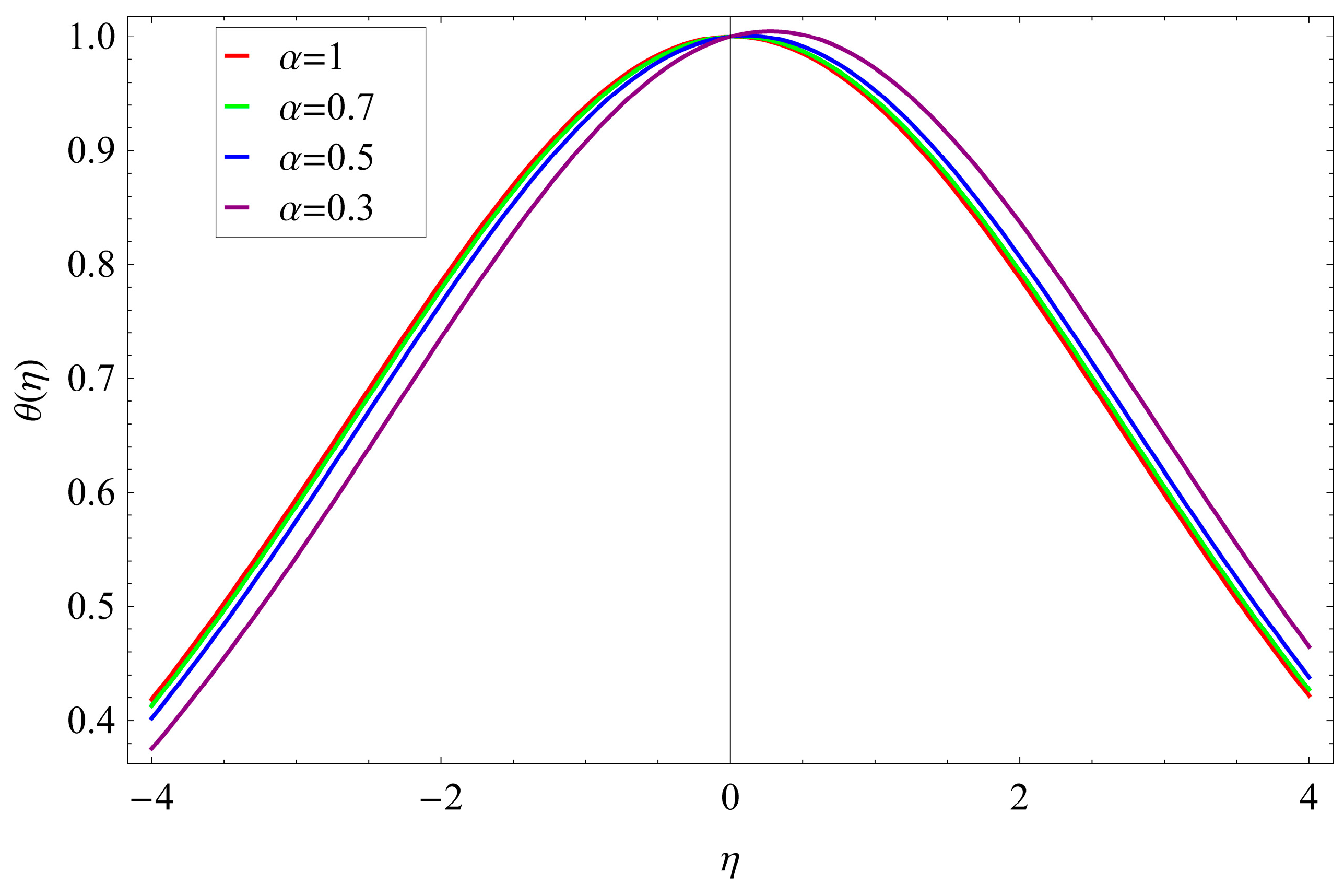
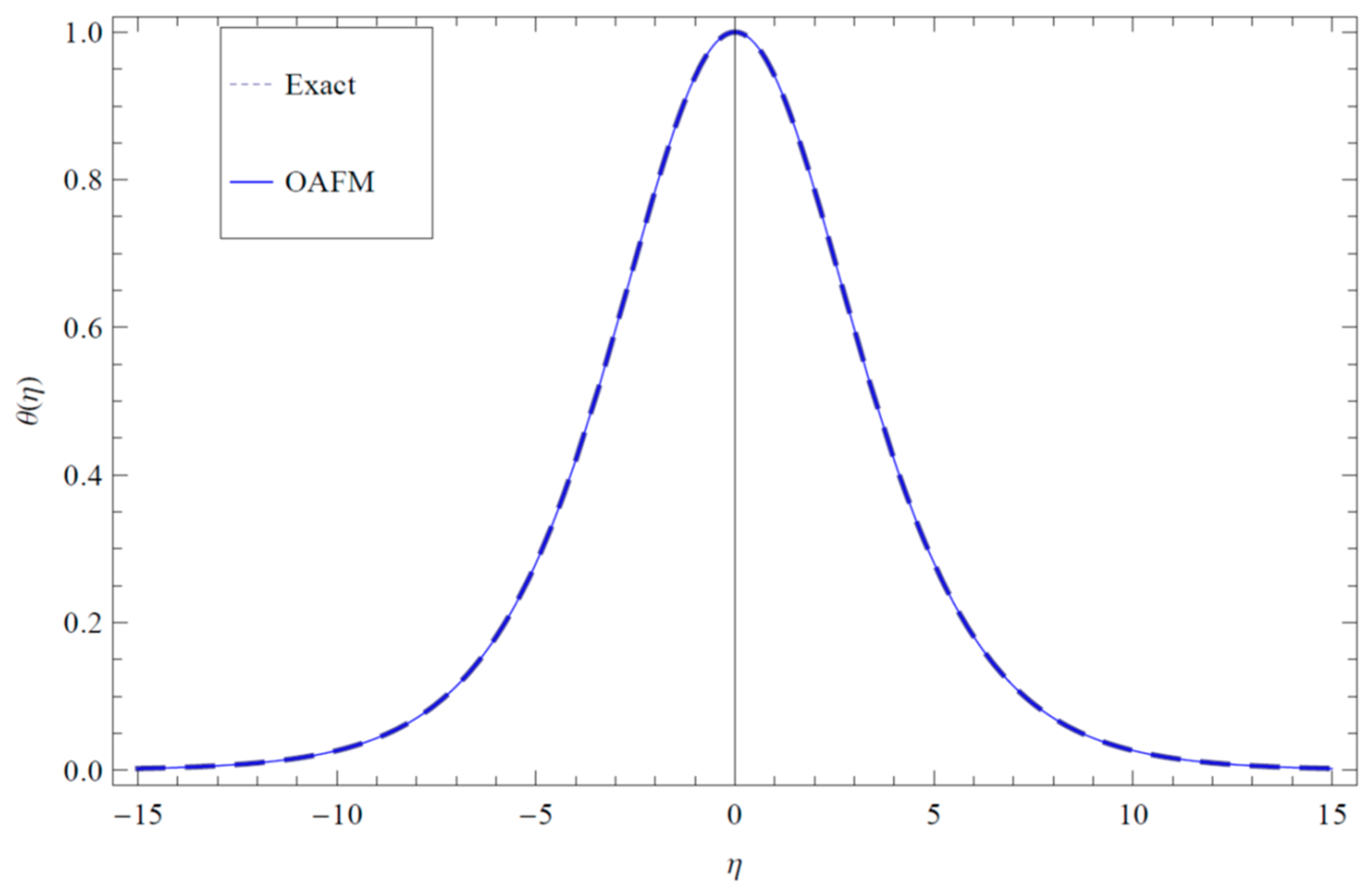
| α = 1 | α = 0.8 | α = 0.7 | α = 0.6 | |
|---|---|---|---|---|
| 0.9999999999999998 | 1.0689593321155948 | 1.1649666232352796 | 1.3213063996776493 | |
| OAFM Solution | Exact Solution | NIM Error [39] | q-HAM Error [39] | OAFM Error | |||||
|---|---|---|---|---|---|---|---|---|---|
| α = 0.6 | α = 0.7 | α = 0.8 | α = 1 | ||||||
| 0.01 | 0.0 | 0.065975 | 0.0361 | 0.020385 | 0.007070 | 0.007070 | 1.151971 × 10−7 | 2.35697 × 10−12 | 4.77049 × 10−17 |
| 1.0 | 0.650199 | 0.63147 | 0.621632 | 0.613291 | 0.613291 | 1.810671 × 10−7 | 2.82376 × 10−10 | 9.99201 × 10−16 | |
| 2.0 | 0.902204 | 0.89594 | 0.892655 | 0.889867 | 0.889867 | 6.167394 × 10−8 | 5.74951 × 10−11 | 9.99201 × 10−16 | |
| 3.0 | 0.975328 | 0.97367 | 0.972799 | 0.972060 | 0.972060 | 1.165205 × 10−9 | 3.75726 × 10−11 | 1.11022 × 10−16 | |
| 0.05 | 0.0 | 0.173216 | 0.11130 | 0.073843 | 0.035340 | 0.035340 | 1.306675 × 10−5 | 7.361971 × 10−9 | 3.72481 × 10−12 |
| 1.0 | 0.715566 | 0.67742 | 0.65435 | 0.630632 | 0.630632 | 2.224480 × 10−5 | 1.736922 × 10−7 | 1.39521 × 10−11 | |
| 2.0 | 0.923783 | 0.91113 | 0.903476 | 0.895608 | 0.895608 | 7.794449 × 10−6 | 3.622408 × 10−8 | 1.85728 × 10−11 | |
| 3.0 | 0.981023 | 0.97768 | 0.975656 | 0.973577 | 0.973577 | 1.257660 × 10−7 | 2.328496 × 10−8 | 1.11566 × 10−12 | |
| 0.08 | 0.0 | 0.229497 | 0.15456 | 0.10748 | 0.056508 | 0.056508 | 4.940148 × 10−5 | 7.713501 × 10−8 | 9.99082 × 10−11 |
| 1.0 | 0.748476 | 0.70289 | 0.674246 | 0.643237 | 0.643237 | 8.990891 × 10−5 | 1.124520 × 10−6 | 2.17279 × 10−10 | |
| 2.0 | 0.934445 | 0.91940 | 0.909956 | 0.899727 | 0.899727 | 3.218897 × 10−5 | 2.387229 × 10−7 | 3.08464 × 10−10 | |
| 3.0 | 0.983821 | 0.97985 | 0.977359 | 0.974662 | 0.974662 | 4.548965 × 10−7 | 1.516340 × 10−7 | 1.89203 × 10−11 | |
| 0.1 | 0.0 | 0.262219 | 0.18058 | 0.128409 | 0.070593 | 0.070593 | 9.109940 × 10−5 | 2.352262 × 10−7 | 4.76052 × 10−10 |
| 1.0 | 0.767071 | 0.71788 | 0.686336 | 0.651452 | 0.651452 | 1.740220 × 10−4 | 2.722916 × 10−6 | 7.86751 × 10−10 | |
| 2.0 | 0.940392 | 0.92420 | 0.913853 | 0.902386 | 0.902386 | 6.321236 × 10−5 | 5.848640 × 10−7 | 1.16877 × 10−9 | |
| 3.0 | 0.985376 | 0.98111 | 0.978381 | 0.975358 | 0.975358 | 8.108096 × 10−7 | 3.686350 × 10−7 | 7.26751 × 10−11 | |
| −0.9999870166919811 | −1.1189030434611396 | −1.208213789561331 | |
| 0.33313615275841246 | 0.9544139953390676 | 1.341269491284959 | |
| −0.4945108518067398 | −6.4337069205146395 | −10.808604146484456 | |
| 0.4503627958849215 | 20.772596091262024 | 37.507958650955004 | |
| −0.2727180163051805 | −29.1932425180932 | −54.58723568118725 | |
| HPM Sol. [40] | OAFM Solution | Exact Solution | Abs. HPM [40] | Abs. OAFM | ||||
|---|---|---|---|---|---|---|---|---|
| 0.9 | 0.2 | 0.5804 | 0.583333 | 0.342866 | 0.217758 | 0.583333 | 2.933 × 10−3 | 9.39489 × 10−8 |
| 1.2 | 0.2 | 0.8304 | 0.833333 | 0.554898 | 0.410035 | 0.833333 | 2.933 × 10−3 | 1.08783 × 10−7 |
| 1.5 | 0.2 | 1.08 | 1.08333 | 0.766929 | 0.602313 | 1.08333 | 3.33 × 10−3 | 1.23617 × 10−7 |
| 1.8 | 0.2 | 1.3296 | 1.33333 | 0.978961 | 0.79459 | 1.33333 | 3.73 × 10−3 | 1.38451 × 10−7 |
| 2 | 0.2 | 1.496 | 1.5 | 1.12032 | 0.922775 | 1.5 | 4.0 × 10−3 | 1.4834 × 10−7 |
| 1 | 0.3 | 0.526 | 0.538435 | 0.271101 | 0.124476 | 0.538462 | 2.462 × 10−3 | 2.64625 × 10−5 |
| 1 | 0.35 | 0.45925 | 0.481359 | 0.168277 | −0.03724 | 0.481481 | 2.223 × 10−2 | 1.2237 × 10−4 |
| 1 | 0.4 | 0.392 | 0.428173 | −0.00623 | −0.35796 | 0.428571 | 3.657 × 10−2 | 3.98493 × 10−4 |
| 1 | 0.45 | 0.32275 | 0.378264 | −0.31461 | −0.96298 | 0.37931 | 5.656 × 10−2 | 1.04634 × 10−3 |
| 1 | 0.5 | 0.25 | 0.330963 | −0.84290 | −2.02297 | 0.333333 | 8.333 × 10−2 | 2.3706 × 10−3 |
| RPSM [41] Sol. at | OAFM Solution at | Exact Solution | Abs. RPSM [41] | Abs. OAFM | ||||
|---|---|---|---|---|---|---|---|---|
| −15 | 0.001 | 0.0022087864 | 0.00220879 | 0.0021987 | 0.00218763 | 0.00220879 | 2.44 × 10−9 | 9.17574 × 10−10 |
| 0.01 | 0.0021988584 | 0.00219885 | 0.0021540 | 0.00212126 | 0.00219888 | 2.41 × 10−8 | 3.39094 × 10−8 | |
| 0.1 | 0.0021019994 | 0.00209946 | 0.0019299 | 0.00185702 | 0.00210223 | 2.29 × 10−7 | 2.77232 × 10−6 | |
| −10 | 0.001 | 0.0265787633 | 0.0265791 | 0.0264598 | 0.0263276 | 0.02657911 | 349 × 10−7 | 1.08249 × 10−8 |
| 0.01 | 0.0264579103 | 0.026461 | 0.0259285 | 0.0255388 | 0.02646140 | 3.45 × 10−6 | 3.94981 × 10−7 | |
| 0.1 | 0.0252801959 | 0.0252796 | 0.0232655 | 0.0223983 | 0.02531183 | 3.16 × 10−5 | 3.21803 × 10−5 | |
| −5 | 0.001 | 0.2802626306 | 0.280296 | 0.2792140 | 0.2780160 | 0.28029508 | 3.33 × 10−5 | 8.95206 × 10−8 |
| 0.01 | 0.2788971245 | 0.279225 | 0.2743971 | 0.2708640 | 0.27922753 | 3.30 × 10−4 | 2.72217 × 10−6 | |
| 0.1 | 0.2656871698 | 0.268514 | 0.2502531 | 0.2423990 | 0.26872355 | 3.30 × 10−3 | 2.09181 × 10−4 | |
| 0 | 0.001 | 0.9999997500 | 1 | 1 | 1 | 1 | 1.88 × 10−7 | 6.25000 × 10−8 |
| 0.01 | 0.9999750000 | 1 | 1 | 1 | 0.99999475 | 1.88 × 10−6 | 6.24997 × 10−6 | |
| 0.1 | 0.9974997396 | 1 | 1 | 1 | 0.99937526 | 1.88 × 10−3 | 6.24740 × 10−4 | |
| 5 | 0.001 | 0.2805672046 | 0.280534 | 0.2816160 | 0.282814 | 0.28053822 | 3.34 × 10−5 | 4.89041 × 10−8 |
| 0.01 | 0.2819428891 | 0.281605 | 0.2864333 | 0.289966 | 0.28160625 | 3.37 × 10−4 | 1.33948 × 10−6 | |
| 0.1 | 0.2961686088 | 0.292315 | 0.3105766 | 0.318439 | 0.29251226 | 3.66 × 10−3 | 1.96911 × 10−4 | |
| 10 | 0.001 | 0.0266056972 | 0.0266054 | 0.0267247 | 0.0268568 | 0.02660534 | 3.49 × 10−7 | 4.44199 × 10−9 |
| 0.01 | 0.0267272511 | 0.0267235 | 0.0272560 | 0.0276457 | 0.02672372 | 3.52 × 10−6 | 2.43308 × 10−7 | |
| 0.1 | 0.0279748560 | 0.0279048 | 0.0299189 | 0.0307862 | 0.02793650 | 3.84 × 10−5 | 3.16596 × 10−5 | |
| 15 | 0.001 | 0.0022109987 | 0.002211 | 0.0022210 | 0.0022321 | 0.00221109 | 2.44 × 10−9 | 3.66932 × 10−10 |
| 0.01 | 0.0022209817 | 0.00222094 | 0.0022657 | 0.0022985 | 0.00222096 | 2.46 × 10−8 | 2.11548 × 10−8 | |
| 0.1 | 0.0023233232 | 0.00232033 | 0.0024898 | 0.0025628 | 0.00232306 | 2.59 × 10−7 | 2.73523 × 10−6 | |
| Exact Solution | OAFM Solution | Error RPSM [42] | Error [42] FHATM | Error OAFM | ||
|---|---|---|---|---|---|---|
| 10 | 0.01 | 2.672 × 10−2 | 2.672 × 10−2 | 3523 × 10−6 | 4529 × 10−5 | 2.4331 × 10−7 |
| 0.001 | 2.661 × 10−2 | 2.661 × 10−2 | 3492 × 10−7 | 4501 × 10−6 | 4.4419 × 10−9 | |
| 15 | 0.01 | 2.221 × 10−3 | 2.221 × 10−3 | 2464 × 10−8 | 3717 ×10−6 | 2.1155 × 10−8 |
| 0.001 | 2.211 × 10−3 | 2.211 × 10−3 | 2441 × 10−9 | 3697 × 10−7 | 3.6690 × 10−10 | |
| 20 | 0.01 | 1.825 × 10−4 | 1.825 × 10−4 | 1663 × 10−10 | 3034 × 10−7 | 1.7446 × 10−9 |
| 0.001 | 1.817 × 10−8 | 1.817 × 10−4 | 1640 × 10−11 | 3018 × 10−8 | 3.0135 × 10−11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashraf, R.; Nawaz, R.; Alabdali, O.; Fewster-Young, N.; Ali, A.H.; Ghanim, F.; Alb Lupaş, A. A New Hybrid Optimal Auxiliary Function Method for Approximate Solutions of Non-Linear Fractional Partial Differential Equations. Fractal Fract. 2023, 7, 673. https://doi.org/10.3390/fractalfract7090673
Ashraf R, Nawaz R, Alabdali O, Fewster-Young N, Ali AH, Ghanim F, Alb Lupaş A. A New Hybrid Optimal Auxiliary Function Method for Approximate Solutions of Non-Linear Fractional Partial Differential Equations. Fractal and Fractional. 2023; 7(9):673. https://doi.org/10.3390/fractalfract7090673
Chicago/Turabian StyleAshraf, Rashid, Rashid Nawaz, Osama Alabdali, Nicholas Fewster-Young, Ali Hasan Ali, Firas Ghanim, and Alina Alb Lupaş. 2023. "A New Hybrid Optimal Auxiliary Function Method for Approximate Solutions of Non-Linear Fractional Partial Differential Equations" Fractal and Fractional 7, no. 9: 673. https://doi.org/10.3390/fractalfract7090673
APA StyleAshraf, R., Nawaz, R., Alabdali, O., Fewster-Young, N., Ali, A. H., Ghanim, F., & Alb Lupaş, A. (2023). A New Hybrid Optimal Auxiliary Function Method for Approximate Solutions of Non-Linear Fractional Partial Differential Equations. Fractal and Fractional, 7(9), 673. https://doi.org/10.3390/fractalfract7090673









