Abstract
A class of generalized fractional Zener-type viscoelastic models with general fractional derivatives is considered. Two integral representations are derived for the corresponding relaxation modulus. The first representation is established by applying the Laplace transform to the constitutive equation and using the Bernstein functions technique to justify the change of integration contour in the complex Laplace inversion formula. The second integral representation for the relaxation modulus is obtained by applying the subordination principle for the relaxation equation with generalized fractional derivatives. Two particular examples of the considered class of models are discussed in more detail: a model with fractional derivatives of uniformly distributed order and a model with general fractional derivatives, the kernel of which is a multinomial Mittag-Leffler-type function. To illustrate the analytical results, some numerical examples are presented.
Keywords:
fractional Zener model; completely monotone function; Stieltjes function; complete Bernstein function; multinomial Mittag-Leffler function MSC:
26A33; 33E12; 74D05
1. Introduction
Analytical methods play an essential role in the study of linear viscoelastic models [1,2]: this is, in general, due to the fact that in such models the rheological properties of a viscoelastic medium are described by a linear constitutive relation between stress and strain . Such a stress–strain relation can be studied analytically by employing the Laplace transform.
Let us consider the uniaxial case, in which and , where and are spatial and temporal variables, respectively. For systems that are at rest before some starting time, , the relaxation modulus is defined via the convolutional relation [2]
which allows us to study the relaxation modulus by the use of the Laplace transform with respect to time.
Fractional calculus has been extensively employed in linear viscoelasticity, due to its ability to model phenomena with memory [1,2,3]. For instance, incorporating non-integer time derivatives in viscoelastic equations provides an appropriate framework for the description of properties of polymer solution and melts [4]. One of the most used fractional viscoelastic models of solid-like behavior is the fractional Zener model, which is defined by the following stress–strain constitutive relation [1,2]:
Here, is the fractional Riemann–Liouville derivative of order , defined by (see, e.g., [5])
In the limiting case , the stress–strain relation (2) represents the classical Zener model, which is also referred to as the Standard Linear Solid model [2].
The relaxation modulus , in the case of the fractional Zener model (2), admits the explicit representation
where denotes the Mittag-Leffler function
Different integral representations for the relaxation modulus (4) can be derived based on such representations for the Mittag-Leffler function. First, the integral representation formula for the Mittag-Leffler function in [6], Equation (A30), yields
where the spectral function is defined as follows:
Since under the restrictions on the parameters in (2), representation (6) implies that the function is completely monotone.
Another type of integral representation follows from the formula (see, e.g., [2])
where is the following function of Wright type:
This function is usually referred to as the Mainardi function.
Various types of generalizations of the classical fractional Zener constitutive model (2) have been proposed and studied in the literature. In [7,8,9,10,11,12], different Zener-type models of distributed order are studied. In [7], the following stress–strain relation of distributed order was proposed:
where the weight functions and are non-negative. By setting
where and for all and denotes the Dirac delta function, the following constitutive equation is obtained:
The multi-term stress–strain relation (11) was studied in [8], and restrictions on the parameters were found, which guarantee thermodynamic compatibility. When the weight functions in (10) have the form
then the model is the so-called power-type distributed-order model. It was proved in [7] that the rheological model (10) with power weight functions (12) is thermodynamically compatible, provided . The constitutive Equation (10) and the related mechanical models are studied in [9,10]. Integral representations of the relaxation moduli, which generalize representation (6), were deduced in [11] for the model (11) and the model with continuous power-type distribution (10)–(12) under the above-mentioned thermodynamic restrictions on the parameters. The obtained representations imply that the corresponding relaxation moduli are completely monotone functions. In [12], restrictions on the parameters guaranteeing thermodynamic compatibility were formulated for the distributed-order model (10), with weight functions of a more general form:
where and are non-negative integrable functions defined for . In recent works [13,14], constitutive models of the Zener type, containing both fractional integrals and derivatives, have been formulated and their thermodynamical consistency has been studied. Relaxation moduli were calculated, and restrictions on model parameters narrowing thermodynamical constraints were posed, in order to ensure complete monotonicity.
A Zener-type model with general fractional derivatives was proposed in [15], and restrictions on the coefficients were derived that followed from the dissipation inequality. General fractional differential operators are a subject of increasing interest—see, e.g., [16,17,18], to mention only a few of many recent publications.
Motivated by [15], where a generalization of model (2) was proposed, with fractional derivative replaced by a general convolutional derivative , we consider the generalized fractional Zener model with the constitutive equation
Here, is the convolutional derivative in the Riemann–Liouville sense, defined by
where is a locally integrable memory kernel. Further assumptions on the kernel are specified later in Section 3.
Based on the properties of completely monotone, Stieltjes, and complete Bernstein functions, in [19] the complete monotonicity of the relaxation modulus for the generalized Zener model (13) was proved and the subordination principle for the corresponding Zener-type wave equation was established.
Integral representations for the relaxation moduli of viscoelastic models have proven useful for the analytical and numerical study of the corresponding models. Therefore, the aim of the present work is to establish integral representations for the relaxation modulus of the Zener model (13), which generalize representations (6) and (9).
First, we establish a representation of the form (6), based on deforming the contour of integration in the complex inversion formula for the Laplace transform. Such a technique has been extensively used in the literature. In [20], sufficient conditions were formulated under which the change of integration contour to the so-called Hankel path was justified. In [1,10], the method was applied to different fractional evolution equations. Applications to distributed-order relaxation equations can be found in [21,22].
To obtain an alternative integral representation for , which generalises (9), we use the relation of this function and the solution of a relaxation equation with a general fractional Caputo derivative with kernel , and we apply the subordination principle for this equation [16,23,24]. The concept of subordination, originally introduced by Bochner in the theory of stochastic processes, has developed recently into a powerful tool in the study of anomalous relaxation and diffusion processes and the physics of complex systems (see, e.g., [25,26,27] and the recent review paper [28]).
The present work is organized as follows. Section 2 contains preliminaries on completely monotone, Stieltjes and complete Bernstein functions. In Section 3, the generalized fractional Zener model is formulated and some basic properties are discussed. In Section 4, the first integral representation for the relaxation modulus is derived. Section 5 contains two particular examples: the Zener model with fractional derivatives of uniformly distributed order and the one with general fractional derivatives, the kernel of which is a multinomial Mittag-Leffler-type function. Numerical results, based on the first integral representation, are given. Applying the subordination principle for the generalized fractional relaxation equation, a second integral representation for the relaxation modulus is obtained in Section 6. Concluding remarks are given in Section 7.
2. Preliminaries
The sets of real and complex numbers are denoted by and , respectively, and .
The Laplace transform of a function is denoted by or :
The class of completely monotone functions, which we denote by , consists of all real-valued functions , defined on the half-line , such that and
According to Bernstein’s theorem, a function is completely monotone if and only if it can be represented as the Laplace transform of a measure on .
The class of Stieltjes functions consists of all non-negative functions defined on that admit the representation (see [16])
where , and the Laplace transform of f exists for any . The constants A and B in (16) are determined by the identities
Any Stieltjes function is completely monotone.
The class of complete Bernstein functions consists of all non-negative functions defined on , which admit the representation [29]
where , and is a completely monotone function, such that
Any complete Bernstein function is a Bernstein function: that is, , and .
Next, some properties of the above special classes of functions are summarized for further use in this work.
Theorem 1
([29]). Suppose that φ is a non-negative function on and . The following statements hold true:
- (P1)
- The sets , , and are convex cones, closed under pointwise limits.
- (P2)
- if and only if .
- (P3)
- Let . Then, if and only if .
- (P4)
- Any function has an analytic continuation to the upper half-plane,which is defined by the expressionwhere are the constants defined in (19) and ν is a Borel measure on satisfying
- (P5)
- Any function φ from the classes or admits an analytic extension to the complex plane cut along the negative real axis , such thatwhere ∗ stands for complex conjugate. Moreover, if , thenand
- (P6)
- Let φ be the analytic extension of a complete Bernstein function to . Then, the limitexists and is real.
- (P7)
- If , then
For details on the proofs, we refer to [29].
The following result is usually referred to as the Karamata–Feller theorem.
Theorem 2
([30]). Let be a slowly varying function at ∞, i.e., for every fixed it holds as . Let and be such that its Laplace transform exists for all . Then,
if and only if
where is the function defined in (3).
Here, and later in this work, the notation as stands for
3. Model Formulation
We consider the generalized fractional Zener model defined by constitutive Equation (13) with the convolutional derivative in the Riemann–Liouville sense (14). We assume that the Laplace transform of the kernel exists for all and
where denotes the class of Stieltjes functions (see (16)). Moreover, we suppose
in the Laplace domain (1), yielding
Here, and denote the Laplace transforms of the functions and with respect to t, while x is considered as a parameter. Applying the Laplace transform to constitutive Equation (13), and using the identity
we deduce the relation
In this way, we obtain
Let us mention some basic characteristics of the model. Based on (29) and assumption (27) in [19] we found that
Furthermore, assumption (26) is equivalent to (see (P2))
which, according to property (P6), implies
where denotes . Therefore, applying the final value theorem for the Laplace transform, we obtain
Since , i.e., there is no full relaxation, constitutive Equation (13) is a model for solid-like viscoelastic behavior as the classical fractional one (2).
It was proven in [15] that condition is sufficient for the thermodynamic compatibility of model (13). In [19], it was established that this condition implies a stronger property of complete monotonicity of the relaxation modulus. Moreover, it appears that the constraint is also a necessary condition for the physical acceptability of model (13). Indeed, in a physically meaningful model, the function should be monotonically decreasing, in particular : this, by taking into account (30) and (33), implies .
In the rest of this work, we assume , where is defined in (32). This is a normal assumption for the kernels of general fractional derivatives (see [16]). In the present work, this restriction is posed only for technical convenience.
4. First Integral Representation
To derive an integral representation for , we use the derived Laplace transform , given in (29), which we rewrite in the form
where
with , as defined in (31). Since , admits an analytic extension to —see (P5)—and is a non-negative and monotonically non-decreasing function for . Therefore, for , and (35) can be written in the form
Applying properties (P1) and (P3), it follows that . Then, by (P2),
Applying again (P3), we obtain . This, by (P5), in particular, implies that the function admits an analytic extension to the complex plane cut along the negative real axis . Therefore, to derive a representation for , we can apply the inverse Laplace integral formula to (34) and change the integration contour in the complex plane. The result is given in the next theorem. As usual, the notation stands for .
Theorem 3.
Assume and let the kernel be such that and
Suppose, moreover, that there exists , such that
where is a function, which does not depend on ϕ and for any . Assume the limit exists for almost all . Then, the relaxation modulus for constitutive model (13) is a continuous function for , infinitely differentiable and completely monotone for , and admits the integral representation
Here, the function is defined by the identity
with
Proof.
Applying the inversion formula for the Laplace transform to (34), and taking into account that , we obtain
where function is defined in (35). The function has the Stieltjes function representation (16) with , calculated by applying (17) and (37). Therefore, is the Laplace transform of a completely monotone function, denoted by —that is, . Then, and, in particular, it is infinitely differentiable for . It follows from (37) that
Applying Theorem 2, (35) implies
In this way, we prove that is continuous for and . Next, our aim is to find a representation for .
By applying Cauchy’s theorem, the integration contour in (41) can be replaced by the composite contour with appropriate orientation, where
with and letting , .
We first prove that
uniformly on for any . This follows from the fact that for any real constant and ,
Indeed, since , it satisfies (22), which yields
Therefore, for some , . Applying the elementary inequality
it follows that
which implies (43). This, together with (35), yields the estimate (42).
By the use of (42), we prove that the integrals on the contours and vanish as . Indeed, for the integral on the contour we obtain
The integral on is evaluated analogously. For the integration on , (42) implies
where we have used the fact that . The integral on is evaluated analogously.
In order to prove that the integral over vanishes as , we show first that
To this end, we use representation (20) in the upper half-plane for the complete Bernstein function . As , the constant A defined in (20) vanishes, . Since, for and
it follows by the integration properties of the measure
Plugging this limit in representation (20) implies that (46) is satisfied in the upper half-plane . For , the function is real-valued and satisfies (46) by assumption. Since for s in the lower half-plane is defined by the Schwarz reflection principle (see (21)), it follows that (46) is satisfied for all .
This estimate, together with (46), implies that for
Therefore, the contour of the integral in (41) can be replaced by the contour , with and , which implies
Since satisfies (21) as a Stieltjes function, it follows that
5. Examples
In this section, we consider two examples of kernels k in the definition (14) of the convolutional derivative , and we show that for both examples the conditions of Theorem 3 are satisfied. Asymptotic expansions of the corresponding relaxation moduli are also discussed.
5.1. Fractional Derivative of Uniformly Distributed Order
Consider first the following particular case of the Zener-type model (13).
Example 1.
Let (14) be the distributed-order fractional derivative with uniform distribution in the interval . In this case,
Therefore, assumption (38) is satisfied.
Let us establish the asymptotic expansion of the relaxation modulus for in the case of Example 1. We use the expansion
which follows from (49). Applying the Karamata–Feller theorem (Theorem 2) with and , and taking into account relation (34), we derive
Therefore, the function exhibits a slow logarithmic decay for large times and .
Theorem 3 is applied for numerical computation of for the model in Example 1. The results obtained for several values of the parameters a and b are plotted in Figure 1.
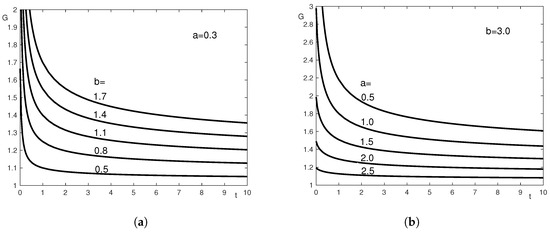
Figure 1.
Relaxation modulus for the model of Example 1: (a) and different values of b; (b) and different values of a.
5.2. Convolutional Derivative with Multinomial Mittag-Leffler-Type Kernel
The multinomial Mittag-Leffler function, introduced in [31], is defined by the series
where , , , . Consider the following multinomial Mittag-Leffler-type function of a single variable :
where , , . It obeys the Laplace transform pair
Viscoelastic models with memory kernels given in terms of completely monotone multinomial Mittag-Leffler functions were studied in our previous work [33].
For other types of multi-index and multi-variable generalizations of the classical Mittag-Leffler function (5), we refer to [34,35,36,37].
In this subsection, we consider the following special case of the generalized Zener model.
Example 2.
Assume the kernel in definition (14) is given by the completely monotone function of multinomial Mittag-Leffler type:
where
In this case, is given by (55), limits (37) hold, and as the Laplace transform of a completely monotone function. Inserting (55) into (29) yields
A comparison to the fractional Zener model with multiple fractional derivatives (11) studied in [8] shows that the model of Example 2 is a special case of it and corresponds to the constitutive equation
Furthermore, inserting with from (55) into (36) yields
where . By the use of identity (55), we deduce that (58) is a Laplace transform of a multinomial Mittag-Leffler-type function, which leads to the following explicit representation
Therefore, the relaxation modulus has the explicit representation with given in (59), which is a generalization of Formula (4) for the classical fractional Zener model.
Let us check the rest of the conditions of Theorem 3. Since (58) implies
estimate (38) is satisfied.
Let us note that in the case of kernel (57) estimate (42) is satisfied for all . This can be deduced from the property (c.f., Proposition 3.1 in [32]) for the function
This property implies by the use of (22) the inequality
which leads to estimate (43) (in the same way as in the proof of Theorem 3), which, in turn, implies (42). This estimate guarantees the integrability of for all s except those near the origin.
Let us establish the asymptotic behavior of the function as and . For the series expansion (53) implies
For we use the asymptotic expansion of the multinomial Mittag-Leffler function, given in [32], for the function in the representation (59), which yields
Therefore, the relaxation modulus in the case of Example 2 exhibits an algebraic decay for large times to the final value .
Although in the case of Example 2 there exists an explicit representation for the function , in terms of the multinomial Mittag-Leffler-type function (59), the integral representation of Theorem 3 is still useful. For instance, it is convenient for numerical computation of the relaxation modulus and, respectively, the multinomial Mittag-Leffler-type function (59) (the infinite series (53) is not suitable for this purpose).
Theorem 3 is applied for the numerical computation of for the model with kernel (57) with , , , , . Figure 2 presents the numerical results obtained for several values of the parameters a and b. In order to enable comparison, we have chosen the same values of a and b as in Figure 1. Compared to the slow (logarithmic) decay in Figure 1, in Figure 2 we observe a faster (algebraic) decay for large times: this is in agreement with the asymptotic expansions (60) and (52). For all plots, the numerical initial value is in agreement with formula (30).
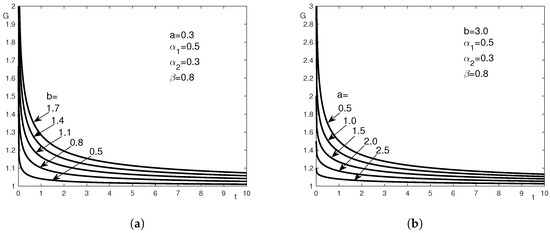
Figure 2.
Relaxation modulus for the model of Example 2 with , , , , : (a) and different values of b; (b) and different values of a.
6. Second Integral Representation
Another integral representation for the function can be derived by applying the subordination principle for the generalized fractional relaxation equation [16,23,24]:
where and is the convolutional derivative in Caputo sense [16]:
Problem (61) is studied in [16], see also [23,24]. Detailed study in the case of distributed order derivatives can be found in [21,22].
The subordination relation for the solution to problem (61) is given next, adapted for use here (see [23,24]).
Theorem 4
From the relation between the convolutional derivatives in Riemann–Liouville and Caputo sense in (62) and identity (28), we obtain for the solution of problem (61) the following expression in the Laplace domain:
Applying the uniqueness property of the Laplace transform, the obtained identity compared to (35) implies that the function in the representation is the solution of the relaxation Equation (61), with convolutional derivative in Caputo sense and with the same kernel k as in (14), and
Applying the subordination relation (63), we deduce the following:
Theorem 5.
We close this section with an estimate, which follows from the established relation of and the solution of the generalized fractional relaxation Equation (61), by applying Theorem 5.8 in the dissertation [24].
Corollary 1.
Assume the conditions of Theorem 5 are satisfied. Then, the relaxation modulus to model (13) obeys the estimate
where the function is related to the kernel via the identity
For instance, in the case of Example 2, by applying the Laplace transform we obtain
where the functions are defined in (3).
7. Concluding Remarks
In the present work, two integral representations are derived for the relaxation modulus of the generalized fractional Zener model (13). The results are formulated in Theorems 3 and 5. The main difficulty in the proof of Theorem 3 is to justify the change of the integration contour for the considered class of kernels. This is done based on the relevant properties of Stieltjes functions and related classes of functions. On the other hand, Theorem 5 is a straightforward implication of the subordination principle for the generalized fractional relaxation equation.
The first representation, (39), demonstrates that is a completely monotone function under the assumptions of Theorem 3: this is implied by the non-negativity of the spectral function . For some models, deriving such a representation with a non-negative spectral function is the most convenient way to establish complete monotonicity of the relaxation modulus (see e.g., [11]). In addition, representation (39) is appropriate for numerical computation of the relaxation modulus.
The second integral representation, (66), splits the relaxation modulus into two parts: a probability density function , which depends only on the kernel k and is independent of the model parameters a and b, and the function . Such a decomposition makes representation (66) suitable for obtaining estimates for the relaxation modulus , as well as for the study of the effect of the parameters a and b on its behavior, which will be a subject of future work.
The technique presented in this paper could be applied to other viscoelastic constitutive equations, to obtain integral representations for the corresponding relaxation moduli. Such representations would be useful for the analytical and numerical study of the models.
Author Contributions
Conceptualization, E.B. and S.P.; methodology and formal analysis, E.B. and S.P.; writing—original draft preparation and revision, E.B. and S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This study was performed within the bilateral project funded by the Bulgarian National Science Fund, Project number KP-06-Russia/5, from 11 December 2020.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; John Wiley & Sons: London, UK, 2014. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity, 2nd ed.; World Scientific: Sinagapore, 2022. [Google Scholar] [CrossRef]
- Mainardi, F. An historical perspective on fractional calculus in linear viscoelasticity. Fract. Calc. Appl. Anal. 2012, 15, 712–717. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 137–148. [Google Scholar] [CrossRef]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional calculus: Integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: New York, NY, USA, 1997; pp. 223–276. [Google Scholar]
- Atanacković, T.M. On a distributed derivative model of a viscoelastic body. C. R. Méc. 2003, 331, 687–692. [Google Scholar] [CrossRef]
- Atanacković, T.; Konjik, S.; Oparnica, L.; Zorica, D. Thermodynamical restrictions and wave propagation for a class of fractional order viscoelastic rods. Abstr. Appl. Anal. 2011, 2011, 975694. [Google Scholar] [CrossRef]
- Rossikhin, Y.; Shitikova, M. Analysis of the viscoelastic rod dynamics via models involving fractional derivatives or operators of two different orders. Shock Vib. Dig. 2004, 36, 3–26. [Google Scholar] [CrossRef]
- Konjik, S.; Oparnica, L.; Zorica, D. Distributed-order fractional constitutive stress–strain relation in wave propagation modeling. Z. Angew. Math. Phys. 2019, 70, 51. [Google Scholar] [CrossRef]
- Bazhlekova, E.; Bazhlekov, I. Complete monotonicity of the relaxation moduli of distributed-order fractional Zener model. AIP Conf. Proc. 2018, 2048, 050008. [Google Scholar] [CrossRef]
- Atanacković, T.M.; Janev, M.; Pilipović, S. Restrictions on parameters in distributed order fractional linear constitutive equations. Appl. Math. Model. 2022, 110, 99–111. [Google Scholar] [CrossRef]
- Jelić, S.; Zorica, D. Energy balance for fractional anti-Zener and Zener models in terms of relaxation modulus and creep compliance. Appl. Math. Model. 2023, 123, 688–728. [Google Scholar] [CrossRef]
- Jelić, S.; Zorica, D. Fractionalization of anti-Zener and Zener models via rheological analogy. Acta Mech. 2023, 234, 313–354. [Google Scholar] [CrossRef]
- Atanacković, T.M.; Pilipović, S. Zener model with General Fractional Calculus: Thermodynamical restrictions. Fractal Fract. 2022, 617, 6. [Google Scholar] [CrossRef]
- Kochubei, A. General fractional calculus, evolution equations, and renewal processes. Integr. Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Luchko, Y.; Yamamoto, M. The general fractional derivative and related fractional differential equations. Mathematics 2020, 8, 2115. [Google Scholar] [CrossRef]
- Tarasov, V.E. Nonlocal Probability Theory: General Fractional Calculus Approach. Mathematics 2022, 10, 20. [Google Scholar] [CrossRef]
- Bazhlekova, E.; Bazhlekov, I. Subordination principle for generalized fractional Zener models. Fractal Fract. 2023, 7, 298. [Google Scholar] [CrossRef]
- Bobylev, A.; Cercignani, C. The inverse Laplace transform of some analytic functions with an application to the eternal solutions of the Boltzmann equation. Appl. Math. Lett. 2002, 15, 807–813. [Google Scholar] [CrossRef]
- Kochubei, A. Distributed order calculus and equations of ultraslow diffusion. J. Math. Anal. Appl. 2008, 340, 252–281. [Google Scholar] [CrossRef]
- Kubica, A.; Ryszewska, K. Decay of solutions to parabolic-type problem with distributed order Caputo derivative. J. Math. Anal. Appl. 2018, 465, 75–99. [Google Scholar] [CrossRef]
- Bazhlekova, E. Estimates for a general fractional relaxation equation and application to an inverse source problem. Math. Methods Appl. Sci. 2018, 41, 9018–9026. [Google Scholar] [CrossRef]
- Bazhlekova, E. Subordination Principle for Generalized Fractional Evolution Equations. Ph.D. Dissertation, Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Sofia, Bulgaria, 2022. [Google Scholar]
- Awad, E.; Sandev, T.; Metzler, R.; Chechkin, A. Closed-form multi-dimensional solutions and asymptotic behaviors for subdiffusive processes with crossovers: I. Retarding case. Chaos Solitons Fractals 2021, 152, 111357. [Google Scholar] [CrossRef]
- Iomin, A.; Metzler, R.; Sandev, T. Topological Subordination in Quantum Mechanics. Fractal Fract. 2023, 7, 431. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A.; Penson, K.A. Non-Debye Relaxations: The Ups and Downs of the Stretched Exponential vs. Mittag-Leffler’s Matchings. Fractal Fract. 2021, 5, 265. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A. Subordination and memory dependent kinetics in diffusion and relaxation phenomena. Fract. Calc. Appl. Anal. 2023, 26, 480–512. [Google Scholar] [CrossRef]
- Schilling, R.L.; Song, R.; Vondraček, Z. Bernstein Functions: Theory and Applications; De Gruyter: Berlin, Germany, 2010. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley: New York, NY, USA, 1971; Volume 2. [Google Scholar]
- Hadid, S.; Luchko, Y. An operational method for solving fractional differential equations of an arbitrary real order. Panam. Math. J. 1996, 6, 57–73. [Google Scholar]
- Bazhlekova, E. Completely monotone multinomial Mittag-Leffler type functions and diffusion equations with multiple time-derivatives. Fract. Calc. Appl. Anal. 2021, 24, 88–111. [Google Scholar] [CrossRef]
- Bazhlekova, E.; Pshenichnov, S. Wave propagation in viscoelastic half-space with memory functions of Mittag-Leffler type. Int. J. Appl. Math. 2021, 34, 423–440. [Google Scholar] [CrossRef]
- Kiryakova, V. A guide to special functions in fractional calculus. Mathematics 2021, 9, 106. [Google Scholar] [CrossRef]
- Kiryakova, V.; Paneva-Konovska, J. Multi-index Le Roy functions of Mittag-Leffler-Prabhakar type. Int. J. Appl. Math. 2022, 35, 745–768. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A. Special Functions of Fractional Calculus: Applications to Diffusion and Random Search Processes; World Scientific: Singapore, 2022. [Google Scholar] [CrossRef]
- Kürt, C.; Fernandez, A.; Özarslan, M. Two unified families of bivariate Mittag-Leffler functions. Appl. Math. Comput. 2023, 443, 127785. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).