Vertical Distribution of Suspended Sediment Concentration in the Unsaturated Jingjiang Reach, Yangtze River, China
Abstract
1. Introduction
2. Study Area, Data, and Methods
2.1. Study Area
2.2. Data
2.3. Methods
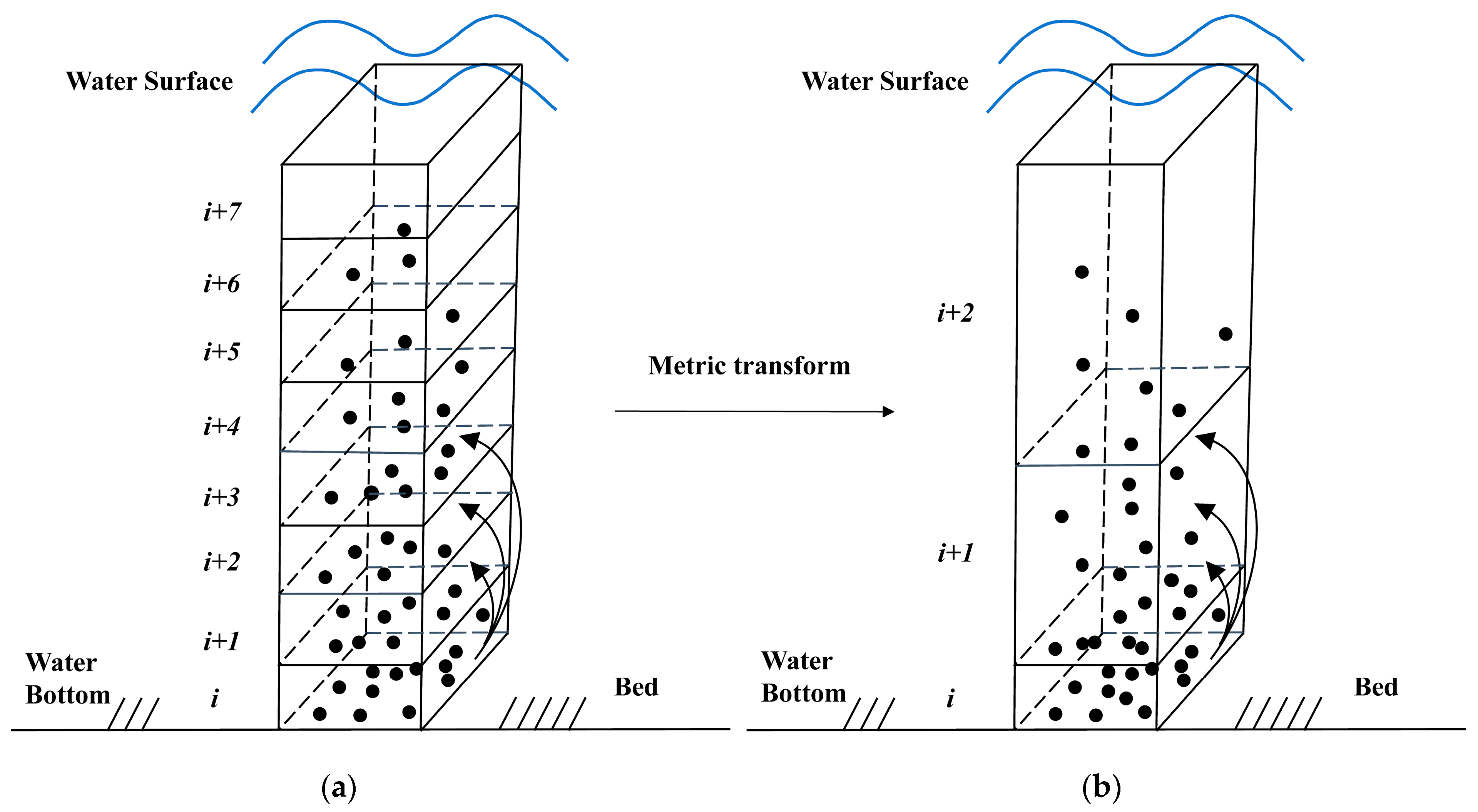
2.3.1. Hausdorff Fractal Space
2.3.2. Hausdorff Fractal Deviation for Non-Equilibrium SSC Vertical Profile
3. Results
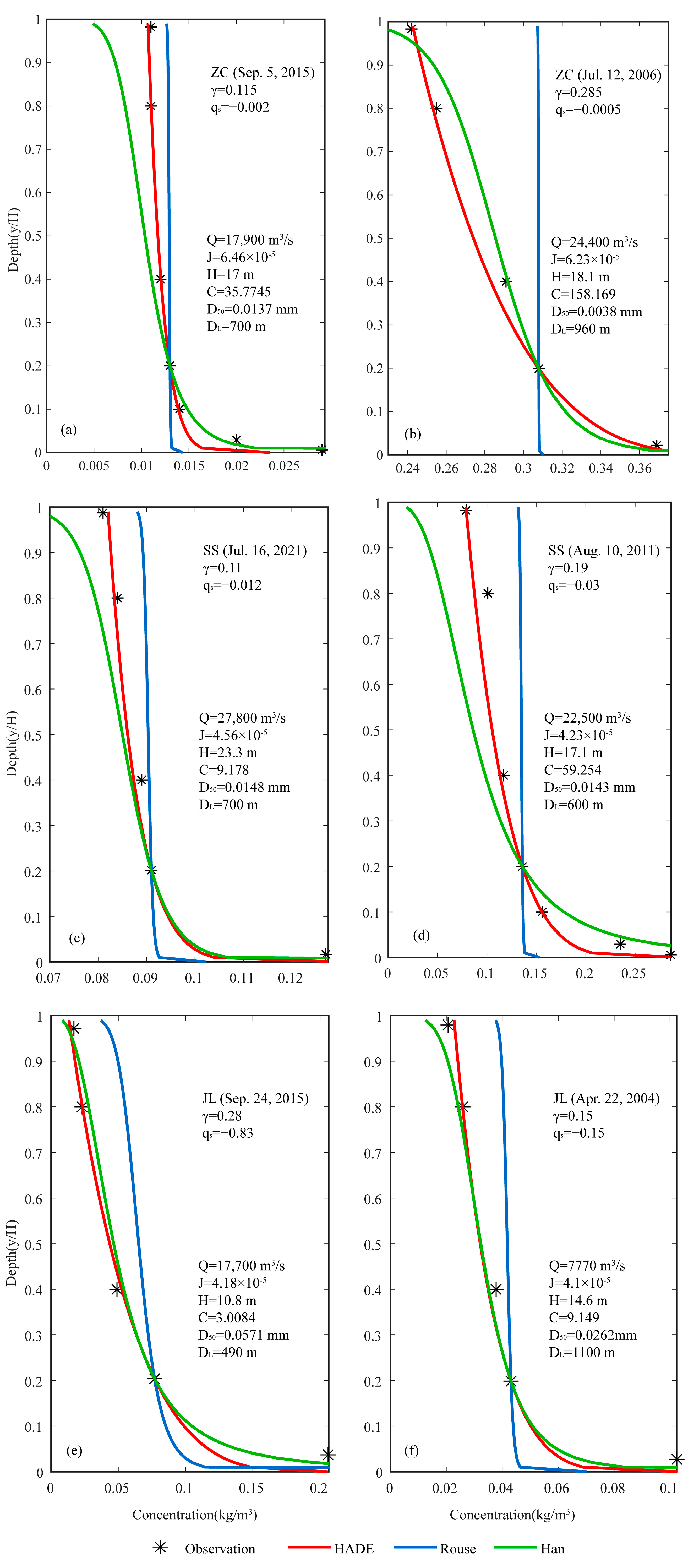
3.1. Comparison of Formulae in Describing Vertical Sediment Profiles
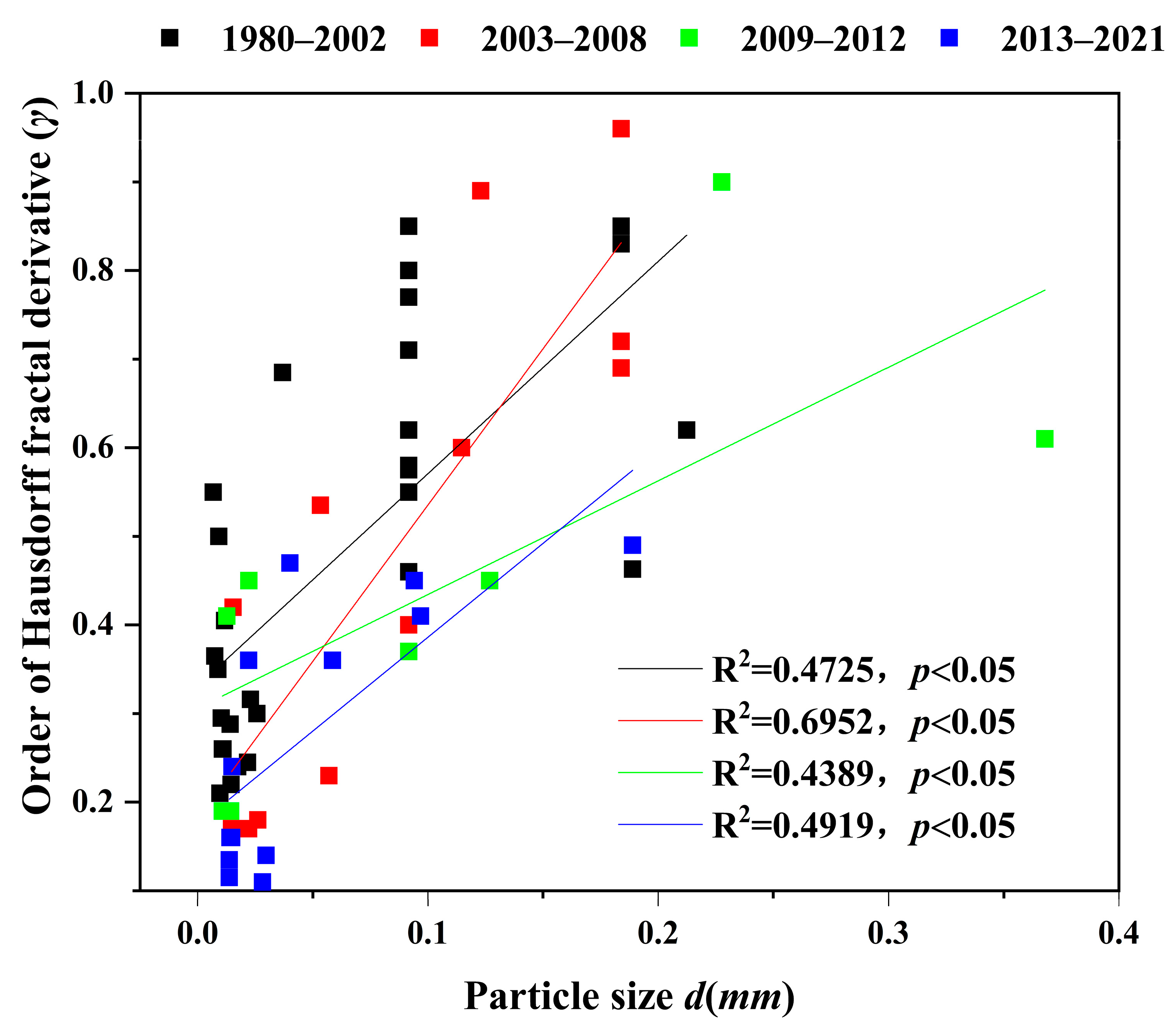
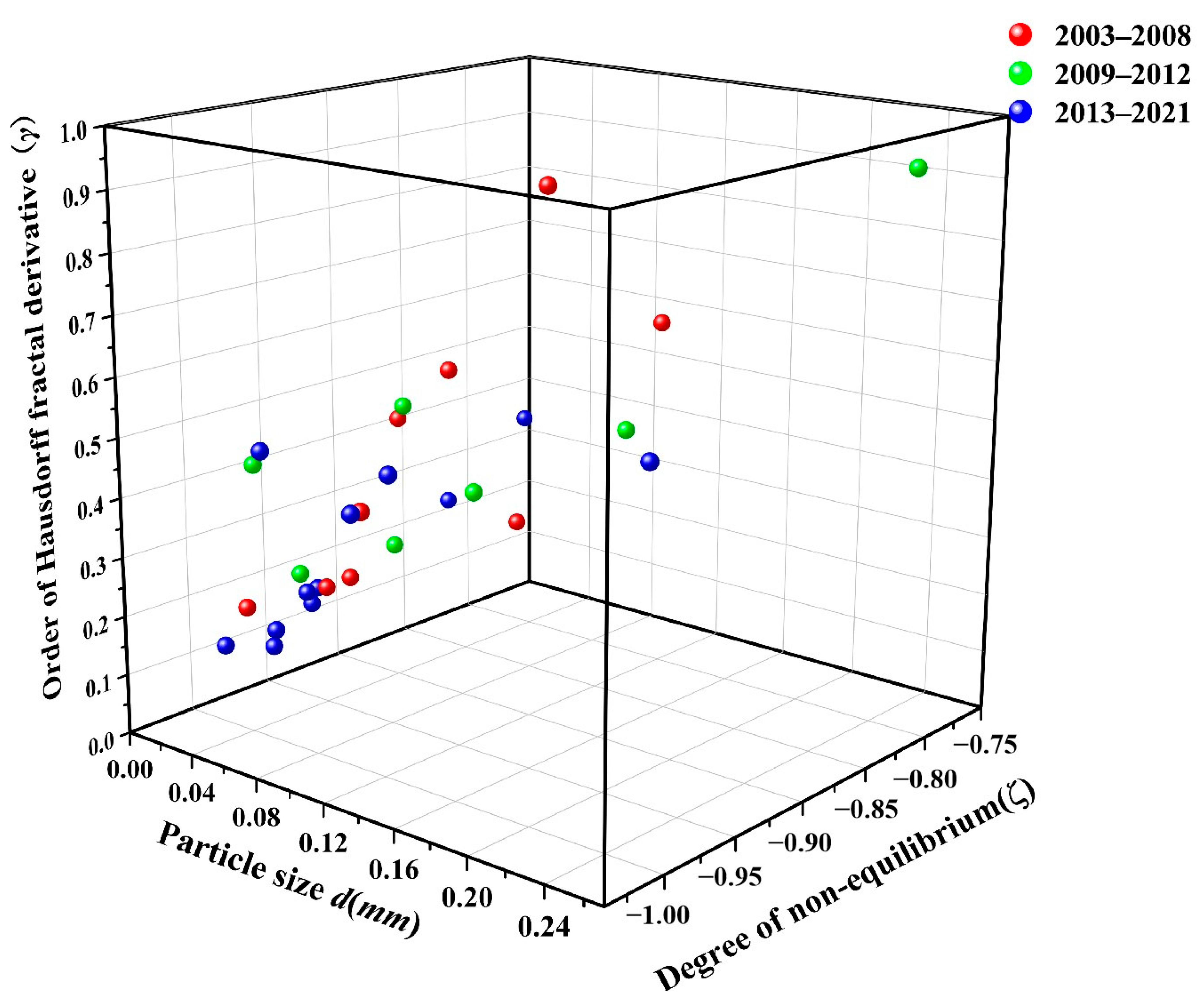
3.2. Parameters That Influence γ
4. Discussion
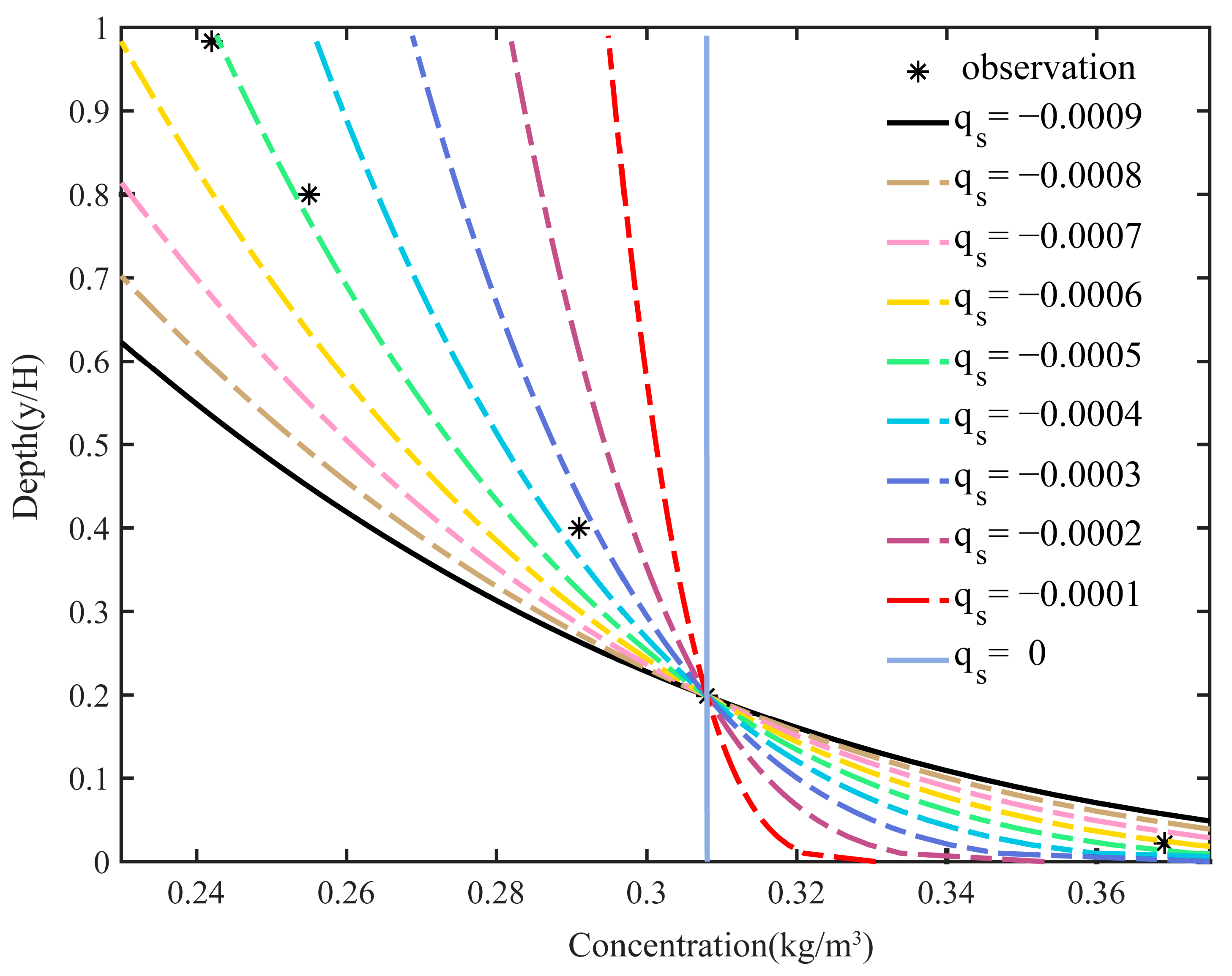
Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, H.C.; Zhang, X.F.; Xu, Q.X. Unprecedented sedimentation in response to emerging cascade reservoirs in the upper Yangtze River Basin. Catena 2022, 209, 105833. [Google Scholar] [CrossRef]
- Guo, X.H.; Qu, G.; Liu, Y.; Liu, X.Y. Sediment transport of different particle size groups in the downstream channel after operation of the Three Gorges Project. J. Lake Sci. 2020, 32, 564–572. [Google Scholar] [CrossRef]
- Li, X.; Xia, J.; Li, J.; Zhou, M. Adjustments in reach-scale bankfull geometry of a braided reach undergoing contrasting channel evolution processes. Arab. J. Geosci. 2019, 12, 535. [Google Scholar] [CrossRef]
- Xia, J.; Deng, S.; Zhou, M.; Lu, J.; Xu, Q. Geomorphic response of the Jingjiang Reach to the Three Gorges Project operation. Earth Surf. Process. Landf. 2017, 42, 866–876. [Google Scholar] [CrossRef]
- Petts, G.E.; Gurnell, A.M. Dams and geomorphology: Research progress and future directions. Geomorphology 2005, 71, 27–47. [Google Scholar] [CrossRef]
- Mccartney, M.P.; Shiferaw, A.; Seleshi, Y. Estimating environmental flow requirements downstream of the Chara Chara weir on the Blue Nile River. Hydrol. Process. 2009, 23, 3751–3758. [Google Scholar] [CrossRef]
- Wohl, E.; Lane, S.N.; Wilcox, A.C. The science and practice of river restoration. Water Resour. Res. 2015, 51, 5974–5997. [Google Scholar] [CrossRef]
- Kamboj, V.; Kamboj, N.; Sharma, A.K. A review on general characteristics, classification and degradation of river systems. Environ. Degrad. Causes Remediat. Strateg. 2020, 1, 47–62. [Google Scholar]
- Yang, X.H.; Xiong, H.B.; Li, D.F.; Li, Y.T.; Hu, Y. Disproportional erosion of the middle-lower Yangtze River following the operation of the Three Gorges Dam. Sci. Total Environ. 2023, 859, 160264. [Google Scholar] [CrossRef]
- Huang, H.Q.; Deng, C.; Nanson, G.C.; Fan, B.; Liu, X.; Liu, T.; Ma, Y. A test of equilibrium theory and a demonstration of its practical application for predicting the morphodynamics of the Yangtze River. Earth Surf. Process. Landf. 2014, 39, 669–675. [Google Scholar] [CrossRef]
- Zuo, S.; Yang, C.; Fu, G.; Xie, H. Variation of water and sediment flux and its influence on the Yangtze River Estuary. Mar. Geol. Front. 2022, 38, 56–64. [Google Scholar] [CrossRef]
- Zuo, S.H.; Zhang, N.C.; Li, B.; Yang, H. Dynamics reasons and temporal-spatial variations of suspended sediment condition in the sea area of Yangshan deep-water harbor. J. East China Norm. Univ. 2009, 3, 72–82. [Google Scholar]
- Li, Y.; Sun, Z.; Deng, J. A Study on Riverbed Erosion Downstream from the Three Gorges Reservoir. J. Basic Sci. Eng. 2003, 11, 283–295. (In Chinese) [Google Scholar]
- Liu, X.Q. Research on riverbed adjustment response of jingjiang reach under the change of flow and sediment. Appl. Ecol. Environ. Res. 2017, 15, 911–922. [Google Scholar] [CrossRef]
- Yang, S.L.; Milliman, J.D.; Xu, K.H.; Deng, B.; Zhang, X.Y.; Luo, X.X. Downstream sedimentary and geomorphic impacts of the Three Gorges Dam on the Yangtze River. Earth-Sci. Rev. 2014, 138, 469–486. [Google Scholar] [CrossRef]
- Sun, H.G.; Nie, S.Q.; Packman, A.I.; Zhang, Y.; Chen, D.; Lu, C.P.; Zheng, C.M. Application of Hausdorff fractal derivative to the determination of the vertical sediment concentration distribution. Int. J. Sediment Res. 2023, 38, 12–23. [Google Scholar] [CrossRef]
- Rouse, H. Modern Conceptions of the Mechanics of Turbulence. Trans. Am. Soc. Civ. Eng. 1937, 102, 463–505. [Google Scholar] [CrossRef]
- Rijn, L. Sediment Transport, Part II: Suspended Load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Qian, N. Experiment study of two-phase turbulent flow with hyper concentration of coarse particles. Chin. Sci. 1984, 8, 766–773. (In Chinese) [Google Scholar]
- Umeyaina, M. Vertical Distribution of Suspended Sediment in Uniform Open-Channel Flow. J. Hydraul. Eng. 1992, 118, 936–941. [Google Scholar] [CrossRef]
- Cao, Z.X. Turbulent bursting-based sediment entrainment function. J. Hydraul. Eng. 1997, 123, 233–236. [Google Scholar] [CrossRef]
- Fu, X.; Wang, G.; Shao, X. Vertical Dispersion of Fine and Coarse Sediments in Turbulent Open-Channel Flows. J. Hydraul. Eng. 2005, 131, 877–888. [Google Scholar] [CrossRef]
- Fu, X.D.; Wang, G.Q. Analysis on the factors affecting the vertical concentration distribution of fine sediment. J. Hydrodyn. 2004, 19, 231–239. (In Chinese) [Google Scholar]
- Zhong, D.; Wang, G.; Sun, Q. Transport Equation for Suspended Sediment Based on Two-Fluid Model of Solid/Liquid Two-Phase Flows. J. Hydraul. Eng. 2011, 137, 530–542. [Google Scholar] [CrossRef]
- Dou, G.R. Suspended sediment movementand calculation of erosion and deposition in tidal flow. J. Hydraul. Eng. 1963, 4, 13–24. (In Chinese) [Google Scholar]
- Han, Q.W.; Chen, X.J.; Xue, X.C. On the vertical distribution of sediment concentration in non-equilibrium transportation. Adv. Water Sci. 2010, 21, 512–523. (In Chinese) [Google Scholar]
- Ma, Z.; Guo, Q.; Guan, J.; Le, M. Non-equilibrium concentration profile formulas of suspended sediment and their preliminary applications. Int. J. Sediment Res. 2022, 37, 505–513. [Google Scholar] [CrossRef]
- Chen, D.; Sun, H.G.; Zhang, Y. Fractional dispersion equation for sediment suspension. J. Hydrol. 2013, 491, 13–22. [Google Scholar] [CrossRef]
- Liang, Y.; Dou, Z.; Zhou, Z.; Chen, W. Hausdorff derivative model for characterization of non-fickian mixing in fractal porous media. Fractals 2019, 27, 1950063. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, D.B.; Yin, M.S.; Sun, H.G.; Wei, W.; Li, S.Y.; Zheng, C.M. Nonlocal-transport models for capturing solute transport in one-dimensional sand columns: Model review, applicability, limitations, and improvement. Hydrol. Process. 2020, 34, 5104–5122. [Google Scholar] [CrossRef]
- Christov, I.C. Soft hydraulics: From Newtonian to complex fluid flows through compliant conduits. J. Physics. Condens. Matter 2021, 34, 063001. [Google Scholar] [CrossRef]
- Al-Raeei, M. Morse potential specific bond volume: A simple formula with applications to dimers and soft–hard slab slider. J. Phys. Condens. Matter 2022, 34, 284001. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Rame, E.; Walker, L.M.; Garoff, S. Dynamic wetting with viscous newtonian and non-newtonian fluids. J. Phys. Condens. Matter 2009, 21, 464126. [Google Scholar] [CrossRef]
- Nie, S.; Sun, H.G.; Zhang, Y.; Zhou, L.; Chen, D. A fractal derivative model to quantify bed-load transport along a heterogeneous sand bed. Environ. Fluid Mech. 2020, 20, 1603–1616. [Google Scholar] [CrossRef]
- Nie, S.; Sun, H.; Liu, X.; Ze, W.; Xie, M. Fractal derivative model for the transport of the suspended sediment in unsteady flows. Therm. Sci. 2018, 22 (Suppl. S1), 109–115. [Google Scholar] [CrossRef]
- Nie, S.; Sun, H.G.; Zhang, Y.; Chen, D.; Wen, C.; Chen, L.; Sydney, S. Vertical Distribution of Suspended Sediment under Steady Flow: Existing Theories and Fractional Derivative Model. Discret. Dyn. Nat. Soc. 2017, 2017, 5481531. [Google Scholar] [CrossRef]
- Meirong, Z.; Junqiang, X.; Shanshan, D.; Yu, M. Longitudinal variation of channel evolution along the middle Yangtze River after the operation of the Three Gorges Project. J. Lake Sci. 2023, 35, 642–649. [Google Scholar] [CrossRef]
- Bureau of Hydrology, Changjiang Water Resources Commission. Analysis on Characteristics of Flow and Sediment Characteristics, Reservoir Sedimentation and Downstream Channel of the Three Gorges Reservoir in 2018; Wuhan Bureau of Hydrology, Changjiang Water Resources Commission: Wuhan, China, 2019. (In Chinese)
- Ren, S.; Zhang, B.; Wang, W.; Yuan, Y.; Guo, C. Sedimentation and its response to management strategies of the Three Gorges Reservoir, Yangtze River, China. Catena 2021, 199, 105096. [Google Scholar] [CrossRef]
- He, L.; Chen, D.; Zhang, S.; Liu, M.; Duan, G. Evaluating Regime Change of Sediment Transport in the Jingjiang River Reach, Yangtze River, China. Water 2018, 10, 329. Available online: https://www.mdpi.com/2073-4441/10/3/329 (accessed on 15 March 2018). [CrossRef]
- He, L.; Chen, D.; Duan, G.L.; Peng, Y.M. Study on vertical distribution of suspended sediment concentration in the Jingjiang reach downstream the Three Gorges Dam. J. Sediment Res. 2020, 45, 27–32. (In Chinese) [Google Scholar]
- Chen, W. Time-space fabric underlying anomalous diffusion. Chaos Solitons Fractals 2006, 28, 923–929. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Z.; Yao, S.; Shan, M.; Guo, C. Case Study: Influence of Three Gorges Reservoir Impoundment on Hydrological Regime of the Acipenser sinensis Spawning Ground, Yangtze River, China. Front. Ecol. Evol. 2021, 9, 624447. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, D.; Chen, L.; Chen, X.; He, L. Using sediment rating parameters to evaluate the changes in sediment transport regimes in the middle yellow river basin, china. Hydrol. Process. 2019, 33, 2481–2497. [Google Scholar] [CrossRef]
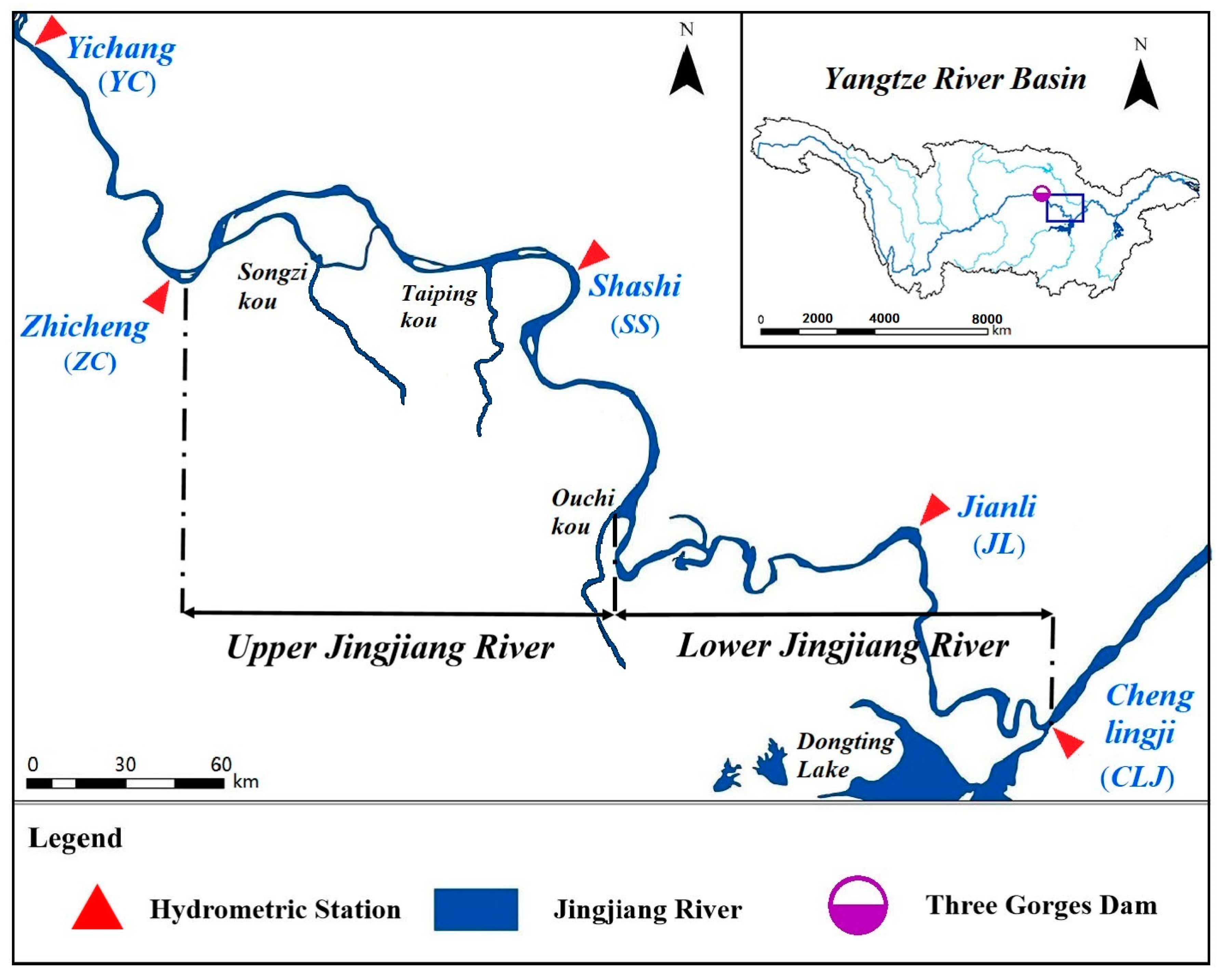

| Station | Before TGR Activation | After TGD Activation | Data Details |
|---|---|---|---|
| ZC | 2000–2001 | 2004–2021 | 3–15 vertical profiles per gauge; measured 1–18 times per year |
| SS | 1981–2002 | ||
| JL | 1982–2002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Chen, D.; Sun, H.-G.; Zhang, F. Vertical Distribution of Suspended Sediment Concentration in the Unsaturated Jingjiang Reach, Yangtze River, China. Fractal Fract. 2023, 7, 456. https://doi.org/10.3390/fractalfract7060456
Liu M, Chen D, Sun H-G, Zhang F. Vertical Distribution of Suspended Sediment Concentration in the Unsaturated Jingjiang Reach, Yangtze River, China. Fractal and Fractional. 2023; 7(6):456. https://doi.org/10.3390/fractalfract7060456
Chicago/Turabian StyleLiu, Meng, Dong Chen, Hong-Guang Sun, and Feng Zhang. 2023. "Vertical Distribution of Suspended Sediment Concentration in the Unsaturated Jingjiang Reach, Yangtze River, China" Fractal and Fractional 7, no. 6: 456. https://doi.org/10.3390/fractalfract7060456
APA StyleLiu, M., Chen, D., Sun, H.-G., & Zhang, F. (2023). Vertical Distribution of Suspended Sediment Concentration in the Unsaturated Jingjiang Reach, Yangtze River, China. Fractal and Fractional, 7(6), 456. https://doi.org/10.3390/fractalfract7060456







