Similarity Reductions, Power Series Solutions, and Conservation Laws of the Time-Fractional Mikhailov–Novikov–Wang System
Abstract
1. Introduction
2. Definition and Properties of the Riemann–Liouville Fractional Derivative
3. Lie Symmetry Analysis for the Time-Fractional Partial Differential System
4. Lie Symmetry Analysis and Reduction
- Case 1:
- Case 2:
5. Power Series Solutions and Convergence Analysis
6. Conservation Laws of the Time-Fractional MNW System
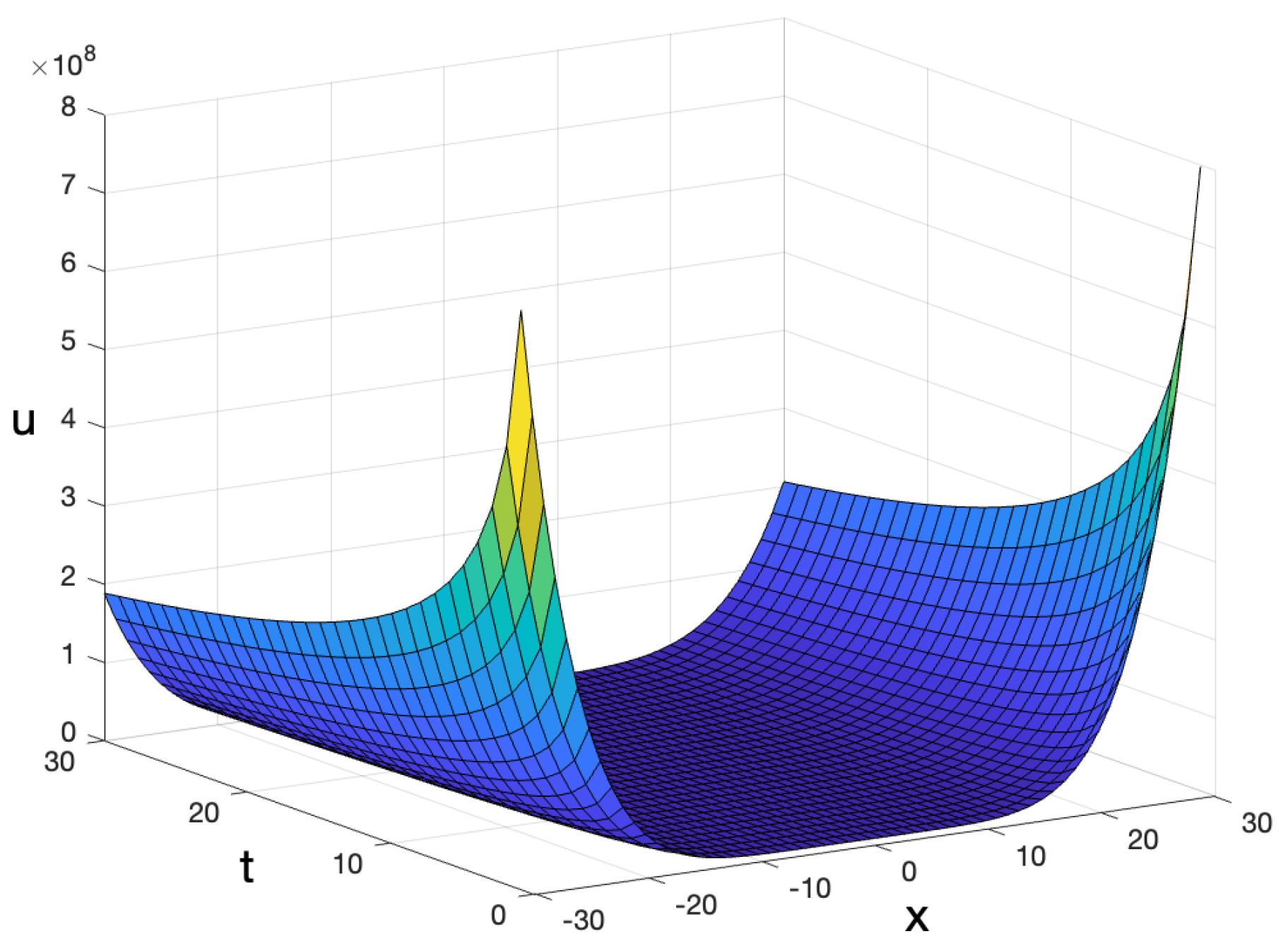
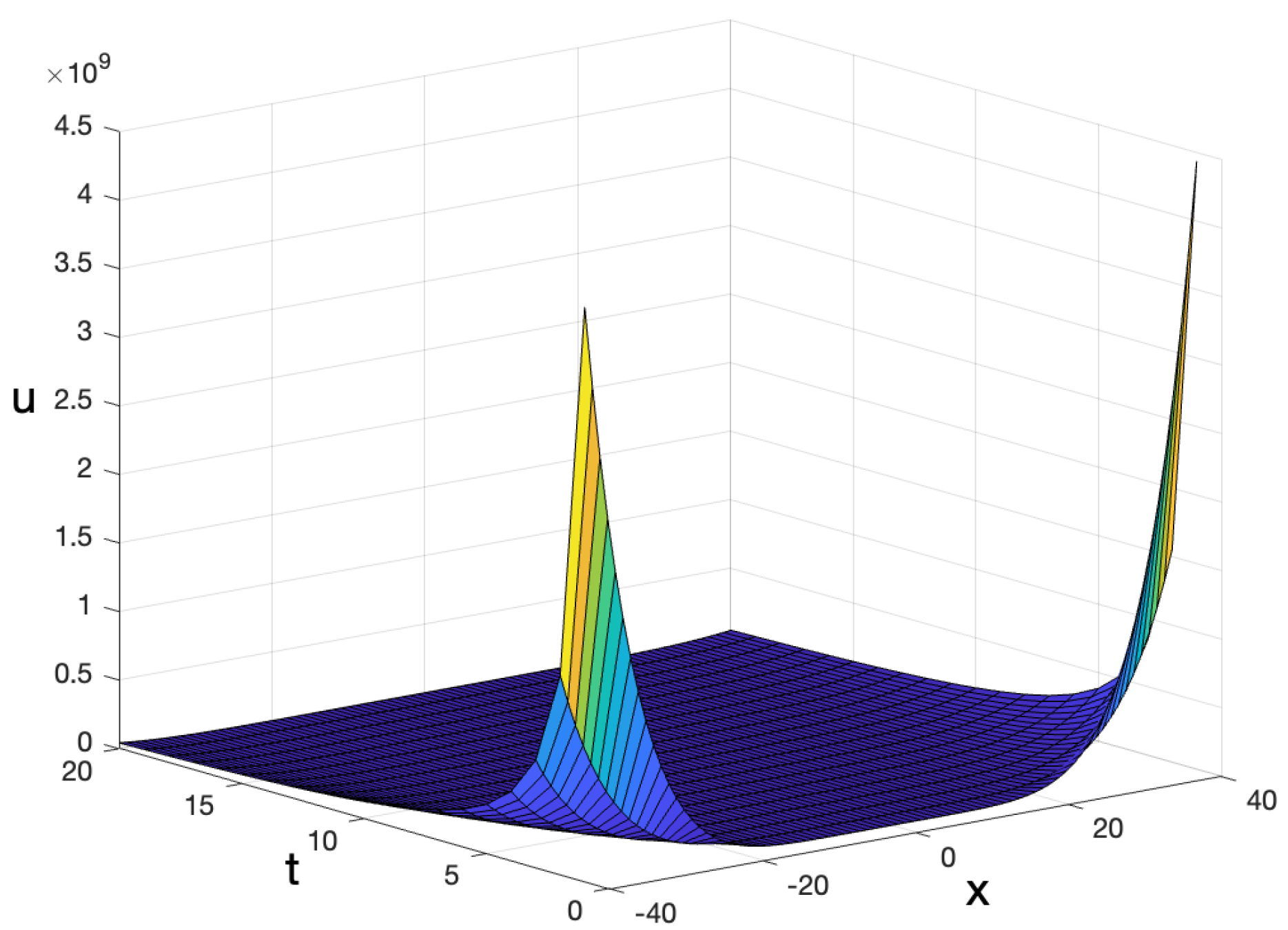
7. Graphical Illustrations of the Power Series Solutions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MNW | Mikhailov–Novikov–Wang |
| FPDE | fractional partial differential equation |
References
- Clarkson, P.A.; Dowie, E. Rational solutions of the Boussinesq equation and applications to rogue waves. Trans. Math. Its Appl. 2017, 1, tnx003. [Google Scholar] [CrossRef]
- Akbar, M.A.; Akinyemi, L.; Yao, S.W.; Jhangeer, A.; Rezazadeh, H.; Khater, M.M.; Ahmad, H.; Inc, M. Soliton solutions to the Boussinesq equation through sine-Gordon method and Kudryashov method. Results Phys. 2021, 25, 104228. [Google Scholar] [CrossRef]
- Mikhailov, A.V.; Novikov, V.S.; Wang, J.P. On classification of integrable nonevolutionary equations. Stud. Appl. Math. 2007, 118, 419–457. [Google Scholar] [CrossRef]
- Akbulut, A.; Kaplan, M.; Kaabar, M.K. New exact solutions of the Mikhailov-Novikov-Wang equation via three novel techniques. J. Ocean Eng. Sci. 2021, 8, 103–110. [Google Scholar] [CrossRef]
- Raza, N.; Seadawy, A.R.; Arshed, S.; Rafiq, M.H. A variety of soliton solutions for the Mikhailov-Novikov-Wang dynamical equation via three analytical methods. J. Geom. Phys. 2022, 176, 104515. [Google Scholar] [CrossRef]
- Ray, S.S.; Singh, S. New various multisoliton kink-type solutions of the (1+ 1)-dimensional Mikhailov–Novikov–Wang equation. Math. Methods Appl. Sci. 2021, 44, 14690–14702. [Google Scholar]
- Ray, S.S. Painlevé analysis, group invariant analysis, similarity reduction, exact solutions, and conservation laws of Mikhailov–Novikov–Wang equation. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150094. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bayrakci, U. A study on the solutions of (1+ 1)-dimensional mikhailov-novikov-wang equation. Math. Model. Numer. Simul. Appl. 2022, 2, 1–8. [Google Scholar] [CrossRef]
- Sergyeyev, A. Zero curvature representation for a new fifth-order integrable system. arXiv 2006, arXiv:nlin/0604064. [Google Scholar] [CrossRef]
- Sierra, C.A.G. A new travelling wave solution of the Mikhail-Novikov-Wang system usint the extended tanh method. Bol. Mat. 2007, 14, 38–43. [Google Scholar]
- Carreno, J.C.L.; Suáres, R.M. Acerca de algunas soluciones de ciertas ecuaciones de onda. Bol. Mat. 2012, 19, 107–118. [Google Scholar]
- Shan, X.; Zhu, J. The Mikhauilov-Novikov-Wang hierarchy and its Hamiltonian structures. Acta Phys. Pol.-Ser. B Elem. Part. Phys. 2012, 43, 1953. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Kılıçman, A. Numerical solutions of nonlinear fractional partial differential equations arising in spatial diffusion of biological populations. Abstr. Appl. Anal. 2014, 2014, 535793. [Google Scholar] [CrossRef]
- Liaskos, K.B.; Pantelous, A.A.; Kougioumtzoglou, I.A.; Meimaris, A.T.; Pirrotta, A. Implicit analytic solutions for a nonlinear fractional partial differential beam equation. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105219. [Google Scholar] [CrossRef]
- Liu, H.Z.; Wang, Z.G.; Xin, X.P.; Liu, X.Q. Symmetries, symmetry reductions and exact solutions to the generalized nonlinear fractional wave equations. Commun. Theor. Phys. 2018, 70, 014. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Baleanu, D. Lie Symmetry Analysis of Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Zhang, Y. A finite difference method for fractional partial differential equation. Appl. Math. Comput. 2009, 215, 524–529. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Finite difference methods for fractional differential equations. Int. J. Bifurc. Chaos 2012, 22, 1230014. [Google Scholar] [CrossRef]
- Odibat, Z. On the optimal selection of the linear operator and the initial approximation in the application of the homotopy analysis method to nonlinear fractional differential equations. Appl. Numer. Math. 2019, 137, 203–212. [Google Scholar] [CrossRef]
- Karaagac, B. New exact solutions for some fractional order differential equations via improved sub-equation method. Discret. Contin. Dyn. Syst. 2019, 12, 447–454. [Google Scholar] [CrossRef]
- Kadkhoda, N.; Jafari, H. Application of fractional sub-equation method to the space-time fractional differential equations. Int. J. Adv. Appl. Math. Mech. 2017, 4, 1–6. [Google Scholar]
- Cheng, X.; Wang, L.; Hou, J. Solving time fractional Keller–Segel type diffusion equations with symmetry analysis, power series method, invariant subspace method and q-homotopy analysis method. Chin. J. Phys. 2022, 77, 1639–1653. [Google Scholar] [CrossRef]
- Maheswari, C.U.; Bakshi, S.K. Invariant subspace method for time-fractional nonlinear evolution equations of the third order. Pramana 2022, 96, 173. [Google Scholar] [CrossRef]
- Prakash, P.; Thomas, R.; Bakkyaraj, T. Invariant subspaces and exact solutions: (1 + 1) and (2 + 1)-dimensional generalized time-fractional thin-film equations. Comput. Appl. Math. 2023, 42, 97. [Google Scholar] [CrossRef]
- Arqub, O.A.; Hayat, T.; Alhodaly, M. Analysis of lie symmetry, explicit series solutions, and conservation laws for the nonlinear time-fractional phi-four equation in two-dimensional space. Int. J. Appl. Comput. Math. 2022, 8, 145. [Google Scholar] [CrossRef]
- Al-Deiakeh, R.; Arqub, O.A.; Al-Smadi, M.; Momani, S. Lie symmetry analysis, explicit solutions, and conservation laws of the time-fractional Fisher equation in two-dimensional space. J. Ocean Eng. Sci. 2022, 7, 345–352. [Google Scholar] [CrossRef]
- Yu, J.; Feng, Y.; Wang, X. Lie symmetry analysis and exact solutions of time fractional Black–Scholes equation. Int. J. Financ. Eng. 2022, 9, 2250023. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Zhu, H.M.; Zheng, J. Lie symmetry analysis, power series solutions and conservation laws of the time-fractional breaking soliton equation. Waves Random Complex Media 2022, 32, 3032–3052. [Google Scholar] [CrossRef]
- Tian, S.F. Lie symmetry analysis, conservation laws and solitary wave solutions to a fourth-order nonlinear generalized Boussinesq water wave equation. Appl. Math. Lett. 2020, 100, 106056. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1993; Volume 107. [Google Scholar]
- Gazizov, R.; Kasatkin, A.; Lukashchuk, S.Y. Continuous transformation groups of fractional differential equations. Vestn. Usatu 2007, 9, 21. [Google Scholar]
- Gazizov, R.; Kasatkin, A.; Lukashchuk, S.Y. Symmetry properties of fractional diffusion equations. Phys. Scr. 2009, 2009, 014016. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Symmetry determination and nonlinearization of a nonlinear time-fractional partial differential equation. Proc. R. Soc. A 2020, 476, 20190564. [Google Scholar] [CrossRef]
- Jefferson, G.; Carminati, J. FracSym: Automated symbolic computation of Lie symmetries of fractional differential equations. Comput. Phys. Commun. 2014, 185, 430–441. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I. Generalized fractional power series solutions for fractional differential equations. Appl. Math. Lett. 2020, 102, 106107. [Google Scholar] [CrossRef]
- Ibragimov, N.H. Nonlinear self-adjointness and conservation laws. J. Phys. A Math. Theor. 2011, 44, 432002. [Google Scholar] [CrossRef]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Li, L. Similarity Reductions, Power Series Solutions, and Conservation Laws of the Time-Fractional Mikhailov–Novikov–Wang System. Fractal Fract. 2023, 7, 457. https://doi.org/10.3390/fractalfract7060457
Jiang X, Li L. Similarity Reductions, Power Series Solutions, and Conservation Laws of the Time-Fractional Mikhailov–Novikov–Wang System. Fractal and Fractional. 2023; 7(6):457. https://doi.org/10.3390/fractalfract7060457
Chicago/Turabian StyleJiang, Xinxin, and Lianzhong Li. 2023. "Similarity Reductions, Power Series Solutions, and Conservation Laws of the Time-Fractional Mikhailov–Novikov–Wang System" Fractal and Fractional 7, no. 6: 457. https://doi.org/10.3390/fractalfract7060457
APA StyleJiang, X., & Li, L. (2023). Similarity Reductions, Power Series Solutions, and Conservation Laws of the Time-Fractional Mikhailov–Novikov–Wang System. Fractal and Fractional, 7(6), 457. https://doi.org/10.3390/fractalfract7060457






