Fractional-Order Impulsive Delayed Reaction-Diffusion Gene Regulatory Networks: Almost Periodic Solutions

Abstract

The paper is oriented on the existence of almost periodic solutions of factional-order impulsive delayed reaction-diffusion gene regulatory networks. Caputo type fractional-order derivatives and impulsive disturbances at not fixed instants of time are considered. New almost periodic and perfect Mittag–Leffler stability criteria are proposed. Lyapunov’s like impulsive functions, the properties of the fractional derivatives and comparison principle are the main tools in the investigation. Illustrative examples are also presented to demonstrate the proposed criteria. Our results contribute to the development of qualitative the theory of fractional-order gene regulatory networks.

1. Introduction

The study of the dynamic behavior of biological network models has attracted an extensive interest of the researchers in the field. In fact, numerous studies in the existing literature considered the complex interactions between molecules, genes and other components that controlled biological functions in the biological networks [1,2].

The gene regulatory networks (GRNs) form an important specific class of biological networks which is applied in the modelling of the connections and communications between the gene expressions (mRNA) and protein molecules. As such the dynamic properties of this class of network models have been an object of enormous research activity using different methods and modelling approaches [3,4,5,6].

The study of delayed GRN models also focused a lot of research interest since delay effects are unavoidable in most of the biological phenomena [7,8,9,10,11,12]. Also, time delays, also known as transmission delays, may affect the dynamical properties of neural networks. Hence, the study of their effects is an interesting and important research topic.

In addition, as one of the powerful tools to represent diffusion phenomena, reaction-diffusion systems have been extensively used as models in numerous research fields of physics, biology and economics. The information about the reaction-diffusion terms has been also widely considered to understand the complexity and the qualitative behavior of the neurons in GRNs. Indeed, the necessary to consider the diffusion of mRNA’s concentrations and proteins expressions lead to the introduction of reaction-diffusion terms into the GRN models. Accordingly, the investigation of reaction-diffusion GRNs has aroused growing research interests, and a great number of excellent results have been announced [13,14,15,16,17,18,19].

The analysis of the effect of some impulsive perturbations on the dynamic behavior of GRN models is another line of research that is intensively developed. Recently there are some very good contributions to the development of the field [20,21,22,23]. The intensive research work in this direction is motivated by the fact that impulsive disturbances are commonly experienced in biological neural network models. In GRNs such short-term perturbations are caused by environmental fluctuations, differentiation cues, and diseases. To analyse the dynamic of a GTN system under impulsive perturbations, the apparatus of impulsive differential systems is mainly applied [24,25,26]. Also, the application of impulsive control approaches is an important focus point of research in investigating impulsive GRNs [27,28]. It is well known that the impulsive controls proceed in some discrete times and can reduce the control cost and the amount of transmitted information. These advantages make it preferred over other control strategies [29,30]. That is why it has been effectively applied as a therapeutic strategy in the study of several biological models used in medicine [31,32,33,34].

However, the research results on impulsive GRNs with reaction-diffusion terms are not enough [35]. Also, in all reported studies on GRNs with impulsive conditions, fixed points of impulsive perturbations are only considered. The case of variable impulsive perturbations which is more general and more relevant to the real physical problems [24,26,29] has been ignored. Indeed, the investigations of impulsive systems with variable impulsive perturbations is related to overcoming difficulties due to the presence of phenomena such as “beating” of the solutions, loss of the property of autonomy, bifurcation, “merging” of solutions, and some others.

Recently, fractional-order gene regulatory networks have been also proposed to extend the theory and consider their memory and hereditary effects in deep [36,37,38,39,40]. Researchers who applied the fractional calculus modelling approach are based on the theory of fractional-order differential equations and their properties. For more information on fractional-order models, see [41,42,43,44] and the references therein, including the impulsive case [45]. In fact, it has been found that the dynamical behavior of many complex nonlinear systems can be properly described by fractional-order models [46,47,48]. Despite of the large number of excellent results reported in the area of applications of fractional calculus in science and engineering, there are still more phenomena unexplored and waiting to be discovered. Therefore, additional aspects of the fractional modeling and applications have to be further developed.

Also, among all defined fractional operators, the Caputo differential operator is extensively used in fractional calculus applications to model many physical phenomena because it has many features that are similar to ordinary ones [46].

Note that, in general, fractional-order operators have non-local characteristics. Important notes about some new concepts related to impulsive fractional differential systems are given in [49,50,51].

Some scholars also considered impulsive fractional-order GRNs. For instance, impulsive effects are taken into account and fractional-order GRNs with time delays and impulsive effects are analysed in [52]. The authors in [53] investigated the finite-time stabilization behavior for a class of impulsive fractional GRNs with reaction-diffusion terms. The impulsive control strategy has been applied and some Mittag–Leffler stability criteria for impulsive Caputo-type fractional GRNs have been proposed in [54]. The almost periodicity of impulsive fractional GRNs has been studied in [55].

However, the research on impulsive fractional GRNs with reaction-diffusion terms is not completed [53,56]. Since reaction-diffusion neural network systems can be used to model the regulation process more accurately, the topic needs further research efforts. In fact, the reaction-diffusion neural network models have been demonstrated to bring many benefits due to the attribute of better recognition of complex dynamic systems [57,58,59,60].

Also, all existing results on impulsive integer-order and fractional-order GRNs considered impulsive effects only at fixed instances of time. A study of variable impulsive perturbations in GRN models, which is essential for both the theory and applications, is not yet reported in the existing literature, so this subject has attracted our attention. In fact, due to the existing challenges in the research on fractional-order systems with variable impulsive perturbations the number of published results is limited [61,62,63,64]. However, such models generalize the impulsive models with fixed instants of impulsive perturbations and are more useful from the applied point of view. Most of the challenges are due to the fact that the impulsive effects such as instantaneous perturbations and abrupt changes on distinct solutions are not, in general, the same. Also, different states of a neural network system have different impulsive perturbations. A novelty in our research is that we will propose an impulsive delayed fractional-order GRN model with variable impulsive perturbations in this paper.

In addition, most of the researchers on impulsive GRNs investigated stability and stabilization problems. Correspondingly, there are only a very small number of established results on their almost periodic properties. Some almost periodic results for several classes of GRNs have been proposed only in [23,55,65]. However, the authors in [23] did not apply the fractional calculus approach. The study [55] does not take into account reaction-diffusion terms and variable impulsive perturbations. The paper [65] is not on an impulsive GRN model with fractional derivatives.

One of the most important concepts in numerous mathematical models associated with the study of neuronal interactions in a periodic environment is that of periodicity. But, in real-world problems the exact periodicity of the states is usually too strong and has limited applicability. Upon considering long-term dynamical behavior, it has been discovered that the periodic parameters often turn out to experience certain perturbations that may lead to changing character. Thus, the investigation of almost periodic behaviour is more accordant with reality.

The concept of almost periodic functions was defined by several mathematicians in equivalent manner. The most common definitions are these of Bohr, Bohner, Stepanov and Weyl [66,67]. The notion has been applied to differential equations and becomes an essential topic in the qualitative analysis of their solutions [68]. It is also applied to impulsive systems of integer and fractional order [45,69,70]. Due to its importance in control theory, the almost periodicity concept attracted considerable interest of the researchers of different classes of neural network models [71,72,73,74,75,76]. The almost periodic notion is of considerable interest because some GRNs are capable of approaching not only one steady state.

Therefore, the almost periodicity direction for impulsive fractional-order GRNs needs further development. Our research interest to this notion is motivated by the fact that the almost periodic behavior of states is a fundamental topic in the study of the mRNA and protein interactions in an almost periodic environment. Indeed, for models with fractional-order dynamic the existence of pure periodic behavior of the state is disproved in [77], where it has been shown that the fractional-order derivative of a periodic function cannot be a periodic function of the same period, underlining a very remarkable difference between integer and fractional-order derivatives and explaining the absence of periodic solutions in a class of fractional-order dynamical systems. Since no exact periodic solutions are possible for a wider class of fractional-order systems, the existence of almost periodic trajectories is a realistic opportunity. Despite the high importance of the concept of almost periodicity, as well as of the Lyapunov’s method for theory and applications they are not yet developed for fractional-order reaction-diffusion GRNs and this is the main aim of the proposed research.

In the present research, inspired by the above analysis, the problem of existence of almost periodic solutions to impulsive fractional GRN models with reaction-diffusion terms is investigated by the application of the fractional Lyapunov method. In addition, the concept of perfect Mittag–Leffler stability is introduced.

The main contributions and novelty of the paper are:

(1) the almost periodicity notion is introduced to a class of impulsive fractional GRNs with reaction-diffusion terms and time delays;

(2) variable impulsive perturbations are considered to generalize the consideration. Note that our study is the first one which propose not-fixed impulsive disturbances to GRN models;

(3) by constructing an appropriate Lyapunov function, new criteria are represented to guarantee the existence and uniqueness of almost periodic states, contributing to the development of the almost periodicity theory for GRNs. The criteria are based on inequalities between the model’s parameters and are convenient for application;

(4) the concept of perfect Mittag–Leffler stability of almost periodic states is considered;

(5) different from the existing works [23,55,65] we apply the fractional calculus approach combined with the consideration of both reaction–diffusion terms and variable impulsive perturbations. Hence, the hybrid approach applied in this paper is more comprehensive.

The organization of the rest of the paper follows the following scheme. Section 2 is devoted to some preliminaries and to the formulation of the hybrid impulsive fractional-order reaction-diffusion delayed GRN model. The main definitions related to the concept of almost periodicity and fractional Lyapunov functions method are also given. The main existence and uniqueness results for almost periodic solutions are presented in Section 3. This section also includes the introduction and analysis of the perfect Mittag–Leffler stability notion for the almost periodic states. In Section 4 illustrative examples are elaborated. Some concluding comments are stated in Section 5.

Notation: Throughout this investigation, ${\mathbb{R}}^q$ will be the notation used for the q-dimensional Euclidean space, the norm of a vector $y={(y_1,y_2,\dots ,y_q)}^T\in {\mathbb{R}}^q$ will be defined as ${\displaystyle {\left|y\right|}_q={\left(\sum _{r=1}^q{y}_r^2\right)}^{\frac{1}{2}}}$, ${\mathbb{R}}_{+}=[0,\infty )$ and $\mathcal{S}$ denotes an open and bounded set in ${\mathbb{R}}^q$ with smooth boundary $\partial \mathcal{S}$ and the measure given by $\mathrm{mes}\mathcal{S}>0$, $\mathbf{0}={(0,0,\dots ,0)}^T\in \mathcal{S}$. Also, we consider the norm

$${\displaystyle \left|\right|\mathcal{C}(t,y)\left|\right|={\left[{\int }_{\mathcal{S}}\sum _{\mathsf{\iota }=1}^n{\mathcal{C}}_{\iota }^2(t,y)dy\right]}^{1/2}}$$

for $\mathcal{C}(t,y)={({\mathcal{C}}_1(t,y),{\mathcal{C}}_2(t,y),\dots ,{\mathcal{C}}_n(t,y))}^T\in {\mathbb{R}}^n,$ $t\in {\mathbb{R}}_{+}$, $y\in \mathcal{S}$. Also, a Hahn class of functions will be used denoted by

$$\mathcal{K}=\{p\in C[\mathbb{R},{\mathbb{R}}^{+}]:m\left(\xi \right)\mathrm{is}\mathrm{increasing}\mathrm{in}\xi ,m\left(0\right)=0,\mathrm{and}m\left(\xi \right)\to \infty \mathrm{as}\xi \to \infty \}.$$

2. Problem Introduction and Preliminary Notes

This section is devoted to some preliminaries and the formulation of the impulsive fractional-order reaction-diffusion GRN model with time-delays. Basic definitions and the fundamentals of the fractional Lyapunov method will also be presented.

Definition 1 

([44]). The Caputo-type partial fractional derivative with respect to time t of order α, $0<\alpha <1$ of a function $\beta \in C^1[{\mathbb{R}}_{+}\times \mathcal{S},\mathbb{R}]$ is defined by

$${\displaystyle \frac{{\partial }^{\alpha }\beta (t,y)}{\partial t^{\alpha }}=\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t\frac{\partial \beta (s,y)}{\partial s}\frac{ds}{{(t-s)}^{\alpha }},t>0,}$$

where Γ is the Gamma function.

Lemma 1 

([59,60]). For a continuous and differentiable with respect to its first argument function $\beta :{\mathbb{R}}_{+}\times \mathcal{S}\to \mathbb{R}$ and $\alpha \in (0,1)$, we have

$$\frac{{\partial }^{\alpha }{\beta }^2(t,y)}{\partial t^{\alpha }}\le 2\beta (t,y)\frac{{\partial }^{\alpha }\beta (t,y)}{\partial t^{\alpha }},t\ge 0,y\in \mathcal{S}.$$

Lemma 2 

([58]). Let $\mathcal{S}$ be the cube $|y_r|<l_r$, $r=1,2,\dots ,q$, and $\overline{\omega }\left(y\right)$ be a real–valued function, $\overline{\omega }\in C^1\left(\mathcal{S}\right)$ such that $\overline{\omega }{\left(y\right)|}_{\partial \mathcal{S}}=0$. Then,

$${\int }_{\mathcal{S}}{\overline{\omega }}^2\left(y\right)dy\le l_r^2{\int }_{\mathcal{S}}|\frac{\partial \overline{\omega }\left(y\right)}{\partial y_r}{|}^{2}dy.$$

2.1. Fractional-Order Impulsive Delayed Reaction-Diffusion GRN Model

We will investigate the class of impulsive delayed fractional-order reaction-diffusion GRNs of the type

$$\left\{{\displaystyle \begin{array}{c}{\displaystyle \frac{{\partial }^{\alpha }{\mathcal{M}}_{\iota }(t,y)}{\partial t^{\alpha }}=\sum _{r=1}^q\frac{\partial }{\partial y_r}\left(D_{\iota r}^{\left(1\right)}\frac{\partial {\mathcal{M}}_{\iota }(t,y)}{\partial y_r}\right)-a_{\iota }{\mathcal{M}}_{\iota }(t,y)}\hfill \\ {\displaystyle +\sum _{j=1}^n{w}_{\iota j}\left(t\right)f_j\left({\mathcal{P}}_j(t-{\upsilon }_j\left(t\right),y)\right)+B_{\iota }\left(t\right),t\ne {\theta }_k\left({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)\right),}\hfill \\ \frac{{\partial }^{\alpha }{\mathcal{P}}_{\iota }(t,y)}{\partial t^{\alpha }}={\displaystyle \sum _{r=1}^q}\frac{\partial }{\partial y_r}\left(D_{\iota r}^{\left(2\right)}\frac{\partial {\mathcal{P}}_{\iota }(t,y)}{\partial y_r}\right)-c_{\iota }{\mathcal{P}}_{\iota }(t,y)\hfill \\ +d_{\iota }\left(t\right){\mathcal{M}}_{\iota }(t-{\delta }_{\iota }\left(t\right),y),t\ne {\theta }_k\left({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)\right),\hfill \\ {\mathcal{M}}_{\iota }(t^{+},y)={\mathcal{M}}_{\iota }(t,y)+I_{\iota k}({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)),t={\theta }_k\left({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)\right),\hfill \\ {\mathcal{P}}_{\iota }(t^{+},y)={\mathcal{P}}_{\iota }(t,y)+J_{\iota k}({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)),t={\theta }_k\left({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)\right),\hfill \end{array}}\right.$$

(1)

where:

a/ $0<\alpha <1$, $\iota =1,2,\dots ,n,n\ge 2,k=\pm 1,\pm 2,\dots ,t\in \mathbb{R},y={(y_1,y_2,\dots ,y_q)}^T\in \mathcal{S}$, the quantities ${\mathcal{M}}_{\iota }(t,y)$ and ${\mathcal{P}}_{\iota }(t,y)$ represent the $\iota$-th mRNA and $\iota$-th protein concentrations, respectively, $\mathcal{M}={({\mathcal{M}}_1,{\mathcal{M}}_2,\dots ,{\mathcal{M}}_n)}^T\in {\mathbb{R}}^n$, $\mathcal{P}={({\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_n)}^T\in {\mathbb{R}}^n$;

b/ $a_{\iota }>0$, $c_{\iota }>0$ stand for the degradation rates of the $\iota$-th mRNA and $\iota$-th protein, respectively, the translation rates are denoted by $d_{\iota }\left(t\right)$, the continuous functions $D_{\iota r}^{\left(l\right)}=D_{\iota r}^{\left(l\right)}(t,y)\ge 0,l=1,2,r=1,2,\dots ,q$ correspond to the transmission diffusion coefficients for $\iota =1,2,\dots ,n$;

c/ $B_{\iota }\left(t\right)={\sum }_{j\in {\mathcal{I}}_{\iota }}{b}_{\iota j}\left(t\right)$, $b_{\iota j}\left(t\right)$ are functions that represent the dimensionless transcriptional rate of transcription factor j to $\iota$ and are bounded, ${\mathcal{I}}_{\iota }$ is the set of all the j which are repressors of gene $\iota$;

d/ The coupling functions $w_{\iota j}\left(t\right)$, $\iota ,j=1,2,\dots ,n$, are 0 if there is no connection from the node j to gene $\iota$, and

$$w_{\iota j}\left(t\right)=\left\{\begin{array}{c}{\displaystyle b_{\iota j}\left(t\right)\mathrm{if}\mathrm{transcription}\mathrm{factor}j\mathrm{is}\mathrm{an}\mathrm{activator}\mathrm{of}\mathrm{gene}\iota ,}\hfill \\ {\displaystyle -b_{\iota j}\left(t\right)\mathrm{if}\mathrm{transcription}\mathrm{factor}j\mathrm{is}\mathrm{a}\mathrm{repressor}\mathrm{of}\mathrm{gene}\iota ;}\hfill \end{array}\right.$$

e/ The function $f_j$, $j=1,2,\dots ,n$, represents the regulatory (activation) of the protein function and is in the form

$${\displaystyle f_j\left({\mathcal{P}}_j\right)=\frac{{({\mathcal{P}}_j/{\beta }_j)}^{{\mathcal{H}}_j}}{1+{({\mathcal{P}}_j/{\beta }_j)}^{{\mathcal{H}}_j}},}$$

where ${\mathcal{H}}_j$ denotes the Hill coefficients and ${\beta }_j$ are positive constants;

f/ ${\delta }_{\iota }={\delta }_{\iota }\left(t\right)$ and ${\upsilon }_j={\upsilon }_j\left(t\right)$ are the transmission time-varying delays, which are continuous functions and satisfy $t>{\upsilon }_j,t>{\delta }_{\iota },j,\iota =1,\dots ,n$, $0\le {\upsilon }_j\left(t\right)\le \upsilon ,0\le {\delta }_i\left(t\right)\le \delta$;

g/ The functions ${\theta }_k$, $I_{\iota k}$ and $J_{\iota k}$, $\iota =1,2,\dots ,n$, $k=\pm 1,\pm 2,\dots$, describe the abrupt changes of the states at the impulsive moments and are all continuous functions. More precisely, the impulsive disturbances for the the concentrations of the $\iota$-th mRNA and i-th protein occur at some instants of time ${\tau }_{p_k}$, which are solutions of the equations $t={\theta }_k({\mathcal{M}}_{\iota },{\mathcal{P}}_{\iota })$, and at which we have

$${\mathcal{M}}_{\iota }({\tau }_{p_k}^{-},y)={\mathcal{M}}_{\iota }({\tau }_{p_k},y),{\mathcal{M}}_{\iota }({\tau }_{p_k}^{+},y)={\mathcal{M}}_{\iota }({\tau }_{p_k},y)+I_{\iota p_k}({\mathcal{M}}_{\iota }({\tau }_{p_k},y),{\mathcal{P}}_{\iota }({\tau }_{p_k},y)),y\in \mathcal{S},$$

$${\mathcal{P}}_{\iota }({\tau }_{p_k}^{-},y)={\mathcal{P}}_{\iota }({\tau }_{p_k},y),{\mathcal{P}}_{\iota }({\tau }_{p_k}^{+},y)={\mathcal{P}}_{\iota }({\tau }_{p_k},x)+J_{\iota p_k}({\mathcal{M}}_{\iota }({\tau }_{p_k},y),{\mathcal{P}}_{\iota }({\tau }_{p_k},y)),y\in \mathcal{S}.$$

The points ${\tau }_{p_k}$, $k=\pm 1,\pm 2,\dots$ are called impulsive moments and in general, they depend on the solutions, i.e., different solutions may have different impulsive moments.

Consider initial functions ${\varphi }_0^1={({\varphi }_{01}^1,{\varphi }_{02}^1,\dots ,{\varphi }_{0n}^1)}^T$ defined on $[-\delta ,0]\times \mathcal{S}$ and ${\varphi }_0^2={({\varphi }_{01}^2,{\varphi }_{02}^2,\dots ,{\varphi }_{0n}^2)}^T$ defined on $[-\upsilon ,0]\times \mathcal{S}$ respectively, ${\varphi }_{0\iota }^l={\varphi }_{0\iota }^l(\xi ,y)$, $\iota =1,2,\dots ,n$, $l=1,2,$ which are piecewise continuous with respect to $\xi$, i.e., if we set $\widehat{\delta }=max\{\delta ,\upsilon \}$ the functions ${\varphi }_{0\iota }^l$ are such that ${\varphi }_{0\iota }^l({\xi }^{+},y)$ and ${\varphi }_{0\iota }^l({\xi }^{-},y)$ exist and ${\varphi }_{0\iota }^l({\xi }^{-},y)={\varphi }_{0\iota }^l(\xi ,y)$ for a finite number of points $\xi \in [-\widehat{\delta },0],$ $\iota =1,2,\dots ,n$, $l=1,2$.

The set of all functions of the type ${\varphi }_0^l$, $l=1,2$ will be denoted by $P{C}^{\widehat{\delta }}=PC[[-\widehat{\delta },0]\times \mathcal{S},{\mathbb{R}}^n]$ and $\mathcal{PC}=P{C}^{\widehat{\delta }}\times P{C}^{\widehat{\delta }}$.

The boundary conditions for the model (1) are of a Dirichlet type:

$${\mathcal{M}}_{\iota }(t,y)=0,{\mathcal{P}}_{\iota }(t,y)=0,t\in [-\widehat{\delta },\infty ),y\in \partial \mathcal{S},$$

(2)

and the initial conditions are given as:

$$\left\{\begin{array}{c}{\mathcal{M}}_{\iota }(\xi ,y)={\varphi }_{0\iota }^1(\xi ,y),{\mathcal{P}}_{\iota }(\xi ,y)={\varphi }_{0\iota }^2(\xi ,y),\xi \in [-\widehat{\delta },0],y\in \mathcal{S},\hfill \\ {\mathcal{M}}_{\iota }(0^{+},y)={\varphi }_{0\iota }^1(0,y),{\mathcal{P}}_{\iota }(0^{+},y)={\varphi }_{0\iota }^2(0,y),y\in \mathcal{S},\hfill \end{array}\right.$$

(3)

$\iota =1,2,\dots ,n.$

Note that it is possible that each ${\left({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)\right)}^T$ meets several or infinitely many times a hypersurface of the type

$${\mathsf{\Theta }}_k=\left\{(t,\mathcal{M},\mathcal{P})\in \mathbb{R}\times {\mathbb{R}}^{2n}:t={\theta }_k(\mathcal{M},\mathcal{P})\right\},k=\pm 1,\pm 2,\dots .$$

Such behavior is defined as “beating” of solutions, which is harmful to the fundamental and qualitative properties of the model. To eliminate any opportunity of beating of solutions, and to assurance existence, uniqueness and continuability of the solution ${\left(\mathcal{M}(t,y),\mathcal{P}(t,y)\right)}^T$ of the problem (1), (2) and (3) we assume that the functions ${\theta }_k$ are continuous, and the following relations hold:

$${\theta }_k(\mathcal{M},\mathcal{P})<{\theta }_{k+1}(\mathcal{M},\mathcal{P})<\dots ,{\theta }_k(\mathcal{M},\mathcal{P})\to \pm \infty \mathrm{as}k\to \pm \infty ,$$

uniformly on $\mathcal{M},\mathcal{P}\in {\mathbb{R}}^n$, and

$$p_k<p_{k+1},k,p_k=\pm 1,\pm 2,\dots .$$

Remark 1. 

The proposed model (1) generalizes many existing GRN models [13,14,15,16,17,18,19,20,21,22,23,52] considering impulsive perturbations, reaction-diffusion terms, Caputo fractional derivatives and delays. Note that fractional-order generalized GRN models are proposed in [52,53,54,55,56]. The authors in [52,54,55] studied some qualitative properties of fractional impulsive GRNs without reaction-diffusion terms. Impulsive effects and not considered in [56].

Remark 2. 

Different from all researchers investigated impulsive GRNs, in this article we consider variable impulsive perturbations, which is a natural extension of the case of impulsive disturbances at fixed moments of time. For $y\in \mathcal{S}$, the notations $\Delta {\mathcal{M}}_{\iota }(t,y)={\mathcal{M}}_{\iota }(t^{+},y)-{\mathcal{M}}_{\iota }(t,y)$ and $\Delta {\mathcal{P}}_{\iota }(t,y)={\mathcal{P}}_{\iota }(t^{+},y)-{\mathcal{P}}_{\iota }(t,y)$ represented the abrupt changes of the trajectories at the impulsive moments, where ${({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y))}^T={({\mathcal{M}}_{\iota }(t^{-},y),{\mathcal{P}}_{\iota }(t^{-},y))}^T$ and ${\displaystyle {({\mathcal{M}}_{\iota }(t^{+},y),{\mathcal{P}}_{\iota }(t^{+},y))}^T=\underset{h\to 0^{+}}{lim}{({\mathcal{M}}_{\iota }(t+h,y),{\mathcal{P}}_{\iota }(t+h,y))}^T}$, are, respectively, the states of the model before and after an impulsive perturbation at t which is one of the impulsive instants ${\tau }_{p_k}$, $p_k=\pm 1,\pm 2,\dots$. Note that by an appropriate choice of the impulsive functions, the variable impulsive perturbations can be applied as an impulsive control strategy to the trajectories of the model.

Now, for a better readability, we will introduce the next notations:

$${\mathsf{\Phi }}_0=({\varphi }_0^1,{\varphi }_0^2),{\varphi }_0^1,{\varphi }_0^2\in P{C}^{\widehat{\delta }},\left|\right|{\mathsf{\Phi }}_0{\left|\right|}_{\widehat{\delta }}=\underset{-\widehat{\delta }\le \xi \le 0}{sup}\left(\left|\right|{\varphi }_0^1(\xi ,y)\left)\right||+\left|\right|{\varphi }_0^2(\xi ,y)\left)\right||\right),y\in \mathcal{S}$$

and

$$\mathcal{U}(t,y)=\mathcal{U}(t,y;{\mathsf{\Phi }}_0)={\left(\mathcal{M}(t,y;{\varphi }_0^1),\mathcal{P}(t,y;{\varphi }_0^2)\right)}^T$$

with $\left|\right|\mathcal{U}\left|\right|=\left|\right|\mathcal{M}\left|\right|+\left|\right|\mathcal{P}\left|\right|$, denotes a solution of (1) corresponding to initial functions $({\varphi }_0^1,{\varphi }_0^2)$.

In addition, we denote

$${\mathcal{B}}_{\rho }=\{\mathcal{U}\in {\mathbb{R}}^{2n}:\left|\right|\mathcal{U}\left|\right|<\rho ,\rho >0\},$$

$${\mathcal{B}}_{\rho }^c=\{\mathcal{U}\in {\mathbb{R}}^{2n}:\left|\right|\mathcal{U}\left|\right|\ge \rho ,\rho >0\}.$$

Definition 2. 

The solutions of model (1) are:

(a) uniformly bounded, if

$$(\forall a>0)(\exists b=b(a)>0)$$

$$(\forall {\mathsf{\Phi }}_0\in \mathcal{PC}:\left|\right|{\mathsf{\Phi }}_0{\left|\right|}_{\widehat{\delta }}<a):||\mathcal{U}(t,y;{\mathsf{\Phi }}_0)\left|\right|<b,t\ge 0,y\in \mathcal{S};$$

(b) quasi-uniformly ultimately bounded, if

$$(\exists b>0)(\forall a>0)(\exists \mathcal{T}=\mathcal{T}(a)>0)$$

$$(\forall {\mathsf{\Phi }}_0\in \mathcal{PC}:\left|\right|{\mathsf{\Phi }}_0{\left|\right|}_{\widehat{\delta }}<a):||\mathcal{U}(t,y;{\mathsf{\Phi }}_0)\left|\right|<b,t\ge \mathcal{T},y\in \mathcal{S};$$

(c) uniformly ultimately bounded, if (a) and (b) hold together.

2.2. Almost Periodicity Definitions

Consider the set

$$\mathrm{T}=\left\{{\displaystyle \left\{{\tau }_{p_k}\right\}:{\tau }_{p_k}\in (-\infty ,\infty ),{\tau }_{p_k}<{\tau }_{p_{k+1}},{\tau }_{p_k}\ne 0,p_k=\pm 1,\pm 2,\dots ,\underset{p_k\to \pm \infty }{lim}{\tau }_{p_k}=\pm \infty }\right\}$$

of all unbounded and strictly increasing sequences for which a distance is defined by $\varrho \left(\left\{{\tau }_{p_k}^{\left(1\right)}\right\},\left\{{\tau }_{p_k}^{\left(2\right)}\right\}\right)$.

Let an element of the set $PC[\mathbb{R}\times \mathcal{S},{\mathbb{R}}^n]\times \mathrm{T}$ be represented as $\mathsf{\Psi }=\left(\psi \right(t,y),T)$ and for any infinite sequence ${\left\{{\sigma }_{\nu }\right\}}_{\nu =1}^{\infty }$, ${\sigma }_{\nu }\in \mathbb{R}$, we introduce the notation ${\eta }_{{\sigma }_{\nu }}\mathsf{\Psi }$ for the sets $\{\psi (t+{\sigma }_{\nu },y),T-{\sigma }_{\nu }\}\subset PC[\mathbb{R}\times \mathcal{S},{\mathbb{R}}^n]\times \mathrm{T}$ where $T-{\sigma }_{\nu }=\{{\tau }_{p_k}-{\sigma }_{\nu }\}$, $p_k=\pm 1,\pm 2,\dots ,$ $\nu =1,2,\dots$.

Definition 3. 

If any sequence of real numbers $\left\{{\sigma }^{\prime }\right\}$ has a subsequence $\left\{{\sigma }_{\nu }\right\},{\sigma }_{\nu }\subset {\sigma }^{\prime }$, such that ${\eta }_{{\sigma }_{\nu }}\mathsf{\Psi }$ is compact in $PC[\mathbb{R}\times \mathcal{S},{\mathbb{R}}^n]\times \mathrm{T}$, then the function $\psi \in PC[\mathbb{R}\times \mathcal{S},{\mathbb{R}}^n]$, $\psi =\psi (t,y)$, is almost periodic piecewise continuous with respect to its first variable with jump discontinuities at the points ${\tau }_{p_k},\left\{{\tau }_{p_k}\right\}\in \mathrm{T}$.

Definition 4. 

The sequence $\left\{{\mathsf{\Psi }}_{\nu }\right\}$, ${\mathsf{\Psi }}_{\nu }=({\psi }_{\nu }(t,y),T_{\nu })\in PC[\mathbb{R}\times \mathcal{S},{\mathbb{R}}^n]\times \mathrm{T}$, converges to Ψ uniformly with respect to t, if the existence of an $\epsilon >0$ implies the existence of a ${\nu }_0>0$ such that both inequalities

$$\varrho (T,T_{\nu })<\epsilon ,\left|\right|{\psi }_{\nu }(t,y)-\psi (t,y)\left|\right|<\epsilon$$

hold uniformly for $\nu \ge {\nu }_0$, $t\in \mathbb{R}\backslash \cap \left\{{\eta }_{\epsilon }\left(\phi (T_{\nu }\cup T)\right)\right\},$ $y\in \mathcal{S}$, where $\phi (T_{\nu }\cup T):\mathcal{T}\to \mathrm{T}$, $\phi (T_{\nu }\cup T)$ forms a strictly increasing sequence, ${\eta }_{\epsilon }\left(\phi (T_{\nu }\cup T)\right)=\{t+\epsilon ,t\in \phi (T_{\nu }\cup T)\}$.

Definition 5. 

If from each infinite sequence of shifts $\{{\tau }_{p_k}-{\sigma }_{\nu }\},p_k=\pm 1,\pm 2,\dots$, $\nu =1,2,\dots$, ${\sigma }_{\nu }\in \mathbb{R}$ it is possible to derive a convergent subsequence in $\mathrm{T}$, then we will call the set of all sequences of the type $\left\{{\tau }_{p_k}^g\right\}$, ${\tau }_{p_k}^g={\tau }_{p_k+g}-{\tau }_{p_k}$, $p_k=\pm 1,\pm 2,\dots$, $g=\pm 1,\pm 2,\dots$ uniformly almost periodic.

In order to study the almost periodic behavior of the states of the model (1), the following hypotheses will be made for the model’s parameters:

H1. 

The functions $B_i\left(t\right)$ are almost periodic on t, $\iota =1,2,\dots ,n$.

H2. 

The functions $w_{ij}\left(t\right)$ and $d_i\left(t\right)$ are almost periodic on t and

$${\displaystyle \underset{t\in \mathbb{R}}{sup}{|w}_{\iota j}|=w_{\iota j}^{+},\underset{t\in \mathbb{R}}{sup}\left|d_{\iota }\right|=d_{\iota }^{+}}$$

where $\iota ,j=1,2,\dots ,n$.

H3. 

There exist constants $E_j^1>0$ and $E_j^2>0$ such that

$$|f_j\left({\chi }_1\right)-f_j\left({\chi }_2\right)|\le E_j^1|{\chi }_1-{\chi }_2|,|f_j\left(\chi \right)|\le E_j^2$$

and $f_j\left(0\right)=0$, for all ${\chi }_1,{\chi }_2\in \mathbb{R},$ ${\chi }_1\ne {\chi }_2$, $j=1,2,\dots ,n$.

H4. 

The diffusion coefficients $D_{\iota r}^{\left(l\right)}=D_{\iota r}^{\left(l\right)}(t,y)\ge 0,l=1,2,r=1,2,\dots ,q$ are almost periodic in t, and there exist constants ${\underline{D}}_{\iota r}^{\left(1\right)}$ and ${\underline{D}}_{\iota r}^{\left(2\right)}$ such that

$$D_{\iota r}^{\left(1\right)}\ge {\underline{D}}_{\iota r}^{\left(1\right)}\ge 0,D_{\iota r}^{\left(2\right)}\ge {\underline{D}}_{\iota r}^{\left(2\right)}\ge 0$$

for $\iota =1,2,\dots ,n$, $r=1,2,\dots ,q$.

H5. 

There exists almost periodic sequences $\left\{{\alpha }_{\iota k}\right\}$, $\left\{{\varsigma }_{\iota k}\right\}$, $\left\{{\gamma }_{\iota k}\right\}$ and $\left\{{\chi }_{\iota k}\right\}$, such that

$$I_{\iota k}={\alpha }_{\iota k}{\mathcal{M}}_{\iota }+{\varsigma }_{\iota k},J_{\iota k}={\gamma }_{\iota k}{\mathcal{P}}_{\iota }+{\chi }_{ik},$$

and

$$-2<{\alpha }_{\iota k}\le 0,-2<{\gamma }_{\iota k}\le 0,$$

$k=\pm 1,\pm 2,\dots ,\iota =1,2,\dots ,n$.

H6. 

The initial functions ${\varphi }_0^1,{\varphi }_0^2\in P{C}^{\widehat{\delta }}$ are almost periodic with respect to their first variables.

H7. 

The set of all sequences of the type $\left\{{\tau }_{p_k}^g\right\}$, ${\tau }_{p_k}^g={\tau }_{p_k+g}-{\tau }_{p_k}$, $p_k=\pm 1,\pm 2,\dots$, $g=\pm 1,\pm 2,\dots$ is uniformly almost periodic, and ${inf}_{p_k}{\tau }_{p_k}^g>0$.

Introduce the notations: $\mathcal{F}(t,\mathcal{U})={({\mathcal{F}}_1(t,\mathcal{U}),{\mathcal{F}}_2(t,\mathcal{U}))}^T,$ and ${\mathcal{I}}_k\left(\mathcal{U}\right)={(I_k\left(\mathcal{U}\right),J_k\left(\mathcal{U}\right))}^T$, where

$$\begin{array}{c}{\mathcal{F}}_1(t,\mathcal{U})={({\mathcal{F}}_{11}(t,\mathcal{U}),{\mathcal{F}}_{12}(t,\mathcal{U}),\dots ,{\mathcal{F}}_{1n}(t,\mathcal{U}))}^T,\hfill \\ {\mathcal{F}}_2(t,\mathcal{U})={({\mathcal{F}}_{21}(t,\mathcal{U}),{\mathcal{F}}_{22}(t,\mathcal{U}),\dots ,{\mathcal{F}}_{2n}(t,\mathcal{U}))}^T,\hfill \\ {\displaystyle {\mathcal{F}}_{1\iota }(t,\mathcal{U})=\sum _{r=1}^q\frac{\partial }{\partial y_r}\left(D_{\iota r}^{\left(1\right)}\frac{\partial {\mathcal{M}}_{\iota }(t,y)}{\partial y_r}\right)-a_{\iota }{\mathcal{M}}_i(t,x)}\hfill \\ {\displaystyle +\sum _{j=1}^n{w}_{\iota j}\left(t\right)f_j\left({\mathcal{P}}_j(t-{\upsilon }_j\left(t\right),y)\right)+B_{\iota }\left(t\right),}\hfill \\ {\displaystyle {\mathcal{F}}_{2i}(t,\mathcal{U})=\sum _{r=1}^q\frac{\partial }{\partial y_q}\left(D_{\iota r}^{\left(2\right)}\frac{\partial {\mathcal{P}}_{\iota }(t,y)}{\partial y_r}\right)-c_{\iota }{\mathcal{P}}_{\iota }(t,y)+d_{\iota }\left(t\right){\mathcal{M}}_{\iota }(t-{\delta }_i\left(t\right),y),}\hfill \\ \\ I_k\left(\mathcal{U}\right)={(I_{1k}\left(\mathcal{U}\right),I_{2k}\left(\mathcal{U}\right),\dots ,I_{nk}\left(\mathcal{U}\right))}^T,\hfill \\ J_k\left(\mathcal{U}\right)={(J_{1k}\left(\mathcal{U}\right),J_{2k}\left(\mathcal{U}\right),\dots ,J_{nk}\left(\mathcal{U}\right))}^T,\hfill \\ I_{\iota k}\left(\mathcal{U}\right)=I_{\iota k}({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)),J_{\iota k}\left(\mathcal{U}\right)=J_{\iota k}({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y))\hfill \end{array}$$

for any $1\le \iota \le n$.

Next, we have from the almost periodicity theory for impulsive systems [69,70] that under the conditions H1–H7 for an arbitrary infinite sequence of real numbers $\left\{{\sigma }^{\prime }\right\}$ there exists a subsequence $\left\{{\sigma }_{\nu }\right\},{\sigma }_{\nu }\subset {\sigma }^{\prime }$ such that the model (1) moves to a system of the type

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{\alpha }\mathcal{U}(t,y)}{\partial t^{\alpha }}={\mathcal{F}}^{\sigma }(t,\mathcal{U}),t\ne {\theta }_k^{\sigma }\left(\mathcal{U}(t,y)\right),}\hfill \\ \Delta \mathcal{U}(t,y)={\mathcal{I}}_k^{\sigma }\left(\mathcal{U}\right),t={\theta }_k^{\sigma }\left(\mathcal{U}(t,y)\right).\hfill \end{array}\right.$$

(4)

We will denote the family of all systems of the type (4) by $\mathcal{H}\left(1\right)$.

2.3. Fundamentals of Fractional Lyapunov Method

Our main results on almost periodicity will be based on the fractional Lyapunov method strategy. The class of Lyapunov functions will be defined in this subsection following [59] and the references therein.

For $k=\pm 1,\pm 2,\dots ,$ define the following sets:

$${\mathcal{G}}_k=\left\{(t,\mathcal{U},\mathcal{V}):{\theta }_{k-1}\left(\mathcal{U}\right)<t<{\theta }_k\left(\mathcal{U}\right),{\theta }_{k-1}\left(\mathcal{V}\right)<t<{\theta }_k\left(\mathcal{V}\right),\mathcal{U},\mathcal{V}\in {\mathbb{R}}^{2n}\right\}.$$

We will also need the set ${\displaystyle \mathcal{G}=\bigcup _{k=\pm 1,\pm 2,\dots }{\mathcal{G}}_k.}$

Definition 6. 

A function $\mathcal{L}:\mathbb{R}\times {\mathbb{R}}^{2n}\times {\mathbb{R}}^{2n}\to {\mathbb{R}}_{+}$ is called piecewise continuous Lyapunov function, if it is continuous in $\mathcal{G}$, Lipschitz continuous with respect to its second and third arguments on each of the sets ${\mathcal{G}}_k$, $\mathcal{L}(t,\mathcal{U}(t,.),\mathcal{V}(t,.\left)\right)=0,t\in \mathbb{R}$, for each $k=\pm 1,\pm 2,\dots$ and $({\tau }_0^{\ast },{\mathcal{U}}_0^{\ast })\in {\mathsf{\Theta }}_k$, $({\tau }_0^{\ast },{\mathcal{V}}_0^{\ast })\in {\mathsf{\Theta }}_k$, $\mathcal{L}({\tau }_0^{\ast -},{\mathcal{U}}_0^{\ast },{\mathcal{V}}_0^{\ast })=\mathcal{L}({\tau }_0^{\ast },{\mathcal{U}}_0^{\ast },{\mathcal{V}}_0^{\ast })$ and $\mathcal{L}({\tau }_0^{\ast +},{\mathcal{U}}_0^{\ast },{\mathcal{V}}_0^{\ast })$ exist.

The class of all piecewise continuous Lyapunov functions defined by Definition 6 will be denoted by ${\mathcal{L}}_0$.

Consider the system

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{\alpha }\mathcal{U}(t,·)}{d{t}^{\alpha }}=\mathcal{K}(t,\mathcal{U}(t-\widehat{\delta },·)),t\ne {\theta }_k\left(\mathcal{U}(t,·)\right),}\hfill \\ \\ \mathcal{U}(t^{+},·)=\mathcal{U}(t,·)+{\mathcal{K}}_k\left(\mathcal{U}(t,·)\right),t={\theta }_k\left(\mathcal{U}(t,·)\right),\hfill \end{array}\right.$$

where $\mathcal{K}:\mathbb{R}\times \mathcal{PC}\to {\mathbb{R}}^{2n}$, $\mathcal{K}(t,\overline{\mathsf{\Phi }})={({\mathcal{K}}_1(t,\overline{\mathsf{\Phi }}),{\mathcal{K}}_2(t,\overline{\mathsf{\Phi }}),\dots ,{\mathcal{K}}_{2n}(t,\overline{\mathsf{\Phi }}))}^T$ is locally Lipschitz continuous in $\overline{\mathsf{\Phi }}\in \mathcal{PC}$ and ${\mathcal{K}}_k:{\mathbb{R}}^{2n}\to {\mathbb{R}}^{2n},k=\pm 1,\pm 2,\dots$.

For a function $\mathcal{L}\in {\mathcal{L}}_0$, $t\ne {\theta }_k\left({\overline{\mathsf{\Phi }}}^1\right)$, $t\ne {\theta }_k\left({\overline{\mathsf{\Phi }}}^2\right)$, $k=\pm 1,\pm 2,\dots$, ${\overline{\mathsf{\Phi }}}^1,{\overline{\mathsf{\Phi }}}^2\in \mathcal{PC}$, we define the notation:

$${\displaystyle {}^C{D}^{\alpha }\mathcal{L}(t,{\overline{\mathsf{\Phi }}}^1(0,·),{\overline{\mathsf{\Phi }}}^2(0,·))=\underset{\xi \to 0^{+}}{lim}sup\frac{1}{{\xi }^{\alpha }}[\mathcal{L}(t,{\overline{\mathsf{\Phi }}}^1(0,·),{\overline{\mathsf{\Phi }}}^2(0,·))}$$

$$-\mathcal{V}(t-\xi ,{\overline{\mathsf{\Phi }}}^1(0,·)-{\xi }^{\alpha }\mathcal{K}(t,{\overline{\mathsf{\Phi }}}^1),{\overline{\mathsf{\Phi }}}^2(0,·)-{\xi }^{\alpha }\mathcal{K}(t,{\overline{\mathsf{\Phi }}}^2))].$$

The following key lemma will be also applied.

Lemma 3 

([59,71]). Suppose that for the piecewise continuous Lyapunov function $\mathcal{L}\in {\mathcal{L}}_0$ and ${\overline{\mathsf{\Phi }}}^1,{\overline{\mathsf{\Phi }}}^2\in \mathcal{PC}$ the following conditions hold:

(i) $\mathcal{L}(t^{+},{\overline{\mathsf{\Phi }}}^1(0,·)+{\mathcal{K}}_k\left({\overline{\mathsf{\Phi }}}^1\right),{\overline{\mathsf{\Phi }}}^2(0,·)+{\mathcal{K}}_k\left({\overline{\mathsf{\Phi }}}^2\right))\le \mathcal{L}(t,{\overline{\mathsf{\Phi }}}^1(0,·),{\overline{\mathsf{\Phi }}}^2(0,·)),t\in {\theta }_k\left({\overline{\mathsf{\Phi }}}^1\right)\cap {\theta }_k\left({\overline{\mathsf{\Phi }}}^2\right),k=\pm 1,\pm 2,\dots$;

(ii) The inequality

$${}^c{D}^{\alpha }\mathcal{L}(t,{\overline{\mathsf{\Phi }}}^1(0,·),{\overline{\mathsf{\Phi }}}^2(0,·))\le -\mu \mathcal{L}(t,{\overline{\mathsf{\Phi }}}^1(0,·),{\overline{\mathsf{\Phi }}}^2(0,·)),t\ne {\theta }_k\left({\overline{\mathsf{\Phi }}}^1\right),t\ne {\theta }_k\left({\overline{\mathsf{\Phi }}}^2\right),\mu =const>0$$

(5)

is valid whenever

$$\mathcal{L}(t+\xi ,{\overline{\mathsf{\Phi }}}^1(\xi ,·),{\overline{\mathsf{\Phi }}}^2(\xi ,·))\le \mathcal{L}(t,{\overline{\mathsf{\Phi }}}^1(0,·),{\overline{\mathsf{\Phi }}}^2(0,·)),-\widehat{\delta }\le \xi \le 0.$$

Then

$${\displaystyle \mathcal{L}(t,\mathcal{U}(t,·),\mathcal{V}(t,·))\le \underset{-\widehat{\delta }\le \xi \le 0}{sup}\mathcal{L}(0,{\overline{\mathsf{\Phi }}}^1(\xi ,·),{\overline{\mathsf{\Phi }}}^2(\xi ,·))E_{\alpha }(-\mu t^{\alpha }),t>0,}$$

where $E_{\alpha }$ is the standard Mittag–Leffler function.

Finally, a class of piecewise continuous Lyapunov functions related to systems of the type (4) will be introduced.

Definition 7. 

${\mathcal{L}}_0^W$ is a class of piecewise continuous Lyapunov functions ${\mathcal{L}}^W(t,\mathcal{U})$, ${\mathcal{L}}^W:\mathbb{R}\times {\mathbb{R}}^{2n}\to {\mathbb{R}}_{+}$ that are continuous for $t\ne {\theta }_k^{\sigma }\left(\mathcal{U}(t,y)\right)$, $k=\pm 1,\pm 2,\dots$, $\mathcal{U}\in {\mathbb{R}}^{2n}$, locally Lipschitz with respect to its second variables, the left-hand and right-hand limits at any t such that $t={\theta }_k^{\sigma }\left(\mathcal{U}(t,y)\right)$ exist and are finite, and ${\mathcal{L}}^W(t,\mathcal{U})$ is left continuous at such t.

3. Almost Periodicity Results

3.1. Boundedness

Since the almost periodic properties of the states of the model (1) depend on their boundedness, in this section we will establish some boundedness results.

Consider the next subset of ${\mathcal{L}}_0$,

$${\mathcal{L}}_1=\{\mathcal{L}\in {\mathcal{L}}_0:\mathcal{L}(t,\mathcal{U},0)=\mathcal{L}(t,\mathcal{U})\}.$$

Theorem 1. 

Under hypotheses H1–H7, if there exists a piecewise continuous Lyapunov function $\mathcal{L}\in {\mathcal{L}}_1$ that satisfies conditions of Lemma 3 for $\mu =0$, and is such that for $m_1,m_2\in \mathcal{K}$

$$m_1\left(\right|\left|\mathcal{U}\right|\left|\right)\le \mathcal{L}(t,\mathcal{U})\le m_2\left(\right|\left|\mathcal{U}\right|\left|\right),(t,\mathcal{U})\in {\mathbb{R}}_{+}\times {\mathcal{B}}_{\rho }^c,$$

(6)

then the solutions of system (1) are uniformly bounded.

Proof. 

Let $a>0$, $y\in \mathcal{S}$ and ${\mathsf{\Phi }}_0\in \mathcal{PC}$. Consider the solution $\mathcal{U}(t,y;{\mathsf{\Phi }}_0)$ of (1) with $\left|\right|{\mathsf{\Phi }}_0{\left|\right|}_{\widehat{\delta }}<a$.

Without loss of generality, suppose that $a\ge \rho$, and choose $b=b\left(a\right)>0$ so that

$$b>max\{a,m_1^{-1}\left(m_2\left(a\right)\right)\}.$$

Hence, we have

$$\left|\right|\mathcal{U}(0,y;{\mathsf{\Phi }}_0)\left|\right|\le \left|\right|{\mathsf{\Phi }}_0{\left|\right|}_{\widehat{\delta }}<a<b.$$

We claim that

$$\left|\right|\mathcal{U}(t,y;{\mathsf{\Phi }}_0)\left|\right|<b,t>0,y\in \mathcal{S}.$$

If it is not true, then there exists some solution $\mathcal{U}(t,y)=\mathcal{U}(t,y;{\mathsf{\Phi }}_0)$ of (1) with $\left|\right|{\mathsf{\Phi }}_0{\left|\right|}_{\widehat{\delta }}<a$ and $t^{\ast }>0$ such that $\left|\right|\mathcal{U}(t^{\ast },y;{\mathsf{\Phi }}_0)\left|\right|\ge b$. Then there exist ${\xi }_1,{\xi }_2,0\le {\xi }_1<{\xi }_2\le t^{\ast }$ and

$$\left|\right|\mathcal{U}({\xi }_1,·)\left|\right|\le a,\left|\right|\mathcal{U}({\xi }_1^{+},·)\left|\right|\ge a,\left|\right|\mathcal{U}({\xi }_2^{+},·)\left|\right|\ge b$$

and

$$\mathcal{U}(t,·)\in {\mathcal{B}}_b\cap {\mathcal{B}}_a^c,t\in [{\xi }_1,{\xi }_2).$$

(7)

First, we shall show that

$$\mathcal{L}({\xi }_1^{+},\mathcal{U}({\xi }_1^{+},·))<m_1\left(b\right).$$

If ${\xi }_1\ne {\theta }_k\left(\mathcal{U}\right)$, then $\left|\right|\mathcal{U}({\xi }_1,·)\left|\right|=a$, and using (6), we have

$$\mathcal{L}({\xi }_1,\mathcal{U}({\xi }_1,·))\le m_2\left(\right||\mathcal{U}({\xi }_1,·)\left)\right|\left|\right)=m_2\left(a\right)<m_1\left(b\right).$$

If ${\xi }_1\in {\theta }_k\left(\mathcal{U}\right)$ for some k, then $\left|\right|\mathcal{U}({\xi }_1,·)\left)\right||\le a$, and

$$\mathcal{L}({\xi }_1,\mathcal{U}({\xi }_1,·))\le m_2\left(\right||\mathcal{U}({\xi }_1,·)\left)\right|\left|\right)\le m_2\left(a\right)<m_1\left(b\right).$$

Thus, by condition (i) of Lemma 3, we obtain

$$\mathcal{L}({\xi }_1^{+},\mathcal{U}({\xi }_1^{+},·))<m_1\left(b\right).$$

Similarly, for $t\in [{\xi }_1,{\xi }_2]$, we have by Lemma 3 or $\mu =0$ and (6)

$${\displaystyle \mathcal{L}(t^{+},\mathcal{U}(t^{+},·))\le \underset{-\widehat{\delta }\le \xi \le 0}{sup}\mathcal{L}(0,{\mathsf{\Phi }}_0(\xi ,·))\le m_2\left(\right||{\mathsf{\Phi }}_0{\left|\right|}_{\widehat{\delta }})\le m_2\left(a\right)<m_1\left(b\right).}$$

(8)

On the other hand, by (6) we get

$$\mathcal{L}({\xi }_2^{+},\mathcal{U}({\xi }_2^{+},·))\ge m_1\left(\right||\mathcal{U}({\xi }_2^{+},·)\left|\right|)\ge m_1\left(b\right),$$

which contradicts (8). Thus

$$\left|\right|\mathcal{U}(t,y)\left|\right|<b,t\ge 0,y\in \mathcal{S}$$

for any solution $\mathcal{U}(t,y;{\mathsf{\Phi }}_0)$ of (1) with $\left|\right|{\mathsf{\Phi }}_0{\left|\right|}_{\widehat{\delta }}<a$ and, therefore, the solutions of (1) are uniformly bounded.

The case $a<\rho$ is treated similarly [45]. □

Theorem 2. 

If condition (5) in Theorem 1 for a piecewise continuous Lyapunov function $\mathcal{L}\in {\mathcal{L}}_1$ is replaced by

$${}^c{D}^{\alpha }\mathcal{L}(t,\mathsf{\Phi }(0,·))\le -m_3\left(\right|\left|\mathsf{\Phi }(0,·)\right|\left|\right),t\ne {\theta }_k\left(\mathsf{\Phi }\right),m_3\in \mathcal{K},$$

for

$$\mathcal{L}(t+\xi ,\mathsf{\Phi }(\xi ,·))\le \mathcal{L}(t,\mathsf{\Phi }(0,·)),-\widehat{\delta }\le \xi \le 0,$$

then the solutions of system (1) are uniformly ultimately bounded.

The steps in the proof of Theorem 2 are essentially similar to these used in the proof of Theorem 1, and we will omit the repetition here.

Remark 3. 

Theorems 1 and 2 offer uniform boundedness and uniform ultimate boundedness criteria for the considered hybrid class of delayed fractional-order impulsive GRNs with reaction-diffusion terms. With the established results, we contribute to the development of the qualitative theory of fractional GRN models. In addition, since both, uniform boundedness and uniform ultimate boundedness, imply boundedness, we can apply both results in the study of the almost periodic properties of the solutions.

3.2. Almost Periodicity

We will use the next notations:

$$w^{+}=\underset{1\le \iota ,j\le n}{max}{w}_{\iota j}^{+},d^{+}=\underset{1\le \iota \le n}{max}{d}_{\iota }^{+},$$

$$a_{min}=\underset{1\le \iota \le n}{min}{a}_{\iota },c_{min}=\underset{1\le \iota \le n}{min}{c}_{\iota }.$$

Theorem 3. 

Under the hypotheses H1–H7, for given scalars $\mathsf{\Lambda }={\lambda }_1-2{\lambda }_2,{\tilde{D}}_{\iota }^{\left(l\right)}$, $l=1,2$. Such that

$${\lambda }_1=min\left({\tilde{D}}_{\iota }^{\left(1\right)},{\tilde{D}}_{\iota }^{\left(2\right)}\right)+min\left(a_{min},c_{min}\right)>0,$$

$${\lambda }_2=max\left(\frac{d^{+}}{2},\frac{w^{+}}{2}\sum _{j=1}^n{E}_j^1\right)>0$$

and

$${\displaystyle {\tilde{D}}_{\iota }^{\left(l\right)}=\sum _{r=1}^q\frac{{\underline{D}}_{\iota r}^{\left(l\right)}}{l_r^2},l=1,2,\iota =1,2,\dots ,n,}$$

if there exists a solution of (1) with $\left|\right|\mathcal{U}(t,y)\left|\right|<{\rm Y},{\rm Y}>0,$ $t\ge 0$, $y\in \mathcal{S}$, then, uniformly on $y\in \mathcal{S}$, there exists a unique almost periodic along t solution $\omega (t,y)$ of the system (1) such that:

(a) $\left|\right|\omega (t,y)\left|\right|\le {{\rm Y}}_1,{{\rm Y}}_1<{\rm Y}$;

(b) $\mathcal{H}(\omega ,{\tau }_{p_k})\subset \mathcal{H}\left(1\right)$.

Proof. 

Let us consider a real sequence $\left\{{\sigma }_{\nu }\right\}$ that moves the nominal model (1) to a system from the set $\mathcal{H}\left(1\right)$, and let ${\sigma }_{\nu }\to \infty$ as $\nu \to \infty$.

For any real number o, let ${\nu }_0={\nu }_0\left(o\right)$ be the smallest value of $\nu$, such that ${\sigma }_{{\nu }_0}+o\ge 0$. Since $\left|\right|\mathcal{U}(t,y)\left|\right|\le {{\rm Y}}_1,{{\rm Y}}_1<{\rm Y}$ for all $t\ge 0$, then $\left|\right|\mathcal{U}(t+{\sigma }_{\nu },y)\left|\right|\le {{\rm Y}}_1$ for $t\ge o,\nu \ge {\nu }_0$.

Suppose that $\mathcal{O},\mathcal{O}\subset (o,\infty )$ is compact. For $\mathcal{U},\mathcal{V}\in {\mathbb{R}}^{2n}$ we will consider the following Lyapunov-type function of the class ${\mathcal{L}}_0$,

$${\displaystyle \mathcal{L}(\mathcal{U}(t,·),\mathcal{V}(t,·))=\frac{1}{2}{\int }_{\mathcal{S}}\sum _{\iota =1}^{2n}{\left({\mathcal{U}}_{\iota }(t,y)-{\mathcal{V}}_{\iota }(t,y)\right)}^{2}dy.}$$

The compactness of $\mathcal{O}$ implies that for a given $\epsilon >0$, there exists an integer number $n_0(\epsilon ,o)\ge {\nu }_0\left(o\right)$, so large that for $\zeta \ge \nu \ge n_0(\epsilon ,o)$ we have

$${\displaystyle \underset{-\widehat{\delta }\le \xi \le 0}{sup}\{{\int }_{\mathcal{S}}\sum _{\iota =1}^n{\left({\varphi }_{0\iota }^1(\xi +{\sigma }_{\nu },y)-{\varphi }_{0\iota }^1(\xi +{\sigma }_{\zeta },y)\right)}^{2}dy}$$

$$+{\int }_{\mathcal{S}}\sum _{\iota =n+1}^{2n}{\left({\varphi }_{0\iota }^2(\xi +{\sigma }_{\nu },y)-{\varphi }_{0\iota }^2(\xi +{\sigma }_{\zeta },y)\right)}^{2}dy\}<\frac{1}{2}{\epsilon }^2{E}_{\alpha }\left(\mathsf{\Lambda }{(t+{\sigma }_{\nu }-{\sigma }_{\zeta })}^{\alpha }\right),$$

(9)

and for any $\iota =1,2,\dots ,n$,

$${\displaystyle |B_{\iota }(t+{\sigma }_{\nu })-B_{\iota }(t+{\sigma }_{\zeta })| < \mathsf{\Lambda }{\epsilon }^2{\left(3n{\rm Y}{2}^{q+3}\prod _{r=1}^q{l}_r\right)}^{-1},}$$

(10)

$${\displaystyle |d_{\iota }(t+{\sigma }_{\nu })-d_{\iota }(t+{\sigma }_{\zeta })| < \mathsf{\Lambda }{\epsilon }^2{\left(3n{\rm Y}{2}^{q+3}\prod _{r=1}^q{l}_r\right)}^{-1},}$$

(11)

$${\displaystyle |w_{\iota j}(t+{\sigma }_{\nu })-w_{\iota j}(t+{\sigma }_{\zeta })| < \mathsf{\Lambda }{\epsilon }^2{\left(3n{\rm Y}{2}^{q+3}\prod _{r=1}^q{l}_r\sum _{j=1}^n{E}_j^2\right)}^{-1}.}$$

(12)

Let $t={\theta }_k\left(\mathcal{U}(t,·)\right)$ and then, by condition H5, we get

$$\mathcal{L}(\mathcal{U}(t^{+}+{\sigma }_{\nu },·),\mathcal{U}(t^{+}+{\sigma }_{\zeta },·))$$

$${\displaystyle =\frac{1}{2}{\int }_{\mathcal{S}}\left\{\sum _{\iota =1}^n\right({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)+{\alpha }_{\iota k}{\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)+{\varsigma }_{\iota k}}$$

$$-\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)+{\alpha }_{\iota k}{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)+{\varsigma }_{\iota k}\right){)}^2$$

$$+\sum _{\iota =n+1}^{2n}({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)+{\gamma }_{\iota k}{\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)+{\chi }_{\iota k}$$

$$-\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)+{\gamma }_{\iota k}{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)+{\chi }_{\iota k}\right){)}^2\}$$

$${\displaystyle =\frac{1}{2}{\int }_{\mathcal{S}}\{\sum _{\iota =1}^n{\left(1+{\alpha }_{\iota k}\right)}^2{\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)\right)}^2}$$

$$+\sum _{\iota =n+1}^{2n}{\left(1+{\gamma }_{\iota k}\right)}^2{\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)\right)}^2\}dy$$

$$\le \mathcal{L}(\mathcal{U}(t+{\sigma }_{\nu },·),\mathcal{U}(t+{\sigma }_{\zeta },·)).$$

(13)

For any t at which the time-derivative of $\mathcal{L}$ of order $\alpha$ exists, we have

$${\displaystyle \frac{d^{\alpha }\mathcal{L}(\mathcal{U}(t,·),\mathcal{V}(t,·))}{d{t}^{\alpha }}=\frac{1}{2}\frac{d^{\alpha }}{d{t}^{\alpha }}\left({\int }_{\mathcal{S}}\sum _{\iota =1}^{2n}{\left({\mathcal{U}}_{\iota }(t,y)-{\mathcal{V}}_{\iota }(t,y)\right)}^{2}dy\right)}$$

$${\displaystyle =\frac{1}{2}\sum _{\iota =1}^{2n}\left(\frac{d^{\alpha }}{d{t}^{\alpha }}\left({\int }_{\mathcal{S}}{\left({\mathcal{U}}_{\iota }(t,y)-{\mathcal{V}}_{\iota }(t,y)\right)}^{2}dy\right)\right).}$$

Also, we have that [59,71] for any $\iota =1,2,\dots ,2n$

$$\frac{d^{\alpha }}{d{t}^{\alpha }}\left({\int }_{\mathcal{S}}{\left({\mathcal{U}}_{\iota }(s,y)-{\mathcal{V}}_{\iota }(s,y)\right)}^{2}dy\right)$$

$$=\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t\left(\frac{d}{ds}{\int }_{\mathsf{\Omega }}{\left({\mathcal{U}}_{\iota }(t,y)-{\mathcal{V}}_{\iota }(t,y)\right)}^{2}dy\right)\frac{ds}{{(t-s)}^{\alpha }}$$

$$={\int }_{\mathsf{\Omega }}\frac{1}{\mathsf{\Gamma }(1-\alpha )}\left({\int }_0^t\frac{\partial }{\partial s}{\left({\mathcal{U}}_{\iota }(s,y)-{\mathcal{V}}_{\iota }(s,y)\right)}^2\frac{ds}{{(t-s)}^{\alpha }}\right)dy$$

$$={\int }_{\mathcal{S}}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}{\left({\mathcal{U}}_{\iota }(t,y)-{\mathcal{V}}_{\iota }(t,y)\right)}^{2}dy.$$

After application of Lemma 1 to the above equality, we obtain

$${\displaystyle \frac{d^{\alpha }}{d{t}^{\alpha }}\left({\int }_{\mathsf{\Omega }}{\left({\mathcal{U}}_{\iota }(t,y)-{\mathcal{V}}_{\iota }(t,y)\right)}^{2}dy\right)}$$

$$\le 2{\int }_{\mathcal{S}}\left({\mathcal{U}}_{\iota }(t,y)-{\mathcal{V}}_{\iota }(t,y)\right)\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left({\mathcal{U}}_{\iota }(t,y)-{\mathcal{V}}_{\iota }(t,y)\right)dy.$$

Now, for $t\ne {\theta }_k\left(\mathcal{U}(t,·)\right)$, we get

$${}^c{D}^{\alpha }\mathcal{L}(\mathcal{U}(t+{\sigma }_{\nu },·),\mathcal{U}(t+{\sigma }_{\zeta },·))\le \sum _{\iota =1}^n{\int }_{\mathcal{S}}({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)$$

$$-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y))(\sum _{r=1}^q\frac{\partial }{\partial y_r}\left(D_{\iota 1}^{\left(1\right)}\frac{\partial }{\partial y_r}\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)\right)\right)$$

$$-a_{\iota }\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)\right)$$

$${\displaystyle +\sum _{j=1}^n(\left(w_{\iota j}(t+{\sigma }_{\nu })-w_{\iota j}(t+{\sigma }_{\zeta })\right)f_j\left({\mathcal{U}}_j(t+{\sigma }_{\nu }-{\upsilon }_j(t+{\sigma }_{\nu }),y)\right)}$$

$$+w_{\iota j}(t+{\sigma }_{\zeta })(f_j\left({\mathcal{U}}_j(t+{\sigma }_{\nu }-{\upsilon }_j(t+{\sigma }_{\nu }),y)\right)$$

$$-f_j\left({\mathcal{U}}_j(t+{\sigma }_{\zeta }-{\upsilon }_j(t+{\sigma }_{\zeta }),y)\right)\left)\right)+B_{\iota }(t+{\sigma }_{\nu })-B_i(t+{\sigma }_{\zeta }))dy$$

$$+\sum _{\iota =n+1}^{2n}{\int }_{\mathcal{S}}\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)\right)(\sum _{r=1}^q\frac{\partial }{\partial y_r}\left(D_{\iota 1}^{\left(2\right)}\frac{\partial }{\partial y_r}\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)\right)\right)$$

$$-c_{\iota }\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)\right)$$

$${\displaystyle +\left(d_{\iota }(t+{\sigma }_{\nu })-d_{\iota }(t+{\sigma }_{\zeta })\right){\mathcal{U}}_{\iota }(t+{\sigma }_{\nu }-{\delta }_{\iota }(t+{\sigma }_{\nu }),y)}$$

$$+d_{\iota }(t+{\sigma }_{\zeta })\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu }-{\delta }_{\iota }(t+{\sigma }_{\nu }),y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta }-{\delta }_{\iota }(t+{\sigma }_{\zeta }),y)\right))dy.$$

To simplify the next calculation we set $h_{\iota }(t,y)={\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)$. By the boundary conditions and the Green’s theorem, we have that

$$\sum _{r=1}^q{\int }_{\mathcal{S}}{h}_{\iota }(t,y)\frac{\partial }{\partial y_r}\left(D_{\iota r}^{\left(1\right)}\frac{\partial h_{\iota }(t,y)}{\partial y_r}\right)dy=-\sum _{r=1}^q{\int }_{\mathcal{S}}{D}_{\iota r}^{\left(1\right)}{\left(\frac{\partial h_{\iota }(t,y)}{\partial y_r}\right)}^{2}dy,$$

$$\sum _{r=1}^q{\int }_{\mathcal{S}}{h}_{\iota }(t,y)\frac{\partial }{\partial y_r}\left(D_{\iota r}^{\left(2\right)}\frac{\partial h_{\iota }(t,y)}{\partial y_r}\right)dy=-\sum _{r=1}^q{\int }_{\mathcal{S}}{D}_{\iota r}^{\left(2\right)}{\left(\frac{\partial h_{\iota }(t,y)}{\partial y_r}\right)}^{2}dy.$$

The application of Lemma 2 implies the following estimates for $t>0$

$$\sum _{r=1}^q{\int }_{\mathcal{S}}{h}_{\iota }(t,y)\frac{\partial }{\partial y_r}\left(D_{\iota r}^{\left(1\right)}\frac{\partial h_{\iota }(t,y)}{\partial y_r}\right)dy\le -\sum _{r=1}^q{\int }_{\mathcal{S}}{\underline{D}}_{\iota r}^{\left(1\right)}{\left(\frac{\partial h_{\iota }(t,y)}{\partial y_r}\right)}^{2}dy$$

$$\le -\sum _{r=1}^q{\int }_{\mathcal{S}}\frac{{\underline{D}}_{\iota r}^{\left(1\right)}}{l_r^2}{h}_{\iota }^2(t,y)dy=-{\tilde{D}}_{\iota }^{\left(1\right)}{\int }_{\mathcal{S}}{h}_{\iota }^2(t,y)dy,$$

(14)

and

$$\sum _{r=1}^q{\int }_{\mathcal{S}}{h}_{\iota }(t,y)\frac{\partial }{\partial y_r}\left(D_{\iota r}^{\left(2\right)}\frac{\partial h_{\iota }(t,y)}{\partial y_r}\right)dy\le -\sum _{r=1}^q{\int }_{\mathcal{S}}{\underline{D}}_{\iota r}^{\left(2\right)}{\left(\frac{\partial h_{\iota }(t,y)}{\partial y_r}\right)}^{2}dy$$

$$\le -\sum _{r=1}^q{\int }_{\mathcal{S}}\frac{{\underline{D}}_{\iota r}^{\left(2\right)}}{l_r^2}{h}_{\iota }^2(t,y)dy=-{\tilde{D}}_{\iota }^{\left(2\right)}{\int }_{\mathcal{S}}{h}_{\iota }^2(t,y)dy.$$

(15)

Next, by the conditions of Theorem 3 and (9)–(12), we get

$$\sum _{j=1}^n(\left(w_{\iota j}(t+{\sigma }_{\nu })-w_{\iota j}(t+{\sigma }_{\zeta })\right){\int }_{\mathcal{S}}{h}_{\iota }(t,y)f_j\left({\mathcal{U}}_j(t+{\sigma }_{\nu }-{\delta }_j(t+{\sigma }_{\nu }),y)\right)dy$$

$$+w_{\iota j}(t+{\sigma }_{\zeta }){\int }_{\mathcal{S}}{h}_{\iota }(t,y)(f_j\left({\mathcal{U}}_j(t+{\sigma }_{\nu }-{\upsilon }_j(t+{\sigma }_{\nu }),y)\right)$$

$$-f_j\left({\mathcal{U}}_j(t+{\sigma }_{\zeta }-{\upsilon }_j(t+{\sigma }_{\zeta }),y)\right)dy)$$

$$<\frac{{\epsilon }^2\mathsf{\Lambda }}{12n}+\sum _{j=1}^n|w_{\iota j}^{+}|E_j^1{\int }_{\mathcal{S}}|h_{\iota }(t,y)\left|\right|h_j(t-{\upsilon }_j,y)|dy$$

$$\le \frac{{\epsilon }^2\mathsf{\Lambda }}{12n}+\frac{1}{2}\sum _{j=1}^n\left|w_{\iota j}^{+}\right|E_j^1{\int }_{\mathcal{S}}\left(h_{\iota }^2(t,y)+h_j^2(t-{\upsilon }_j,y)\right)dy,$$

(16)

and

$${\displaystyle \left(d_{\iota }(t+{\sigma }_{\nu })-d_{\iota }(t+{\sigma }_{\zeta })\right){\int }_{\mathcal{S}}{h}_{\iota }(t,y){\mathcal{U}}_i(t+{\sigma }_{\nu }-{\delta }_i(t+{\sigma }_{\nu }),y)dy}$$

$$+d_{\iota }(t+{\sigma }_{\zeta }){\int }_{\mathcal{S}}{h}_{\iota }(t,y)\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu }-{\delta }_{\iota }(t+{\sigma }_{\nu }),y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta }-{\delta }_{\iota }(t+{\sigma }_{\zeta }),y)\right)dy$$

$$<\frac{{\epsilon }^2\mathsf{\Lambda }}{12n}+|d_i^{+}|{\int }_{\mathcal{S}}|h_{\iota }(t,y)\left|\right|h_{\iota }(t-{\delta }_{\iota },y)|dy\le \frac{{\epsilon }^2\mathsf{\Lambda }}{12n}+\frac{1}{2}\left|d_i^{+}\right|{\int }_{\mathcal{S}}\left(h_{\iota }^2(t,y)+h_{\iota }^2(t-{\delta }_{\iota },y)\right)dy.$$

(17)

After combining (14)–(17), we obtain

$${}^c{D}^{\alpha }\mathcal{L}(\mathcal{U}(t+{\sigma }_{\nu },·),\mathcal{U}(t+{\sigma }_{\zeta },·))$$

$$\le -\left[min\left({\tilde{D}}_{\iota }^{\left(1\right)},{\tilde{D}}_{\iota }^{\left(2\right)}\right)+min\left(a_{min},c_{min}\right)-max\left(\frac{d^{+}}{2},\frac{w^{+}}{2}\sum _{j=1}^n{E}_j^1\right)\right]\sum _{\iota =1}^{2n}{\int }_{\mathcal{S}}{h}_{\iota }^2(t,y)dy$$

$$+max\left(\frac{d^{+}}{2},\frac{w^{+}}{2}\sum _{j=1}^n{E}_j^1\right)\left\{\sum _{\iota =1}^n{\int }_{\mathcal{S}}{h}_{\iota }^2(t-{\upsilon }_{\iota },y)dy+\sum _{\iota =n+1}^{2n}{\int }_{\mathcal{S}}{h}_{\iota }^2(t-{\delta }_{\iota },y)dy\right\}+\frac{{\epsilon }^2\mathsf{\Lambda }}{4}$$

$$\le -({\lambda }_1-{\lambda }_2)\mathcal{L}(\mathcal{U}(t+{\sigma }_{\nu },·),\mathcal{U}(t+{\sigma }_{\zeta },·))$$

$$+{\lambda }_2\underset{t-\widehat{\delta }\le s\le t}{sup}\mathcal{L}(\mathcal{U}(s+{\sigma }_{\nu },·),\mathcal{U}(s+{\sigma }_{\zeta },·)))+\frac{{\epsilon }^2\mathsf{\Lambda }}{4},$$

where

$${\lambda }_1=min\left({\tilde{D}}_{\iota }^{\left(1\right)},{\tilde{D}}_{\iota }^{\left(2\right)}\right)+min\left(a_{min},c_{min}\right)>0,$$

$${\lambda }_2=max\left(\frac{d^{+}}{2},\frac{w^{+}}{2}\sum _{j=1}^n{E}_j^1\right)>0.$$

From the choice of $\mathsf{\Lambda }$ for $t\ne {\theta }_k\left(\mathcal{U}(t,·)\right)$, we obtain

$${}^c{D}^{\alpha }\mathcal{L}(\mathcal{U}(t+{\sigma }_{\nu },·),\mathcal{U}(t+{\sigma }_{\zeta },·))\le -\mathsf{\Lambda }\left(\mathcal{L}(\mathcal{U}(t+{\sigma }_{\nu },·),\mathcal{U}(t+{\sigma }_{\zeta },·))-\frac{{\epsilon }^2}{4}\right),$$

(18)

when $\mathcal{L}(\mathcal{U}(\xi +{\sigma }_{\nu },·),\mathcal{U}(\xi +{\sigma }_{\zeta },·))\le \mathcal{L}(\mathcal{U}(t+{\sigma }_{\nu },·),\mathcal{U}(t+{\sigma }_{\zeta },·))$ for $t-\widehat{\delta }\le \xi \le t$, $t\ge 0$.

Hence, using (13), (18) and Lemma 3, for $t\in [0,\infty )$ we get

$$\mathcal{L}(\mathcal{U}(t+{\sigma }_{\nu },·),\mathcal{U}(t+{\sigma }_{\zeta },·))\le \underset{-\widehat{\delta }\le \xi \le 0}{sup}\mathcal{L}({\mathsf{\Phi }}_0(\xi +{\sigma }_{\nu },·),{\mathsf{\Phi }}_0(\xi +{\sigma }_{\zeta },·))E_{\alpha }(-\mathsf{\Lambda }{(t+{\sigma }_{\nu }-{\sigma }_{\zeta })}^{\alpha })+\frac{{\epsilon }^2}{4},$$

or

$${\int }_{\mathcal{S}}\sum _{\iota =1}^{2n}{\left({\mathcal{U}}_{\iota }(t+{\sigma }_{\nu },y)-{\mathcal{U}}_{\iota }(t+{\sigma }_{\zeta },y)\right)}^{2}dy$$

$$\le \underset{-\widehat{\delta }\le \xi \le 0}{sup}({\int }_{\mathcal{S}}\sum _{\iota =1}^{2n}({\mathsf{\Phi }}_{0\iota }(\xi +{\sigma }_{\nu },y)$$

$$-{\mathsf{\Phi }}_{0\iota }(\xi +{\sigma }_{\zeta },y){)}^{2}dy)E_{\alpha }(-\mathsf{\Lambda }{(t+{\sigma }_{\nu }-{\sigma }_{\nu })}^{\alpha }+\frac{{\epsilon }^2}{2},$$

and then, it follows

$$\left|\right|\mathcal{U}(t+{\sigma }_{\nu },y)-\mathcal{U}(t+{\sigma }_{\zeta },y)\left|\right|\le \left\{\underset{-\widehat{\delta }\le \xi \le 0}{sup}\right({\int }_{\mathcal{S}}\sum _{\iota =1}^{2n}({\mathsf{\Phi }}_{0\iota }(\xi +{\sigma }_{\nu },y)$$

$$-{\mathsf{\Phi }}_{0\iota }(\xi +{\sigma }_{\zeta },y){)}^{2}dy)E_{\alpha }(-\mathsf{\Lambda }{(t+{\sigma }_{\nu }-{\sigma }_{\zeta })}^{\alpha }+\frac{{\epsilon }^2}{2}{\}}^{1/2}.$$

We apply (9) to the above estimate, and we obtain

$$\left|\right|\mathcal{U}(t+{\sigma }_{\nu },y)-\mathcal{U}(t+{\sigma }_{\zeta },y)\left|\right|<{\left(\frac{{\epsilon }^2}{2}+\frac{{\epsilon }^2}{2}\right)}^{\frac{1}{2}}=\epsilon .$$

The last inequality implies the existence of a function

$$\omega (t,y)=({\omega }_1(t,y),{\omega }_2(t,y),\dots ,{\omega }_{2n}(t,y)),$$

such that $\mathcal{U}(t+{\sigma }_{\nu },y)-\omega (t,y)\to 0$ as $\nu \to \infty$. Since o is arbitrary, then $\omega (t,y)$ is defined uniformly on $t\in \mathbb{R}$ and $y\in \mathcal{S}$.

We will show that $\omega (t,y)$ is a solution of one of the systems of the type (4). Following the same arguments as above, for any $\epsilon$ we can prove the next inequality

$$\left|\right|\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\mathcal{U}(t+{\sigma }_{\nu },y)-\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\mathcal{U}(t+{\sigma }_{\zeta },y)\left|\right|<\epsilon ,$$

or ${\displaystyle \underset{\nu \to \infty }{lim}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\mathcal{U}(t+{\sigma }_{\nu },y)}$ exists uniformly on all compact subsets of $\mathbb{R}.$

From ${\displaystyle \underset{\nu \to \infty }{lim}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\mathcal{U}(t+{\sigma }_{\nu },y)=\frac{{\partial }^{\alpha }\omega (t,x)}{\partial t^{\alpha }}}$, we have

$$\frac{{\partial }^{\alpha }\omega (t,y)}{\partial t^{\alpha }}=\underset{\nu \to \infty }{lim}(\mathcal{F}(t+{\sigma }_{\nu },\mathcal{U}(t+{\sigma }_{\nu },y))-\mathcal{F}(t+{\sigma }_{\nu },\omega (t,y))$$

$$+\mathcal{F}(t+{\sigma }_{\nu },\omega (t,y)))={\mathcal{F}}^{\sigma }(t,\omega (t,y)),$$

(19)

where $t\ne {\theta }_k^{\sigma }\left(\omega (t,y)\right)$.

For $t={\theta }_k^{\sigma }\left(\omega (t,y)\right)$, we have

$$\omega (t^{\sigma +},y)-\omega (t^{\sigma -},y)=\underset{\nu \to \infty }{lim}(\mathcal{U}(t^{\sigma }+{\sigma }_{\nu }+0,y)-\mathcal{U}(t^{\sigma }+{\sigma }_{\nu }-0,y))$$

$$=\underset{\nu \to \infty }{lim}{\mathcal{I}}_k\left(\mathcal{U}(t^{\sigma }+{\sigma }_{\nu },y)\right)={\mathcal{I}}_k\left(\omega (t^{\sigma },y)\right).$$

(20)

Since the function $\omega (t,y)$ satisfies both relations (19) and (20), then it is a solution of a system of type (4).

Finally, we will show that $\omega (t,y)$ is almost periodic. Consider a sequence $\left\{{\sigma }_{n}u\right\}$ that moves the model (1) to $\mathcal{H}\left(1\right)$.

For the function

$${\displaystyle \mathcal{L}(\omega (t,·),\omega (t+{\sigma }_{\nu }-{\sigma }_{\zeta },·))=\frac{1}{2}{\int }_{\mathcal{S}}\sum _{\iota =1}^{2n}{\left({\omega }_{\iota }(t,y)-{\omega }_{\iota }(t+{\sigma }_{\nu }-{\sigma }_{\zeta },y)\right)}^{2}dy,}$$

we have $t\ne {\theta }_k^{\sigma }\left(\omega (t,y)\right)$

$${}^c{D}^{\alpha }\mathcal{L}(\omega (t,·),\omega (t+{\sigma }_{\nu }-{\sigma }_{\zeta },·))\le -\mathsf{\Lambda }\left(\mathcal{L}(\omega (t,·),\omega (t+{\sigma }_{\nu }-{\sigma }_{\zeta },·))-\frac{2{\epsilon }^2}{3}\right)$$

(21)

and

$$\mathcal{L}(\omega (t^{\sigma +},·),\omega (t^{\sigma +}+{\sigma }_{\nu }-{\sigma }_{\zeta },·))\le \mathcal{L}(\omega (t^{\sigma },·),\omega (t^{\sigma }+{\sigma }_{\nu }-{\sigma }_{\zeta },·))$$

(22)

for $t={\theta }_k^{\sigma }\left(\omega (t,y)\right)$.

Using (21), (22) and Lemma 3, we get

$$\left|\right|\omega (t+{\sigma }_{\nu },y)-\omega (t+{\sigma }_{\zeta },y)\left|\right|<\epsilon ,\zeta \ge \nu \ge {\nu }_0\left(\epsilon \right).$$

(23)

The definitions of the sequence $\left\{s_{\nu }\right\}$ and the instants ${\tau }_{p_k}$ also guarantee that

$$\varrho (t+{\sigma }_{\nu },t+{\sigma }_{p_k})<\epsilon$$

for $\zeta \ge \nu \ge {\nu }_0\left(\epsilon \right)$.

Hence, it follows from (23) that $\omega (t+{\sigma }_{\nu },y)$ uniformly converges to $\omega (t,y)$, and therefore both statements (a) and (b) of Theorem 3 follow.

This completes the proof. □

Remark 4. 

Ones of the most investigated qualitative properties of GRN models are the stability and stabilization of the trajectories [7,8,9,11,12,14,15,16,19,20,21,22,27,35,38,40,52,56]. Different from the existing results on stability strategies for such models, we investigated the almost periodic behavior of a delayed model with reaction-diffusion terms. Fractional-order dynamics and impulsive disturbances at not fixed moments of time are also considered.

Remark 5. 

Although the established almost periodicity results for GRNs are few [23,55,65] they do not consider the combined approach applied in this paper. For example, the authors in [23] did not apply the fractional calculus approach. The paper [55] does not consider reaction-diffusion terms and variable impulsive perturbations. The impulsive fractional-order approach has not been applied in [65]. Hence, our results extend these few existing almost periodicity criteria and contribute to the development of the topic.

3.3. Perfect Mittag–Leffler Stability

In this section, we will analyze the stability of the almost periodic solution of (1). We will first extend the global perfect Mittag–Leffler stability concept to the hybrid model (1) [71].

Definition 8. 

A solution $\mathcal{U}(t,y;{\mathsf{\Phi }}_0)$ of (1) corresponding to an initial function ${\mathsf{\Phi }}_0\in \mathcal{PC}$ is said to be Mittag–Leffler stable, if for any ${\mathsf{\Phi }}_0^1\in \mathcal{PC}$ such that $\left|\right|{\mathsf{\Phi }}_0-{\mathsf{\Phi }}_0^1{\left|\right|}_{\widehat{\delta }}<\overline{\lambda }$ ($\overline{\lambda }>0$) constants $c>0$ and $d>0$ exist such that for $y\in \mathcal{S}$ we have

$$\left|\right|\mathcal{U}(t,y;{\mathsf{\Phi }}_0)-{\mathcal{U}}^1(t,y;{\mathsf{\Phi }}_0^1)\left|\right|\le {\left\{\mathcal{M}({\mathsf{\Phi }}_0-{\mathsf{\Phi }}_0^1)E_{\alpha }(-c{t}^{\alpha })\right\}}^d,t\ge 0,$$

where $\mathcal{M}\left(0\right)=0$, $\mathcal{M}\left(\mathsf{\Phi }\right)\ge 0$, and $\mathcal{M}\left(\mathsf{\Phi }\right)$ is Lipschitz with respect to $\mathsf{\Phi }\in \mathcal{PC}$.

Definition 9. 

A solution $\mathcal{U}(t,y;{\mathsf{\Phi }}_0)$ of (1) is said to be globally perfectly Mittag–Leffler stable, if it Mittag–Leffler stable and uniformly bounded.

Remark 6. 

The concept of perfect Mittag–Leffler stability is an extension of the Mittag–Leffler stability notion. It is related to bounded solutions, which is a requirement of the existence of almost periodic solutions [45,71].

Theorem 4. 

Under the conditions of Theorem 3 the almost periodic solution $\omega (t,y)$ of (1) is globally perfectly Mittag–Leffler stable.

Proof. 

Denote by

$$\widehat{\omega }(t,y)=\overline{\omega }(t,y)-\omega (t,y),$$

$${\mathcal{F}}^{\sigma }(t,\widehat{\omega }(t,y))={\mathcal{F}}^{\sigma }(t,\widehat{\omega }(t,y)+\omega (t,y))-{\mathcal{F}}^{\sigma }(t,\omega (t,y)),$$

where $\overline{\omega }(t,y)$ is any solution of (4).

Now, we consider the system

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{\alpha }\widehat{\omega }(t,y)}{\partial t^{\alpha }}={\mathcal{F}}^{\sigma }(t,\widehat{\omega }(t,y)),t\ne {\theta }_k^{\sigma }\left(\omega (t,y)\right),}\hfill \\ \Delta \widehat{\omega }(t,y)={\mathcal{I}}_k^{\sigma }\left(\widehat{\omega }(t,y)\right),t={\theta }_k^{\sigma }\left(\omega (t,y)\right),\hfill \end{array}\right.$$

(24)

and let ${\mathcal{L}}^W(t,\widehat{\omega }(t,y))=\mathcal{L}(\omega (t,y),\omega (t,y)+\widehat{\omega }(t,y))$.

After an estimation of the fractional-order derivative of ${\mathcal{L}}^W$ for $t\ne {\theta }_k^{\sigma }\left(\omega (t,y)\right)$ and ${\mathcal{L}}^W(t^{+},\widehat{\omega }(t^{+},y))$ for $t={\theta }_k^{\sigma }\left(\omega (t,y)\right)$ repeating the steps in the proof of Theorem 3, we obtain that the zero solution $\widehat{\omega }(t,y)=0$ of (24) is globally perfectly Mittag–Leffler stable, which implies the global perfect Mittag–Leffler stability of $\omega (t,y)$.

This completes the proof. □

Remark 7. 

Theorem 4 provides sufficient conditions for global perfect Mittag–Leffler stability of an almost periodic solution of a Caputo fractional order impulsive GRN models with delays and reaction-diffusion terms. The proposed results are new and complement the existing stability results for different classes of GRNs [7,8,9,11,12,14,15,16,19,20,21,22,27,35,38,40,52,56].

4. Illustrative Examples

In this section, illustrative examples are addressed to demonstrate the usefulness of the proposed criteria.

Example 1. 

To expose the established results, let us consider a reaction-diffusion impulsive fractional-order GRN model of type (1) for $0<\alpha <1$, $n=q=2$, $\mathcal{S}=\{{(y_1,y_2)}^T:-2\le y_1,y_2\le 2\}\subset {\mathbb{R}}^2$, with parameters defined by $a_1=a_2=2,$ $c_1=c_2=3,$ $B_1\left(t\right)=B_2\left(t\right)=0.02cos\sqrt{2}t$, $0\le {\upsilon }_j\left(t\right)\le 1,$ $0\le {\delta }_{\iota }\left(t\right)\le 1,$ $\iota ,j=1,2,$ $d_1\left(t\right)=0.3+0.1sin\sqrt{2}t,$ $d_2\left(t\right)=0.2+0.2cos\sqrt{2}t,$ $f_j\left({\mathcal{P}}_j\right)=\frac{{\mathcal{P}}_j^2}{1+{\mathcal{P}}_j^2},$ $j=1,2,$

$$\left(w_{\iota j}\right)\left(t\right)=\left(\begin{array}{cc}0.4+0.1sin\left(t\right)\hfill & \hfill 0.5-0.2cos\left(t\right)\\ 0.3+0.1cos\left(t\right)\hfill & \hfill 0.2-0.1sin\left(t\right)\end{array}\right),$$

$$\left(D_{\iota r}^{\left(1\right)}\right)=\left(\begin{array}{cc}0.4\hfill & \hfill 0.8\\ 1.2\hfill & \hfill 0.8\end{array}\right),\left(D_{\iota r}^{\left(2\right)}\right)=\left(\begin{array}{cc}0.8\hfill & \hfill 0.4\\ 0.4\hfill & \hfill 1.2\end{array}\right),$$

impulsive functions, which satisfy H5 for

$${\alpha }_{\iota k}={\gamma }_{\iota k}=-\frac{\iota }{\iota +1},\left\{{\varsigma }_{\iota k}\right\}=\left\{{\chi }_{\iota k}\right\}=0.3,$$

and functions ${\theta }_k\left(\mathcal{U}(t,y)\right)$, $\iota =1,2$, $k=\pm 1,\pm 2,\dots$ that satisfy H7.

For the particular choice of the parameters, we get

$${\lambda }_1=min\left({\tilde{D}}_{\iota }^{\left(1\right)},{\tilde{D}}_{\iota }^{\left(2\right)}\right)+min\left(a_{min},c_{min}\right)=2.3>0,$$

$${\lambda }_2=max\left(\frac{d^{+}}{2},\frac{w^{+}}{2}\sum _{j=1}^n{E}_j^1\right)=0.5>0,$$

and $\mathsf{\Lambda }={\lambda }_1-2{\lambda }_2=1.3>0$.

Hence, Theorem 3 guarantees the existence and uniqueness of an almost periodic solution $\omega (t,y)$ of the considered model.

Furthermore, Theorem 4 implies its global perfect Mittag–Leffler stability.

Example 2. 

We consider a reaction-diffusion impulsive fractional-order GRN model of type (1) for $\alpha =0.97$, $n=2$, $q=1$, $\mathcal{S}=[-1,1]$, $\mathcal{M}(t,y)={({\mathcal{M}}_1(t,y),{\mathcal{M}}_2(t,y))}^T$, $\mathcal{P}(t,y)={({\mathcal{P}}_1(t,y),{\mathcal{P}}_2(t,y))}^T$, $y\in \mathcal{S}$, with parameters defined by $a_1=a_2=4,$ $c_1=c_2=5,$ $B_1\left(t\right)=B_2\left(t\right)=0.01sin\sqrt{3}t$, $0\le {\upsilon }_j\left(t\right)\le 1,$ $0\le {\delta }_{\iota }\left(t\right)\le 1,$ $\iota ,j=1,2,$ $d_1\left(t\right)=0.1+0.3cos\sqrt{3}t,$ $d_2\left(t\right)=0.3+0.5sin\sqrt{3}t,$ $D_{11}^{\left(1\right)}=D_{22}^{\left(1\right)}=D_{11}^{\left(2\right)}=D_{22}^{\left(2\right)}=1$, $D_{12}^{\left(1\right)}=D_{21}^{\left(1\right)}=D_{12}^{\left(2\right)}=D_{21}^{\left(2\right)}=0$, $f_j\left({\mathcal{P}}_j\right)=\frac{{\mathcal{P}}_j^2}{1+{\mathcal{P}}_j^2},$ $j=1,2,$

$$\left(w_{\iota j}\right)\left(t\right)=\left(\begin{array}{cc}0.1+0.2sin\left(t\right)\hfill & \hfill 0.3+0.2cos\left(t\right)\\ 0.2+0.1sin\left(t\right)\hfill & \hfill 0.2-0.1cos\left(t\right)\end{array}\right),$$

impulsive functions, which satisfy H5 for

$${\alpha }_{\iota k}=-1+\frac{1}{4\iota },{\gamma }_{\iota k}=-1+\frac{1}{3\iota },\left\{{\varsigma }_{\iota k}\right\}=\left\{{\chi }_{\iota k}\right\}=0.5,$$

and functions ${\theta }_k\left({\mathcal{M}}_{\iota }(t,y),{\mathcal{P}}_{\iota }(t,y)\right)=|{\mathcal{M}}_{\iota }(t,y)|+|{\mathcal{P}}_{\iota }(t,y)|+\iota$, $\iota =1,2$, $k=\pm 1,\pm 2,\dots$.

For the particular choice of the parameters, we get

$${\lambda }_1=min\left({\tilde{D}}_{\iota }^{\left(1\right)},{\tilde{D}}_{\iota }^{\left(2\right)}\right)+min\left(a_{min},c_{min}\right)=5>0,$$

$${\lambda }_2=max\left(\frac{d^{+}}{2},\frac{w^{+}}{2}\sum _{j=1}^n{E}_j^1\right)=0.5>0,$$

and $\mathsf{\Lambda }={\lambda }_1-2{\lambda }_2=4>0$.

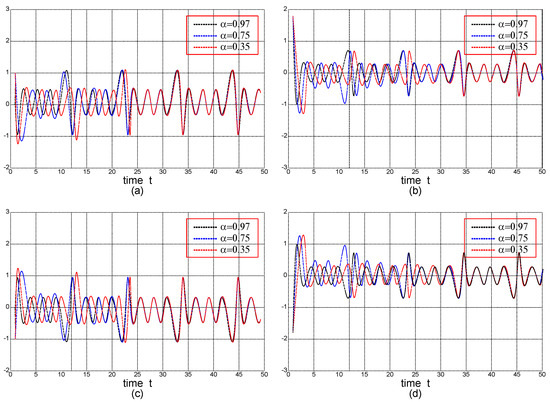
Hence, by Theorems 3 and 4 we conclude that the considered model has a unique almost periodic solution $\omega (t,y)$, which is globally perfectly Mittag–Leffler stable. The almost periodic level curves of the state variables ${\mathcal{M}}_1(t,y)$, ${\mathcal{M}}_2(t,y)$, ${\mathcal{P}}_1(t,y)$, ${\mathcal{P}}_2(t,y)$ for $y=0.8$ are shown on Figure 1. To demonstrate the almost periodic behavior of the solution for $\alpha =0.97$, we take different orders under the same initial conditions. Our simulations show that when the derivative order is larger, the almost periodic solution converges to the solution of the original system faster.

Remark 8. 

In the proposed examples, we investigate the almost periodic behavior of fractional-order reaction-diffusion impulsive GRN models using Theorems 3 and 4. Since the criteria proposed in these results are in the form of bounds on the system’s parameters, including synaptic weights, and impulsive control functions, we demonstrate that the proposed conditions are efficient and can be easily applied to check the existence of an almost periodic solution of the model and its global perfect Mittag–Leffler stability.

5. Conclusions

This article studied the almost periodic behavior of the solutions of a reaction-diffusion impulsive Caputo-fractional-order GRN model with delays. A general type of variable impulsive perturbations are considered for such models for the first time. The notion of almost periodicity is introduced to the generalized model in Section 2. The concept of perfect Mittag–Leffler stability is also introduced to the model by Definition 9. Our main results are presented in Theorems 1, 2, 3 and 4. In Theorems 1 and 2 criteria for uniform boundedness and uniform ultimate boundedness are provided. In Theorems 3 and 4, by applying the fractional Lyapunov functional theory, we established new conditions that ensure the existence and uniqueness of an almost periodic solution, as well as, its global perfect Mittag–Leffler stability. The presented criteria are in terms of bounds on the system’s parameters and impulsive control functions. Finally, illustrative examples are elaborated to demonstrate the efficacy and usefulness of our theoretical results. With the presented results we contributed to the development of the almost periodic theory of GRNs and generalize numerous existing results to the fractional-order impulsive case. The proposed criteria extend the existing results in [23,55,65] considering reaction-diffusion terms, variable impulsive perturbations and fractional calculus dynamics. They also complement the existing stability results for integer-order and fractional-order GRNs.