Dynamical Analysis of the Incommensurate Fractional-Order Hopfield Neural Network System and Its Digital Circuit Realization

Abstract

Dynamical analysis of the incommensurate fractional-order neural network is a novel topic in the field of chaos research. This article investigates a Hopfield neural network (HNN) system in view of incommensurate fractional orders. Using the Adomian decomposition method (ADM) algorithm, the solution of the incommensurate fractional-order Hopfield neural network (FOHNN) system is solved. The equilibrium point of the system is discussed, and the dissipative characteristics are verified and discussed. By varying the order values of the proposed system, different dynamical behaviors of the incommensurate FOHNN system are explored and discussed via bifurcation diagrams, the Lyapunov exponent spectrum, complexity, etc. Finally, using the DSP platform to implement the system, the results are in good agreement with those of the simulation. The actual results indicate that the system shows many complex and interesting phenomena, such as attractor coexistence and an inversion property, with dynamic changes of the order of q₀, q₁, and q₂. These phenomena provide important insights for simulating complex neural system states in pathological conditions and provide the theoretical basis for the later study of incommensurate fractional-order neural network systems.

1. Introduction

The exploration of fractional order calculus theory provides a new way of thinking to create value [1,2]. Fractional order calculus is a theory that studies differential integrals of an arbitrary order, and it has a very important role in many fields [3,4], such as bioinformatics, image enhancement, image encryption, chaos, and complex networks [5,6,7,8]. Fractional order calculus accumulates global information about functions in a weighted form [9]. Its memorability and global relevance enable it to be widely used in engineering applications [10,11]. To facilitate ease of reading and understanding in this article, the full names appearing in the paper correspond to the abbreviations shown in Table 1.

Table 1. Full name corresponding to the abbreviation.

Full Name	Abbreviation
Artificial neural network	ANN
Adomian decomposition method	ADM
Fractional-order neural network	FONN
Fractional-order Hopfield neural network	FOHNN

Artificial neural network (ANN) [12,13] consists of neurons and synapses. It is used to simulate the different electrical activities in the nervous systems [14,15]. Numerous physiological experiments have shown that biological neurons and electrical activity in the nervous system are highly correlated with thinking, memory, and learning skills [16,17]. The chaotic behavior in the human brain is also closely related to the brain’s unique abilities of memory, thinking, and learning [18]. Scholars have subsequently discovered ways to introduce chaos theory into artificial neural network models; in this way, they can better simulate the neural network structure of the brain [19]. The mystery of the brain has inspired many researchers to study chaotic neural networks [20]. In recent years, chaotic neural networks have been widely used in the areas of image identification, biomedicine, pattern recognition, etc. [21,22]. The Hopfield neural network (HNN) is one of the most used neural network models [23,24,25]. For instance, Ma et al. built a novel 4D HNN system with two nonlinear memristors, which are used to simulate the neural synapses in the model. There have also been investigations of how the chaotic state changes when an external stimulus is added to the neuron [26]. Xu et al. proposed a FOHNN system with four neurons. Moreover, a new multi-hash index chain construction method has been designed based on this system [27]. These experiments suggest that studying the dynamical behavior of the HNN can provide a foundation for work associated with neurodynamical behaviors. It is necessary for scholars to study the neural network model in depth [28,29,30,31].

The memory of a neural network model is analogous to the associative global dependence of fractional order calculus [32]. It has been demonstrated that the function of introducing fractional calculus into the neural network is to simulate the complex information processing and memory function of the human brain [33,34]. The fractional-order neural network (FONN) has an infinite “memory” property compared with the integer order; this property can improve the control ability of the network model for many practical problems and has strong application potential. Since the end of the 20th century, attempts to use and studies on FONN have been emerging. Alsaade et al. proposed a model-free and finite-time super-twisting control technique for a variable-order fractional Hopfield-like neural network with the aim of improving the robustness of FONN system control [35]. Boroomand et al. replaced the capacitor in the conventional HNN with this fractional-order partial resistance to build a FOHNN and used it for parameter estimation of second-order systems [36].

Findings indicate that the human brain first classifies information into different levels of importance before memorizing it, and that each segment of memory is stored in the human brain for different lengths of time and profundity [37]. The commensurate fractional-order neural network system can only process all information according to the same level of importance [38]. The incommensurate order can classify information into different levels of importance and then process it [39]. In fact, the commensurate order is only a special case of a FONN system, as each order of equations affects the system differently, such that incommensurate FONN systems can more accurately describe the working mechanism of the brain [40]. However, very few studies have been conducted on incommensurate FONN [41]. Abbes et al. calculated the stability of zero equilibrium points for a novel discrete incommensurate FOHNN [42]. Jia et al. lagged the quasi-synchronization of incommensurate fractional-order memristor neural networks with disparate characteristics, which was achieved via quantization control [43]. Chen et al. established the asymptotic stability criterion of FONN, and this criterion was used to effectively investigate the stability and synchronization of the incommensurate FOHNN system [44]. Jia et al. obtained the global stability of the incommensurate fractional-order memristor-based neural networks [45]. According to current research results, the characteristics of incommensurate FONN systems are more often studied by changing one order when the other orders of the system are equal. No complete order inequality has ever been realized before. Therefore, no ADM decomposition process has been given for the incommensurate fractional-order neural network. There are also relatively few implementations of non-commutative FONN systems. In this paper, a complete ADM decomposition procedure was given when the orders were not equal at all. The effect of the order on the complexity of FOHNN systems with complex activation functions was analyzed, and the effects of synaptic weights change on the system were also explored when the orders were completely unequal. It was found that the incommensurate FOHNN system has complex and rich dynamical behaviors [46,47]. The study of incommensurate FOHNN systems has contributed to a better understanding of the neural function of the human brain [48] and provided a theoretical basis for the subsequent study of incommensurate fractional-order systems.

Based on the above analysis, this paper constructs an incommensurate FOHNN system. The paper has the following structure. In Section 2, a new FOHNN system of an unequal order is presented. The numerical solution is calculated using the ADM algorithm, and then the dissipative nature of the system is analyzed and the equilibrium point and stability are explored. Section 3 provides a dynamical analysis of the system, and the effects of different synaptic weights and orders on the system are investigated. The system is implemented using the DSP platform in Section 4, and Section 5 is the conclusion of the whole paper.

2. The Incommensurate FOHNN System

2.1. Fractional Calculus

Definition 1

[49]. The definition of the Caputo fractional-order derivative is introduced as

$$(\ast D_{t_0+}^{q}f)(t)=\frac{1}{\mathsf{\Gamma }(s-q)}{\displaystyle {\int }_{t_0}^t\frac{f^{(s)}(\tau )}{{(t-\tau )}^{q+1-s}}}\mathrm{d}\tau ,$$

(1)

where Γ represents the Gamma function, q stands for order, s represents the first integer greater than q, and ${*D}_{t_0+}^q$ represents the Caputo differential operator.

Theorem 1

[50]. For the given fractional-order chaotic function ${(*D}_{t_0+}^{q}x\left)\right(t)=f(x\left(t\right))+$ c(t), where x(t) is the given function variable, c(t) is the constant term, and f denotes a functional equation containing linear and nonlinear components, the ADM algorithm expressed the system as

$$\left(\ast D_{t_0+}^{q}x\right)(t)=Lx(t)+Nx(t)+c(t),$$

(2)

where L and N are the linear and nonlinear parts of the system, respectively. Both sides of the equation are subjected to some calculus operations, and the following can be obtained

$$x=J_{t_0}^{q}Lx+J_{t_0}^{q}Nx+\mathsf{\Phi },$$

(3)

where Φ is the initial condition that satisfies the system and $J_{t_0}^q$ indicates the R-L fractional integral operator of order q. The nonlinear term is decomposed as

$$\left\{\begin{array}{l}{A}_j^i=\frac{1}{i!}{\left[\frac{{\mathrm{d}}^i}{\mathrm{d}{\alpha }^i}N(u_j^i(\alpha ))\right]}_{\alpha =0}\\ u_j^i(\alpha )={\displaystyle \sum _{g=0}^i{\alpha }^g{x}_j^g}\end{array}\right.,$$

(4)

in which i = 0, 1, 2, 3... ∞ and j = 1, 2, 3... n.

2.2. Solution of the Incommensurate FOHNN-Based System

HNN is a recurrent neural network suitable for computing complex dynamical behaviors in simulated neurons. The novel Hopfield neural network can be represented as

$${\dot{x}}_i=-x_i+{\displaystyle \sum _{j=1}^G{k}_{ij}\tanh (x_j)},$$

(5)

x_i (i = 1, 2, 3) indicates the status variable associated with the membrane potential of the i-th neuron, k_ij represents the G × G matrix of synaptic weights, and tanh(x_j) (j = 1, 2, 3) denotes the activation function responsible for mapping its input to the output on a neuron that is nonlinear. The topology is shown in Figure 1 and the matrix can be expressed as

$$K=\left[\begin{array}{ccc}{k}_{11}& k_{12}& k_{13}\\ k_{21}& k_{22}& k_{23}\\ k_{31}& k_{32}& k_{33}\end{array}\right]=\left[\begin{array}{ccc}{k}_{11}& -1.8& 0.7\\ 2.8& 0& k_{23}\\ k_{31}& 1.4& k_{33}\end{array}\right].$$

(6)

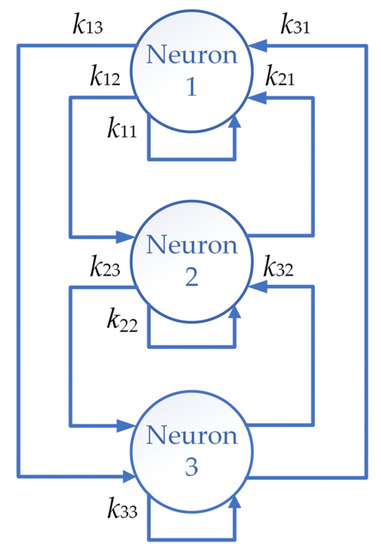
Figure 1. The topology structure of the neural network.

Combining Equations (5) and (6), a nonlinear dimensionless form of the 3-neuron HNN is written as

$$\left\{\begin{array}{l}{\dot{x}}_1=-x_1+k_{11}\tanh (x_1)-1.8\tanh (x_2)+0.7\tanh (x_3)\\ {\dot{x}}_2=-x_2+2.8\tanh (x_1)+k_{23}\tanh (x_3)\\ {\dot{x}}_3=-x_3+k_{31}\tanh (x_1)+1.4\tanh (x_2)+k_{33}\tanh (x_3)\end{array}\right..$$

(7)

Based on the compliant derivative, the incommensurate fractional-order nonlinear system can be written as

$$\left\{\begin{array}{l}\ast D_{t_0}^{q_0}{x}_1(t)=-x_1+k_{11}\tanh (x_1)-1.8\tanh (x_2)+0.7\tanh (x_3)\\ \ast D_{t_0}^{q_1}{x}_2(t)=-x_2+2.8\tanh (x_1)+k_{23}\tanh (x_3)\\ \ast D_{t_0}^{q_2}{x}_3(t)=-x_3+k_{31}\tanh (x_1)+1.4\tanh (x_2)+k_{33}\tanh (x_3)\end{array}\right.,$$

(8)

q₀, q₁, and q₂ are the systems of three disparate orders. The linear and nonlinear terms of the system are

$$\left[\begin{array}{c}L{x}_1\\ L{x}_2\\ L{x}_3\end{array}\right]=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right],\left[\begin{array}{c}N{x}_1\\ N{x}_2\\ N{x}_3\end{array}\right]=\left[\begin{array}{c}\tanh (x_1)\\ \tanh (x_2)\\ \tanh (x_3)\end{array}\right].$$

(9)

The nonlinear terms possess similar expressions; as such, here, only the decomposition Nx₁ through Equation (4) can be obtained as

$$\left\{\begin{array}{c}{A}_1^0=\tanh (x_1^0)\hfill \\ A_1^1=x_1^1{\mathrm{sech}}^2(x_1^0)\hfill \\ A_1^2=x_1^2{\mathrm{sech}}^2(x_1^0)-{(x_1^1)}^2{\mathrm{sech}}^2(x_1^0)\tanh (x_1^0)\hfill \\ A_1^3=x_1^3{\mathrm{sech}}^2(x_1^0)-2x_1^2{x}_1^1{\mathrm{sech}}^2(x_1^0)\tanh (x_1^0)\hfill \\ \hspace{1em}+\frac{1}{3}{(x_1^1)}^3(4{\mathrm{sech}}^3(x_1^0){\tanh }^2(x_1^0)-{\mathrm{sech}}^4(x_1^0))\hfill \\ A_1^4=x_1^4{\mathrm{sech}}^2(x_1^0)-\left(2x_1^3{x}_1^1+x_1^2{x}_1^2\right){\mathrm{sech}}^2(x_1^0)\tanh (x_1^0)\hfill \\ \hspace{1em}+{\left(x_1^1\right)}^2{x}_1^2(4{\mathrm{sech}}^3(x_1^0){\tanh }^2(x_1^0)-{\mathrm{sech}}^4(x_1^0))\hfill \\ \hspace{1em}+\frac{1}{3}{(x_1^1)}^4({\mathrm{sech}}^3(x_1^0)\tanh (x_1^0)-3{\mathrm{sech}}^3(x_1^0){\tanh }^3(x_1^0))\hfill \end{array}\right.,$$

(10)

and the first term can be obtained as

$$\left\{\begin{array}{l}{x}_1^0=x_1(t_{0^{+}})=c_1^0\\ x_2^0=x_2(t_{0^{+}})=c_2^0\\ x_3^0=x_3(t_{0^{+}})=c_3^0\end{array}\right..$$

(11)

The second term of the state parameter is represented as

$$\left\{\begin{array}{l}{x}_1^1=(-c_1^0+k_{11}\tanh (c_1^0)-1.8\tanh (c_2^0)+0.7\tanh (c_3^0))\frac{{(t-t_0)}^{q_0}}{\mathsf{\Gamma }(q_0+1)}\\ x_2^1=(-c_2^0+2.8\tanh (c_1^0)+k_{23}\tanh (c_3^0))\frac{{(t-t_0)}^{q_1}}{\mathsf{\Gamma }(q_1+1)}\\ x_3^1=(-c_3^0+k_{31}\tanh (c_1^0)+1.4\tanh \left(c_2^0\right)+k_{33}\tanh (c_3^0))\frac{{(t-t_0)}^{q_2}}{\mathsf{\Gamma }(q_2+1)}\end{array}\right..$$

(12)

Let

$$\left\{\begin{array}{l}{c}_1^1=-c_1^0+k_{11}\tanh (c_1^0)-1.8\tanh (c_2^0)+0.7\tanh (c_3^0)\\ c_2^1=-c_2^0+2.8\tanh (c_1^0)+k_{23}\tanh (c_3^0)\\ c_3^1=-c_3^0+k_{31}\tanh (c_1^0)+1.4\tanh \left(c_2^0\right)+k_{33}\tanh (c_3^0)\end{array}\right..$$

(13)

The coefficient decompositions of the other three terms are listed in Appendix A. The first five terms of the solutions to the incommensurate FOHNN chaotic systems are

$$\left\{\begin{array}{l}{x}_1(t)=c_1^0+c_1^1\frac{{(t-t_0)}^{q_0}}{\mathsf{\Gamma }(q_0+1)}+c_1^2\frac{{(t-t_0)}^{2q_0}}{\mathsf{\Gamma }(2q_0+1)}+c_1^3\frac{{(t-t_0)}^{3q_0}}{\mathsf{\Gamma }(3q_0+1)}+c_1^4\frac{{(t-t_0)}^{4q_0}}{\mathsf{\Gamma }(4q_0+1)}\\ x_2(t)=c_2^0+c_2^1\frac{{(t-t_0)}^{q_1}}{\mathsf{\Gamma }(q_1+1)}+c_2^2\frac{{(t-t_0)}^{2q_1}}{\mathsf{\Gamma }(2q_1+1)}+c_2^3\frac{{(t-t_0)}^{3q_1}}{\mathsf{\Gamma }(3q_1+1)}+c_2^4\frac{{(t-t_0)}^{4q_1}}{\mathsf{\Gamma }(4q_1+1)}\\ x_3(t)=c_3^0+c_3^1\frac{{(t-t_0)}^{q_2}}{\mathsf{\Gamma }(q_2+1)}+c_3^2\frac{{(t-t_0)}^{2q_2}}{\mathsf{\Gamma }(2q_2+1)}+c_3^3\frac{{(t-t_0)}^{3q_2}}{\mathsf{\Gamma }(3q_2+1)}+c_3^4\frac{{(t-t_0)}^{4q_2}}{\mathsf{\Gamma }(4q_2+1)}\end{array}\right..$$

(14)

According to the ADM process, the whole region is divided into an infinite number of small regions, and the solution obtained from the previous small region is used as the initial condition for the next small region for iteration, with iteration step h = 0.01. The setting was k₁₁ = 3.7, k₂₃ = 1, k₃₁ = −7, k₃₃ = 0, initial value x₀ = (1, 1, 1), incommensurate order q₀ = 0.88, q₁ = 0.86, and q₂ = 0.83. The incommensurate FOHNN-based system’s Lyapunov exponents are L₁ = 0.2502, L₂ = 0, and L₃ = −1.6173. The system has a chaotic state because L₁ > 0, L₂ = 0, and L₁ + L₂ + L₃ < 0. The relative phase diagram of the attractor is presented in Figure 2.

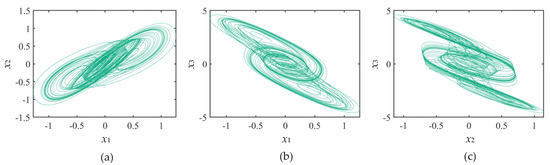
Figure 2. Phase portraits of the system. (a) x₁-x₂ plane; (b) x₁-x₃ plane; (c) x₂-x₃ plane.

2.3. Dissipation

The volume of the phase space of a system in dissipation is always contracting during motion; this state is expressed in mathematics as Λ < 0, and its properties guarantee the existence of bounded global attractors. The dissipative of the system is obtained as

$$\mathsf{\Lambda }=\frac{\partial {\dot{x}}_1}{\partial x_1}+\frac{\partial {\dot{x}}_2}{\partial x_2}+\frac{\partial {\dot{x}}_3}{\partial x_3}=-3+k_{11}(1-{\tanh }^2(x_1))+k_{33}(1-{\tanh }^2(x_3)).$$

(15)

Because −1 < tanh(x_i) < 1, the model is guaranteed to be dissipative for all x_i (i = 1, 2, 3) if the self-synaptic weights k₃₃, k₁₁ are properly selected. A positive definite Lyapunov function is introduced as

$$V\left(x_1,x_2,x_3\right)=\frac{1}{2}{x}_1^2+\frac{1}{2}{x}_2^2+\frac{1}{2}{x}_3^2,$$

(16)

the time derivative of Equation (16) can be deduced as

$$\begin{array}{cc}\dot{V}\left(x_1,x_2,x_3\right)\hfill & =x_1^{}{\dot{x}}_1+x_2^{}{\dot{x}}_2+x_3^{}{\dot{x}}_3\hfill \\ & =-(x_1^2+x_2^2+x_3^2)\hfill \\ & +\tanh (x_1)(k_{11}{x}_1+2.8x_2-k_{31}{x}_3)+\tanh (x_2)(-1.8x_1+1.4x_3)\hfill \\ & +\tanh (x_3)(0.7x_1+k_{23}{x}_2+k_{33}{x}_3)\hfill \end{array},$$

(17)

$$\begin{array}{cc}h\left(x_1,x_2,x_3\right)\hfill & =\tanh (x_1)(k_{11}{x}_1+2.8x_2-k_{31}{x}_3)+\tanh (x_2)(-1.8x_1+1.4x_3)\hfill \\ & +\tanh (x_3)(0.7x_1+k_{23}{x}_2+k_{33}{x}_3)\hfill \end{array},$$

(18)

next, the equation can become

$$\dot{V}\left(x_1,x_2,x_3\right)=-2V\left(x_1,x_2,x_3\right)+h\left(x_1,x_2,x_3\right).$$

(19)

Because tanh(x_i) < 1 for all x_i (i = 1, 2, 3).

$$\begin{array}{cc}h\left(x_1,x_2,x_3\right)\hfill & \le \left|\tanh (x_1)(k_{11}{x}_1+2.8x_2-k_{31}{x}_3)\right|+\left|\tanh (x_2)(-1.8x_1+1.4x_3)\right|\hfill \\ & +\left|\tanh (x_3)(0.7x_1+k_{23}{x}_2+k_{33}{x}_3)\right|\hfill \\ & <\left|k_{11}{x}_1+2.8x_2-k_{31}{x}_3\right|+\left|(-1.8x_1+1.4x_3)\right|+\left|0.7x_1+k_{23}{x}_2+k_{33}{x}_3\right|\hfill \\ & \le \left|x_1\right|(\left|k_{11}\right|-1.1)+\left|x_2\right|(\left|k_{31}\right|+2.8)+\left|x_3\right|(\left|k_{23}\right|+\left|k_{33}\right|+1.4)\hfill \end{array},$$

(20)

put D₀ > 0, which is a wirelessly extensive range of values. Let the range of all x_i (i = 1, 2, 3) be D with D > D₀, and obtain

$$\begin{array}{cc}h\left(x_1,x_2,x_3\right)\hfill & <\left|x_1\right|(k_{11}-1.1)+\left|x_2\right|(k_{23}+2.8)+\left|x_3\right|(-k_{31}+k_{33}+1.4)\hfill \\ & <x_1^2+x_2^2+x_3^2=2V\left(x_1,x_2,x_3\right)\hfill \end{array},$$

(21)

where k₁₁ − 1.1 > 0, k₂₃ + 2.8 > 0, and k₃₃ − k₃₁ + 1.4 > 0, and they are both constants on the surface

$$\{\left(x_1,x_2,x_3\right)\left|V\left(x_1,x_2,x_3\right)\right.=D\},$$

(22)

$$\dot{V}\left(x_1,x_2,x_3\right)=-2V\left(x_1,x_2,x_3\right)+h\left(x_1,x_2,x_3\right)<0,$$

(23)

therefore, it yields

$$\{\left(x_1,x_2,x_3\right)\left|V\left(x_1,x_2,x_3\right)\right.\le D\}.$$

(24)

The restricted region of all solutions of Equation (7) is obtained by a series of calculations.

2.4. Equilibrium Points and Stabilities

To obtain the dynamical behavior of stretching, contraction, and folding transformations of chaotic attractors in FOHNN systems with respect to the nature of equilibrium points, set the left side of Equation (8) to 0.

$$\left\{\begin{array}{l}0=-x_1+k_{11}\tanh (x_1)-1.8\tanh (x_2)+0.7\tanh (x_3)\\ 0=-x_2+2.8\tanh (x_1)+k_{23}\tanh (x_3)\\ 0=-x_3+k_{31}\tanh (x_1)+1.4\tanh (x_2)+k_{33}\tanh (x_3)\end{array}\right..$$

(25)

The Jacobian matrix corresponding to it is

$$J=\left[\begin{array}{ccc}-1+k_{11}{\mathrm{sech}}^2(x_1)& -1.8{\mathrm{sech}}^2(x_2)& 0.7{\mathrm{sech}}^2(x_3)\\ 2.8{\mathrm{sech}}^2(x_1)& -1& k_{23}{\mathrm{sech}}^2(x_3)\\ k_{31}{\mathrm{sech}}^2(x_1)& 1.4{\mathrm{sech}}^2(x_2)& -1-k_{33}{\mathrm{sech}}^2(x_3)\end{array}\right],$$

(26)

The equilibrium point is [0, 0, 0] obtained by calculating. The setting is k₁₁ = 3.7, k₂₃ = 0.8, k₃₁ = −6.6, and k₃₃ = 0.1. The equilibrium equation is

$${\lambda }^3+6.4{\lambda }^2-29.32\lambda -22.74=0,$$

(27)

and the solution is

$$\left\{\begin{array}{l}{\lambda }_1=-9.29\\ {\lambda }_2=-0.68\\ {\lambda }_3=3.58\end{array}\right..$$

(28)

According to Equation (25), all three eigenvalues are real roots, and λ₁ < 0, λ₂ < 0, and λ₃ > 0. λ₁ is a positive real root corresponding to an unstable solution, while λ₂ and λ₃ are two negative real roots corresponding to two stable solutions. As shown in Figure 3, this is a saddle point with an unstable manifold and the confluence of two stable manifolds for indicator 2.

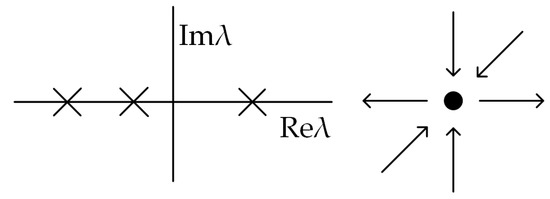
Figure 3. Model for indicator 2 saddle point.

3. The Dynamical Analysis of the Incommensurate FOHNN System

3.1. Dynamical Behaviors with the Incommensurate Fractional Order

The setting is k₁₁ = 3.7, k₂₃ = 0.7, k₃₁ = −7.1, k₃₃ = 1, initial value x₀ = (1, 1, 1), incommensurate order q₀ = 0.85, q₁ = 0.75, and q₂ = 0.6. The incommensurate order is varied. The setting q₀, q₁, and q₂ in the range of 0.75 to 0.85, in turn, was studied. The Lyapunov exponent spectrum and the bifurcation diagram are displayed in Figure 4, and the max Lyapunov exponent spectrum is displayed in Figure 5. To obtain a better view of the changes in the Lyapunov exponents of the system, only values greater than −4 are shown in Figure 4.

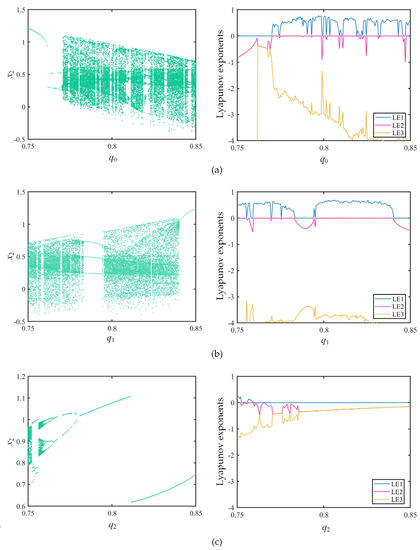
Figure 4. The bifurcation diagram and LEs when the incommensurate fractional order changes. (a) q₀ ∈ (0.75, 0.85); (b) q₁ ∈ (0.75, 0.85); (c) q₂ ∈ (0.75, 0.85).

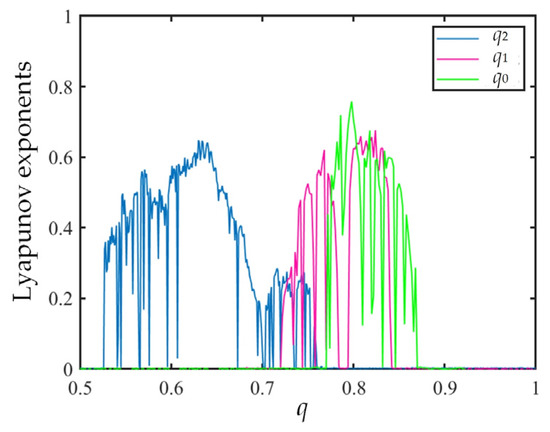
Figure 5. Max Lyapunov exponents spectrum when q₀, q₁, and q₂ vary.

Observe that q₀ in Figure 4a enters chaos from 0.772, with occasional brief periodic states in a continuous chaotic state. q₁ in Figure 4b is already in a chaotic state at 0.75; it has a longer period-3 window at 0.782, enters chaos again at 0.795 via a tangent bifurcation, and then changes back to a periodic state at 0.84. q₂ in Figure 4c undergoes a brief chaotic state and then enters the periodic state through an inverse multiplicative periodic bifurcation. As shown in Figure 5, the max Lyapunov diagram for q_i is (i = 1, 2, 3), unfolding the range of local instability of chaotic attractors caused by each order.

Analysis of Figure 4 and Figure 5 reveals that when the orders of the FOHNN system are not the same, by changing the order, the dynamical behavior of the system changes more. This indicates that the incommensurate order is more accurate in describing the physical phenomena of the system.

3.2. The Dynamical Behavior of Distinct Synaptic Weights

3.2.1. The Self-Synaptic Weight k₁₁ Varies

Auto synapses play an important role in regulating the accuracy of their own action potential delivery. Altering the self-synaptic weight can enhance neuronal responsiveness and make the FOHNN system appear as a complex chaotic phenomenon. Consider the effects of shifts in the self-synaptic weight k₁₁ on the system. The setting is k₂₃ = 0.9, k₃₁ = −7.1, k₃₃ = 0.1, initial value x₀ = (1, 1, 1), incommensurate order q₀ = 0.88, q₁ = 0.84, q₂ = 0.8, and self-synaptic weight k₁₁ ∈ (3.4, 3.9). The diagrams of the bifurcation and the Lyapunov exponents spectrum of the system are drawn in Figure 6. Observe a and b of Figure 6 at k₁₁ = 3.4. The system has entered a chaotic state, which lasts until k₁₁ = 3.58. At k₁₁ = 3.58, the system degenerates back to the periodic state; at k₁₁ = 0.61, it enters the chaotic state again and lasts until k₁₁ = 3.73, when it returns to the periodic state; at k₁₁ = 3.76, it enters the chaotic state again; and, in the interval from k₁₁ = 3.76 to 3.9, it is mostly in the chaotic state. The phase diagram in the x₂-x₃ plane of the attractor obtained by varying k₁₁ in this range is given in Figure 7.

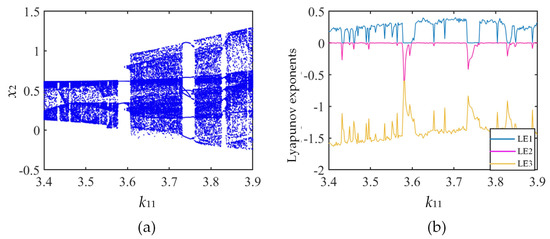
Figure 6. The dynamical behaviors with k₁₁ vary. (a) Diagram of bifurcation; (b) Lyapunov exponents of the system.

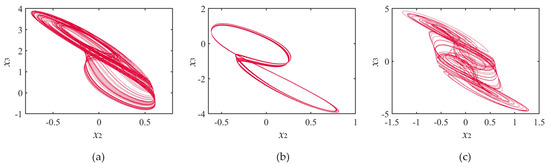
Figure 7. The attractor phase diagram with different k₁₁. (a) k₁₁ = 3.4; (b) k₁₁ = 3.6; (c) k₁₁ = 3.8.

3.2.2. The Synaptic Weight k₃₁ Varies

Varying the synaptic weights between neurons, the incommensurate FOHNN system harvests complex and research-worthy dynamical properties when k₁₁ = 3.9, k₂₃ = 0.8, k₃₃ = 1.3, incommensurate order q₀ = 0.94, q₁ = 0.86, q₂ = 0.8, the remaining characters are the same as described above, and synaptic weight k₃₁ ∈ (−5, −10). The Lyapunov exponent spectrum and bifurcation diagram are displayed in Figure 8. The system enters a chaotic state at k₃₁ = −5.1 via a tangent bifurcation, and then the period-7 attractor appears at k₃₁ ∈ (−6, −6.95). At k₃₁ = −6.95, the system enters the chaotic state again through a short period of doubling bifurcation lasting until k₃₁ = −7.3; during k₃₁ ∈ (−7.3, −7.5), the system is in period-7 states and then enters a chaotic state at k₃₁ = −7.5; after, it returns to the periodic state at k₃₁ = −8.2 through the internal crisis bifurcation at k₃₁ = −8.36, and then it enters a longer chaotic state, other conditions being unchanged. The attractor phase diagram obtained by choosing different k₃₁ is shown in Figure 9.

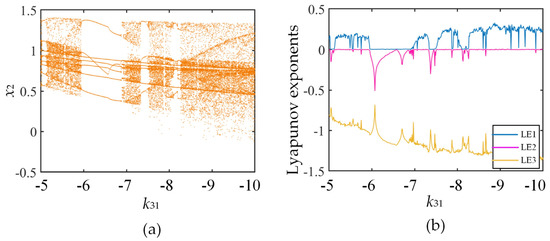
Figure 8. The dynamical behaviors with k₃₁ vary. (a) Diagram of bifurcation; (b) Lyapunov exponents of the system.

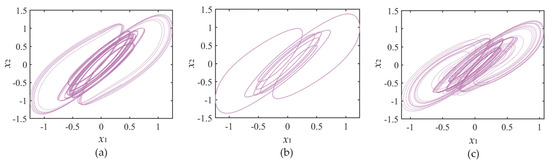
Figure 9. The attractor phase diagram with different k₃₁. (a) k₃₁ = −5; (b) k₃₁ = −6; (c) k₃₁ = −8.

3.3. Complexity Analysis

Spectral entropy complexity (SE) belongs to structural complexity. The main analysis is whether the sequence has the complexity of frequency component. The spectral entropy value is obtained using the energy distribution in the Fourier transform domain.

The setting is k₁₁ = 3.7, k₂₃ = 0.7, k₃₁ = −7.1, k₃₃ = 1, initial value x₀ = (1, 1, 1), incommensurate order q₀ = 0.85, q₁ = 0.75, and q₂ = 0.6. The incommensurate order is varied. q₀ and q₁ are set in the range of 0.75 to 0.85 and q₂ is set in the range of 0.65 to 0.75. The 3D SE complexity of various order planes is plotted in Figure 10, and, as shown, the maximum spectral entropy value reaches 0.55. The larger the SE value, the larger the average uncertainty of all possible events of the system. In a neural network system, the greater the complexity, the nearer it is to the brain’s proper working state. Therefore, the parameter values should be selected in the dark red area of Figure 10a,b.

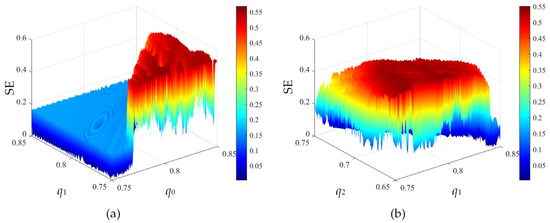
Figure 10. SE complexity with the incommensurate fractional order. (a) q₀-q₁ plane; (b) q₁-q₂ plane.

3.4. Coexistence of the Attractors for the Incommensurate Fractional Order

In the field of neural networks, there are multiple pathological states in brain dynamics, which include both normal and pathogenic states, and the coexistence of the two states corresponds to the phenomenon of attractor coexistence. Brain activity is highly dynamical; in normal conditions, the brain is in a chaotic state, while in the pathogenic state, the brain’s behavior is periodic.

The coexistence of incommensurate fractional orders was observed by adjusting the order of the system. The setting was k₁₁ = 3.7, k₂₃ = 0.8, k₃₁ = −8, and k₃₃ = 1. The attractor is blue when the initial value x₀ = (1, 1, 1) and pink when the initial value x₀ = (1, −5, −5); incommensurate order q₀ = 0.91, q₁ = 0.89, and q₂ = 0.8. The coexistence attractor phase diagram is shown in Figure 11a. By fixing q₀ = 0.91 and q₂ = 0.8 and changing the value of q₁ so that it is equal to 0.88 and 0.86, the different types of coexistence attractors are plotted in Figure 11b,c.

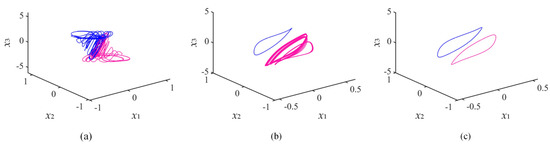
Figure 11. Phase portraits of coexisting symmetric attractors in the x₁-x₂-x₃ plane. (a) q₁ = 0.89; (b) q₁ = 0.88; (c) q₁ = 0.86.

4. Circuit Design and Simulation of the FOHNN System

The hardware implementation of the chaotic system is the key step in its application in engineering practice. DSP becomes the core of the electronic system with its programmability and easy implementation. This part uses DSP to obtain the chaotic signal of the system based on a typical TMS320F28335 DSP chip to study the implementation of FOHNN. The DSP hardware block diagram to realize the incommensurate FOHNN system is shown in Figure 12.

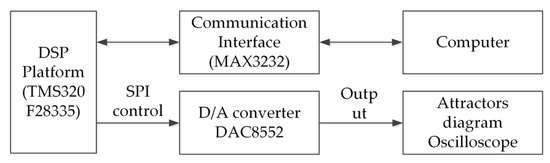
Figure 12. The hardware design of the DSP platform.

The software flow chart is shown in Figure 13.

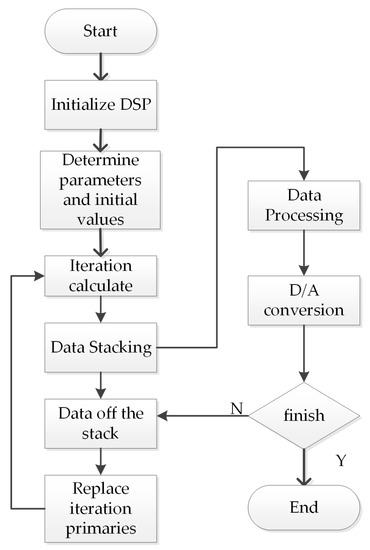
Figure 13. DSP software implementation flow chart.

The entire experimental system is shown in Figure 14.

Figure 14. DSP implementation platform.

The phase diagram realized by the oscilloscope DSP in Figure 15.

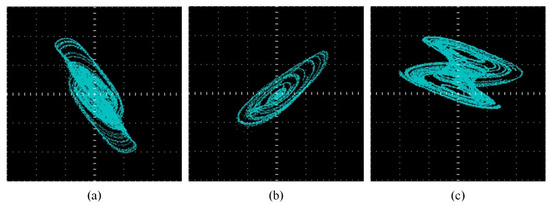
Figure 15. Chaotic attractor. (a) k₁₁ = 3.7, k₂₃ = 1, k₃₁ = −7, k₃₃ = 0, initial value x₀ = (1, 1, 1), incommensurate order q₀ = 0.88, q₁ = 0.86, and q₂ = 0.83; (b) k₁₁ = 3.7, k₂₃ = 0.8, k₃₁ = −7.1, k₃₃ = 0.1, initial value x₀ = (1, 1, 1), incommensurate order q₀ = 0.88, q₁ = 0.85, and q₂ = 0.82; (c) k₁₁ = 3.7, k₂₃ = 1, k₃₁ = −7, k₃₃ = 0.1, initial value x₀ = (1, 1, 1), incommensurate order q₀ = 0.88, q₁ = 0.86, and q₂ = 0.84.

5. Conclusions

In this article, an incommensurate FOHNN system is designed and solved by the ADM algorithm. The dissipative properties of the system are given and the stabilization point at fixed values is calculated. The effects of the order q₀, q₁, q₂ and the changes of the synaptic weights k₃₁ and self-synaptic weight k₁₁ in the system on the dynamic characteristics were analyzed. The results indicate that the system shows complex dynamical behaviors with the dynamic changes of the five parameters. Interestingly, the coexistence of attractors is found for many cases and its inversion property is found. Finally, the digital circuit of the incommensurate FOHNN system is implemented on the DSP platform, and the Matlab simulation results match those obtained by the DSP. The rich nonlinear phenomena, exhibited by the incommensurate FOHNN system, offer an additional experimental basis for the study of this system in fractional-order chaotic systems and the practical application of neural networks. The next step will be to consider its application in medical image encryption, and the actual circuit realization of the system.