Abstract
Since each rock type represents different deformation characteristics, prediction of the damage beforehand is one of the most fundamental problems of industrial activities and rock engineering studies. Previous studies have predicted the stress–strain behaviors preceding rock failure; however, quantitative analyses of the progressive damage in different rocks under stress have not been accurately presented. This study aims to quantify pre-failure rock damage by investigating the stress-induced microscale cracking process in three different rock types, including diabase, ignimbrite, and marble, representing strong, medium-hard, and weak rock types, respectively. We demonstrate crack intensity at critical stress levels where cracking initiates (σci), propagates (σcd), and where failure occurs (σpeak) based on scanning electron microscope (SEM) images. Furthermore, the progression of rock damage was quantified for each rock type through the fractal analyses of crack patterns on these images. Our results show that the patterns in diabase have the highest fractal dimensions (DB) for all three stress levels. While marble produces the lowest DB value up to σci stress level, it presents greater DB values than those of ignimbrite, starting from the σcd level. This is because rock damage in ignimbrite is controlled by the groundmass, proceeding from such stress level. Rock texture controls the rock stiffness and, hence, the DB values of cracking. The mineral composition is effective on the rock strength, but the textural pattern of the minerals has a first-order control on the rock deformation behavior. Overall, our results provide a better understanding of progressive damage in different rock types, which is crucial in the design of engineering structures.
1. Introduction
Because rock deformation and failure processes are controlled by the initiation, propagation, and coalescence of microcracks, the stability of engineering structures (e.g., dams and tunnels), based on various rock types, is primarily dependent on robust assessments of the cracking process. Since the pioneering work of Griffith [1], researchers have produced numerous methods and theories to explain progressive rock damage regarding such stress-induced microcracking [2,3,4,5,6,7,8,9,10,11,12].
In order to obtain a better understanding of the micro-interaction mechanisms within rocks, laboratory loading experiments have been accompanied by mineralogical analyses. For instance, Simmon et al. [13] and Kranz [14] classified microcracks on thin sections to detect the source of stress concentration. Zhao et al. [15] observed the failure development of marble under compression through SEM images. Similarly, Eberhardt [16] identified the changing orientations of stress-induced cracks on SEM images as well.
Moreover, studies focusing on the quantification of rock texture [17,18] have provided a solid basis for the investigation of the effects of mineralogical composition and textural distribution on rock strength and deformation characteristics. Fahy and Guccione [19] identified the strength of sandstones by using the mineralogical properties of quartz. Shakoor and Bonelli [20] studied the effects of grain properties and the textural structure of sandstones on compressive strength. Ulusay et al. [21] determined rock engineering properties through petrographic characteristics using correlation and multivariate statistical techniques. Ersoy and Waller [22] proposed a relation between the mechanical properties and the textural coefficient of various rock types. El Bied et al. [23] suggested that the textural features control damage localization, forming shear bands in rocks. Later on, Coggan et al. [24] revealed the effect of mineralogical changes on strength reduction. Öztürk et al. [25] proposed regression models to predict the approximate value of compressive strength from the textural coefficient. Ündül [26] determined the effect of textural and mineralogical properties on the strength and deformation parameters of volcanic rocks. More recently, Askaripour et al. [27] summarized the influences of rock textural features on the geomechanical properties of a rock by regression equations.
Besides these microscopic insights, it has also been discovered that cracking patterns in rocks causing failure and deformation have fractal characteristics [28,29,30,31,32,33]. More specifically, fractal properties of crack propagation and crack network development in rock specimens have been investigated at various types and levels of stresses in the laboratory. For instance, Zhao et al. [15] and Zhao [34] captured images of crack initiation, extension, and coalescence from direct SEM observation of microcracks developing on marble plates. To understand the extent of deformation and cracking behavior, authors calculated the box fractal dimension of the cracks, showing that the fractal dimension increases with increasing stress. On the other hand, the results of these studies can not be considered for the evaluation of the findings derived from the standard testing methods because they were obtained from an unconventional strength test. Ju et al. [35] recently developed a methodology that incorporates computed tomography (CT) and servo-controlled triaxial test techniques. Namely, box-counting fractal dimensions of crack networks developed inside coal cores for different stages of axial stresses show that the fractal dimension of the crack network tended to decrease initially before subsequently increasing during the further stages of loading. Accordingly, Wang et al. [36] performed X-ray CT scans of coal samples under uniaxial and triaxial compressive loading conditions. The 3D box-counting fractal dimensions of crack networks that developed within the coal samples exhibited a good linear correlation with crack volume, crack rate, crack density, and crack connectivity.
While Ju et al. [35] and Wang et al. [36] have provided quite important insights into the progressive crack development in rocks, but the influence of mineralogical composition on rock damage evolution has not been considered. Considering the mineralogical properties in the cracking process, Liu and Zhao [37] examined the effects of impact times on cracking in various rock types under dynamic loadings to represent the field (outcrop) -scale deformation processes (e.g., faulting). Under quasi-static loading conditions, Lai et al. [38] studied the role of various loading rates on the box fractal dimension of the fragmentation distribution and microcracks of the internal structure. Nevertheless, Lai et al. [38] did not identify the cracking process along different stages of loading for the demonstration of damage progression in rocks.
The novelty of this study is in revealing the progressive damage by comparing the microcracking processes in three different rock types through a combined assessment of experimental measurements, mineralogical analysis, and fractal characterizations. Since the identification of the critical stress levels, where cracking initiates (σci), propagates (σcd), and failure occurs (σpeak) has been required to reveal the incremental damage accumulation in rock [8,16,39,40], the microcracking in the examined rocks was captured during different stages of the loading. The effects of mineralogical composition and textural features on the cracking evolution, quantified by fractal dimensions, have been interpreted. As is different from previous studies, our study was conducted under quasi-static loading conditions through conventional laboratory strength tests.
For this purpose, the macro mechanical parameters of three different rock types, such as diabase, ignimbrite, and marble, were determined in the laboratory, and then their critical stress levels (σci, σcd, and σpeak) related to microcracking were detected in representative numerical models generated through the discrete element method (DEM). Core samples recovered from each rock type were subjected to uniaxial compressive loading up to these critical stress levels using a stress-controlled press. These samples were then cut parallel to the loading direction to reveal the traces of cracks along such parallel surfaces, through which thin sections and SEM images were taken. Through the box-counting technique, fractal dimension values were calculated to quantify the crack patterns on digital reconstructions derived from SEM images. The fractal dimension values corresponding to each stress level were evaluated together with the mineralogical properties. The damage developments in different rock types were compared to each other to explain the role of rock microstructure on the damage.
2. Material
Three different rock types, diabase, marble, and ignimbrite, are used in this study. These rocks have no visible (macro) fractures/cracks and a relatively homogeneous internal structure. This property enables the minimization of the effect of pre-existing defects on mechanical behavior (Figure 1). For each rock type, 40 cylindrical (core) samples in ASTM [41] standards (2 ≤ L/D ≤ 2.5, L: length, and D: diameter) were subjected to uniaxial and triaxial compressive strength tests and tensile strength tests. From these experiments, four fundamental mechanical parameters of these rocks, such as uniaxial compressive strength (UCS), tensile strength (UTS), Young’s (Elasticity) Modulus (E), and Poisson’s ratio (ν), were determined, and Hoek–Brown failure envelopes [42] were plotted. These macro properties were then used in the calibration of numerical models whose details are given in the following section.

Figure 1.
Rock types used in this study: (a) Marble; (b) Diabase; (c) Ignimbrite.
3. Method
3.1. Three-Dimensional DEM Modeling
A numerical modeling technique based on the discrete element method (DEM) was used to determine the critical cracking stress levels in rocks. The macro mechanical properties determined from laboratory experiments were used in the calibration of three-dimensional DEM-based numerical models. Numerical models were generated through Yade open-source DEM code [43]. According to the bonded particle model (BPM), first proposed by Potyondy and Cundall [44] and later modified by Scholtes and Donze [45], a rock material consists of an assembly of polydisperse, discrete, rigid, and spherical particles (discrete elements, DEs). The particles are bonded together in an interaction range and follow the elastic–brittle contact law. Following the elastic–brittle contact law, the particles are bonded together in an interaction range (γint) such as:
Here, Deq is the initial equilibrium distance and Rx and Ry are the radii of particles x and y. This parameter (γint) adjusts the average number of bonds per particle, N (coordination number), and is defined before the start of the test simulation. The interaction forces between the particles are subdivided into a normal component Fn and a shear component Fs. Fn is calculated in Equation (2) as:
where kn is the normal stiffness as a function of equivalent elastic modulus Y (in Pa), and un is the normal relative displacement. Under compression, Fn can increase indefinitely. However, under tension, Fn can increase up to a significant threshold such as . t is the interparticle tensile strength (in Pa) and A is a surface regarding the size of the particles (). When , the bond breaks, and a tensile crack occurs at the bond location.
Fs is the shear force and is calculated incrementally, as shown in Equation (4):
Here, ks, the shear stiffness computed as , and P is as a constant between ks and the normal stiffness, kn, between the values 0 < P < 1. Δus is the relative incremental displacement and Fs,t−Δt is the shear force at the previous timestep. The maximum shear force, Fs,max, is calculated according to the generalized Mohr–Coulomb criterion:
In Equation (5), c (in Pa) is the cohesion, and φ (in °) is the friction angle. When Fs ≥ Fs,max, shear failure develops, and a shear crack occurs at the bond location.
The calibration process is driven by micromodel parameters, given above (Y, P, t, c, φ, and N), that are assigned to these particles to obtain the macro mechanical rock parameters (UCS, UTS, E, and ν). The calibrated microparameters of each rock type are given in Table 1. The details of the methodology are presented in Scholtes and Donze [45], and some applications regarding simulation procedure can be found in Dinç Göğüş [46] and Dinç Göğüş and Avşar [47].

Table 1.
Calibrated microparameters of DEM model samples based on macro mechanical properties obtained in the laboratory.
A total of 149 uniaxial and triaxial compression and tensile strength test simulations were performed with the same stress conditions in the laboratory (e.g., the same lateral pressures, using frictionless plates to apply loading, etc.). Numerical samples with the dimensions of 1 × 2 × 1 (model unit), each containing 10,000 particles (discrete element, DE), represent accurately the failure and deformation parameters of real rocks (Table 2). In the simulation of the uniaxial compressive strength test, the loading is applied to the model sample through two rigid and frictionless plates, placed at the bottom and top surfaces of the sample (Figure 2). The strain rate was chosen as 0.025 m/s, according to the preliminary sensitivity analysis results.

Table 2.
Comparison of macro mechanical parameters obtained from laboratory measurements and DEM modeling.
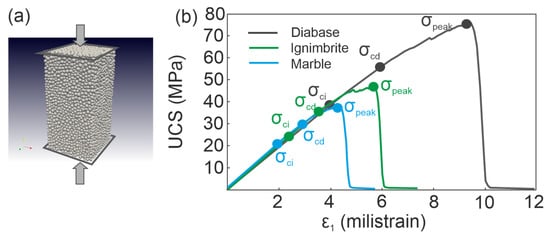
Figure 2.
(a) Configuration of 3D DEM model under uniaxial compressive loading; (b) stress–strain responses and critical stress levels of the rock materials.
In the DEM analyses, the models were examined in an open-source interface program called Paraview to determine the stress levels (σci and σcd, respectively) at which cracks emerge and progress by coalescence. In the uniaxial compressive strength test simulations, 150,000 iterations were made for each sample, and cracking was examined from the beginning of the loading. During the analysis, it was determined how many cracks occurred in the model sample at which stage of the iteration, and the stress level corresponding to the relevant strain was determined. The detected critical stress thresholds from DEM modeling are presented in Table 3.

Table 3.
Critical stress levels (σci, σcd, σpeak) for the rock types.
3.2. Experimental Setup
Core samples were loaded up to the determined stress levels under uniaxial compression (see Table 3). The tests were carried out in a stress-controlled hydraulic press and the loading rate was set up to 0.1 MPa/s for ignimbrite and marble, and 0.2 MPa/s for diabase, according to the preliminary experimental results.
Three micro-cameras with 90× magnification at 4 cm and 20× at 15 cm and a 1.3-megapixel sensor were integrated into the experimental setup to observe the cracking at the mesoscale as well (Figure 3). Camera images were recorded by using Dino Capture software on two different computers. Synchronously, stress–strain responses of rocks were recorded through the control panel. Three samples of each rock type were loaded up to the stress level σci, and then the experiment was ended. After that, 3 new samples were loaded up to the σcd, and the experiment was stopped again. Finally, 2 core samples were loaded up to the σpeak until reaching the ultimate rock failure (up to the UCS value). Looking at the digital micro-camera recordings (Figure 4), one can see that there is no mesoscale cracking in the diabase and marble cores loaded up to the σci level. In addition, just a few cracks are observed in all samples at the σcd levels. The most prominent mesoscale cracking develops in samples of ignimbrites once the sample reaches its ultimate stress level (σpeak). All loaded core samples and the unloaded samples representing the primary texture of the rocks were cut parallel to the loading direction, as shown in Figure 5. A total of 72 thin sections and 51 polished sections were prepared from these cut surfaces to be analyzed mineralogically under the polarized microscope (PM) and scanning electron microscope (SEM), respectively. The images taken under microscopes and the details of the analyses are given in the following section.

Figure 3.
Experimental setup for the stress-controlled uniaxial compressive strength test.

Figure 4.
Incremental cracking (mesoscale) with increasing stress under uniaxial compressive loading (i: σci, ii: σcd, iii: σpeak stress levels, and yellow lines: mesoscale cracks).
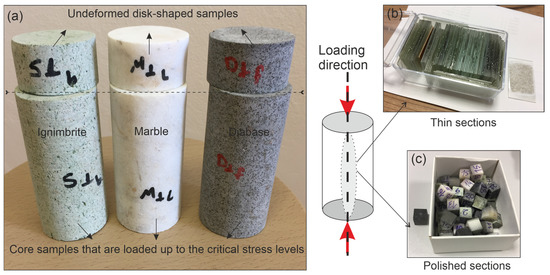
Figure 5.
(a) Loaded core- and unloaded disk-shaped samples; (b,c) thin and polished sections prepared from these samples.
3.3. Mineralogical Analysis
In the mineralogical analysis, firstly, thin sections taken from unloaded samples were assessed, and the primary texture and mineralogy of the rocks were identified. Then the general pattern of pre-existing microcracks in the texture of rocks at different microscales was determined on both the thin sections and the SEM images to be able to distinguish the new cracks induced by stress. The undeformed (unloaded) views of the rock samples in both under the SEM and thin section imaging are shown in Figure 6.

Figure 6.
Images of all rock types under the polarizing microscope (top) and SEM (bottom): (a) diabase; (b) ignimbrite; (c) marble. (The thin sections were viewed at 4× in crossed polarized light (XPL). Mineral abbreviations based on the study by Whitney and Evans [48]: Afs—alkali feldspar, Bt—biotite, Cal—calcite, Chl—chlorite, Pl—plagioclase, Px—pyroxene).
In the mineralogical analysis, the composition of the diabase sample was determined mainly as plagioclase, pyroxene, and olivine (Figure 6a). There are also secondary opaque minerals. Plagioclase crystals are euhedral and subhedral, columnar, or flat prismatic. They show polysynthetic twinning. A typical ophitic texture is identified because of observing high-relief anhedral pyroxene crystals among plagioclase crystals. Olivine crystals are in the form of small, circular grains and are relatively less abundant than other minerals in the samples. In the ignimbrites, mainly volcanic glass and fragments of existing crystals were detected in the fine-grained groundmass (Figure 6b). The crystals are plagioclase, alkali feldspar (sanidine), and biotite minerals. Quartz is observed in very small amounts. There is also some chlorination in the groundmass. The third rock type, marble, only consists of calcite. There are also small amounts of opaque minerals. Anhedral calcite crystals with cleaved, rhombohedral twins present granoblastic texture (Figure 6c).
The principal results of the mineralogical analyses under the polarized microscope can be summarized as follows:
- Diabase and marble consist only of crystals. The ignimbrite has a groundmass-dominated structure, and the crystals are dispersed within the groundmass. Diabase has an equidimensional and interlocking texture. Similarly, calcite crystals in marble also clamp together.
- In SEM images, marble presents a relatively smoother surface than ignimbrite and diabase in the undeformed state (Figure 6). However, the increase in the number of cracks with increasing stress was clearly observed in the SEM images of all three rock types (detailed hereafter in the following section).
- Looking at the compositions of all rock types, plagioclase, pyroxene, and alkali feldspars are the hardest minerals. Calcite and biotite have relatively lower hardness. However, since biotite is very cleaved, it deforms more easily under loading (for instance, the bending of biotites in ignimbrites is demonstrated in Figure 6b).
3.4. Fractal Analysis
The concept of fractal geometry [49] has been a very useful and robust tool in the practical solution of many complex problems in the earth sciences and, especially, in rock mechanics, as in many other disciplines. With the recognition of the fractal properties of metal crack surfaces [50], the application of the fractal concept of topologically 2D rock crack surfaces and 1D profiles taken from these surfaces is of great interest and many works have been published in the literature for this purpose, e.g., [51,52,53,54,55,56,57,58,59,60,61,62,63].
Fractal characterization of the cracks has been investigated at various scales. For instance, Barton and Larsen [28], by using the box-counting technique, examined the fractality of three crack-trace network maps prepared from tuff outcrops at Yucca Mountain in the western US, and they found that these complex networks were fractal with fractal dimensions values such as 1.12, 1.14, and 1.16. Later on, Hirata [30] studied the fractal properties of fault systems in Japan and revealed that the fractal dimensions varied between 1.05 and 1.60. Barton [31] provided a series of crack trace maps at various scales and listed the calculated fractal dimensions for each, ranging between 1.32 and 1.70. This study also introduced variations of the conventional box method, such as the box-rotate, box-flex, and box-density methods, to improve the box method’s accuracy and reproducibility. Some authors, on the other hand, have claimed non-fractal structures for the crack network patterns, e.g., [64,65,66]. Further, it was emphasized that natural crack patterns might not be characterized by a single fractal dimension over a significant scale range [67]. Due to these contradictory findings, Berkowitz and Hadad [32] addressed the fundamental question of whether crack networks are fractal or not. They analyzed the fractality of a series of natural crack trace maps as well as several synthetical crack networks generated using various probability distribution functions. The authors concluded that both crack network types exhibited fractal properties [32]. Later, by using a modified version of the box-counting technique, the previously obtained results of Barton [31] were re-examined by Roy et al. [33]. It was also highlighted that some crack networks are certainly self-similar, such that their geometries should be described by a single fractal dimension.
In this study, for the calculation of fractal dimension values of 2D microcrack patterns that developed at different stress levels and were then visualized through the SEM inspections, we performed the box-counting (grid) technique [68,69]. The technique is quite practical and applicable to one- and two-dimensional data sets [70]. A map of crack traces is covered by a grid of square boxes or cells with a side length of r. Then the number of square cells Nbox(r), including any part of crack traces, is counted. Recursively running this process for a sequence of grids with decreasing box sizes will result in an increase in the number of boxes occupied by any portion of the cracks. The relationship between Nbox(r) and r is given as:
If the log-log plot of Nbox(r) versus r is drawn and the slope β of the linear fit adjusted to the data in this plot is read, the fractal dimension (DB) is estimated by the following relationship:
4. Analysis of Progressive Rock Damage
In the SEM analysis, 522 images were taken at different magnitudes of scales ranging between 40 μm and 500 μm. The images were selected in which cracks are obviously visible and that also demonstrate the overall crack pattern for the fractal analysis (Figure 7a, Figure 8a and Figure 9a). Therefore, the scale magnitude of the images was selected as 200 μm (equivalent to 400× magnification), which is the same for all of the images taken in high vacuum mode, 10,000 kV with an ET detector. These images that represent the cracking in samples for three different critical stress levels, σci, σcd, and σpeak, were scaled in pixels through the digital image processing technique by using ImageJ software. The stress-induced cracks in the images were first drawn as lines representing crack traces. To distinguish these crack traces from the rest of the image, they were converted to 8-bit images, and then black-and-white thresholds were applied to them. As a result, binary images with white backgrounds and black crack traces were derived, and the crack pattern for each image was digitized (Figure 7b, Figure 8b, and Figure 9b). The box-counting method in the FracLac plugin was applied to these binary images. The image type was selected as binary and the background was set as white. Six grid positions (scan types) in fixed grid scanning were used to find an optimal covering. The scale was arranged such that the smallest box size was 2 pixels and the largest box size was 30% of the binary image size. By running the software with this configuration of input parameters, log Nbox(r) vs. log r plots were drawn and the slopes (β) of the linear fits adjusted to the data on these plots were read. By substituting these slope values in Equation (7), the fractal dimension (DB) values of the crack patterns for three loading stages were determined (Figure 7c, Figure 8c, and Figure 9c).
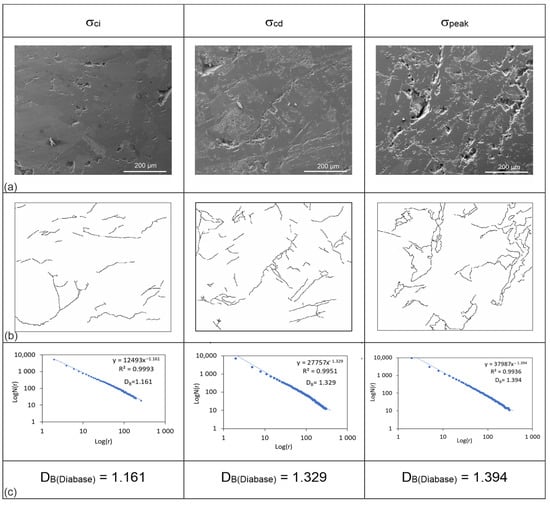
Figure 7.
(a) SEM images of the diabase; (b) the 8-bit black and white binary images of the crack patterns for different stress levels; (c) the logN(r)-log(r) graphs derived from the fractal analyses of these images.
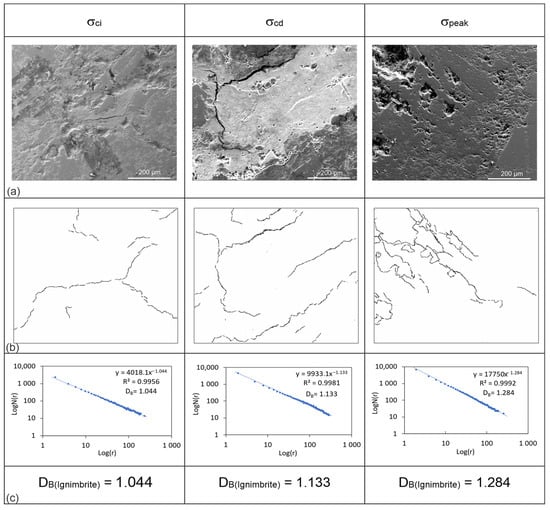
Figure 8.
(a) SEM images of the ignimbrite; (b) the 8-bit black and white binary images of the crack patterns for different stress levels; (c) the logN(r)-log(r) graphs derived from the fractal analyses of these images.
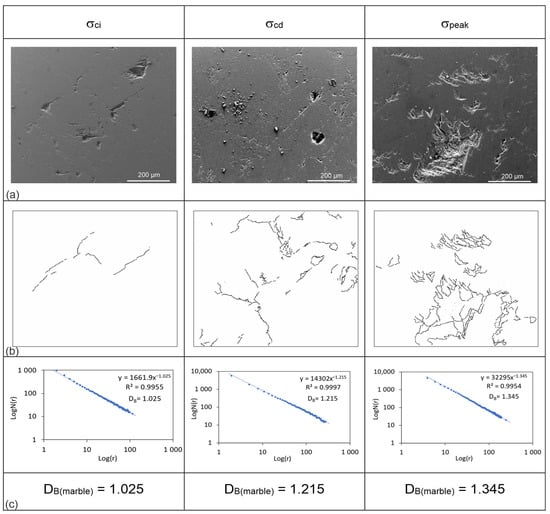
Figure 9.
(a) SEM images of the marble; (b) the 8-bit black and white binary images of the crack patterns for different stress levels; (c) the logN(r)-log(r) graphs derived from the fractal analyses of these images.
Our results show that the DB values increase with increasing stress, indicating that the microcrack intensity in the rocks increases as well. The diabase has the greatest DB values for all three stress levels (DBdiabase = 1.161, 1.329, 1.394). For the σci stress level, the DB value of the ignimbrite (1.044) is greater than that of the marble (1.025), while the DB value of the marble is greater than the ignimbrite’s once the σcd is reached (DBmarble = 1.215 and DBignimbrite = 1.133). Similarly, the DB value of marble is more than that of ignimbrite at the σpeak stress level (DBmarble = 1.345 and DBignimbrite = 1.284).
5. Discussion
Increasing DB values has been interpreted as increasing microcrack intensity in rocks [34,36,37,71]. Although the calculation of the DB values to assess the cracking process in rocks has paramount importance, it has to be interpreted accompanying the mineralogical composition of the rock to have a better understanding of progressive rock damage [37,38]. Therefore, the cracking process in three different rock types here was quantified by fractal analysis, and DB values were interpreted together with mineralogical observations in terms of their hardness, interlocking, and texture.
Our results show that the DB values increase with increasing cracking intensity induced by the incremental stress in all rock types. The greatest DB values were obtained in diabase, demonstrating that it displays the most intensive cracking at all critical stress levels. It consists of hard minerals (pyroxene and plagioclase) representing strong rock characteristics [72]. Furthermore, its interlocking texture has a great influence on its strength properties as increasing rigidity [19,23,24,25,27]. These findings point out that the diabase is the most brittle rock compared to the others.
Marble is the weakest rock in terms of strength parameters (UCS and UTS) in this study (see Table 2) However, it has a greater ratio of UCS to UTS and the E value than ignimbrite. It has the lowest DB value at σci stress level. On the other hand, once the σcd stress level is reached, it has a greater DB value than that of ignimbrite. This shows a more significant decrease in stiffness in marble, compared to ignimbrite, with increasing stress, so the DB values become greater with more intense cracking. This is because the groundmass-dominated texture in ignimbrite exhibits a more plastic (ductile) behavior than the granoblastic texture in marble, which consists of only crystals (calcites) [24,26,27]. In other words, the laboratory measurements show that the strength values of ignimbrite are greater than those of marble, but ignimbrite’s groundmass-dominant composition [20,21,22] controls the rock damage starting from the σcd stress level.
These findings show that the mineralogical composition and texture exert an important control on the rock stiffness and, hence, the DB values. However, mineral hardness is strongly effective on the rock strength parameters, and the textural pattern of the minerals predominantly drives the rock deformation behaviors. Therefore, since the damage accumulation strongly depends on textural characteristics, each rock type exhibits different cracking intensities at the relevant critical stress level. The DB values during the loading paths are marked on the stress–strain curves, representing the quantitative progressive rock damage for each rock type (Figure 10). The damage regarding the cracking process in all rock model samples is predominantly driven by tensile/extensional mechanisms rather than shearing, representing brittle rock response. Please note that the blue and red dashed lines in Figure 10 demonstrate the tensile and shear microcrack numbers, respectively.
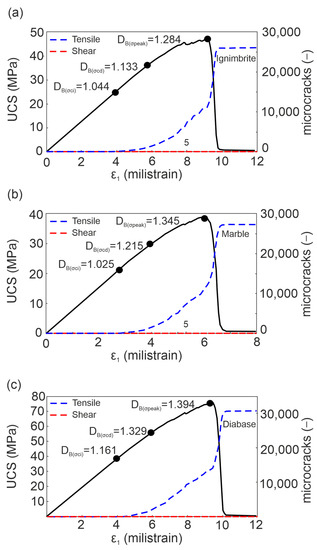
Figure 10.
Quantification of progressive rock damage regarding the cracking process in all rock types based on fractal calculations (a) Ignimbrite (b) Marble (c) Diabase (Blue and red dashed lines show the numbers of tensile and shear microcracks, respectively).
Overall, the DB values of cracking patterns at the critical stress levels demonstrate an explicit increment with increasing stress (Figure 11). Thus, the progressive crack accumulation was assessed using fractal theory to have an explicit quantitative data platform for the damage mechanics in rocks.
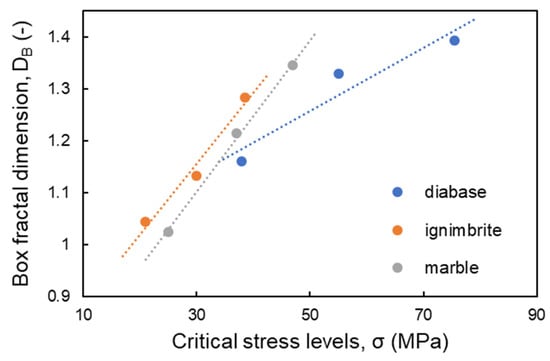
Figure 11.
Variation of the DB values of crack patterns at the critical stress levels.
6. Conclusions
In this study, progressive rock damage was investigated through laboratory tests, numerical modeling, and mineralogical observations integrated with fractal analysis. Macro mechanical parameters of three different rock types, diabase, ignimbrite, and marble, representing strong, medium-hard, and weak rock types, respectively, were calibrated through a 3D DEM modeling technique according to the laboratory measurements (see Table 2). The critical stress levels where cracking initiates (σci), propagates (σcd), and failure occurs (σpeak) were detected in 3D DEM model samples in order to reveal the progressive rock damage. After that, the core samples of these three different rock types were subjected to uniaxial compressive loading up to the critical stress levels (σci, σcd, and σpeak) in the laboratory. Thin section and SEM images taken from these loaded samples were examined to identify the cracking intensity and pattern developing at the relevant stress levels. The progression of rock damage in each rock type was quantified through the determination of the fractal dimension (DB) of the crack patterns.
The main results of our research can be summarized as follows:
- The 3D DEM model predictions are in good agreement with the laboratory measurements in terms of mechanical parameters. In all DEM samples, the rocks display brittle rock response, and damage is most likely driven by the tensile mechanisms.
- During the recording of the loading process, the mesoscale cracking patterns could not be detected in marble and diabase by digital cameras, while ignimbrite presented visible crack development. Contrarily, at the microscale (under polarizing and scanning electron microscopes), intensive cracking is mostly detected in marble and diabase.
- In the mineralogical analyses, it is identified that diabase has the hardest minerals, with an equidimensional and interlocking texture. Marble consists only of crystals clamping together. On the other hand, the ignimbrite has a groundmass-dominated texture, and the crystals are dispersed in this groundmass.
- In all rock types, the DB values increase with increasing critical stress levels (σci, σcd, and σpeak). The diabase has the greatest DB values at all stress levels, demonstrating that it displays the most intensive cracking during the loading due to the hard minerals and interlocking texture.
- Marble is the weakest rock in terms of strength parameters, and it has the lowest DB value at σci stress level. However, marble has a greater DB value than that of ignimbrite once the σcd stress level is reached. This is because the groundmass-dominated texture in ignimbrite controls the rock damage, and it presents a more plastic behavior than the one in crystalline marble after the σcd level.
The mechanical parameters obtained from the rock mechanics laboratory experiments give fundamental information about the rock’s strength and deformation properties. Moreover, the evaluation of both results of fractal dimension and mineralogical analyses show that the entire damage process of rocks may exhibit different tendencies depending on micro-interactions under stress. Therefore, the quantification of progressive damage and mineralogical assessments in various rocks at the microscale provides a more accurate and robust interpretation of the load-bearing capacity and deformation issues encountered in rock engineering applications.
Author Contributions
Conceptualization, Ö.D.G.; methodology, Ö.D.G., E.A., K.D. and A.Ç.; software, Ö.D.G. and E.A.; validation, Ö.D.G.; formal analysis, Ö.D.G., E.A. and A.Ç.; investigation, Ö.D.G., E.A. and K.D.; resources, Ö.D.G. and E.A.; writing—original draft preparation, Ö.D.G., E.A. and K.D.; visualization, Ö.D.G. and E.A.; project administration, Ö.D.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Scientific and Technological Research Council of Türkiye (TÜBİTAK) through the research project with the number 121Y031.
Data Availability Statement
This work is based on the data derived from laboratory and numerical experiments, which are available through contacting the authors.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Griffith, A.A. The Phenomena of Rupture and Flow in Solids. Philos. Trans. R. Soc. A 1921, 221, 163–198. [Google Scholar]
- Hoek, E.; Bieniawski, Z.T. Brittle rock fracture propagation in rock under compression South African Council for scientific and industrial research pretoria. Int. J. Fract. Mech. 1965, 1, 137–155. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Mechanism of brittle fracture of rock: Part I—Theory of the fracture process. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1967, 4, 395–406. [Google Scholar] [CrossRef]
- Lajtai, E.Z. Brittle fracture in compression. Int. J. Fract. 1974, 5, 25–36. [Google Scholar] [CrossRef]
- Tapponnier, P.; Brace, W.F. Development of stress-induced microcracks in Westerly granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1976, 13, 103–112. [Google Scholar] [CrossRef]
- Horii, H.; Nemat-Nasser, S. Brittle failure in compression: Splitting faulting and brittle-ductile transition. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1986, 319, 337–374. [Google Scholar]
- Martin, C.D.; Chandler, N.A. The progressive fracture of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B.; Read, R.S. Identifying crack initiation and propagation thresholds in brittle rock. Can. Geotech. J. 1998, 35, 222–233. [Google Scholar] [CrossRef]
- Wong, L.N.; Einstein, H.H. Systematic evaluation of cracking behavior in specimens containing single flaws under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2009, 46, 239–249. [Google Scholar] [CrossRef]
- Renard, F.; Bernard, D.; Jacques Desrues, J.; Ougier-Simonin, A. 3D imaging of fracture propagation using synchrotron X-ray microtomography. Earth Planet. Sci. Lett. 2009, 286, 285–291. [Google Scholar] [CrossRef]
- Renard, F.; Cordonnier, B.; Kobchenko, M.; Kandula, N.; Weiss, J.; Zhu, W. Microscale characterization of rupture nucleation unravels precursors to faulting in rocks. Earth Planet. Sci. Lett. 2017, 476, 69–78. [Google Scholar] [CrossRef]
- McBeck, J.; Ben-Zion, Y.; Renard, F. Predicting fault reactivation and macroscopic failure in discrete element method simulations of restraining and releasing step overs. Earth Planet. Sci. Lett. 2022, 593, 117667. [Google Scholar] [CrossRef]
- Simmons, G.; Richter, D. Microcracks in Rocks. In The Physics and Chemistry of Minerals and Rocks; Strens, R.G.J., Ed.; Wiley: Toronto, ON, Canada, 1976; pp. 105–137. [Google Scholar]
- Kranz, R.L. Microcracks in rocks: A review. Tectonophysics 1983, 100, 449–480. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, J.; Wang, R. Real-time SEM observations of the microfracturing process in rock during a compression test. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 643–652. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 361–380. [Google Scholar] [CrossRef]
- Howarth, D.F.; Rowlands, J.C. Development of an index to quantify rock texture for qualitative assessment of intact rock properties. Geotech. Test. J. 1986, 9, 169–179. [Google Scholar]
- Howarth, D.F.; Rowlands, J.C. Quantitative assessment of rock texture and correlation with drillability and strength properties. Rock Mech. Rock Eng. 1987, 20, 57–85. [Google Scholar] [CrossRef]
- Fahy, M.P.; Guccione, M.J. Estimating strength of sandstone using petrographic thin-section data. Bull. Int. Assoc. Eng. Geol. 1979, 16, 467–485. [Google Scholar] [CrossRef]
- Shakoor, A.; Bonelli, R.E. Relationship between petrographic characteristics, engineering index properties, and mechanical properties of selected sandstones. Bull. Assoc. Eng. Geol. 1991, 28, 55–71. [Google Scholar] [CrossRef]
- Ulusay, R.; Türeli, K.; Ider, M.H. Prediction of engineering properties of a selected litharenite sandstone from its petrographic characteristics using correlation and multivariate statistical techniques. Eng. Geol. 1994, 38, 135–157. [Google Scholar] [CrossRef]
- Ersoy, A.; Waller, M.D. Textural characterization of rocks. Eng. Geol. 1995, 39, 123–136. [Google Scholar] [CrossRef]
- El Bied, A.; Sulem, J.; Martineau, F. Microstructure of shear zones in Fontainebleau sandstone. Int. J. Rock Mech. Min. Sci. 2002, 39, 917–932. [Google Scholar] [CrossRef]
- Coggan, J.S.; Stead, D.; Howe, J.H.; Faulks, C.I. Mineralogical controls on the engineering behavior of hydrothermally altered granites under uniaxial compression. Eng. Geol. 2013, 160, 89–102. [Google Scholar]
- Özturk, C.A.; Nasuf, E.; Kahraman, S.A. Estimation of rock strength from quantitative assessment of rock texture. J. S. Afr. Inst. Min. Metall. 2014, 114, 471–480. [Google Scholar]
- Ündül, Ö. Assessment of mineralogical and petrographic factors affecting petro-physical properties, strength and cracking processes of volcanic rocks. Eng. Geol. 2016, 210, 10–22. [Google Scholar] [CrossRef]
- Askaripour, M.; Saeidi, A.; Mercier-Langevin, P.; Rouleau, A. A Review of Relationship between Texture Characteristic and Mechanical Properties of Rock. Geotechnics 2022, 2, 262–296. [Google Scholar] [CrossRef]
- Barton, C.C.; Larsen, E. Fractal geometry of two-dimensional fracture networks at Yucca Mountain, southwestern Nevada. In Proceedings of the International Symposium on Fundamentals of Rock Joints, Björkliden, Sweden, 15–20 September 1985; Stephansson, O., Ed.; Centek: Björkliden, Sweden, 1985; pp. 77–84. [Google Scholar]
- Anderson, T.L. Application of fractal geometry to damage development and brittle fracture in materials. Scr. Metall. 1989, 25, 97–102. [Google Scholar] [CrossRef]
- Hirata, T. Fractal dimension of fault systems in Japan: Fractal structure in rock fracture geometry at various scales. Fractals Geophys. 1989, 131, 157–170. [Google Scholar]
- Barton, C.C. Fractal Analysis of Scaling and Spatial Clustering of Fractures. In Fractals in the Earth Sciences; Barton, C.C., La Pointe, P.R., Eds.; Springer Science Business Media: New York, NY, USA, 1995; pp. 141–178. [Google Scholar]
- Berkowitz, B.; Hadad, A. Fractal and multifractal measures of natural and synthetic fracture networks. J. Geophys. Res. Solid Earth 1997, 102, 12205–12218. [Google Scholar] [CrossRef]
- Roy, A.; Perfect, E.; Dunne, W.M.; McKay, L.D. Fractal characterization of fracture networks: An improved box-counting technique. J. Geophys. Res. 2007, 112, B12201. [Google Scholar] [CrossRef]
- Zhao, Y. Crack pattern evolution and a fractal damage constitutive model for rock. Int. J. Rock Mech. Min. Sci. 1998, 35, 349–366. [Google Scholar] [CrossRef]
- Ju, Y.; Xi, C.; Zhang, Y.; Mao, L.; Gao, F.; Xie, H. Laboratory in situ CT observation of the evolution of 3D fracture networks in coal subjected to confining pressures and axial compressive loads: A novel approach. Rock Mech. Rock Eng. 2018, 51, 3361–3375. [Google Scholar] [CrossRef]
- Wang, D.; Zeng, F.; Wei, J.; Zhang, H.; Wu, Y.; Wei, Q. Quantitative analysis of fracture dynamic evolution in coal subjected to uniaxial and triaxial compression loads based on industrial CT and fractal theory. J. Pet. Sci. Eng. 2021, 196, 108051. [Google Scholar] [CrossRef]
- Liu, K.; Zhao, J. Progressive damage behaviours of triaxially confined rocks under multiple dynamic loads. Rock Mech. Rock Eng. 2021, 54, 3327–3358. [Google Scholar] [CrossRef]
- Lai, Y.; Zhao, K.; He, Z.; Yu, X.; Yan, Y.; Li, Q.; Shao, H.; Zhang, X.; Zhou, Y. Fractal characteristics of rocks and mesoscopic fractures at different loading rates. Géomeéch. Energy Environ. 2022, 33, 100431b. [Google Scholar] [CrossRef]
- Nicksiar, M.; Martin, C.D. Evaluation of methods for determining crack initiation in compression tests on low-porosity rocks. Rock Mech. Rock Eng. 2012, 45, 607–617. [Google Scholar] [CrossRef]
- Moradian, Z.; Einstein, H.H.; Ballivy, G. Detection of cracking levels in brittle rocks by parametric analysis of the acoustic emission signals. Rock Mech Rock Eng. 2015, 49, 785–800. [Google Scholar] [CrossRef]
- ASTM. Annual Book of ASTM Standards-Soil and Rock, Building Stones, Section-4, Construction Vol. 04.08; ASTM Publications: Philadelphia, PA, USA, 2000. [Google Scholar]
- Hoek, E.; Carranza-Torres, C.T.; Corkum, B. Hoek–Brown failure criterion—2002 edition. In Proceedings of the Fifth North American Rock Mechanics Symposium, Toronto, ON, Canada, 7–10 July 2002; pp. 267–273. [Google Scholar]
- Smilauer, V.; Catalano, E.; Chareyre, B.; Dorofeenko, S.; Duriez, J.; Dyck, N.; Elias, J.; Er, B.; Eulitz, A.; Gladky, A.; et al. Yade Documentation, 2nd ed.; The Yade Project; Zenodo: Honolulu, HI, USA, 2015. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Scholtes, L.; Donze, F.V. A DEM model for soft and hard rocks: Role of grain interlocking on strength. J. Mech. Phys. Solids 2013, 61, 352–369. [Google Scholar] [CrossRef]
- Dinç Göğüş, Ö.D. 3D discrete analysis of damage evolution of hard rock under tension. Arab. J. Geosci. 2020, 13, 661. [Google Scholar] [CrossRef]
- Dinç Göğüş, Ö.; Avşar, E. Stress levels of precursory strain localization subsequent to the crack damage threshold in brittle rock. PLoS ONE 2022, 17, e0276214. [Google Scholar] [CrossRef]
- Whitney, D.L.; Evans, B.W. Abbreviations for names of rock-forming minerals. Am. Min. 2010, 95, 185–187. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. How long is the coast of Britain? Statistical Self-Similarity and Fractal Dimension. Science 1967, 155, 636–638. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Brown, S.R.; Scholz, C.H. Broad bandwidth study of the topography of natural rock surfaces. J. Geophys. Res. 1985, 90, 575–582. [Google Scholar] [CrossRef]
- Carr, J.R.; Warriner, J.B. Rock mass classification using fractal dimension. In Proceedings of the 28th US Rock Mechanics Symposium, Tucson, AZ, USA, 29 June–1 July 1987; Balkema: Rotterdam, The Netherlands, 1987; pp. 73–80. [Google Scholar]
- Turk, N.; Greig, M.J.; Dearman, W.R.; Amin, F.F. Characterization of rock joint surfaces by fractal dimension. In Proceedings of the 28th US Rock Mechanics Symposium, Tucson, AZ, USA, 29 June–1 July 1987; Balkema: Rotterdam, The Netherlands, 1987; pp. 1223–1236. [Google Scholar]
- Lee, Y.H.; Carr, J.R.; Barr, D.J.; Haas, C.J. The fractal dimension as a measure of the roughness of rock discontinuity profiles. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1990, 27, 453–464. [Google Scholar] [CrossRef]
- Power, W.L.; Tullis, T.E. Euclidean and fractal models for the description of rock surface roughness. J. Geophys. Res. 1991, 96, 415–424. [Google Scholar] [CrossRef]
- Sakellariou, M.; Nakosi, B.; Mitsakaki, C. On the fractal character of rock surfaces. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 527–533. [Google Scholar] [CrossRef]
- Odling, N.E. Natural fracture profiles, fractal dimension and joint roughness coefficients. Rock Mech. Rock Eng. 1994, 27, 135–153. [Google Scholar] [CrossRef]
- Develi, K.; Babadagli, T. Quantification of natural fracture surfaces using fractal geometry. Math. Geol. 1998, 30, 971–998. [Google Scholar] [CrossRef]
- Develi, K.; Babadagli, T. Experimental and visual analysis of single-phase flow through rough fracture replicas. Int. J. Rock Mech. Min. Sci. 2015, 73, 139–155. [Google Scholar] [CrossRef]
- Fardin, N.; Stephansson, O.; Jing, L. The scale dependence of rock joint surface roughness. Int. J. Rock Mech. Min. Sci. 2001, 38, 659–669. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, B.; Tanabashi, Y. Estimating the relation between surface roughness and mechanical properties of rock joints. Int. J. Rock Mech. Min. Sci. 2006, 43, 837–846. [Google Scholar] [CrossRef]
- Develi, K. Computation of direction dependent joint surface parameters through the algorithm of triangular prism surface area method: A theoretical and experimental study. Int. J. Solids Struct. 2020, 202, 895–911. [Google Scholar] [CrossRef]
- Avşar, E. An experimental investigation of shear strength behavior of a welded bimrock by meso-scale direct shear tests. Eng. Geol. 2021, 294, 106321. [Google Scholar] [CrossRef]
- Chiles, J.P. Fractal and geostatistical methods for modeling of a fracture network. Math. Geol. 1988, 20, 631–654. [Google Scholar] [CrossRef]
- Odling, N.E. Network properties of a two-dimensional natural fracture pattern. Pure Appl. Geophys. 1992, 138, 95–114. [Google Scholar] [CrossRef]
- Gillespie, P.A.; Howard, C.B.; Walsh, J.J.; Watterson, J. Measurement and characterisation of spatial distribution of fractures. Tectonophysics 1993, 226, 113–141. [Google Scholar] [CrossRef]
- Walsh, J.J.; Watterson, J. Fractal analysis of fracture pattern using the standard box-counting technique: Valid and invalid methodologies. J. Struct. Geol. 1993, 15, 1509–1512. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982; p. 468. [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988; 283p. [Google Scholar]
- Barton, C.C.; La Pointe, P.R. Fractals in the Earth Sciences; Springer Science Business Media: New York, NY, USA, 1995; 265p. [Google Scholar]
- Yaohui, W.; Tingjie, L. The Fractal Characteristics of Micro-cracks in Rock under Uniaxial Compression. In Proceedings of the ISRM International Symposium—2nd Asian Rock Mechanics Symposium, Beijing, China, 11–14 September 2001. [Google Scholar]
- Yılmaz, N.G.; Goktan, R.M.; Kibici, Y. An investigation of the petrographic and physico mechanical properties of true granites influencing diamond tool wear performance, and development of a new wear index. Wear 2011, 271, 960–969. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).