An Implicit Numerical Method for the Riemann–Liouville Distributed-Order Space Fractional Diffusion Equation

Abstract

This paper investigates a two-dimensional Riemann–Liouville distributed-order space fractional diffusion equation (RLDO-SFDE). However, many challenges exist in deriving analytical solutions for fractional dynamic systems. Efficient and reliable methods need to be explored for solving the RLDO-SFDE numerically. We develop an alternating direction implicit scheme and prove that the numerical method is unconditionally stable and convergent with an accuracy of $O({\sigma }^2+{\rho }^2+\tau +h_x+h_y)$. After employing an extrapolated technique, the convergence order is improved to second order in time and space. Furthermore, a fast algorithm is constructed to reduce computational costs. Two numerical examples are presented to verify the effectiveness of the numerical methods. This study may provide more possibilities for simulating diffusion complexities by fractional calculus.

1. Introduction

In past centuries, the classical differential equation was regarded as a powerful tool to describe many physical phenomena. However, there exist many challenges in modelling some abnormal diffusion processes and physical behaviours in complex systems only by integer-order differential equations. Fractional derivative operators can be used to describe the memory effect and heterogeneous properties that are not covered by integer-order models, which give a more realistic description of complex physical processes [1]. Increasing interest has been given to the application of fractional differential equations in various fields, such as finance [2], information security [3], viscoelasticity [4], imaging processing [5,6], and control problems [7,8]. By virtue of the non-local property, fractional derivatives have shown great potential for simulating diffusion processes in complex and heterogeneous media [9,10]. In recent years, extensive attention has been drawn to distributed-order differential equations since they are more effective in modelling phenomena exhibiting varying non-local properties over multiple scales.

The distributed-order operator, generalised by integrating the order of fractional derivatives over a given range, has accumulated considerable popularity during recent years [11]. Due to the utility of this operator in describing behaviours with multi-scale varying characteristics, extensive attention has been attracted to the investigation of distributed-order differential equations [12,13]. In 1969, Caputo [14] first presented the idea of the distributed-order equation, which was solved in 1995 [15]. Li et al. [16] studied fractional differential equations involving the distributed-order operator to investigate ultra-slow diffusion. Some physical processes exhibit non-local behaviours that are variable with time or space. It was found that the distributed-order fractional diffusion equation is an efficient tool to describe complex diffusion processes, especially when the diffusion exponent varies over multi-scales [17]. Lorenzo and Hartley [18] concluded that both integer-order and fractional-order systems are special cases of distributed-order systems. Space distributed-order fractional equations are more flexible in their ability to capture diffusion phenomena with multi-scale memory characteristics [19]. However, studies on space distributed-order diffusion equations are still limited, especially for the Riemann–Liouville fractional derivative. Furthermore, high-dimensional partial differential equations (PDEs) will be more suitable for the simulation of diffusion phenomena in the real world. Motivated by this, we consider the Riemann–Liouville distributed-order space fractional diffusion equation (RLDO-SFDE) in two dimensions.

Since it is difficult to derive the analytical solutions of fractional dynamic systems, many numerical methods for solving distributed-order fractional PDEs have been proposed [20,21,22,23]. By using numerical integration techniques, one-dimensional time distributed-order fractional models have been transformed into multi-term fractional systems which were finally solved by spectral methods [20,21]. A meshless method was proposed for solving the time distributed-order anomalous sub-diffusion equation [22]. However, efficient and robust numerical schemes are still under development, especially for high-dimensional cases. The computational cost of solving two-dimensional distributed-order fractional equations is very large, and highly accurate techniques are demanded [24]. Further research needs to be focused on exploring effective numerical methods.

The discretised fractional diffusion equation generates a dense coefficient matrix; it requires high computational costs and memory storage, especially for high-dimensional problems. To tackle this issue, we employ the alternating direction implicit method (ADIM) [25] to solve a complex two-dimension fractional system. Peaceman and Rachford [26] proposed the ADIM to solve classical parabolic and elliptic PDEs efficiently. This efficient method has gained considerable popularity for solving large matrix equations numerically, such as diffusion equations in two or higher dimensions [26]. Meerschaert et al. [25] developed a variation on the classical ADIM to solve two-dimensional fractional PDEs with variable coefficients. The theory of this fractional ADIM is based on splitting the finite difference equations into two iteration systems, first solving the x-direction iteration to calculate the intermediate solution and then dealing with the y-direction iteration system. Compared with the Gaussian elimination, the ADIM has the advantage of reducing the two-dimensional problem into two one-dimensional problems, which improves the efficiency and reduces the computational cost remarkably [27,28]. Therefore, we develop the ADIM to solve the two-dimensional RLDO-SFDE. Furthermore, to improve the convergence order of the numerical method, an extrapolated technique [29] is employed to solve the fractional system efficiently. This Richardson extrapolated technique is a more general approach that can also be combined with other numerical methods to improve the convergence order further. For example, the modified Crank–Nicolson scheme with Richardson extrapolation has been investigated for solving many PDEs [30,31]. This extrapolated technique may offer more possibilities for the research on developing numerical methods with higher-order accuracy.

The coefficient matrices in iterated systems of the ADIM are very dense for high-dimensional problems with fine meshes, which leads to high computational costs and memory storage. In view of the Toeplitz-like structure of these coefficient matrices, we develop a fast algorithm by constructing circulant matrices and employing fast Fourier transform. The idea of this fast method has been investigated extensively [32,33,34]. The fast ADIM does not require the assembly of coefficient matrices, which saves memory storage remarkably. The implemented fast Fourier transform accelerates the calculation with lower computational costs.

In this paper, we investigate the two-dimensional RLDO-SFDE. Firstly, some preliminary knowledge related to this research is introduced in Section 2. Section 3 discretises the RLDO-SFDE as a multi-term fractional equation by employing the midpoint quadrature rule. Distributed-order fractional PDEs can be regarded as the limiting case of multi-term fractional PDEs [35]. Diethelm and Ford [36] have observed that small changes in the order of a fractional PDE lead to only slight changes in the final solution, which gives initial support to the employed numerical integration method. Then, we use an implicit Euler method, which includes a left-shifted Grünwald–Letnikov approximation [29] to discretise the Riemann–Liouville fractional derivative. Moreover, the discretised equation is solved by the ADIM. In Section 4, we provide the stability and convergence of the numerical scheme. More importantly, an extrapolated technique and a fast algorithm are constructed to improve the ADIM in Section 5. Section 6 verifies the effectiveness of the developed numerical schemes by comparing the error between the exact solutions and numerical results. Finally, some conclusions are drawn in Section 7.

2. Preliminaries

When we discretise a space fractional diffusion equation by applying the standard Grünwald–Letnikov fractional derivative, the finite difference approximation is unstable whether the difference method is the explicit Euler method, implicit Euler method, or the Crank–Nicholson method. Thus, we take the use of a left-shifted Grünwald–Letnikov approximation, which is unconditionally stable, to discretise the Riemann–Liouville fractional derivative.

Theorem 1

([1]). Suppose $\alpha \in (1,2),f\left(x\right)\in C^2[a,b]$; then, the definite left-shifted Grünwald –Letnikov fractional derivative is defined as:

$${}_a^G{D}_{x,1}^{\alpha }f\left(x\right)=\frac{1}{h^{\alpha }}\sum _{j=0}^{(x-a)/h+1}{g}_j^{\left(\alpha \right)}f(x-(j-1)h)$$

(1)

Equation (1) is the approximation of the left Riemann–Liouville fractional derivative if and only if $f\left(a\right)=0$, i.e.,

$${}_a^G{D}_{x,1}^{\alpha }f\left(x\right)={}_a^R{D}_x^{\alpha }f\left(x\right)+O\left(h\right).$$

where the left Riemann–Liouville fractional derivative is defined as [1]

$${}_a^R{D}_x^{\alpha }f\left(x\right)=\frac{1}{\Gamma (2-\alpha )}\frac{d^2}{d{x}^2}{\int }_a^x\frac{f\left(\xi \right)}{{(x-\xi )}^{\alpha -1}}d\xi ,$$

where $\Gamma (·)$ refers to the gamma function.

When $f\left(a\right)\ne 0$, then

$${}_a^G{D}_{x,1}^{\alpha }f\left(x\right)={}_a^R{D}_x^{\alpha }f\left(x\right)+O\left(h\right)+O\left(f\left(a\right)\right).$$

Lemma 1

([37]). When $1<\alpha <2$, the coefficients $g_k^{\left(\alpha \right)}={(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{k}}\right)(k=0,\pm 1,\pm 2,\cdots )$ satisfy

1. 

$g_0^{\left(\alpha \right)}=1,g_1^{\left(\alpha \right)}=-\alpha ,g_k^{\left(\alpha \right)}>0(k=0,2,3,\cdots )$;

2. 

${\displaystyle \sum _{k=0}^{\infty }}{g}_k^{\left(\alpha \right)}=0$;

3. 

${\displaystyle \sum _{k=0}^N}{g}_k^{\left(\alpha \right)}<0$ for any positive integer N.

Lemma 2

([29]). Let $X={[x_1,x_2,\cdots ,x_m]}^T$, ${\parallel X\parallel }_{\infty }={max}_{1\le i\le m}\left|x_i\right|$. If the matrix $D={\left(d_{i,l}\right)}_{m\times m}\in {\mathbb{R}}^{m\times m}$ satisfies the following conditions,

$$\sum _{l=1,l\ne i}^m|d_{i,l}|\le |d_{i,i}|-1,(i=1,2,\cdots ,m),$$

then

$${\parallel X\parallel }_{\infty }\le {\parallel DX\parallel }_{\infty }.$$

3. Numerical Methods

Meerschaert et al. [25] investigated the following two-dimensional fractional diffusion equation with variable coefficients:

$$\frac{\partial u(x,y,t)}{\partial t}=K_1(x,y)\frac{{\partial }^{\alpha }u(x,y,t)}{\partial x^{\alpha }}+K_2(x,y)\frac{{\partial }^{\beta }u(x,y,t)}{\partial y^{\beta }}+f(x,y,t),$$

(2)

where $K_1(x,y)$ and $K_2(x,y)$ refer to variable diffusion coefficients. ${\partial }^{\alpha }u(x,y,t)/\partial x^{\alpha }$ and ${\partial }^{\beta }u(x,y,t)/\partial y^{\beta }$ are Riemann–Liouville fractional derivative operators.

It is difficult to simulate the diffusion processes in heterogeneous media with varying characteristics only by the fixed fractional parameters [38]. Based on the above fractional diffusion model (2), this study generalises space fractional derivatives by using distributed-order operators, which can describe diffusion behaviours exhibited varying non-local properties. Regarding diffusion coefficients as constants, we consider the following two-dimensional RLDO-SFDE:

$$\frac{\partial u(x,y,t)}{\partial t}=K_x{\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }u(x,y,t)}{\partial x^{\alpha }}d\alpha +K_y{\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }u(x,y,t)}{\partial y^{\beta }}d\beta +f(x,y,t),$$

(3)

$$x\in (a,b),y\in (c,d),\mathsf{\Omega }=(a,b)\times (c,d),t\in (0,T],$$

where $K_x$ and $K_y$ refer to diffusion coefficients. $P\left(\alpha \right)$ and $Q\left(\beta \right)$ are weight functions satisfying the following conditions:

$$P\left(\alpha \right)\ge 0,P\left(\alpha \right)\not\equiv 0,{\int }_1^{2}P\left(\alpha \right)d\alpha <\infty ,\alpha \in [1,2],$$

(4)

$$Q\left(\beta \right)\ge 0,Q\left(\beta \right)\not\equiv 0,{\int }_1^{2}Q\left(\beta \right)d\beta <\infty ,\beta \in [1,2].$$

(5)

The boundary and initial conditions of the two-dimensional fractional diffusion Equation (3) are

$$u(x,y,t)=0,(x,y,t)\in (R^2\backslash \mathsf{\Omega })\times (0,T],$$

(6)

$$u(x,y,0)=u_0(x,y),(x,y)\in \mathsf{\Omega }\cup \partial \mathsf{\Omega },$$

(7)

where $\partial \mathsf{\Omega }$ is the boundary of the domain $\mathsf{\Omega }$.

3.1. The Discretisation of Integral Intervals

Firstly, the integral intervals [1, 2] of $\alpha$ and [1, 2] of $\beta$ are discretised as $1={\xi }_0<{\xi }_1<\cdots <{\xi }_S=2$, $1={\eta }_0<{\eta }_1<\cdots <{\eta }_{\overline{S}}=2$. We denote $\Delta {\xi }_j={\xi }_j-{\xi }_{j-1}=1/S=\sigma$, ${\alpha }_j=({\xi }_j+{\xi }_{j-1})/2=1+(2j-1)/2S$, $j=1,2,\cdots ,S$, $S\in N$, and $\Delta {\eta }_j={\eta }_j-{\eta }_{j-1}=1/\overline{S}=\rho$, ${\beta }_j=({\eta }_j+{\eta }_{j-1})=1+(2j-1)/2\overline{S}$, $j=1,2,\cdots ,\overline{S}$, $\overline{S}\in N$. Then, adopting the midpoint quadrature formula [39], we can obtain

$$\begin{array}{ccc}& & {\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }u(x,y,t)}{\partial x^{\alpha }}d\alpha +{\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }u(x,y,t)}{\partial y^{\beta }}d\beta \hfill \\ & & =\sum _{j=1}^{S}P\left({\alpha }_j\right)\frac{{\partial }_j^{\alpha }u(x,y,t)}{\partial x_j^{\alpha }}\Delta {\xi }_j+\sum _{j=1}^{\overline{S}}Q\left({\beta }_j\right)\frac{{\partial }_j^{\beta }u(x,y,t)}{\partial y_j^{\beta }}\Delta {\eta }_j+O({\sigma }^2+{\rho }^2).\hfill \end{array}$$

(8)

Then, the two-dimensional Riemann–Liouville space distributed-order diffusion Equation (3) is discretised as follows:

$$\begin{array}{cc}\hfill \frac{\partial u(x,y,t)}{\partial t}& =K_x\sum _{j=1}^{S}P\left({\alpha }_j\right)\frac{{\partial }_j^{\alpha }u(x,y,t)}{\partial x_j^{\alpha }}\Delta {\xi }_j+K_y\sum _{j=1}^{\overline{S}}Q\left({\beta }_j\right)\frac{{\partial }_j^{\beta }u(x,y,t)}{\partial y_j^{\beta }}\Delta {\eta }_j\hfill \\ & +f(x,y,t)+O({\sigma }^2+{\rho }^2).\hfill \end{array}$$

(9)

3.2. The ADIM

The interval $\mathsf{\Omega }\times (0,T]$ is divided by $x_i=a+i{h}_x(i=0,1,2,\cdots ,M_1)$, $y_l=c+l{h}_y(l=0,1,2,\cdots ,M_2)$, and $t_n=n\tau (n=0,1,2,\cdots ,N)$, where $h_x=\frac{b-a}{M_1}$, $h_y=\frac{d-c}{M_2}$ are space steps, and $\tau =T/N$ is the time step. According to the backward difference, the integer-order term can be written as:

$$\frac{\partial u(x_i,y_l,t_{n-1/2})}{\partial t}=\frac{u(x_i,y_l,t_n)-u(x_i,y_l,t_{n-1})}{\tau }+O\left(\tau \right).$$

(10)

Using the implicit Euler method [29], which contains a left-shifted Grünwald–Letnikov approximation, the Riemann–Liouville space fractional derivative operators can be discretised as the following forms:

$$\frac{{\partial }^{{\alpha }_j}u(x_i,y_l,t_n)}{\partial x^{{\alpha }_j}}=\frac{1}{h_x^{{\alpha }_j}}\sum _{k=0}^{i+1}{g}_k^{{\alpha }_j}u(x_{i-k+1},y_l,t_n)+O\left(h_x\right),$$

(11)

$$\frac{{\partial }^{{\beta }_j}u(x_i,y_l,t_n)}{\partial y^{{\beta }_j}}=\frac{1}{h_y^{{\beta }_j}}\sum _{k=0}^{l+1}{g}_k^{{\beta }_j}u(x_i,y_{l-k+1},t_n)+O\left(h_y\right),$$

(12)

where $g_k^{{\alpha }_j}={(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_j}{k}}\right)$.

Thus, the implicit difference method of Equation (3) can be approximated by the following equation:

$$\begin{array}{cc}\hfill & \frac{u(x_i,y_l,t_n)-u(x_i,y_l,t_{n-1})}{\tau }\hfill \\ \hfill =& K_x\sum _{j=0}^S\frac{P\left({\alpha }_j\right)}{S}\frac{1}{h_x^{{\alpha }_j}}\sum _{k=0}^{i+1}{g}_k^{{\alpha }_j}u(x_{i-k+1},y_l,t_n)+K_y\sum _{j=1}^{\overline{S}}\frac{Q\left({\beta }_j\right)}{\overline{S}}\frac{1}{h_y^{{\beta }_j}}\sum _{k=0}^{l+1}{g}_k^{{\beta }_j}u(x_i,y_{l-k+1},t_n)\hfill \\ \hfill & +f(x_i,y_l,t_n)+O({\sigma }^2+{\rho }^2+\tau +h_x+h_y),\hfill \end{array}$$

(13)

which can be written as:

$$\begin{array}{cc}\hfill & \frac{u(x_i,y_l,t_n)-u(x_i,y_l,t_{n-1})}{\tau }\hfill \\ \hfill =& K_x\sum _{j=0}^S\frac{P\left({\alpha }_j\right)}{S}\frac{1}{h_x^{{\alpha }_j}}\sum _{k=0}^{i+1}{g}_{i-k+1}^{{\alpha }_j}u(x_k,y_l,t_n)+K_y\sum _{j=1}^{\overline{S}}\frac{Q\left({\beta }_j\right)}{\overline{S}}\frac{1}{h_y^{{\beta }_j}}\sum _{k=0}^{l+1}{g}_{l-k+1}^{{\beta }_j}u(x_i,y_k,t_n)\hfill \\ \hfill & +f(x_i,y_l,t_n)+R_{i,l}^n,\hfill \\ \hfill & (i=0,1,2,\cdots ,M_1,l=0,1,2,\cdots ,M_2,n=0,1,2,\cdots ,N),\hfill \end{array}$$

(14)

where the truncation error is denoted as $R_{i,l}^n=O({\sigma }^2+{\rho }^2+\tau +h_x+h_y)$.

After the truncation error is neglected, the implicit numerical method for Equation (3) is obtained as:

$$\frac{u_{i,l}^n-u_{i,l}^{n-1}}{\tau }=K_x\sum _{j=0}^S\frac{P\left({\alpha }_j\right)}{S}\frac{1}{h_x^{{\alpha }_j}}\sum _{k=0}^{i+1}{g}_{i-k+1}^{{\alpha }_j}{u}_{k,l}^n+K_y\sum _{j=1}^{\overline{S}}\frac{Q\left({\beta }_j\right)}{\overline{S}}\frac{1}{h_y^{{\beta }_j}}\sum _{k=0}^{l+1}{g}_{l-k+1}^{{\beta }_j}{u}_{i,k}^n+f_{i,l}^n,$$

(15)

$$u_{0,l}^n=u_{M_1,l}^n=0,u_{i,0}^n=u_{i,M_2}^n=0,(0\le n\le N),$$

(16)

$$u_{i,l}^0=u_0(x_i,y_l),(0\le i\le M_1,0\le l\le M_2).$$

(17)

In order to solve the above Equations (15)–(17), two fractional partial difference operators are defined as follows:

$$\begin{array}{c}\hfill {\delta }_x{u}_{i,l}^n=K_x\sum _{j=0}^S\frac{P\left({\alpha }_j\right)}{S}\frac{1}{h_x^{{\alpha }_j}}\sum _{k=0}^{i+1}{g}_{i-k+1}^{{\alpha }_j}{u}_{k,l}^n,\end{array}$$

(18)

$$\begin{array}{c}\hfill {\delta }_y{u}_{i,l}^n=K_y\sum _{j=1}^{\overline{S}}\frac{Q\left({\beta }_j\right)}{\overline{S}}\frac{1}{h_y^{{\beta }_j}}\sum _{k=0}^{l+1}{g}_{l-k+1}^{{\beta }_j}{u}_{i,k}^n.\end{array}$$

(19)

Thus, the difference method can be rewritten as the following form:

$$(1-\tau {\delta }_x-\tau {\delta }_y)u_{i,l}^n=u_{i,l}^{n-1}+\tau f_{i,l}^n.$$

(20)

After introducing the truncation error ${\tau }^2{\delta }_x{\delta }_y{u}_{i,l}^n$, which is far smaller than the original error, Equation (20) is written as:

$$(1-\tau {\delta }_x)(1-\tau {\delta }_y)u_{i,l}^n=u_{i,l}^{n-1}+\tau f_{i,l}^n,0\le i\le M_1,0\le l\le M_2.$$

(21)

The above Equation (21) is the ADIM of the two-dimensional Riemann–Liouville space distributed-order diffusion equation, and the perturbation error is $O({\sigma }^2+{\rho }^2+\tau +h_x+h_y)$.

Then, we can employ the following iteration techniques to find the numerical solution of the ADIM (21):

$$\begin{array}{c}\hfill (1-\tau {\delta }_x)u_{i,l}^{\ast }=u_{i,l}^{n-1}+\tau f_{i,l}^n,\end{array}$$

(22)

$$\begin{array}{c}\hfill (1-\tau {\delta }_y)u_{i,l}^n=u_{i,l}^{\ast },\\ \hfill 1\le i\le M_1,1\le l\le M_2.\end{array}$$

(23)

• Solve Equation (22) in the x-direction for each fixed value of l, so the intermediate solution $u_{i,l}^{\ast }$ can be obtained;
• Solve Equation (23) in the y-direction for each fixed i, so we can obtain the final solution $u_{i,l}^n$.

4. The Stability and Convergence of the ADIM

The ADIM Equation (21) can be rewritten as

$$GH{U}^n=U^{n-1}+\tau F^n,$$

(24)

where $U^n={(u_{1,1}^n,\cdots ,u_{M_1-1,1}^n,u_{1,2}^n,\cdots ,u_{M_1-1,2}^n,\cdots ,u_{1,M_2-1}^n,\cdots ,u_{M_1-1,M_2-1}^n)}^T$, $F^n={(f_{1,1}^n,\cdots ,f_{M_1-1,1}^n,f_{1,2}^n,\cdots ,f_{M_1-1,2}^n,\cdots ,f_{1,M_2-1}^n,\cdots ,f_{M_1-1,M_2-1}^n)}^T$.

Additionally, the matrices G and H represent the difference operators $(1-\tau {\delta }_x)$ and $(1-\tau {\delta }_y)$, respectively. The matrix $G=diag(A_1,A_2,\cdots ,A_{M_2-1})$ is a block diagonal matrix where the $(M_1-1)\times (M_1-1)$ block $A_l$ is obtained by Equation (22). Similarly, the $(M_2-1)\times (M_2-1)$ blocks $B_i$ resulting from Equation (23) lead to the diagonal matrix $H=diag(B_1,B_2,\cdots ,B_{M_1-1})$.

Here, the matrices $A_l={\left(a_{i,k}\right)}_{(M_1-1)\times (M_1-1)}^{\left(l\right)}$, $1\le l\le M_2-1$, note $r_1=\frac{\tau K_x}{S}>0$,

$$a_{i,k}=\left\{\begin{array}{cc}0\hfill & \mathrm{for}k>i+1,\hfill \\ {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_0^{\left({\alpha }_j\right)}}\hfill & \mathrm{for}k=i+1,\hfill \\ {\displaystyle 1-r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_1^{\left({\alpha }_j\right)}}\hfill & \mathrm{for}k=i,\hfill \\ {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_{i-k+1}^{\left({\alpha }_j\right)}}\hfill & \mathrm{for}k<i.\hfill \end{array}\right.$$

(25)

The matrices $B_i={\left(b_{k,l}\right)}_{(M_2-1)\times (M_2-1)}^{\left(i\right)}$, $1\le i\le M_2-1$, note $r_2=\frac{\tau K_y}{\overline{S}}>0$,

$$b_{k,l}=\left\{\begin{array}{cc}0\hfill & \mathrm{for}l>k+1,\hfill \\ {\displaystyle -r_2\sum _{j=1}^{\overline{S}}\frac{Q\left({\beta }_j\right)}{h_y^{{\beta }_j}}{g}_0^{\left({\beta }_j\right)}}\hfill & \mathrm{for}l=k+1,\hfill \\ {\displaystyle 1-r_2\sum _{j=1}^{\overline{S}}\frac{Q\left({\beta }_j\right)}{h_y^{{\beta }_j}}{g}_1^{\left({\beta }_j\right)}}\hfill & \mathrm{for}l=k,\hfill \\ {\displaystyle -r_2\sum _{j=1}^{\overline{S}}\frac{Q\left({\beta }_j\right)}{h_y^{{\beta }_j}}{g}_{k-l+1}^{\left({\beta }_j\right)}}\hfill & \mathrm{for}l<k.\hfill \end{array}\right.$$

(26)

Equation (22) can be rewritten as

$$A_l{U}_l^{\ast }=U_l^{n-1}+\tau F_l^n+\left(\begin{array}{c}0\\ ⋮\\ 0\\ {\displaystyle r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_0^{\left({\alpha }_j\right)}{u}_{M_1,l}^{\ast }}\end{array}\right),1\le l\le M_2-1,$$

(27)

where $U_l^{\ast }={(u_{1,l}^{\ast },u_{2,l}^{\ast },\cdots ,u_{M_1-1,l}^{\ast })}^T$, $F_l^n={(f_{1,l}^n,f_{2,l}^n,\cdots ,u_{M_1-1,l}^n)}^T$.

Similarly, Equation (23) can also be written as

$$B_i{U}_i^n=U_i^{\ast }+\left(\begin{array}{c}0\\ ⋮\\ 0\\ {\displaystyle r_2\sum _{j=1}^{\overline{S}}\frac{Q\left({\beta }_j\right)}{h_y^{{\beta }_j}}{g}_0^{\left({\beta }_j\right)}{u}_{i,M_2}^n}\end{array}\right),1\le i\le M_1-1,$$

(28)

where $U_i^n={(u_{i,1}^n,u_{i,2}^n,\cdots ,u_{i,M_2-1}^n)}^T$, $U_i^{\ast }={(u_{i,1}^{\ast },u_{i,2}^{\ast },\cdots ,u_{i,M_2-1}^{\ast })}^T$.

The framework of the numerical method is listed in the following Algorithm 1.

Algorithm 1: Framework of the ADIM for the RLDO-SFDE.

Input: Mesh generation

The total number of time steps N, the total number of spatial nodes $M_1$ (x-direction) and $M_2$ (y-direction);

The partitions of integral intervals ${\alpha }_j=1+(2j-1)/2S,(j=1,2,\dots ,S)$ and ${\beta }_j=1+(2j-1)/2\overline{S},(j=1,2,\dots ,\overline{S})$;

Output: Numerical solutions $U^n$ Generation of weight functions $P\left({\alpha }_j\right),Q\left({\beta }_j\right),g_k^{{\alpha }_j}$ and $g_k^{{\beta }_j}$; Assemble matrices $A_l$ (by Equation (25)), $B_i$ (by Equation (26)), and the vector $F_l^n$;

for $n=1:N$do

for $l=1:M_2-1$ do

Compute $U_l^{\ast }$ by the system (27).

end for

for $i=1:M_1-1$ do

Compute $U_i^n$ by the system (28).

end for

Obtain numerical solutions $U^n$.

end for

4.1. Stability

Theorem 2.

The ADIM (Equation (21)) is unconditionally stable.

Proof. 

In order to prove the stability of the numerical method, we assume that $u_{i,l}^n$ and ${\overline{u}}_{i,l}^n$ are the numerical solutions and the approximation solutions, respectively. Their corresponding error is ${\epsilon }_{i,l}^n={\overline{u}}_{i,l}^n-u_{i,l}^n$, noting that

$$\begin{array}{c}\hfill Y^n={({\epsilon }_{1,1}^n,{\epsilon }_{2,1}^n,\cdots ,{\epsilon }_{M_1-1,1}^n,\cdots ,{\epsilon }_{1,M_2-1}^n,{\epsilon }_{2,M_2-1}^n,\cdots ,{\epsilon }_{M_1-1,M_2-1}^n)}^T.\end{array}$$

According to Lemma 1, we can obtain that $a_{i,l}<0$ ($i\ne l$), $a_{i,i}>0$. Thus,

$$\begin{array}{cc}\hfill \sum _{l=1,l\ne i}^{M_1-1}\left|a_{i,l}\right|& {\displaystyle =r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_0^{\left({\alpha }_j\right)}+r_1\sum _{l=1}^{i-1}\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_{i-k+1}^{\left({\alpha }_j\right)}}\hfill \\ \hfill & {\displaystyle =r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_0^{\left({\alpha }_j\right)}+r_1\sum _{k=2}^i\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_k^{\left({\alpha }_j\right)}}\hfill \\ \hfill & {\displaystyle =-r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_1^{\left({\alpha }_j\right)}-r_1\sum _{k=i+1}^{\infty }\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_k^{\left({\alpha }_j\right)}}\hfill \\ \hfill & {\displaystyle =|a_{i,i}|-1-r_1\sum _{k=i+1}^{\infty }\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_k^{\left({\alpha }_j\right)}.}\hfill \end{array}$$

It is obtained from Lemma 1 that $g_k^{\left({\alpha }_j\right)}>0(k=0,2,3,\cdots )$, which leads to the expression ${\displaystyle r_1\sum _{k=i+1}^{\infty }\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_k^{\left({\alpha }_j\right)}>0}$, so there yields

$$\begin{array}{c}\hfill {\displaystyle \sum _{l=1,l\ne i}^{M_1-1}|a_{i,l}|=|a_{i,i}|-1-r_1\sum _{k=i+1}^{\infty }\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_k^{\left({\alpha }_j\right)}<\left|a_{i,i}\right|-1.}\end{array}$$

Therefore, the matrices $A_l$($1\le l\le M_2-1$) satisfy Lemma 2. Similarly, the matrices $B_i$($1\le i\le M_1-1$) also satisfy Lemma 2.

According to the relationships between $A_l$ and G, as well as $B_i$ and H, it is clear that matrices G and H meet the conditions of Lemma 2 as well. Thus,

$$\begin{array}{c}\hfill \parallel Y^n{\parallel }_{\infty }\le \parallel H{Y}^n{\parallel }_{\infty }\le \parallel GH{Y}^n{\parallel }_{\infty }=\parallel Y^{n-1}{\parallel }_{\infty }\le {\parallel Y^0\parallel }_{\infty }.\end{array}$$

Therefore, the ADIM is unconditionally stable. □

4.2. Convergence

Theorem 3.

The ADIM (Equation (21)) is convergent, and the convergence order is $O({\sigma }^2+{\rho }^2+\tau +h_x+h_y)$.

Proof. 

Let $u(x_i,y_l,t_n)$ be the exact solutions of Equations (3), (6), and (7), let $u_{i,l}^n$ be the numerical solutions of the ADIM, and note that

$$\begin{array}{ccc}& & e_{i,l}^n=u(x_i,y_l,t_n)-u_{i,l}^n,\hfill \\ & & E^n={(e_{1,1}^n,e_{2,1}^n,\cdots ,e_{M_1-1,1}^n,\cdots ,e_{1,M_2-1}^n,e_{2,M_2-1}^n,\cdots ,e_{M_1-1,M_2-1}^n)}^T;\hfill \end{array}$$

then, the error $E^n$ satisfies the following perturbed equations:

$$\begin{array}{ccc}& & GH{E}^n=E^{n-1}+\tau R^n,\hfill \end{array}$$

(29)

$$\begin{array}{ccc}& & e_{0,l}^n=e_{M_1,l}^n=0,e_{i,0}^n=e_{i,M_2}^n=0,0\le n\le N,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}& & e_{i,l}^0=0,0\le i\le M_1,0\le l\le M_2,\hfill \end{array}$$

(31)

where $R_{i,l}^n=O({\sigma }^2+{\rho }^2+\tau +h_x+h_y)$.

Using Lemma 2, we can obtain

$$\begin{array}{cc}\hfill \parallel E^n\parallel \infty & \le \parallel H{E}^n\parallel \infty \le \parallel GH{E}^n\parallel \infty =\parallel E^{n-1}+\tau R^n\parallel \infty \hfill \\ \hfill & \le \parallel E^{n-1}\parallel \infty +\tau \parallel R^n\parallel \infty \hfill \\ \hfill & \le \parallel E^{n-2}\parallel \infty +2\tau \parallel R^n\parallel \infty \hfill \\ \hfill & \le \parallel E^0\parallel \infty +n\tau \parallel R^n\parallel \infty \hfill \\ \hfill & \le C({\sigma }^2+{\rho }^2+\tau +h_x+h_y),\hfill \end{array}$$

where C is a positive constant.

Therefore, the ADIM is convergent, and the convergence order is $O({\sigma }^2+{\rho }^2+\tau +h_x+h_y)$. □

5. Improved Algorithms

This section develops two improved numerical algorithms. An extrapolated technique is employed to increase the convergence order of the ADIM. Then, we provide a fast algorithm to solve the fractional diffusion model more efficiently with lower memory usage and computational costs.

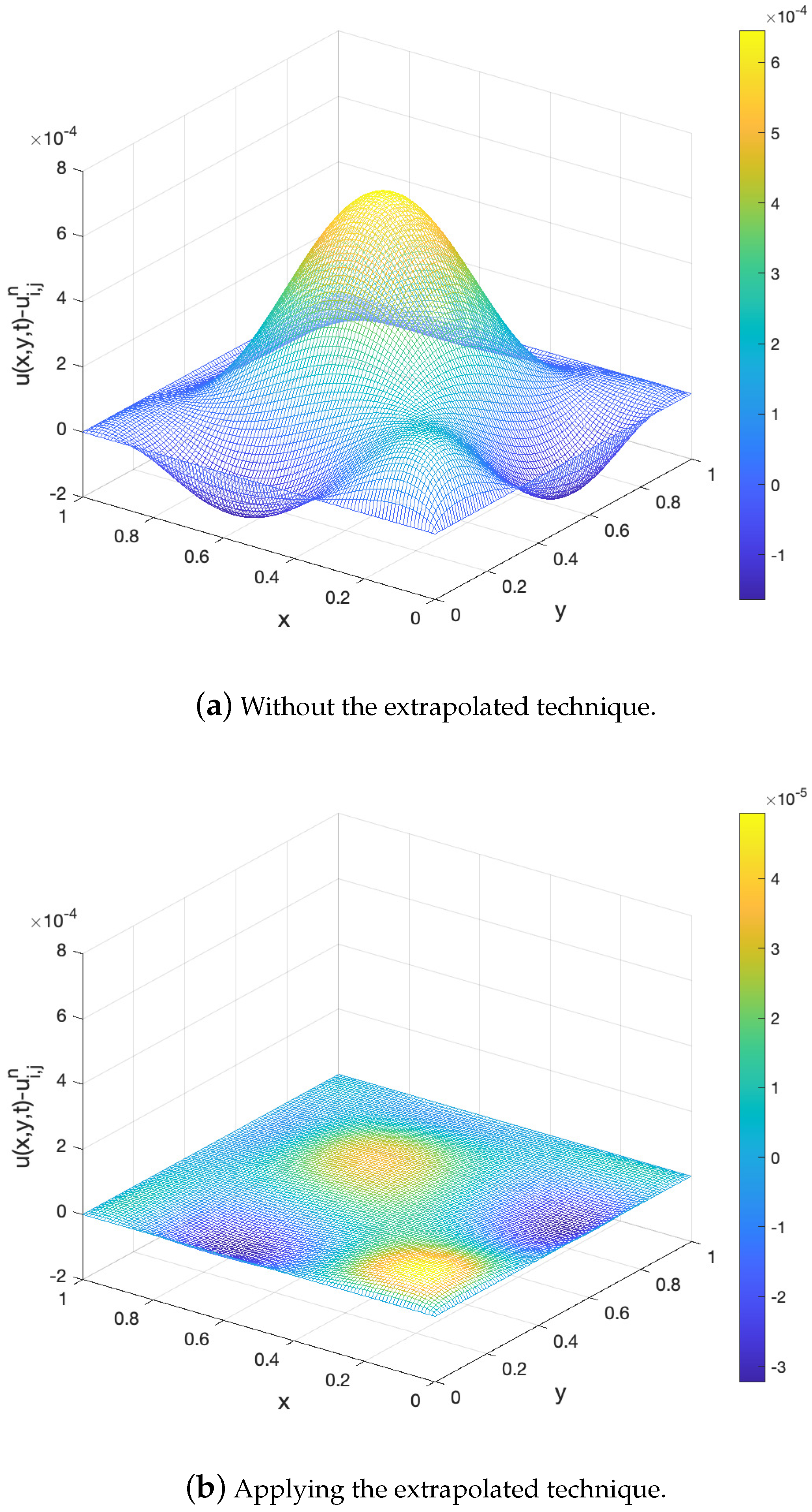
5.1. An Extrapolated Technique

In order to improve the convergence of the numerical method discussed above, we adopt an extrapolated technique [29] at a time step ($\tau$) and space steps ($h_{x}and{h}_y$). An extrapolated technique of the Euler method for a one-dimensional fractional diffusion equation has been analysed [35]. The procedures of the extended extrapolation for this research are summarized as follows:

• Employ the ADIM that contains a left-shifted Grünwald–Letnikov approximation to obtain the numerical solutions $u_{i,l}^n(h_x,h_y,\tau )$ on the coarse grid $\Delta t=\tau ,\Delta x=h_x,\Delta y=h_y$.
• Solve Equation (3) by the implicit Euler method on the fine grid $\Delta t=\tau /2,\Delta x=h_x/2,\Delta y=h_y/2$; then, the numerical solutions $u_{2i,2l}^{2n}(h_x/2,h_y/2,\tau /2)$ can be obtained.
• The new extrapolated solutions can be written as:

  $$\begin{array}{cc}\hfill & {\tilde{u}}_{i,l}^n\approx 2u_{2i,2l}^{2n}(h_x/2,h_y/2,\tau /2)-u_{i,l}^n(h_x,h_y,\tau ),\hfill \\ \hfill & i=1,2,\cdots ,M_1-1,l=1,2,\cdots ,M_2-1.\hfill \end{array}$$

Therefore, we can obtain the second-order-accuracy numerical solutions by applying the proposed extrapolated technique, and the convergence order of the new extrapolated solution ${\tilde{u}}_{i,l}^n$ is $O({\tau }^2+h_x^2+h_y^2)$.

5.2. A Fast Algorithm for the ADIM

The numerical solutions of the RLDO-SFDE can be obtained by solving two matrix systems ((27)–(28)). The Gaussian elimination for solving the system $Ax=b$ with $A\in {\mathbb{R}}^{M\times M}$ requires $O\left(M^2\right)$ memory and $O\left(M^3\right)$ operations per time step when A is a full matrix. The coefficient matrices $A_l\in {\mathbb{R}}^{(M_1-1)\times (M_1-1)}$ and $B_i\in {\mathbb{R}}^{(M_2-1)\times (M_2-1)}$ in systems ((27) and (28)) are lower Hessenberg–Toeplitz-like matrices. The computational work for solving the matrix system $A_{l}x=b$ is approximately $M_1\times (M_1-1)$ arithmetic operations [25]. Although it requires less computational work compared with the Gaussian elimination for a full coefficient matrix system, further efficient algorithms need to be explored to reduce the computational complexity for fine meshes. Since the coefficient matrices $A_l$ and $B_i$ are Toeplitz-like matrices, we develop a fast algorithm based on the circulant matrix and the fast Fourier transform to accelerate the computation. This fast algorithm is implemented with the Bi-CGSTAB iterative method, which is suitable for solving non-symmetric linear systems [40]. The main tasks of the fast Bi-CGSTAB ADIM are matrix-vector multiplications $A_{l}v$ and $B_i\overline{v}$ with $v\in {\mathbb{R}}^{M_1-1}$ and $\overline{v}\in {\mathbb{R}}^{M_2-1}$. Taking the matrix-vector multiplication $A_{l}v$ as an example, we can obtain the following lemma.

Lemma 3.

The matrix-vector multiplication $A_{l}v$ can be performed in $O((M_1-1)log(M_1-1))$ operations for any $v\in {\mathbb{R}}^{M_1-1}$.

Proof. 

The coefficient matrix $A_l$ of the ADIM is a lower Hessenberg–Toeplitz-like matrix formulated in the following form:

$$A_l:=\left[\begin{array}{ccccc}{\displaystyle 1-r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_1^{\left({\alpha }_j\right)}}& {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_0^{\left({\alpha }_j\right)}}& 0& \cdots & 0\\ {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_2^{\left({\alpha }_j\right)}}& {\displaystyle 1-r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_1^{\left({\alpha }_j\right)}}& {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_0^{\left({\alpha }_j\right)}}& \ddots & 0\\ ⋮& \ddots & \ddots & \ddots & 0\\ {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_{M_1-2}^{\left({\alpha }_j\right)}}& \ddots & \ddots & \ddots & {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_0^{\left({\alpha }_j\right)}}\\ {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_{M_1-1}^{\left({\alpha }_j\right)}}& {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_{M_1-2}^{\left({\alpha }_j\right)}}& \cdots & \cdots & {\displaystyle 1-r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_1^{\left({\alpha }_j\right)}}\end{array}\right].$$

(32)

The Toeplitz matrix can be embedded into the following $2(M_1-1)\times 2(M_1-1)$ circulant matrix $C^{\alpha ,2(M_1-1)}$:

$$C^{\alpha ,2(M_1-1)}:=\left[\begin{array}{cc}{A}_l& S^{\alpha ,M_1-1}\\ S^{\alpha ,M_1-1}& A_l\end{array}\right],$$

(33)

where

$$S^{\alpha ,M_1-1}=\left[\begin{array}{ccccc}0& {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_{M_1-1}^{\left({\alpha }_j\right)}}& \cdots & {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_3^{\left({\alpha }_j\right)}}& {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_2^{\left({\alpha }_j\right)}}\\ 0& 0& \ddots & \ddots & {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_3^{\left({\alpha }_j\right)}}\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & \ddots & 0& {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_{M_1-1}^{\left({\alpha }_j\right)}}\\ {\displaystyle -r_1\sum _{j=1}^S\frac{P\left({\alpha }_j\right)}{h_x^{{\alpha }_j}}{g}_0^{\left({\alpha }_j\right)}}& 0& \cdots & 0& 0\end{array}\right].$$

For any $\widehat{v}:={[v^T,0^T]}^T\in {\mathbb{R}}^{2(M_1-1)}$, we have

$$C^{\alpha ,2(M_1-1)}\widehat{v}=\left[\begin{array}{c}{A}_{l}v\\ S^{\alpha ,M_1-1}v\end{array}\right].$$

(34)

Then, we can obtain the matrix-vector multiplication $A_{l}v$ from the first half of $C^{\alpha ,2(M_1-1)}\widehat{v}$. The circulant matrix $C^{\alpha ,2(M_1-1)}$ can be diagonalised as follows by using a discrete Fourier transform [41,42]:

$$C^{\alpha ,2(M_1-1)}=F_{2(M_1-1)}^{-1}\mathrm{diag}\left(\mathsf{\Lambda }\right)F_{2(M_1-1)},$$

(35)

where $\mathsf{\Lambda }=F_{2(M_1-1)}{c}^{\alpha ,2(M_1-1)}$, with $c^{\alpha ,2(M_1-1)}$ being the first column vector of the matrix $C^{\alpha ,2(M_1-1)}$, and $F_{2(M_1-1)}$ is a $2(M_1-1)\times 2(M_1-1)$ discrete Fourier transform. For any $w\in {\mathbb{R}}^{2(M_1-1)}$, it is known that $F_{2(M_1-1)}w$ and $F_{2(M_1-1)}^{-1}w$ can be performed in $O(2(M_1-1)log\left(2(M_1-1)\right))=O((M_1-1)log(M_1-1))$ operations via the fast Fourier transform and the inverse fast Fourier transform, respectively [43]. Thus, the computation work of $A_{l}v$ requires $O((M_1-1)log(M_1-1))$ operations. □

Similarly, the matrix-vector multiplication $B_i\overline{v}$ can be performed in $O((M_2-1)log(M_2-1))$ operations for any $\overline{v}\in {\mathbb{R}}^{M_2-1}$.

Therefore, this fast algorithm based on the fast Fourier transform reduces computational costs. Furthermore, coefficient matrices $A_l$ and $B_i$ do not need to be assembled in the fast algorithm. Only the first column vectors of circulant matrices $C^{\alpha ,2(M_1-1)}$ and $C^{\beta ,2(M_2-1)}$ are required to be stored in this fast ADIM. Both the memory requirement and computational costs can be reduced in solving the fractional system by the fast Bi-CGSTAB ADIM compared to the classical Gaussian elimination and standard Bi-CGSTAB method.

The algorithm of the fast Bi-CGSTAB iterative method is illustrated in Algorithm 2.

Algorithm 2: Framework of the fast Bi-CGSTAB iterative method.

Input: The eigenvalue vector $\mathsf{\Lambda }$ of the corresponding circulant matrix;

The numerical solution at the previous time level $U^{n-1}$;

The right-hand-side vector b;

Output: Numerical solutions $U^n$ $x_0=U^{n-1}$ is an initial guess, $M=length\left(x_0\right)$, defining a zero vector $I_1=zeros(M,1)$; Compute the product of the circulant matrix C and the vector ${\widehat{x}}_0=[x_0;I_1]$ using Equations (34) and (35), and let the first M elements be the Toeplitz-like matrix-vector multiplication $A_l{x}_0=C{\widehat{x}}_0(1:M)$; Compute $r_0=b-A_l{x}_0$, where ${\widehat{r}}_0$ is an arbitrary vector such that $({\widehat{r}}_0,r_0)\ne 0$, e.g., ${\widehat{r}}_0=r_0$; Let ${\rho }_0={\alpha }_0={\omega }_0=1$, $v_0=p_0=0$;

for$i=1,2,3,\cdots ,$do

${\rho }_i=({\widehat{r}}_0,r_{i-1})$; $\beta =({\rho }_i/rh{o}_{i-1})({\alpha }_{i-1}/{\omega }_{i-1})$;

$p_i=r_{i-1}+\beta (p_{i-1}-{\omega }_{i-1v_{i-1}})$;

Compute the product of the circulant matrix C and the vector ${\widehat{p}}_i=[p_i;I_1]$ using Equations (34) and (35);

$v_i=C{\widehat{p}}_i(1:M)$; ${\alpha }_i={\rho }_i/({\widehat{r}}_0,v_i)$;

$s=r_{i-1}-{\alpha }_i{v}_i$;

Compute the product of the circulant matrix C and the vector $\widehat{s}=[s;I_1]$ using Equations (34) and (35);

$t=C\widehat{s}(1:M)$; $x_i=x_{i-1}+{\alpha }_i{p}_i+{\omega }_{i}s$;

if $x_i$ is accurate enough, then quit;

$r_i=s-{\omega }_{i}t$;

end for

Obtain numerical solutions $U^n=x_i$.

6. Numerical Example

This section provides two numerical examples. The effectiveness and reliability of the developed numerical methods are discussed. The numerical computations were performed using MATLAB R2021b on a MacBook Air with the following configuration: Apple M1 chip, 8-core CPU, 16 GB RAM, 512 GB storage, and macOS Ventura 13.1.

In the following numerical examples, the $L_{\infty }$ error refers to the maximum value of the absolute value of the difference between the numerical solution and the exact solution at $t_n=T$, which is calculated by

$$L_{\infty }error=\underset{(x,y)\in \mathsf{\Omega }}{max}|u_{i,j}^n-u(x,y,t_n)|.$$

(36)

Example 1.

We consider the two-dimensional RLDO-SFDE:

$$\frac{\partial u}{\partial t}={\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}d\alpha +{\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }u}{\partial y^{\beta }}d\beta +f(x,y,t),$$

(37)

in a finite domain $\mathsf{\Omega }\in (0,1)\times (0,1)$, $t\in (0,1]$, where $P\left(\alpha \right)=\Gamma (5-\alpha )$, $Q\left(\beta \right)=\Gamma (5-\beta )$.

The boundary and initial conditions are

$$\begin{array}{cc}\hfill & u(x,y,t)=0,(x,y,t)\in (R^2\backslash \mathsf{\Omega })\times (0,1],\hfill \\ \hfill & u(x,y,0)=x^2{(1-x)}^2{y}^2{(1-y)}^2,(x,y)\in \mathsf{\Omega }\cup \partial \mathsf{\Omega }.\hfill \end{array}$$

The exact solution of Equation (29) is

$$u(x,y,t)=(t^2+1)x^2{(1-x)}^2{y}^2{(1-y)}^2.$$

Employing the Riemann–Liouville fractional derivative of power functions, we can obtain

$$\begin{array}{cc}\hfill \frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}& =(t^2+1)y^2{(1-y)}^2{}_a^R{D}_x^{\alpha }\left(x^2{(1-x)}^2\right)\hfill \\ \hfill & =(t^2+1)y^2{(1-y)}^2{}_a^R{D}_x^{\alpha }(x^4-2x^3+x^2)\hfill \\ \hfill & =(t^2+1)y^2{(1-y)}^2\left[{}_a^R{D}_x^{\alpha }{x}^4-2{}_a^R{D}_x^{\alpha }{x}^3+{}_a^R{D}_x^{\alpha }{x}^2\right]\hfill \\ \hfill & =(t^2+1)y^2{(1-y)}^2\left[\frac{\Gamma \left(5\right)x^{4-\alpha }}{\Gamma (5-\alpha )}-2\frac{\Gamma \left(4\right)x^{3-\alpha }}{\Gamma (4-\alpha )}+\frac{\Gamma \left(3\right)x^{2-\alpha }}{\Gamma (3-\alpha )}\right].\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill & {\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}d\alpha \hfill \\ \hfill =& (t^2+1)y^2{(1-y)}^2{\int }_1^2\left[\Gamma \left(5\right)x^{4-\alpha }-2(4-\alpha )\Gamma \left(4\right)x^{3-\alpha }+(4-\alpha )(3-\alpha )\Gamma \left(3\right)x^{2-\alpha }\right]d\alpha \hfill \\ \hfill =& (t^2+1)y^2{(1-y)}^2{\int }_1^2\left[24x^{4-\alpha }-12(4-\alpha )x^{3-\alpha }+2({\alpha }^2-7\alpha +12)x^{2-\alpha }\right]d\alpha \hfill \\ \hfill =& 2(t^2+1)y^2{(1-y)}^2\frac{1}{{ln}^{3}x}\left[2(x-1)+(6x^2-11x+3)lnx+2(6x^3-15x^2+9x-1){ln}^{2}x\right].\hfill \end{array}$$

Likewise,

$$\begin{array}{c}\hfill {\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }u}{\partial y^{\beta }}d\beta =2(t^2+1)x^2{(1-x)}^2\frac{1}{{ln}^{3}y}\left[2(y-1)+(6y^2-11y+3)lny+2(6y^3-15y^2+9y-1){ln}^{2}y\right].\end{array}$$

Therefore,

$$\begin{array}{cc}\hfill f(x,y,t)=& \frac{\partial u(x,y,t)}{\partial t}-{\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}d\alpha -{\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }u}{\partial y^{\beta }}d\beta \hfill \\ \hfill =& 2t{x}^2{(1-x)}^2{y}^2{(1-y)}^2\hfill \\ \hfill & -2(t^2+1)y^2{(1-y)}^2\frac{1}{{ln}^{3}x}\left[2(x-1)+(6x^2-11x+3)lnx+2(6x^3-15x^2+9x-1){ln}^{2}x\right]\hfill \\ \hfill & -2(t^2+1)x^2{(1-x)}^2\frac{1}{{ln}^{3}y}\left[2(y-1)+(6y^2-11y+3)lny+2(6y^3-15y^2+9y-1){ln}^{2}y\right].\hfill \end{array}$$

To verify the effectiveness of the proposed numerical methods, Figure 1 displays the error between the exact solutions $u(x,y,t)$ and numerical solutions $u_{i,j}^n$ with $\sigma =\rho =1/200$ and $\tau =h_x=h_y=1/100$ at $t=1$. Both error distributions in Figure 1 suggest that the results produced by the proposed two numerical methods are in great agreement with the exact solutions. Furthermore, it is demonstrated that the error distributions in Figure 1b decrease dramatically after the implementation of the extrapolated technique as compared to the error without the extrapolated technique shown in Figure 1a. The result implies that the applied extrapolated technique is very efficient in solving the fractional system numerically.

The $L_{\infty }$ error and the corresponding convergence order of implicit alternating direction methods without and with the extrapolated technique for different mesh partitions with $\sigma =\rho =1/200$ at $t=1$ are compared in

Table 1. The comparison of $L_{\infty }$ error and convergence order between ADIM without and with the extrapolated method for different meshes with $\sigma =\rho =1/200$ at $t=1$.

	Without Extrapolated Technique		Extrapolated Technique
$\mathit{\tau }={\mathit{h}}_{\mathit{x}}={\mathit{h}}_{\mathit{y}}$	${\mathit{L}}_{\infty }$  Error	Order	${\mathit{L}}_{\infty }$  Error	Order
1/50	1.2000 $\times {10}^{-3}$	-	1.3159 $\times {10}^{-4}$	-
1/100	6.4413 $\times {10}^{-4}$	0.90	4.9333 $\times {10}^{-5}$	1.42
1/200	3.3766 $\times {10}^{-4}$	0.93	1.5396 $\times {10}^{-5}$	1.68
1/400	1.7308 $\times {10}^{-4}$	0.96	4.3243 $\times {10}^{-6}$	1.83

. It is observed that the $L_{\infty }$ error of the original ADIM maintains $O(\tau +h_x+h_y)$ accuracy. The $L_{\infty }$ error decreases dramatically after applying the extrapolated technique, as shown in Table 1. More importantly, the convergence order is improved to second-order accuracy by implementing the extrapolated technique.

Example 2.

Consider the two-dimensional RLDO-SFDE in $\mathsf{\Omega }\in (0,1)\times (0,1)$:

$$\begin{array}{cc}\hfill & \frac{\partial u}{\partial t}={\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}d\alpha +{\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }u}{\partial y^{\beta }}d\beta +f(x,y,t),\hfill \\ \hfill & u(x,y,t)=0,(x,y,t)\in (R^2\backslash \mathsf{\Omega })\times (0,1],\hfill \\ \hfill & u(x,y,0)=x^2{(1-x)}^2{y}^2{(1-y)}^2,(x,y)\in \mathsf{\Omega }\cup \partial \mathsf{\Omega }.\hfill \end{array}$$

where $t\in (0,1]$, $P\left(\alpha \right)=\Gamma (5-\alpha )$, $Q\left(\beta \right)=\Gamma (5-\beta )$.

The exact solution of this example is given by

$$u(x,y,t)=e^t{x}^2{(1-x)}^2{y}^2{(1-y)}^2.$$

The source term is formulated as

$$\begin{array}{cc}\hfill f(x,y,t)=& \frac{\partial u(x,y,t)}{\partial t}-{\int }_1^{2}P\left(\alpha \right)\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}d\alpha -{\int }_1^{2}Q\left(\beta \right)\frac{{\partial }^{\beta }u}{\partial y^{\beta }}d\beta \hfill \\ \hfill =& e^t{x}^2{(1-x)}^2{y}^2{(1-y)}^2\hfill \\ \hfill & -2e^t{y}^2{(1-y)}^2\frac{1}{{ln}^{3}x}\left[2(x-1)+(6x^2-11x+3)lnx+2(6x^3-15x^2+9x-1){ln}^{2}x\right]\hfill \\ \hfill & -2e^t{x}^2{(1-x)}^2\frac{1}{{ln}^{3}y}\left[2(y-1)+(6y^2-11y+3)lny+2(6y^3-15y^2+9y-1){ln}^{2}y\right].\hfill \end{array}$$

To test the effectiveness of the proposed fast algorithm, we compare the computational costs of three different ADIMs (Gaussian elimination, Bi-CGSTAB, and fast Bi-CGSTAB). The stopping criterion on the relative residual was ${10}^{-9}$ for the standard and fast Bi-CGSTAB algorithms. The $L_{\infty }$ error between exact solutions $u(x,y,t)$ and numerical solutions $u_{i,j}^n$ and the corresponding convergence order of two different algorithms (Gaussian elimination and fast Bi-CGSTAB) are illustrated in

Table 2. The comparison of $L_{\infty }$ error and convergence order between the ADIM and fast Bi-CGSTAB ADIM for different meshes with $\sigma =\rho =1/200$ at $t=1$.

	Gauss		Fast Bi-CGSTAB
$\mathbf{\tau }={\mathit{h}}_{\mathit{x}}={\mathit{h}}_{\mathit{y}}$	${\mathit{L}}_{\infty }$  Error	Order	${\mathit{L}}_{\infty }$  Error	Order
100	8.7548 $\times {10}^{-4}$	-	8.7548 $\times {10}^{-4}$	-
200	4.5894 $\times {10}^{-4}$	0.93	4.5901 $\times {10}^{-4}$	0.93
400	2.3524 $\times {10}^{-4}$	0.96	2.3523 $\times {10}^{-4}$	0.96
600	1.5817 $\times {10}^{-4}$	0.98	1.5814 $\times {10}^{-4}$	0.98

with $\sigma =\rho =1/200$ at $t=1$. Table 2 shows that the $L_{\infty }$ error of the numerical methods can achieve first-order convergence both for Gaussian elimination and the fast Bi-CGSTAB method. Furthermore, the comparison of CPU time consumed by Gaussian elimination and the standard and fast Bi-CGSTAB is demonstrated in

Table 3. The comparison of the consumed CPU time for three ADIMs (Gauss, Bi-CGSTAB, and fast Bi-CGSTAB) for different meshes with $\sigma =\rho =1/200$ at $t=1$.

	Gauss	Bi-CGSTAB	Fast Bi-CGSTAB
$\mathbf{\tau }={\mathit{h}}_{\mathit{x}}={\mathit{h}}_{\mathit{y}}$	CPU Time	CPU Time	CPU Time
25	0.73 s	0.75 s	0.31 s
50	2.65 s	3.03 s	1.53 s
100	11.99 s	13.84 s	9.58 s
200	89.15 s	5 min 14 s	82.63 s
400	14 min 54 s	32 min 39 s	10 min 52 s
600	1 h 6 min 4 s	3 h 7 min 15 s	1 h 1 min 12 s

. The fast Bi-CGSTAB method requires less CPU time than Gaussian elimination, as displayed in Table 3. More importantly, it is observed from Table 3 that the fast Bi-CGSTAB algorithm leads to a significant reduction of the CPU running time compared to the CPU time consumed by the standard Bi-CGSTAB method. This result indicates that the fast algorithm plays a significant role in reducing computational costs, especially compared with the standard Bi-CGSTAB method. Due to the fact that coefficient matrices in ADIM systems are lower Hessenberg–Toeplitz-like matrices, these systems can be effectively solved by first reducing the system to a lower triangular system using a backward sweep. The solution can be obtained by using Gaussian elimination in a relatively efficient way. This leads to the result that the fast Bi-CGSTAB method shows a slight acceleration of the computation than Gaussian elimination. When the coefficient matrix is a full matrix, the fast Bi-CGSTAB method might show better performance in reducing computational costs. Additionally, this fast algorithm offers great potential to speed up the calculation of the standard Bi-CGSTAB method. Some preconditioned techniques and parallel algorithms can further improve the efficiency of the fast Bi-CGSTAB method. The study of these issues and more effective numerical algorithms will be the goal of our future research.

7. Conclusions

In this work, we investigated the two-dimensional RLDO-SFDE by the ADIM. The stability and convergence of the numerical method were provided. An extrapolated technique was implemented to improve the convergence order of the implicit scheme. More importantly, a fast algorithm applied to the ADIM was developed to accelerate the computation. Finally, two numerical examples were provided to verify the effectiveness of the proposed numerical methods. The main highlights of this paper can be summarised as follows:

• The distributed-order operator allows for simulating anomalous diffusion processes exhibiting varying memory effects.
• The ADIM is unconditionally stable and convergent with an accuracy of $O({\sigma }^2+{\rho }^2+\tau +h_x+h_y)$.
• An extrapolated scheme maintains the higher-order accuracy of the implicit numerical method.
• The fast Bi-CGSTAB method shows excellent performance in reducing computational costs.
• This research may offer more insights into the application of fractional calculus and numerical techniques for solving fractional systems.

The offered work in this paper can be extended for more advanced fractional definitions (e.g., generalised fractal-fractional Caputo derivatives [44]). This research provides more possibilities for improving the effectiveness of the standard Bi-CGSTAB method. Further investigations into exploring efficient preconditioned techniques and parallel algorithms will be a potential direction in our future research.