Abstract
Although the literature presents promising techniques for the control of integer-order systems, control and synchronizing fractional systems still need further improvement to ensure their robustness and convergence time. This study aims to address this issue by proposing a model-free and finite-time super-twisting control technique for a variable-order fractional Hopfield-like neural network. The proposed controller is enhanced with an intelligent observer to account for disturbances and uncertainties in the chaotic model of the Hopfield-like neural network. The controller is able to regulate the system even when its complex variable-order fractional dynamic is completely unknown. Moreover, the proposed technique guarantees finite-time convergence of the closed-loop system. First, the dynamics of the variable-order fractional Hopfield-like neural network are examined. Then, the control design is described and its finite-time stability is proven. The controller is then applied to the variable-order fractional system and tested under two different scenarios to evaluate its performance. The results of the simulations demonstrate the excellent performance of the proposed method in both scenarios.
1. Introduction
Fractional-order neural networks are a relatively recent development in the field of neural networks [1,2]. They employ fractional calculus to represent the network’s behavior, which allows them to capture the complex and memory-dependent behavior of many physical systems more accurately [3]. This is because fractional calculus extends the concept of differentiation and integration to non-integer orders, enabling a more comprehensive representation of the system’s dynamics [4,5]. The major advantage of fractional-order neural networks is their ability to model complex and memory-dependent systems with a high degree of accuracy [6,7]. This is due to the fact that traditional integer-order neural networks are often unable to capture non-local, non-linear, and multi-fractal behaviors that are exhibited by these systems [8,9]. By utilizing fractional-order derivatives, neural networks can accurately represent these complex dynamics and improve their performance in a variety of applications [10,11].
Recently, some studies have shown that variable-order fractional (VOF) can capture the dynamic of some systems more accurately [12]. The applications of VOF neural networks are vast and promising. They have been successfully applied in signal processing for noise reduction, feature extraction, and signal classification. In addition, VOF neural networks have been used in image and speech recognition, as well as for modeling and controlling various physical systems such as robots, drones, and power systems. In VOF neural networks, the order of the fractional derivative is not fixed but varies as a function of time or the system state [13,14,15]. This enables the network to model systems that exhibit complex and time-varying behavior, which is neither possible with traditional integer order nor with constant fractional-order neural networks [16,17]. In addition, VOF neural networks are highly flexible and adaptive to changes in the system’s behavior. Unlike traditional neural networks, which have a fixed and pre-defined order of derivative, VOF neural networks can vary the order of derivative as a function of time or the system’s state [18,19]. This allows the network to model time-varying and non-stationary systems that cannot be captured by traditional neural networks [20,21].
Furthermore, VOF neural networks are capable of real-time learning and adaptation to new information, which is crucial in many applications. Therefore, VOF neural networks have been used to provide better performance in various applications, such as signal processing, image and speech recognition, and control systems [22,23]. However, VOF neural networks also present certain challenges that must be addressed. One of the main challenges is the increased computational complexity compared to traditional neural networks. Fractional-order derivatives require more computational resources, which can result in slower training and inference times. Additionally, designing effective control strategies for VOF neural networks is a challenging task due to the system’s complex and memory-dependent behavior [24,25].
One of the most widely used control techniques for complex systems is sliding mode control [26,27,28]. This robust control technique has been employed to stabilize and regulate neural networks [29]. By introducing a sliding mode surface, SMC can ensure the stability and robustness of the network, even in the presence of disturbances and uncertainties [30,31]. Adaptive control is another effective technique used for neural networks [32,33]. It utilizes feedback to adjust the network’s parameters in real time, depending on the system’s behavior [34]. By adapting to the changing behavior of the system, adaptive control techniques can improve the network’s performance in different environments [35]. Robust control is another control technique that has been successfully implemented for neural networks [36]. Its aim is to ensure the stability and robustness of the network, even in the presence of uncertainties and disturbances. By designing a robust controller, the network can maintain its stability and performance in various environments [37].
Although the latest control techniques such as SMC, adaptive control, and robust control show promising results for VOF neural networks’ reliable operation, they still suffer from some significant issues. For instance, most VOF controllers depend on the accuracy of the models provided in the simulations, and their finite-time convergence has not been proven in most studies. Hence, controlling VOF neural networks needs more attention to achieve successful deployment in various applications. Motivated by this, in the current study, we focus on the control of VOF Hopfield-like neural networks using a new super-twisting control technique. The proposed controller is enhanced by an intelligent observer, which accounts for disturbances and uncertainties that exist in the model of the chaotic neural network. The proposed technique offers several advantages, with its main advantage being its model-free nature that enables it to control the system even when the dynamics of the fractional systems are entirely unknown. Furthermore, the proposed controller is designed to guarantee finite-time convergence of the closed-loop system while avoiding chattering in the results. Thus, the proposed approach aims to overcome the technical challenges posed by the uncertain nature of the system by combining super-twisting control with an intelligent observer to provide a model-free control solution that can achieve finite-time convergence while handling uncertainties in the system. We describe the design of the controller and prove its finite-time stability. We conduct numerical simulations to examine the dynamics of the VOF Hopfield-like neural network, and then apply the proposed controller to the system.
The paper is organized as follows: In Section 2, we present the modeling and mathematical representation of VOF neural networks. Section 3 is dedicated to the design process of the controller, along with a discussion of its guaranteed stability. The proposed controller’s application to the system under uncertain scenarios for synchronization and control is explored in Section 4. Finally, we summarize the key findings and future prospects in Section 5.
2. Modeling and Mathematical Formulation of the System
In this paper, we have utilized a fractional version of a theoretical model originally presented in [38]. This model represents a generalization of the basic Hopfield neural network model originally proposed by Hopfield in [39], where neuronal self-connections are not present. The following variable-order fractional model of neural networks will be analyzed in this paper:
where denotes the number of neurons in the network. The state of the ith neuron is denoted by . The term represents the fractional-order derivative which is time-dependent, and is a positive constant. The function denotes the nonlinear function of the system, and is the external input to the ith neuron. Additionally, indicates the constant connection memristive weights. The VOF derivative captures the complex and memory-dependent behavior of the system, which is not possible with traditional integer-order derivatives. The nonlinear function captures the non-linear and non-local behavior of the system, which is essential for modeling complex systems such as neural networks. The present study focuses on a neural network that has three neurons and is characterized by the following governing equation:
where and . Additionally, , and It is noteworthy that all parameters and variables in the model are dimensionless. In this study, all calculations are performed using the Caputo definition, which is a widely used definition for fractional derivatives. Figure 1 displays the phase portraits of the VOF neural network for a value of equal to The figure clearly illustrates the chaotic behavior exhibited by the system.
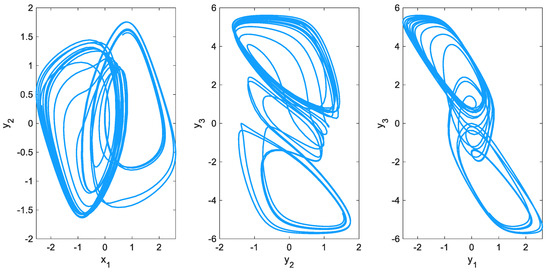
Figure 1.
Phase portraits of the VOF neural network.
To further analyze the impact of the variable-order derivative on the system’s behavior, we have presented the Lyapunov exponents and bifurcation diagrams. Figure 2 depicts the Lyapunov exponents of the system with the aforementioned parameters, providing clear evidence of the chaotic nature of the system.
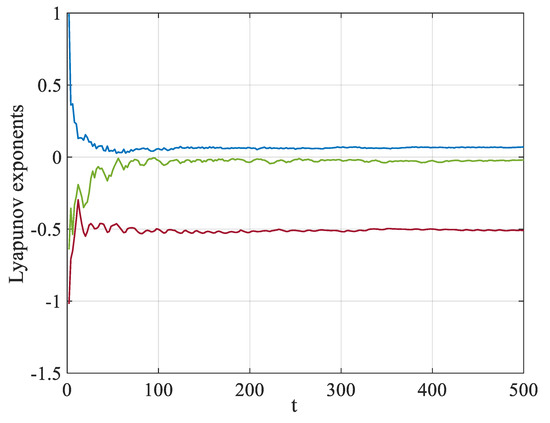
Figure 2.
Lyapunov exponents of the VOF neural network.
3. Controller Design and Its Stability
In this section, a new control technique is proposed for nonlinear memristive neural networks, and the stability of the closed-loop system is proven. The following nonlinear fractional-order slave system is under consideration:
where represents the state of the slave system, indicates the fractional-order derivative of the equations, and is the uncertain fractional-order function of the system. and indicate the control input and external disturbance, respectively. Considering the unknown external disturbance and uncertain dynamic function as an unknown compound term , the equation of the slave system can be written as:
Furthermore, we define the master system as:
Here, represents the states of the master system, while represents the nonlinear functions that define the behavior of the system. The synchronization error is defined as the difference between the states of the slave system and the states of the master system, .
3.1. Neural Network Estimator
The radial basis function (RBF) neural network estimator is a powerful tool for approximating functions and making predictions. It consists of an input layer, a hidden layer, and an output layer. The hidden layer is made up of several radial basis functions that transform the input data into a higher-dimensional space. The final output is generated by combining the outputs of the hidden layer using linear combinations.
RBF neural networks are particularly useful for tasks that involve interpolation or extrapolation. They have been applied in a wide range of fields, including control systems, pattern recognition, and function approximation [40,41].
In Figure 3, the structure of the RBF neural network estimator is shown, and the output of the estimator is denoted as . The output is calculated as a linear combination of the hidden layer outputs, where the weights are determined through a training process. The RBF neural network estimator is capable of learning and approximating complex functions, and its output is given by:
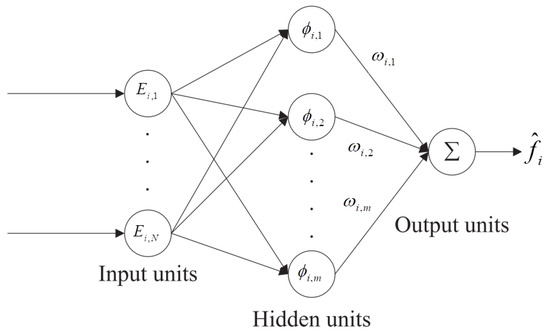
Figure 3.
The schematic structure of RBF neural network.
In the equation above, the RBF weight, denoted by , is a constant value used to adjust the importance or strength of each function in the hidden layer. The RBF function is represented by , and the number of hidden nodes is denoted by m, while the number of outputs is denoted by . The width value of the basis function, , determines the spread or influence of the function. The input vector for the RBF is denoted by , which includes the input data for the network. The bounded RBF approximation error, ε, measures the difference between the output of the network and the true value. Finally, determines the position of the basis function in the input space by representing the center of the basis function [40].
3.2. Super-Twisting Controller
In this section, we present the proposed finite-time control scheme, which aims to achieve finite-time stability. Finite-time stability is a property of a dynamic system, wherein its state variables remain bounded within a finite time interval, even when the system is subjected to disturbances or uncertainties. This property is desirable in control systems as it ensures that the system will reach a stable state within a finite time frame, regardless of external factors. To achieve finite-time stability in the system, we utilize the super-twisting algorithm. The super-twisting algorithm is a well-known and widely used second-order sliding mode control and observation technique. It was first introduced by Levant [42]. Since then, the super-twisting algorithm has been applied to a variety of control and observation problems, including mechanical systems, power electronics, robotics, and aerospace systems. However, the literature on super-twisting algorithms for fractional-order systems is relatively limited. The present study proposes a dependable control scheme for VOF neural networks that utilize the neural networks’ approximation ability and the robustness of super-twisting sliding mode controllers. The goal is to enhance control performance by merging these two potent techniques. We define the following sliding surface:
where τ is a positive value constant defined by the user. Our suggested strategy for the system (4) is a finite-time model-free super-twisting controller that is expressed as:
In the provided equation, both and are positive parameters that are defined by the user. The discrepancy between the calculated weights and the factual weights is called the weight estimation error, which is expressed as:
The proposed process for weight evolution of the neural network is described by the following adaptation law equation:
in which denotes a positive design parameter.
Remark 1.
In contrast to traditional training processes for neural networks, we utilized an online approach to update the weights of the network in real time. Specifically, the weights were updated based on a proposed adaptive law, which enabled the network to continuously adjust and improve its performance as new data became available. This approach is commonly used in control applications where fast and accurate estimations are necessary. By updating the weights in an online manner, the network is able to respond quickly to changes in the input and produce reliable output predictions in real time.
Theorem 1:
Given slave system (4) and master system (6), and the following assumptions:
- the states of the slave and master system are continuous and Lipschitz,
- the external disturbance and uncertainties are all bounded,
- the design parameters , and are positive;
Proposed control law (10) pushes the states of the slave system to those of the master system within a finite time interval.
Proof.
Equation (13) denotes the rate of change of the sliding surface over time as follows:
Using Equation (19), we have = which yields
Thus, by substituting the proposed control law , we can obtain the following equations.
By reformulating the equation and introducing new variables and , we can obtain:
where is a bounded estimation error. Equation (16) expresses a second-order super-twisting algorithm. As per Theorem 2 in the article [43] we adopt the given Lyapunov function:
in which is a matrix that is both symmetric and positive definite, while is a quadratic Lyapunov function. The variable is a vector that consists of two components, and , and is defined as . Additionally, the following equality holds:
in which is a symmetric and positive definite matrix. It is guaranteed that the error’s path will be bounded globally and ultimately. The time required for convergence is defined by , which can be expressed as:
By following the procedure described in [43], the matrices P and Q in the Lyapunov function can be selected such that the variables and reach zero in finite time. Additionally, the error trajectory will be globally ultimately bounded and the convergence time is given by . □
Remark 2.
The proposed technique offers several benefits compared to conventional control methods. It is model-free, which means it does not require knowledge of the exact system dynamics, which can be difficult to obtain in practice. Therefore, it can effectively manage the nonlinearity and uncertainty of the VOF system using an intelligent observer. Moreover, it employs a finite-time convergence algorithm, which guarantees that the system will attain the desired equilibrium state within a fixed duration (as opposed to exponential convergence), irrespective of initial conditions or system parameters. However, it is noteworthy that designing the parameters and structure of the RBF neural network can be considered a technical challenge in the proposed method.
4. Simulation Study by Applying Controller
In this section, we illustrate the numerical simulations of the proposed controller, highlighting the excellent performance of the suggested control method on a VOF neural network system, even under highly unpredictable dynamics. Taking into account the presence of external disturbances and the control input, the VOF neural network’s equation is formulated for simulation purposes as follows:
This equation shows the governing equation of the salve system. The parameters of the slave system are assumed to be identical to those of the master system. Across all numerical examples, the RBF network employed in the study consists of a hidden layer comprised of 30 neurons, each of which is associated with an RBF. The inputs to the network are the synchronization error and its time derivative. The initial weights of all neurons in the RBF network are set to 0.1, and these weights are updated based on the proposed adaptive law (Equation (12)). The biases of all neurons in the network are considered constant and equal to 20. To enable the network to output continuous values, a linear activation function is used.
To consider the impact of disturbances, the system is assumed to be affected by unknown perturbations that vary over time, as follows:
To evaluate the performance of our proposed method, we compared it against a state-of-the-art control approach designed for variable-order fractional chaotic systems. Specifically, we considered the Finite-Time Sliding Mode (FTSM) method presented in [44]. FTSM in that reference employs VOF integral-type and derivative-type sliding surfaces, leveraging the theory of VOF calculus. Here we applied the integral-type sliding surface, which is given by:
where is a positive design parameter. Additionally, the control law of FTSM is described in [44] as follows:
where and are positive design parameters.
It is worth noting that in our proposed super-twisting sliding mode controller, we utilized the integral of the sign function to avoid chattering. In contrast, the FTSM described in Equations (22) and (23) directly incorporates the sign function into the controller input, which can result in chattering and necessitates careful parameter tuning. Consequently, designing parameters for FTSM involves a trade-off between minimizing chattering and minimizing errors in the control results. Therefore, to compare the performance of the two controllers, we tested FTSM with two different sets of parameters.
In Section 4.1, we compare the performance of our developed method against that of FTSM when the latter has been optimized to produce a control signal that is free from any unwanted chatter. Additionally, in Section 4.2, we evaluate our proposed method against FTSM by selecting a set of parameters that minimize the error in FTSM.
4.1. Comparison 1
Here the FTSM parameters have been carefully selected to ensure that the resulting control signal is free from any undesirable chatter. Figure 4, Figure 5 and Figure 6 present the results of our comparison between the proposed super-twisting sliding mode controller and FTSM in [44].
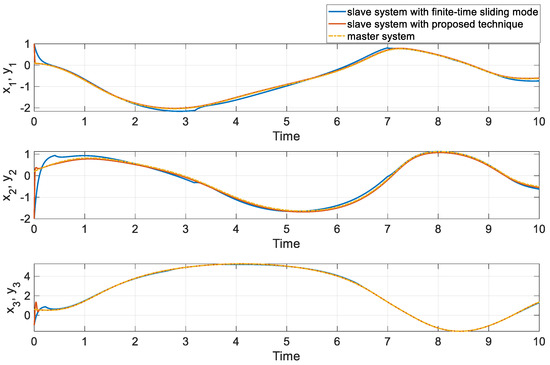
Figure 4.
The states of VOF neural network under both methods in comparison 1.

Figure 5.
The synchronization error under both methods in comparison 1.
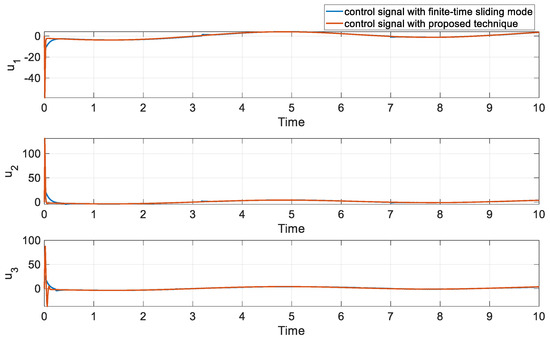
Figure 6.
The control input of both methods in comparison 1.
By analyzing the results presented in these figures, we can observe that our proposed super-twisting sliding mode controller outperforms FTSM in terms of achieving accurate synchronization. Notably, our controller achieves lower error (see Figure 5). These findings highlight the effectiveness of our proposed method in controlling variable-order fractional chaotic systems.
4.2. Comparison 2
To further evaluate the performance of our proposed super-twisting sliding mode controller, we compared it with FTSM [44] by selecting a set of parameters that minimize the error in FTSM. In this part, we consider the same disturbance as described in Equation (21). While the parameters of FTSM are changed to result in smaller synchronization errors, the parameters of our controller are the same as in the previous section. The results of this comparison are presented in Figure 7, Figure 8 and Figure 9.
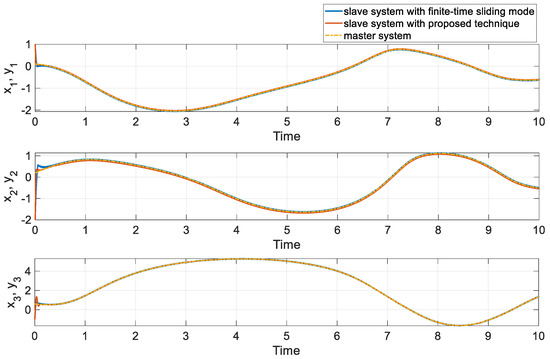
Figure 7.
The states of VOF neural network under both methods in comparison 2.
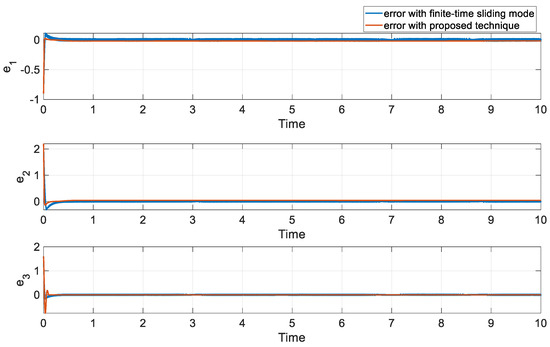
Figure 8.
The synchronization error under both methods in comparison 2.
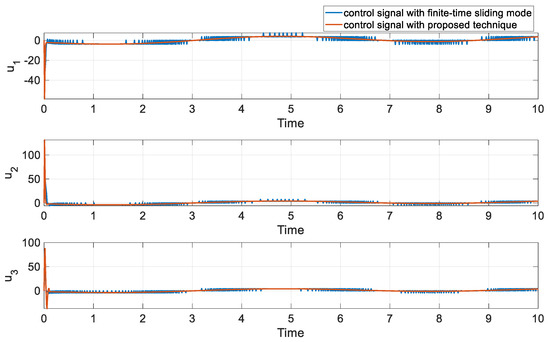
Figure 9.
The control input of both methods in comparison 2.
Figure 7 and Figure 8 show that both controllers achieve similar levels of synchronization error. However, upon closer examination of Figure 9, we observed that FTSM suffers from significant chattering, which is an undesired effect in practical applications. This behavior highlights the limitation of FTSM and reinforces the advantages of our proposed super-twisting sliding mode controller, which achieves accurate and smooth control signals with minimal chattering.
4.3. Quantitative Results of Comparisons 1 and 2
To better compare the performance of the controllers, we carried out quantitative analysis based on the average norm of errors and control inputs, as summarized in Table 1. Lower values indicate better performance, and it is worth noting that all approaches had the same control input range. Our analysis showed that, with the first set of parameters, the FTSM controller produced higher synchronization errors than our proposed approach. However, when the parameters of the FTSM controller were optimized to minimize errors, its performance in terms of synchronization errors resembled that of our proposed control technique. Unfortunately, the control signal of FTSM displayed significant chattering (as depicted in Figure 9), which cannot be ignored.

Table 1.
Quantitative results of the synchronization results.
To recapitulate briefly, even when we found a set of parameters that resulted in small errors for the FTSM controller, the chattering issue persisted. Considering all factors, our results suggest that the proposed control technique is a more practical and effective solution compared to FTSM, despite their similar performance in terms of synchronization error with optimized parameters.
4.4. Model-Free Control
In order to evaluate the effectiveness of the suggested control scheme, we investigated a scenario where the dynamics of the slave system are entirely unknown. In this scenario, the suggested neural network observation should gauge the dynamics of the VOF system and supply this information to the controller signals. This case serves as a reference point for assessing the efficacy of the suggested method for controlling the slave system when its dynamics are completely unknown.
Figure 7 and Figure 8 depict the states of the system and the synchronization error, respectively. The results of the synchronization displayed in these figures indicate that the suggested control approach can successfully achieve the desired performance. Additionally, Figure 9 illustrates the time history of the control signal. The system behavior and control input are both stable and smooth, without any noticeable fluctuations or unstable behavior. These findings suggest that the proposed control method is effective in regulating the system and generating consistent and stable outcomes, even when the dynamic of the system is completely unknown.
5. Conclusions
In this article, we examined the synchronization of VOF neural networks without relying on any specific model of the slave system. We proposed an extended super-twisting sliding mode control scheme that can produce finite-time responses while taking advantage of an RBF neural network estimator. We proved the system’s finite-time convergence and stability using the Lyapunov stability theorem, accounting for any disturbances and unknown models of the slave system. We evaluated the effectiveness of the proposed method through several numerical simulations in two different scenarios, including synchronization with time-varying disturbances and synchronization of a totally unknown slave system. The numerical simulations confirmed the validity of the theoretical claims about the proposed control technique, showcasing its outstanding performance. The proposed method in this paper is a step towards addressing existing challenges in the control of VOF neural networks, and the findings of this study pave the way for future practical research on the application of these complex systems. As a future direction, we suggest that the proposed controller could be further enhanced using self-tuning algorithms and that it has immense potential for customization and adaptation to various systems, including those with discrete-time dynamics.
Author Contributions
Conceptualization, F.W.A., M.S.A.-z., Q.Y. and H.J.; methodology, F.W.A., M.S.A.-z., Q.Y. and H.J.; software, F.W.A., M.S.A.-z., Q.Y. and H.J.; validation, F.W.A., M.S.A.-z., Q.Y. and H.J.; formal analysis, F.W.A., M.S.A.-z., Q.Y. and H.J.; writing—original draft preparation, F.W.A., M.S.A.-z., Q.Y. and H.J.; writing—review and editing, F.W.A., M.S.A.-z., Q.Y. and H.J.; supervision, F.W.A., M.S.A.-z., Q.Y. and H.J. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia, for funding this research work (Project number INSTR005).
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaslik, E.; Rădulescu, I.R. Dynamics of complex-valued fractional-order neural networks. Neural Netw. 2017, 89, 39–49. [Google Scholar] [CrossRef]
- Maiti, M.; Sunder, M.; Abishek, R.; Bingi, K.; Shaik, N.B.; Benjapolakul, W. Recent Advances and Applications of Fractional-Order Neural Networks. Eng. J. 2022, 26, 49–67. [Google Scholar] [CrossRef]
- Viera-Martin, E.; Gómez-Aguilar, J.F.; Solís-Pérez, J.E.; Hernández-Pérez, J.A.; Escobar-Jiménez, R.F. Artificial neural networks: A practical review of applications involving fractional calculus. Eur. Phys. J. Spéc. Top. 2022, 231, 2059–2095. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Cao, J. Dynamics in fractional-order neural networks. Neurocomputing 2014, 142, 494–498. [Google Scholar] [CrossRef]
- Cao, J.; Udhayakumar, K.; Rakkiyappan, R.; Li, X.; Lu, J. A comprehensive review of continuous-/discontinuous-time fractional-order multidimensional neural networks. IEEE Trans. Neural. Netw. Learn. Syst. 2021; ahead of print. [Google Scholar]
- Chen, Y.Q.; Petras, I.; Xue, D. Fractional order control—A tutorial. In Proceedings of the 2009 American Control Conference (ACC), St. Louis, MO, USA, 10–12 July 2009; pp. 1397–1411. [Google Scholar]
- Gutiérrez, R.E.; Rosário, J.M.; Machado, J.T. Fractional Order Calculus: Basic Concepts and Engineering Applications. Math. Probl. Eng. 2010, 2010, 375858. [Google Scholar] [CrossRef]
- David, S.A.; Linares, J.L.; Pallone, E.M.J.A. Fractional order calculus: Historical apologia, basic concepts and some applications. Rev. Bras. Ensino Física 2011, 33, 4302. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Zhang, S.; Chen, Y.; Yu, Y. A survey of fractional-order neural networks. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, Cleveland, OH, USA, 6–9 August 2017; Volume 58233, p. V009T07A024. [Google Scholar]
- Alsaade, F.W.; Jahanshahi, H.; Yao, Q.; Al-zahrani, M.S.; Alzahrani, A.S. On the Development of a Data-Driven-Based Fractional-Order Controller for Unmanned Aerial Vehicles. Fractal and Fractional. 2023, 7, 236. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Castillo, O. Application of variable-order fractional calculus in neural networks: Where do we stand? Eur. Phys. J. Spec. Top. 2022, 231, 1753–1756. [Google Scholar] [CrossRef]
- Çavuşoğlu, Ü. S-Box-based video stenography application of variable-order fractional hopfield neural network (VFHNN). Eur. Phys. J. Spec. Top. 2022, 231, 2017–2035. [Google Scholar] [CrossRef]
- Zhou, M.; Feng, Y.; Xue, C.; Han, F. Deep convolutional neural network based fractional-order terminal sliding-mode control for robotic manipulators. Neurocomputing 2020, 416, 143–151. [Google Scholar] [CrossRef]
- Aslipour, Z.; Yazdizadeh, A. Identification of nonlinear systems using adaptive variable-order fractional neural networks (Case study: A wind turbine with practical results). Eng. Appl. Artif. Intell. 2019, 85, 462–473. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Zambrano-Serrano, E.; Bekiros, S.; Wei, Z.; Volos, C.; Castillo, O.; Aly, A.A. On the dynamical investigation and synchronization of variable-order fractional neural networks: The Hopfield-like neural network model. Eur. Phys. J. Spéc. Top. 2022, 231, 1757–1769. [Google Scholar] [CrossRef]
- Huang, L.-L.; Park, J.H.; Wu, G.-C.; Mo, Z.-W. Variable-order fractional discrete-time recurrent neural networks. J. Comput. Appl. Math. 2020, 370, 112633. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Nguyen, T.G.; Fathurrochman, I.; Sadat, R.; Ali, M.R. Applications of neural networks for the novel designed of nonlinear fractional seventh order singular system. Eur. Phys. J. Spéc. Top. 2022, 231, 1831–1845. [Google Scholar] [CrossRef]
- Din, A.; Li, Y.; Yusuf, A.; Liu, J.; Aly, A.A. Impact of information intervention on stochastic hepatitis B model and its variable-order fractional network. Eur. Phys. J. Spéc. Top. 2022, 231, 1859–1873. [Google Scholar] [CrossRef] [PubMed]
- Yasami, A.; Beigi, A.; Yousefpour, A. Application of long short-term memory neural network and optimal control to variable-order fractional model of HIV/AIDS. Eur. Phys. J. Spec. Top. 2022, 231, 1875–1884. [Google Scholar] [CrossRef]
- Kaçar, S. Digital circuit implementation and PRNG-based data security application of variable-order fractional Hopfield neural network under electromagnetic radiation using Grünwald-Letnikov method. Eur. Phys. J. Spéc. Top. 2022, 231, 1969–1981. [Google Scholar] [CrossRef]
- Gu, C.-Y.; Zheng, F.-X.; Shiri, B. Mittag-leffler stability analysis of tempered fractional neural networks with short memory and variable-order. Fractals 2021, 29, 21400296. [Google Scholar] [CrossRef]
- Wang, B.; Jahanshahi, H.; Arıcıoğlu, B.; Boru, B.; Kacar, S.; Alotaibi, N.D. A variable-order fractional neural network: Dynamical properties, data security application, and synchronization using a novel control algorithm with a finite-time estimator. J. Frankl. Inst. 2022; in press. [Google Scholar] [CrossRef]
- Yang, J.; Yao, H.; Wu, B. An efficient numerical method for variable order fractional functional differential equation. Appl. Math. Lett. 2018, 76, 221–226. [Google Scholar] [CrossRef]
- Heydari, M.H.; Avazzadeh, Z.; Yang, Y. A computational method for solving variable-order fractional nonlinear diffusion-wave equation. Appl. Math. Comput. 2019, 352, 235–248. [Google Scholar] [CrossRef]
- Yousefpour, A.; Vahidi-Moghaddam, A.; Rajaei, A.; Ayati, M. Stabilization of nonlinear vibrations of carbon nanotubes using observer-based terminal sliding mode control. Trans. Inst. Meas. Control. 2019, 42, 1047–1058. [Google Scholar] [CrossRef]
- Yousefpour, A.; Hosseinloo, A.H.; Yazdi, M.R.H.; Bahrami, A. Disturbance observer–based terminal sliding mode control for effective performance of a nonlinear vibration energy harvester. J. Intell. Mater. Syst. Struct. 2020, 31, 1495–1510. [Google Scholar] [CrossRef]
- Wang, B.; Derbeli, M.; Barambones, O.; Yousefpour, A.; Jahanshahi, H.; Bekiros, S.; Aly, A.A.; Alharthi, M.M. Experimental validation of disturbance observer-based adaptive terminal sliding mode control subject to control input limitations for SISO and MIMO systems. Eur. J. Control. 2022, 63, 151–163. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Bekiros, S.; Muñoz-Pacheco, J.M. Robust adaptive control of fractional-order memristive neural networks. In Mem-Elements for Neuromorphic Circuits with Artificial Intelligence Applications; Elsevier: Amsterdam, The Netherlands, 2021; pp. 501–515. [Google Scholar]
- Yousefpour, A.; Jahanshahi, H.; Gan, D. Fuzzy integral sliding mode technique for synchronization of memristive neural networks. In Mem-Elements for Neuromorphic Circuits with Artificial Intelligence Applications; Elsevier: Amsterdam, The Netherlands, 2021; pp. 485–500. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: Berlin/Heidelberg, Germany, 2014; Volume 10. [Google Scholar]
- Kao, Y.; Li, Y.; Park, J.H.; Chen, X. Mittag–Leffler Synchronization of Delayed Fractional Memristor Neural Networks via Adaptive Control. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 2279–2284. [Google Scholar] [CrossRef] [PubMed]
- Mani, P.; Rajan, R.; Shanmugam, L.; Joo, Y.H. Adaptive control for fractional order induced chaotic fuzzy cellular neural networks and its application to image encryption. Inf. Sci. 2019, 491, 74–89. [Google Scholar] [CrossRef]
- Tao, G. Adaptive Control Design and Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 37. [Google Scholar] [CrossRef]
- Åström, K.J. Theory and applications of adaptive control—A survey. Automatica 1983, 19, 471–486. [Google Scholar] [CrossRef]
- Xi, Y.; Yu, Y.; Zhang, S.; Hai, X. Finite-time robust control of uncertain fractional-order Hopfield neural networks via sliding mode control. Chin. Phys. B 2018, 27, 010202. [Google Scholar] [CrossRef]
- Petersen, I.R.; Tempo, R. Robust control of uncertain systems: Classical results and recent developments. Automatica 2014, 50, 1315–1335. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Farrell, M.H.; Liang, T.; Misra, S. Deep Neural Networks for Estimation and Inference. Econometrica 2021, 89, 181–213. [Google Scholar] [CrossRef]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control. 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Meng, X.; Wu, Z.; Gao, C.; Jiang, B.; Karimi, H.R. Finite-Time Projective Synchronization Control of Variable-Order Fractional Chaotic Systems via Sliding Mode Approach. IEEE Trans. Circuits Syst. II: Express Briefs 2021, 68, 2503–2507. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).