Numerical Identification of External Boundary Conditions for Time Fractional Parabolic Equations on Disjoint Domains
Abstract
1. Introduction
2. Direct and Inverse Problems
3. Existence and Uniqueness of the Solution of the Direct Problem
4. Solution of the Semidiscrete Direct and Inverse Problem
4.1. Time Semidiscretization of the Direct Problem
4.2. Solving the Inverse Problems
5. Numerical Realization
5.1. Full Discretizations
5.2. Correctness
5.3. Implementation
6. Extension to 2D Problem
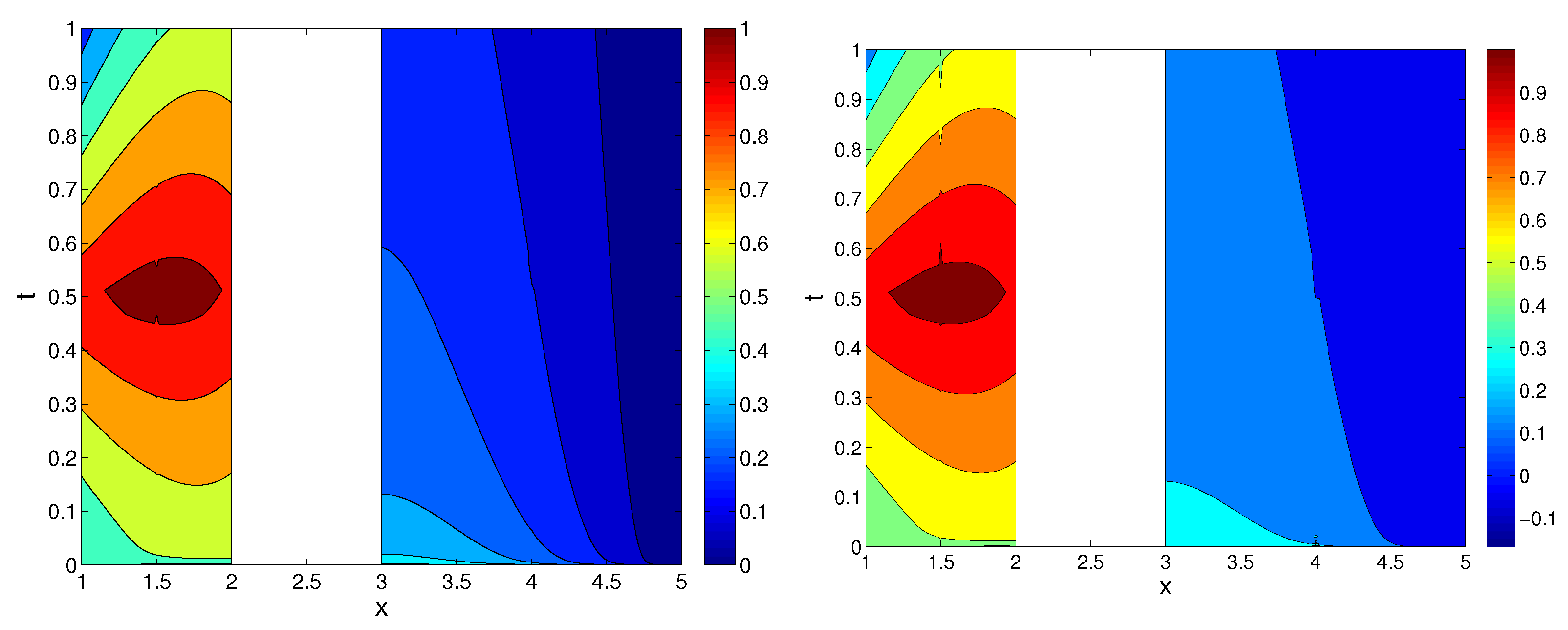
7. Numerical Simulations
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hasanoglu, A.H.; Romanov, V.G. Introduction to Inverse Problems for Differential Equations, 1st ed.; Springer: Cham, Switzerland, 2017; 261p. [Google Scholar]
- Lesnic, D. Inverse Problems with Applications in Science and Engineering; CRC Press: Abingdon, UK, 2021; p. 349. [Google Scholar]
- Samarskii, A.A.; Vabishchevich, P.N. Numerical Methods for Solving Inverse Problems in Mathematical Physics; de Gruyter: Berlin, Germany, 2007; p. 438. [Google Scholar]
- Koleva, M.; Milovanović Jeknić, Z.D.; Vulkov, L. Determination of external boundary conditions of a stationary nonlinear problem on disjoint intervals at point observation. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Zhuo, L.; Lesnic, D.; Meng, S. Reconstruction of the heat transfer coefficient at the interface of a bi-material. Inverse Probl. Sci. Eng. 2020, 28, 374–401. [Google Scholar] [CrossRef]
- Alifanov, O.M. Inverse Heat Transfer Problems, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1994; 348p. [Google Scholar]
- Amann, H. Maximal regularity of parabolic transmission problems. J. Evol. Equ. 2021, 21, 3375–3420. [Google Scholar] [CrossRef]
- Caffarelli, L. A monotonicity formula for heat functions in disjoint domains, boundary value problems for partial differential equations and applications. RMA Res. Notes Appl. Math. 1993, 29, 53–60. [Google Scholar]
- Calabro, F.; Zunino, P. Analysis of parabolic problems on partitioned domains withnonlinearconditions at the interface: Application to mass transfer trough semi-permeable membranes. Math. Model. Methods Appl. Sci. 2006, 164, 479–501. [Google Scholar] [CrossRef]
- Datta, A.K. Biological and Bioenvironmental Heat and Mass Transfer, 1st ed.; Marcel Dekker: New York, NY, USA, 2002; 424p. [Google Scholar]
- Givoli, D. Exact representation on artificial interfaces and applications in mechanics. Appl. Mech. Rev. 1999, 52, 333–349. [Google Scholar] [CrossRef]
- Kinash, N.; Janno, J. An inverse problem for a generalized fractional derivative with an application in reconstruction of time- and space-dependent Sources in fractional diffusion and wave equations. Mathematics 2019, 7, 1138. [Google Scholar] [CrossRef]
- Qatanani, N.; Barham, A.; Heeh, Q. Existence and uniqueness of the solution of the coupled conduction radiation energy transfer on diffuse gray surfaces. Surv. Math. Its Appl. 2007, 2, 43–58. [Google Scholar]
- Caputo, M. Vibrations of infinite viscoelastic layer with a dissipative memory. J. Acoust. Soc. Am. 1974, 56, 897–904. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Stynes, M.; O’Riordan, E.; Gracia, J.L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z.; Liao, H. Finite difference methods for the time fractional diffusion equationo non-uniform meshes. J. Comput. Phys. 2014, 265, 195–210. [Google Scholar] [CrossRef]
- Lancia, M.R.; Cefalo, M.; Dell’Acqua, G. Numerical approximation of transmission problems across Koch-type highly conductive layers. Appl. Math. Comput. 2012, 218, 5453–5473. [Google Scholar] [CrossRef]
- El Hamidi, A.; Kirane, M.; Tfayli, A. An Inverse Problem for a Non-Homogeneous Time-Space Fractional Equation. Mathematics 2022, 10, 2586. [Google Scholar] [CrossRef]
- Jovanovic, B.S.; Milovanovic, Z.D. Numerical approximation of a 2D parabolic transmission problem in disjoint domains. Appl. Math. Comput. 2014, 228, 508–519. [Google Scholar] [CrossRef]
- Jovanovic, B.; Koleva, M.; Vulkov, L. Convergence of a FEM and two-grid algorithms for elliptic problems on disjoint domains. J. Comput. Appl. Math. 2011, 236, 364–374. [Google Scholar] [CrossRef]
- Koleva, M. Finite element solution of 1D boundary value linear and nonlinear problems with nonlocal jump conditions. AIP Conf. Proc. 2007, 946, 163. [Google Scholar]
- L’vov, P.E.; Sibatov, R.T.; Yavtushenko, I.O.; Kitsyuk, E.P. Time-Fractional phase field model of electrochemical impedance. Fractal Fract. 2021, 5, 191. [Google Scholar] [CrossRef]
- Milovanovic, Z. Finite difference scheme for a parabolic transmission problem in disjoint domains. Lect. Notes Comput. Sci. 2013, 8236, 403–410. [Google Scholar]
- Prilepko, A.I.; Kamynin, V.L.; Kostin, A.B. Inverse source problem for parabolic equation with the condition of integral observation in time. J. Inverse -Ill-Posed Probl. 2018, 46, 523–539. [Google Scholar] [CrossRef]
- Teresi, L.; Vacca, E. Transmission phenomena across highly conductive interfaces. In Applied and Industrial Mathematics in Italy II; Series on Advances in Mathematics for Applied Sciences; World Scientific: Singapore, 2007; pp. 585–596. [Google Scholar]
- Vulkov, L. Well posedness and monotone iterative method for nonlinear interface problem on disjoint intervals. AIP Conf. Proc. 2007, 946, 188. [Google Scholar]
- Zhang, Y.; Mazzucato, A.L. Transmission problems for parabolic operators on polygonal domains and applications to the finite element method. La Mat. 2022, 1, 225–262. [Google Scholar] [CrossRef]
- Jovanovic, B.S.; Vulkov, L.G.; Delic, A. Boundary value problems for fractional PDE and their numerical approximation. In Numerical Analysis and Its Applications; Dimov, I., Farago, I., Vulkov, L., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8236, pp. 38–49. [Google Scholar]
- Jovanovic, B.S.; Vulkov, L.G.; Delic, A. About some boundary value problems for fractional PDE and their numerical solution. Proc. Appl. Math. Mech. 2013, 13, 445–446. [Google Scholar] [CrossRef]
- Al-Masaeed, R.; Maayah, B.; Abu-Ghurra, S. Adaptive technique for solving 1-D interface problems of fractional order. Int. J. Appl. Comput. Math 2022, 8, 214. [Google Scholar] [CrossRef] [PubMed]
- Vasil’ev, V.I.; Su, L. Numerical method for solving boundary inverse problem for one-dimensional parabolic equation. Math. Model. 2017, 24, 108–117. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, D.; Wang, H. Simultaneous identification of initial value and source strength in a transmission problem for a parabolic equation. Adv. Comput. Math. 2022, 48, 77. [Google Scholar] [CrossRef]
- Kiana, Y.; Oksanenb, L.; Soccorsia, E.; Yamamoto, M. Global uniqueness in an inverse problem for time fractional diffusion equations. J. Differ. Equ. 2018, 264, 1146–1170. [Google Scholar] [CrossRef]
- Ashurov, R.; Fayziev, Y. On the nonlocal problems in time for time-fractional subdiffusion equations. Fractal Fract. 2022, 6, 41. [Google Scholar] [CrossRef]
- Ozbilge, E.; Kanca, F.; Özbilge, E. Inverse problem for a time fractional parabolic equation with nonlocal boundary conditions. Mathematics 2022, 10, 1479. [Google Scholar] [CrossRef]
- Klibas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; p. 540. [Google Scholar]
- Hadamard, J. Lectures on Cauchy’s Problem in Linear Partial Differential Equations; Yale University Press: New Haven, CT, USA, 1923. [Google Scholar]
- Evans, L.C. Partial Differential Equations, 2nd ed.; American Mathematical Society: Prividence, RI, USA, 2010; Volume 19. [Google Scholar]
- Varga, R.S. Matrix Iterative Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2000; p. 358. [Google Scholar]





| 0.5 | 0.5 | 5.699 | 1.965 | 6.157 | 2.142 | 7.418 | 2.600 | 9.118 | |
| 1.536 | 1.674 | 1.523 | 1.530 | 1.512 | 1.512 | ||||
| 1.844 | 6.665 | 2.213 | 7.720 | 2.653 | 9.398 | 3.286 | |||
| 1.468 | 1.591 | 1.519 | 1.541 | 1.497 | 1.516 | ||||
| 0.3 | 0.6 | 1.014 | 3.113 | 1.046 | 3.873 | 1.462 | 5.453 | 2.040 | |
| 1.703 | 1.573 | 1.433 | 1.406 | 1.423 | 1.419 | ||||
| 3.166 | 1.075 | 3.496 | 1.333 | 4.911 | 1.859 | 6.930 | |||
| 1.559 | 1.620 | 1.391 | 1.441 | 1.401 | 1.424 | ||||
| 0.9 | 0.4 | 2.672 | 9.865 | 4.230 | 1.988 | 8.263 | 3.832 | 1.684 | |
| 1.438 | 1.222 | 1.089 | 1.267 | 1.109 | 1.186 | ||||
| 9.591 | 3.127 | 1.535 | 6.830 | 2.907 | 1.331 | 6.159 | |||
| 1.617 | 1.026 | 1.168 | 1.232 | 1.127 | 1.112 |
| 1.037 | 2.583 | 6.445 | 1.610 | 4.022 | 1.005 | 2.512 | |
| 2.005 | 2.003 | 2.002 | 2.001 | 2.000 | 2.000 | ||
| 3.725 | 9.320 | 2.330 | 5.822 | 1.455 | 3.637 | 9.093 | |
| 1.999 | 2.000 | 2.000 | 2.000 | 2.000 | 2.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koleva, M.N.; Vulkov, L.G. Numerical Identification of External Boundary Conditions for Time Fractional Parabolic Equations on Disjoint Domains. Fractal Fract. 2023, 7, 326. https://doi.org/10.3390/fractalfract7040326
Koleva MN, Vulkov LG. Numerical Identification of External Boundary Conditions for Time Fractional Parabolic Equations on Disjoint Domains. Fractal and Fractional. 2023; 7(4):326. https://doi.org/10.3390/fractalfract7040326
Chicago/Turabian StyleKoleva, Miglena N., and Lubin G. Vulkov. 2023. "Numerical Identification of External Boundary Conditions for Time Fractional Parabolic Equations on Disjoint Domains" Fractal and Fractional 7, no. 4: 326. https://doi.org/10.3390/fractalfract7040326
APA StyleKoleva, M. N., & Vulkov, L. G. (2023). Numerical Identification of External Boundary Conditions for Time Fractional Parabolic Equations on Disjoint Domains. Fractal and Fractional, 7(4), 326. https://doi.org/10.3390/fractalfract7040326






