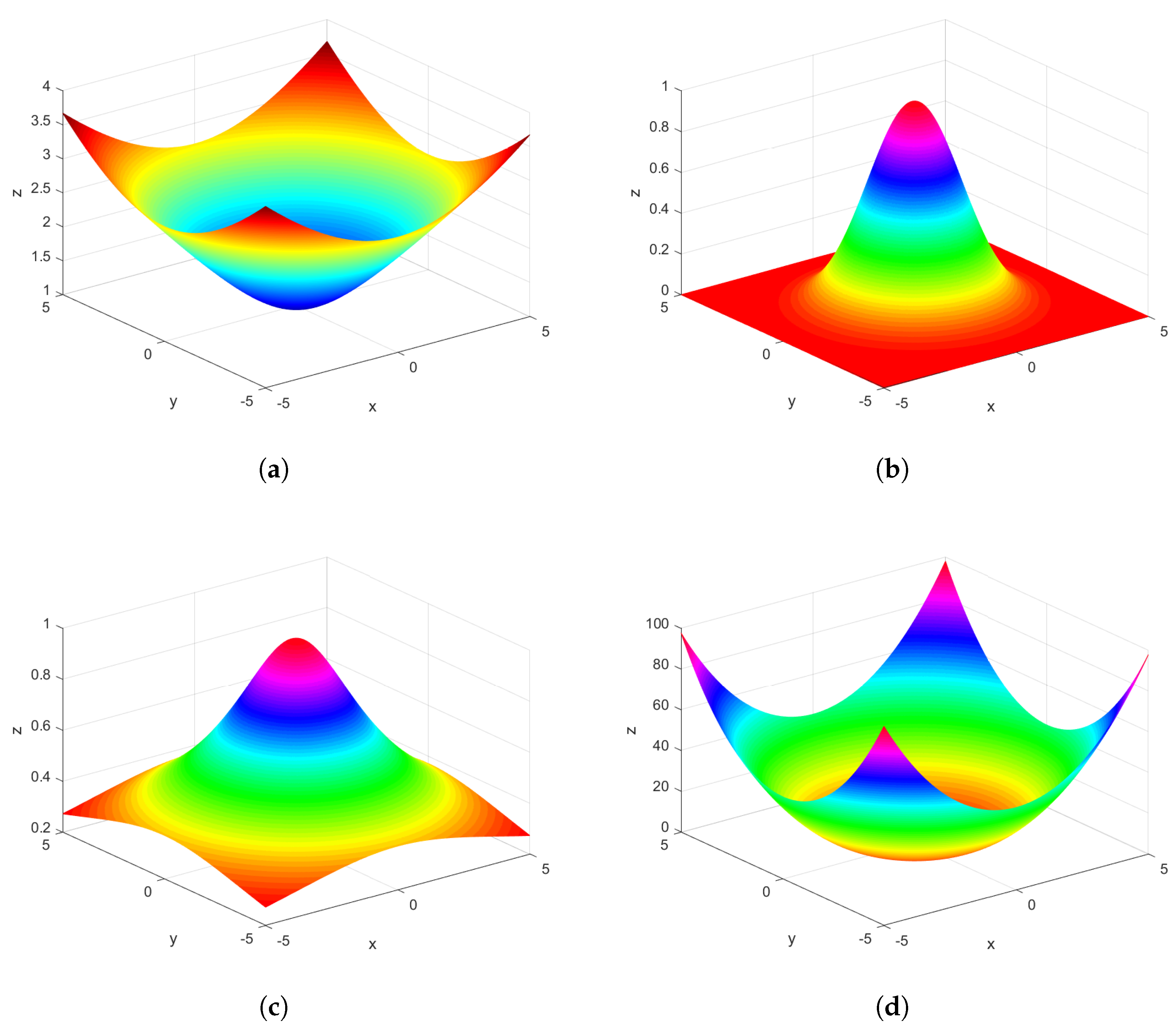
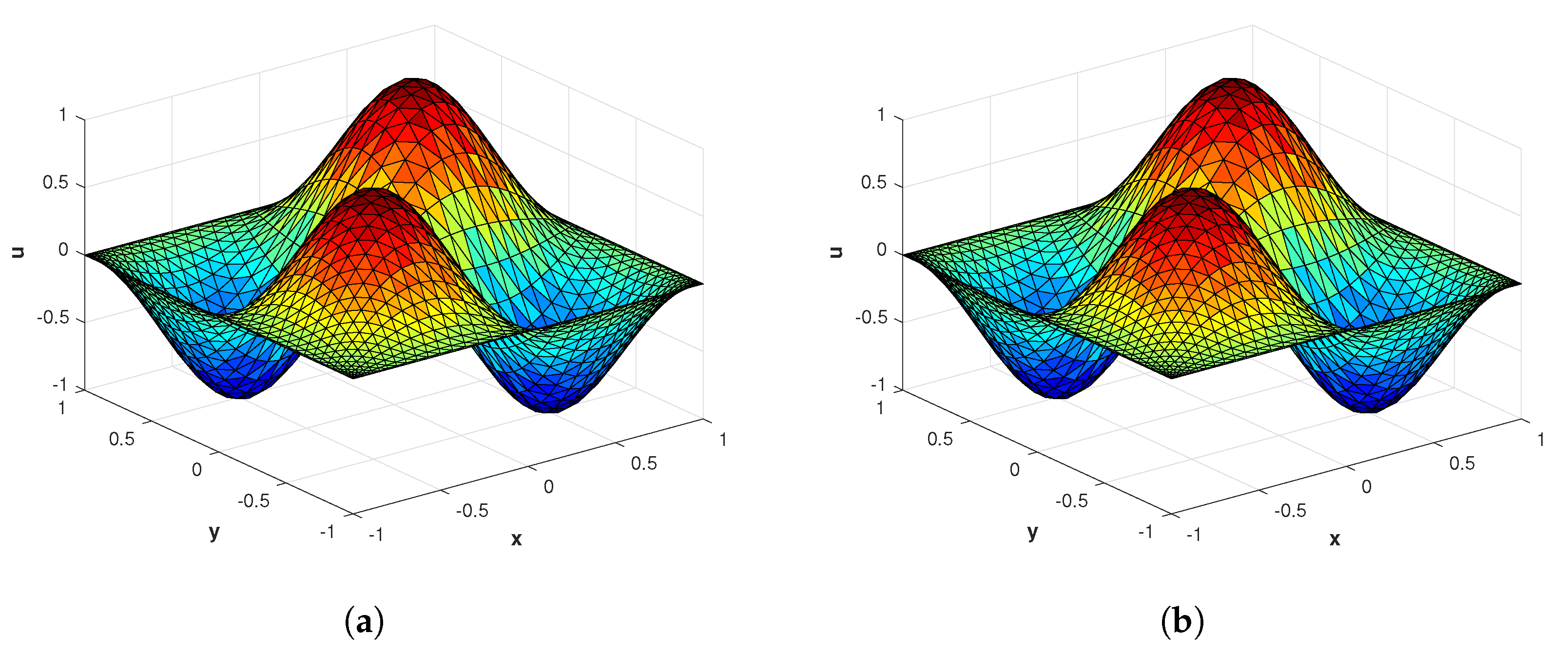
Figure 1.
(a) The MQ RBF plot in the domain with ; (b) the GA RBF plot in the domain with ; (c) the IMQ RBF plot in the domain with ; (d) the TPS RBF plot in the domain with .
Figure 1.
(a) The MQ RBF plot in the domain with ; (b) the GA RBF plot in the domain with ; (c) the IMQ RBF plot in the domain with ; (d) the TPS RBF plot in the domain with .
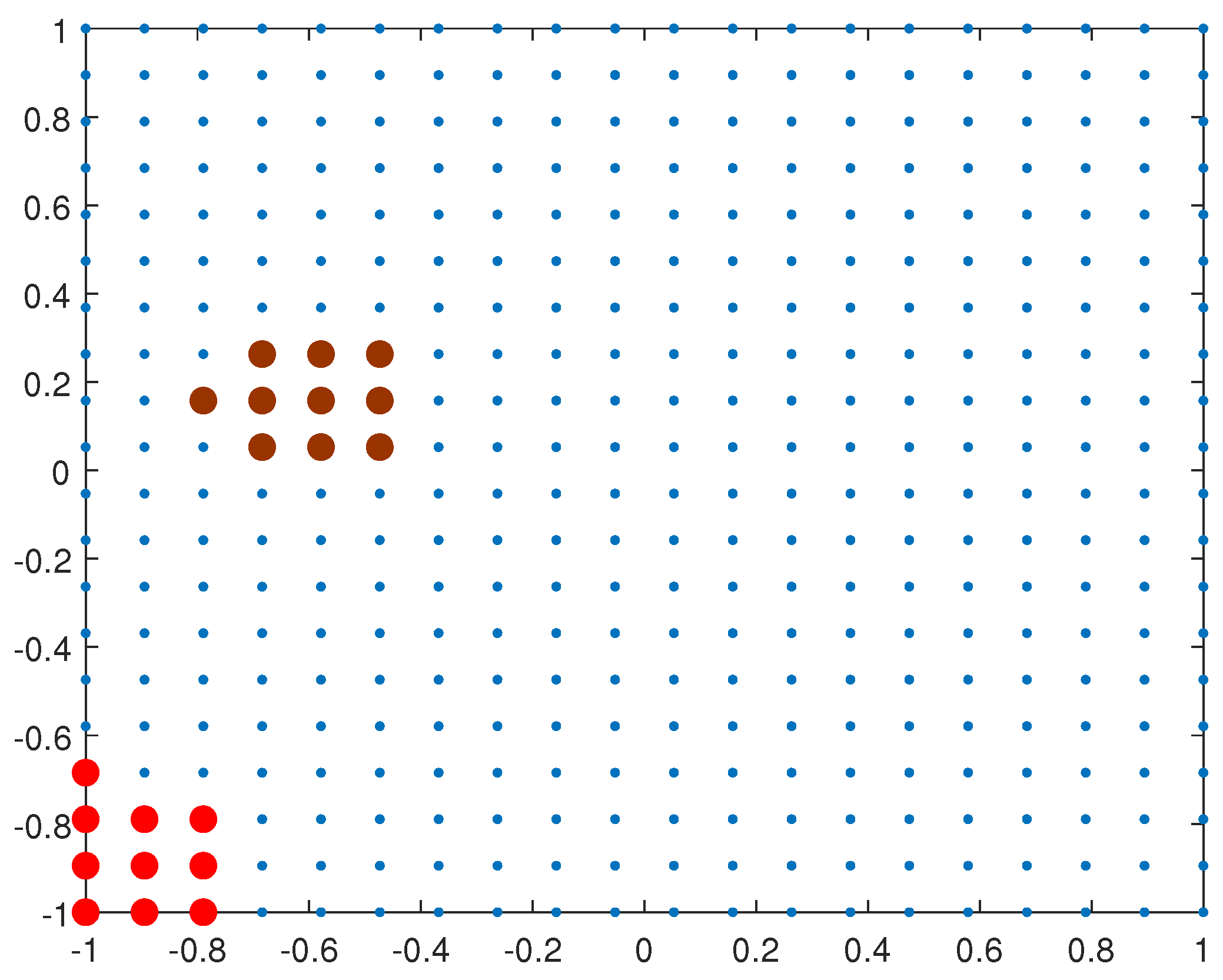
Figure 2.
A stencil for , red corresponds to the boundary node and brown to the interior node.
Figure 2.
A stencil for , red corresponds to the boundary node and brown to the interior node.
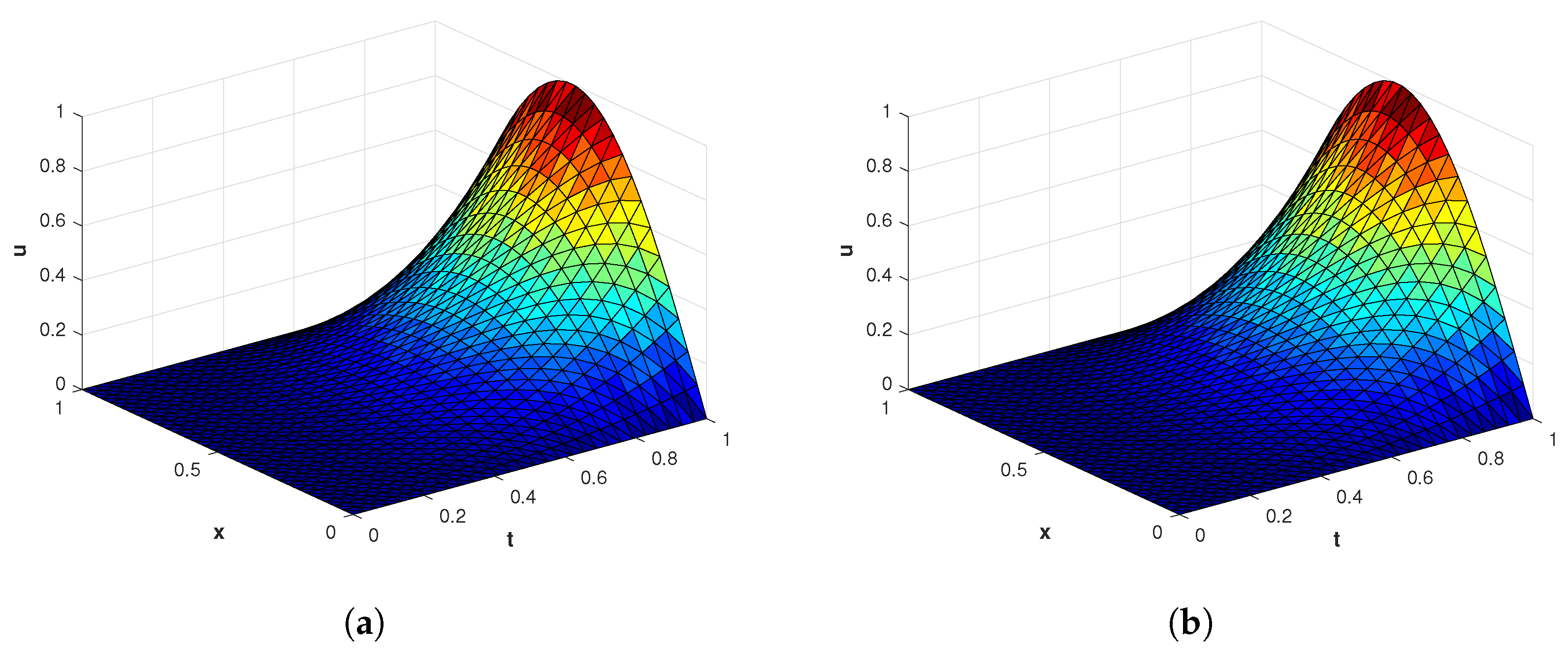
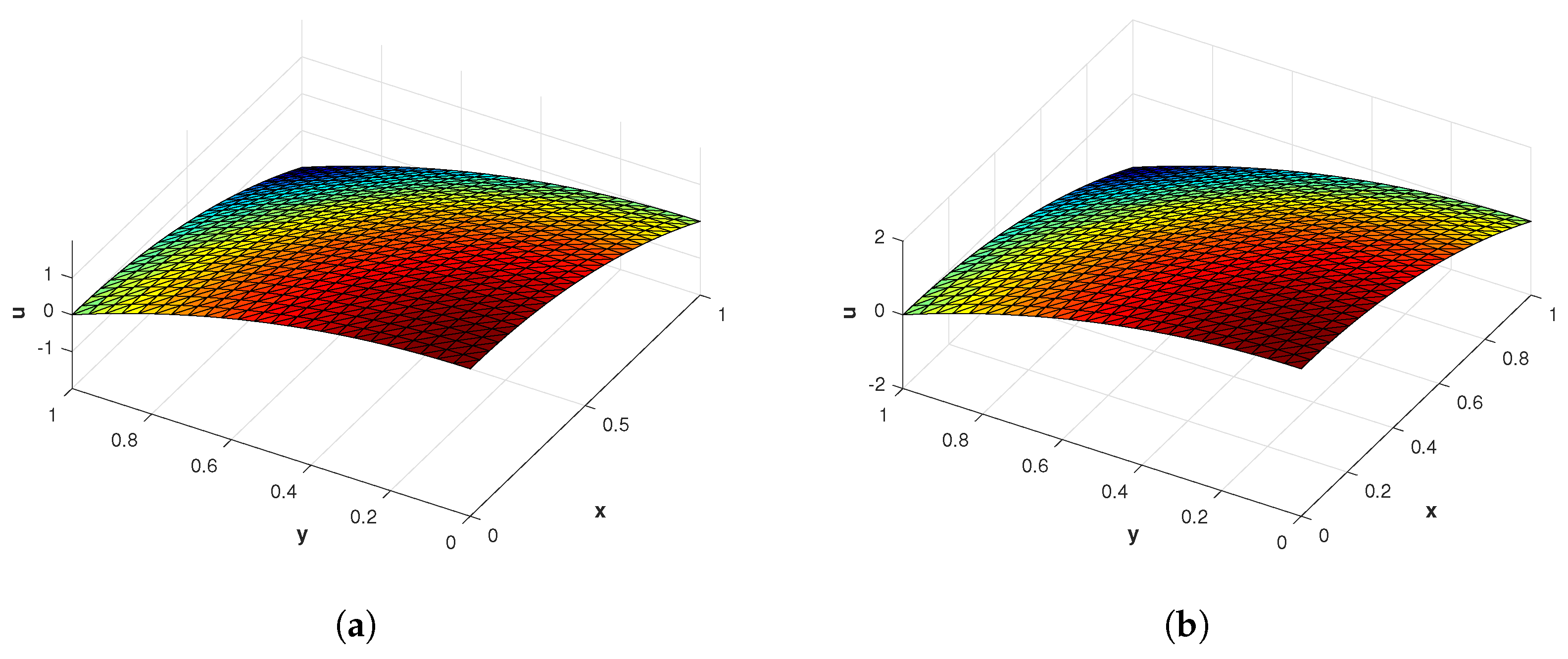
Figure 3.
(a) The numerical solution of problem 1 with (b) The exact solution of problem 1 with .
Figure 3.
(a) The numerical solution of problem 1 with (b) The exact solution of problem 1 with .
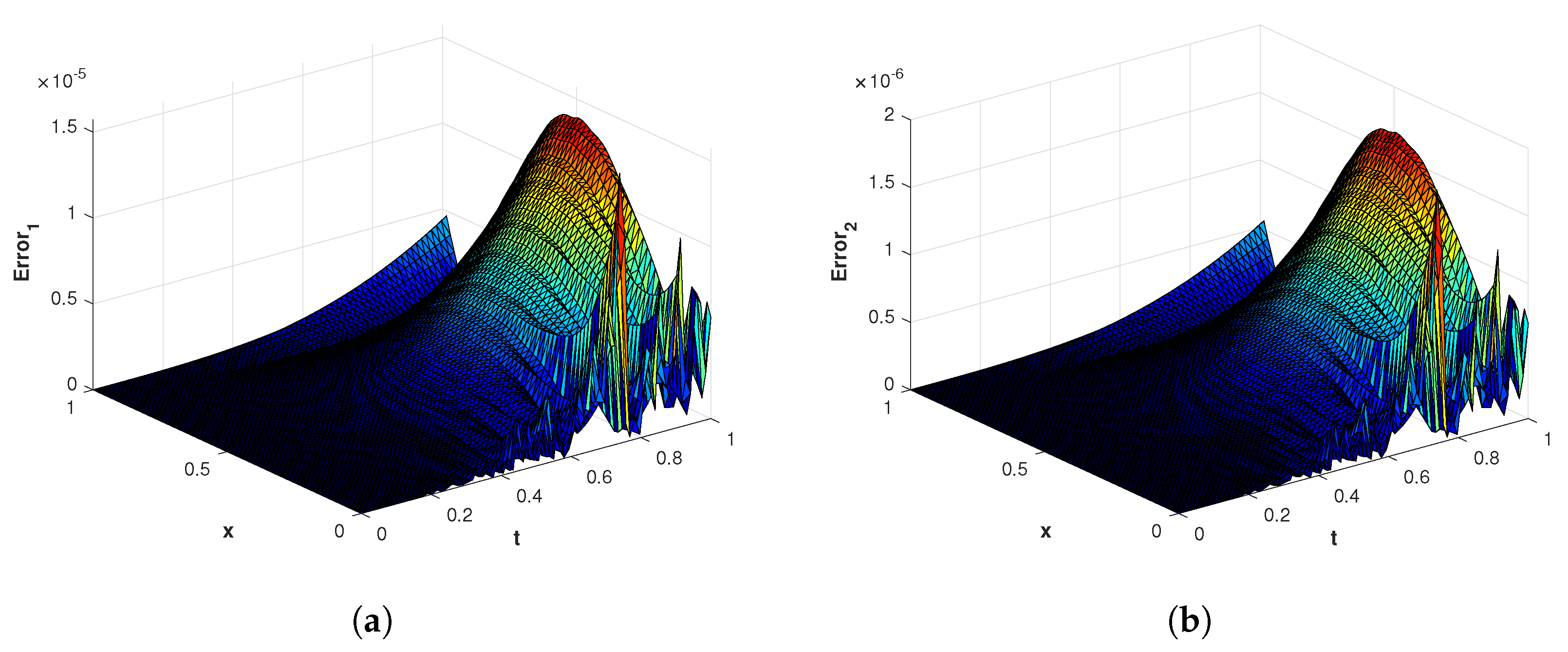
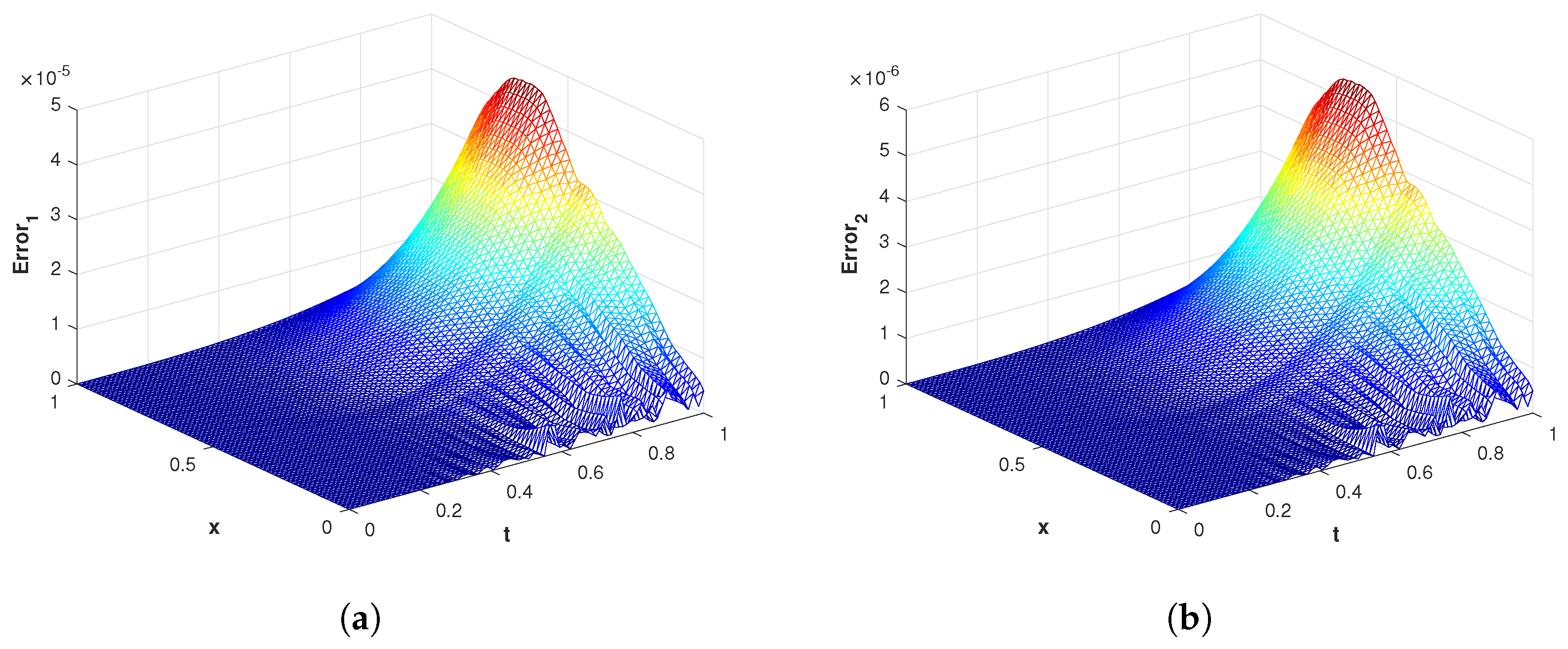
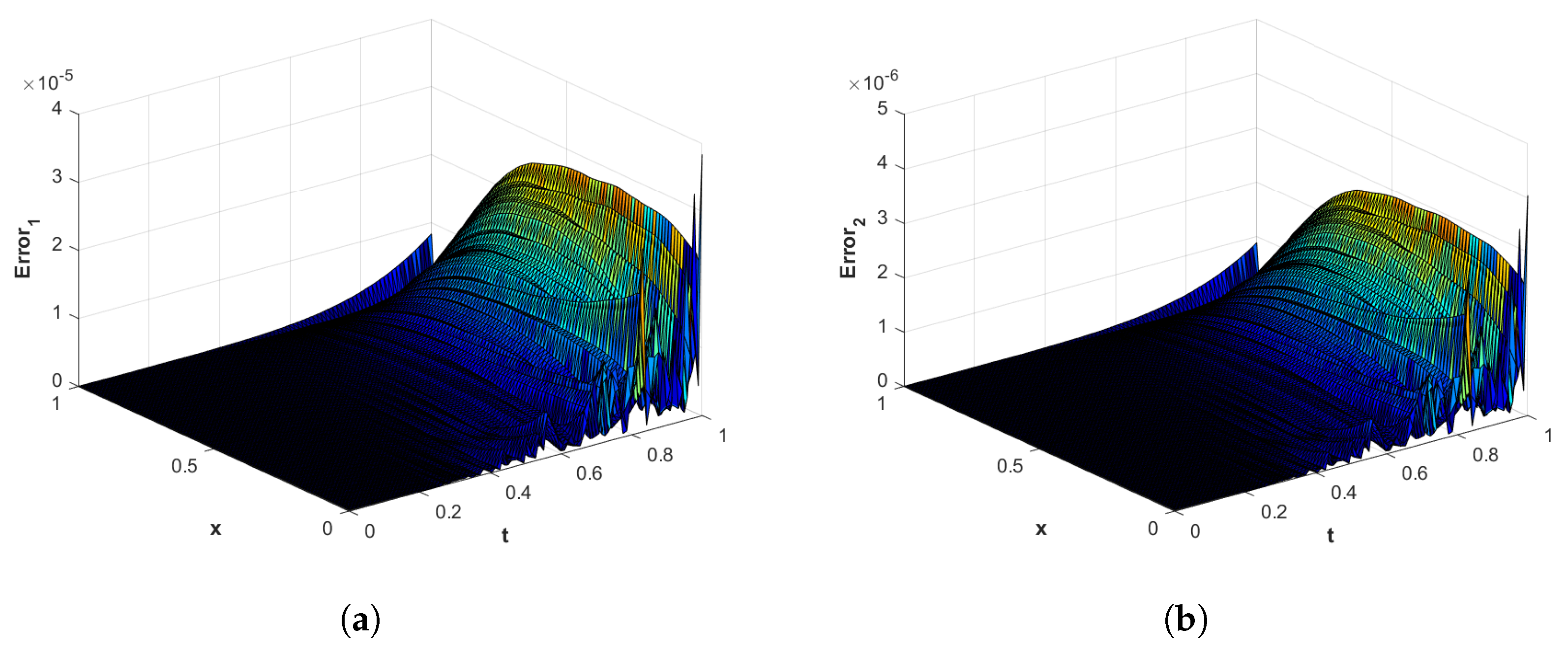
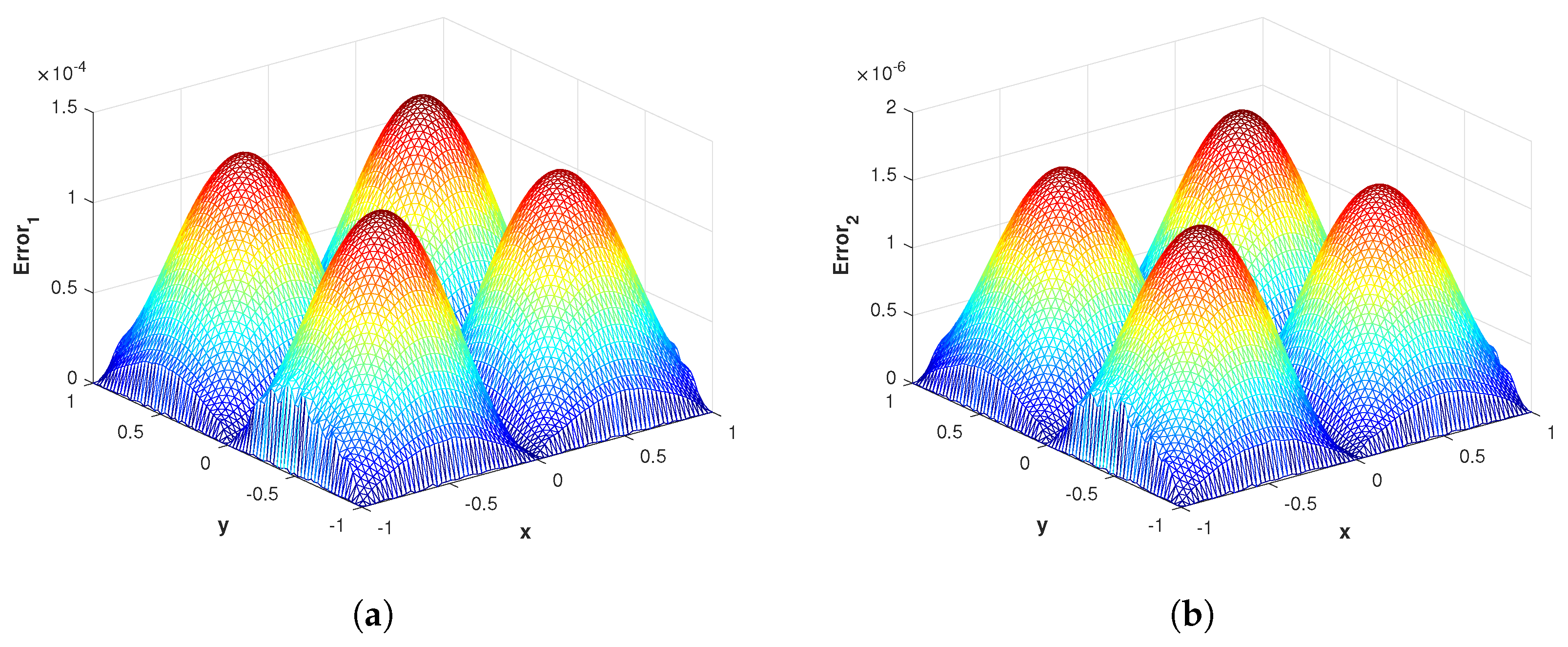
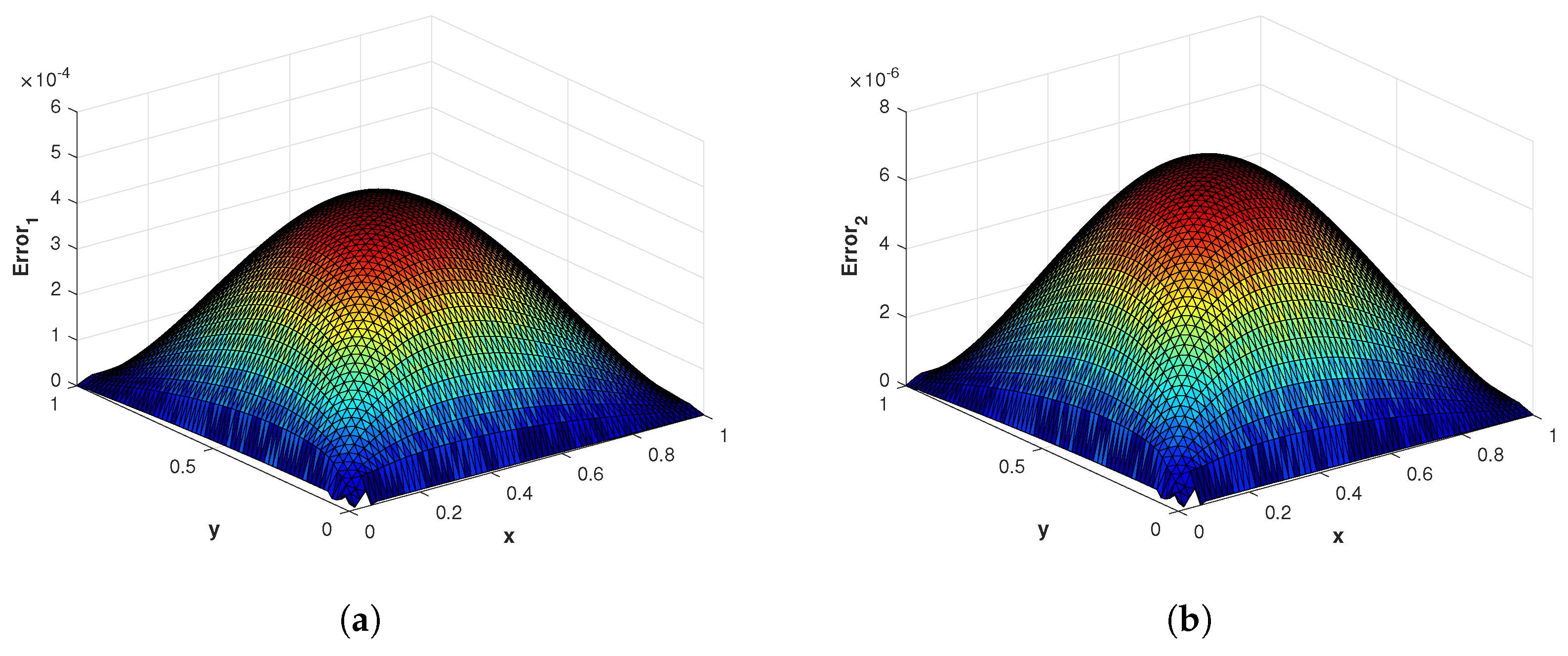
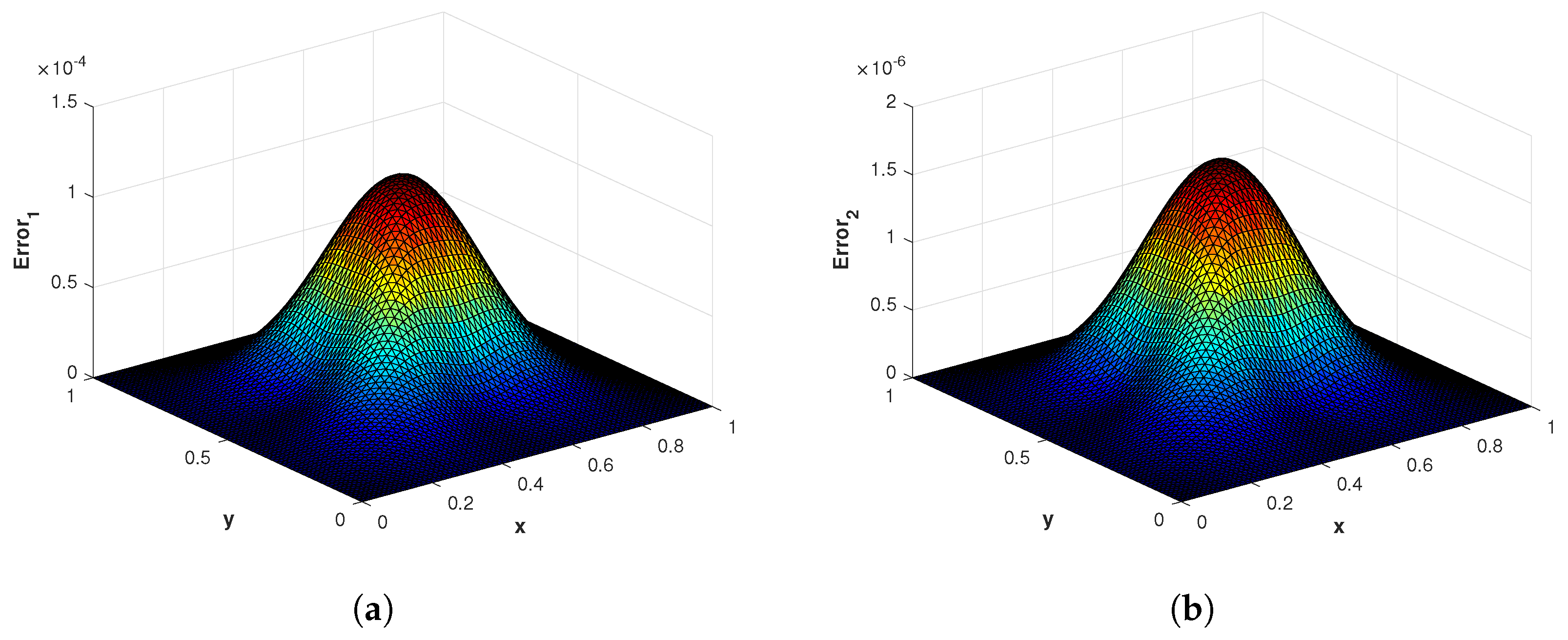
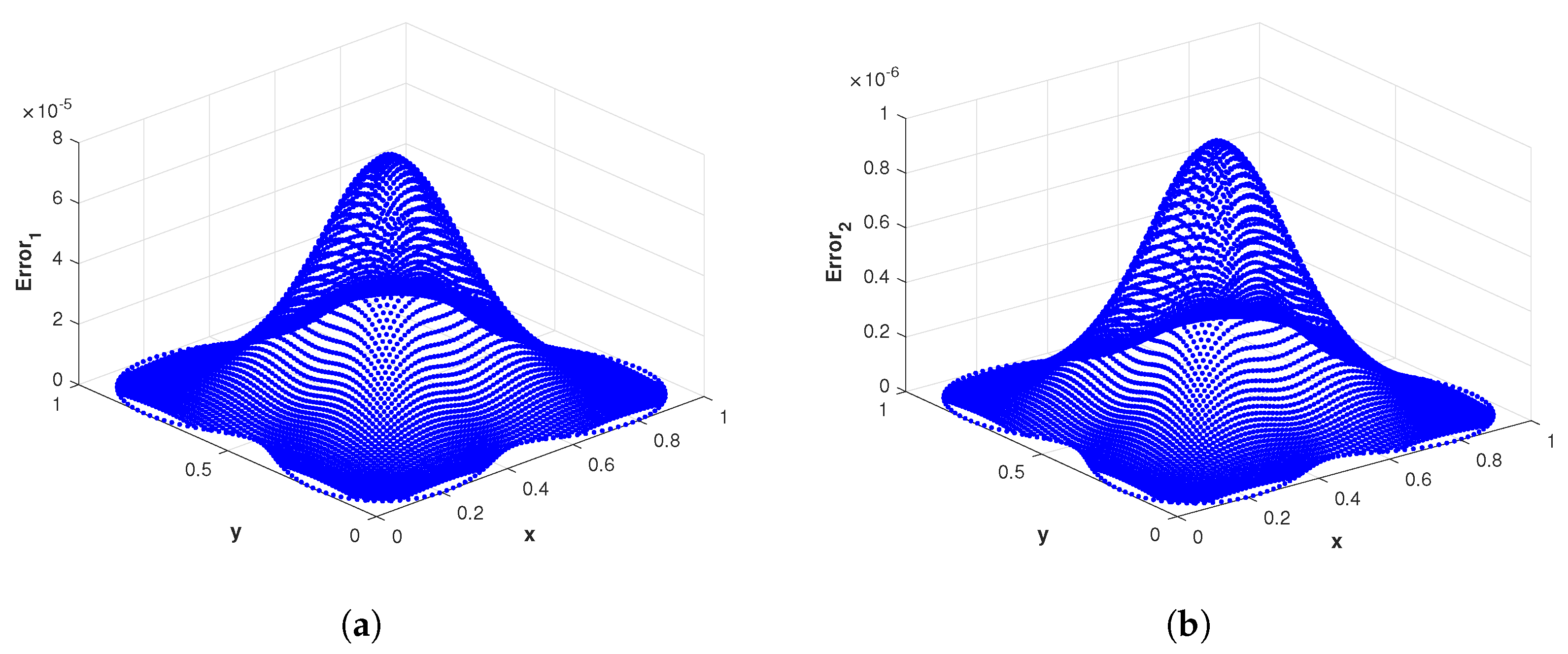
Figure 4.
(a) The surface plot of of the proposed method corresponding to problem 1 with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 1 with using MQ RBF.
Figure 4.
(a) The surface plot of of the proposed method corresponding to problem 1 with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 1 with using MQ RBF.
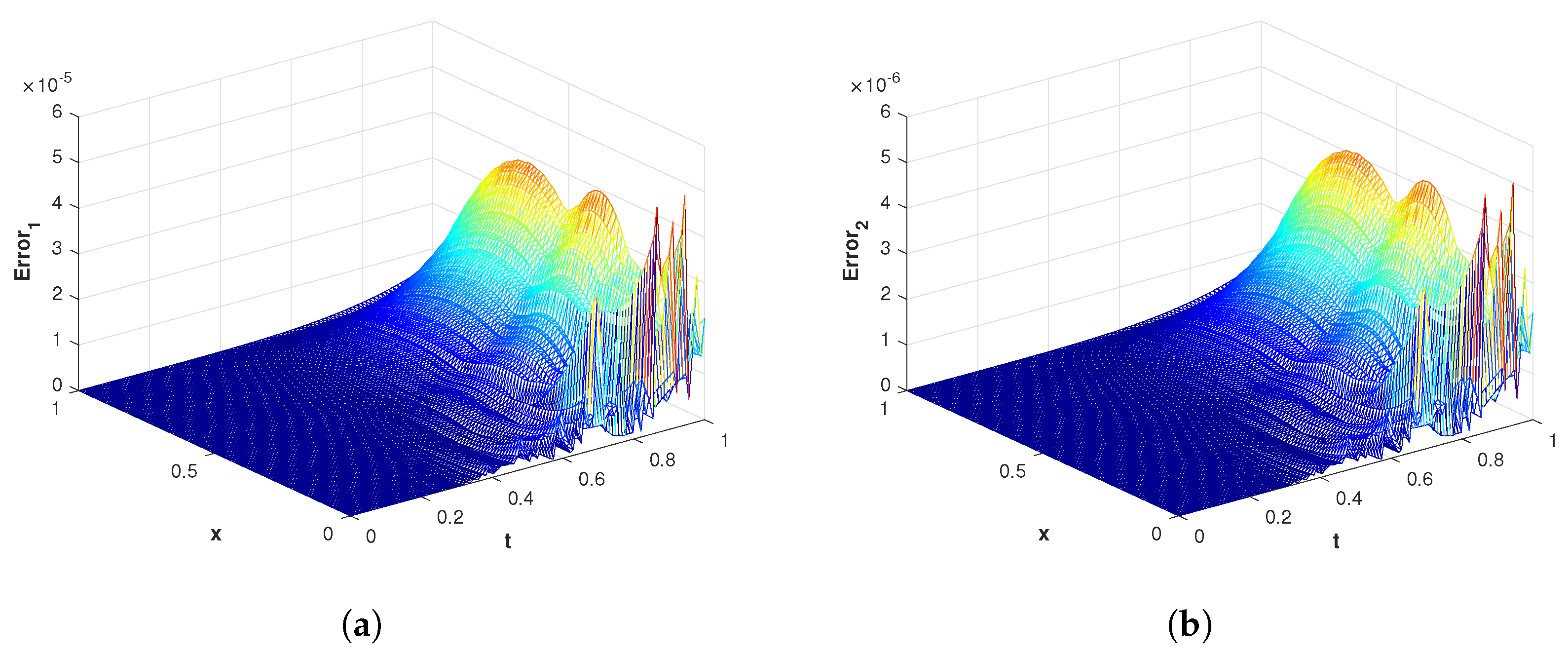
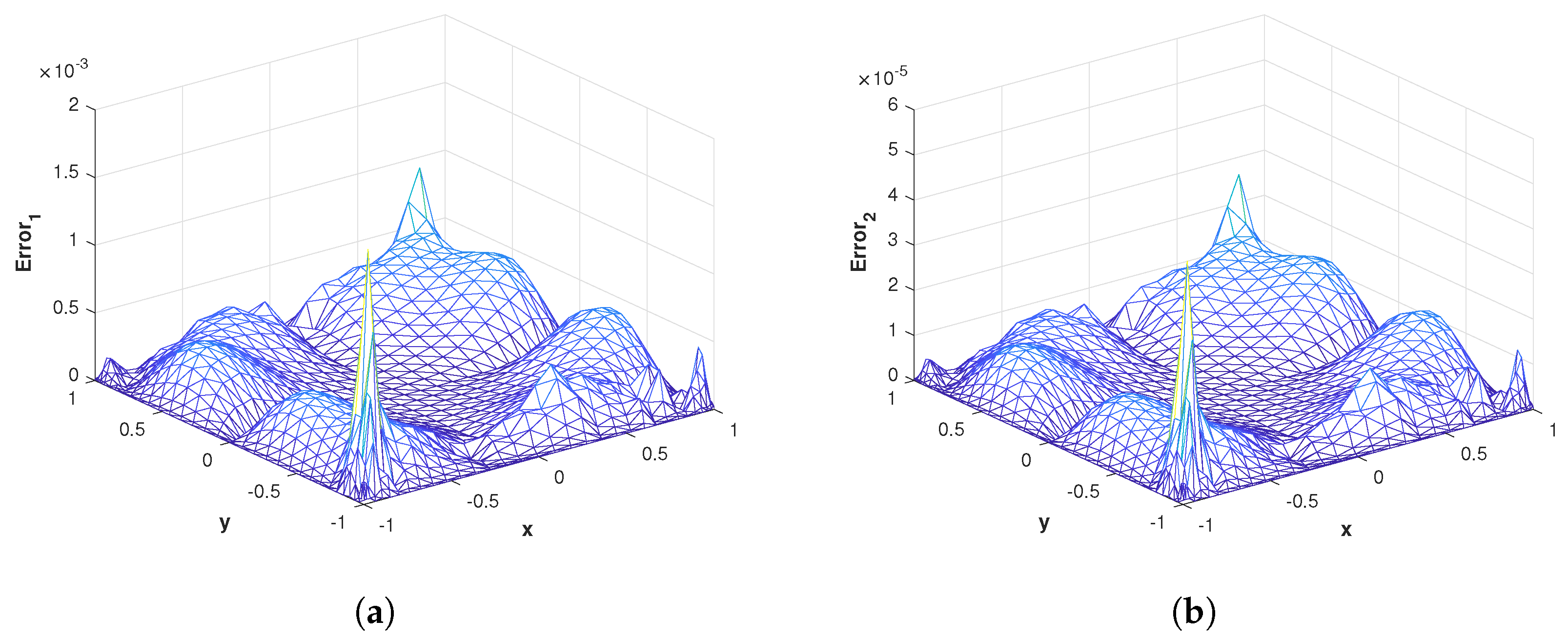
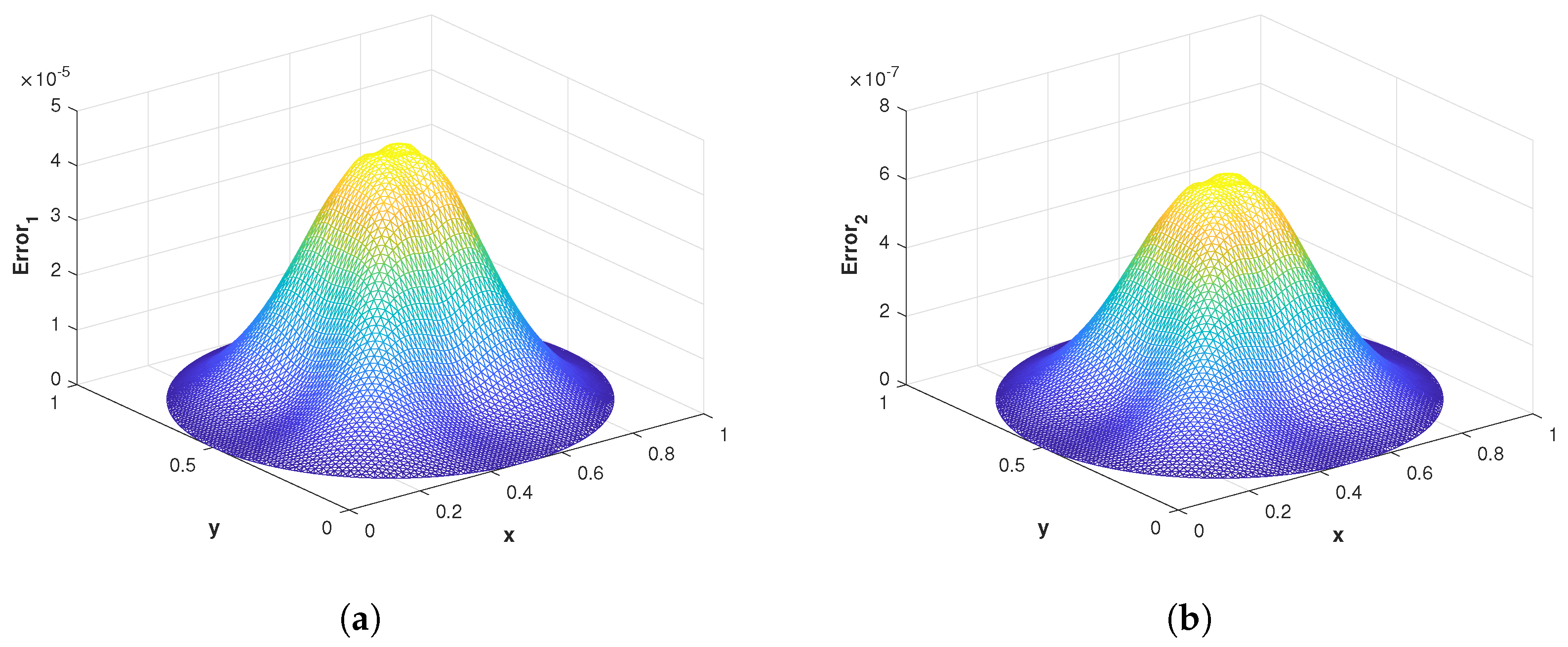
Figure 5.
(a) The mesh plot of of the proposed method corresponding to problem 1 with using GA RBF. (b) The mesh plot of of the proposed method corresponding to problem 1 with using GA RBF.
Figure 5.
(a) The mesh plot of of the proposed method corresponding to problem 1 with using GA RBF. (b) The mesh plot of of the proposed method corresponding to problem 1 with using GA RBF.
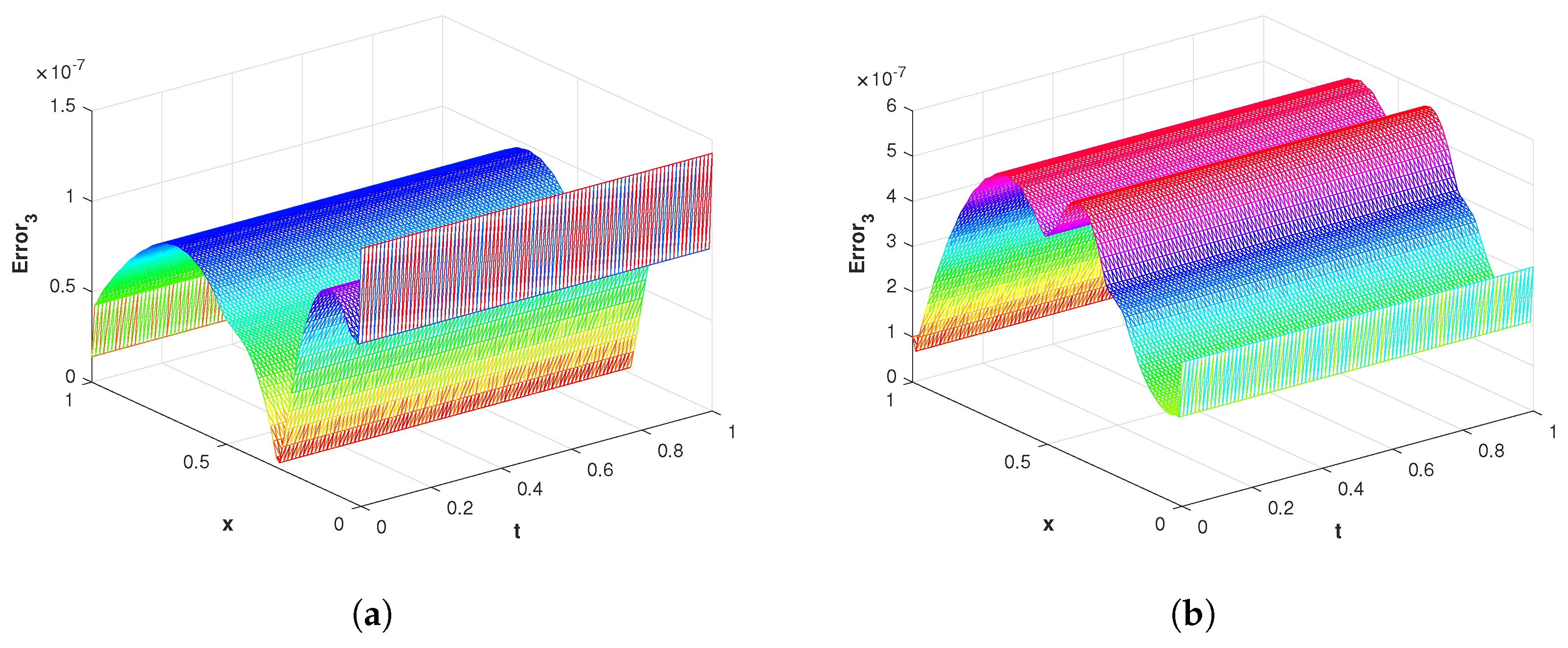
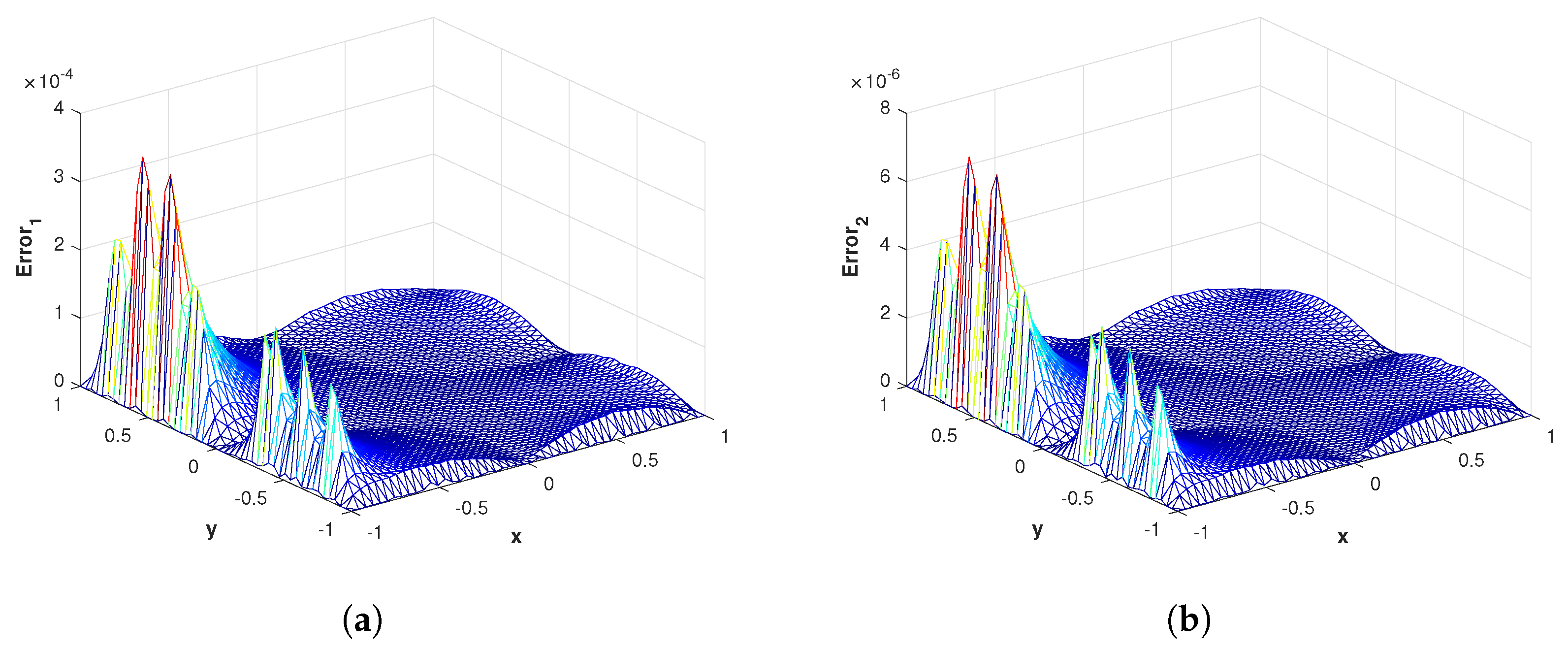
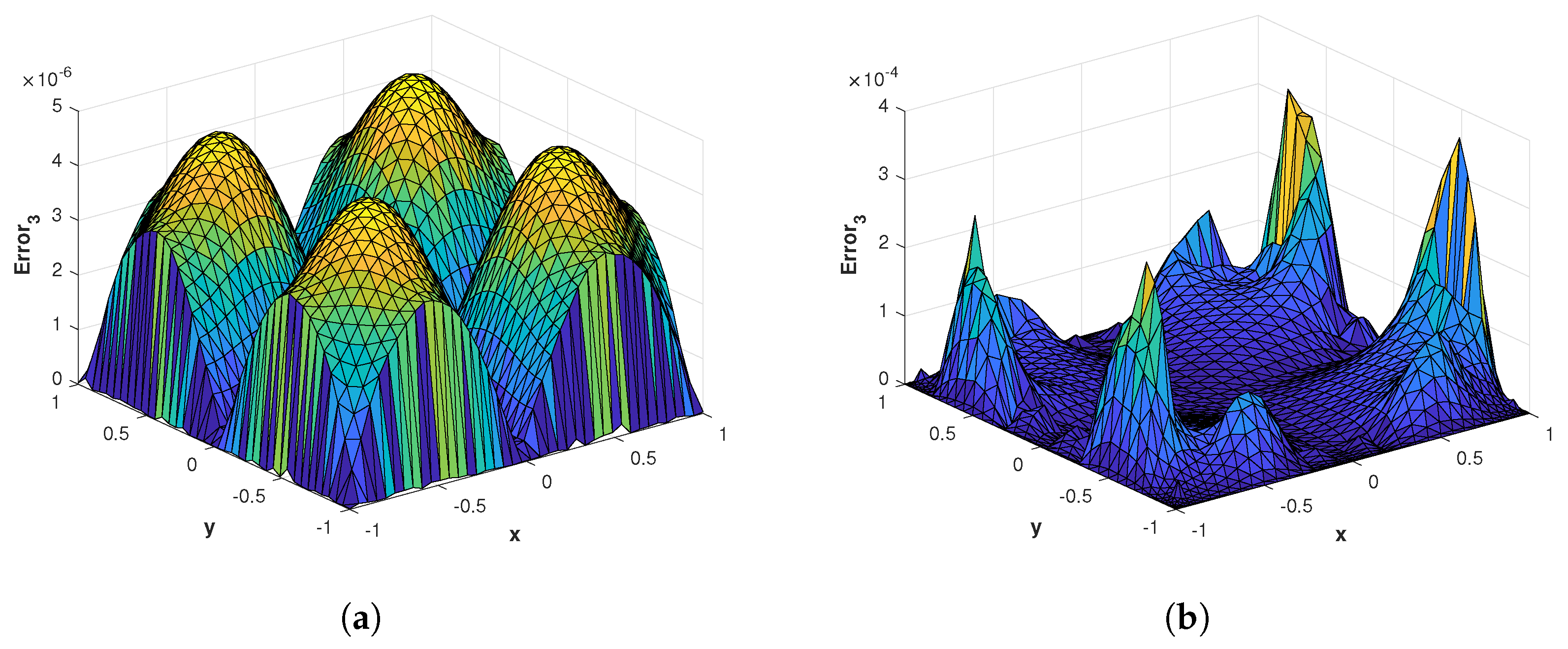
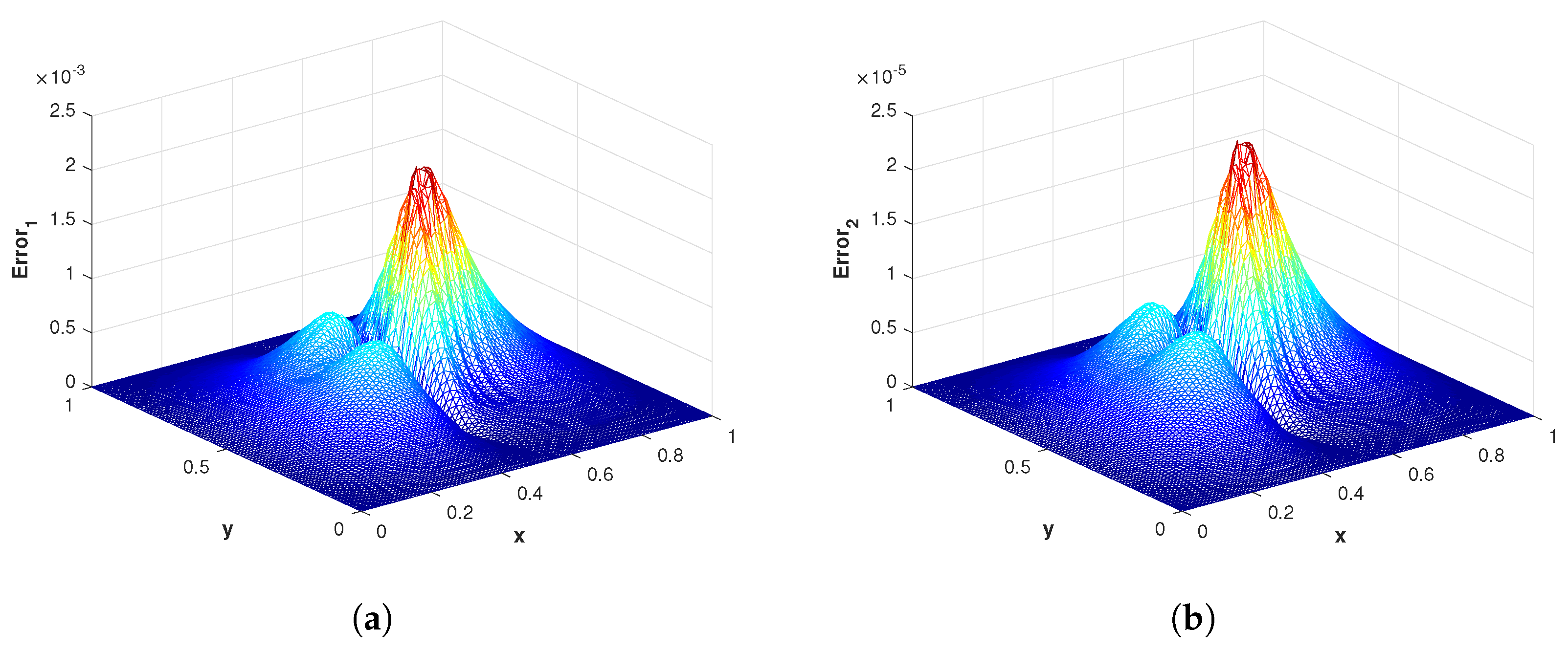
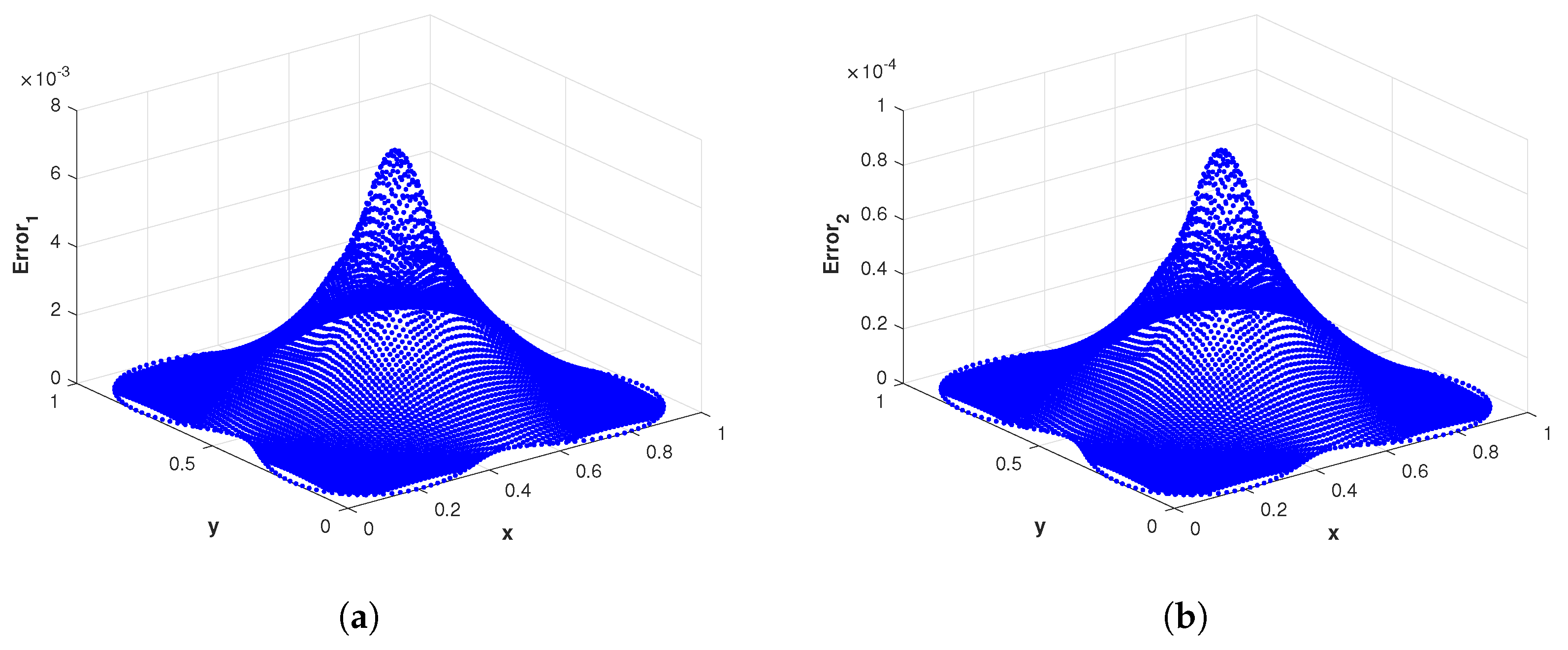
Figure 6.
(a) The surface plot of of the proposed method corresponding to problem 1 with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 1 with using GA RBF.
Figure 6.
(a) The surface plot of of the proposed method corresponding to problem 1 with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 1 with using GA RBF.
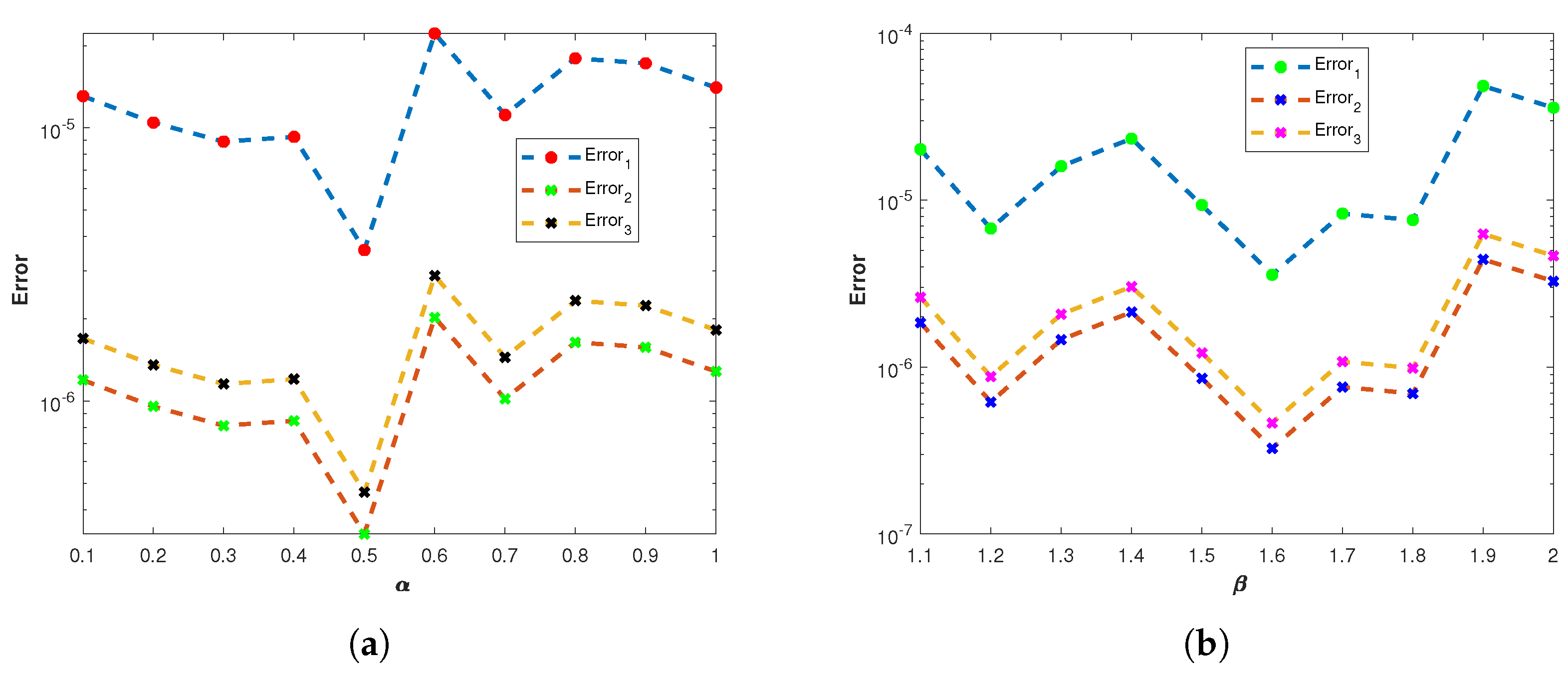
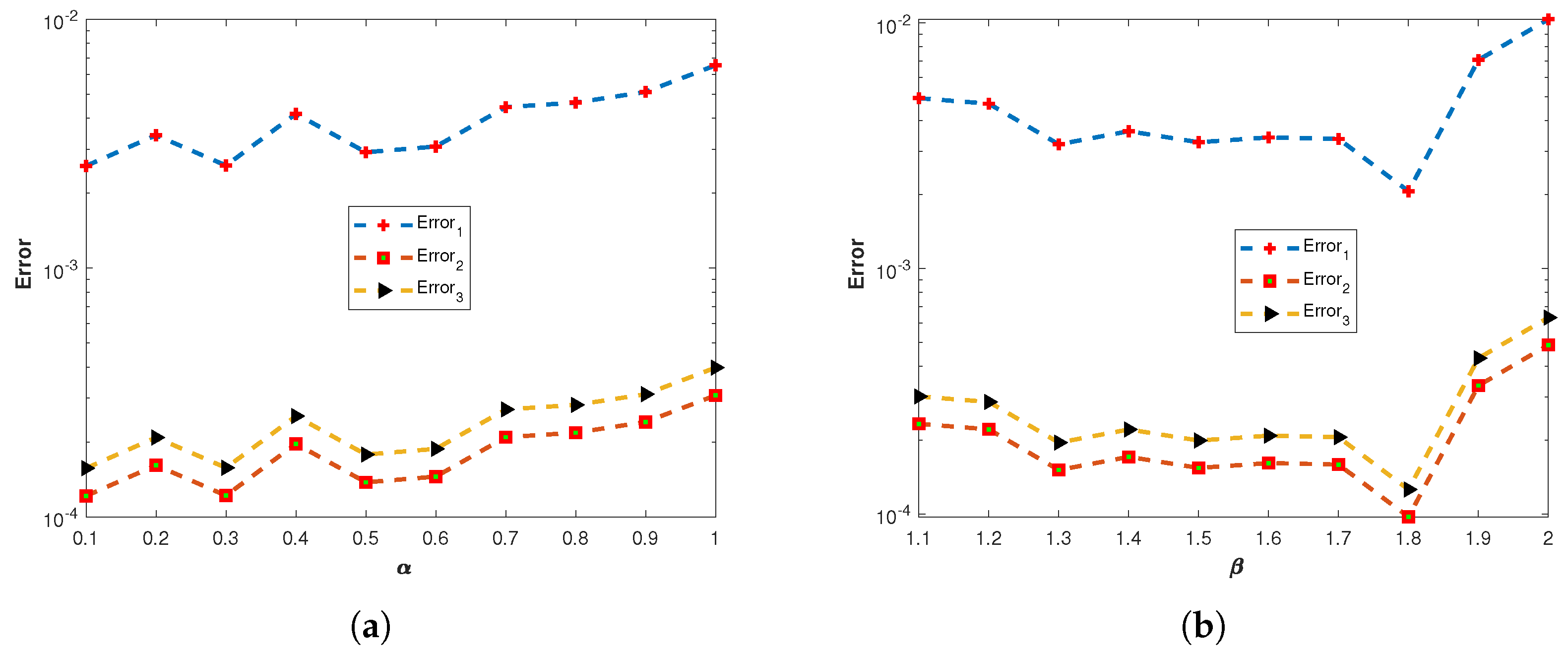
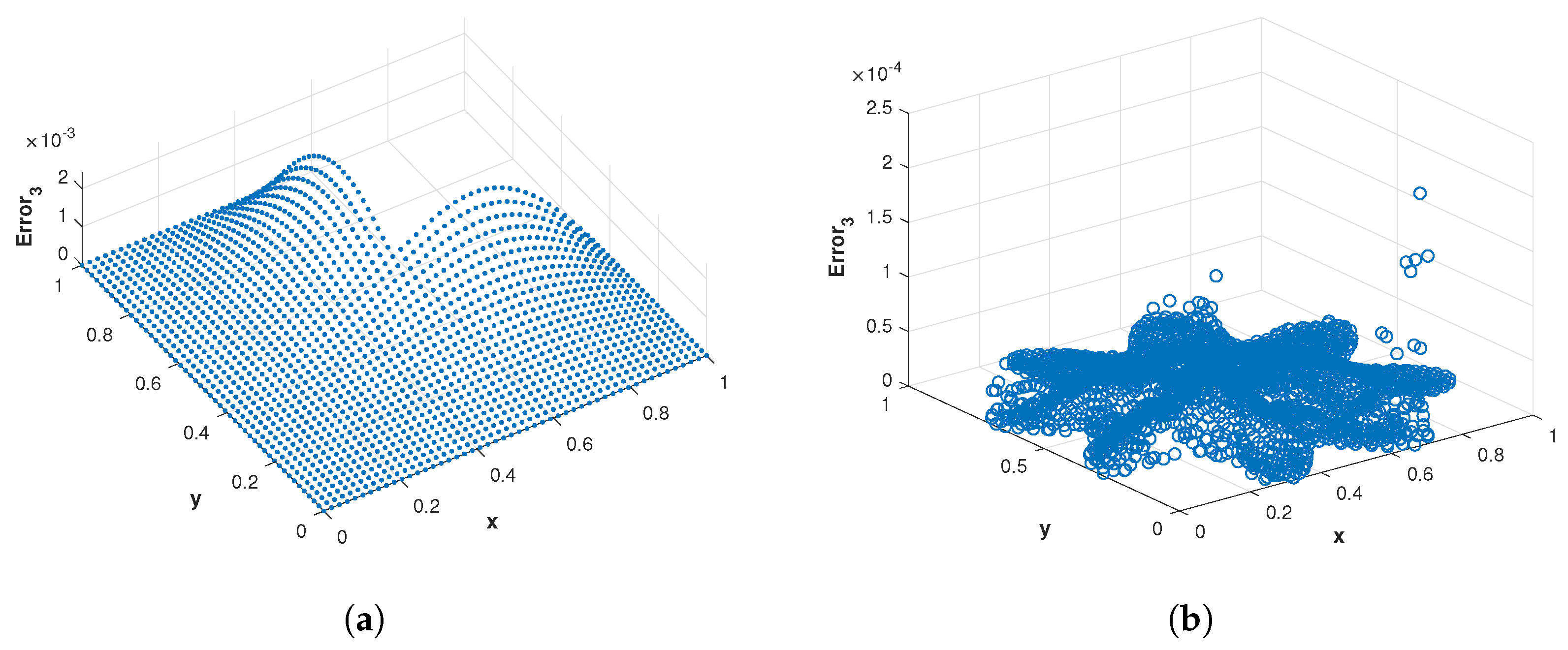
Figure 7.
(a) The plots of , , and of the proposed method corresponding to problem 1 with various values of and using the MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 1 with various values of and using the MQ RBF.
Figure 7.
(a) The plots of , , and of the proposed method corresponding to problem 1 with various values of and using the MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 1 with various values of and using the MQ RBF.
Figure 8.
(a) The plots of , , and of the proposed method corresponding to problem 1 with various values of and using the GA RBF. (b) The plots , , and of the proposed method corresponding to problem 1 with various values of and using the GA RBF.
Figure 8.
(a) The plots of , , and of the proposed method corresponding to problem 1 with various values of and using the GA RBF. (b) The plots , , and of the proposed method corresponding to problem 1 with various values of and using the GA RBF.
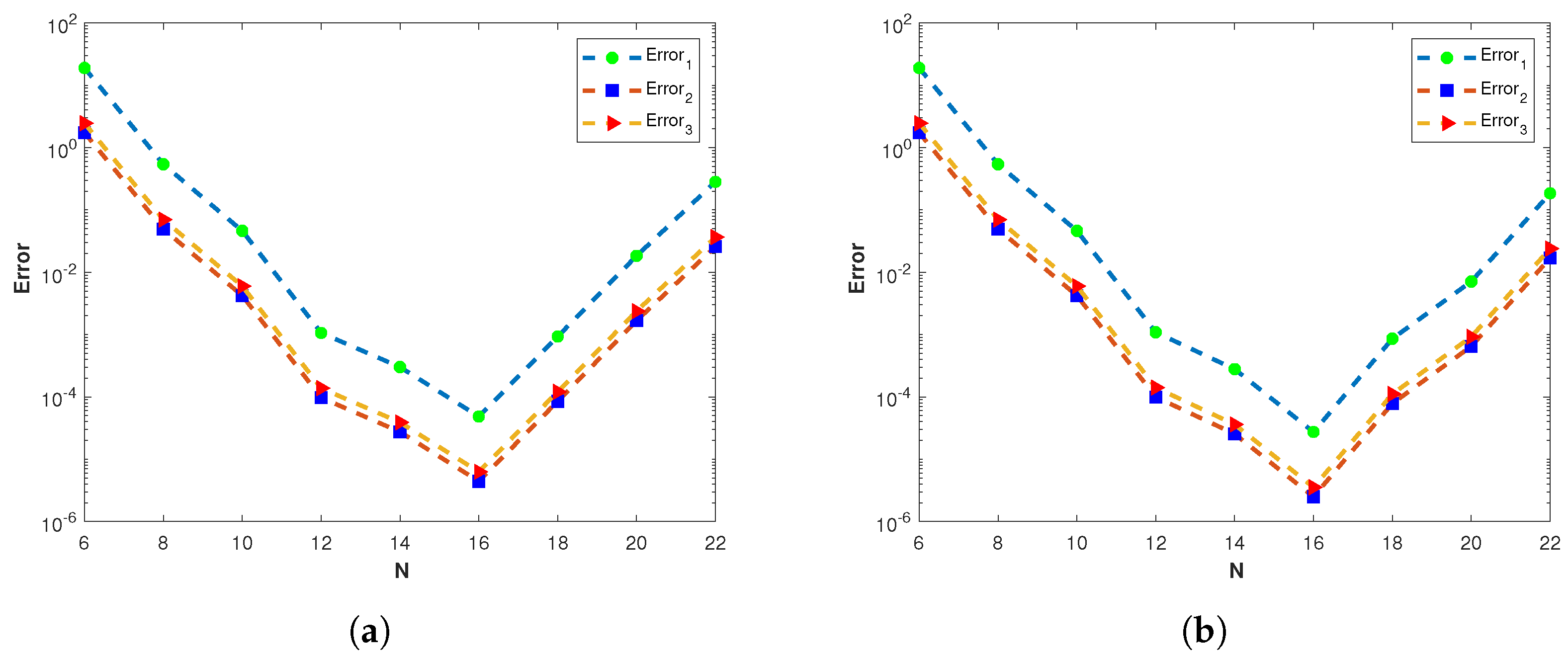
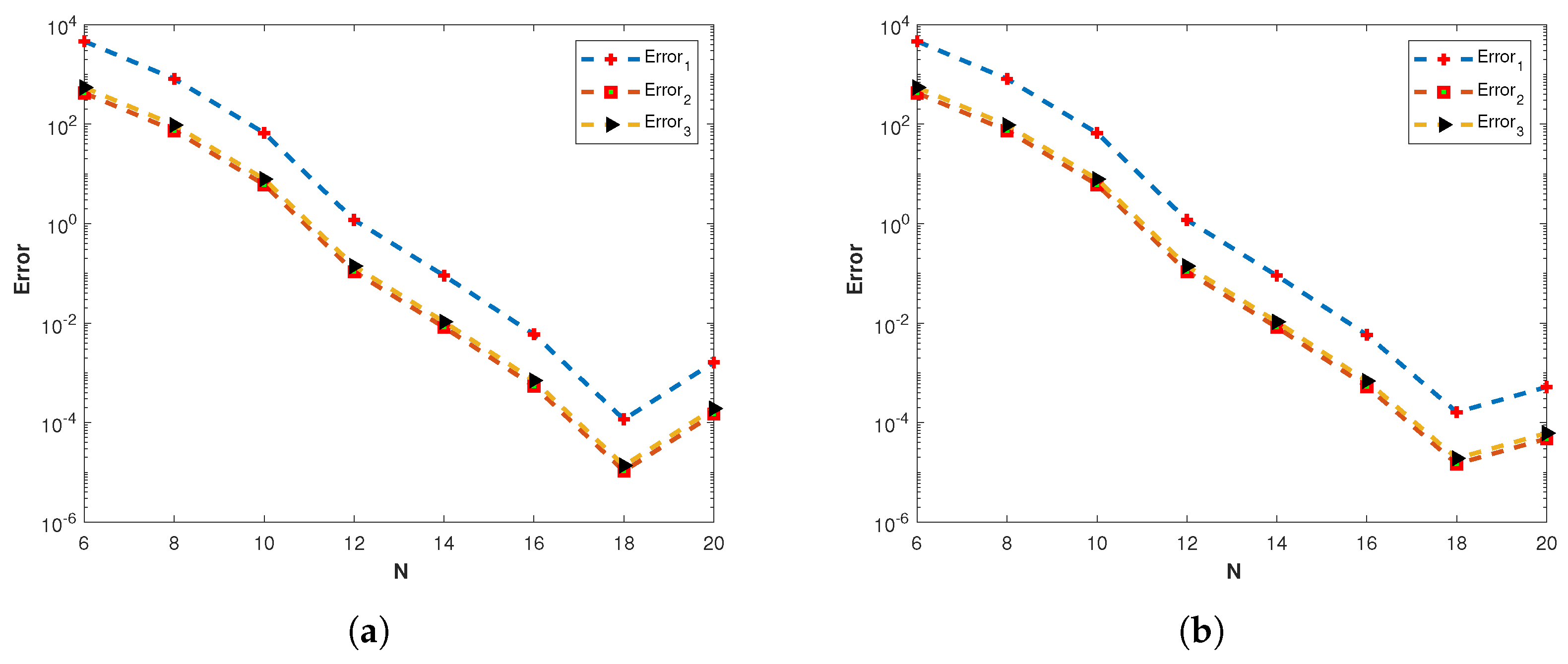
Figure 9.
(a) The plots of , , and of the proposed method corresponding to problem 1 with various values of N and using the MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 1 with various values of N and using the GA RBF.
Figure 9.
(a) The plots of , , and of the proposed method corresponding to problem 1 with various values of N and using the MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 1 with various values of N and using the GA RBF.
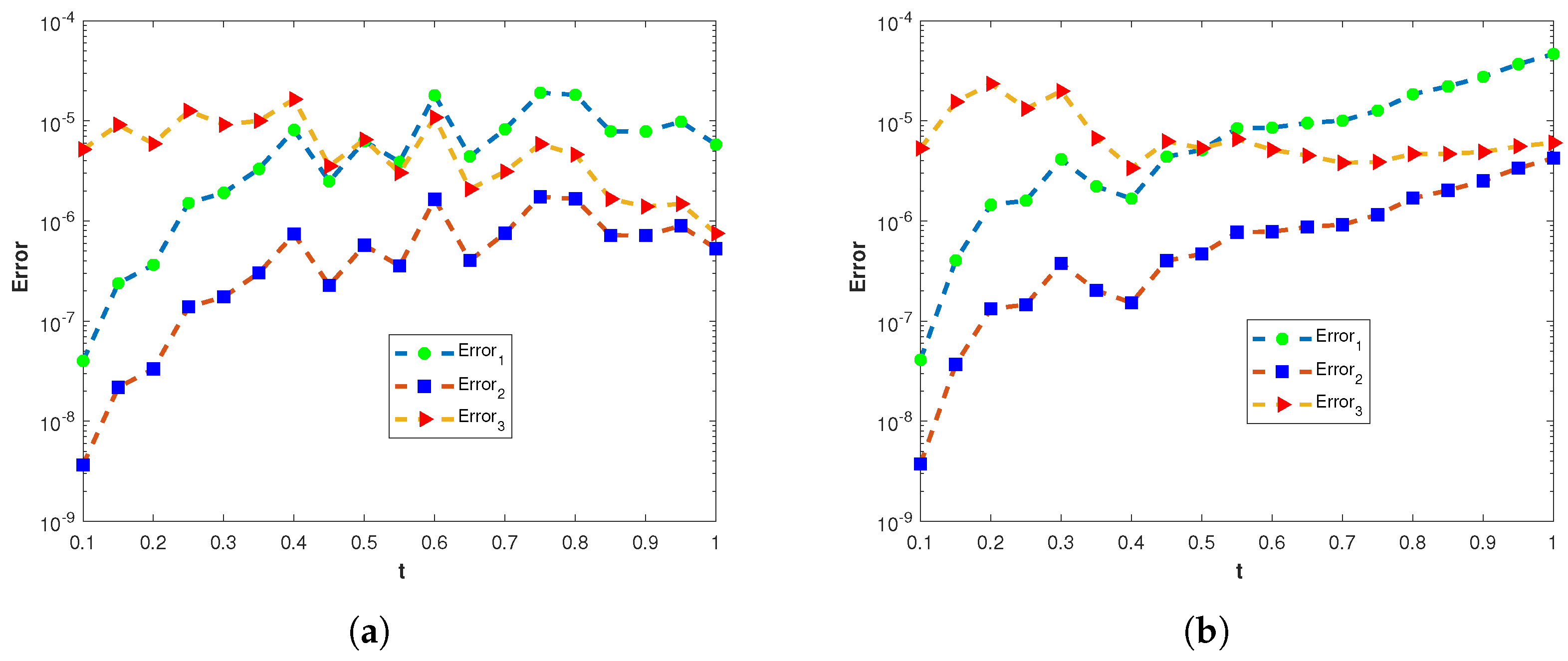
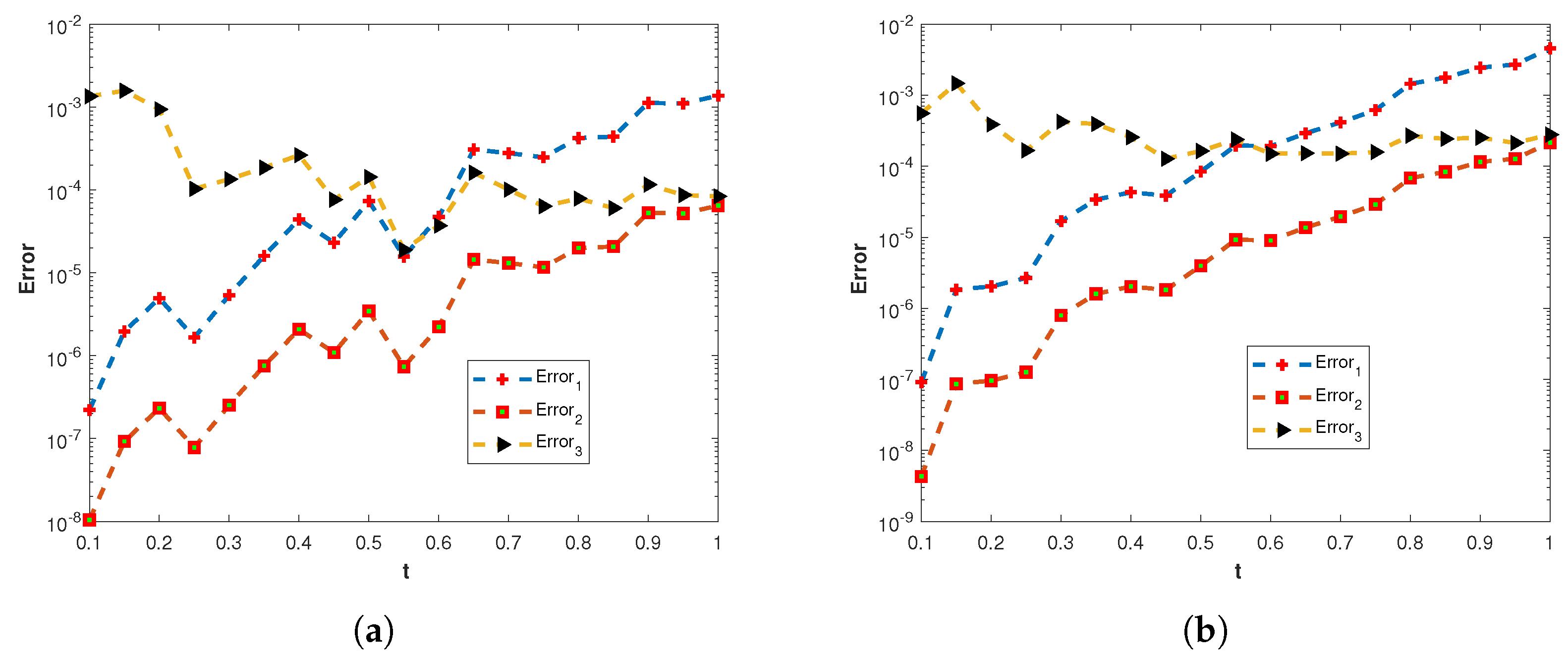
Figure 10.
(a) The plots of , , and of the proposed method corresponding to problem 1 with various values of t and using the MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 1 with various values of t and using the GA RBF.
Figure 10.
(a) The plots of , , and of the proposed method corresponding to problem 1 with various values of t and using the MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 1 with various values of t and using the GA RBF.
Figure 11.
(a) The numerical solution of problem 2 with (b) The exact solution of problem 2 with .
Figure 11.
(a) The numerical solution of problem 2 with (b) The exact solution of problem 2 with .
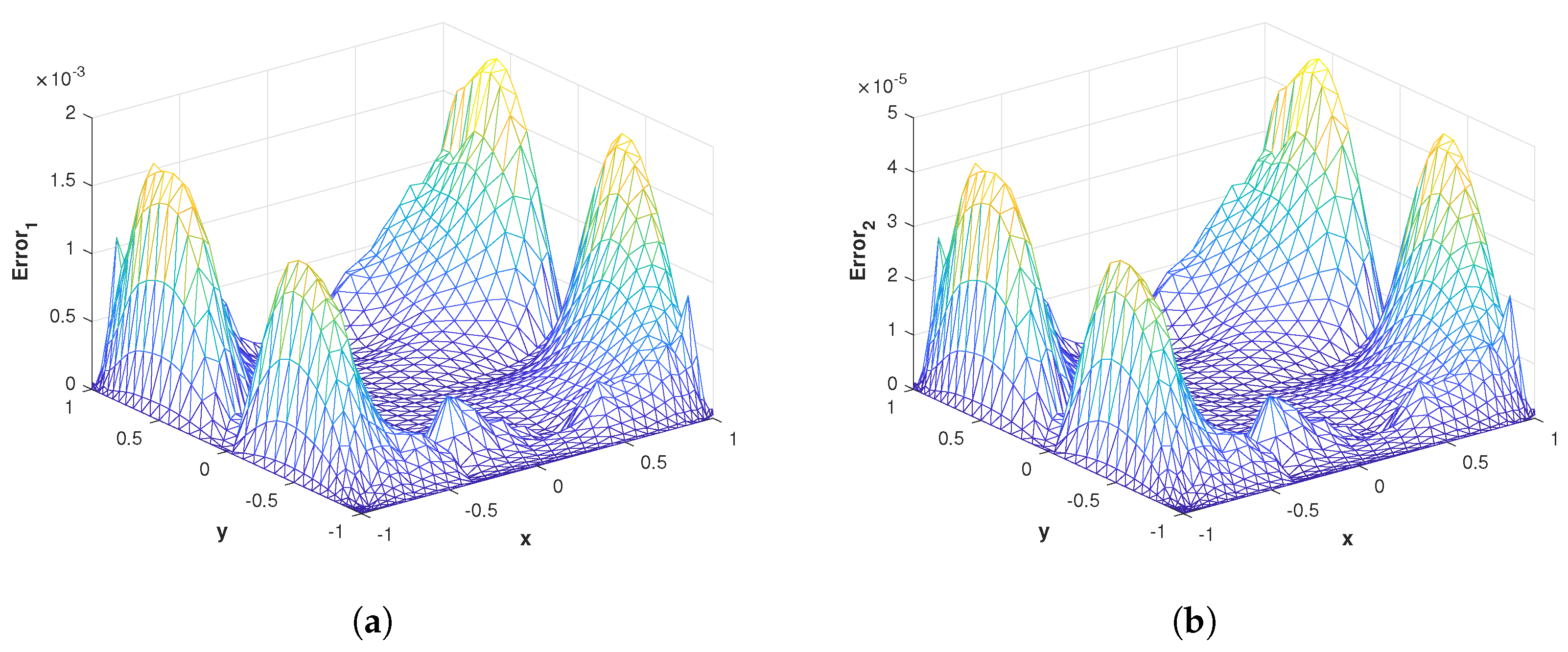
Figure 12.
(a) The surface plot of of the proposed method corresponding to problem 2 with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 2 with using MQ RBF.
Figure 12.
(a) The surface plot of of the proposed method corresponding to problem 2 with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 2 with using MQ RBF.
Figure 13.
(a) The mesh plot of of the proposed method corresponding to problem 2 with using GA RBF. (b) The mesh plot of of the proposed method corresponding to problem 2 with using GA RBF.
Figure 13.
(a) The mesh plot of of the proposed method corresponding to problem 2 with using GA RBF. (b) The mesh plot of of the proposed method corresponding to problem 2 with using GA RBF.
Figure 14.
(a) The surface plot of of the proposed method corresponding to problem 2 with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 2 with using GA RBF.
Figure 14.
(a) The surface plot of of the proposed method corresponding to problem 2 with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 2 with using GA RBF.
Figure 15.
(a) The plots of , , and of the proposed method corresponding to problem 2 with various values of and using MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 2 with various values of and using MQ RBF.
Figure 15.
(a) The plots of , , and of the proposed method corresponding to problem 2 with various values of and using MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 2 with various values of and using MQ RBF.
Figure 16.
(a) The plots of , , and of the proposed method corresponding to problem 2 with various values of and using GA RBF. (b) The plots , , and of the proposed method corresponding to problem 2 with various values of and using GA RBF.
Figure 16.
(a) The plots of , , and of the proposed method corresponding to problem 2 with various values of and using GA RBF. (b) The plots , , and of the proposed method corresponding to problem 2 with various values of and using GA RBF.
Figure 17.
(a) The plots of , , and of the proposed method corresponding to problem 2 with various values of N and using MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 2 with various values of N and using GA RBF.
Figure 17.
(a) The plots of , , and of the proposed method corresponding to problem 2 with various values of N and using MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 2 with various values of N and using GA RBF.
Figure 18.
(a) The plots of , , and of the proposed method corresponding to problem 2 with various values of t and using MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 2 with various values of t and using GA RBF.
Figure 18.
(a) The plots of , , and of the proposed method corresponding to problem 2 with various values of t and using MQ RBF. (b) The plots , , and of the proposed method corresponding to problem 2 with various values of t and using GA RBF.
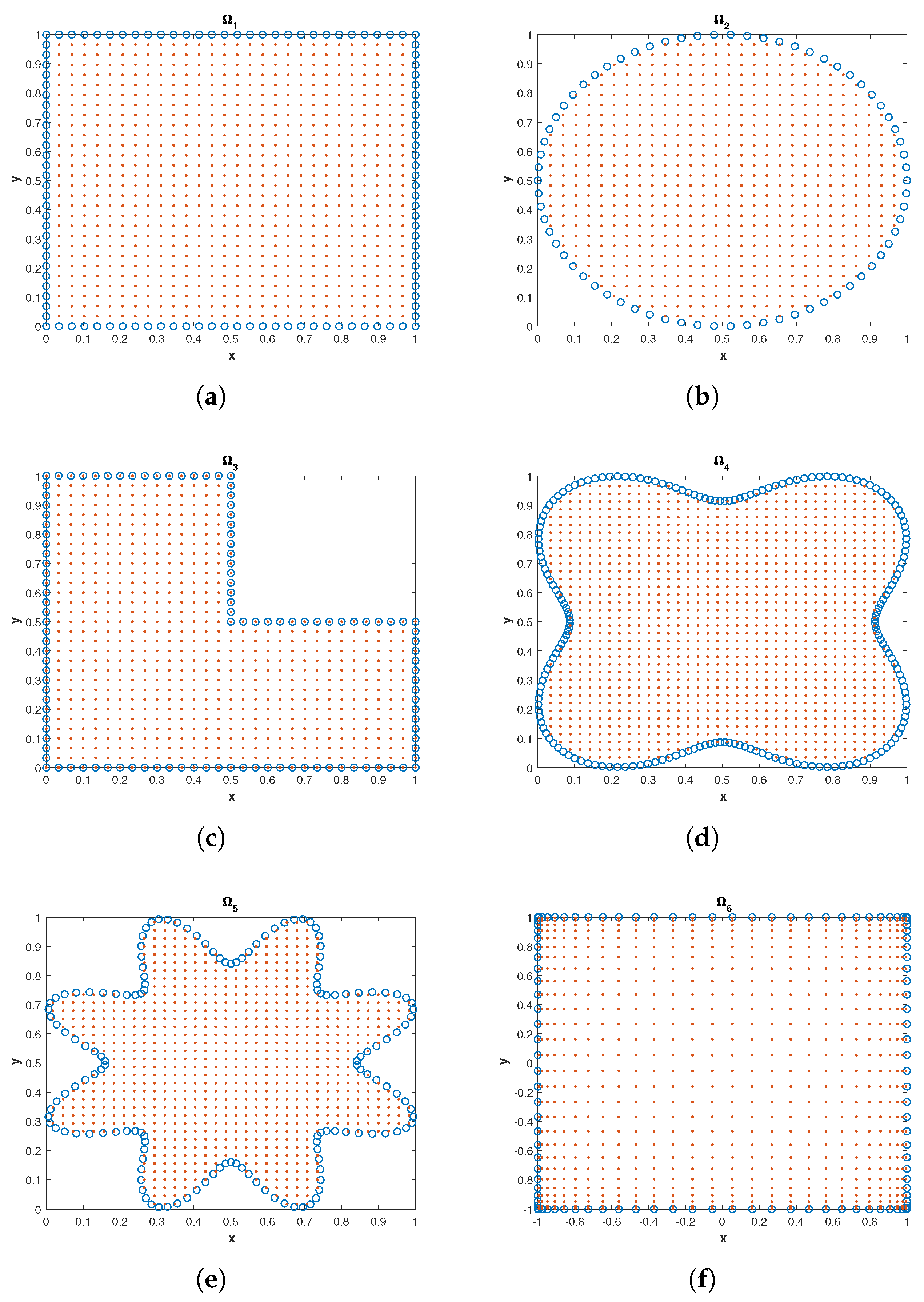
Figure 19.
(a) Uniform nodes distribution in the square domain; (b) Uniform nodes distribution in the circular domain; (c) Uniform nodes distribution in the L shaped domain; (d) Uniform nodes distribution in the nut shaped domain; (e) Uniform nodes distribution in the star shaped domain; (f) Chebyshev nodes distribution in the square domain.
Figure 19.
(a) Uniform nodes distribution in the square domain; (b) Uniform nodes distribution in the circular domain; (c) Uniform nodes distribution in the L shaped domain; (d) Uniform nodes distribution in the nut shaped domain; (e) Uniform nodes distribution in the star shaped domain; (f) Chebyshev nodes distribution in the square domain.
Figure 20.
(a) The numerical solution of problem 3 on (b) The exact solution of problem 3 on .
Figure 20.
(a) The numerical solution of problem 3 on (b) The exact solution of problem 3 on .
Figure 21.
(a) The mesh plot of of the proposed method corresponding to problem 3 using MQ RBF on with (b) The mesh plot of of the proposed method corresponding to problem 3 using MQ RBF on with .
Figure 21.
(a) The mesh plot of of the proposed method corresponding to problem 3 using MQ RBF on with (b) The mesh plot of of the proposed method corresponding to problem 3 using MQ RBF on with .
Figure 22.
(a) The mesh plot of of the proposed method corresponding to problem 3 using MQ RBF on with (b) The mesh plot of of the proposed method corresponding to problem 3 using MQ RBF on with .
Figure 22.
(a) The mesh plot of of the proposed method corresponding to problem 3 using MQ RBF on with (b) The mesh plot of of the proposed method corresponding to problem 3 using MQ RBF on with .
Figure 23.
(a) The mesh plot of of the proposed method corresponding to problem 3 using GA RBF on with (b) The mesh plot of of the proposed method corresponding to problem 3 using GA RBF on with .
Figure 23.
(a) The mesh plot of of the proposed method corresponding to problem 3 using GA RBF on with (b) The mesh plot of of the proposed method corresponding to problem 3 using GA RBF on with .
Figure 24.
(a) The mesh plot of of the proposed method corresponding to problem 3 using GA RBF on with (b) The mesh plot of of the proposed method corresponding to problem 3 using GA RBF on with .
Figure 24.
(a) The mesh plot of of the proposed method corresponding to problem 3 using GA RBF on with (b) The mesh plot of of the proposed method corresponding to problem 3 using GA RBF on with .
Figure 25.
(a) The surface plot of of the proposed method corresponding to problem 3 using MQ RBF on with (b) The surface plot of of the proposed method corresponding to problem 3 using GA RBF on with .
Figure 25.
(a) The surface plot of of the proposed method corresponding to problem 3 using MQ RBF on with (b) The surface plot of of the proposed method corresponding to problem 3 using GA RBF on with .
Figure 26.
(a) The numerical solution of problem 4 on (b) The exact solution of problem 4 on .
Figure 26.
(a) The numerical solution of problem 4 on (b) The exact solution of problem 4 on .
Figure 27.
(a) The surface plot of of the proposed method corresponding to problem 4 using MQ RBF on with (b) The surface plot of of the proposed method corresponding to problem 4 using MQ RBF on with .
Figure 27.
(a) The surface plot of of the proposed method corresponding to problem 4 using MQ RBF on with (b) The surface plot of of the proposed method corresponding to problem 4 using MQ RBF on with .
Figure 28.
(a) The surface plot of of the proposed method corresponding to problem 4 using GA RBF on with (b) The surface plot of of the proposed method corresponding to problem 4 using GA RBF on with .
Figure 28.
(a) The surface plot of of the proposed method corresponding to problem 4 using GA RBF on with (b) The surface plot of of the proposed method corresponding to problem 4 using GA RBF on with .
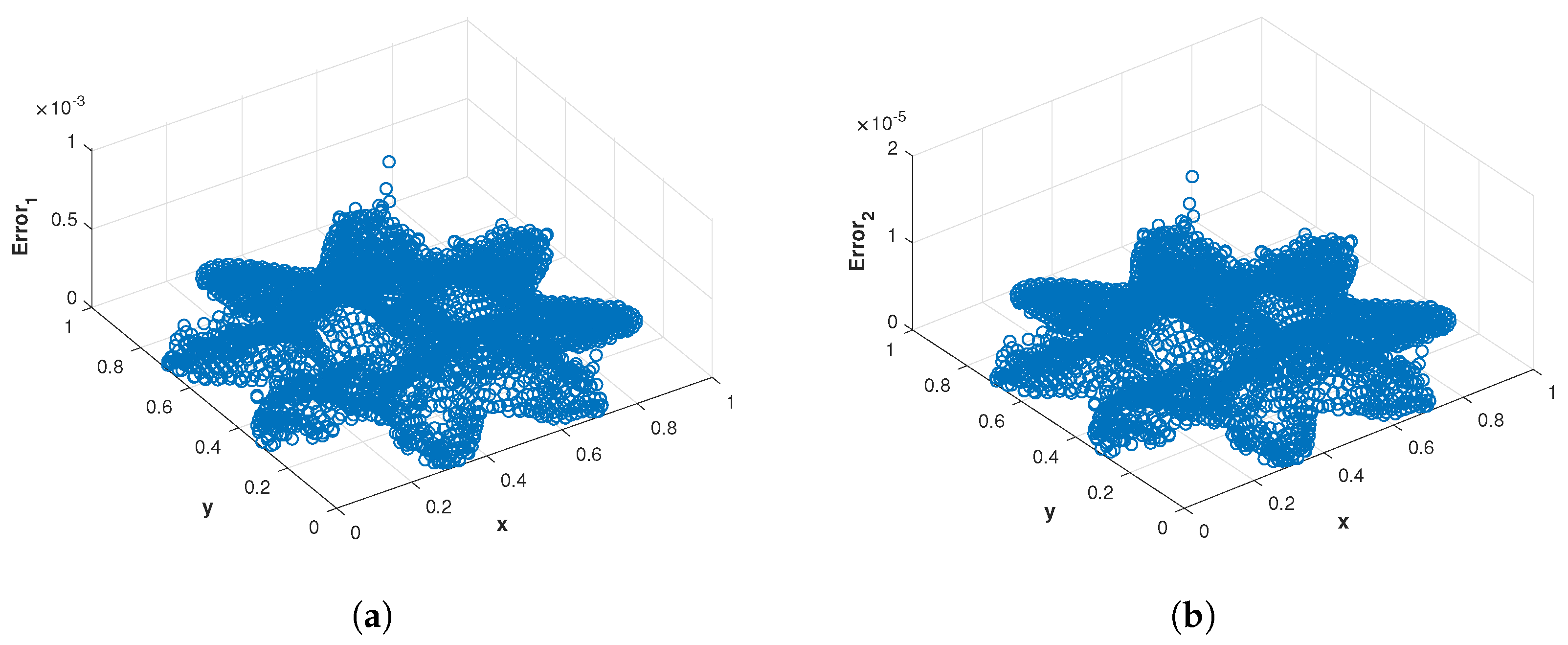
Figure 29.
(a) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with .
Figure 29.
(a) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with .
Figure 30.
(a) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with .
Figure 30.
(a) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with .
Figure 31.
(a) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with .
Figure 31.
(a) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with .
Figure 32.
(a) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with .
Figure 32.
(a) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with .
Figure 33.
(a) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with .
Figure 33.
(a) The scatter plot of of the proposed method corresponding to problem 4 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 4 using GA RBF on with .
Figure 34.
(a) The numerical solution of problem 5 on domain . (b) The exact solution of problem 5 on domain .
Figure 34.
(a) The numerical solution of problem 5 on domain . (b) The exact solution of problem 5 on domain .
Figure 35.
(a) The surface plot of of the proposed method corresponding to problem 5 on with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 5 on with using MQ RBF.
Figure 35.
(a) The surface plot of of the proposed method corresponding to problem 5 on with using MQ RBF. (b) The surface plot of of the proposed method corresponding to problem 5 on with using MQ RBF.
Figure 36.
(a) The surface plot of of the proposed method corresponding to problem 5 using GA RBF on domain with (b) The surface plot of of the proposed method corresponding to problem 5 using GA RBF on domain with .
Figure 36.
(a) The surface plot of of the proposed method corresponding to problem 5 using GA RBF on domain with (b) The surface plot of of the proposed method corresponding to problem 5 using GA RBF on domain with .
Figure 37.
(a) The mesh plot of of the proposed method corresponding to problem 5 using MQ RBF on with (b) The mesh plot of of the proposed method corresponding to problem 5 using MQ RBF on with .
Figure 37.
(a) The mesh plot of of the proposed method corresponding to problem 5 using MQ RBF on with (b) The mesh plot of of the proposed method corresponding to problem 5 using MQ RBF on with .
Figure 38.
(a) The mesh plot of of the proposed method corresponding to problem 5 using GA RBF on with (b) The mesh plot of of the proposed method corresponding to problem 5 using GA RBF on with .
Figure 38.
(a) The mesh plot of of the proposed method corresponding to problem 5 using GA RBF on with (b) The mesh plot of of the proposed method corresponding to problem 5 using GA RBF on with .
Figure 39.
(a) The scatter plot of of the proposed method corresponding to problem 5 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 5 using MQ RBF on with .
Figure 39.
(a) The scatter plot of of the proposed method corresponding to problem 5 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 5 using MQ RBF on with .
Figure 40.
(a) The scatter plot of of the proposed method corresponding to problem 5 using GA RBF on with (b) The scatter plot of of the proposed method corresponding to problem 5 using GA RBF on with .
Figure 40.
(a) The scatter plot of of the proposed method corresponding to problem 5 using GA RBF on with (b) The scatter plot of of the proposed method corresponding to problem 5 using GA RBF on with .
Figure 41.
(a) The mesh plot of of the proposed method corresponding to problem 5 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 5 using GA RBF on with .
Figure 41.
(a) The mesh plot of of the proposed method corresponding to problem 5 using MQ RBF on with (b) The scatter plot of of the proposed method corresponding to problem 5 using GA RBF on with .
Table 1.
Different types of finite and infinite smooth RBFs.
Table 1.
Different types of finite and infinite smooth RBFs.
| Multiquadric (MQ) | |
| Inverse multiquadric (IMQ) | |
| Gaussian (GA) | |
| Wendlan | , is a polynomial, |
| Duchon spline | |
| Thin Plate Spline (TPS) | , |
Table 2.
The errors obtained using the proposed method for problem 1 using MQ RBF.
Table 2.
The errors obtained using the proposed method for problem 1 using MQ RBF.
| | | N | | | | C.Time(s) |
|---|
| | 95 | 10 | 16 | 2.72 × | 2.79 × | 3.97 × | 0.132263 |
| | | 15 | | 8.99 × | 9.22 × | 1.31 × | 0.183286 |
| | | 20 | | 7.34 × | 7.53 × | 1.07 × | 0.228481 |
| | | 22 | | 6.32 × | 6.48 × | 9.22 × | 0.258556 |
| | 120 | 21 | 12 | 9.12 × | 8.32 × | 1.18 × | 0.242945 |
| | | | 14 | 4.59 × | 4.19 × | 5.95 × | 0.248445 |
| | | | 16 | 1.74 × | 1.59 × | 2.26 × | 0.238210 |
| | | | 18 | 8.95 × | 8.17 × | 1.16 × | 0.237966 |
| | 82 | 21 | 16 | 9.20 × | 1.01 × | 1.44 × | 0.226662 |
| | 85 | | | 8.70 × | 9.44 × | 1.34 × | 0.227972 |
| | 88 | | | 7.08 × | 7.55 × | 1.07 × | 0.234824 |
| | 95 | | | 6.88 × | 7.06 × | 1.00 × | 0.239582 |
| [32] | | | | 1.69 × | | | |
Table 3.
The errors obtained using the proposed method for problem 1 using GA RBF.
Table 3.
The errors obtained using the proposed method for problem 1 using GA RBF.
| | | N | | | | C.Time(s) |
|---|
| | 115 | 10 | 12 | 9.86 × | 9.19 × | 1.30 × | 0.188929 |
| | 125 | | | 6.69 × | 5.98 × | 8.50 × | 0.185436 |
| | 130 | | | 5.69 × | 4.99 × | 7.09 × | 0.223009 |
| | 135 | | | 4.92 × | 4.23 × | 6.01 × | 0.213365 |
| | 95 | 8 | 12 | 7.69 × | 7.89 × | 1.12 × | 0.173427 |
| | | 13 | | 3.06 × | 3.14 × | 4.47 × | 0.220220 |
| | | 14 | | 2.92 × | 3.00 × | 4.27 × | 0.202532 |
| | | 15 | | 1.08 × | 1.11 × | 1.58 × | 0.196352 |
| | 74 | 10 | 12 | 6.84 × | 7.95 × | 1.13 × | 0.102373 |
| | | | 14 | 4.09 × | 4.75 × | 6.77 × | 0.136801 |
| | | | 16 | 2.01 × | 2.33 × | 3.33 × | 0.129105 |
| | | | 18 | 1.73 × | 2.01 × | 2.87 × | 0.148823 |
| [32] | | | | 9.47 × | | | |
Table 4.
The errors obtained using the proposed method for problem 2 using MQ RBF.
Table 4.
The errors obtained using the proposed method for problem 2 using MQ RBF.
| | | N | | | | C.Time(s) |
|---|
| | 120 | 15 | 18 | 3.76 × | 3.44 × | 4.45 × | 0.203494 |
| | | 16 | | 3.34 × | 3.05 × | 3.95 × | 0.216352 |
| | | 17 | | 1.65 × | 1.51 × | 1.95 × | 0.198863 |
| | | 18 | | 1.15 × | 1.05 × | 1.36 × | 0.259377 |
| | 90 | 16 | 14 | 9.20 × | 9.64 × | 1.20 × | 0.193569 |
| | | | 16 | 2.10 × | 2.22 × | 2.87 × | 0.199498 |
| | | | 18 | 2.65 × | 2.79 × | 3.62 × | 0.188744 |
| | | | 20 | 1.98 × | 2.08 × | 2.70 × | 0.202167 |
| | 110 | 18 | 18 | 2.38 × | 2.27 × | 2.94 × | 0.232646 |
| | 112 | | | 9.76 × | 9.22 × | 1.19 × | 0.228243 |
| | 115 | | | 9.75 × | 9.09 × | 1.17 × | 0.223190 |
| | 116 | | | 4.45 × | 4.13 × | 5.34 × | 0.233154 |
| [32] | | | | 4.38 × | | | |
Table 5.
The errors obtained using the proposed method for problem 2 using GA RBF.
Table 5.
The errors obtained using the proposed method for problem 2 using GA RBF.
| | | N | | | | C.Time(s) |
|---|
| | 80 | 11 | 18 | 3.42 × | 3.83 × | 4.95 × | 0.147621 |
| | 90 | | | 2.53 × | 2.66 × | 3.44 × | 0.148642 |
| | 100 | | | 1.26 × | 1.26 × | 1.63 × | 0.161187 |
| | 101 | | | 8.43 × | 8.39 × | 1.08 × | 0.156145 |
| | 99 | 10 | 14 | 9.20 × | 9.87 × | 1.30 × | 0.206573 |
| | | | 16 | 2.40 × | 2.46 × | 3.18 × | 0.272171 |
| | | | 18 | 5.02 × | 5.05 × | 6.53 × | 0.225353 |
| | | | 20 | 4.87 × | 4.90 × | 6.33 × | 0.247079 |
| | 95 | 10 | 18 | 4.94 × | 5.07 × | 6.56 × | 0.205846 |
| | | 11 | | 4.22 × | 4.33 × | 5.60 × | 0.200952 |
| | | 12 | | 3.22 × | 3.30 × | 4.27 × | 0.216622 |
| | | 15 | | 2.33 × | 2.39 × | 3.09 × | 0.201578 |
| [32] | | | | 5.72 × | | | |
Table 6.
The errors obtained using the proposed method for problem 3 on domain using MQ RBF.
Table 6.
The errors obtained using the proposed method for problem 3 on domain using MQ RBF.
| | | N | | | | C.Time(s) |
|---|
| | 4624 | 13 | 14 | 1.27 × | 1.86 × | 3.78 × | 28.244165 |
| | | | 16 | 9.32 × | 1.37 × | 2.78 × | 21.367193 |
| | | | 18 | 3.91 × | 5.75 × | 1.16 × | 25.048697 |
| | | | 20 | 3.62 × | 5.33 × | 1.08 × | 25.466929 |
| | 4225 | 13 | 16 | 1.20 × | 1.82 × | 3.71 × | 24.562205 |
| | | 14 | | 9.56 × | 1.47 × | 2.99 × | 25.343475 |
| | | 15 | | 4.42 × | 6.80 × | 1.38 × | 25.994300 |
| | | 17 | | 4.16 × | 6.40 × | 1.30 × | 26.284367 |
| | 4096 | 16 | 16 | 5.86 × | 9.16 × | 1.86 × | 26.098623 |
| | 4356 | | | 5.84 × | 8.85 × | 1.79 × | 27.673088 |
| | 4761 | | | 5.51 × | 7.99 × | 1.62 × | 31.860493 |
| | 4900 | | | 5.30 × | 7.58 × | 1.53 × | 37.681474 |
| [32] | | | | 1.44 × | | | |
Table 7.
The errors obtained using the proposed method for problem 3 on domain using GA RBF.
Table 7.
The errors obtained using the proposed method for problem 3 on domain using GA RBF.
| | | N | | | | C.Time(s) |
|---|
| | 1600 | 15 | 16 | 6.10 × | 1.51 × | 3.98 × | 10.247910 |
| | | | 18 | 5.90 × | 1.47 × | 3.87 × | 10.275675 |
| | | | 20 | 5.80 × | 1.45 × | 3.83 × | 10.530108 |
| | | | 22 | 5.70 × | 1.43 × | 3.78 × | 13.210822 |
| | 1521 | 13 | 16 | 8.00 × | 2.04 × | 5.38 × | 6.366293 |
| | | 14 | | 6.30 × | 1.61 × | 4.25 × | 6.503034 |
| | | 15 | | 6.20 × | 1.59 × | 4.18 × | 7.186865 |
| | | 18 | | 6.18 × | 1.58 × | 4.17 × | 8.509750 |
| | 1600 | 13 | 18 | 8.30 × | 2.08 × | 5.48 × | 7.300554 |
| | 1764 | | | 6.80 × | 1.62 × | 4.26 × | 8.319459 |
| | 1936 | | | 6.60 × | 1.49 × | 3.91 × | 9.356419 |
| | 2401 | | | 6.30 × | 1.28 × | 3.36 × | 12.664379 |
| [32] | | | | 1.98 × | | | |
Table 8.
The errors obtained using the proposed method for problem 4 on domain using MQ RBF.
Table 8.
The errors obtained using the proposed method for problem 4 on domain using MQ RBF.
| | | N | | | | C.Time(s) |
|---|
| | 625 | 40 | 20 | 9.75 × | 3.90 × | 2.29 × | 5.780576 |
| | 676 | | | 8.36 × | 3.21 × | 1.88 × | 5.887121 |
| | 729 | | | 7.78 × | 2.88 × | 1.69 × | 6.109537 |
| | 784 | | | 7.69 × | 2.74 × | 1.60 × | 6.602348 |
| | 1444 | 55 | 12 | 8.18 × | 2.15 × | 1.24 × | 18.340002 |
| | | | 14 | 7.57 × | 1.99 × | 1.15 × | 18.271623 |
| | | | 16 | 6.07 × | 1.59 × | 9.26 × | 18.396910 |
| | | | 18 | 5.87 × | 1.54 × | 8.96 × | 19.094877 |
| | 841 | 50 | 22 | 1.10 × | 3.84 × | 2.24 × | 9.939883 |
| | | 51 | | 1.00 × | 3.55 × | 2.07 × | 10.480804 |
| | | 52 | | 6.16 × | 2.12 × | 1.24 × | 10.572760 |
| | | 53 | | 5.45 × | 1.88 × | 1.09 × | 10.763141 |
| [32] | | | | 9.54 × | | | |
Table 9.
The errors obtained using the proposed method for problem 4 on domain using GA RBF.
Table 9.
The errors obtained using the proposed method for problem 4 on domain using GA RBF.
| | | N | | | | C.Time(s) |
|---|
| | 1444 | 10 | 16 | 9.00 × | 2.36 × | 2.18 × | 3.095921 |
| | 1521 | | | 8.70 × | 2.22 × | 2.05 × | 3.330961 |
| | 1600 | | | 8.60 × | 2.14 × | 1.98 × | 3.742602 |
| | 1764 | | | 8.50 × | 2.03 × | 1.87 × | 4.456763 |
| | 2025 | 11 | 18 | 7.90 × | 1.75 × | 1.62 × | 5.512489 |
| | | 17 | | 7.60 × | 1.69 × | 1.56 × | 6.991000 |
| | | 18 | | 5.60 × | 1.24 × | 1.15 × | 6.989841 |
| | | 19 | | 3.30 × | 7.36 × | 6.81 × | 6.974949 |
| | 676 | 19 | 14 | 3.40 × | 1.29 × | 1.19 × | 2.241376 |
| | | 51 | 16 | 3.10 × | 1.17 × | 1.07 × | 3.233400 |
| | | 52 | 18 | 3.00 × | 1.15 × | 1.06 × | 2.891570 |
| | | 53 | 20 | 2.80 × | 1.08 × | 9.96 × | 2.693629 |
| [32] | | | | 8.90 × | | | |
Table 10.
The errors obtained using the proposed method for problem 4 on domain using MQ RBF.
Table 10.
The errors obtained using the proposed method for problem 4 on domain using MQ RBF.
| | | N | | | | C.Time(s) |
|---|
| | 560 | 23 | 18 | 9.91 × | 4.19 × | 3.59 × | 2.342120 |
| | | 30 | | 8.62 × | 3.64 × | 3.13 × | 3.562138 |
| | | 31 | | 8.49 × | 3.58 × | 3.08 × | 3.845987 |
| | | 32 | | 8.27 × | 3.49 × | 3.00 × | 4.054985 |
| | 481 | 65 | 12 | 1.60 × | 7.47 × | 6.41 × | 10.473426 |
| | | | 14 | 1.00 × | 4.71 × | 4.04 × | 10.964542 |
| | | | 16 | 7.50 × | 3.42 × | 2.93 × | 10.637479 |
| | | | 18 | 7.48 × | 3.41 × | 2.93 × | 10.676450 |
| | 481 | 74 | 18 | 8.04 × | 3.66 × | 3.15 × | 13.894779 |
| | 560 | | | 7.56 × | 3.19 × | 2.74 × | 15.420818 |
| | 645 | | | 7.28 × | 2.87 × | 2.46 × | 16.253816 |
| | 736 | | | 7.11 × | 2.62 × | 2.25 × | 17.652880 |
| [32] | | | | 6.22 × | | | |
Table 11.
The errors obtained using the proposed method for problem 4 on domain using GA RBF.
Table 11.
The errors obtained using the proposed method for problem 4 on domain using GA RBF.
| | | N | | | | C.Time(s) |
|---|
| | 800 | 70 | 18 | 4.70 × | 1.65 × | 1.59 × | 16.835572 |
| | 805 | | | 3.60 × | 1.26 × | 1.21 × | 18.014559 |
| | 819 | | | 1.90 × | 6.54 × | 6.31 | 17.489709 |
| | 839 | | | 1.70 × | 5.80 | 5.59 × | 17.416943 |
| | 905 | 38 | 16 | 4.70 × | 1.56 × | 1.50 × | 8.011904 |
| | | 39 | | 3.40 × | 1.13 × | 1.09 × | 8.525006 |
| | | 40 | | 2.80 × | 9.44 × | 9.08 × | 6.758216 |
| | | 41 | | 2.20 × | 7.23 × | 6.95 × | 6.854242 |
| | 824 | 58 | 10 | 8.91 × | 3.10 × | 3.00 × | 8.248187 |
| | | | 12 | 3.10 × | 1.07 × | 1.03 × | 9.049039 |
| | | | 14 | 2.40 × | 8.23 × | 7.93 × | 9.104889 |
| | | | 16 | 2.30 × | 7.95 × | 7.67 × | 9.238572 |
| [32] | | | | 3.19 × | | | |
Table 12.
The errors obtained using the proposed method for problem 5 on domain using MQ RBF.
Table 12.
The errors obtained using the proposed method for problem 5 on domain using MQ RBF.
| | | N | | | | C.Time(s) |
|---|
| | 1296 | 18 | 20 | 7.11 × | 1.97 × | 1.14 × | 4.254578 |
| | 1369 | | | 6.30 × | 1.70 × | 9.87 × | 4.517336 |
| | 1444 | | | 6.03 × | 1.58 × | 9.20 × | 5.330350 |
| | 1600 | | | 5.92 × | 1.48 × | 8.57 × | 5.933110 |
| | 2304 | 15 | 12 | 1.10 × | 2.38 × | 1.37 × | 6.226840 |
| | | | 14 | 4.60 × | 9.58 × | 5.52 × | 6.486711 |
| | | | 16 | 2.86 × | 5.96 × | 3.43 × | 7.310871 |
| | | | 18 | 2.81 × | 5.85 × | 3.37 × | 7.713956 |
| | 1600 | 13 | 18 | 6.47 × | 1.61 × | 9.36 × | 3.810299 |
| | | 14 | | 5.98 × | 1.49 × | 8.66 × | 4.302964 |
| | | 15 | | 5.94 × | 1.48 × | 8.59 × | 4.404455 |
| | | 16 | | 5.03 × | 1.25 × | 7.28 × | 4.543246 |
| [32] | | | | 1.01 × | | | |
Table 13.
The errors obtained using the proposed method for problem 5 on domain using GA RBF.
Table 13.
The errors obtained using the proposed method for problem 5 on domain using GA RBF.
| | | N | | | | C.Time(s) |
|---|
| | 2025 | 16 | 18 | 3.33 × | 7.42 × | 4.28 × | 6.454437 |
| | 2500 | | | 1.98 × | 3.97 × | 2.28 × | 8.824310 |
| | 3025 | | | 1.25 × | 2.28 × | 1.31 × | 11.457521 |
| | 3600 | | | 1.06 × | 1.77 × | 1.02 × | 15.700804 |
| | 3969 | 12 | 18 | 9.70 × | 1.53 × | 8.80 × | 21.993975 |
| | | 13 | | 1.49 × | 2.37 × | 1.36 × | 24.161273 |
| | | 14 | | 1.48 × | 2.35 × | 1.34 × | 23.322577 |
| | | 16 | | 1.16 × | 1.85 × | 1.06 × | 24.757581 |
| | 3721 | 16 | 12 | 1.40 × | 2.35 × | 1.35 × | 16.911628 |
| | | | 14 | 4.58 × | 7.52 × | 4.31 × | 18.235145 |
| | | | 16 | 1.10 × | 1.80 × | 1.03 × | 20.645716 |
| | | | 18 | 9.52 × | 1.56 × | 8.95 × | 21.862306 |
| [32] | | | | 1.01 × | | | |
Table 14.
The errors obtained using the proposed method for problem 5 on domain using MQ RBF.
Table 14.
The errors obtained using the proposed method for problem 5 on domain using MQ RBF.
| | | N | | | | C.Time(s) |
|---|
| | 718 | 53 | 23 | 3.90 × | 1.45 × | 7.60 × | 9.462843 |
| | 822 | | | 2.99 × | 1.04 × | 5.44 × | 10.868986 |
| | 893 | | | 2.62 × | 8.77 × | 4.62 × | 11.586178 |
| | 1115 | | | 2.61 × | 7.83 × | 4.10 × | 13.733598 |
| | 1286 | 50 | 12 | 7.92 × | 2.21 × | 1.14 × | 13.692401 |
| | | | 14 | 6.78 × | 1.89 × | 9.81 × | 13.796613 |
| | | | 16 | 4.95 × | 1.38 × | 7.16 × | 14.059077 |
| | | | 18 | 4.70 × | 1.31 × | 6.81 × | 14.525208 |
| | 1357 | 45 | 18 | 5.19 × | 1.41 × | 7.33 × | 14.082632 |
| | | 46 | | 4.68 × | 1.27 × | 6.61 × | 13.687417 |
| | | 47 | | 4.03 × | 1.09 × | 5.68 × | 14.141039 |
| | | 48 | | 1.96 × | 5.33 × | 2.77 × | 14.555474 |
| [32] | | | | 1.01 × | | | |
Table 15.
The errors obtained using the proposed method for problem 5 on domain using GA RBF.
Table 15.
The errors obtained using the proposed method for problem 5 on domain using GA RBF.
| | | N | | | | C.Time(s) |
|---|
| | 1765 | 28 | 18 | 2.70 × | 6.32 × | 3.48 × | 12.738675 |
| | | 29 | | 7.78 × | 1.85 × | 1.02 × | 12.319389 |
| | | 30 | | 7.03 × | 1.67 × | 9.23 × | 12.649178 |
| | | 32 | | 5.20 × | 1.23 × | 6.82 × | 13.501318 |
| | 2031 | 15 | 16 | 8.69 × | 1.93 × | 1.06 × | 10.713900 |
| | 2108 | | | 7.38 × | 1.60 × | 8.80 × | 6.853962 |
| | 2292 | | | 5.97 × | 1.24 × | 6.81 × | 7.950902 |
| | 2367 | | | 3.93 × | 8.09 × | 4.39 × | 8.201278 |
| | 2460 | 15 | 12 | 9.49 × | 1.91 × | 1.03 × | 7.867139 |
| | | | 14 | 8.75 × | 1.76 × | 9.56 × | 7.951785 |
| | | | 16 | 5.96 × | 1.20 × | 6.52 × | 8.449387 |
| | | | 18 | 5.57 × | 1.12 × | 6.09 × | 8.862747 |
| [32] | | | | 1.01 × | | | |