Abstract
Recent studies have demonstrated the benefits of using fractional derivatives to simulate a blood pressure profile. In this work we propose to combine a one-dimensional model of coronary blood flow with fractional-order Windkessel boundary conditions. This allows us to obtain a greater variety of blood pressure profiles for better model personalization An algorithm of parameter identification is described, which is used to fit the measured mean value of arterial pressure and estimate the fractional flow reserve (FFR) for a given patient. The proposed framework is used to investigate sensitivity of mean blood pressure and fractional flow reserve to fractional order. We demonstrate that the fractional derivative order significantly affects the fractional flow reserve (FFR), which is used as an indicator of stenosis significance.
1. Introduction
Atherosclerotic diseases of coronary vessels are the main reason for myocardial ischemia frequently resulting in disability or death. These diseases are mainly caused by blockages due to an abnormal narrowing in a blood vessel—stenosis [1]. The choice of medical treatment involves evaluation of stenosis significance, which may require invasive measurements. To assess the severity of each stenosis case, clinicians use various hemodynamic indices. The most popular and well-developed index is the fractional flow reserve (FFR), which is a ratio between mean pressure distal (downstream) to stenosis and mean aortic pressure during artificially induced hyperemia [2,3]. Stenoses with values of FFR below 0.8 are considered to be significant and should be surgically treated.
Measuring FFR involves expensive pressure sensors and specialized equipment. Some patients have multiple stenoses with complicated interactions. These problems led to the development of coronary blood flow models capable of estimating FFR from coronary computed tomography angiography (CCTA) and patient’s data (age, heart rate, stroke volume, blood pressure, etc.). Some of these models are based on solving three-dimensional Navier–Stokes equations [4], but in this work, we concentrate on one-dimensional (1D) models of blood flow [5,6,7,8]. The 1D approach is less time-consuming, and it was shown that 3D and 1D FFR calculations demonstrate similar results [9].
One-dimensional models with fractional derivatives can provide a compromise between accuracy and computational cost. Fractional-order models extend the concept of differentiability and incorporate nonlocal and memory effects using a small amount of parameters. This feature can be used to describe complex flows over different space and time scales without splitting the problem into smaller subproblems. Fractional-order models have been proposed in hemodynamic applications. Some examples are the model of blood flow in viscoelastic vessels [10,11] and the model of heat and mass transfer through an arterial segment, which takes into account the interaction with a magnetic field [12]. Fractional derivatives are used to obtain a more realistic prediction of pulse wave forms, which involves the development of parameter identification procedures [13,14]. The latter task has become especially relevant in recent years with the development of computer technology and increasing interest in inverse problems.
In order to extract the patient-specific data of coronary arteries, CCTA images are used. However, there is no geometry data for arteries of systemic circles beyond coronary vessels which can be accounted for in the model. One approach to resolving this issue is to simulate the whole systemic circle with some averaged parameters [8]. This is a physiologically based approach, and it requires a lot of computational resources and includes many parameters that are difficult to estimate. Another option is to impose pressure-derived boundary conditions directly on the inlet of coronary arteries [9], which represents the impact of smaller arteries and microcirculation. This approach simplifies the model but makes it difficult to investigate the effect of various heart conditions on coronary blood flow. Another approach is to take into account the impact of smaller arteries and microcirculation using a submodel coupled with the blood flow model in coronary arteries. A popular choice is Windkessel-type models which are based on the representation of blood vessels (or the whole systemic circulation) as elastic reservoirs with resistance [5]. This leads to small amount (from 2 to 4) of parameters to describe the influence of systemic circulation. An alternative option, similar to the one we use in this work, is to include a part of the aorta in the model and impose a boundary condition on the end of ascending aorta [15]. This approach allows us to use cardiac output as an inlet boundary condition and calculate pressure in the aorta.
Boundary conditions in blood flow models usually imitate the impact of smaller arteries and microcirculation. A porous media-based approach was previously used to simulate microcirculation [16], and fractional derivatives were used to describe flow in porous media [17]. Fractional derivatives were also used to simulate blood flow in capillary vessels [18].
We describe the flow in the systemic circle and microcirculation using Windkessel-type boundary conditions that utilize fractional derivatives. Fractional derivatives have already been used in Windkessel models to simulate hypertensive and normal blood pressure profiles [14]. We propose to couple the Windkessel fractional derivative model with a 1D coronary blood flow model to obtain a greater variety of aortic pressure profiles. We demonstrate that the resulting shape of the aortic pressure profile allows for better personalization of the model and affects the calculated FFR as well as the patient’s diagnosis.
2. Materials and Methods
2.1. Coronary Blood Flow Model
We simulated coronary blood flow and calculated the FFR with a 1D hemodynamic model [19,20]. This model is based on the flow of incompressible viscous fluid through a network of one-dimensional elastic tubes. The conditions for mass and momentum conservation within the network are expressed as a system of hyperbolic equations for each tube:
where t is time, x is the coordinate along the vessel (tube), is the cross-sectional area, is the velocity averaged over the cross-section, is the blood pressure, g/cm is the blood density, and is the blood viscosity. The right-hand side of Equation (2) represents friction force. An additional relation between the blood pressure and cross-sectional area of the vessel wall is required to close the system:
where g/cm is the blood vessel wall density, is the cross-sectional area of the unstressed vessel, and c is elasticity index. The physiological meaning of c is the pulse wave velocity or velocity of small disturbances propagated in the vessel wall [21]. Equation (3) is an analytical approximation of the pressure–area curves obtained in experimental studies [22].
The computational domain consists of the aortic root, aorta, left coronary artery (with branches), and right coronary artery (with branches). The diameters, lengths, and topology of vessels can be extracted from CCTA scans. A simplified version of arterial network is presented in Figure 1. We simulated stenosis as a separate segment with decreased diameter.
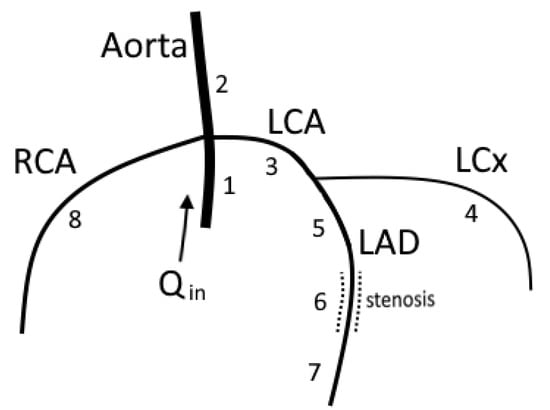
Figure 1.
A simplified network of major coronary arteries. Segment 6 represents 66% stenosis. The model parameters for each segment are presented in Table A1 in Appendix A. We impose cardiac output function (Figure 2) on the inlet of segment 1. On the terminal ends of segments 4, 7, and 8, we impose hydraulic resistance and outflow pressure (6). Boundary condition on the terminal end of the aorta (segment 2) involves a 2-element Windkessel model (7).
One-dimensional vessels are connected to each other in junction points to create an arterial structure. The conditions of mass conservation and total pressure continuity are imposed at the junction points:
Equation (4) represents an algebraic sum of influxes and effluxes, where i is the index of a vessel connected to a junction. , and , and in (5) are the velocities and blood pressures of vessels with indices i and j near the junction point.
On the inlet of the aorta (segment 1 on Figure 1), we set cardiac the output as a periodic time function (Figure 2). The shape of the cardiac output was proposed in [23]. It can be adjusted according to the patient’s heart rate (HR), stroke volume (SV), or other data (peak-to-mean flow ratio, QT-interval).
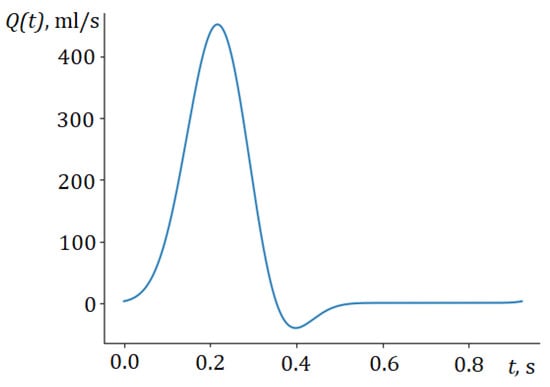
Figure 2.
Cardiac output function.
On the outlet of coronary arteries (segments 4,7,8 on Figure 1), we impose a pressure drop condition:
where k is the index of a segment, is the blood pressure at the boundary point, is the blood flux at the boundary point, and is the hydraulic resistance, is the outflow pressure. Outflow pressure can be described as a value of blood pressure at which the microcirculation between arteries and veins stops. It ranges between 20 and 60 mm Hg [5] and can be adjusted according to the patient’s data. Resistances are distributed according to empiric Murray’s law through an algorithm described in [24]. Resistances increase during the systolic phase to simulate contractions of myocardium tissue that hinder coronary blood flow [19].
The boundary condition on the outlet of the aorta (segment 2 on Figure 1) differs from boundary condition on the terminal coronary arteries (6) since the former one represents the whole systemic circle as well as microcirculation. In order to describe the behavior of the microcirculation vessels, the two-element Windkessel model [25] is extensively used:
where and are the blood flow and pressure in the aorta, and is the hydraulic resistance of the systemic circle and microcirculation. In (7), compliance C is introduced. which represents the ability of blood vessels to distend and store blood volume. Larger values of C correspond to greater vessel elasticity. Compliance C can be adjusted according to patient’s systolic and diastolic blood pressures, and resistance can be derived from the systemic vascular resistance—the ratio between mean blood pressure and cardiac output [24]. The elastic index c from (3), on the other hand, increases with the rigidity of the vessels and, thus, has a different physiological interpretation.
We solve the hyperbolic system (1) and (2) inside each vessel numerically with the help of an explicit grid-characteristic method [26], which is monotone and first-order accurate. Compatibility conditions imposed on junctions with Equations (4) and (5) and boundary points with conditions (6) and (7) form the system of nonlinear equations which is solved with the Newton method. Compatibility conditions are discretized implicitly with a first-order approximation. Discretizations and convergence studies are presented in [27].
The described model can be used to calculate FFR at any point of the coronary arteries. We calculate FFR as a ratio between mean pressure in the coronary artery distal to stenosis () and mean aortic pressure () during vasodilation of the coronary vessels (hyperemia) [2]:
Hyperemia is simulated by decreasing terminal resistances by 70% [28]. FFR values below 0.8 are considered to be significant. This means that the coronary vessel has an abnormal narrowing (stenosis) that should be surgically treated.
By adjusting C and in (6) and (7), we can reproduce patient’s systolic and diastolic blood pressures. However, the range of possible blood profiles is quite limited. To improve the mathematical model, additional elements can be introduced into the arterial structure and the Windkessel model [8]. Instead, in this paper, we propose to use the fractional time derivative in Equation (7).
2.2. Fractional-Order Boundary Conditions
We impose boundary condition on the terminal end of the aorta using the fractional-order Windkessel model, which can be written as follows:
where is a fractional differentiation operator; is a fractional differentiation order, which is assumed to be between 0 and 2 in this work; and is a pseudo-compliance (pseudo-capacitance). Fractional differentiation order determines the relative degree of interaction between the capacitance of the microvasculature vessels, elastic compliance of the vessels, and the dissipation forces inside them. This, in turn, defines the physiological meaning of .
Windkessel models with fractional derivatives were extensively studied before [13,29]. However, combining a one-dimensional hemodynamic model with the fractional-order Windkessel boundary condition is a new approach that allows us to represent a greater variety of storage and dissipation effects that can be represented with a single additional parameter .
A large number of different definitions have been proposed for the fractional differentiation operator [30]. We use the Caputo fractional derivative in this work:
where is a gamma function, is a ceiling of (smallest integer greater than ), and is a derivative with an integer order . There are many other definitions of the fractional derivative: the Atangana–Baleanu fractional integral [31], Riemann–Liouville fractional derivative [32], Riesz derivative [33], etc. The choice of the Caputo fractional derivative is due to its simplicity in representation (relative to other fractional derivatives) and availability of well-studied numerical methods with approximation estimates for various problems. Another useful representation derived in [34] can be obtained using integration by parts in (10):
This representation is valid for . We use it to approximate the integral in (11) with a trapezoidal rule. For the interval with a grid , assuming a constant time-step and , numerical approximation of can be expressed as
where coefficients are
The error and stability analysis of this numerical approximation was described in detail in [30,35]. It was demonstrated that the order of approximation error is .
We use an explicit approximation scheme for (9) with the discretization of fractional derivative described above. This allows us to determine the blood pressure at the terminal end of the aorta from the values of pressure and flux at the previous time steps. Then, we calculate the outflow at the terminal end of the aorta using compatibility conditions (1) and (2) and wall-state Equation (3).
2.3. Model Personalization
One of the most important problems in patient-specific blood flow modeling is to identify the parameters of the model. Diameters, lengths, and overall arterial structure can be extracted from CCTA images with the help of segmentation and skeletonization algorithms [36]. Parameter c in (3) represents the pulse wave velocity and can be estimated from the patient’s age, blood pressure, heart rate, and stroke volume with the help of machine learning methods [20]. Terminal resistances in (6), (7) and (9) are calculated from systemic vascular resistance (the ratio between mean pressure and cardiac output) and the diameters of the terminal arteries [24].
Outflow pressure and compliance C in (7) are estimated to reproduce measured systolic and diastolic blood pressure. A number of algorithms for and C estimation are presented in [25]. The following procedure to estimate these parameters is used in this work. We calculate initial value of C as a ratio between stroke volume and pulse pressure () and the initial value of as 50% of diastolic pressure. After this, C and are iteratively adjusted until the measured diastolic and systolic blood pressures match:
Adjustment of in (9) is performed using the same procedure, but initial estimation is usually less precise since the dimension and interpretation of changes with .
Unfortunately, relying solely on systolic and diastolic pressures may produce incorrect diagnostic outcomes. For example, the hemodynamic significance of stenosis may vary for the same values of systolic and diastolic pressures. In order to obtain more accurate estimates, additional available information about the pressure profile, such as mean pressure, must be taken into account.
We propose to estimate an additional parameter, fractional derivative order , based on the value of the mean pressure . To do this, we first iteratively adjust to match the mean pressure and then adjust and for each to match the systolic and diastolic blood pressures. After this, we calculate and compare it with the measured mean pressure. If the calculated mean pressure is higher than the measured one, the order should be decreased, and vice-versa. As we will see from the results, the relationship between and is very close to linear. Therefore, in most situations, it is sufficient to perform two preliminary calculations for and or to estimate , which provides the appropriate value for the mean pressure.
The procedure of parameter identification described above is summarized on Figure 3.
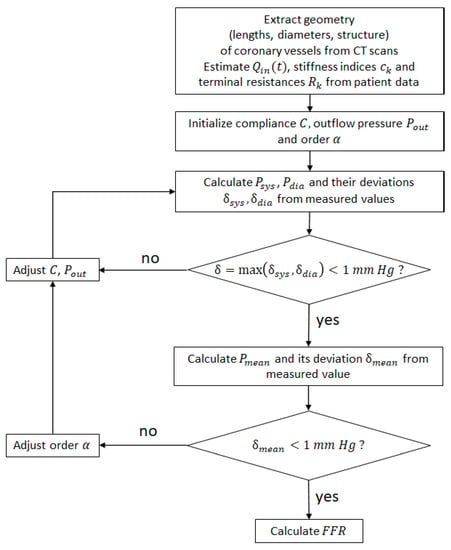
Figure 3.
Parameter identification procedure.
2.4. Patient Data
We tested the parameter identification procedure (Figure 3) on a publicly available dataset [5]. This dataset contains data from ten patients, including the geometry of arterial networks and the location stenoses in various coronary vessels. We kept the numeration of patients from [5] but we excluded Patient 9 from our study since the measurement of mean pressure is unavailable. As a result, our study included nine patients (Table 1 with 13 stenoses).

Table 1.
Characteristics of the patient dataset (mean ± standard deviation). Details are presented in [5]. is a measure of blood profile thickness.
Figure 4 presents examples of two patient-specific structures for Patient 1 and Patient 4. Table 2 presents patient metadata as well as measured FFR values. These two patients were chosen based on the value , which is the measure of the blood profile thickness:
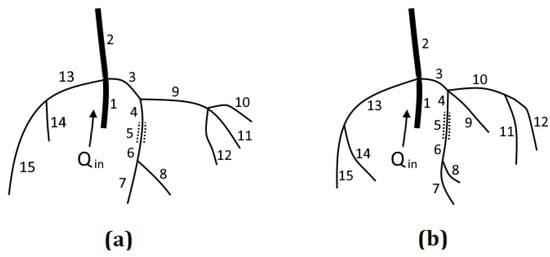

Table 2.
Characteristics of Patient 1 and Patient 4. Stroke volume (SV) was estimated from patient age and BMI values presented in [5].
The average value of across all nine patients is . Patient 1 has the lowest value , and Patient 4 has the closest to the average value . As a result, Patient 1 has the thinnest blood pressure profile and Patient 4 has the most typical profile.
3. Results
3.1. Blood Pressure and FFR Sensitivity to Order
The proposed model was applied to calculate the blood pressure profiles for various fractional differentiation orders in a simplified network of coronary arteries (Figure 1). We also calculated the FFR for 66% of the stenoses for various .
First, we calculated aortic blood pressure for and adjusted the model parameters to acquire the physiological systolic (125 mm Hg) and diastolic (75 mm Hg) blood pressures. Then, we performed calculations for other values of with the same set of model parameters. The value of compliance C remains constant for various . This is technically incorrect since the physiological meaning and dimensional formula for C depend on , but it helps us to explore changes in pressure profiles with the change of (Figure 5a).
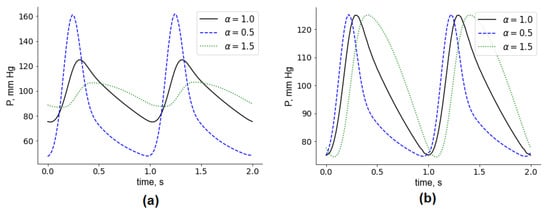
Figure 5.
Aortic blood pressure for various orders . (a) All parameters, except for , are fixed. (b) Model parameters were adjusted to yield the same values of the systolic and diastolic blood pressure.
Second, we adjusted C and for each order to obtain the same values of systolic and diastolic blood pressures (Figure 5b). As decreases, the pressure peak shifts to the left, and the pressure profile becomes thinner. This results in a drop in mean pressure. Conversely, as increases, the profile peak shifts to the right, the profile becomes thicker, and the mean pressure grows.
Systolic and diastolic blood pressures are one of the most commonly available patient-specific parameters. All blood profiles on Figure 5b have the same systolic and diastolic blood pressures, but the mean pressures are different for each . If the mean pressure is available for a given patient, we can use it to select an appropriate and calculate FFR. Figure 6 demonstrates how the calculated mean pressure and FFR depend on , assuming that the systolic and diastolic blood pressures are the same (125/75 mm Hg). The relationship between mean pressure and is very close to linear within the considered interval (from 0.25 to 1.5). Therefore, this simplifies the process of identification from patient’s mean pressure: if we calculate the mean pressures for any two values of , we can derive an appropriate for a given mean pressure value using linear interpolation.
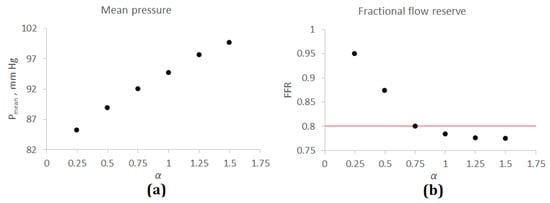
Figure 6.
Mean pressure and FFR for a simplified network of coronary arteries. (a) Mean pressure and . (b) FFR and . The horizontal red line corresponds to FFR = 0.8—threshold value between significant (FFR < 0.8) and insignificant (FFR > 0.8) stenoses.
At the same time, FFR drops with increasing (Figure 6b). This relation resembles exponential decay. For , FFR drops rapidly from 0.95 () to 0.78 (). The threshold between the significant and insignificant lesions is 0.8, so the choice of affects the diagnostic outcome. For , FFR is almost constant.
3.2. Patient-Specific Calculations
In this section, we describe applying a parameter estimation algorithm (Figure 3) to estimate FFR for nine patients (Table 1). We start with two examples: Patient 1 and Patient 4.
Patient 1 had stenosis in the left anterior descending artery (LAD) with a corresponding measured FFR value of 0.89 and a mean aortic pressure of 111 mm Hg. Blood flow calculations for (utilizing boundary condition (7)) yielded and mm Hg. Then, we applied the proposed model with fractional-order Windkessel boundary conditions (9) with the parameter identification procedure to fit the given systolic, diastolic, and mean pressures. As a result, the following estimates were obtained: mm Hg was achieved for , and the resulting FFR was . The error in FFR estimation was significantly reduced after applying optimization of for mean pressure.
Patient 4 had stenosis in the LAD with a corresponding measured FFR value of 0.82 and a mean aortic pressure of 94 mm Hg. Blood flow calculations for (utilizing boundary condition (7)) yielded and mm Hg. No further optimization was required in this case since the calculated mean pressure matched the measured mean pressure with good accuracy. The calculated FFR value also matched the measured one.
FFR estimations for other patients are presented in Table 3. The original approach to estimate FFR involves a boundary condition (7) without fractional derivative. We ignored the measured mean pressure and adjusted our model to achieve the measured systolic and diastolic blood pressures. The fractional-order approach involves adjusting the fractional derivative order to obtain measured mean pressure. The RMSE for the original approach was 0.05, and the RMSE for the fractional order approach was 0.04. The RMSE was mainly defined by large errors in the FFR estimations of patients 6, 8, and 10. We assumed that stenosis degree and length were not identified properly for these patients. The FFR estimation was improved for patients with a “thin” blood profile (), including Patient 1, Patient 5, and Patient 7. Patients 2, 3, 4, and 6 had am optimal fractional order close to 1.0 (or equal to 1.0), so FFR estimations for both approaches were similar. The FFR estimations for patient 6 were less precise for the fractional order approach, but the difference was very small. Patients 8 and 10 had an optimal fractional order , and the FFR estimation was similar for both approaches. This is due to the fact that FFR is almost constant for (Figure 6).

Table 3.
FFR estimations for the patient dataset. Patient data: is the measured mean pressure, mm Hg; is a measure of the pressure profile thickness (14); Loc. is a location of stenosis; is the invasively measured FFR. The original approach for FFR estimation (order ): is the calculated FFR value with a boundary condition (7); is the calculated mean pressure with order . The fractional derivative approach (order ) involves adjusting order so that the calculated mean pressure matches the measured one: is the calculated FFR value with the boundary condition (9), and fractional order ; is the optimal fractional order. Patient 9 was excluded due to the absence of a mean pressure measurement.
Results of the FFR estimation showed that the fractional-order approach provided benefits for a certain group of patients (patients 1, 5, and 7) with a thin blood pressure profile. These patients may have a common cardiovascular pathology. According to [14], low fractional orders can be used to simulate the blood profiles of patients with hypertension. Patients 1, 5, and 7 have a BMI > 30 kg/m which is a good predictor of hypertension. However, their blood pressure levels are not the highest in the dataset. We need a larger sample of patients to make further conclusions.
4. Discussion
We proposed coupling the well-established one-dimensional hemodynamic model of coronary blood flow with a fractional-order boundary condition, as well as a procedure for estimating its parameters. The fractional derivative can be a useful tool for more accurate modeling of the pressure profile. The actual blood pressure profiles depend on many factors, such as age, height, weight, medical history, and artery elasticity. The most commonly available characteristics of blood pressure profiles are systolic and diastolic blood pressures. Unfortunately, relying solely on these two values alone may produce incorrect diagnostic outcomes. For example, the hemodynamic significance of stenosis may vary for the same systolic and diastolic blood pressures. This fact has motivated researchers to look for new tools to model blood pressure profiles.
We used the fractional derivative order to match calculated mean blood pressure with the measured one. Adjusting mean pressure can be performed in other ways: introducing a larger Windkessel model, expanding the arterial network, etc. The fractional-derivative Windkessel model is a good compromise: we introduced a very small amount of new parameters (1–2) and gained the ability to simulate a whole spectrum of dissipative and storage mechanisms with the help of fractional order . Our approach does require additional information on the blood pressure profile. These data can be obtained with simple noninvasive procedures. Unfortunately, in many cases, these data are unavailable, and all the pressure profile information is reduced to systolic and diastolic pressure values. This was the case for Patient 9 who was excluded from our study.
The proposed approach has a number of shortcomings that need to be resolved in the future. First, in some cases, the only data available regarding a patient’s pressure profile were systolic and diastolic blood pressures. Identifying the fractional derivative order in this case would require a completely different approach that can be based on other data, such as patient medical history. Second, calculating fractional derivatives calls for significant computational resources. This negates one of the main advantages of one-dimensional blood flow models—computational efficiency. Instead of the basic approach presented in this work, new efficient numerical approximations can be used. Third, the proposed approach should be tested on a larger number of patients with a wide range of FFR values. The FFR is nearly constant for fractional differentiation orders , so for some patients, its adjustment will be useless.
Further research will focus on integrating more efficient approaches to identify model parameters and to approximate a fractional derivative. Other areas of work include collaborating with clinicians to find effective methods for pulse wave assessment and further validation on a larger amount of patients. The proposed approach has great potential to provide an alternative means to simulating arterial stiffness and pulse waves.
Author Contributions
Conceptualization, T.G. and R.Y.; methodology, T.G.; software, T.G.; validation, T.G.; formal analysis, R.Y.; investigation, T.G.; data curation, T.G.; writing—original draft preparation, T.G.; writing—review and editing, R.Y.; visualization, T.G. and R.Y.; supervision, T.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation under project no. 22-71-10087.
Data Availability Statement
The datasets used in this work are described in [5] and are freely available at https://doi.org/10.6084/m9.figshare.8047742.v2 (accessed on 2 April 2023).
Acknowledgments
We thank Alexander Lapin (Sechenov University) for useful discussion and literature recommendations.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CCTA | coronary computed tomography angiography |
| DA | diagonal artery |
| FFR | fractional flow reserve |
| HR | heart rate |
| LCA | left coronary artery |
| LCx | left circumflex artery |
| LAD | left anterior descending artery |
| LADd | distal part of the left anterior descending artery |
| LADp | proximal part of the left anterior descending artery |
| RCA | right coronary artery |
| RMSE | root mean square error |
| SV | stroke volume |
Appendix A

Table A1.
Parameters of the vessels for simplified structure (Figure 1).
Table A1.
Parameters of the vessels for simplified structure (Figure 1).
| Segment № | Length, cm | Diameter, mm | c, m/s |
|---|---|---|---|
| 1 | 3.2 | 22.0 | 7.5 |
| 2 | 5.0 | 25.0 | 7.5 |
| 3 | 1.3 | 3.9 | 9.0 |
| 4 | 6.0 | 2.8 | 9.0 |
| 5 | 3.0 | 3.0 | 9.0 |
| 6 | 0.7 | 0.9 | 9.0 |
| 7 | 4.0 | 0.3 | 9.0 |
| 8 | 7.5 | 3.0 | 9.0 |

Table A2.
Parameters of the vessels for Patient 1 (Figure 4).
Table A2.
Parameters of the vessels for Patient 1 (Figure 4).
| Segment № | Length, cm | Diameter, mm | c, m/s |
|---|---|---|---|
| 1 | 3.1 | 21.0 | 9.7 |
| 2 | 5.0 | 23.0 | 9.7 |
| 3 | 1.3 | 3.9 | 11.6 |
| 4 | 2.3 | 2.3 | 11.6 |
| 5 | 1.1 | 0.7 | 11.6 |
| 6 | 1.0 | 2.6 | 11.6 |
| 7 | 2.7 | 1.4 | 11.6 |
| 8 | 3.9 | 1.9 | 11.6 |
| 9 | 2.1 | 3.1 | 11.6 |
| 10 | 1.8 | 2.0 | 11.6 |
| 11 | 6.8 | 2.0 | 11.6 |
| 12 | 7.6 | 1.4 | 11.6 |
| 13 | 4.6 | 1.7 | 11.6 |
| 14 | 1.1 | 1.3 | 11.6 |
| 15 | 7.5 | 1.3 | 11.6 |

Table A3.
Parameters of the vessels for Patient 4 (Figure 4).
Table A3.
Parameters of the vessels for Patient 4 (Figure 4).
| Segment № | Length, cm | Diameter, mm | c, m/s |
|---|---|---|---|
| 1 | 2.9 | 21.0 | 8.8 |
| 2 | 5.0 | 22.0 | 8.8 |
| 3 | 0.6 | 2.4 | 10.6 |
| 4 | 0.9 | 3.0 | 10.6 |
| 5 | 2.3 | 1.3 | 10.6 |
| 6 | 2.2 | 2.0 | 10.6 |
| 7 | 9.7 | 1.9 | 10.6 |
| 8 | 2.8 | 1.3 | 10.6 |
| 9 | 4.7 | 1.8 | 10.6 |
| 10 | 3.0 | 3.0 | 10.6 |
| 11 | 6.5 | 2.2 | 10.6 |
| 12 | 9.4 | 2.8 | 10.6 |
| 13 | 1.2 | 1.6 | 10.6 |
| 14 | 4.6 | 1.3 | 10.6 |
| 15 | 9.9 | 1.7 | 10.6 |
References
- Van der Wal, A.C. Coronary artery pathology. Heart 2007, 93, 1484–1489. [Google Scholar] [CrossRef] [PubMed]
- Pijls, N.H.; de Bruyne, B.; Peels, K.; van der Voort, P.H.; Bonnier, H.J.; Koolen, J.J.B.J.; Koolen, J.J. Measurement of Fractional Flow Reserve to Assess the Functional Severity of Coronary-Artery Stenoses. N. Engl. J. Med. 1996, 334, 1703–1708. [Google Scholar] [CrossRef] [PubMed]
- Tebaldi, M.; Campo, G.; Biscaglia, S. Fractional flow reserve: Current applications and overview of the available data. World J. Clin. Cases 2015, 3, 678–681. [Google Scholar] [CrossRef] [PubMed]
- Norgaard, B.L.; Leipsic, J.; Gaur, S.; Seneviratne, S.; Ko, B.S.; Ito, H.; Jensen, J.M.; Mauri, L.; De Bruyne, B.; Bezerra, H.; et al. Group NXTTS Diagnostic performance of noninvasive fractional flow reserve derived from coronary computed tomography angiography in suspected coronary artery disease: The NXT trial (Analysis of Coronary Blood Flow Using CT Angiography: Next Steps). J. Am. Coll. Cardiol. 2014, 63, 1145–1155. [Google Scholar] [CrossRef] [PubMed]
- Carson, J.M.; Pant, S.; Roobottom, C.; Alcock, R.; Blanco, P.J.; Carlos Bulant, C.A.; Vassilevski, Y.; Simakov, S.; Gamilov, T.; Pryamonosov, R.; et al. Non-invasive coronary CT angiography-derived fractional flow reserve: A benchmark study comparing the diagnostic performance of four different computational methodologies. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3235. [Google Scholar] [CrossRef]
- Gognieva, D.; Mitina, Y.; Gamilov, T.; Pryamonosov, R.; Vasilevskii, Y.; Simakov, S.; Liang, F.; Ternovoy, S.; Serova, N.; Tebenkova, E.; et al. Noninvasive assessment of the fractional flow reserve with the CT FFRc 1D method: Final results of a pilot study. Glob. Heart 2020, 16, 837. [Google Scholar] [CrossRef]
- Boileau, E.; Pant, S.; Roobottom, C.; Sazonov, I.; Deng, J.; Xie, X.; Nithiarasu, P. Estimating the accuracy of a reduced-order model for the calculation of fractional flow reserve (FFR). Int. J. Numer. Methods Biomed. Eng. 2017, 34, e2908. [Google Scholar] [CrossRef]
- Ge, X.; Liu, Y.; Yin, Z.; Tu, S.; Fan, Y.; Vassilevski, Y.; Simakov, S.; Liang, F. Comparison of instantaneous wave-free ratio (iFR) and fractional flow reserve (FFR) with respect to their sensitivities to cardiovascular factors: A computational model-based study. J. Interv. Cardiol. 2020, 2020, 4094121. [Google Scholar] [CrossRef]
- Blanco, P.J.; Bulant, C.A.; Muller, L.O.; Talou, G.D.M.; Bezerra, C.G.; Lemos, P.A.; Feijoo, R.A. Comparison of 1D and 3D models for the estimation of fractional flow reserve. Sci. Rep. 2018, 8, 17275. [Google Scholar] [CrossRef]
- Craiem, D.O.; Rojo, F.J.; Atienza, J.M.; Guinea, G.V.; Armentano, R.L. Fractional calculus applied to model arterial Viscoelasticity. Lat. Am. Appl. Res. 2008, 38, 141–145. [Google Scholar]
- Perdikaris, P.; Karniadakis, G.E. Fractional-order viscoelasticity in one-dimensional blood flow models. Ann. Biomed. Eng. 2014, 42, 1012–1023. [Google Scholar] [CrossRef]
- Shah, N.A.; Vieru, D.; Fetecau, C. Effects of the fractional order and magnetic field on the blood flow in cylindrical domains. J. Magn. Magn. Mater. 2016, 409, 10–19. [Google Scholar] [CrossRef]
- Bahloul, M.A.; Laleg Kirati, T.M. Fractional-order model representations of apparent vascular compliance as an alternative in the analysis of arterial stiffness: An in-silico study. Physiol. Meas. 2021, 42, 42. [Google Scholar] [CrossRef]
- Bahloul, M.A.; Aboelkassem, Y.; Laleg-Kirati, T.M. Human Hypertension Blood Flow Model Using Fractional Calculus. Front. Physiol. 2022, 13, 838593. [Google Scholar] [CrossRef]
- Carson, J.M.; Roobottom, C.; Alcock, R.; Nithiarasu, P. Computational instantaneous wave-free ratio (IFR) for patient-specific coronary artery stenoses using 1D network models. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3255. [Google Scholar] [CrossRef] [PubMed]
- Coccarelli, A.; Prakash, A.; Nithiarasu, P. A novel porous media-based approach to outflow boundary resistances of 1D arterial blood flow models. Biomech. Model Mechanobiol. 2019, 18, 939–951. [Google Scholar] [CrossRef]
- Zhou, H.W.; Yang, S. Fractional derivative approach to non-Darcian flow in porous media. J. Hydrol. 2018, 566, 910–918. [Google Scholar] [CrossRef]
- Alotta, G.; Bologna, E.; Failla, G.; Zingales, M. A Fractional Approach to Non-Newtonian Blood Rheology in Capillary Vessels. J. Peridyn. Nonlocal. Model 2019, 1, 88–96. [Google Scholar] [CrossRef]
- Simakov, S.; Gamilov, T.; Liang, F.; Gognieva, D.G.; Gappoeva, M.K.; Kopylov, P.Y. Numerical evaluation of the effectiveness of coronary revascularization. Russian J. Num. Anal. Math. Mod. 2021, 36, 303–312. [Google Scholar] [CrossRef]
- Gamilov, T.; Liang, F.; Kopylov, P.; Kuznetsova, N.; Rogov, A.; Simakov, S. Computational Analysis of Hemodynamic Indices Based on Personalized Identification of Aortic Pulse Wave Velocity by a Neural Network. Mathematics 2023, 11, 1358. [Google Scholar] [CrossRef]
- Matthys, K.S.; Alastruey, J.; Peiro, J.; Khir, A.W.; Segers, P.; Verdonck, P.R.; Parker, K.H.; Sherwin, S.J. Pulse wave propagation in a model human arterial network: Assessment of 1D numerical simulations against in-vitro measurements. J. Biomech. 2007, 40, 3476–3486. [Google Scholar] [CrossRef] [PubMed]
- Caro, C.; Pedley, T.; Schroter, R.; Seed, W.; Parker, K. The Mechanics of the Circulation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Stevens, S.A.; Lakin, W.D.; Goetz, W. A differentiable, periodic function for pulsatile cardiac output based on heart rate and stroke volume. Math. Biosci. 2003, 182, 201–211. [Google Scholar] [CrossRef]
- Simakov, S.; Gamilov, T.; Liang, F.; Kopylov, P. Computational analysis of haemodynamic indices in synthetic atherosclerotic coronary netwroks. Mathematics 2021, 9, 2221. [Google Scholar] [CrossRef]
- Mariscal-Harana, J.; Charlton, P.; Vennin, S.; Aramburu, J.; Florkow, M.; Van Engelen, A.; Schneider, T.; Bliek, H.; Ruijsink, B.; Valverde, I.; et al. Estimating central blood pressure from aortic flow: Development and assessment of algorithms. Am. J. Physiol. Heart Circ. Physiol. 2020, 320. [Google Scholar] [CrossRef] [PubMed]
- Magomedov, K.M.; Kholodov, A.S. Grid—Characteristic Numerical Methods; Nauka: Moscow, Russia, 1988; 287p. (In Russian) [Google Scholar]
- Simakov, S.; Gamilov, T. Computational Study of the Cerebral Circulation Accounting for the Patient-specific Anatomical Features. In Smart Modeling for Engineering Systems; Petrov, I., Favorskaya, A., Favorskaya, M., Simakov, S., Jain, L., Eds.; Springer: Cham, Switzerland, 2019; Volume 133. [Google Scholar]
- Lo, E.W.C.; Menezes, L.J.; Torii, R. On outflow boundary conditions for CT-based computation of FFR: Examination using PET images. Med Eng. Phys. 2020, 76, 79–87. [Google Scholar] [CrossRef]
- Bahloul, M.A.; Laleg-Kirati, T.M. Assessment of Fractional-Order Arterial Windkessel as a Model of Aortic Input Impedance. IEEE Open J. Eng. Med. Biol. 2020, 22, 123–132. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Liu, J.-B.; Butt, S.I.; Nasir, J.; Aslam, A.; Fahad, A.; Soontharanon, J. Jensen-Mercer variant of Hermite-Hadamard type inequalities via Atangana-Baleanu fractional operator. AIMS Math. 2022, 7, 2123–2141. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Haghighi, A.; Dadvand, A.; Ghejlo, H. Solution of the fractional diffusion equation with the Riesz fractional derivative using McCormack method. Commun. Adv. Comput. Sci. Appl. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Elliot, D. An asymptotic analysis of two algorithms for certain Hadamard finite-part integrals. Ima J. Numer. Anal. 1993, 13, 445–462. [Google Scholar] [CrossRef]
- Diethelm, K. Generalized compound quadrature formulae for finite-part integrals. IMA J. Numer. Anal. 1997, 17, 479–493. [Google Scholar] [CrossRef]
- Vassilevski, Y.; Olshanskii, M.; Simakov, S.; Kolobov, A.; Danilov, A. Personalized Computational Haemodynamics: Models, Methods, and Applications for Vascular Surgery and Antitumor Therapy; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).