Bifurcation of Traveling Wave Solution of Sakovich Equation with Beta Fractional Derivative

Abstract

The current work is devoted to studying the dynamical behavior of the Sakovich equation with beta derivatives. We announce the conditions of problem parameters leading to the existence of periodic, solitary, and kink solutions by applying the qualitative theory of planar dynamical systems. Based on these conditions, we construct some new solutions by integrating the conserved quantity along the possible interval of real wave propagation in order to obtain real solutions that are significant and desirable in real-world applications. We illustrate the dependence of the solutions on the initial conditions by examining the phase plane orbit. We graphically show the fractional order beta effects on the width of the solutions and keep their amplitude approximately unchanged. The graphical representations of some 3D and 2D solutions are introduced.

1. Introduction

In recent years, time evolution phenomena, such as nonlinear waves, are best described by partial differential equations [1,2]. These equations are hard to analyze, and there are no common analytical approaches to solve them. Exact traveling wave solutions of nonlinear evolution equations are one of the fundamental objects of study in mathematical physics. These exact solutions, when they exist, can help one to understand the mechanism of the complicated physical phenomena and dynamical processes modeled by these nonlinear evolution equations. Among traveling wave solutions, solitary waves with nonlinear dispersive effects, called solitons, are of great interest due to their additional property of permanently retaining [3,4]. Solitons play a momentous role in the telecommunication industry as signals can proceed far away without any distortion in the form of solitons, see for example [5]. As a sequence, numerous techniques have been proposed in the literature to obtain different solutions [6,7,8,9,10,11,12,13]. The Korteweg–de Vries (KdV) equation and its modifications are nonlinear differential equations, whose solutions were analytically described. The family of the KdV equations model a number of nonlinear processes such as waves in shallow water, ion acoustic waves in plasma, and many physics and engineering phenomena [14,15]. In his work on the Painlevé analysis of a class of second-order equations, Sakovich formed a new equation using the KdV-equation and the fifth order KdV-equation [16]. The equation obtained, named after Sakovich, takes the following form:

$$u_{xt}+u_{yy}+2u{u}_{xy}+6u^2{u}_{xx}+2u_{xx}^2=0$$

(1)

where u is a wave function in three independent variables, representing time and two spatial variables. The Sakovich equation was extended several time to obtain versions with more independent variables [17,18]. It is worth noting that the Sakovich equation and all its extended versions are Painlevé integrable [16,17,18]. The Painlevé test [19] provides a criterion for the integrability of nonlinear partial differential equations. In [16], Sakovich showed that Equation (1) satisfies the Painlevé test and possesses multiple solutions that satisfy, simultaneously, the Korteweg–de Vries (KdV) equation and the fifth-order KdV equation.

In fact, numerous evolutionary systems with memory effects on dynamics have been mathematically modeled using fractional calculus. Several different derivative definitions such as Riemman–Liouville, Caputo, Grünwald–Letnikov, etc., have arisen (see for example [20,21]. Fractional derivatives have their geometric and physical interpretations [22]. In [23], Atangana introduced the “beta-derivative”, which complies with numerous requirements that were restrictions for fractional derivatives. The introduced derivative can be thought of as a natural extension of the classical derivative rather than fractional derivatives. For more information about the $\beta$-derivative, see Appendix A. The $\beta$-derivative version of Equation (1) is given by

$${}^A{D}_x^{\beta }{(}^A{D}_t^{\beta }u){+}^A{D}_y^{\beta }{(}^A{D}_y^{\beta }u)+2u{}^A{D}_x^{\beta }{(}^A{D}_y^{\beta }u)+6u^2{}^A{D}_x^{\beta }{(}^A{D}_x^{\beta }u)+2{{(}^A{D}_x^{\beta }{(}^A{D}_x^{\beta }u))}^2=0,$$

(2)

where $0<\beta \le 1$ and ${}^A{D}_x^{\beta },{}^A{D}_t^{\beta }$ represents the $\beta$-derivative with respect to space and time, respectively. Notice, when $\beta =1$, Equation (2) will be reduced to Equation (1). The solutions for several fractional nonlinear equations were investigated in the literature [24,25]. Bifurcation is one of the methods used to describe the solutions of many fractional and classical differential equations [26,27,28,29,30,31,32,33,34,35]. In this work, we use bifurcation methods to investigate the dynamical behavior of Equation (2). To the extent of the authors’ knowledge, the study of the $\beta$-time derivative Sakovich equation has not been investigated in the literature. We construct some wave solutions of the equation, and study the influence of the order $\beta$-derivative on the obtained solutions.

This paper is organized as follows: Section 2 contains the mathematical analysis covering the conversion of Equation (2) into a traveling wave system by using appropriate wave transformation and applying the qualitative theory for a planar integrable system to this system. Section 3 is devoted to constructing a wave solution for Equation (2). In Section 4, we provide 3D-graphical representations and illustrate the effect of the order $\beta$ on the solutions. Finally, Section 5 gives a summary of the obtained result.

2. Bifurcation Analysis

We search for a wave solution in the form

$$u=\psi (\rho ),\rho =\frac{k}{\beta }{(x+\frac{1}{\Gamma (\beta )})}^{\beta }+\frac{m}{\beta }{(y+\frac{1}{\Gamma (\beta )})}^{\beta }+\frac{w}{\beta }{(t+\frac{1}{\Gamma (\beta )})}^{\beta },$$

(3)

where $k,m,\omega$ are arbitrary constants and $\Gamma (·)$ is the Gamma function. Applying Proposition A2, we obtain

$$\begin{array}{cc}\hfill {}^A{D}_x^{\beta }u& ={(x+\frac{1}{\Gamma (\beta )})}^{1-\beta }\frac{\partial u}{\partial x}={(x+\frac{1}{\Gamma (\beta )})}^{1-\beta }{\psi }^{\prime }(\rho )\frac{\partial \rho }{\partial x}\hfill \\ \hfill & ={(x+\frac{1}{\Gamma (\beta )})}^{1-\beta }{\psi }^{\prime }(\rho )k{(x+\frac{1}{\Gamma (\beta )})}^{\beta -1}=k{\psi }^{\prime },\hfill \\ \hfill & {}^A{D}_y^{\beta }u=m{\psi }^{\prime },{}^A{D}_t^{\beta }u=\omega {\psi }^{\prime },\hfill \end{array}$$

(4)

where primes indicate a derivative with respect to $\rho$. Taking into account the results provided in the appendix, and the expressions (4), we obtain

$$\begin{array}{cc}\hfill & {}^A{D}_x^{\beta }{(}^A{D}_t^{\beta }u){=}^A{D}_x^{\beta }(\omega {\psi }^{\prime }(\rho ))=k\omega {\psi }^{″},{}^A{D}_y^{\beta }{(}^A{D}_y^{\beta }u)=m^2{\psi }^{″},{}^A{D}_x^{\beta }{(}^A{D}_x^{\beta }u)=k^2{\psi }^{″}.\hfill \end{array}$$

(5)

Inserting Equation (5) into Equation (2), we obtain

$${\psi }^{″}\left[kw+m^2+2mk\psi +6k^2{\psi }^2+2k^4{\psi }^{″}\right]=0.$$

(6)

Thus, we have two possibilities, either ${\psi }^{″}=0$, or $kw+m^2+2mk\psi +6k^2{\psi }^2+2k^4{\psi }^{″}=0$. The first equation, ${\psi }^{″}=0$, gives a solution of the form

$$\psi \left(\rho \right)=A\rho +B,$$

(7)

where $A,B$ are two constants. The second equation

$${\psi }^{″}\left(\rho \right)+\frac{3}{k^2}{\psi }^2\left(\rho \right)+\frac{m}{k^3}\psi \left(\rho \right)+\frac{k\omega +m^2}{2k^4}=0,$$

(8)

can be written as a dynamical system in the form

$$\begin{array}{cc}\hfill {\psi }^{\prime }& =z,\hfill \\ \hfill z^{\prime }& =\frac{-3}{k^2}{\psi }^2-\frac{m}{k^3}\psi -\frac{kw+m^2}{2k^4}.\hfill \end{array}$$

(9)

System (9) can be obtained using the canonical Hamilton equations with Hamiltonian function

$$H=\frac{1}{2}{z}^2+V\left(\psi \right),$$

(10)

where

$$V\left(\psi \right)=\frac{1}{k^2}{\psi }^3+\frac{m}{2k^3}{\psi }^2+\frac{k\omega +m^2}{2k^4}\psi ,$$

(11)

Since H does not explicitly depend on $\rho$, which plays the role of the time in Hamiltonian mechanics, it is a conserved quantity, i.e., it takes a constant value along all the phase orbits. Thus, we obtain

$$\frac{1}{2}{z}^2+V\left(\psi \right)=f,$$

(12)

where f is an arbitrary constant. Using Equation (12), we can rewrite the first equation in (9) as

$$\frac{d\psi }{\sqrt{F_3\left(\psi \right)}}=d\rho ,$$

(13)

where $F_3\left(\psi \right)$ is given by

$$F_3\left(\psi \right)=2[f-V\left(\psi \right)]=\frac{2}{k^2}\left[-{\psi }^3-\frac{m}{2k}{\psi }^2-\frac{k\omega +m^2}{2k^2}\psi +f{k}^2\right].$$

(14)

To integrate both sides of Equation (13), we need to determine the range of the parameters $m,k,\omega$, and f. The desired range can be determined by using bifurcation analysis. For more details about the bifurcation theory, see, e.g., [36,37]. First, we find the equilibrium points for the Hamiltonian system (9). These are the critical points for the potential function (11), i.e., they are $({\psi }_0,0)$, where ${\psi }_0$ satisfies the quadratic equation $\frac{dV}{d\psi }=\frac{3}{k^2}{\psi }_0^2+\frac{m}{k^3}{\psi }_0+\frac{k\omega +m^2}{2k^4}=0$. The number of the equilibrium points is determined by the sign of the discriminant $\mathsf{\Delta }=\frac{-1}{k^6}(5m^2+6k\omega )$. We will consider the different possibilities individually and utilize MATLAB software to sketch phase portraits:

(a)

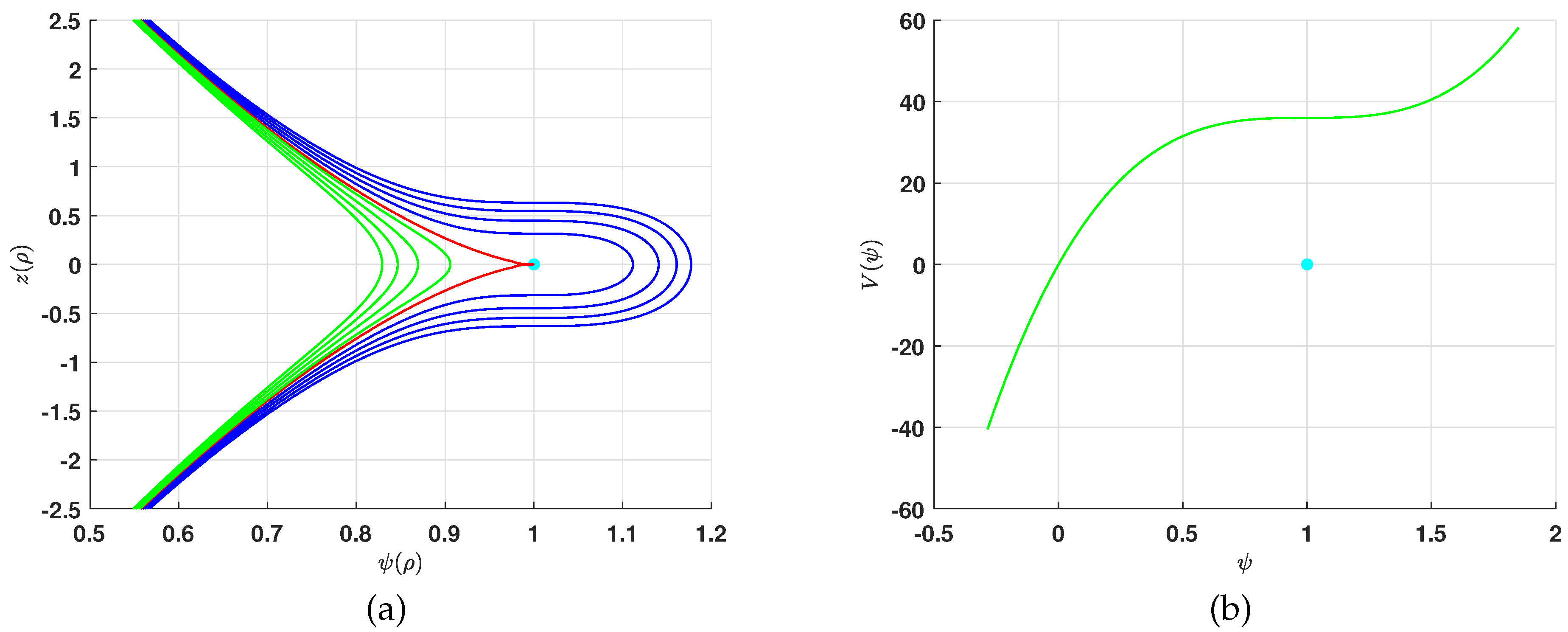
If $k=-\frac{5m^2}{6\omega }$, then there is a unique equilibrium point $E_1=(\frac{\omega }{5m},0)$ for system (9). This point is a cusp since $V^{″}\left(\frac{\omega }{5m}\right)=0$. The phase portrait and potential function for system (9) are shown in Figure 1a,b, respectively. For fixed values of the parameters $\omega ,m,k$, there are three type of phase orbits depending on whether $f>f_1$, shown in blue, $f<f_1$, shown in green, or $f=f_1$, shown in red, where $f_1=V\left(E_1\right)=\frac{36{\omega }^6}{3125m^7}$ is the value of the conserved quantity at the cusp point $E_1$. All the phase orbits in these cases are unbounded and, consequently, they will imply unbounded solutions.

(b)

If $m^2>-\frac{6}{5}k\omega$, then there are no equilibrium points for the Hamiltonian system (9). The phase plane consists of one family of unbounded phase orbits for any value of the parameter f as shown in Figure 2a. This type of phase orbit will lead to unbounded solutions. The potential function (11) is given by Figure 2b.

(c)

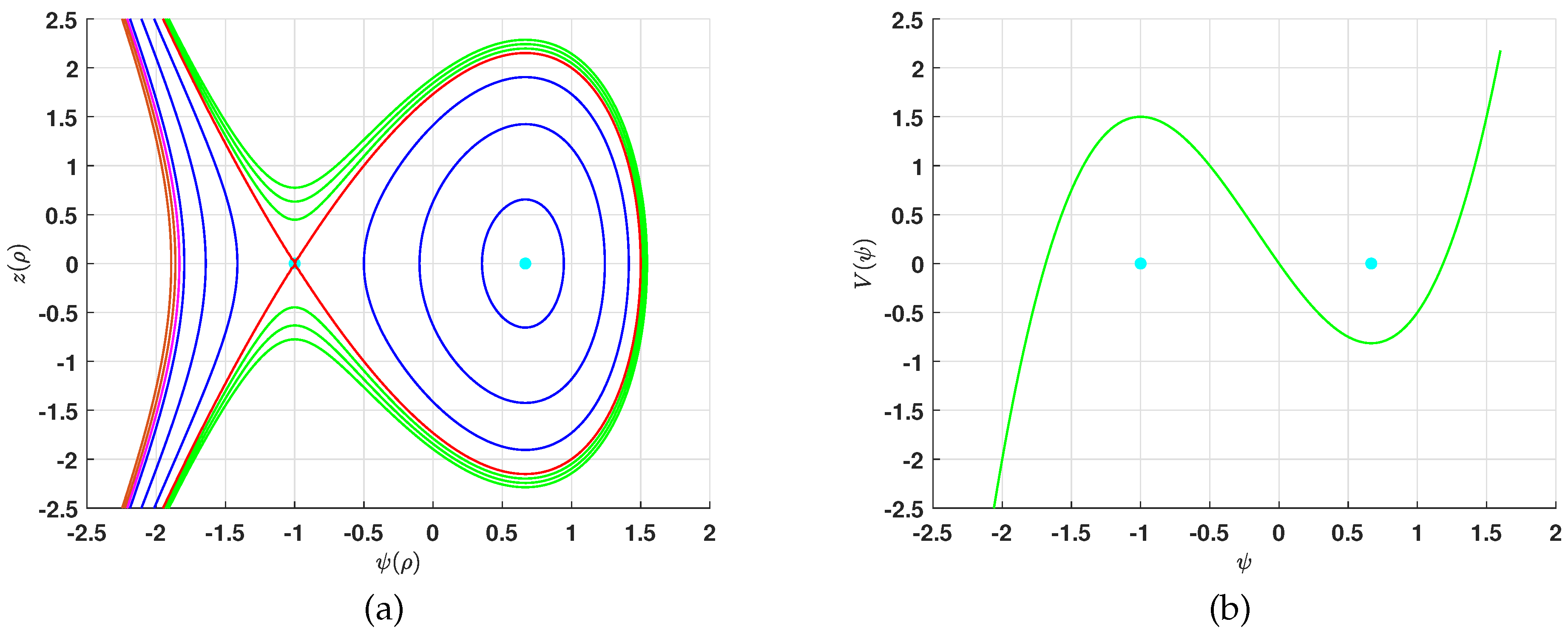
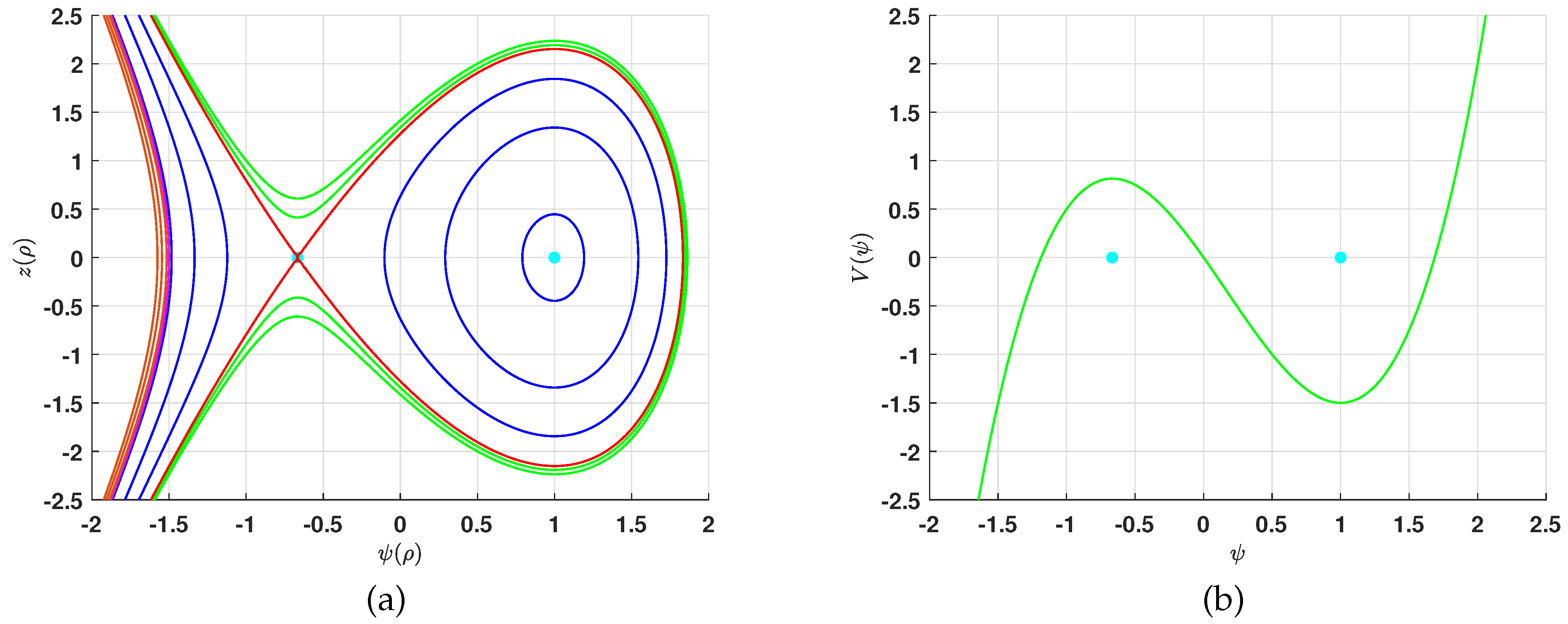
If $m^2<-\frac{6}{5}k\omega$, then there are two equilibrium points for the Hamiltonian system (9). They are $E_{2,3}=\left(\frac{-m\pm \sqrt{-5m^2-6k\omega }}{6k},0\right)$. To determine the nature of these equilibrium points, we calculate

$$V^{″}\left(E_2\right)=\frac{1}{k^3}\sqrt{-(5m^2+6k\omega )},V^{″}\left(E_3\right)=\frac{-1}{k^3}\sqrt{-(5m^2+6k\omega )}.$$

(15)

Since reversing the signs of k and $\omega$ exchanges $V^{″}\left(E_2\right)$ and $V^{″}\left(E_3\right)$, we may assume $k>0$, hence $\omega <0$. Under this assumption, $E_2$ will be a center while $E_3$ will be a saddle point. Figure 3a,b show the phase portrait and potential function (11), respectively. To describe the phase portrait for this case, we defined the two constants $f_2$ and $f_3$, which are the values of the conserved quantity at the equilibrium points $E_{2,3}$, i.e.,

$$f_{2,3}=V\left(E_{2,3}\right)=\frac{1}{216k^5}(m\pm \sqrt{-5m^2-6k\omega })(\pm \sqrt{-5m^2-6k\omega }-12k\omega -11m^2),$$

(16)

Figure 1. (a) Phase portrait when $\mathsf{\Delta }=0$ ($k=\frac{1}{6},m=-1,\omega =-5$) and (b) the potential function. The cyan solid circle is the equilibrium point.

Figure 1. (a) Phase portrait when $\mathsf{\Delta }=0$ ($k=\frac{1}{6},m=-1,\omega =-5$) and (b) the potential function. The cyan solid circle is the equilibrium point.

Figure 2. (a) Phase portrait when $\mathsf{\Delta }<0$ ($k=1,m=1,\omega =-\frac{1}{2}$) and (b) the potential function.

Figure 2. (a) Phase portrait when $\mathsf{\Delta }<0$ ($k=1,m=1,\omega =-\frac{1}{2}$) and (b) the potential function.

Figure 3. (a) Phase portrait when $\mathsf{\Delta }>0$ with $k>0,\omega <0$ ($k=1,m=1,\omega =-5$) and (b) the potential function. The cyan solid circles are the equilibrium points.

Figure 3. (a) Phase portrait when $\mathsf{\Delta }>0$ with $k>0,\omega <0$ ($k=1,m=1,\omega =-5$) and (b) the potential function. The cyan solid circles are the equilibrium points.

For all the energy levels $f>f_3$, system (9) has a family of unbounded orbits, shown in green in Figure 3a. Corresponding to the energy level $f=f_3$, there is a homoclinic orbit, shown in red, which connects the saddle point $E_3$ with itself and has unbounded extensions. For $f\in ]f_2,f_3[$, there are two families of orbits, shown in blue, one of which is periodic enclosing the center point $E_2$ and contained inside the homoclinic orbit while the other one is unbounded. For $f=f_2$, there is a single unbounded orbit, shown in pink. Finally, when $f<f_2$, there is a family of unbounded orbits, shown in brown.

Note that if instead of assuming $k>0$, we had assumed that $k<0$, then the equilibrium point $E_2$ will be a saddle while $E_3$ will be a center. The phase portrait for this case can be described as in the previous one. Figure 4a,b show the phase plane and the potential function (11) in this case.

3. Solutions

The present section aims to obtain solutions for Equation (2) taking into account the bifurcations constraints on the parameters introduced in the previous section. Equation (13) can be written as

$$\frac{d\psi }{\sqrt{Q_3\left(\psi \right)}}=\frac{2}{\left|k\right|}d\rho ,$$

(17)

where

$$Q_3\left(\psi \right)=-{\psi }^3-\frac{m}{2k}{\psi }^2-\frac{k\omega +m^2}{2k^2}\psi +f{k}^2.$$

(18)

The procedure of finding the solutions is given in the following Theorems:

Theorem 1.

(a) 

If $k=-\frac{5m^2}{6\omega },f\in ]-\infty ,f_1[\cup ]f_1,\infty [$, then Equation (2) has a solution of the form

$$\psi (x,y,t)={\psi }_1+A_1-\frac{2A_1}{1+\mathrm{c}\mathrm{n}({\mathsf{\Omega }}_1\rho ,k_1)},$$

(19)

where ${\psi }_1,{\psi }_2,{\psi }_2^{*}$ are the roots of the polynomial (18), ${\mathsf{\Omega }}_1=\frac{2\sqrt{A_1}}{|k_1|}$, $k_1=\sqrt{\frac{A_1-{\psi }_1+\mathit{Re}.{\psi }_2}{2A_1}}$, and $A_1^2={(\mathit{Re}.{\psi }_2-{\psi }_1)}^2+{\psi }_1^2$.

(b) 

If $k=-\frac{5m^2}{6\omega }$ and $f=f_1$, then Equation (2) has the solution

$$\psi (x,y,t)=\frac{\omega }{5m}-\frac{k^2}{16{\rho }^2}.$$

(20)

Proof. 

(a)

For the given range of the parameters, system (9) has two families of unbounded orbits shown in blue and in green in Figure 1a. This shows that the polynomial (18) has one real root ${\psi }_1$ and two complex conjugate roots ${\psi }_2,{\psi }_2^{*}$, where ${}^{*}$ denotes the complex conjugate. Note that ${\psi }_1>\frac{\omega }{5m}$ if $f>f_1$ while ${\psi }_1<\frac{\omega }{5m}$ if $f<f_1$. The domain of the solution in both cases is $\psi \in ]-\infty ,{\psi }_1[$. Assuming $\psi \left(0\right)={\psi }_1$, and integrating both sides of Equation (17), we obtain the solution of Equation (2) given in (19).

(b)

For the selected range of the parameters, system (9) has a single phase orbit passing through the cusp point $E_1$, shown in red in Figure 1a. This shows that the polynomial (18) has $\psi =\frac{\omega }{5m}$ as a repeated root. Hence, $Q\left(\psi \right)={(\frac{\omega }{5m}-\psi )}^3$. The domain of the solution is $\psi \in ]-\infty ,\frac{\omega }{5m}[$. Assuming $\psi \left(0\right)=-\infty$, and integrating both sides of Equation (2) gives us the solution (20).

□

Theorem 2.

For $m^2>-\frac{6}{5}k\omega$ and for an arbitrary value of f, Equation (2) has a solution of the form (19).

Proof. 

For the given range of the parameters, system (9) has no equilibrium point as shown in Figure 2a and any phase orbit intersects the $\psi$–axis at exactly one point. Thus, the polynomial (18) has one real root ${\psi }_1$, and two complex conjugate roots ${\psi }_2,{\psi }_2^{*}$. The domain of the solution is $\psi \in ]-\infty ,{\psi }_1[$. Assuming $\psi \left(0\right)={\psi }_1$ and integrating both sides of Equation (17), we obtain a solution in the form (19) for Equation (2). □

Theorem 3.

Assuming $(m,k,\omega )\in ]-\sqrt{\frac{-6}{5}k\omega },\sqrt{\frac{-6}{5}k\omega }[\times {\mathbb{R}}^{-}\times {\mathbb{R}}^{+}$, we have

(a) 

If $f=f_3$, then Equation (2) has the solution

$$\psi (x,y,t)={\psi }_e-({\psi }_3-{\psi }_e){\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^2\left(\frac{\sqrt{{\psi }_3-{\psi }_e}}{\left|k\right|}\rho \right),\mathit{if}-\infty <\psi <{\psi }_e,$$

(21)

or,

$$\psi (x,y,t)={\psi }_e+({\psi }_3-{\psi }_e){\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left(\frac{\sqrt{{\psi }_3-{\psi }_e}}{\left|k\right|}\rho \right),\mathit{if}{\psi }_e<\psi <{\psi }_3,$$

(22)

where ${\psi }_e$ is the $\psi -$ coordinate of the equilibrium point $E_3$ and ${\psi }_3=\frac{-m-2\sqrt{\mathsf{\Delta }}}{6k}$.

(b) 

If $f\in ]f_2,f_3[$, then Equation (2) has the solution

$$\psi (x,y,t)={\psi }_5+({\psi }_4-{\psi }_5){\mathrm{n}\mathrm{c}}^2({\mathsf{\Omega }}_2\rho ,k_2),\mathit{if}-\infty <\psi <{\psi }_4,$$

(23)

or,

$$\psi (x,y,t)={\psi }_6-({\psi }_6-{\psi }_5){\mathrm{s}\mathrm{n}}^2({\mathsf{\Omega }}_2\rho ,k_2),\mathit{if}{\psi }_5<\psi <{\psi }_6,$$

(24)

where ${\psi }_4<{\psi }_5<{\psi }_6$ are the roots of the polynomial (18), ${\mathsf{\Omega }}_2=\frac{\sqrt{{\psi }_6-{\psi }_4}}{\left|k\right|}$, and $k_2=\sqrt{\frac{{\psi }_6-{\psi }_5}{{\psi }_6-{\psi }_4}}$.

(c) 

If $f\le f_2$, then Equation (2) has a solution in the form (19).

Proof. 

(a)

For the given range of the parameters, system (9) has a homoclinic orbit, shown in red in Figure 3a. This shows that the polynomial (18) has one double root, which is ${\psi }_e$, and another simple root denoted by ${\psi }_3$. Thus, $Q_3\left(\psi \right)={(\psi -{\psi }_e)}^2({\psi }_3-\psi )$. There are two possible domains of the solution $\psi \in ]-\infty ,{\psi }_e[\cup ]{\psi }_e,{\psi }_3[$. If $\psi \in ]-\infty ,{\psi }_e[$ and $\psi \left(0\right)=-\infty$, then integrating both sides of Equation (17) gives the solution (21). If $\psi \in ]{\psi }_e,{\psi }_3[$ and $\psi \left(0\right)={\psi }_3$, we obtain the solution (22) by integrating both sides of Equation (17).

(b)

The bifurcation analysis shows that for the given range of the parameters, the system (9) has two families of orbits; one is periodic and the other unbounded. This shows that the polynomial (18) has three real zeros, ${\psi }_4,{\psi }_5,{\psi }_6$, where ${\psi }_4<{\psi }_5<{\psi }_6$. Thus, $Q_3\left(\psi \right)=({\psi }_4-\psi )(\psi -{\psi }_5)(\psi -{\psi }_6)$. There are two possible domains of the solution, namely $\psi \in ]-\infty ,{\psi }_4[\cup ]{\psi }_5,{\psi }_6[$. Assuming $\psi \in ]-\infty ,{\psi }_4[$, $\psi \left(0\right)=-\infty$, and integrating both sides of Equation (17), we obtain a new solution (23) for Equation (2). On other hand, if $\psi \in ]{\psi }_5,{\psi }_6[$, $\psi \left(0\right)={\psi }_6$, then integrating both sides of Equation (13) yields to a new solution (24) for Equation (2).

(c)

The proof of this statement is completely analogous to the proof of part (a) in Theorem 1.

□

The next proposition gives the procedures of obtaining the solutions for Equation (2) corresponding to the phase orbits shown in Figure 4a.

Proposition 1.

For $(m,k,\omega )\in ]-\sqrt{\frac{-6}{5}k\omega },\sqrt{\frac{-6}{5}k\omega }[\times {\mathbb{R}}^{+}\times {\mathbb{R}}^{-}$, the solutions of Equation (2) can be obtained from those in Theorem 3 by replacing $\omega ⟼-\omega$, $k⟼-k$, $f_2⟷f_3$.

Remark 1.

All solutions obtained in the previous theorems are new solutions for Equation (2). Moreover, if $\beta \to 1$, Equation (2) becomes Equation (1) and the solutions for Equation (1) can be obtained from those given in the previous theorems by letting $\beta \to 1$ and these solutions are also new.

Note that the roots after carrying out the replacement in Proposition 1 are different from those in Theorem 3 due to the dependence of the roots on the coefficients of the polynomial (18). Thus, the solutions obtained in Proposition 1 are different from those in Theorem 3.

Finding the domain of the solution is important since it enables us to construct all possible solutions for Equation (2). This deserves some elaboration. It should be noted that from part (a) in Theorem 3, we have two solutions, (21) and (22), for the same conditions on the parameters $m,k,\omega$, and f, that are completely different mathematically and physically. Solution (22) is a solitary solution that corresponds to the red homoclinic phase orbit in Figure 3a. The other solution (21) is unbounded and corresponds to the unbounded extension of the homoclinic orbit. The two solutions are the results of integrating Equation (17) along all possible intervals of real wave propagation.

Remark 2.

The degeneracy of the obtained solutions can be investigated through the transition between the phase plane orbits. This shows the consistency of the obtained results. In Figure 3a, when $f\to f_3$, the periodic family of blue orbits will be transformed to the homoclinic orbit, shown in red. Thus, the periodic solution (24) corresponding to a periodic orbit will be transformed to the solitary solution (22). The correctness of this statement can be seen by letting $f\to f_3$, then ${\psi }_6\to {\psi }_3$ and ${\psi }_4,{\psi }_5\to {\psi }_e$, and the solution (24) converges to:

$$\begin{array}{cc}\hfill \psi (x,y,t)& ={\psi }_6-({\psi }_6-{\psi }_5){\mathrm{s}\mathrm{n}}^2\left({\mathsf{\Omega }}_2\rho ,k_2\right),\hfill \\ \hfill & ={\psi }_3-({\psi }_3-{\psi }_e){tanh}^2\left(\frac{\sqrt{{\psi }_3-{\psi }_e}}{|k}\right),\hfill \\ \hfill & ={\psi }_e+({\psi }_3-{\psi }_e){\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left(\frac{\sqrt{{\psi }_3-{\psi }_e}}{|k}\right),\hfill \end{array}$$

(25)

which agrees with the solution (22).

4. Graphical Representation

In this sections, we give 2D and 3D representations of the solutions obtained above and clarify the influence of the fractional order $\beta$ on the solutions.

For the fixed values $k=-0.1$ and $\omega =0.2$, m is restricted to fall in the interval $]-0.154919338,0.154919338[$. We will take $m=0.01$. The solution of Equation (2) can be obtained from Theorem 3 as determined by the value of the conserved quantity (12) and the domain of the solution. We have the following cases:

(a)

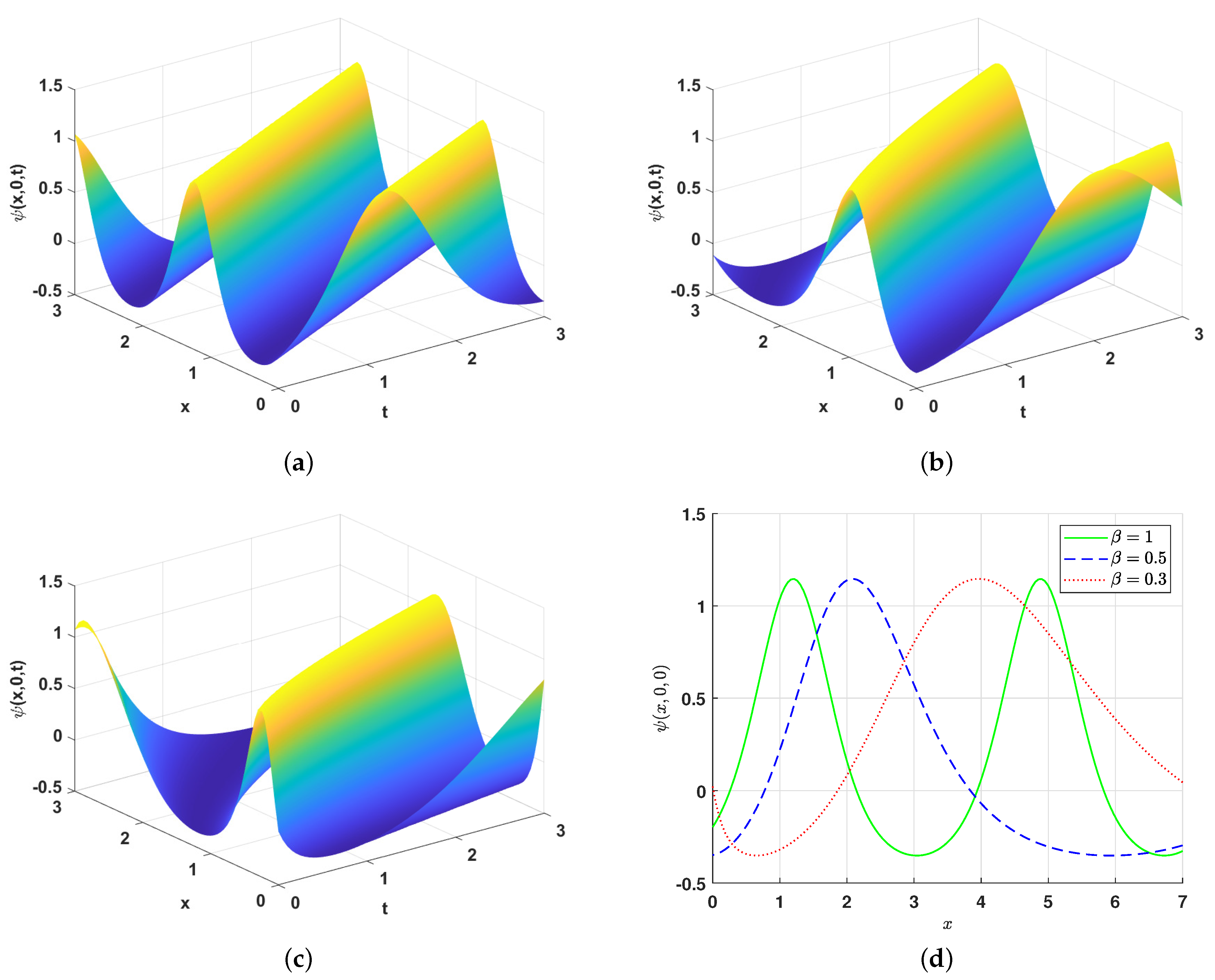
For $f=f_3=36.59044683$, Equation (2) has either the solution (21) or (22) depending on the chosen domain of the solution. Thus, if we select $\psi \in ]{\psi }_e,{\psi }_3[$, where ${\psi }_e=-0.5594795338,{\psi }_3=1.168959068$ are the zeros of the polynomial (18), then Equation (2) has the solution (22), which can be rewritten in the form

$$\begin{array}{cc}\hfill \psi (x,y,t)& =-0.5594795338+1.728438602{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left(\frac{1.314700955}{\beta }[{(y+\frac{1}{\Gamma \left(\beta \right)})}^{\beta }-{(x+\frac{1}{\Gamma \left(\beta \right)})}^{\beta }]\right.\hfill \\ & \left.+\frac{2.629401910}{\beta }{(t+\frac{1}{\Gamma \left(\beta \right)})}^{\beta }\right).\hfill \end{array}$$

(26)

Solution (26) is a solitary wave solution for Equation (2) corresponding to the homoclinic orbit in red as outlined by Figure 3a. This type of solutions is also named a compressive solitary wave solution; for more details, see, e.g., [36]. Figure 5a–c show the 3D-graphical representation of the solution (26) for several values of the order $\beta$ ($\beta =0.6,0.8,1$) while Figure 5d shows the 2D representation of the solutions. It should be noted that the amplitude of the solution is left approximately unchanged by changing the value of the order $\beta$ while the solution’s width decreases with the increasing of the order $\beta$.

(b)

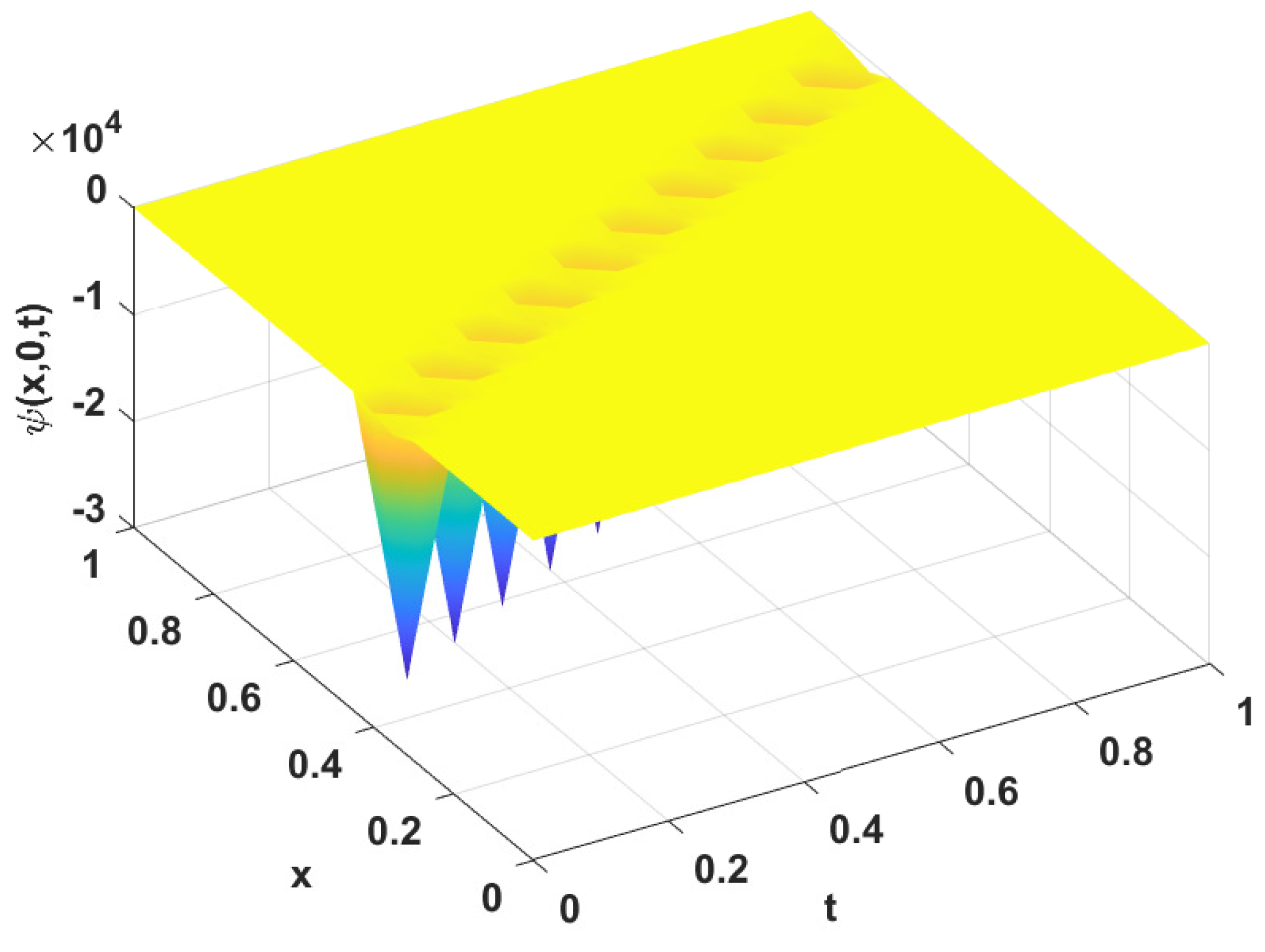
We take $f=30$, which falls in the interval $]f_2,f_3[=]-39.90896535,36.59044683[$. From Theorem (3), Equation (2) has either the solution (23) or the solution (24) depending on the chosen domain of the solution. Direct calculations give ${\psi }_4=-0.7450404543$, ${\psi }_5=-0.3512688151$, and ${\psi }_6=1.146309269$, which are the roots of the polynomial (18). Choosing the interval of the real solution as $\psi \in ]{\psi }_5,{\psi }_6[$, will result in the solution for Equation (2) having the form

$$\begin{array}{cc}\hfill \psi (x,y,t)& =1.146309269-1.497578084{\mathrm{s}\mathrm{n}}^2\left(\frac{1.375263510}{\beta }[{(y+\frac{1}{\Gamma \left(\beta \right)})}^{\beta }-{(x+\frac{1}{\Gamma \left(\beta \right)})}^{\beta }]\right.\hfill \\ & \left.+\frac{2.750527020}{\beta }{(t+\frac{1}{\Gamma \left(\beta \right)})}^{\beta },0.8898336352\right).\hfill \end{array}$$

(27)

The solution (27) is a periodic solution for Equation (2) and this solution corresponds to the periodic family of orbit in blue around the equilibrium point $E_2$ as is clarified by Figure 3a. Figure 6a–c show the 3D-graphical representation of the solution (27) for different values of $\beta$ ($\beta =1,0.5,0.3$) while Figure 6d shows the 2D representation of the solution. Figure 6d shows that the amplitude of the solution (27) remains unchanged for changing values of the order $\beta$ while the solution’s width decreases as the value of the order $\beta$ increases.

To illustrate the importance of the choice of the domain of the solution, we give the graphical representation for two solutions having the same condition on the parameters, but with different domains of the solution. The solution (23) with $\beta =1$ takes the form

$$\begin{array}{cc}\hfill \psi (x,y,t)& =-0.3512688151-0.3937716392{\mathrm{n}\mathrm{c}}^2(0.1375263510(y-x)+2.750527020t\hfill \\ & +1.512789861,0.8898336352).\hfill \end{array}$$

(28)

The two solutions (27) and (28) were obtained with the same conditions on the parameters $f,m,k$, and $\omega$, but with different domains of the solution. The two solutions are completely different physically and mathematically, as shown in Figure 6a and Figure 7. One of them is periodic and the other is singular. This can be also seen by examining the phase orbits. The phase orbit for this case consists of two orbits, shown in blue in Figure 3a. One of the orbits is periodic, which gives a periodic solution, and the other is unbounded, which gives an unbounded solution.

Figure 5. Graphic representation of the solution (22) for different values of the fractional order $\beta$. (a) $\beta =1$. (b) $\beta =0.8$. (c) $\beta =0.6$. (d) 2D representation with various $\beta$.

Figure 5. Graphic representation of the solution (22) for different values of the fractional order $\beta$. (a) $\beta =1$. (b) $\beta =0.8$. (c) $\beta =0.6$. (d) 2D representation with various $\beta$.

Figure 6. Graphic representation of the solution (24) for different values of the fractional order $\beta$. (a) $\beta =1$. (b) $\beta =0.5$. (c) $\beta =0.3$. (d) 2D representation with various $\beta$.

Figure 6. Graphic representation of the solution (24) for different values of the fractional order $\beta$. (a) $\beta =1$. (b) $\beta =0.5$. (c) $\beta =0.3$. (d) 2D representation with various $\beta$.

Figure 7. Graphic representation of the solution (23) with $\beta =1$.

Figure 7. Graphic representation of the solution (23) with $\beta =1$.

5. Conclusions

This paper studied the dynamical behavior of the solutions of the fractional Sakovich equation with beta derivatives for time and space variables. This equation was transformed in an appropriate manner to create a Hamiltonian system that describes time evolution. Bifurcation analysis was carried out, the phase portrait was generated, and possible domains of the solution were determined. To create some novel solutions for the Sakovich equation with beta derivatives, the conserved quantity was integrated along these intervals. The dependence of the solutions on the initial conditions was illustrated by examining the phase plane orbit. The 3D- and 2D-graphical representations of these solutions were generated. We showed that the fractional order $\beta$ affected the width of the solitary and periodic solutions while leaving the amplitude of the solutions approximately unchanged. Furthermore, we have illustrated the significance of the choice of the domain of the solution by producing two solutions with the same conditions on the parameters, but with different domains of the solution. We have found that one of them is periodic while the other is singular, i.e., they are mathematically and physically different, as shown in Figure 6a and Figure 7. This point also illustrated the effectiveness of applying bifurcation analysis since the latter solutions correspond to the phase orbit in blue, in Figure 3a, which consists of two families, where one of them is periodic and the other is unbounded. The upcoming work may include the study of chaotic behavior for system (9) after adding the periodic term and its applications to image encryption. Additionally, the geometric and physical interpretation for Equation (2) will be considered.