Applications of Fractional Differentiation Matrices in Solving Caputo Fractional Differential Equations

Abstract

This paper pursues obtaining Jacobi spectral collocation methods to solve Caputo fractional differential equations numerically. We used the shifted Jacobi–Gauss–Lobatto or Jacobi–Gauss–Radau quadrature nodes as the collocation points and derived the fractional differentiation matrices for Caputo fractional derivatives. With the fractional differentiation matrices, the fractional differential equations were transformed into linear systems, which are easier to solve. Two types of fractional differential equations were used for the numerical simulations, and the numerical results demonstrated the fast convergence and high accuracy of the proposed methods.

1. Introduction

The Caputo fractional derivative is used to model phenomena that involve interactions with the past and also problems with nonlocal properties [1,2,3,4,5]. The most-popular definition of the left-side Caputo derivative [1] is given below.

Definition 1.

Suppose that function u is defined in $(0,l)$, $n-1\le \nu <n$,$n\in \mathbb{N}$, then the left-side Caputo fractional derivative of order ν is defined by

$${\partial }_x^{\nu }u(x,t)={}_0^C{D}_x^{\nu }u\left(x\right):=\frac{1}{\mathsf{\Gamma }(n-\nu )}{\int }_0^x{(x-t)}^{n-\nu -1}{u}^{\left(n\right)}\left(t\right)\mathrm{d}t.$$

(1)

Given the above definition, it can be observed that the fractional derivative’s value at $x_0$ depends on the function values at $x<x_0$. In this sense, one can think of the derivative as having “memory”. Thus, the fractional partial differential equations (FDEs) are more suitable than the traditional partial differential equations to study the processes of memory, hereditary properties, and heterogeneous materials.

For the fractional differential equations with an initial value, the existence and uniqueness of the solutions were studied in [6]. To achieve the analytical solutions, the Adomian decomposition methods [7] and the variational iteration methods [8,9] are the two common methods. The above literature showed that the exact solutions of FDEs are usually very hard to acquire or contain some special functions. Therefore, more and more researchers turn to numerical methods, for example finite-difference methods [10,11,12] and spectral methods [13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Spectral methods are well-known high-accuracy methods [27,28,29,30,31,32,33,34,35], normally carried out by a Galerkin, Tau, or collocation approach in practical problems. Because fractional derivative operators are nonlocal and spectral methods are global methods, it is very natural to apply spectral methods to solve FDEs.

Recently, the methods of operational matrices combined with spectral techniques have been widely used to solve FDEs due to their efficiency, stability, and usability. Suppose that $u\left(x\right)$ is the solution of an FDE and ${\left\{{\phi }_n\left(x\right)\right\}}_{n=0}^N$ are orthogonal polynomials. The solution $u\left(x\right)$ can be approximated by $u_N\left(x\right)={\sum }_{n=0}^N{c}_n{\phi }_n\left(x\right)$. The operational matrix $\mathbf{O}$ of the fractional derivative is a matrix satisfying

$${\partial }_x^{\nu }\Phi \left(x\right)\approx \mathbf{O}\Phi \left(x\right),$$

with $\Phi \left(x\right)={[{\phi }_0\left(x\right),{\phi }_1\left(x\right),\cdots ,{\phi }_N\left(x\right)]}^T.$ By the operational matrices,

$${\partial }_x^{\nu }{u}_N\left(x\right)\approx [c_0,c_1,\cdots ,c_N]\mathbf{O}\Phi \left(x\right),$$

the FDEs, hence, can be transformed into algebraic equations of coefficients $c_n,n=0,1,\cdots ,N$. The operational matrices based on all kinds of shifted orthogonal polynomials have been discussed by scholars, such as Laguerre operational matrices [14,15], Legendre operational matrices [16], Bernstein operational matrices [17], Chebyshev operational matrices [18,19], Jacobi operational matrices [20,21], and Genocchi operational matrices [22]. The analysis of the exponential convergence of the operational matrix methods for some FDEs can be found in [36,37,38].

Suppose that ${\left\{x_n\right\}}_{n=0}^N$ are a collection of $N+1$ collocation points and $u_n=u_N\left(x_n\right)$, $n=0,1,\cdots ,N$. The approximation $u_N$ can be written in the Lagrange interpolating formula:

$$u_N\left(x\right)=\sum _{n=0}^N{u}_n{h}_n\left(x\right),$$

with $h_j\left(x_i\right)={\delta }_{ij}$.

Let $\mathbf{u}={[u_0,u_1,\cdots ,u_N]}^T$ and ${\partial }_x\mathbf{u}={[{\partial }_x^{\nu }{u}_N\left(x_0\right),{\partial }_x^{\nu }{u}_N\left(x_1\right),\cdots ,{\partial }_x^{\nu }{u}_N\left(x_N\right)]}^T$; it then follows that

$${\partial }_x\mathbf{u}={}^c{\mathbf{D}}_s^{\left(\nu \right)}\mathbf{u},$$

where the matrix ${}^c{\mathbf{D}}_s^{\left(\nu \right)}=\left({\partial }_x^{\nu }{h}_j\left(x_i\right)\right)$ is the fractional differentiation matrix (FDM) of the Caputo fractional derivative of order $\nu$. The Lagrange cardinal polynomial can be formulated by $h_j\left(x\right)={\sum }_{i=0}^N{t}_{ij}{\phi }_i\left(x\right).$ The corresponding operational matrix, therefore, can be used to obtain the fractional differentiation matrix as

$${}^c{\mathbf{D}}_s^{\left(\nu \right)}\approx {[\Phi \left(x_0\right),\Phi \left(x_1\right),\cdots ,\Phi \left(x_N\right)]}^{\prime }{\mathbf{O}}^{\prime }\mathbf{T},$$

with $\mathbf{T}=\left(t_{ij}\right)$. However, to achieve the operational matrices, one often uses a polynomial expansion to approximate the non-integer power of x resulting from the fractional order derivative, which lowers the accuracy of the approaches. In this paper, we focused on deriving a new fractional differentiation matrix based on Jacobi polynomials to solve FDEs numerically.

This paper is structured as follows. Section 2 provides the preliminaries for standard Jacobi spectral collocation methods. In Section 3, the shifted Jacobi polynomials are introduced and the expressions of the fractional differentiation matrices for the fractional derivative are deduced using the shifted Jacobi–Gauss–Lobatto (JGL) and shifted Jacobi–Gauss–Radau (JGR) collocation points. The fractional differentiation matrix based on the shifted JGL points is used to numerically solve the generalized space–fractional Burgers’ equations in Section 4, and the fractional differentiation matrix based on the shifted JGR points is used to numerically solve fractional integro-differential equations in Section 5. The conclusion is made in the last section.

2. Jacobi Polynomials and Differentiation Matrix

Let $P_n^{\alpha ,\beta }(·)$ stand for the common nth-degree Jacobi polynomials defined on $[-1,1]$. Jacobi polynomials $P_n^{\alpha ,\beta }(·)$ for $n\in {\mathbb{N}}_0$ are orthogonal in regard to the weight function ${\omega }^{\alpha ,\beta }\left(x\right)={(1-x)}^{\alpha }{(1+x)}^{\beta }$ with $\alpha >-1$ and $\beta >-1$. From [34], $P_n^{\alpha ,\beta }\left(x\right)$ has the following representation:

$$P_n^{\alpha ,\beta }\left(x\right)=\frac{\mathsf{\Gamma }(n+\alpha +1)}{n!\mathsf{\Gamma }(n+\alpha +\beta +1)}\sum _{k=0}^n{(-1)}^k\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{\mathsf{\Gamma }(n+k+\alpha +\beta +1)}{\mathsf{\Gamma }(k+\alpha +1)}{\left(\frac{1-x}{2}\right)}^k.$$

(2)

Suppose that ${\left\{x_j^{\alpha ,\beta }\right\}}_{j=0}^N$ are the corresponding Jacobi–Gauss–Lobatto (JGL) quadrature nodes ($x_0^{\alpha ,\beta }=-1$, $x_N^{\alpha ,\beta }=1$, ${\left\{x_i^{\alpha ,\beta }\right\}}_{i=1}^{N-1}$ are the zeros of ${\partial }_x{P}_N^{\alpha ,\beta }\left(x\right)$) or Jacobi–Gauss–Radau (JGR) quadrature nodes ($x_0^{\alpha ,\beta }=-1$ and ${\left\{x_i^{\alpha ,\beta }\right\}}_{i=1}^N$ are the zeros of $P_N^{\alpha ,\beta +1}\left(x\right)$) and taken as the collocation points.

Let function u be defined on $[-1,1]$ and ${\left\{h_j^{\alpha ,\beta }\left(x\right)\right\}}_{j=0}^N$ be Lagrange cardinal polynomials; the interpolation of u then is

$$\begin{array}{c}\hfill u_N\left(x\right)=\sum _{j=0}^{N}u\left(x_j\right)h_j^{\alpha ,\beta }\left(x\right).\end{array}$$

(3)

The Lagrange cardinal polynomials $h_j^{\alpha ,\beta }\left(x\right)$ can be expressed by the linear combination of Jacobi polynomials as

$$\begin{array}{}\hfill h_j^{\alpha ,\beta }\left(x\right)=\sum _{i=0}^N{t}_{ij}^{\alpha ,\beta }{P}_i^{\alpha ,\beta }\left(x\right),\end{array}$$

with the coefficients:

$$t_{ij}^{\alpha ,\beta }=\frac{{\omega }_j^{\alpha ,\beta }}{{\gamma }_i^{\alpha ,\beta }}{P}_i^{\alpha ,\beta }\left(x_j\right),$$

(4)

where

$${\omega }_j^{\alpha ,\beta }={\int }_{-1}^1{h}_j^{\alpha ,\beta }\left(x\right){\omega }^{\alpha ,\beta }\left(x\right)dx,$$

(5)

and

$${\gamma }_i^{\alpha ,\beta }=\left\{\begin{array}{cc}\hfill & {\int }_{-1}^1{\left[P_i^{\alpha ,\beta }\left(x\right)\right]}^2{\omega }^{\alpha ,\beta }\left(x\right)dx,i=0,\cdots ,N-1,\hfill \\ \hfill & {\int }_{-1}^1{\left[P_N^{\alpha ,\beta }\left(x\right)\right]}^2{\omega }^{\alpha ,\beta }\left(x\right)dx,i=N,\mathrm{if}\mathrm{JGR}\mathrm{quadrature}\mathrm{nodes}\mathrm{are}\mathrm{used},\hfill \\ \hfill & (2+\frac{\alpha +\beta +1}{N}){\int }_{-1}^1{\left[P_N^{\alpha ,\beta }\left(x\right)\right]}^2{\omega }^{\alpha ,\beta }\left(x\right)dx,i=N,\mathrm{if}\mathrm{JGL}\mathrm{quadrature}\mathrm{nodes}\mathrm{are}\mathrm{used}.\hfill \end{array}\right.$$

(6)

The coefficients ${\left\{{\gamma }_i^{\alpha ,\beta }\right\}}_{i=0}^N$ and ${\left\{{\omega }_j^{\alpha ,\beta }\right\}}_{j=0}^N$ can be calculated as below.

When the JGL collocation points are used,

$${\gamma }_i^{\alpha ,\beta }=\left\{\begin{array}{cc}\hfill & \frac{2^{\alpha +\beta +1}\mathsf{\Gamma }(i+\alpha +1)\mathsf{\Gamma }(i+\beta +1)}{(2i+\alpha +\beta +1)i!\mathsf{\Gamma }(i+\alpha +\beta +1)},i=0,\cdots ,N-1,\hfill \\ \hfill & (2+\frac{\alpha +\beta +1}{N})\frac{2^{\alpha +\beta +1}\mathsf{\Gamma }(N+\alpha +1)\mathsf{\Gamma }(N+\beta +1)}{(2N+\alpha +\beta +1)N!\mathsf{\Gamma }(N+\alpha +\beta +1)},i=N,\hfill \end{array}\right.$$

(7)

and

$${\omega }_j^{\alpha ,\beta }=\left\{\begin{array}{cc}\hfill & \frac{2^{\alpha +\beta +1}(\beta +1){\mathsf{\Gamma }}^2(\beta +1)\mathsf{\Gamma }\left(N\right)\mathsf{\Gamma }(N+\alpha +1)}{\mathsf{\Gamma }(N+\beta +1)\mathsf{\Gamma }(N+\alpha +\beta +2)},j=0,\hfill \\ \hfill & \frac{{\tilde{G}}_{N-2}^{\alpha +1,\beta +1}}{{(1-x_j^2)}^2{\left({\partial }_x{P}_{N-1}^{\alpha +1,\beta +1}\left(x_j\right)\right)}^2},j=1,\cdots ,N-1,\hfill \\ \hfill & \frac{2^{\alpha +\beta +1}(\alpha +1){\mathsf{\Gamma }}^2(\alpha +1)\mathsf{\Gamma }\left(N\right)\mathsf{\Gamma }(N+\beta +1)}{\mathsf{\Gamma }(N+\alpha +1)\mathsf{\Gamma }(N+\alpha +\beta +2)},j=N,\hfill \end{array}\right.$$

(8)

with ${\tilde{G}}_{N-2}^{\alpha +1,\beta +1}=\frac{2^{\alpha +\beta +3}\mathsf{\Gamma }(N+\alpha +1)\mathsf{\Gamma }(N+\beta +1)}{(N-1)!\mathsf{\Gamma }(N+\alpha +\beta +2)}$; when the JGR collocation points are used,

$${\gamma }_i^{\alpha ,\beta }=\frac{2^{\alpha +\beta +1}\mathsf{\Gamma }(i+\alpha +1)\mathsf{\Gamma }(i+\beta +1)}{(2i+\alpha +\beta +1)i!\mathsf{\Gamma }(i+\alpha +\beta +1)},i=0,\cdots ,N$$

(9)

and

$${\omega }_j^{\alpha ,\beta }=\left\{\begin{array}{cc}\hfill & \frac{2^{\alpha +\beta +1}(\beta +1){\mathsf{\Gamma }}^2(\beta +1)\mathsf{\Gamma }(N+1)\mathsf{\Gamma }(N+\alpha +1)}{\mathsf{\Gamma }(N+\beta +2)\mathsf{\Gamma }(N+\alpha +\beta +2)},j=0,\hfill \\ \hfill & \frac{{\tilde{G}}_{N-1}^{\alpha ,\beta +1}}{(1+x_j)(1-x_j^2){\left({\partial }_x{P}_N^{\alpha ,\beta +1}\left(x_j\right)\right)}^2},j=1,\cdots ,N,\hfill \end{array}\right.$$

(10)

with ${\tilde{G}}_{N-1}^{\alpha ,\beta +1}=\frac{2^{\alpha +\beta +2}\mathsf{\Gamma }(N+\alpha +1)\mathsf{\Gamma }(N+\beta +2)}{N!\mathsf{\Gamma }(N+\alpha +\beta +2)}$.

After differentiation on Equation (3), one has

$$\begin{array}{c}\hfill {\partial }_x{u}_N\left(x\right)=\sum _{j=0}^{N}u\left(x_j\right){\partial }_x{h}_j^{\alpha ,\beta }\left(x\right).\end{array}$$

The vector with its components being the values of the first-order derivative of $u_N$ at the collocation points can be retrieved by a matrix $\mathit{D}$ multiplying a vector composed of function values of $u_N$, i.e.,

$${\mathbf{u}}^{\prime }=\mathit{D}\mathit{u},$$

(11)

where

$$\left\{\begin{array}{cc}\hfill & \mathbf{u}={\left[u\left(x_0^{\alpha ,\beta }\right),u\left(x_1^{\alpha ,\beta }\right),\dots ,u\left(x_N^{\alpha ,\beta }\right)\right]}^T,\hfill \\ \hfill & {\mathbf{u}}^{\prime }={\left[{\partial }_{x}u\left(x_0^{\alpha ,\beta }\right),{\partial }_{x}u\left(x_1^{\alpha ,\beta }\right),\dots ,{\partial }_{x}u\left(x_N^{\alpha ,\beta }\right)\right]}^T,\hfill \\ \hfill & \mathbf{D}=\left(d_{ij}\right)=\left({\partial }_x{h}_j^{\alpha ,\beta }\left(x_i^{\alpha ,\beta }\right)\right).\hfill \end{array}\right.$$

The matrix $\mathit{D}$ is the first-order differentiation matrix, and the exact formula of $\mathit{D}$ for the JGL or JGR collocation points can be found in [34]. The differentiation matrix of higher-integer-order derivatives of $u_N$ can be obtained by calculating the corresponding power of $\mathit{D}$. For example, the differentiation matrix of the second-order derivative is ${\mathit{D}}^2$.

3. Jacobi Fractional Differentiation Matrix

The Caputo fractional differentiation matrix at the shifted Jacobi collocation points is derived in this section. The matrix will be used to solve FDEs in the next sections.

The shifted Jacobi polynomials, $P_{0,l,n}^{\alpha ,\beta }\left(x\right),n=0,1,2,\cdots$, which are defined on $[0,l]$, can be obtained by a translation and dilation of general Jacobi polynomials, i.e.,

$$P_{0,l,n}^{\alpha ,\beta }\left(x\right)=P_n^{\alpha ,\beta }(\frac{2x}{l}-1),n=0,1,2,\cdots .$$

The shifted JGL collocation points then become

$$y_j^{\alpha ,\beta }=\frac{l}{2}(x_j^{\alpha ,\beta }+1),j=0,1,\cdots ,N.$$

According to (2), the analytic expression of shifted Jacobi polynomials is

$$\begin{array}{ccc}\hfill P_{0,l,n}^{\alpha ,\beta }\left(x\right)& =& \sum _{k=0}^n{(-1)}^{n-k}\frac{\mathsf{\Gamma }(n+\beta +1)\mathsf{\Gamma }(n+k+\alpha +\beta +1)}{k!(n-k)!\mathsf{\Gamma }(n+\alpha +\beta +1)\mathsf{\Gamma }(k+\beta +1)}{\left(\frac{1}{l}\right)}^k{x}^k.\hfill \end{array}$$

Similarly, the approximation $u_N$ of function u defined on $[0,l]$ has the following representation:

$$\begin{array}{c}\hfill u_N\left(x\right)=\sum _{j=0}^{N}u\left(y_j^{\alpha ,\beta }\right)\sum _{i=0}^N{t}_{ij}^{\alpha ,\beta }{P}_{0,l,i}^{\alpha ,\beta }\left(x\right).\end{array}$$

(12)

The differentiation matrix ${\mathit{D}}_s$ associated with the shifted Jacobi polynomials $P_{0,l,n}^{\alpha ,\beta }\left(x\right)$ can be calculated by $2\mathit{D}/l$ with $\mathit{D}$ defined in Section 2.

Take the Caputo derivative of order $\nu$ on Equation (12); one has

$$\begin{array}{c}\hfill {\partial }_x^{\nu }{u}_N\left(x\right)=\sum _{j=0}^{N}u\left(y_j^{\alpha ,\beta }\right)\sum _{i=0}^N{t}_{ij}^{\alpha ,\beta }{\partial }_x^{\nu }{P}_{0,l,i}^{\alpha ,\beta }\left(x\right).\end{array}$$

According to [1,26], we have the following lemma for the Caputo derivative.

Lemma 1.

Suppose that C is a constant, then ${\partial }_x^{\nu }C=0$; $\forall x\in (0,l)$, $\nu \in (n-1,n]$, $n\in \mathbb{N}$, then

$${\partial }_x^{\nu }{x}^m=\left\{\begin{array}{cc}0\hfill & ifm\in {\mathbb{N}}_0,m<\lceil \nu \rceil ,\hfill \\ \frac{\mathsf{\Gamma }(m+1)}{\mathsf{\Gamma }(m+1-\nu )}{x}^{m-\nu },\hfill & ifm\in {\mathbb{N}}_0,m\ge \lceil \nu \rceil ,orm\notin \mathbb{N},m>\lfloor \nu \rfloor .\hfill \end{array}\right.$$

It follows from the above lemma that

$$\begin{array}{ccc}\hfill & & {\partial }_x^{\nu }{P}_{0,l,i}^{\alpha ,\beta }\left(x\right)\hfill & & =& \sum _{k=\lceil \nu \rceil }^i\frac{{(-1)}^{i-k}\mathsf{\Gamma }(i+\beta +1)\mathsf{\Gamma }(i+k+\alpha +\beta +1)}{l^k(i-k)!\mathsf{\Gamma }(k+1-\nu )\mathsf{\Gamma }(i+\alpha +\beta +1)\mathsf{\Gamma }(k+\beta +1)}{x}^{k-\nu }.\hfill \end{array}$$

(13)

The formulas of the FDMs for Caputo fractional derivatives are, hence, presented in the following theorem.

Theorem 1.

The Jacobi–Caputo fractional differentiation matrix of order ν with the shifted JGL or JGR collocation points ${\left\{y_j^{\alpha ,\beta }\right\}}_{j=0}^N$ is formulated as follows:

$${}^c{\mathit{D}}_s^{\left(\nu \right)}:=\mathit{ZA}\mathit{T},$$

where $\mathit{T}:=\left(t_{ij}^{\alpha ,\beta }\right)$ with $t_{ij}^{\alpha ,\beta }$ defined in (4), $\mathit{Z}:=\left(z_{jm}\right)$ with for $j=0,1,\cdots ,N$:

$$z_{jm}=\left\{\begin{array}{cc}0,\hfill & m=0,\cdots ,\lceil \nu \rceil -1,\hfill \\ {\left(y_j^{\alpha ,\beta }\right)}^{m-\nu },\hfill & m=\lceil \nu \rceil ,\cdots ,N,\hfill \end{array}\right.$$

(14)

and $\mathit{A}:=\left(a_{mi}\right)$ with for $i=0,1,\cdots ,N$,

$$a_{mi}=\left\{\begin{array}{cc}{l}^{-m}{(-1)}^{i-m}\frac{\mathsf{\Gamma }(i+\beta +1)\mathsf{\Gamma }(i+m+\alpha +\beta +1)}{(i-m)!\mathsf{\Gamma }(m+1-\nu )\mathsf{\Gamma }(i+\alpha +\beta +1)\mathsf{\Gamma }(m+\beta +1)}\hfill & m=\lceil \nu \rceil ,\cdots ,i,\hfill \\ 0\hfill & m=0,\cdots ,\lceil \nu \rceil -1,\hfill \\ 0\hfill & i<m\le N.\hfill \end{array}\right.$$

(15)

The Chebyshev polynomial of first kind is related to the Jacobi polynomials of $\alpha =\beta =-1/2$ as

$$P_n^{-\frac{1}{2},-\frac{1}{2}}\left(x\right)=\frac{\mathsf{\Gamma }(n+\frac{1}{2})}{\mathsf{\Gamma }(n+1)\mathsf{\Gamma }\left(\frac{1}{2}\right)}{T}_n\left(x\right),$$

(16)

where $T_n\left(x\right)=cos(narccosx)$ is the nth-degree Chebyshev polynomial. The Chebyshev–Gauss–Lobatto (CGL) collocation points are

$$x_j^{-\frac{1}{2},-\frac{1}{2}}=-cos\left(\frac{j\pi }{N}\right),j=0,\cdots ,N,$$

and the Chebyshev–Gauss–Radau (CGR) collocation points are

$$x_j^{-\frac{1}{2},-\frac{1}{2}}=-cos\left(\frac{2j\pi }{2N+1}\right),j=0,\cdots ,N.$$

The following corollary gives the formulas of the Chebyshev fractional differentiation matrix for the Caputo fractional derivative.

Corollary 1.

The Chebyshev–Caputo fractional differentiation matrix of order ν with the shifted CGL or CGR collocation points ${\left\{y_j^{-\frac{1}{2},-\frac{1}{2}}\right\}}_{j=0}^N$ is formulated as follows:

$${}^c{\mathit{D}}_s^{\left(\nu \right)}:=\mathit{ZA}{\mathit{T}}_C,$$

where $\mathit{Z}:=\left(z_{jm}\right)$ with $z_{jm}$ defined in (14), $\mathit{A}:=\left(a_{mi}\right)$ with for $i=0,1,\cdots ,N$:

$$a_{mi}=\left\{\begin{array}{cc}\frac{l^{-m}{(-1)}^{i-m}i\mathsf{\Gamma }(1/2)\mathsf{\Gamma }(i+m)}{(i-m)!\mathsf{\Gamma }(m+1-\nu )\mathsf{\Gamma }(m+1/2)}\hfill & m=\lceil \nu \rceil ,\cdots ,i,\hfill \\ 0\hfill & m=0,\cdots ,\lceil \nu \rceil -1,\hfill \\ 0\hfill & i<m\le N,\hfill \end{array}\right.$$

and ${\mathit{T}}_C:=\left(t_{ij}\right)$ with for $i=0,1,\cdots ,N$:

$$t_{ij}={(-1)}^i\frac{2cos\left(\frac{ij\pi }{N}\right)}{c_i{c}_{j}N},c_0=c_N=2,c_i=1,i=1,\cdots ,N-1$$

for the CGL collocation points, and

$$t_{ij}={(-1)}^i\frac{4cos\left(\frac{2ij\pi }{2N+1}\right)}{{\tilde{c}}_i{\tilde{c}}_j(2N+1)},{\tilde{c}}_0=2,{\tilde{c}}_i=1,i=1,\cdots ,N$$

for the CGR collocation points.

Proof. 

Using (4), (12) and (16), we have

$$u_N\left(x\right)=\sum _{j=0}^{N}u\left(y_j^{\alpha ,\beta }\right)\sum _{i=0}^N{C}_i^2\frac{{\omega }_j}{{\gamma }_i}{T}_i\left(x_j^{-\frac{1}{2},-\frac{1}{2}}\right)T_{0,l,i}\left(x\right),$$

where $C_i=\frac{\mathsf{\Gamma }(i+\frac{1}{2})}{\mathsf{\Gamma }(i+1)\mathsf{\Gamma }\left(\frac{1}{2}\right)}$ and $T_{0,l,i}\left(x\right)$ is the shifted ith-degree Chebyshev polynomial. By the definition of ${\gamma }_i$ in (6), we have

$${\gamma }_i=C_i^2{\int }_{-1}^1{\left[T_i\left(x\right)\right]}^2{(1-x^2)}^{-\frac{1}{2}}dx:=C_i^2{\tilde{\gamma }}_i,$$

thus for the CGL collocation points,

$$u_N\left(x\right)=\sum _{j=0}^{N}u\left(y_j^{\alpha ,\beta }\right)\sum _{i=0}^N\frac{{\omega }_j}{{\tilde{\gamma }}_i}cos\left(\frac{ij\pi }{N}\right)T_{0,l,i}\left(x\right),$$

and for the CGR collocation points,

$$u_N\left(x\right)=\sum _{j=0}^{N}u\left(y_j^{\alpha ,\beta }\right)\sum _{i=0}^N\frac{{\omega }_j}{{\tilde{\gamma }}_i}cos\left(\frac{2ij\pi }{2N+1}\right)T_{0,l,i}\left(x\right).$$

According to [34], when the CGL collocation points are used,

$${\omega }_j=\frac{\pi }{N},j=1,\cdots ,N-1,{\omega }_0={\omega }_N=\frac{\pi }{2N},\mathrm{and}{\tilde{\gamma }}_i=\frac{\pi }{2},i=1,\cdots ,N-1,{\tilde{\gamma }}_0={\tilde{\gamma }}_N=\pi ;$$

when the CGR collocation points are used,

$${\omega }_0=\frac{\pi }{2N+1},{\omega }_j=\frac{2\pi }{2N+1},j=1,\cdots ,N,\mathrm{and}{\tilde{\gamma }}_i=\frac{\pi }{2},i=1,\cdots ,N,{\tilde{\gamma }}_0=\pi .$$

Hence, the formula of the elements of ${\mathit{T}}_C$ is verified.

The Caputo fractional derivative of order $\nu$ of $T_{0,l,i}\left(x\right)$ is

$${\partial }_x^{\nu }{T}_{0,l,i}\left(x\right)=\mathsf{\Gamma }\left(\frac{1}{2}\right)\sum _{k=\lceil \nu \rceil }^i\frac{l^{-k}{(-1)}^{i-k}i\mathsf{\Gamma }(i+k)}{(i-k)!\mathsf{\Gamma }(k+1-\nu )\mathsf{\Gamma }(k+\frac{1}{2})}{x}^{k-\nu },$$

which verifies the the formula of the elements of $\mathit{Z}$, $\mathit{A}$ and completes the proof. □

When $\alpha =\beta =0,$ the Jacobi polynomials $P_i^{0,0}\left(x\right)$ become Legendre polynomials $L_i\left(x\right)$. The Legendre–Gauss–Lobatto (LGL) quadrature nodes ${\left\{x_j^{0,0}\right\}}_{j=0}^N$ are zeros of $(1-x^2){\partial }_x{L}_{N+1}\left(x\right)$, and the Legendre–Gauss–Radau (LGR) quadrature nodes ${\left\{x_j^{0,0}\right\}}_{j=0}^N$ are zeros of $L_N\left(x\right)+L_{N+1}\left(x\right)$. The following corollary delivers the expression of Legendre–Caputo fractional differentiation matrix.

Corollary 2.

The Legendre–Caputo fractional differentiation matrix of order ν with the shifted LGL or LGR collocation points ${\left\{y_j^{0,0}\right\}}_{j=0}^N$ is formulated as follows:

$${}^c{\mathit{D}}_s^{\left(\nu \right)}:=\mathit{ZA}{\mathit{T}}_L,$$

where $\mathit{Z}:=\left(z_{jm}\right)$ with $z_{jm}$ defined in (14), $\mathit{A}:=\left(a_{mi}\right)$ with for $i=0,1,\cdots ,N$:

$$a_{mi}=\left\{\begin{array}{cc}{l}^{-m}{(-1)}^{i-m}\frac{\mathsf{\Gamma }(i+m+1)}{(i-m)!\mathsf{\Gamma }(m+1-\nu )\mathsf{\Gamma }(m+1)}\hfill & m=\lceil \nu \rceil ,\cdots ,i,\hfill \\ 0\hfill & m=0,\cdots ,\lceil \nu \rceil -1,\hfill \\ 0\hfill & i<m\le N,\hfill \end{array}\right.$$

and ${\mathit{T}}_L:=\left(t_{ij}\right)$ with for $j=0,1,\cdots ,N$:

$$t_{ij}=\left\{\begin{array}{cc}\hfill & \frac{2i+1}{N(N+1)L_N^2\left(x_j\right)}{L}_i\left(x_j\right),i=0,1,\cdots ,N-1,\hfill \\ \hfill & \frac{1}{(N+1)L_N\left(x_j\right)},i=N,\hfill \end{array}\right.$$

for the LGL collocation points, and

$$t_{ij}=\frac{(2i+1)(1-x_j)}{2{(N+1)}^2{L}_N^2\left(x_j\right)}{L}_i\left(x_j\right),i=0,1,\cdots ,N,$$

(17)

for the LGR collocation points.

Proof. 

The formula of the elements of $\mathit{Z}$ and $\mathit{A}$ can be easily verified by taking $\alpha =\beta =0$ in Theorem 1. According to [34], when the LGL collocation points are used,

$${\omega }_j=\frac{2}{N(N+1)L_N^2\left(x_j\right)},j=0,1,\cdots ,N,\mathrm{and}{\gamma }_i=\frac{2}{2i+1},i=0,\cdots ,N-1,{\gamma }_N=\frac{2}{N};$$

when the LGR collocation points are used,

$${\omega }_j=\frac{1-x_j}{{(N+1)}^2{L}_N^2\left(x_j\right)},j=0,1,\cdots ,N,\mathrm{and}{\gamma }_i=\frac{2}{2i+1},i=0,\cdots ,N.$$

Thus, the formula of the elements in ${\mathit{T}}_L$ is proven. □

Corollary 3.

The Caputo fractional differentiation matrix of order ν with the shifted JGL or JGR collocation points ${\left\{y_j^{\alpha ,0}\right\}}_{j=0}^N$ is formulated as follows:

$${}^c{\mathbf{D}}_s^{\left(\nu \right)}:={\mathbf{R}}^{\prime }\mathit{T},$$

where $\mathit{T}:=\left(t_{ij}^{\alpha ,0}\right)$ with $t_{ij}^{\alpha ,0}$ defined in (4) by taking $\beta =0$ and $\mathbf{R}:=\left(r_{ij}\right)$ with

$$r_{ij}=\left\{\begin{array}{cc}\frac{\mathsf{\Gamma }(i+1)}{\mathsf{\Gamma }(i-\nu +1)}{\left(y_j^{\alpha ,0}\right)}^{-\nu }{P}_{0,l,i}^{\alpha +\nu ,-\nu }\left(y_j^{\alpha ,0}\right)-\sum _{k=0}^{\lfloor \nu \rfloor }\frac{{(-1)}^{i-k}\left(\genfrac{}{}{0pt}{}{i}{k}\right)\mathsf{\Gamma }(i+k+\alpha +1)}{l^k\mathsf{\Gamma }(k+1-\nu )\mathsf{\Gamma }(i+\alpha +1)}{\left(y_j^{\alpha ,0}\right)}^{k-\nu },\hfill & \mathrm{if}i>\lfloor \nu \rfloor ,j>0,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Proof. 

When $x=0$, ${\partial }_x^{\nu }{P}_{0,l,i}^{\alpha ,0}\left(0\right)=0$. When $\beta =0$, $x\ne 0$, and $i>\nu$, we have

$$\begin{array}{lll}& {\partial }_x^{\nu }{P}_{0,l,i}^{\alpha ,0}\left(x\right)\hfill & & =& \sum _{k=\lceil \nu \rceil }^i\frac{{(-1)}^{i-k}\mathsf{\Gamma }(i+1)\mathsf{\Gamma }(i+k+\alpha +1)}{l^k(i-k)!k!\mathsf{\Gamma }(k+1-\nu )\mathsf{\Gamma }(i+\alpha +1)}{x}^{k-\nu }\hfill \\ & =& x^{-\nu }\frac{\mathsf{\Gamma }(i+1)}{\mathsf{\Gamma }(i-\nu +1)}\sum _{k=\lceil \nu \rceil }^i\frac{{(-1)}^{i-k}\mathsf{\Gamma }(i-\nu +1)\mathsf{\Gamma }(i+k+\alpha +1)}{l^k(i-k)!k!\mathsf{\Gamma }(k+1-\nu )\mathsf{\Gamma }(i+\alpha +1)}{x}^k\hfill \\ & =& x^{-\nu }\left(\frac{\mathsf{\Gamma }(i+1)}{\mathsf{\Gamma }(i-\nu +1)}{P}_{0,l,i}^{\alpha +\nu ,-\nu }\left(x\right)-\sum _{k=0}^{\lfloor \nu \rfloor }\frac{{(-1)}^{i-k}\left(\genfrac{}{}{0pt}{}{i}{k}\right)\mathsf{\Gamma }(i+k+\alpha +1)}{l^k\mathsf{\Gamma }(k+1-\nu )\mathsf{\Gamma }(i+\alpha +1)}{x}^k\right).\hfill \end{array}$$

The proof is complete according to (12) and (18). □

When $\beta =0$ and if $0<\nu <1$, according to the proof of the above corollary, we have

$$\begin{array}{ccc}& & {\partial }_x^{\nu }{P}_{0,l,i}^{\alpha ,0}\left(x\right)=x^{-\nu }\left(\frac{\mathsf{\Gamma }(i+1)}{\mathsf{\Gamma }(i-\nu +1)}{P}_{0,l,i}^{\alpha +\nu ,-\nu }\left(x\right)-\frac{{(-1)}^i}{\mathsf{\Gamma }(1-\nu )}\right),\hfill \end{array}$$

then the element $r_{ij},i>\lfloor \nu \rfloor ,j>0$ of matrix $\mathbf{R}$ in the above corollary has the following form:

$$\frac{\mathsf{\Gamma }(i+1)}{\mathsf{\Gamma }(i-\nu +1)}{\left(y_j^{\alpha ,0}\right)}^{-\nu }{P}_{0,l,i}^{\alpha +\nu ,-\nu }\left(y_j^{\alpha ,0}\right)-\frac{{(-1)}^i}{\mathsf{\Gamma }(1-\nu )}{\left(y_j^{\alpha ,0}\right)}^{-\nu }.$$

4. Algorithm and Numerical Examples for the Generalized Space–Fractional Burgers’ Equations

The generalized space–fractional Burgers’ equation depicts the acoustic phenomenon of a sound wave with weak nonlinearity propagating through a gas-filled tube in one direction [12]. In this section, we intended to apply the Jacobi–Caputo fractional differentiation matrix derived in the previous section to solve the generalized space–fractional Burgers’ equation defined as follows:

$$\left\{\begin{array}{c}{\partial }_{t}u(x,t)-\eta {\partial }_x^{\nu }u(x,t)+ϵu(x,t){\partial }_{x}u(x,t)-\mu {\partial }_x^{2}u(x,t)=g\left(x\right),\hfill \\ 0<t<T,0<x<1,\hfill \\ u(0,t)=u(1,t)=0,0<t<T,\hfill \\ u(x,0)=u_0\left(x\right),0<x<1,\hfill \end{array}\right.$$

(18)

where $\eta$, $\mu$, and $ϵ$ are arbitrary positive numbers and the fractional order of the Caputo derivative $\nu$ is a positive number less than 1.

Firstly, let ${\left\{y_j^{\alpha ,\beta }\right\}}_{j=0}^N$ be a set of the shifted JGL collocation points. The shifted Jacobi spectral collocation method for (18) is to find $u_N(·,t)\in P_N\left([0,1]\right)$, such that

$$\left\{\begin{array}{c}{\partial }_t{u}_N\left(y_j^{\alpha ,\beta },t\right)=\eta {\partial }_x^{\nu }{u}_N\left(y_j^{\alpha ,\beta },t\right)-ϵu_N\left(y_j^{\alpha ,\beta },t\right){\partial }_x{u}_N\left(y_j^{\alpha ,\beta },t\right)\hfill \\ +\mu {\partial }_x^2{u}_N\left(y_j^{\alpha ,\beta },t\right)+g(y_j^{\alpha ,\beta },t),j=1,2,\dots ,N-1,0<t<T,\hfill \\ u_N\left(y_0^{\alpha ,\beta },t\right)=0,u_N\left(y_N^{\alpha ,\beta },t\right)=0,0<t<T,\hfill \\ u_N\left(y_j^{\alpha ,\beta },0\right)=u_0\left(y_j^{\alpha ,\beta }\right),j=0,1,\dots ,N.\hfill \end{array}\right.$$

(19)

Let ${}^c{\mathit{D}}_{1:N-1}^{\left(\nu \right)}$, ${\mathit{D}}_{1:N-1}$, and ${\mathit{D}}_{1:N-1}^{\left(2\right)}$ be $(N-1)\times (N-1)$ square matrices by removing the 1st, $N+1$st columns and rows, respectively from ${}^c{\mathit{D}}_s^{\left(\nu \right)}$, $\mathbf{D}$, and ${\mathit{D}}^2$. In accordance with (11), (19) can be rewritten in the following matrix–vector representation:

$$\left\{\begin{array}{c}{\partial }_t\mathit{u}\left(t\right)=\eta {}^c{\mathit{D}}_{1:N-1}^{\left(\nu \right)}\mathit{u}\left(t\right)-ϵ\mathit{u}\left(t\right)·{\mathit{D}}_{1:N-1}\mathit{u}\left(t\right)+\mu {\mathit{D}}_{1:N-1}^{\left(2\right)}\mathit{u}\left(t\right)+\mathit{g}\left(t\right),\hfill \\ \mathit{u}\left(0\right)={\mathit{u}}_0,\hfill \end{array}\right.$$

(20)

where

$$\begin{array}{cc}\hfill & {\partial }_t\mathbf{u}\left(t\right)={\left[{\partial }_t{u}_N\left(y_1^{\alpha ,\beta },t\right),{\partial }_t{u}_N\left(y_2^{\alpha ,\beta },t\right),\dots ,{\partial }_t{u}_N\left(y_{N-1}^{\alpha ,\beta },t\right)\right]}^T,\hfill \\ \hfill & \mathbf{u}\left(t\right)={\left[u_N\left(y_1^{\alpha ,\beta },t\right),u_N\left(y_2^{\alpha ,\beta },t\right),\dots ,u_N\left(y_{N-1}^{\alpha ,\beta },t\right)\right]}^T,\hfill \\ \hfill & {\mathbf{u}}_0={\left[u_0\left(y_1^{\alpha ,\beta }\right),u_0\left(y_2^{\alpha ,\beta }\right),\dots ,u_0\left(y_{N-1}^{\alpha ,\beta }\right)\right]}^T,\hfill \\ \hfill & \mathbf{g}\left(t\right)={\left[g\left(y_1^{\alpha ,\beta },t\right),g\left(y_2^{\alpha ,\beta },t\right),\dots ,g\left(y_{N-1}^{\alpha ,\beta },t\right)\right]}^T.\hfill \end{array}$$

Two examples of the generalized space–fractional Burgers’ equation are given below.

Example 1.

In this example, the function on the right-hand side of (18) is chosen to be

$$\begin{array}{ccc}\hfill g(x,t)& =& g_1(x,t)+g_2(x,t)+g_3(x,t)+g_4(x,t),\hfill \\ \hfill g_1(x,t)& =& -\left(e^{\sigma x}-(e^{\sigma }-1)x-1\right)e^{-t},\hfill \\ \hfill g_2(x,t)& =& \epsilon \left(e^{\sigma x}-(e^{\sigma }-1)x-1\right)\left(\sigma e^{\sigma x}-e^{\sigma }+1\right)e^{-2t},\hfill \\ \hfill g_3(x,t)& =& -\mu {\sigma }^2{e}^{-t+\sigma x},\hfill \\ \hfill g_4(x,t)& =& \eta \left({\sigma }^{\lceil \nu \rceil }{x}^{\lceil \nu \rceil -\nu }{E}_{1,\lceil \nu \rceil +1-\nu }\left(\sigma x\right)-\frac{\mathsf{\Gamma }\left(2\right)}{\mathsf{\Gamma }(2-\nu )}(e^{\sigma }-1)x^{1-\nu }\right)e^{-t},\hfill \end{array}$$

where $E_{a,b}\left(x\right)$ is the two-parameter Mittag–Leffler function. The exact solution of (18) is $\left(e^{\sigma x}-(e^{\sigma }-1)x-1\right)e^{-t}$.

Example 2.

Let $g(x,t)$ in (18) be chosen as

$$\begin{array}{ccc}\hfill g(x,t)& =& g_1(x,t)+g_2(x,t)+g_3(x,t)+g_4(x,t),\hfill \\ \hfill g_1(x,t)& =& -sin\left(\pi x\right)e^{-t},\hfill \\ \hfill g_2(x,t)& =& ϵ\frac{\pi }{2}sin\left(2\pi x\right)e^{-2t},\hfill \\ \hfill g_3(x,t)& =& \mu {\pi }^{2}sin\left(\pi x\right)e^{-t},\hfill \\ \hfill g_4(x,t)& =& \eta \frac{\pi x^{1-\nu }}{(1-\nu )\mathsf{\Gamma }(1-\nu )}{}_1{F}_2(1;1-\frac{\nu }{2},\frac{3}{2}-\frac{\nu }{2};-\frac{1}{4}{\pi }^2{x}^2)e^{-t},\hfill \end{array}$$

where ${}_1{F}_2$ is the generalized hypergeometric function. The exact solution of (18) is $sin\left(\pi x\right)e^{-t}$.

In the numerical simulations, we used the fourth-order Runge–Kutta method, a highly accurate algorithm, to solve the system of ODEs (20) and chose $\Delta t$ = 1.0 × 10${}^{-4}$ to make sure that the error resulting in the direction of time was small enough. We performed the numerical simulations with the fractional orders $\nu$ being $0.3$, $0.6$, and $0.9$ and chose the CGL, LGL, and JGL($\alpha =-\nu ,\beta =0$) quadrature nodes as collocation points. In Table 1 and Table 2, we show the root-mean-squared (RMS) errors of the numerical solution at the collocation points at $T=1$ of Examples 1 and 2, respectively. The RMS errors of these two numerical examples with $\nu =0.6$ using our method and the Jacobi operational matrix method proposed in [21] are plotted in Figure 1. The numerical results indicated the fast convergence of the methods and illustrated that our proposed algorithm in this section performed much better than the methods in [21].

Table 1. RMS errors of numerical solutions of Example 1 at $T=1$ when $ϵ=\mu =\eta =1$, $\sigma =1$, and $\tau$ = 1.0 × 10${}^{-4}$.

	N	$\mathit{\nu }=0.3$	$\mathit{\nu }=0.6$	$\mathit{\nu }=0.9$
	4	6.0362 × 10${}^{-6}$	5.9249 × 10${}^{-6}$	6.2110 × 10${}^{-6}$
$\alpha =-\frac{1}{2}$	8	3.4641 × 10${}^{-12}$	3.4508 × 10${}^{-12}$	3.5460 × 10${}^{-12}$
$\beta =-\frac{1}{2}$	12	1.0282 × 10${}^{-15}$	9.6164 × 10${}^{-16}$	9.4303 × 10${}^{-16}$
	4	5.5072 × 10${}^{-7}$	1.3705 × 10${}^{-7}$	6.5986 × 10${}^{-7}$
$\alpha =0$	8	1.8781 × 10${}^{-13}$	2.6166 × 10${}^{-14}$	4.2505 × 10${}^{-13}$
$\beta =0$	12	7.9866 × 10${}^{-16}$	7.7894 × 10${}^{-16}$	7.9360 × 10${}^{-16}$
	4	2.5969 × 10${}^{-6}$	3.8212 × 10${}^{-6}$	5.6797 × 10${}^{-6}$
$\alpha =-\nu$	8	1.7825 × 10${}^{-12}$	2.2046 × 10${}^{-12}$	3.1671 × 10${}^{-12}$
$\beta =0$	12	8.8606 × 10${}^{-16}$	1.1035 × 10${}^{-15}$	1.5604 × 10${}^{-15}$

Table 2. RMS errors of numerical solutions of Example 2 at $T=1$ when $ϵ=\mu =\eta =1$ and $\tau$ = 1.0 × 10${}^{-4}$.

	N	$\mathit{\nu }=0.3$	$\mathit{\nu }=0.6$	$\mathit{\nu }=0.9$
	4	8.8219 × 10${}^{-4}$	8.9389 × 10${}^{-4}$	9.2472 × 10${}^{-4}$
$\alpha =-\frac{1}{2}$	8	1.8921 × 10${}^{-8}$	1.8993 × 10${}^{-8}$	1.9393 × 10${}^{-8}$
$\beta =-\frac{1}{2}$	12	1.7631 × 10${}^{-13}$	1.7707 × 10${}^{-13}$	1.8036 × 10${}^{-13}$
	16	2.9591 × 10${}^{-15}$	3.6478 × 10${}^{-15}$	5.5501 × 10${}^{-15}$
	4	3.1279 × 10${}^{-4}$	3.1274 × 10${}^{-4}$	3.2005 × 10${}^{-4}$
$\alpha =0$	8	9.6568 × 10${}^{-9}$	9.6444 × 10${}^{-9}$	9.7385 × 10${}^{-9}$
$\beta =0$	12	9.6773 × 10${}^{-14}$	9.6694 × 10${}^{-14}$	9.7314 × 10${}^{-14}$
	16	2.4675 × 10${}^{-15}$	2.6880 × 10${}^{-15}$	3.4963 × 10${}^{-15}$
	4	4.0505 × 10${}^{-4}$	4.9560 × 10${}^{-4}$	6.1909 × 10${}^{-4}$
$\alpha =-\nu$	8	1.2005 × 10${}^{-8}$	1.3271 × 10${}^{-8}$	1.4142 × 10${}^{-8}$
$\beta =0$	12	1.2032 × 10${}^{-13}$	1.2645 × 10${}^{-13}$	1.3179 × 10${}^{-13}$
	16	2.5721 × 10${}^{-15}$	4.3107 × 10${}^{-15}$	1.8257 × 10${}^{-14}$

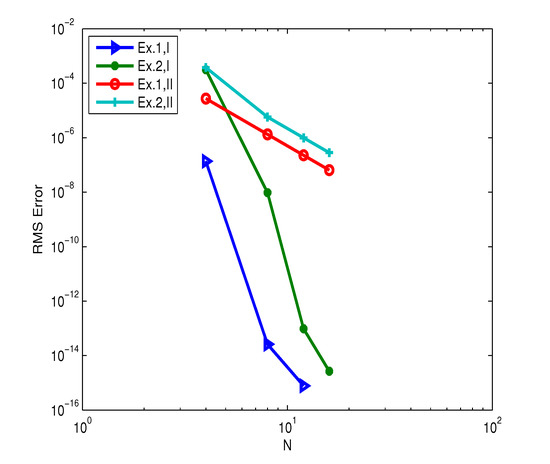
Figure 1. Numerical results of Examples 1 and 2 when $\nu =0.6$ and $\alpha =\beta =0$. I: results by using methods proposed in this paper; II: results by using methods proposed in [21].

5. Algorithm and Numerical Examples for Initial Fractional Integro-Differential Equations

In this section, we numerically solved the initial fractional integro-differential equation (FIDE) in the following form:

$$\left\{\begin{array}{cc}\hfill {\partial }_t^{\nu }u\left(t\right)& =f\left(t\right)u\left(t\right)+{\int }_0^{t}K(t,s)u\left(s\right)ds+g\left(t\right),0<t\le T,\hfill \\ \hfill u\left(0\right)& =u_0,\hfill \end{array}\right.$$

(21)

with the fractional order of the Caputo derivative $\nu \in (0,1)$.

The algorithm developed in the section for (21) is to find $u_N\left(t\right)\in P_N\left([0,T]\right)$, such that

$$\left\{\begin{array}{cc}\hfill {\partial }_t^{\nu }{u}_N\left(y_m^{\alpha ,\beta }\right)& =f\left(y_m^{\alpha ,\beta }\right)u_N\left(y_m^{\alpha ,\beta }\right)\hfill \\ \hfill & +{\int }_0^{y_m^{\alpha ,\beta }}K(y_m^{\alpha ,\beta },s)u_N\left(s\right)ds+g\left(y_m^{\alpha ,\beta }\right),m=1,\cdots ,N,\hfill \\ \hfill u\left(0\right)& =u\left(y_0^{\alpha ,\beta }\right)=u_0.\hfill \end{array}\right.$$

(22)

where $y_m^{\alpha ,\beta },m=0,\cdots ,N,$ are the JGR points.

Let $s(\theta ,y_m^{\alpha ,\beta })=\frac{y_m^{\alpha ,\beta }}{2}(\theta +1),-1\le \theta \le 1$. By the change of variable, one has

$${\int }_0^{y_m^{\alpha ,\beta }}K(y_m^{\alpha ,\beta },s)u_N\left(s\right)ds=\frac{y_m^{\alpha ,\beta }}{2}{\int }_{-1}^{1}K(y_m^{\alpha ,\beta },\frac{y_m^{\alpha ,\beta }}{2}(\theta +1))u_N\left(\frac{y_m^{\alpha ,\beta }}{2}(\theta +1)\right)d\theta .$$

Suppose that ${\theta }_k^{0,0},k=0.\cdots ,N$ is the LGR quadrature nodes and the integration can be approximated by a corresponding LGR quadrature rule with respect to the Jacobi weights ${\omega }_k^{0,0},k=0.\cdots ,N$; we hence have

$$\left\{\begin{array}{cc}\hfill {\partial }_t^{\nu }{u}_N\left(y_m^{\alpha ,\beta }\right)& =f\left(y_m^{\alpha ,\beta }\right)u_N\left(y_m^{\alpha ,\beta }\right)+g\left(y_m^{\alpha ,\beta }\right)\hfill \\ & +\frac{y_m^{\alpha ,\beta }}{2}\sum _{k=0}^{N}K\left(y_m^{\alpha ,\beta },\frac{y_m^{\alpha ,\beta }}{2}({\theta }_k^{0,0}+1)\right)u_N\left(\frac{y_m^{\alpha ,\beta }}{2}({\theta }_k^{0,0}+1)\right){\omega }_k^{0,0},m=1,\cdots ,N,\hfill \\ \hfill u\left(y_0^{\alpha ,\beta }\right)& =u_0.\hfill \end{array}\right.$$

(23)

Let $u_j=u\left(y_j^{\alpha ,\beta }\right)$,$f_j=f\left(y_j^{\alpha ,\beta }\right)$, $g_j=g\left(y_j^{\alpha ,\beta }\right),j=0,\cdots ,N$. According to (12) and (13), we have

$$\begin{array}{cc}\hfill & \sum _{i=0}^N\sum _{j=1}^N{u}_j{t}_{ij}\sum _{k=\lceil \nu \rceil }^i\frac{{(-1)}^{i-k}\mathsf{\Gamma }(i+\beta +1)\mathsf{\Gamma }(i+k+\alpha +\beta +1)}{L^k(i-k)!\mathsf{\Gamma }(k+1-\nu )\mathsf{\Gamma }(i+\alpha +\beta +1)\mathsf{\Gamma }(k+\beta +1)}{\left(y_m^{\alpha ,\beta }\right)}^{k-\nu }\hfill \\ \hfill & =\frac{y_m^{\alpha ,\beta }}{2}\sum _{i=0}^N\sum _{j=1}^N{u}_j{t}_{ij}\sum _{k=0}^{N}K\left(y_m^{\alpha ,\beta },\frac{y_m^{\alpha ,\beta }({\theta }_k^{0,0}+1)}{2}\right)P_{0,L,i}^{\alpha ,\beta }\left(\frac{y_m^{\alpha ,\beta }({\theta }_k^{0,0}+1)}{2}\right){\omega }_k^{0,0}\hfill \\ \hfill & +\frac{y_m^{\alpha ,\beta }}{2}{u}_0\sum _{i=0}^N{t}_{i0}\sum _{k=0}^{N}K\left(y_m^{\alpha ,\beta },\frac{y_m^{\alpha ,\beta }({\theta }_k^{0,0}+1)}{2}\right)P_{0,L,i}^{\alpha ,\beta }\left(\frac{y_m^{\alpha ,\beta }({\theta }_k^{0,0}+1)}{2}\right){\omega }_k^{0,0}\hfill \\ \hfill & -u_0\sum _{i=0}^N{t}_{i0}\sum _{k=\lceil \nu \rceil }^i\frac{{(-1)}^{i-k}\mathsf{\Gamma }(i+\beta +1)\mathsf{\Gamma }(i+k+\alpha +\beta +1)}{L^k(i-k)!\mathsf{\Gamma }(k+1-\nu )\mathsf{\Gamma }(i+\alpha +\beta +1)\mathsf{\Gamma }(k+\beta +1)}{\left(y_m^{\alpha ,\beta }\right)}^{k-\nu }\hfill \\ \hfill & +f_m{u}_m+g_m,m=1,\cdots ,N.\hfill \end{array}$$

(24)

In the next step, we worked on converting (24) into a vector–matrix form and started with the quadrature part first.

Let $\mathit{W}=\left(w_{mi}\right)$ with

$$w_{mi}=\frac{y_m^{\alpha ,\beta }}{2}\sum _{k=0}^{N}K\left(y_m^{\alpha ,\beta },\frac{y_m^{\alpha ,\beta }({\theta }_k^{0,0}+1)}{2}\right)P_{0,L,i}^{\alpha ,\beta }\left(\frac{y_m^{\alpha ,\beta }({\theta }_k^{0,0}+1)}{2}\right){\omega }_k^{0,0}.$$

The operational matrix for the quadrature part can, hence, be written as

$$\mathit{M}=\mathit{W}\mathit{T},$$

(25)

where the elements in $\mathit{T}$ are defined in (4). Let $\mathit{f}={(f_0,f_1,\cdots ,f_N)}^{\prime }$, $\mathbf{u}={\left(u_0,u_1,\cdots ,u_N\right)}^{\prime }$, and $\mathit{g}={\left(g_0,g_1,\cdots ,g_N\right)}^{\prime }$. Suppose that ${}^c{\mathit{D}}_{1:N}^{\left(\nu \right)}$ and ${\mathit{M}}_{1:N}$ are $N\times N$ square matrices by removing the first row and column, respectively, from ${}^c{\mathit{D}}_s^{\left(\nu \right)}$ and $\mathit{M}$, while ${}^c{\mathit{d}}_i^{\left(\nu \right)}$ and ${\mathit{m}}_i$ are the $(i+1)$th column of ${}^c{\mathit{D}}_s^{\left(\nu \right)}$ and $\mathit{M}$ without the first element; ${\mathit{f}}_{1:N}$, ${\mathit{g}}_{1:N}$, and ${\mathbf{u}}_{1:N}$ are vectors formed by the last N elements of $\mathit{f}$, $\mathit{g}$, and $\mathit{u}$, respectively. The vector–matrix form of (24) is

$${}^c{\mathit{D}}_{1:N}^{\left(\nu \right)}{\mathit{u}}_{1:N}={\mathit{f}}_{1:N}·{\mathit{u}}_{1:N}+{\mathit{M}}_{1:N}{\mathit{u}}_{1:N}+{\mathit{g}}_{1:N}+u_0{\mathit{m}}_0-u_0{}^c{\mathit{d}}_0^{\left(\nu \right)}.$$

(26)

Example 3.

$$\left\{\begin{array}{cc}\hfill {\partial }_t^{\nu }u\left(t\right)& =u\left(t\right)+{\int }_0^t(t+s)u\left(s\right)ds-t^3+t^2\hfill \\ & -\frac{\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(3-\nu )}{t}^{2-\nu }+\frac{\mathsf{\Gamma }\left(4\right)}{\mathsf{\Gamma }(4-\nu )}{t}^{3-\nu }+\frac{7}{12}{t}^4-\frac{9}{20}{t}^5,\hfill \\ \hfill u\left(0\right)& =0,\hfill \end{array}\right.$$

(27)

in association with the analytic solution $u\left(t\right)=t^2(t-1)$.

Example 4.

$$\left\{\begin{array}{cc}\hfill {\partial }_t^{\nu }u\left(t\right)& =u\left(t\right)+{\int }_0^t(t-s)u\left(s\right)ds\hfill \\ & +\frac{t^{1-\nu }}{(1-\nu )\mathsf{\Gamma }(1-\nu )}{}_1{F}_2(1;1-\frac{\nu }{2},\frac{3}{2}-\frac{\nu }{2};-\frac{t^2}{4})-t,\hfill \\ \hfill u\left(0\right)& =0,\hfill \end{array}\right.$$

(28)

with ${}_1{F}_2$ being the generalized hypergeometric function and the exact solution $u\left(t\right)=sin\left(t\right)$.

We took the fractional order to be $\nu =0.6$, used the LGR collocation points, and chose $N=16$ in the numerical simulations. The absolute errors at the collocation points of Example 3 and 4 are plotted in the right panel in Figure 2 together with the numerical results produced by the methods proposed in [39]. The FIDE (21) was converted into an integral equation by taking the fractional-order integral and then approximated by the Gaussian quadrature rule with Jacobi collocation points in [39]. One can observe from the figure that the algorithm proposed in the section performs better compared to the methods in [39]. The numerical results matched well with the analytic solutions of the two examples, which demonstrated that the proposed scheme (26) worked accurately for the initial fractional integro-differential Equation (21).

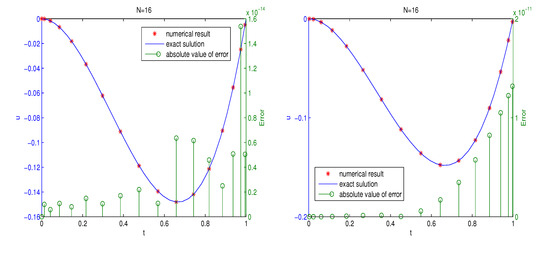
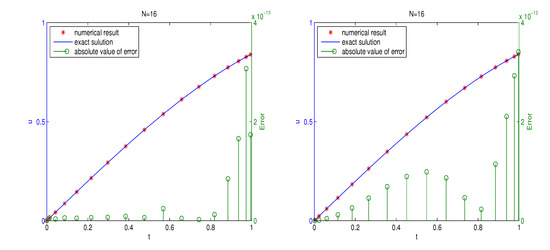
Figure 2. Numerical results of Examples 3 (top) and 4 (bottom) when $\nu =0.6$ and $N=16$. left: results by using methods proposed in this paper; right: results by using methods proposed in [39].

6. Conclusions

In summary, Jacobi collocation spectral methods with the fractional differentiation matrices using shifted JGL or JGR collocation points were presented in this paper. We employed the matrices to numerically solve the generalized space–fractional Burgers’ equations and the initial fractional integro-differential equations. The numerical results of these two types of fractional differential equations fit very well with the analytic solutions, which indicated that the proposed approach can effectively solve the FDE problems.