Doubling Smith Method for a Class of Large-Scale Generalized Fractional Diffusion Equations

Abstract

The implicit difference approach is used to discretize a class of generalized fractional diffusion equations into a series of linear equations. By rearranging the equations as the matrix form, the separable forcing term and the coefficient matrices are shown to be low-ranked and of nonsingular M-matrix structure, respectively. A low-ranked doubling Smith method with determined optimally iterative parameters is presented for solving the corresponding matrix equation. In comparison to the existing Krylov solver with Fast Fourier Transform (FFT) for the sequence Toeplitz linear system, numerical examples demonstrate that the proposed method is more effective on CPU time for solving large-scale problems.

1. Introduction

Consider a class of generalized fractional diffusion equations (GFDE)

$${}_0^C{D}_t^{\gamma ,\lambda \left(t\right)}u(x,t)=\kappa [p_a{D}_x^{\alpha }u(x,t)+(1-p){}_x{D}_b^{\alpha }u(x,t)]+f(x,t),(x,t)\in (a,b)\times (0,T)$$

(1)

with the initial values $u(x,0)=\varphi \left(x\right)$, $x\in [a,b]$ and zero boundary conditions $u(a,t)=u(b,t)=0$, $t\in [0,T]$, where the parameters $\alpha \in (1,2]$, $\gamma \in (0,1)$, $p\in [0,1]$, and $\lambda \left(t\right)>0$ are the weighting function for $t\in [0,T]$ with ${\lambda }^{\prime }\left(t\right)\le 0$. This equation arises from the continuous time random walks (CTRWs) model, with some complicated power-law waiting time distributions WTDs [1,2,3]. The weight function $\lambda \left(t\right)$ are of significant importance in the CTRW model, where biological particles have a finite lifespan. In such cases, it is more reasonable to employ the tempered power-law waiting time distribution, $e^{-bt}{t}^{-\gamma }$, instead of the divergent power-law distribution, $t^{-\gamma }$. This selection allows the model to describe the gradual transitions from subdiffusion to normal diffusion and, finally, to superdiffusion. These characteristics of the model have numerous potential applications in physical, biological, and chemical processes. For further details, please refer to [4,5]. The desired function $u(x,t)$ represents the concentration of a particle plume undergoing anomalous diffusion with a diffusion coefficient $\kappa \in (0,+\infty )$, and the forcing function $f(x,t)$ denotes the source or sink term. Throughout the paper, we assume that the function $f(x,t)$ is separable (or decoupled) with respect to x on $[a,b]$ and t on $[0,T]$, that is,

$$f(x,t)=\sum _{i=1}^l{f}_{s_i}\left(x\right)f_{t_i}\left(t\right)\mathrm{for} \mathrm{all}(x,t)\in [a,b]\times [0,T].$$

The GFDE (1) reduces to the space fractional diffusion equation (SFDE) when $\gamma =\lambda \left(t\right)=1$. Robust numerical schemes for SFDE have been studied extensively, as outlined in [6,7,8,9,10] and references therein. For GFDE, the time fractional derivative is the $\gamma$-order generalized Caputo fractional derivative [1,11], defined as

$${}_0^C{D}_t^{\gamma ,\lambda \left(t\right)}u(x,t)=\frac{1}{\Gamma (1-\gamma )}{\int }_0^t\frac{\lambda (t-\eta )}{{(t-\eta )}^{\gamma }}\frac{\partial u(x,\eta )}{\partial \eta }d\eta ,$$

while the left-handed and the right-handed space fractional derivatives are the $\alpha$-order Riemann–Liouville (R-L) fractional derivatives of the form [12]

$$\begin{array}{ccc}\hfill {}_{x_{{}_L}}{D}_x^{\alpha }u(x,t)& =& \hfill \frac{1}{\Gamma (2-\alpha )}\frac{{\partial }^2}{\partial x^2}{\int }_{x_{{}_L}}^x\frac{u(\xi ,t)}{{(x-\xi )}^{\alpha -1}}d\xi ,\hfill \\ \hfill {}_x{D}_{x_{{}_R}}^{\alpha }u(x,t)& =& \hfill \frac{1}{\Gamma (2-\alpha )}\frac{{\partial }^2}{\partial x^2}{\int }_x^{x_{{}_R}}\frac{u(\xi ,t)}{{(\xi -x)}^{\alpha -1}}d\xi .\hfill \end{array}$$

There are various ways to solve mathematical models that involve fractional order derivatives. One such approach is to use cubic splines, which are useful in modeling anomalous diffusion. In this technique, piece-wise polynomial functions are used to interpolate the data points, allowing for the diffusion coefficient to vary with time or space [13]. Another approach is to adapt the finite element method to include fractional order derivatives, which has been applied to determine the rheological properties of biomaterials that exhibit fractal structures. This method has been useful in studying the viscoelastic behavior of collagen and elastin [14]. The Galerkin method is yet another technique used to obtain numerical solutions for fractional differential equations. This method approximates the solution as a linear combination of basis functions and derives a system of algebraic equations, which can then be numerically solved using the Galerkin orthogonality [15].

To obtain an unconditionally stable difference scheme, the implicit difference scheme can be developed for Equation (1), which inherits $(2-\gamma )$-order temporal and 2-order spatial convergence [11]. The corresponding Toeplitz linear system is then solved efficiently by using preconditioned Krylov subspace solvers with fast Fourier transformation (FFT), costing about $O(n_{s}log\left(n_s\right))$ flops and $O\left(n_s\right)$ memory for each temporal node, where $n_s$ is the number of spatial nodes. However, the derivation of the entire $n_t$ temporal nodes requires about $O(n_t{n}_{s}log\left(n_s\right))$ flops, which is not suitable for large-scale computations.

In this paper, we observe that the discretized coefficient matrices in the linear system are the nonsingular Toeplitz M-matrix, fitting well with the frame of the M-matrix Sylvester equation. This allows us to present a doubling Smith method [16,17] to deal with GFDE (1). The main contributions of this paper include the following aspects:

• The transformation of the linear systems corresponding to the GFDE (1) into a low-ranked matrix equation is explained in detail.
• The low-ranked doubling Smith method with two optimal parameters is proposed under the separable forcing function.
• Numerical results demonstrate that, for large-scale problems, the low-ranked doubling Smith method equipped with truncation and compression is faster than the sequential Krylov solver (Bi-CGSTA) [18] with FFT for solving Equation (1).

Some notations and definitions are required in this paper. Let $L_1\left(\mathbb{R}\right)$ be the set of all integrable functions in real space. Symbols ${\mathbb{R}}^2$ and ${\mathbb{R}}^{n\times n}$ are the real plane and the $n\times n$ real matrices, respectively. For matrices A, $B\in {\mathbb{R}}^{n\times n}$, we write $A\ge B(A>B)$ if their respective elements satisfy $a_{ij}\ge b_{ij}(a_{ij}>b_{ij})$ for all i, j. A real square matrix A is called a Z-matrix if all its off-diagonal elements are nonpositive. It is clear that any Z-matrix A can be written as $sI-B$ with $B\ge 0$. A Z-matrix $A=sI-B$ with $B\ge 0$ is called an M-matrix if $s\ge \rho \left(B\right)$, where $\rho (·)$ denotes the spectral radius. It is called a singular M-matrix if $s=\rho \left(B\right)$ and a nonsingular M-matrix if $s>\rho \left(B\right)$. The (non)symmetric Toeplitz matrix is denoted by $\mathrm{Toep}(c,r)$ with vectors c and r being its first column and row, respectively. The matrix $A\in {\mathbb{R}}^{n\times n}$ is numerically low-ranked if there is a constant $c_{\tau }$ independent of n such that ${\mathrm{rank}}_{\tau }\left(A\right)\le c_{\tau }$.

The following results about M-matrix are well known (see [19] (Section 3.5), [20] (Lem. 2.2) for an example).

Lemma 1.

For a Z-matrix A, the following statements are equivalent:

(a) 

A is a nonsingular M-matrix.

(b) 

A is nonsingular and satisfies $A^{-1}\ge 0$.

(c) 

$Av>0$ for some vector $v>0$.

(d) 

All eigenvalues of A have positive real parts.

Lemma 2.

Suppose that A is an M-matrix and B is a Z-matrix.

(a) 

If $B\ge A$, then B is an M-matrix. Particularly, $\gamma I+A$ is an M-matrix for $\gamma \ge 0$ and a nonsingular M-matrix for $\gamma >0$.

(b) 

The one with the smallest absolute value among all eigenvalues of A, denoted by ${\lambda }_1^A$, is nonnegative, and ${\lambda }_1^A\le {max}_i{A}_{ii}$.

2. Implicit Difference Scheme and the Linear Systems

We will construct an implicit difference scheme for temporal and spatial discretization by using the generalized Caputo fractional derivative [1] for the temporal direction and the second-order WSGD [21,22,23] spatial discretization for the spatial direction.

2.1. Temporal and Spatial Discretization

We first introduce the temporal discretization of the function $u(x,t)$ on the rectangle area $\mathrm{Rec}=\{(x,t):a\le x\le b,0\le t\le T\}\in {\mathbb{R}}^2$ with the discretized mesh $m_h\times m_{\tau }=\{x_i\times t_j:x_i=a+ih,t_j=j\tau ,0\le i\le n_s,0\le j\le n_t,h=(b-a)/n_s,\tau =T/n_t\}$.

Define the linear interpolation

$${\Pi }_{1,s}u(·,t)=u(·,t_{s+1})\frac{t-t_s}{\tau }+u(·,t_s)\frac{t_{s+1}-t}{\tau }$$

over the time interval $(t_i,t_j)$ with $0\le j\le n_t-1$. Then, at the time $t_{j+1}$, one has

$$\begin{array}{c}\hfill {}_0^C{D}_t^{\gamma ,\lambda \left(t\right)}u(·,t)|{}_{t=t_{j+1}}=\frac{{\tau }^{1-\gamma }}{\Gamma (2-\gamma )}\sum _{s=0}^j[{\lambda }_{j-s+1/2}{a}_{j-s}+({\lambda }_{j-s}-{\lambda }_{j-s+1})b_{j-s}]u_{t,s}+R_1^j+R_2^j,\hfill \end{array}$$

where

$$\begin{array}{c}{\lambda }_s=\lambda \left(t_s\right),u_{t,s}=\frac{u(·,t_{s+1})-u(·,t_s)}{\tau },\hfill \\ a_i={(i+1)}^{1-\gamma }-i^{1-\gamma },\hfill \\ b_i=\frac{1}{2-\gamma }[{(i+1)}^{2-\gamma }-i^{2-\gamma }]-\frac{1}{2}[{(i+1)}^{1-\gamma }+i^{1-\gamma }],\hfill \end{array}$$

with $i\ge 1$ and $R_1^j$ and $R_2^j$ being residuals defined in [1]. The following Lemma concludes the truncation error of the above discretized scheme [1] (Lem. 4.1).

Lemma 3.

Let $\gamma \in (0,1)$, $\lambda \left(t\right)>0$, ${\lambda }^{\prime }\left(t\right)\le 0$, and $\lambda \left(t\right)$, $u(·,t)\in {\mathcal{C}}^2[0,t_{j+1}]$. Then,

$${}_0^C{D}_t^{\gamma ,\lambda \left(t\right)}u(·,t_{j+1})={\Delta }_{0,t_{j+1}}^{\gamma ,\lambda \left(t\right)}{u}^{j+1}+O\left({\tau }^{2-\gamma }\right)$$

with

$${\Delta }_{0,t_{j+1}}^{\gamma ,\lambda \left(t\right)}{u}^{j+1}=\sum _{s=0}^j{c}_{j-s}(u^{s+1}-u^s)$$

(2)

and

$$c_k=\frac{{\tau }^{-\gamma }}{\Gamma (2-\gamma )}[{\lambda }_{k+1/2}{a}_k+({\lambda }_k-{\lambda }_{k+1})b_k]$$

for $k\ge 0$. Furthermore, elements in sequences $\left\{a_k\right\}$, $\left\{b_k\right\}$, and $\left\{c_k\right\}$ are all decreasing with respect to k, i.e.,

$$\left\{\begin{array}{c}{a}_0>a_1>\dots >a_k>\frac{1-\gamma }{{(k+1)}^{\gamma }},\hfill \\ b_0>b_1>\dots >b_k>0,\hfill \\ c_0>c_1>\dots >c_k>\frac{\lambda \left(t_{k+1/2}\right)}{\Gamma (1-\gamma )t_{k+1}^{\gamma }}.\hfill \end{array}\right.$$

(3)

We next consider the spatial discretization. Let ${\mathcal{L}}^{n+\alpha }\left(\mathbb{R}\right)=\left\{u\right|u\in L_1\left(\mathbb{R}\right),{\int }_{-\infty }^{+\infty }{(1+k)}^{n+\alpha }|\widehat{u}\left(k\right)|dk<\infty \}$ with $\widehat{u}\left(k\right)={\int }_{-\infty }^{+\infty }{e}^{\mathbf{i}kx}u\left(x\right)dx$ being the Fourier transformation of $u\left(x\right)$. Here, i represents the imaginary unit. The spatial WSGD discretized format for the R–L fractional derivative is summarized in the following lemma, as proposed in [11] (Lem. 2.3); see also in [21,22,23].

Lemma 4.

Let $u(x,·)\in {\mathcal{L}}^{2+\alpha }\left(\mathbb{R}\right)$. Then, for some fixed space step-length h, one has

$${}_a{D}_x^{\alpha }u(x,·)={\delta }_{x,+}^{\alpha }u(x,·)+O\left(h^2\right),{}_x{D}_b^{\alpha }u(x,·)={\delta }_{x,-}^{\alpha }u(x,·)+O\left(h^2\right),$$

where

$$\begin{array}{ccc}\hfill {\delta }_{x,+}^{\alpha }u(x,·)& =& \hfill \frac{1}{h^{\alpha }}\sum _{k=0}^{\left[\left[\frac{x-a}{h}\right]\right]}{w}_k^{\left(\alpha \right)}u(x-(k-1)h,·)),\hfill \\ \hfill {\delta }_{x,-}^{\alpha }u(x,·)& =& \hfill \frac{1}{h^{\alpha }}\sum _{k=0}^{\left[\left[\frac{b-x}{h}\right]\right]}{w}_k^{\left(\alpha \right)}u(x+(k-1)h,·))\hfill \end{array}$$

are difference operators with $\left[\right[·\left]\right]$ being the floor function and

$$w_0^{\left(\alpha \right)}={\kappa }_1{g}_0^{\left(\alpha \right)},w_1^{\left(\alpha \right)}={\kappa }_1{g}_1^{\left(\alpha \right)}+{\kappa }_0{g}_0^{\left(\alpha \right)},w_k^{\left(\alpha \right)}={\kappa }_1{g}_k^{\left(\alpha \right)}+{\kappa }_0{g}_{k-1}^{\left(\alpha \right)}+{\kappa }_{-1}{g}_{k-2}^{\left(\alpha \right)},(k\ge 2).$$

Here, ${\kappa }_1=\frac{{\alpha }^2+3\alpha +2}{12}$, ${\kappa }_0=\frac{4-{\alpha }^2}{6}$, ${\kappa }_{-1}=\frac{{\alpha }^2-3\alpha +2}{12}$, and $g_k^{\left(\alpha \right)}={(-1)}^k\left(\begin{array}{c}\alpha \\ k\end{array}\right)$. Furthermore, for $\alpha \in (1,2)$, the sequence $\left\{w_k^{\left(\alpha \right)}\right\}$ satisfies

$$\begin{array}{c}\hfill w_0^{\left(\alpha \right)}>0,w_1^{\left(\alpha \right)}<0,w_k^{\left(\alpha \right)}>0,(k\ge 3),\hfill \\ \hfill \sum _{k=0}^{\infty }{w}_k^{\left(\alpha \right)}=0,\sum _{k=0}^n{w}_k^{\left(\alpha \right)}<0,(n>1).\hfill \end{array}$$

(4)

2.2. Derivation of the Sequence of Linear Systems

By employing the above implicit difference scheme, we can obtain a sequence of discretized linear systems. In fact, for $i=1,\dots ,n_s-1$ and $j=0,1,\dots ,n_t-1$, the GFDE (1) at the grid point $(x_i,t_j)$ is

$${}_0^C{D}_t^{\gamma ,\lambda \left(t\right)}u(x_i,t_j)=\kappa {[p{}_a{D}_x^{\alpha }u(x,t)+(1-p){}_x{D}_b^{\alpha }u(x,t)]}_{(x_i,t_j)}+f(x_i,t_j).$$

(5)

Recalling Lemmas 3 and 4, Equation (5) can be rewritten as

$${\Delta }_{0,t_{j+1}}^{\gamma ,\lambda \left(t\right)}{u}_i^{j+1}=\kappa ·{\delta }_h^{\alpha }{u}_i^{j+1}+f_i^{j+1}+R_i^{j+1},$$

where $u_i^j=u(x_i,t_j)$, $f_i^j=f(x_i,t_j)$,

$${\delta }_h^{\alpha }{u}_i^{j+1}=\frac{1}{h^{\alpha }}[p\sum _{k=0}^{i+1}{w}_k^{\left(\alpha \right)}{u}_{i-k+1}^{j+1}+(1-p)\sum _{k=0}^{n_s-i+1}{w}_k^{\left(\alpha \right)}{u}_{i+k-1}^{j+1}],$$

(6)

and $R_i^{j+1}$ is the error. We then omit the error and arrive at the implicit difference scheme

$${\Delta }_{0,t_{j+1}}^{\gamma ,\lambda \left(t\right)}{u}_i^{j+1}=\kappa ·{\delta }_h^{\alpha }{u}_i^{j+1}+f_i^{j+1},1\le i\le n_s-1,0\le j\le n_t-1$$

(7)

with the initial condition $u_i^0=\varphi \left(x_i\right)$ for $0\le i\le n_s$ and the zero boundary conditions $u_0^j=0$, $u_{n_s}^j=0$ for $0\le j\le n_t$.

Before we proceed with the derivation of the linear system, we show that the implicit difference scheme presented in Equation (7) is stable. In fact, by setting ${\xi }_i^j=\kappa$ for all i and j in [11] (Thm 2.2), one has the following stability theorem.

Theorem 1.

By defining $\parallel f^{j+1}{\parallel }^2=h{\sum }_{i=1}^{n_s-1}{f}^2(x_i,t_{j+1})$, the implicit difference scheme (7) is unconditionally stable, and there exists a constant c such that a priori estimate is

$$\parallel u^{j+1}\parallel \le \parallel u^0{\parallel }^2+\frac{\Gamma (1-\gamma )T^{\gamma }}{2c\kappa ln2\lambda \left(T\right)}\underset{0\le j\le n_t-1}{max}{\parallel f^{j+1}\parallel }^2,$$

where $u^{j+1}={[u_1^{j+1},u_2^{j+1},\dots ,u_{n_s-1}^{j+1}]}^{\top }$, $u^0={[u_1^0,u_2^0,\dots ,u_{n_s-1}^0]}^{\top }$.

According to [11] (Thm 2.3), the implicit difference scheme (7) exhibits a 2-$\gamma$ order of convergence in time and a quadratic order of convergence in space variables when the solution of the GFDE (1) is sufficiently smooth.

Theorem 2.

Suppose that $u_{\mathrm{true}}(x,t)\in {\mathcal{C}}_{x,t}^{4,2}([a,b]\times [0,T])$ is the solution of GFDE (1) and $u_i^j$ derives from the implicit difference scheme (7). Define

$$E_i^j=u_{\mathrm{true}}(x_i,t_j)-u_i^j,1\le i\le n_s-1,0\le j\le n_t-1.$$

Then, there exists a constant $\tilde{c}$ such that for $j\le n_t-1$,

$$\parallel E^j\parallel \le \tilde{c}({\tau }^{2-\gamma }+h^2).$$

Now, we construct the Toeplitz matrix

$$\begin{array}{c}{W}_{\alpha }=\mathrm{Toep}([w_1^{\left(\alpha \right)},\dots ,w_{n_s-1}^{\left(\alpha \right)}],[w_1^{\left(\alpha \right)},w_0^{\left(\alpha \right)},\stackrel{n_s-3}{\overbrace{0,\dots ,0}}])\in {\mathbb{R}}^{(n_s-1)\times (n_s-1)}\end{array}$$

and set

$$B=-\frac{\kappa }{h^{\alpha }}(p{W}_{\alpha }+(1-p)W_{\alpha }^{\top }).$$

(8)

Then, for each temporal node j ($0\le j\le n_t-1$), Equation (7) with $1\le i\le n_s-1$ are equivalent to the linear system

$$(c_0{I}_{n_s-1}+B)u^{j+1}=c_j{u}^0+\sum _{k=1}^j(c_{k-1}-c_k)u^{j+1-k}+f^{j+1}$$

(9)

with $u^j={[u_1^j,\dots ,u_{n_s-1}^j]}^{\top }$ and $f^j={[f_1^j,\dots ,f_{n_s-1}^j]}^{\top }$. It is clear that the fast Fourier transform (FFT) method is well-suited for the linear system sequence (7), and the computational complexity for solving the j-th equation is $O((n_s-1)log(n_s-1))$ [24] (Chap. 3). As a result, the total computational cost for the entire sequence of linear systems in Equation (9) is about $O(n_t(n_s-1)log(n_s-1))$ flops.

3. Low-Ranked Matrix Equation and Doubling Smith Method

In this section, we will further transform the sequence of linear systems (9) into a low-ranked matrix equation via the separable forcing function $f(x,t)$, which is then efficiently solved by the presented doubling Smith method, equipped with two determined optimal parameters.

3.1. Matrix Equation with Structured Coefficients

To construct the matrix equation, we rewrite the linear systems (9) into

$$\begin{array}{cc}& \left[\begin{array}{ccccc}-c_0{I}_{n_s-1}& c_0{I}_{n_s-1}& & & \\ -c_1{I}_{n_s-1}& (c_1-c_0)I_{n_s-1}& c_0{I}_{n_s-1}& & \\ -c_2{I}_{n_s-1}& (c_2-c_1)I_{n_s-1}& (c_1-c_0)I_{n_s-1}& c_0{I}_{n_s-1}& \\ ⋮& ⋮& \ddots & \ddots & \\ -c_{n_t-1}{I}_{n_s-1}& (c_{n_t-1}-c_{n_t-2})I_{n_s-1}& \cdots & (c_1-c_0)I_{n_s-1}& c_0{I}_{n_s-1}\end{array}\right]\left[\begin{array}{c}{u}^0\\ u^1\\ u^2\\ ⋮\\ u^{n_t}\end{array}\right]\\ & +\left[\begin{array}{ccccc}B& & & & \\ & B& & & \\ & & \ddots & & \\ & & & & B\end{array}\right]\left[\begin{array}{c}{u}^1\\ u^2\\ ⋮\\ u^{n_t}\end{array}\right]=\left[\begin{array}{c}{f}^1\\ f^2\\ ⋮\\ f^{n_t}\end{array}\right].\end{array}$$

(10)

By setting the Toeplitz matrix

$$A=\mathrm{Toep}([c_0,\stackrel{n_t-1}{\overbrace{0,\dots ,0}}],[c_0,c_1-c_0,c_2-c_1,\dots ,c_{n_t-1}-c_{n_t-2}])\in {\mathbb{R}}^{n_t\times n_t},$$

(11)

the linear system (10) is the one-shot equation of the scale $n_t(n_s-1)\times n_t(n_s-1)$, i.e.,

$$(A^{\top }\otimes I_{n_s-1}+I_{n_t}\otimes B)u=f+c\otimes u^0,$$

where $f={({f^1}^{\top },{f^2}^{\top },\dots ,{f^{n_t}}^{\top })}^{\top }\in {\mathbb{R}}^{(n_s-1)n_t}$ is the forcing term, $c={(c_0,c_1,\dots ,c_{n_t-1})}^{\top }\in {\mathbb{R}}^{n_t}$ is the constant vector, and $u={({u^1}^{\top },{u^2}^{\top },\dots ,{u^{n_t}}^{\top })}^{\top }\in {\mathbb{R}}^{(n_s-1)n_t}$ is the desired unknown vector.

Furthermore, by rearranging vectors $u^i$ and $f^i$ as matrices $U=[u^1,u^2,\dots ,u^{n_t}]\in {\mathbb{R}}^{(n_s-1)\times n_t}$ and $F=[f^1+c_0{u}^0,f^2+c_1{u}^0,\dots ,f^{n_t}+c_{n_t-1}{u}^0]\in {\mathbb{R}}^{(n_s-1)\times n_t}$, respectively, we arrive at the Sylvester matrix equation

$$UA+BU=F,$$

(12)

with F being the constant term.

Remark 1.

When the forcing function $f(x,t)$ is separable, the constant matrix F in (12) is a product of two low-rank factors, i.e.,

$$F=F_s{F}_t^{\top }=[F_{s1},u^0]{[F_{t1},c]}^{\top },$$

where $F_{s1}\in {\mathbb{R}}^{(n_s-1)\times r_f}$ ($r_f\ll n_s$) and $F_{t1}\in {\mathbb{R}}^{n_t\times r_f}$ ($r_f\ll n_t$) are discretized spatial and time matrices from $f(x,t)$.

The following theorem states the nice property of matrices A and B, which also contributes to the motivation of developing the doubling Smith method with the optimal parameters.

Theorem 3.

Let $\lambda \left(t\right)\in {\mathcal{C}}^2[0,T]$ be the weight function satisfying $\lambda \left(t\right)>0$ and ${\lambda }^{\prime }\left(t\right)\le 0$ for all $t\in [0,T]$. Let $\{w_k^{\left(\alpha \right)}\}$ be the sequence generated by the WSGD format in Lemma 4. Then, matrices A given in (11) and B given in (8) are both nonsingular M-matrices.

Proof. 

Let $\mathbf{1}={(1,1,\dots ,1)}^{\top }$ be a vector with all its elements equal to 1. According to Equation (3) and the assumption that the weight function $\lambda \left(t\right)$ is positive, we can conclude that the minimum value of the sequence $c_k$ is greater than zero. As a result, we have

$$A\mathbf{1}={(c_{n_t-1},c_{n_t-2},\dots ,c_1,c_0)}^{\top }>\frac{\lambda (n_t-1/2)}{\Gamma (1-\gamma )t_{n_t}^{\gamma }}\mathbf{1}>0,$$

and A is a nonsingular M-matrix based on Lemma 1.

Moreover, from ${\sum }_{i=0}^{\infty }{w}_i^{\left(\alpha \right)}=0$ in Equation (4), we can derive that ${\sum }_{i=n_s}^{\infty }{w}_i^{\left(\alpha \right)}=-{\sum }_{i=0}^{n_s-1}{w}_i^{\left(\alpha \right)}>0$, which implies that ${\sum }_{i=1}^{n_s-1}{w}_i^{\left(\alpha \right)}=-(w_0^{\left(\alpha \right)}+{\sum }_{i=n_s}^{\infty }{w}_i^{\left(\alpha \right)})<0$. Therefore,

$$\begin{array}{c}\hfill W_{\alpha }\mathbf{1}={[\sum _{i=0}^1{w}_i^{\left(\alpha \right)},\sum _{i=0}^2{w}_i^{\left(\alpha \right)},\dots ,\sum _{i=0}^{n_s-2}{w}_i^{\left(\alpha \right)},\sum _{i=1}^{n_s-1}{w}_i^{\left(\alpha \right)}]}^{\top }<0,\hfill \\ \hfill W_{\alpha }^{\top }\mathbf{1}={[\sum _{i=1}^{n_s-1}{w}_i^{\left(\alpha \right)},\sum _{i=0}^{n_s-2}{w}_i^{\left(\alpha \right)},\dots ,\sum _{i=0}^2{w}_i^{\left(\alpha \right)},\sum _{i=0}^1{w}_i^{\left(\alpha \right)}]}^{\top }<0.\hfill \end{array}$$

Since $\kappa$, $h^{\alpha }$, and p in (8) are all positive, we can find a vector 1 such that $B\mathbf{1}>0$, and B is a nonsingular M-matrix via Lemma 1.    □

3.2. Doubling Smith Method with the Optimal Parameters

To develop the doubling Smith method, we first use the generalized Cayley transform [17,20,25] (Section 2) to convert the Sylvester Equation (12) to the Stein equation. By introducing two positive parameters $\mu$ and $\nu$, Equation (12) can be rewritten as

$$(B-\nu I_{n_s-1})U(A-\mu I_{n_t})-(B+\mu I_{{}_{n_s-1}})U(A+\nu I_{n_t})=-(\mu +\nu )F,$$

or the corresponding Stein equation

$$\tilde{B}U\tilde{A}-U+\tilde{F}=0,$$

(13)

where

$$\tilde{A}=(A-\mu I_{n_t}){(A+\nu I_{n_t})}^{-1},\tilde{B}=(B-\nu I_{n_s-1}){(B+\mu I_{n_s-1})}^{-1}$$

and $\tilde{F}=(\mu +\nu ){(B+\mu I_{n_s-1})}^{-1}F{(A+\nu I_{n_t})}^{-1}$. As A and B are nonsingular M-matrices, Lemma 2 implies that $\tilde{A}$ and $\tilde{B}$ are non-positive matrices when

$$\mu \ge \underset{1\le i\le n_t}{max}{A}_{ii}\mathrm{and}\nu \ge \underset{1\le i\le n_s-1}{max}{B}_{ii}.$$

We can rewrite the Stein equation as $U=\mathcal{S}\left(U\right)=\tilde{B}U\tilde{A}+\tilde{F}$ and substitute $U=\mathcal{S}\left(U\right)$ into the right-hand side. This gives the equation $U={\mathcal{S}}^2\left(U\right)=\mathcal{S}(\tilde{B}U\tilde{A}+\tilde{F})={\tilde{B}}^{2}U{\tilde{A}}^2+\tilde{B}\tilde{F}\tilde{A}+\tilde{F}.$ By repeatedly substituting $U={\mathcal{S}}^2\left(U\right)$ for the right-hand side of itself, we can derive the k-th iteration in the form

$$U={\tilde{B}}^{2^k}U{\tilde{A}}^{2^k}+\sum _{i=0}^{2^k-1}{\tilde{B}}^i\tilde{F}{\tilde{A}}^i,$$

which contributes to the doubling Smith (DS) iteration

$${\tilde{A}}_{k+1}={\tilde{A}}_k^2,{\tilde{B}}_{k+1}={\tilde{B}}_k^2,{\tilde{U}}_{k+1}={\tilde{U}}_k+{\tilde{B}}_k{\tilde{U}}_k{\tilde{A}}_k,(k\ge 0)$$

(14)

where ${\tilde{A}}_0=\tilde{A}$, ${\tilde{B}}_0=\tilde{B}$, and ${\tilde{U}}_0=\tilde{F}$.

The following theorem describes how the convergence rate of the DS iteration is a function of the Cayley parameters $(\mu ,\nu )$ and can attain the optimal by using the M-matrix property.

Theorem 4.

Let the sequence $\{{\tilde{U}}_k\}$ be generated by the DS iteration. Assume that ${\tilde{U}}_{\infty }={\sum }_{i=0}^{\infty }{\tilde{B}}^i\tilde{F}{\tilde{A}}^i$ is the solution of the Stein Equation (13). Then,

$$\begin{array}{c}\underset{k\to \infty }{lim\; sup}{\parallel {\tilde{U}}_{\infty }-{\tilde{U}}_k\parallel }^{1/2^k}\le \rho (\tilde{A})\rho (\tilde{B}).\end{array}$$

(15)

Furthermore, $\rho (\tilde{A})\rho (\tilde{B})$ will arrive at the minimal value when

$$({\mu }^{*},{\nu }^{*})=(\underset{i}{max}{A}_{ii},\underset{i}{max}{B}_{ii})=(c_0,-\kappa w_1^{\left(\alpha \right)}/h^{\alpha }),$$

(16)

where $c_0$ is given in (11) and κ, $w_1^{\left(\alpha \right)}$, $h^{\alpha }$ are given in (8).

Proof. 

The DS iteration (14) yields that the error at the k-th iteration is ${\tilde{U}}_{\infty }-{\tilde{U}}_k={\sum }_{i=2^k}^{\infty }{\tilde{B}}^i\tilde{F}{\tilde{A}}^i={\tilde{B}}^{2^k}{\tilde{U}}_{\infty }{\tilde{A}}^{2^k}$ and then the inequality (15) holds true. To ensure that the DS converges as fast as possible, one needs to select appropriate values for $\mu$ and $\nu$ to minimize the convergence rate.

We first consider $\rho (\tilde{A})$. Since all eigenvalues of A are the same and equal to $c_0$, let $Av=c_{0}v$ with v be the corresponding eigenvector. Then, we have

$$\tilde{A}v=(A-\mu I_{n_t}){(A+\nu I_{n_t})}^{-1}v=\frac{c_0-\mu }{c_0+\nu }v,$$

which implies that

$$\rho (\tilde{A})=\frac{\mu -c_0}{c_0+\nu }.$$

On the other hand, let $B=sI-N_B$ with $s>0$ and $N_B\ge 0$ be irreducible. According to the Perron–Frobenius theorem [19] (Thm. 2.7), there exists a positive vector u such that $N_{B}u=\rho \left(N_B\right)u$. Therefore, the minimal eigenvalue of B, i.e., ${\lambda }_{\min }^B=s-\rho \left(N_B\right)$, is positive, and this leads to

$$\tilde{B}u=(B-\nu I_{n_s-1}){(B+\mu I_{n_s-1})}^{-1}u=\frac{{\lambda }_{\min }^B-\nu }{{\lambda }_{\min }^B+\mu }u.$$

Since $\tilde{B}=(B-\nu I_{n_s-1}){(B+\mu I_{n_s-1})}^{-1}$ is non-positive and irreducible for $\nu \ge {max}_i{B}_{ii}$ and $\mu >0$ (see Lemma 2), it follows from the Perron–Frobenius theorem again that

$$\rho (\tilde{B})=\rho (-\tilde{B})=\frac{\nu -{\lambda }_{\min }^B}{{\lambda }_{\min }^B+\mu }.$$

Construct the functions

$$g_1\left(\mu \right)=\frac{\mu -c_0}{{\lambda }_{\min }^B+\mu }\mathrm{and}{g}_2\left(\nu \right)=\frac{\nu -{\lambda }_{\min }^B}{c_0+\nu }.$$

They are obviously monotonically increasing with respect to $\mu \in [{\mu }^{*},+\infty )$ and $\nu \in [{\nu }^{*},+\infty )$, respectively. Then, $\rho (\tilde{A})\rho (\tilde{B})=g_1\left(\mu \right)·g_2\left(\nu \right)$ achieves the minimal value at $({\mu }^{*},{\nu }^{*})$.    □

For the large-scale Equation (12) with separable $F=F_s{F}_t^{\top }$, the DS method (14) can be further organized as the following low-ranked version [16,17] (Alg. 1)

$$\left\{\begin{array}{c}{\tilde{U}}_{k+1}={\tilde{G}}_{k+1}{\tilde{T}}_{k+1}{\tilde{H}}_{k+1}^{\top },{\tilde{T}}_{k+1}=\left[\begin{array}{cc}{\tilde{T}}_k& 0\\ 0& {\tilde{T}}_k\end{array}\right],\hfill \\ {\tilde{G}}_{k+1}=[{\tilde{G}}_k,{\tilde{B}}_k{\tilde{G}}_k],{\tilde{H}}_{k+1}=[{\tilde{H}}_k,{\tilde{A}}_k^{\top }{\tilde{H}}_k]\hfill \end{array}\right.$$

(17)

with ${\tilde{G}}_0=F_s$, ${\tilde{H}}_0=F_t$, ${\tilde{T}}_0=I$. Then, the solution ${\tilde{U}}_{\infty }$ is numerically low-ranked. If FFT is still used for coping with the Toeplitz system and the number of the DS iteration is not large (in a sense of $2^k=O\left(1\right)$), the entire complexity is expected to be reduced to $O((n_s-1)log(n_s-1))$.

4. Numerical Examples

In this section, we will illustrate the effectiveness of the low-ranked DS method in computing the solution of large-scale GFDE using the implicit difference scheme. We compare the DS method with the Bi-CGSTAB solver [18] (Alg. 3.6.3) (referred to as “ST”), which is used to solve the sequence of Toeplitz linear systems (9) at each temporal node. The same solver is also used to construct $\tilde{A}$ and $\tilde{B}$ in (13) for the DS method. Additionally, both algorithms employ the Gohber–Semecul formula [24,26] to solve their respective Toeplitz systems, and the algorithm terminates when the relative residual of the Toeplitz system is less than ${10}^{-14}$.

In the DS method, we use the technique of truncation and compression of the economic QR decomposition [25] (Section 2.2) (see also in [16,17] with a tolerance of ${10}^{-30}$) to reduce the columns of ${\tilde{G}}_k$ and ${\tilde{H}}_k$ as much as possible. We also set the upper bound of the truncated maximal number of columns to ${10}^3$. The DS method stops either when the number of iterations exceeds six or when the low-ranked residual form [16,17] of the Stein Equation (13) is less than ${10}^{-11}$. We implemented both algorithms using MATLAB 2019a on a 64-bit PC with a 3.0 GHz Intel Core i5 processor and 32G RAM, with the machine error eps = $2.22\times {10}^{-16}$.

To assess the accuracy of both algorithms, we calculate their errors as

$$\mathrm{Err}=\underset{0\le j\le n_t}{max}{\parallel u^j-u_{\mathrm{true}}^j\parallel }_{\infty }$$

and record the convergent rate as

$$\mathrm{Rate}={log}_{h_1/h_2}({\mathrm{Err}}_{h_1}/{\mathrm{Err}}_{h_2}),$$

where $h_1$ and $h_2$ are different step-lengths in two consecutively temporal nodes.

Example 1.

Consider the GFDE (1) with the diffusion coefficient $\kappa =1$ and $p=1$. The weight function is $\lambda \left(t\right)=e^{-t}$, and the forcing function on the RHS of GFDE is

$$f(x,t)=\frac{-t^{1-\gamma }{e}^{-t}}{\Gamma (2-\gamma )}{x}^3(1-x)-\frac{6e^{-t}}{\Gamma (4-\alpha )}{x}^{3-\alpha }+\frac{24e^{-t}}{\Gamma (5-\alpha )}{x}^{4-\alpha }.$$

The initial-boundary value conditions for this problem are $u(x,0)=x^3(1-x)$ and $u(0,t)=u(1,t)=0$. It is not difficult to see the exact solution function of this problem is $u(x,t)=e^{-t}{x}^3(1-x)$ (see Appendix A).

To test the numerical performance of the two algorithms, we take $\gamma =0.2$ and test the values of $\alpha$ at 1.1, 1.5, and 1.9. The obtained results are listed in

Table 1. Numerical performances of two different methods when $\gamma =0.2$ in Example 1.

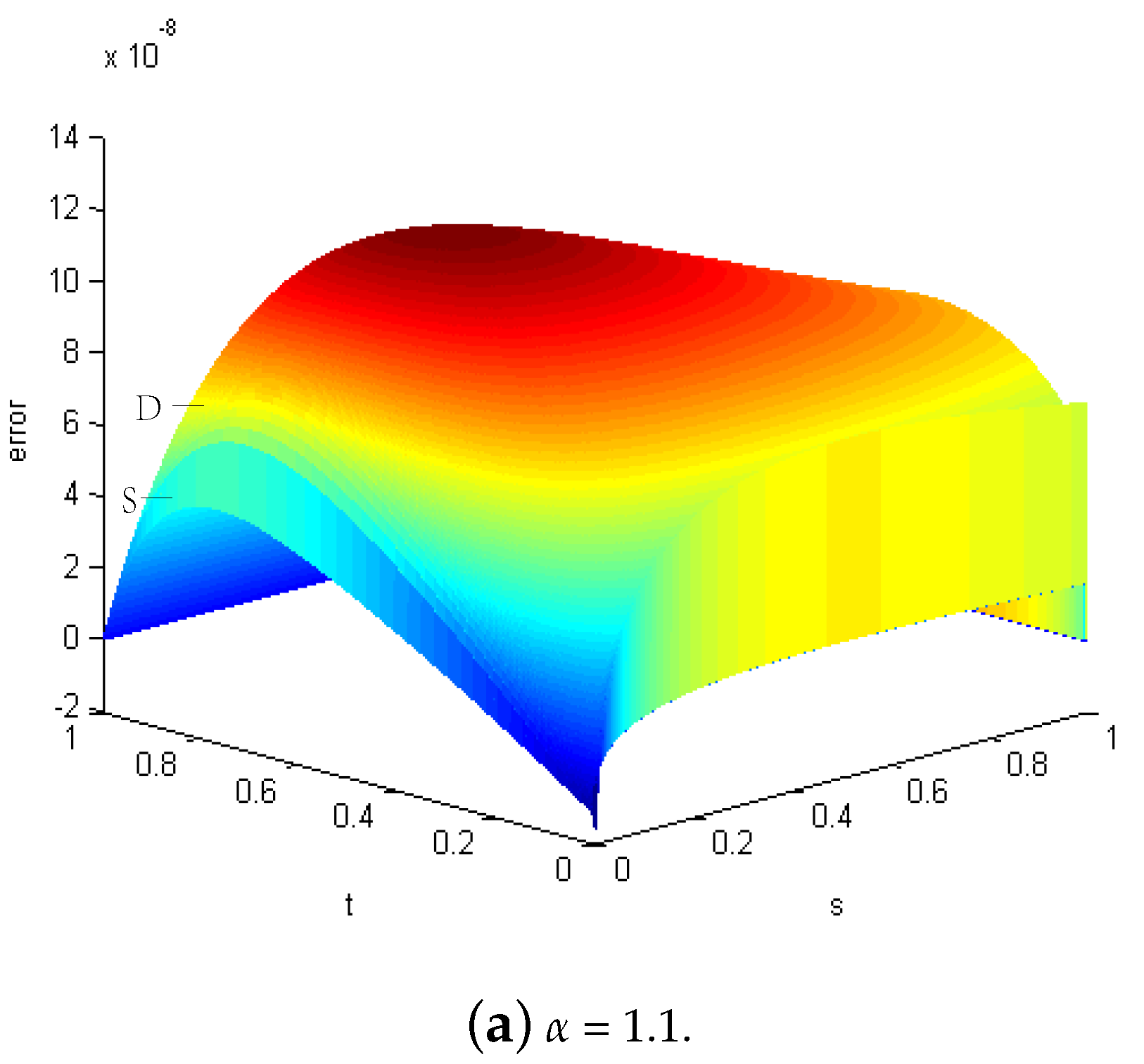
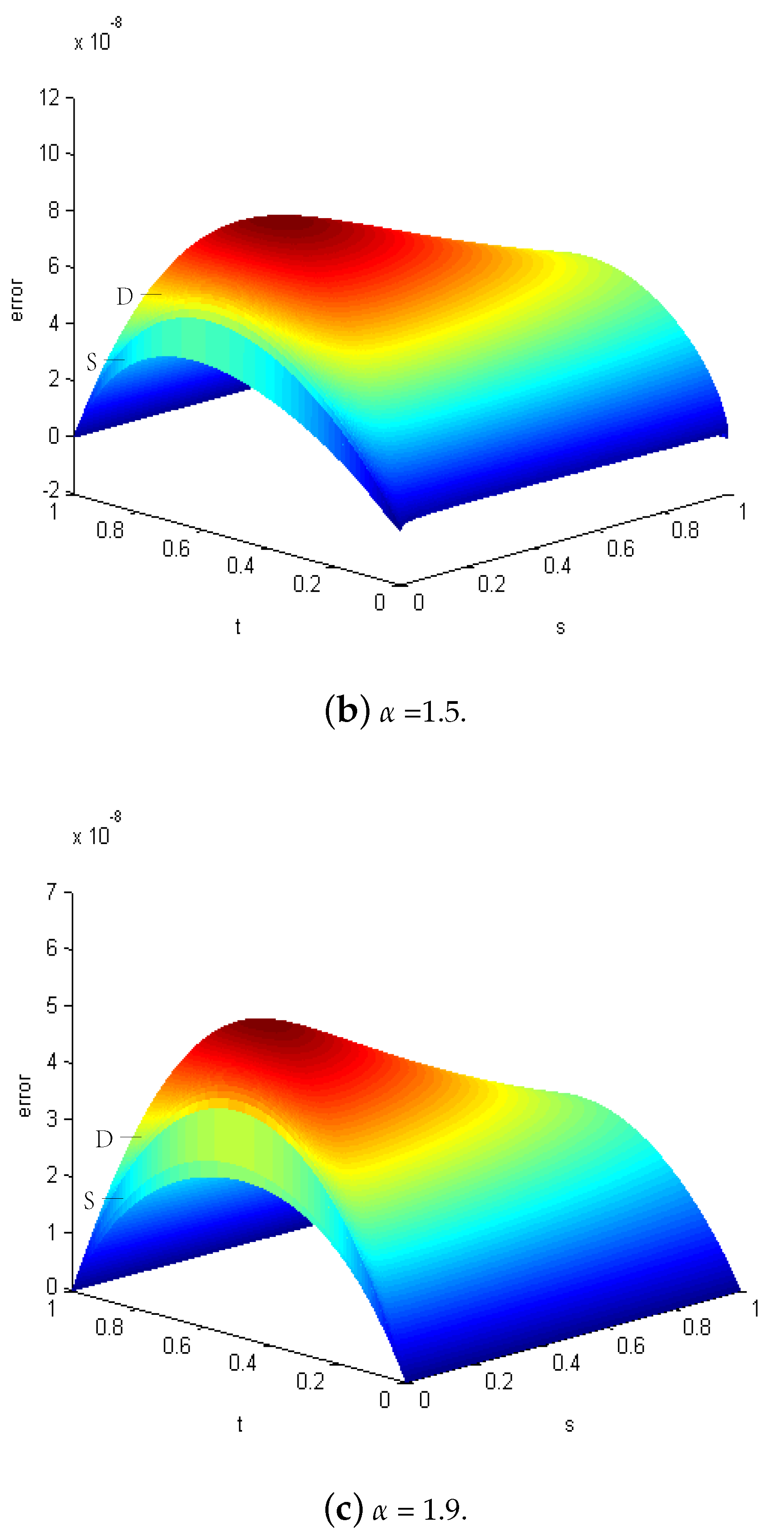
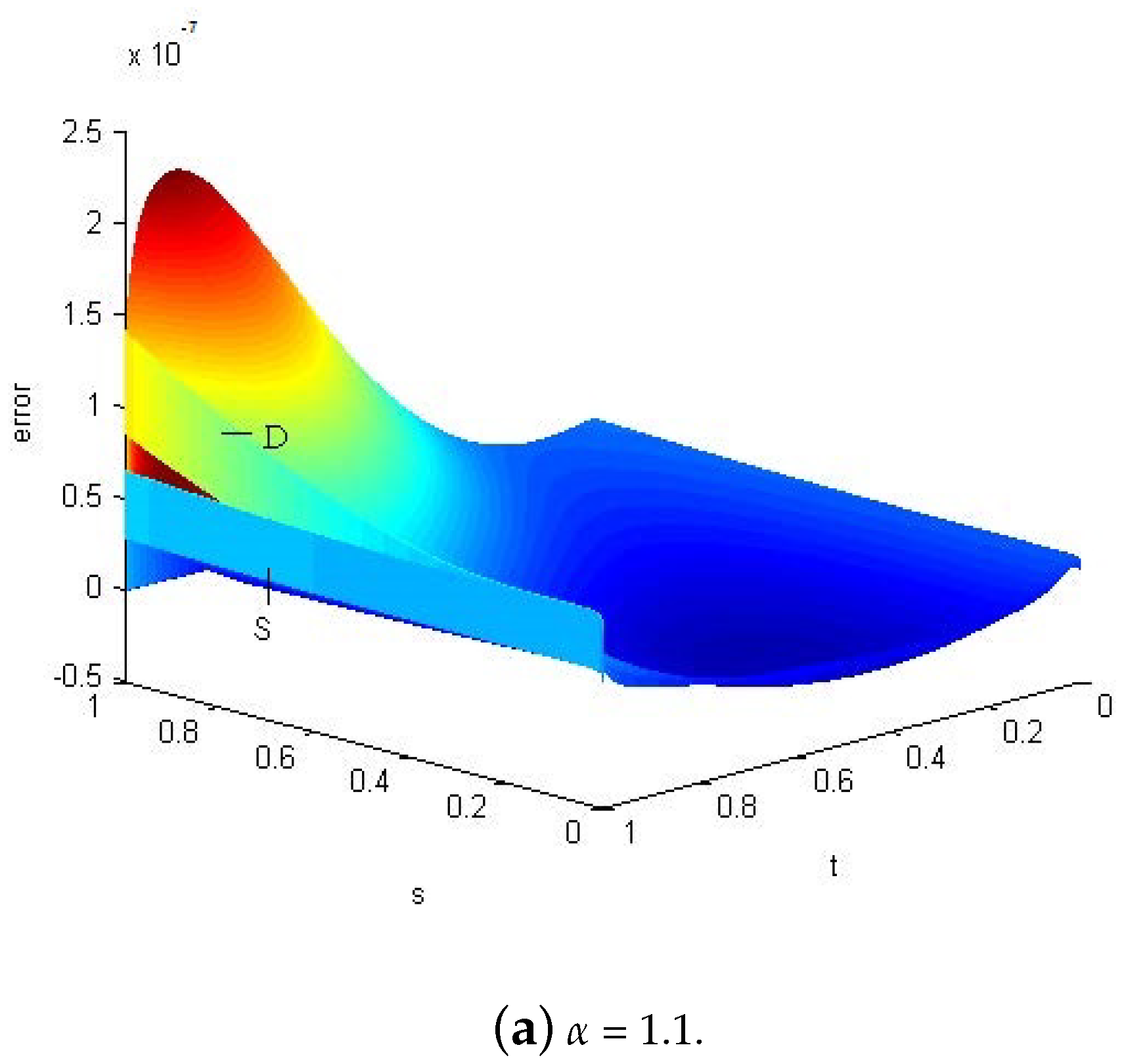
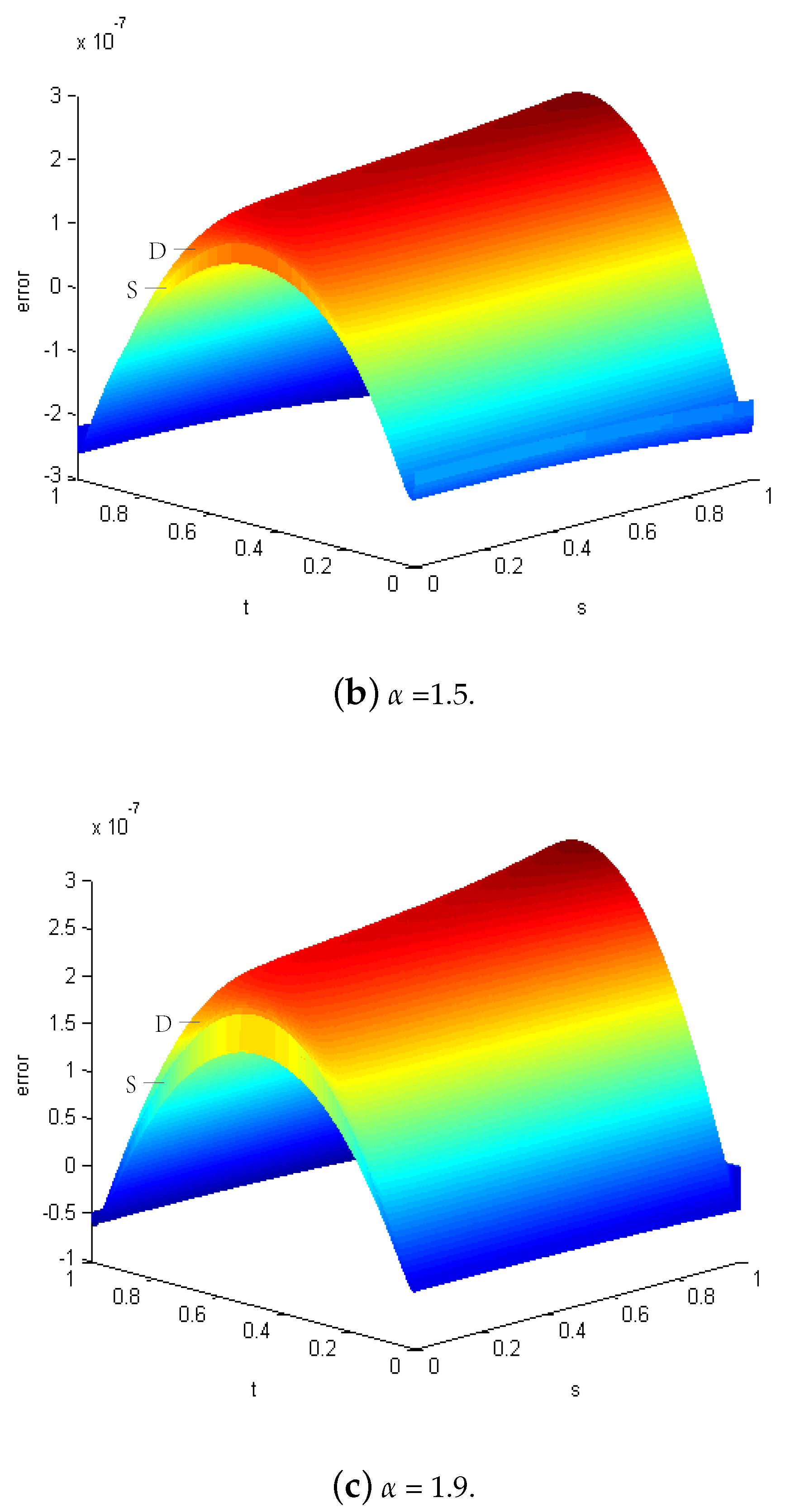
$\mathit{\gamma }=0.2$	h	CPU_ST	CPU_DS (It.)	Rate_DS	Err_ST	Err_DS
	1/2048	4.27	2.31 (5)	—	1.38 $\times {10}^{-7}$	1.38 $\times {10}^{-7}$
	1/4096	17.00	3.83 (5)	2.005	3.44 $\times {10}^{-8}$	3.44 $\times {10}^{-8}$
$\alpha =1.1$	1/8192	116.52	8.02 (5)	2.006	8.57 $\times {10}^{-9}$	8.57 $\times {10}^{-9}$
	1/16,384	792.30	15.54 (6)	2.008	2.13 $\times {10}^{-9}$	2.13 $\times {10}^{-9}$
	1/32,768	5805.97	111.84 (6)	2.004	5.31 $\times {10}^{-10}$	5.31 $\times {10}^{-10}$
	1/2048	4.32	2.34 (5)	—	9.71 $\times {10}^{-8}$	9.71 $\times {10}^{-8}$
	1/4096	16.62	3.79 (5)	2.005	2.42 $\times {10}^{-8}$	2.42 $\times {10}^{-8}$
$\alpha =1.5$	1/8192	120.03	8.19 (5)	2.133	6.03 $\times {10}^{-9}$	5.52 $\times {10}^{-9}$
	1/16,384	789.31	15.55 (5)	2.005	1.30 $\times {10}^{-9}$	1.37 $\times {10}^{-9}$
	1/32,768	5830.86	38.36 (5)	1.186	3.64 $\times {10}^{-10}$	6.02 $\times {10}^{-10}$
	1/2048	4.28	0.73 (4)	—	5.81 $\times {10}^{-8}$	5.62 $\times {10}^{-8}$
	1/4096	15.93	3.57 (4)	2.001	1.45 $\times {10}^{-8}$	1.41 $\times {10}^{-8}$
$\alpha =1.9$	1/8192	117.38	8.04(5)	1.827	3.62 $\times {10}^{-9}$	3.96 $\times {10}^{-9}$
	1/16,384	786.57	15.12 (5)	1.281	8.41 $\times {10}^{-10}$	1.71 $\times {10}^{-9}$
	1/32,768	5838.16	431.24 (6)	1.039	2.95 $\times {10}^{-10}$	8.32 $\times {10}^{-10}$

, where the column labeled “h” indicates the spatial step-length (corresponding to the number of nodes $n_s$). The columns “$\mathrm{CPU}\_\mathrm{ST}$” and “$\mathrm{CPU}\_\mathrm{DS}$” represent the elapsed CPU time for the sequence solver with the Bi-CGSTAB method (abbreviated as “ST”) and our DS method, respectively. The letters “It.” behind “$\mathrm{CPU}\_\mathrm{DS}$” represent the required number of the DS iteration. The columns labeled “$\mathrm{Err}\_\mathrm{ST}$” and “$\mathrm{Err}\_\mathrm{DS}$” represent the calculated errors of the ST method and our DS method, respectively, after termination. As both algorithms reach similar error levels, we only report the convergent rate of the DS method at various scales in the “Rate_DS” column.

We can see from Table 1 that both methods efficiently compute the solution for various values of $\alpha$ with errors ranging from $O\left({10}^{-7}\right)$ to $O\left({10}^{-10}\right)$. Our DS method requires only 4–5 iterations for middle-scale problems ($n_s=2048,4098,8192$) and 5–6 iterations for large-scale problems ($n_s$ = 16,384 to 32,768) to achieve the prescribed residual level of the Stein equation, resulting in similar error levels as the ST method. Although the Rate_DS column shows that the convergence rate gradually decreases with increasing scale, the DS method still requires less CPU time than the ST method for all different $\alpha$, especially at $n_s$ = 32,768. At this scale, the DS method takes only 1/14 of the CPU time required by the ST method to obtain a solution of almost the same order $O\left({10}^{-10}\right)$.

We also carried out further numerical experiments to validate the efficacy of our DS method, with the aim of comparing the error surfaces of the DS and ST methods, and observe any differences in their respective performances. Figure 1 presents the results of our experiments. The figure displays the error surfaces of the DS and ST methods, labeled as “D” and “S” respectively, at specific values of $\gamma =0.3$ and $n_s=2048$. The variables t and s in Figure 1 represent the discretized temporal and spatial values, respectively, within the interval [0, 1] in the error functions. Our analysis of the figure revealed that the error surface of the DS method encompasses that of the ST method, but the errors for both methods are at the level of $O\left({10}^{-8}\right)$, which is a relatively low level of error. This result reinforces the effectiveness and reliability of our proposed DS method.

We subsequently increase the value of $\gamma$ for different $\alpha$ and compare the numerical performance of the DS method with that of the ST method. The obtained results are listed in

Table 2. Numerical performances of two different methods when $\gamma =0.5$ in Example 1.

$\mathit{\gamma }=0.5$	h	CPU_ST	CPU_DS (It.)	Rate_DS	Err_ST	Err_DS
	1/2048	4.14	25.21(6)	—	7.48 $\times {10}^{-8}$	7.52 $\times {10}^{-8}$
	1/4096	15.88	42.74 (6)	2.023	1.33 $\times {10}^{-8}$	1.85 $\times {10}^{-7}$
$\alpha =1.1$	1/8192	117.33	99.25 (6)	2.088	2.24 $\times {10}^{-9}$	4.35 $\times {10}^{-9}$
	1/16,384	803.19	197.31 (6)	1.957	6.27 $\times {10}^{-10}$	1.12 $\times {10}^{-9}$
	1/32,768	5568.40	420.32 (6)	1.559	2.02 $\times {10}^{-10}$	3.80 $\times {10}^{-10}$
	1/2048	5.14	24.69 (6)	—	5.96 $\times {10}^{-8}$	6.13 $\times {10}^{-8}$
	1/4096	16.12	43.80 (6)	2.120	1.17 $\times {10}^{-8}$	1.41 $\times {10}^{-8}$
$\alpha =1.5$	1/8192	117.78	98.53 (6)	2.010	1.83 $\times {10}^{-9}$	3.50 $\times {10}^{-9}$
	1/16,384	798.62	198.50 (6)	1.845	1.27 $\times {10}^{-10}$	9.74 $\times {10}^{-10}$
	1/32,768	5584.45	420.80 (6)	1.633	3.11 $\times {10}^{-11}$	3.14 $\times {10}^{-10}$
	1/2048	6.39	29.16 (6)	—	3.83 $\times {10}^{-8}$	3.96 $\times {10}^{-8}$
	1/4096	16.36	44.39 (6)	2.150	8.00 $\times {10}^{-9}$	8.92 $\times {10}^{-9}$
$\alpha =1.9$	1/8192	118.96	99.52 (6)	2.066	1.31 $\times {10}^{-9}$	2.13 $\times {10}^{-9}$
	1/16,384	792.86	194.41 (6)	1.115	5.71 $\times {10}^{-10}$	9.83 $\times {10}^{-10}$
	1/32,768	5544.37	429.55 (6)	0.916	9.34 $\times {10}^{-11}$	5.21 $\times {10}^{-10}$

. We can see that for different $\alpha$, the DS method requires 6 iterations to reach the prescribed residual level. For middle-scale problems ($n_s=2048,4098$), the ST method is faster than the DS method in terms of CPU time. However, with increasing scale (from $n_s=8192$ to 32,768), the DS method gradually becomes faster than the ST method, albeit sacrificing some accuracy. In particular, at the scale of $n_s$ = 32,768, the DS method takes only about 1/14 of the CPU time required by the ST method to obtain a solution of the order $O\left({10}^{-10}\right)$, indicating that the DS method is more suitable for dealing with large-scale problems. Furthermore, we conducted numerical experiments with a value of $\gamma =0.9$. The results, as shown in

Table 3. Numerical performances of two different methods when $\gamma =0.9$ in Example 1.

$\mathit{\gamma }=0.9$	h	CPU_ST	CPU_DS (It.)	Rate_DS	Err_ST	Err_DS
	1/2048	4.72	25.73(6)	—	2.34 $\times {10}^{-6}$	9.64 $\times {10}^{-6}$
	1/4096	16.49	45.68 (6)	1.072	1.12 $\times {10}^{-6}$	4.75 $\times {10}^{-6}$
$\alpha =1.1$	1/8192	125.95	112.17 (6)	0.911	5.32 $\times {10}^{-7}$	2.43 $\times {10}^{-6}$
	1/16,384	857.63	226.60 (6)	1.029	2.50 $\times {10}^{-7}$	1.19 $\times {10}^{-6}$
	1/32,768	5416.31	405.57 (6)	0.523	1.05 $\times {10}^{-7}$	8.30 $\times {10}^{-7}$
	1/2048	5.03	29.10 (6)	—	1.16 $\times {10}^{-6}$	9.84 $\times {10}^{-6}$
	1/4096	20.55	45.28 (6)	0.922	5.61 $\times {10}^{-7}$	5.19 $\times {10}^{-6}$
$\alpha =1.5$	1/8192	122.46	100.14 (6)	0.805	2.67 $\times {10}^{-7}$	2.97 $\times {10}^{-6}$
	1/16,384	802.23	196.10 (6)	1.137	1.26 $\times {10}^{-7}$	1.35 $\times {10}^{-6}$
	1/32,768	5496.12	428.64 (6)	0.537	9.42 $\times {10}^{-8}$	9.32 $\times {10}^{-7}$
	1/2048	4.32	24.58 (6)	—	6.31 $\times {10}^{-7}$	4.26 $\times {10}^{-6}$
	1/4096	16.36	42.56 (6)	0.696	3.06 $\times {10}^{-7}$	2.63 $\times {10}^{-6}$
$\alpha =1.9$	1/8192	121.83	98.89 (6)	0.772	1.46 $\times {10}^{-7}$	1.54 $\times {10}^{-7}$
	1/16,384	803.47	194.59 (6)	0.874	6.91 $\times {10}^{-8}$	8.42 $\times {10}^{-7}$
	1/32,768	5521.86	435.56 (6)	0.573	4.75 $\times {10}^{-8}$	5.66 $\times {10}^{-7}$

, indicate that while the DS method may sacrifice some accuracy, it still outperforms the ST method in terms of CPU time when $n_s$ is no less than 8192.

Example 2.

Consider the GFDE (1) with the diffusion coefficient $\kappa =5$ and the weight function $\lambda \left(t\right)=e^{-bt}$ with $b\ge 0$ [11]. The source term is

$$\begin{array}{ccc}\hfill f(x,t)& =& \frac{10t^{3-\gamma }{e}^{-bt}}{\Gamma (4-\gamma )}{x}^2{(1-x)}^2-25g\left(t\right)\{\frac{\Gamma \left(3\right)}{\Gamma (3-\alpha )}[p{x}^{2-\alpha }+(1-p){(1-x)}^{2-\alpha }]\hfill \\ & & -2\frac{\Gamma \left(4\right)}{\Gamma (4-\alpha )}[p{x}^{3-\alpha }+(1-p){(1-x)}^{3-\alpha }]+\frac{\Gamma \left(5\right)}{\Gamma (5-\alpha )}[p{x}^{4-\alpha }+(1-p){(1-x)}^{4-\alpha }]\}.\hfill \end{array}$$

The corresponding initial-boundary value conditions are $u(x,0)=5g\left(0\right)x^2{(1-x)}^2$, $u(0,t)=u(1,t)=0$. It can be verified that the exact solution function is $u(x,t)=5g\left(t\right)x^2{(1-x)}^2$ ( see Appendix A) with

$$g\left(t\right)=1+\frac{2-(2+2bt+b^2{t}^2)e^{-bt}}{b^3}.$$

We chose values of $p=0.4$ and $\gamma =0.2$ and implemented both algorithms for the discretized Stein equation from Example 2. The results obtained are displayed in

Table 4. Numerical performances of two different methods when $\gamma =0.2$, $p=0.4$ in Example 2.

$\mathit{\gamma }=0.2$, $\mathit{p}=0.4$	h	CPU_ST	CPU_DS (It.)	Rate_DS	Err_ST	Err_DS
	1/2048	4.43	2.23 (5)	—	6.59 $\times {10}^{-7}$	6.59 $\times {10}^{-7}$
	1/4096	16.62	14.57 (6)	1.9872	1.66 $\times {10}^{-7}$	1.66 $\times {10}^{-7}$
$\alpha =1.1$	1/8192	121.85	32.28 (6)	1.9912	4.16 $\times {10}^{-8}$	4.16 $\times {10}^{-8}$
	1/16,384	779.27	64.17 (6)	1.9938	1.04 $\times {10}^{-8}$	1.04 $\times {10}^{-8}$
	1/32,768	5579.25	521.88 (6)	1.9956	2.62 $\times {10}^{-9}$	2.62 $\times {10}^{-9}$
	1/2048	4.16	23.58 (6)	—	2.99 $\times {10}^{-7}$	2.99 $\times {10}^{-7}$
	1/4096	15.86	44.47 (6)	1.9929	7.76 $\times {10}^{-8}$	7.75 $\times {10}^{-8}$
$\alpha =1.5$	1/8192	127.21	103.13 (6)	1.7647	2.00 $\times {10}^{-8}$	2.28 $\times {10}^{-8}$
	1/16,384	791.21	221.25 (6)	1.3760	5.14 $\times {10}^{-9}$	8.78 $\times {10}^{-9}$
	1/32,768	5742.21	532.20 (6)	1.1816	1.31 $\times {10}^{-9}$	3.86 $\times {10}^{-9}$
	1/2048	6.14	19.69 (6)	—	2.94 $\times {10}^{-7}$	2.94 $\times {10}^{-7}$
	1/4096	16.72	37.14 (6)	1.9582	7.23 $\times {10}^{-8}$	7.53 $\times {10}^{-8}$
$\alpha =1.9$	1/8192	120.83	83.25 (6)	1.8630	1.83 $\times {10}^{-8}$	2.07 $\times {10}^{-8}$
	1/16,384	795.98	169.03 (6)	1.4210	2.94 $\times {10}^{-9}$	5.73 $\times {10}^{-9}$
	1/32,768	5813.56	478.80 (6)	0.4961	1.05 $\times {10}^{-9}$	4.07 $\times {10}^{-9}$

, which demonstrates that both methods are capable of efficiently computing the solution with an error range of approximately between $O\left({10}^{-7}\right)$ to $O\left({10}^{-9}\right)$ for different values of $\alpha$. With the exception of when $h=1/2048$ and $\alpha =1.1$, our DS method required six iterations to achieve the desired residual level. In addition, for $\alpha =1.1$, the DS method was less time-consuming than the ST method but achieved almost the same level of accuracy. For cases where $\alpha =1.5$ and $1.9$, our DS method took more CPU time to compute the solution for middle-scale cases where $n_s$ was 2048 and 4098. However, as the scale increased, the DS method required less CPU time than the ST method, with only a slight decrease in accuracy.

Additionally, we generated error surfaces for both methods and denoted them as “D” for the DS method and “S” for the ST method. These surfaces were plotted at $\gamma =0.4$ and $n_s=2048$, and the results are shown in Figure 2. The figure indicates that the error surface of the DS method covers that of the ST method, while both methods have similar error levels of approximately $O\left({10}^{-7}\right)$.

We also raised the parameter $\gamma$ to 0.5 and executed both algorithms once more.

Table 5. Numerical performances of two different methods when $\gamma =0.5$, $p=0.4$ in Example 2.

$\mathit{\gamma }=0.5$, $\mathit{p}=0.4$	h	CPU_ST	CPU_DS (It.)	Rate_DS	Err_ST	Err_DS
	1/2048	4.41	30.12 (6)	—	6.41 $\times {10}^{-7}$	6.41 $\times {10}^{-7}$
	1/4096	16.82	55.45 (6)	1.9579	1.60 $\times {10}^{-7}$	1.65 $\times {10}^{-7}$
$\alpha =1.1$	1/8192	122.68	111.99 (6)	1.8652	4.00 $\times {10}^{-8}$	4.53 $\times {10}^{-8}$
	1/16,384	739.46	246.17 (6)	1.8234	9.95 $\times {10}^{-9}$	1.28 $\times {10}^{-8}$
	1/32,768	5954.71	520.47 (6)	1.7597	2.47 $\times {10}^{-9}$	3.78 $\times {10}^{-9}$
	1/2048	4.16	28.98 (6)	—	2.98 $\times {10}^{-7}$	2.98 $\times {10}^{-7}$
	1/4096	15.77	55.01 (6)	1.9428	7.72 $\times {10}^{-8}$	7.76 $\times {10}^{-8}$
$\alpha =1.5$	1/8192	117.98	101.78 (6)	1.8448	1.99 $\times {10}^{-8}$	2.16 $\times {10}^{-8}$
	1/16,384	785.39	246.42 (6)	1.5690	5.10 $\times {10}^{-9}$	7.28 $\times {10}^{-9}$
	1/32,768	5744.93	536.89.26 (6)	1.5721	1.29 $\times {10}^{-9}$	2.45 $\times {10}^{-9}$
	1/2048	4.38	29.96 (6)	—	3.01 $\times {10}^{-7}$	3.01 $\times {10}^{-7}$
	1/4096	16.74	55.44 (6)	2.005	7.46 $\times {10}^{-8}$	7.53 $\times {10}^{-8}$
$\alpha =1.9$	1/8192	118.82	103.35 (6)	1.8423	1.89 $\times {10}^{-8}$	2.10 $\times {10}^{-8}$
	1/16,384	810.04	246.57 (6)	1.3030	4.14 $\times {10}^{-9}$	8.53 $\times {10}^{-9}$
	1/32,768	5816.90	550.72 (6)	0.0051	1.96 $\times {10}^{-9}$	8.50 $\times {10}^{-9}$

illustrates the results, indicating that our DS method produces similar error levels to the ST method. Moreover, when $n_s=8192$, our DS method performs better than the ST method in terms of CPU time. This tendency becomes increasingly apparent as the scale increases, demonstrating that the complexity of the DS method is roughly $O((n_s-1)log(n_s-1))$ and that it is more suitable for larger-scale problems. In

Table 6. Numerical performances of two different methods when $\gamma =0.9$, $p=0.4$ in Example 2.

$\mathit{\gamma }=0.9$, $\mathit{p}=0.4$	h	CPU_ST	CPU_DS (It.)	Rate_DS	Err_ST	Err_DS
	1/2048	4.53	29.75 (6)	—	3.78 $\times {10}^{-6}$	4.08 $\times {10}^{-6}$
	1/4096	17.29	54.29 (6)	1.0213	1.72 $\times {10}^{-6}$	2.01 $\times {10}^{-6}$
$\alpha =1.1$	1/8192	126.29	128.06 (6)	0.9368	7.94 $\times {10}^{-7}$	1.05 $\times {10}^{-6}$
	1/16,384	814.66	243.67 (6)	0.7124	3.68 $\times {10}^{-7}$	6.42 $\times {10}^{-7}$
	1/32,768	6043.21	518.66 (6)	0.6225	1.53 $\times {10}^{-7}$	4.17 $\times {10}^{-7}$
	1/2048	4.31	29.78 (6)	—	9.72 $\times {10}^{-7}$	1.23 $\times {10}^{-6}$
	1/4096	16.45	54.31 (6)	1.0105	4.07 $\times {10}^{-7}$	6.12 $\times {10}^{-7}$
$\alpha =1.5$	1/8192	122.19	124.77 (6)	0.7416	1.79 $\times {10}^{-7}$	3.66 $\times {10}^{-7}$
	1/16,384	802.35	243.98 (6)	0.8936	8.06 $\times {10}^{-8}$	1.97 $\times {10}^{-7}$
	1/32,768	5804.55	522.53 (6)	0.9970	3.90 $\times {10}^{-8}$	9.88 $\times {10}^{-8}$
	1/2048	4.52	29.63 (6)	—	5.79 $\times {10}^{-7}$	9.54 $\times {10}^{-7}$
	1/4096	17.44	54.40 (6)	1.0121	2.11 $\times {10}^{-7}$	4.73 $\times {10}^{-7}$
$\alpha =1.9$	1/8192	124.43	123.46 (6)	0.6425	8.37 $\times {10}^{-8}$	3.03 $\times {10}^{-7}$
	1/16,384	810.55	244.26 (6)	0.8508	3.46 $\times {10}^{-8}$	1.68 $\times {10}^{-7}$
	1/32,768	5978.33	562.76 (6)	0.5979	1.41 $\times {10}^{-8}$	1.11 $\times {10}^{-7}$

, we resumed conducting numerical experiments with $\gamma =0.9$ and similarly found that while the DS method may compromise some accuracy, it still outperforms the ST method in terms of CPU time when $n_s>8192$.

5. Conclusions

We have presented a doubling Smith iteration method for solving discretized Stein equations arising from a class of generalized fractional diffusion equations (GFDEs). The method takes advantage of the implicit difference scheme, resulting in coefficient matrices with nonsingular M-matrix structures. The two optimal parameters are then determined based on this property, and the separable forcing term of the GFDE contributes to the low-ranked version of the doubling Smith method. Numerical experiments demonstrate that our method outperforms the ST method with the Bi-CGSTAB solver in terms of CPU time, particularly as the scale increases, although it sacrifices some accuracy. However, our approach is limited to GFDEs with the case of $\lambda \left(t\right)=1$. It may not be appropriate for solving other types of fractional diffusion equations. Additionally, if the coefficient matrices do not have nonsingular M-matrix structures, the optimal parameters in the presented doubling Smith method may not be determined. As future work, we plan to explore the applicability of the low-ranked doubling Smith methods for solving other large-scale GFDEs. In addition, it should be noted that the GFDE discussed in this paper is limited to zero boundary conditions. It is important to acknowledge that previous studies have shown that the shifted Grunwald–Letnikov formula requires modification when dealing with absorbing boundary conditions. Researchers have explored this area in depth, as evidenced by works such as [27,28,29]. As such, it would be beneficial for future research to focus on extending the technique of the classical method of manufactured solutions [30,31,32,33] to convert non-zero boundary conditions into zero ones. This would allow the GFDE to be applied to a wider range of problems, improving its practicality and usefulness in real-world scenarios.