Doubling Smith Method for a Class of Large-Scale Generalized Fractional Diffusion Equations
Abstract
1. Introduction
- The transformation of the linear systems corresponding to the GFDE (1) into a low-ranked matrix equation is explained in detail.
- The low-ranked doubling Smith method with two optimal parameters is proposed under the separable forcing function.
- (a)
- A is a nonsingular M-matrix.
- (b)
- A is nonsingular and satisfies .
- (c)
- for some vector .
- (d)
- All eigenvalues of A have positive real parts.
- (a)
- If , then B is an M-matrix. Particularly, is an M-matrix for and a nonsingular M-matrix for .
- (b)
- The one with the smallest absolute value among all eigenvalues of A, denoted by , is nonnegative, and .
2. Implicit Difference Scheme and the Linear Systems
2.1. Temporal and Spatial Discretization
2.2. Derivation of the Sequence of Linear Systems
3. Low-Ranked Matrix Equation and Doubling Smith Method
3.1. Matrix Equation with Structured Coefficients
3.2. Doubling Smith Method with the Optimal Parameters
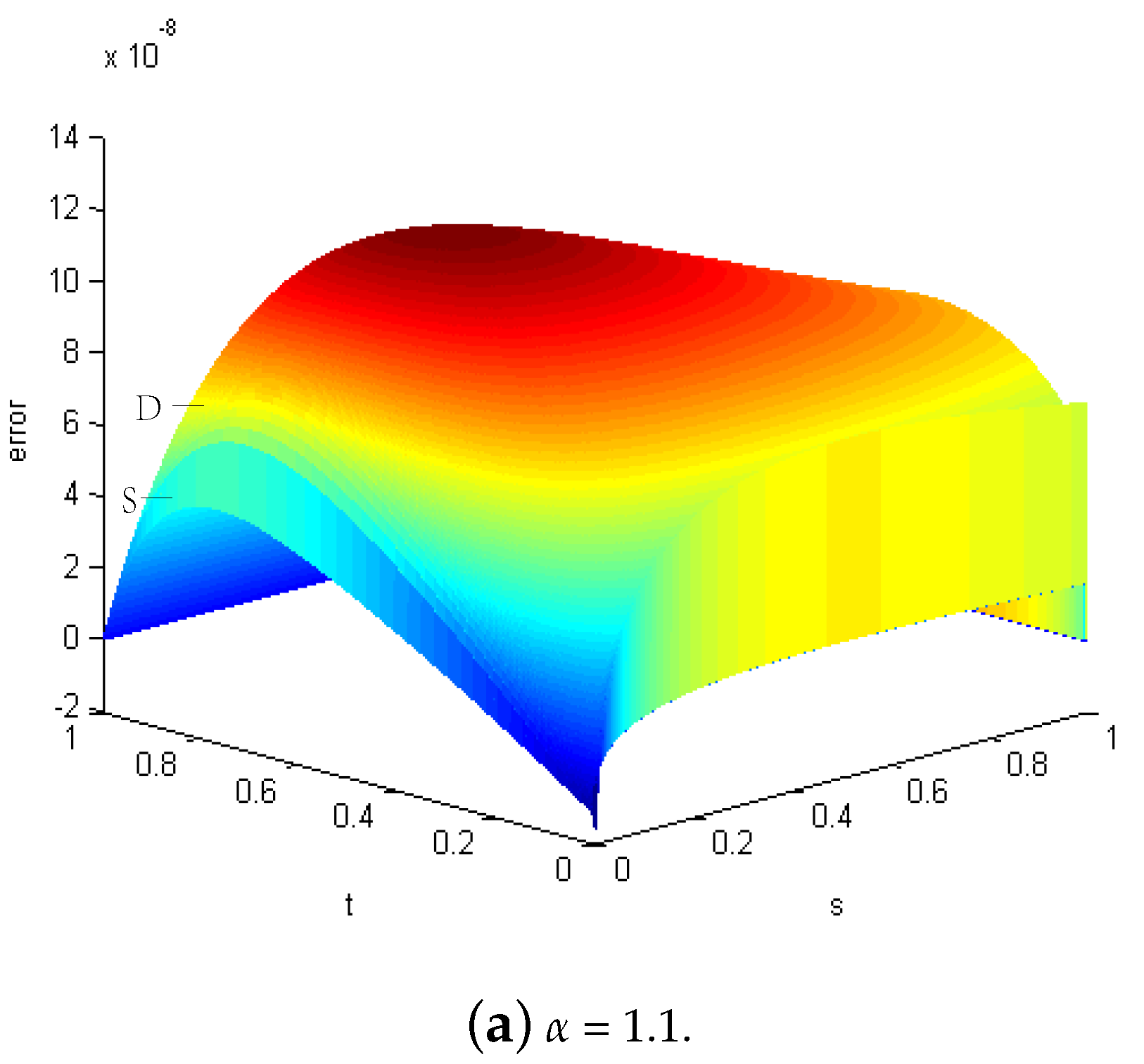
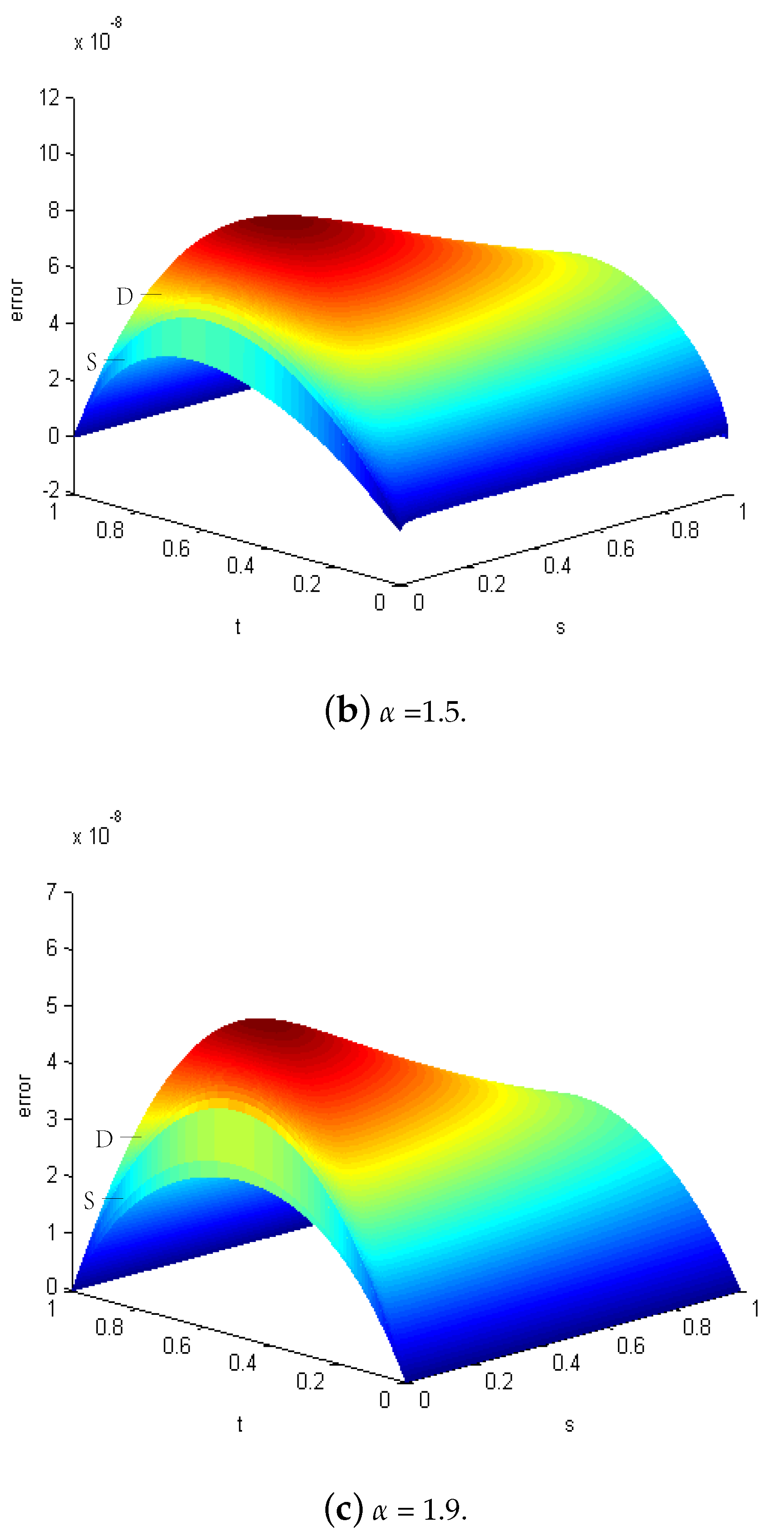
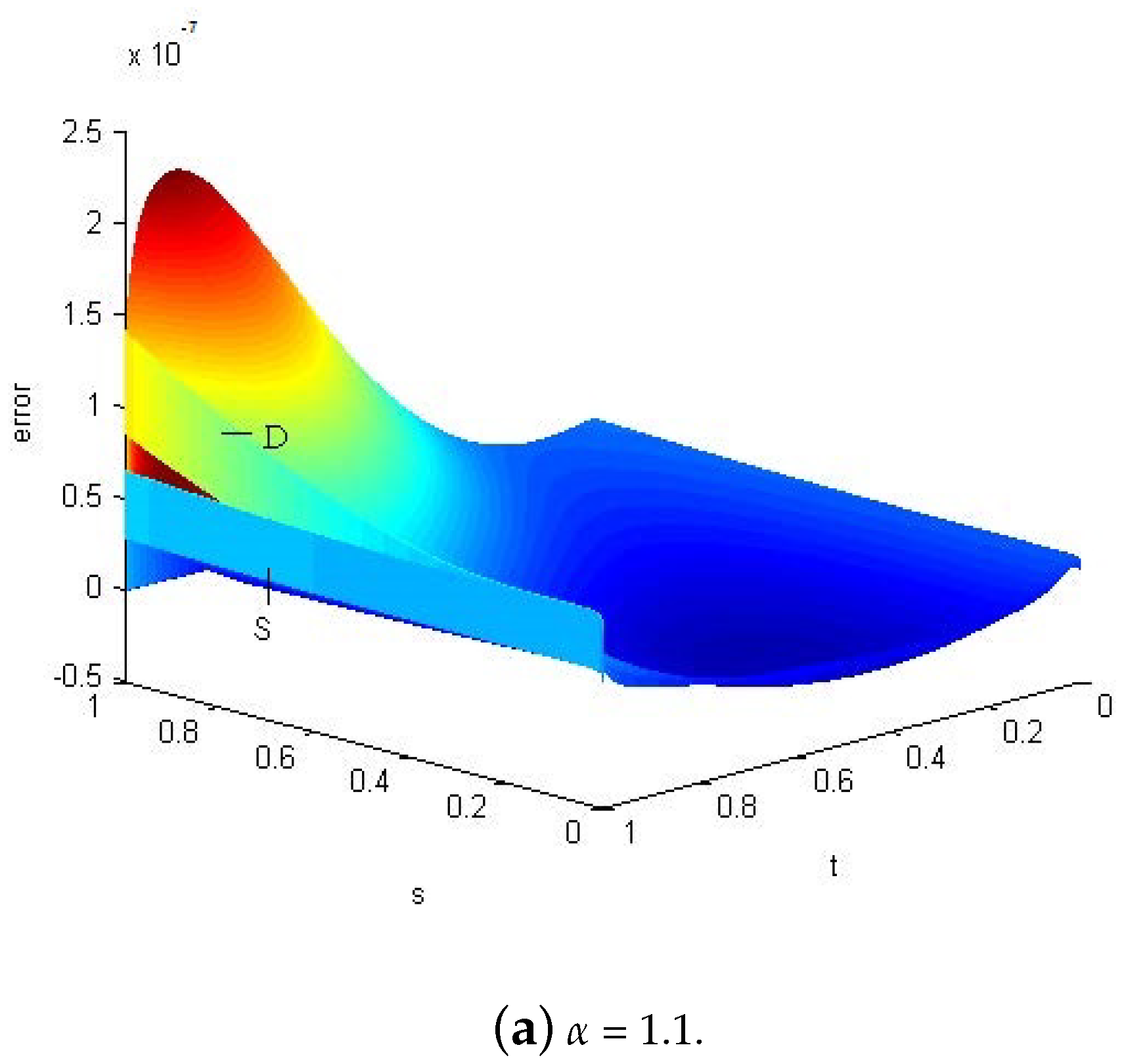
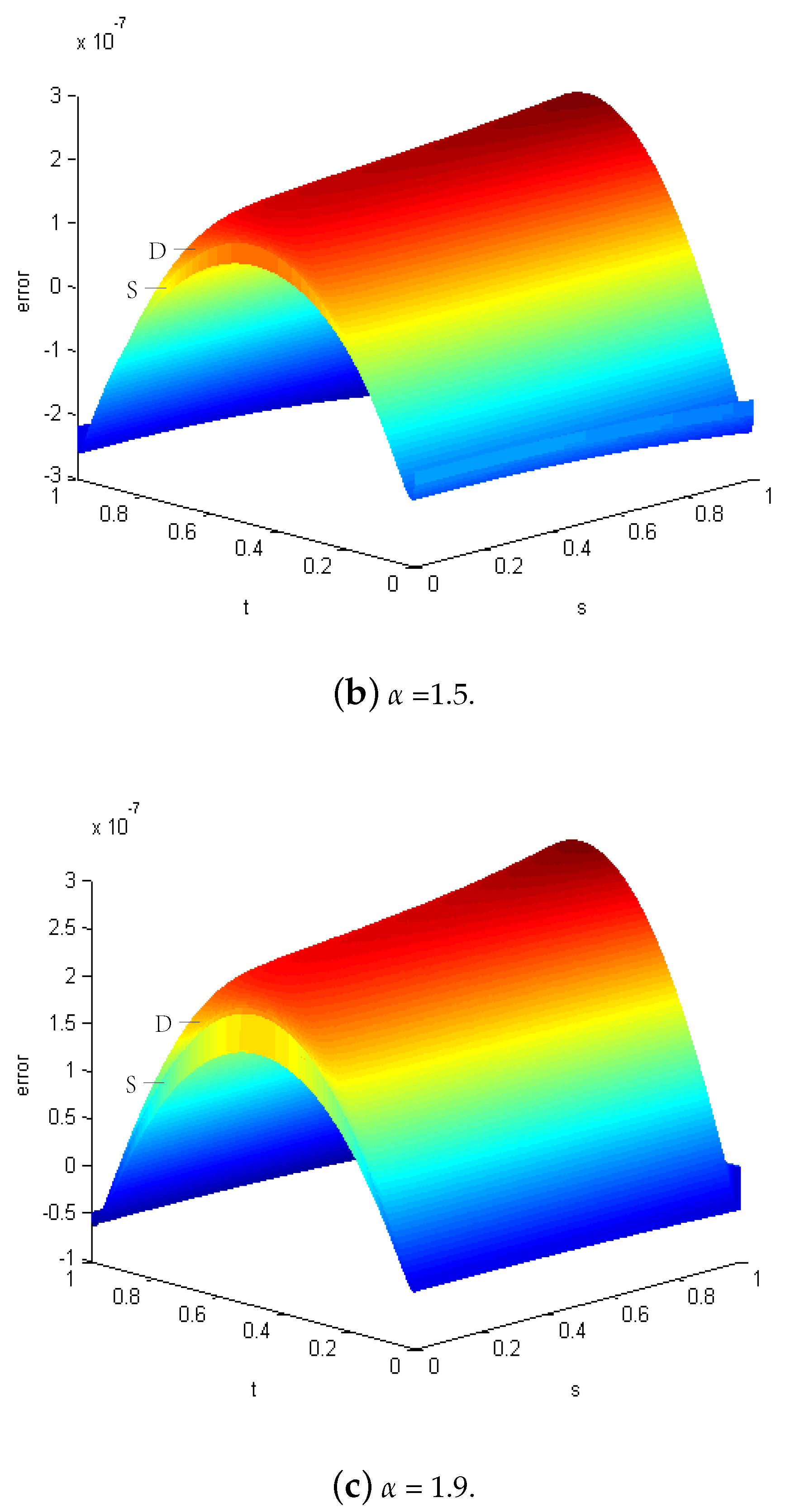
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Validation of True Solutions in Example 1 and 2
References
- Alikhanov, A.A. A time-fractional diffusion equation with generalized memory kernel in differential and difference settings with smooth solutions. Comput. Methods Appl. Math. 2017, 17, 647–660. [Google Scholar] [CrossRef]
- Sandev, T.; Chechkin, A.; Kantz, H.; Metzler, R. Diffusion and Fokker-Planck-Smoluchowski equations with generalized memory kernel. Fract. Calc. Appl. Anal. 2015, 18, 1006–1038. [Google Scholar] [CrossRef]
- Santos, M.A.F. Mittag-Leffler memory kernel in Lévy flights. Mathematics 2019, 7, 766. [Google Scholar] [CrossRef]
- Chen, M.; Deng, W. High order algorithm for the time-tempered fractional Feynman-Kac equation. J. Sci. Comput. 2018, 76, 867–887. [Google Scholar] [CrossRef]
- Wu, X.; Deng, W.; Barkai, E. Tempered fractional Feynman-Kac equation: Theory and examples. Phys. Rev. E 2016, 93, 032151. [Google Scholar] [CrossRef]
- Kostić, M. Abstract Volterra Integro-Differential Equations; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Lin, F.-R.; Yang, S.-W.; Jin, X.-Q. Preconditioned iterative methods for fractional diffusion equation. J. Comput. Phys. 2014, 256, 109–117. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Bazhlekova, E. Fractional Evolution Equations in Banach Spaces. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2001. [Google Scholar]
- Tadjeran, C.; Meerschaert, M.M.; Scheffler, H.-P. A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys. 2006, 213, 205–213. [Google Scholar] [CrossRef]
- Gu, X.-M.; Huang, T.-Z.; Zhao, Y.-L.; Lyu, P.; Carpentieri, B. A fast implicit difference scheme for solving the generalized time-space fractional diffusion equations with variable coefficients. Numer. Meth. Part. Differ. Equ. 2021, 37, 1136–1162. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential Equations, Mathematics in Science; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Pitolli, F.; Sorgentone, C.; Pellegrino, E. Approximation of the Riesz–Caputo Derivative by Cubic Splines. Algorithms 2022, 15, 69. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, T. Finite element calculation of the linear elasticity problem for biomaterials with fractal structure. Open Bioinform. J. 2021, 14 (Suppl. M1), 114–122. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. A Discretization Approach for the Nonlinear Fractional Logistic Equation. Entropy 2020, 22, 1328. [Google Scholar] [CrossRef]
- Li, T.-X.; Weng, P.C.-Y.; Chu, E.K.-W.; Lin, W.-W. Large-scale Stein and Lyapunov equtions, Smith method, and applications. Numer. Algorithms 2013, 63, 727–752. [Google Scholar] [CrossRef]
- Yu, B.; Fan, H.-Y.; Chu, E.K.-W. Smith method for projected Lyapunov and Stein equations. Univ. Politeh. Buchar. Sci. Bull.-Ser. A-Appl. Math. Phys. 2018, 80, 191–204. [Google Scholar]
- Kelly, C.T. Iterative Methods for Linear and Nonlinear Equations; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Varga, R. Matrix Iterative Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germeny, 2000. [Google Scholar]
- Wang, W.-G.; Wang, W.-C.; Li, R.-C. Alternating-directional doubling algorithm for M-matrix algebraic Riccati equations. SIAM J. Matrix Anal. Appl. 2012, 33, 170–194. [Google Scholar] [CrossRef]
- Gu, X.-M.; Huang, T.-Z.; Ji, C.-C.; Carpentieri, B.; Alikhanov, A.A. Fast iterative method with a second-order implicit difference scheme for time-space fractional convection-diffusion equation. J. Sci. Comput. 2017, 72, 957–985. [Google Scholar] [CrossRef]
- Hao, Z.-P.; Sun, Z.-Z.; Cao, W.-R. A fourth-order approximation of fractional derivatives with its applications. J. Comput. Phys. 2015, 281, 787–805. [Google Scholar] [CrossRef]
- Tian, W.-Y.; Zhou, H.; Deng, W.-H. A class of second order difference approsimation for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Ng, M. Iterative Methods for Toeplitz Systems; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Chu, E.K.-W.; Weng, P.C.-Y. Large-scale discrete-time algebraic Riccati equations—Doubling algorithm and error analysis. J. Comput. Appl. Math. 2015, 277, 115–126. [Google Scholar] [CrossRef]
- Gohberg, I.; Semencul, A. On the inversion of finite Toeplitz matrices and their continuous analogues. Mat. Issled. 1972, 7, 201–223. (In Russian) [Google Scholar]
- Kelly, F.; Sankaranarayanan, H.; Meerschaert, M. Boundary conditions for two-sided fractional diffusion. J. Comput. Phys. 2019, 376, 1089–1107. [Google Scholar] [CrossRef]
- Krepysheva, N.; Di Pietro, L.; Néel, C. Space-fractional advection-diffusion and reflective boundary condition. Phys. Rev. E 2006, 73, 021104. [Google Scholar] [CrossRef]
- Baeumer, B.; Kovács, M.; Meerschaert, M.; Sankaranarayanan, H. Reprint of: Boundary conditions for fractional diffusion. J. Comput. Appl. Math. 2018, 339, 414–430. [Google Scholar] [CrossRef]
- Tremblay, D.; Stephane, E.; Dominique, P. Code verification and the method of manufactured solutions for fluid-structure interaction problems. In Proceedings of the 36th AIAA Fluid Dynamics Conference and Exhibit, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Krueger, M.; Mousseau, A.; Hassan, A. Rigorous code verification: An additional tool to use with the method of manufactured solutions. In Verification and Validation; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 41174, p. V001T04A002. [Google Scholar]
- Vedovoto, J.M.; da Silveira, N.A.; Mura, A.; da Silva, L.F.F. Application of the method of manufactured solutions to the verification of a pressure-based finite-volume numerical scheme. Comput. Fluids 2011, 51, 85–99. [Google Scholar] [CrossRef]
- Shunn, L.; Ham, F. Method of manufactured solutions applied to variable-density flow solvers. In Annual Research Briefs-2007; Center for Turbulence Research: San Francisco, CA, USA, 2007; pp. 155–168. [Google Scholar]
| h | CPU_ST | CPU_DS (It.) | Rate_DS | Err_ST | Err_DS | |
|---|---|---|---|---|---|---|
| 1/2048 | 4.27 | 2.31 (5) | — | 1.38 | 1.38 | |
| 1/4096 | 17.00 | 3.83 (5) | 2.005 | 3.44 | 3.44 | |
| 1/8192 | 116.52 | 8.02 (5) | 2.006 | 8.57 | 8.57 | |
| 1/16,384 | 792.30 | 15.54 (6) | 2.008 | 2.13 | 2.13 | |
| 1/32,768 | 5805.97 | 111.84 (6) | 2.004 | 5.31 | 5.31 | |
| 1/2048 | 4.32 | 2.34 (5) | — | 9.71 | 9.71 | |
| 1/4096 | 16.62 | 3.79 (5) | 2.005 | 2.42 | 2.42 | |
| 1/8192 | 120.03 | 8.19 (5) | 2.133 | 6.03 | 5.52 | |
| 1/16,384 | 789.31 | 15.55 (5) | 2.005 | 1.30 | 1.37 | |
| 1/32,768 | 5830.86 | 38.36 (5) | 1.186 | 3.64 | 6.02 | |
| 1/2048 | 4.28 | 0.73 (4) | — | 5.81 | 5.62 | |
| 1/4096 | 15.93 | 3.57 (4) | 2.001 | 1.45 | 1.41 | |
| 1/8192 | 117.38 | 8.04(5) | 1.827 | 3.62 | 3.96 | |
| 1/16,384 | 786.57 | 15.12 (5) | 1.281 | 8.41 | 1.71 | |
| 1/32,768 | 5838.16 | 431.24 (6) | 1.039 | 2.95 | 8.32 |
| h | CPU_ST | CPU_DS (It.) | Rate_DS | Err_ST | Err_DS | |
|---|---|---|---|---|---|---|
| 1/2048 | 4.14 | 25.21(6) | — | 7.48 | 7.52 | |
| 1/4096 | 15.88 | 42.74 (6) | 2.023 | 1.33 | 1.85 | |
| 1/8192 | 117.33 | 99.25 (6) | 2.088 | 2.24 | 4.35 | |
| 1/16,384 | 803.19 | 197.31 (6) | 1.957 | 6.27 | 1.12 | |
| 1/32,768 | 5568.40 | 420.32 (6) | 1.559 | 2.02 | 3.80 | |
| 1/2048 | 5.14 | 24.69 (6) | — | 5.96 | 6.13 | |
| 1/4096 | 16.12 | 43.80 (6) | 2.120 | 1.17 | 1.41 | |
| 1/8192 | 117.78 | 98.53 (6) | 2.010 | 1.83 | 3.50 | |
| 1/16,384 | 798.62 | 198.50 (6) | 1.845 | 1.27 | 9.74 | |
| 1/32,768 | 5584.45 | 420.80 (6) | 1.633 | 3.11 | 3.14 | |
| 1/2048 | 6.39 | 29.16 (6) | — | 3.83 | 3.96 | |
| 1/4096 | 16.36 | 44.39 (6) | 2.150 | 8.00 | 8.92 | |
| 1/8192 | 118.96 | 99.52 (6) | 2.066 | 1.31 | 2.13 | |
| 1/16,384 | 792.86 | 194.41 (6) | 1.115 | 5.71 | 9.83 | |
| 1/32,768 | 5544.37 | 429.55 (6) | 0.916 | 9.34 | 5.21 |
| h | CPU_ST | CPU_DS (It.) | Rate_DS | Err_ST | Err_DS | |
|---|---|---|---|---|---|---|
| 1/2048 | 4.72 | 25.73(6) | — | 2.34 | 9.64 | |
| 1/4096 | 16.49 | 45.68 (6) | 1.072 | 1.12 | 4.75 | |
| 1/8192 | 125.95 | 112.17 (6) | 0.911 | 5.32 | 2.43 | |
| 1/16,384 | 857.63 | 226.60 (6) | 1.029 | 2.50 | 1.19 | |
| 1/32,768 | 5416.31 | 405.57 (6) | 0.523 | 1.05 | 8.30 | |
| 1/2048 | 5.03 | 29.10 (6) | — | 1.16 | 9.84 | |
| 1/4096 | 20.55 | 45.28 (6) | 0.922 | 5.61 | 5.19 | |
| 1/8192 | 122.46 | 100.14 (6) | 0.805 | 2.67 | 2.97 | |
| 1/16,384 | 802.23 | 196.10 (6) | 1.137 | 1.26 | 1.35 | |
| 1/32,768 | 5496.12 | 428.64 (6) | 0.537 | 9.42 | 9.32 | |
| 1/2048 | 4.32 | 24.58 (6) | — | 6.31 | 4.26 | |
| 1/4096 | 16.36 | 42.56 (6) | 0.696 | 3.06 | 2.63 | |
| 1/8192 | 121.83 | 98.89 (6) | 0.772 | 1.46 | 1.54 | |
| 1/16,384 | 803.47 | 194.59 (6) | 0.874 | 6.91 | 8.42 | |
| 1/32,768 | 5521.86 | 435.56 (6) | 0.573 | 4.75 | 5.66 |
| , | h | CPU_ST | CPU_DS (It.) | Rate_DS | Err_ST | Err_DS |
|---|---|---|---|---|---|---|
| 1/2048 | 4.43 | 2.23 (5) | — | 6.59 | 6.59 | |
| 1/4096 | 16.62 | 14.57 (6) | 1.9872 | 1.66 | 1.66 | |
| 1/8192 | 121.85 | 32.28 (6) | 1.9912 | 4.16 | 4.16 | |
| 1/16,384 | 779.27 | 64.17 (6) | 1.9938 | 1.04 | 1.04 | |
| 1/32,768 | 5579.25 | 521.88 (6) | 1.9956 | 2.62 | 2.62 | |
| 1/2048 | 4.16 | 23.58 (6) | — | 2.99 | 2.99 | |
| 1/4096 | 15.86 | 44.47 (6) | 1.9929 | 7.76 | 7.75 | |
| 1/8192 | 127.21 | 103.13 (6) | 1.7647 | 2.00 | 2.28 | |
| 1/16,384 | 791.21 | 221.25 (6) | 1.3760 | 5.14 | 8.78 | |
| 1/32,768 | 5742.21 | 532.20 (6) | 1.1816 | 1.31 | 3.86 | |
| 1/2048 | 6.14 | 19.69 (6) | — | 2.94 | 2.94 | |
| 1/4096 | 16.72 | 37.14 (6) | 1.9582 | 7.23 | 7.53 | |
| 1/8192 | 120.83 | 83.25 (6) | 1.8630 | 1.83 | 2.07 | |
| 1/16,384 | 795.98 | 169.03 (6) | 1.4210 | 2.94 | 5.73 | |
| 1/32,768 | 5813.56 | 478.80 (6) | 0.4961 | 1.05 | 4.07 |
| , | h | CPU_ST | CPU_DS (It.) | Rate_DS | Err_ST | Err_DS |
|---|---|---|---|---|---|---|
| 1/2048 | 4.41 | 30.12 (6) | — | 6.41 | 6.41 | |
| 1/4096 | 16.82 | 55.45 (6) | 1.9579 | 1.60 | 1.65 | |
| 1/8192 | 122.68 | 111.99 (6) | 1.8652 | 4.00 | 4.53 | |
| 1/16,384 | 739.46 | 246.17 (6) | 1.8234 | 9.95 | 1.28 | |
| 1/32,768 | 5954.71 | 520.47 (6) | 1.7597 | 2.47 | 3.78 | |
| 1/2048 | 4.16 | 28.98 (6) | — | 2.98 | 2.98 | |
| 1/4096 | 15.77 | 55.01 (6) | 1.9428 | 7.72 | 7.76 | |
| 1/8192 | 117.98 | 101.78 (6) | 1.8448 | 1.99 | 2.16 | |
| 1/16,384 | 785.39 | 246.42 (6) | 1.5690 | 5.10 | 7.28 | |
| 1/32,768 | 5744.93 | 536.89.26 (6) | 1.5721 | 1.29 | 2.45 | |
| 1/2048 | 4.38 | 29.96 (6) | — | 3.01 | 3.01 | |
| 1/4096 | 16.74 | 55.44 (6) | 2.005 | 7.46 | 7.53 | |
| 1/8192 | 118.82 | 103.35 (6) | 1.8423 | 1.89 | 2.10 | |
| 1/16,384 | 810.04 | 246.57 (6) | 1.3030 | 4.14 | 8.53 | |
| 1/32,768 | 5816.90 | 550.72 (6) | 0.0051 | 1.96 | 8.50 |
| , | h | CPU_ST | CPU_DS (It.) | Rate_DS | Err_ST | Err_DS |
|---|---|---|---|---|---|---|
| 1/2048 | 4.53 | 29.75 (6) | — | 3.78 | 4.08 | |
| 1/4096 | 17.29 | 54.29 (6) | 1.0213 | 1.72 | 2.01 | |
| 1/8192 | 126.29 | 128.06 (6) | 0.9368 | 7.94 | 1.05 | |
| 1/16,384 | 814.66 | 243.67 (6) | 0.7124 | 3.68 | 6.42 | |
| 1/32,768 | 6043.21 | 518.66 (6) | 0.6225 | 1.53 | 4.17 | |
| 1/2048 | 4.31 | 29.78 (6) | — | 9.72 | 1.23 | |
| 1/4096 | 16.45 | 54.31 (6) | 1.0105 | 4.07 | 6.12 | |
| 1/8192 | 122.19 | 124.77 (6) | 0.7416 | 1.79 | 3.66 | |
| 1/16,384 | 802.35 | 243.98 (6) | 0.8936 | 8.06 | 1.97 | |
| 1/32,768 | 5804.55 | 522.53 (6) | 0.9970 | 3.90 | 9.88 | |
| 1/2048 | 4.52 | 29.63 (6) | — | 5.79 | 9.54 | |
| 1/4096 | 17.44 | 54.40 (6) | 1.0121 | 2.11 | 4.73 | |
| 1/8192 | 124.43 | 123.46 (6) | 0.6425 | 8.37 | 3.03 | |
| 1/16,384 | 810.55 | 244.26 (6) | 0.8508 | 3.46 | 1.68 | |
| 1/32,768 | 5978.33 | 562.76 (6) | 0.5979 | 1.41 | 1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Li, X.; Dong, N. Doubling Smith Method for a Class of Large-Scale Generalized Fractional Diffusion Equations. Fractal Fract. 2023, 7, 380. https://doi.org/10.3390/fractalfract7050380
Yu B, Li X, Dong N. Doubling Smith Method for a Class of Large-Scale Generalized Fractional Diffusion Equations. Fractal and Fractional. 2023; 7(5):380. https://doi.org/10.3390/fractalfract7050380
Chicago/Turabian StyleYu, Bo, Xiang Li, and Ning Dong. 2023. "Doubling Smith Method for a Class of Large-Scale Generalized Fractional Diffusion Equations" Fractal and Fractional 7, no. 5: 380. https://doi.org/10.3390/fractalfract7050380
APA StyleYu, B., Li, X., & Dong, N. (2023). Doubling Smith Method for a Class of Large-Scale Generalized Fractional Diffusion Equations. Fractal and Fractional, 7(5), 380. https://doi.org/10.3390/fractalfract7050380








