Bernoulli-Type Spectral Numerical Scheme for Initial and Boundary Value Problems with Variable Order
Abstract
1. Introduction
2. Basic Results
- i.
- ,
- ii.
- ,
- iii.
- ,
- iv.
- , ,
- i.
- ,
- ii.
- iii.
- iv.
- v.
- vi.
- ,
- vii.
- ,
The Fractional-Order Bernoulli Polynomials
3. Procedure for Approximation of Functions
Extended Bernoulli Operational Matrices
4. Establishment of Numerical Algorithms
4.1. Variable-Order Initial Value Problems
4.2. Variable-Order Boundary Value Problems
4.3. Convergence Analysis
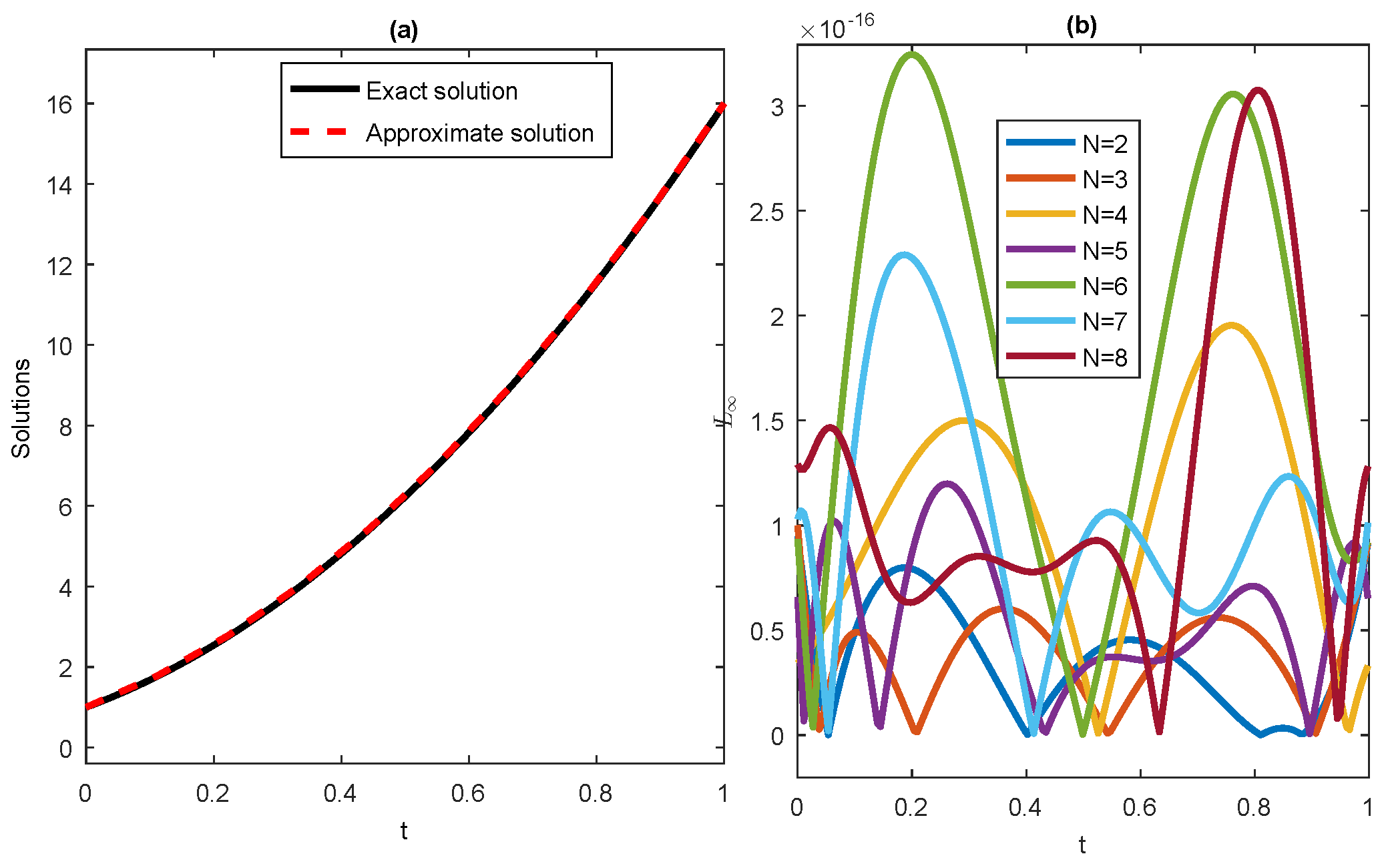
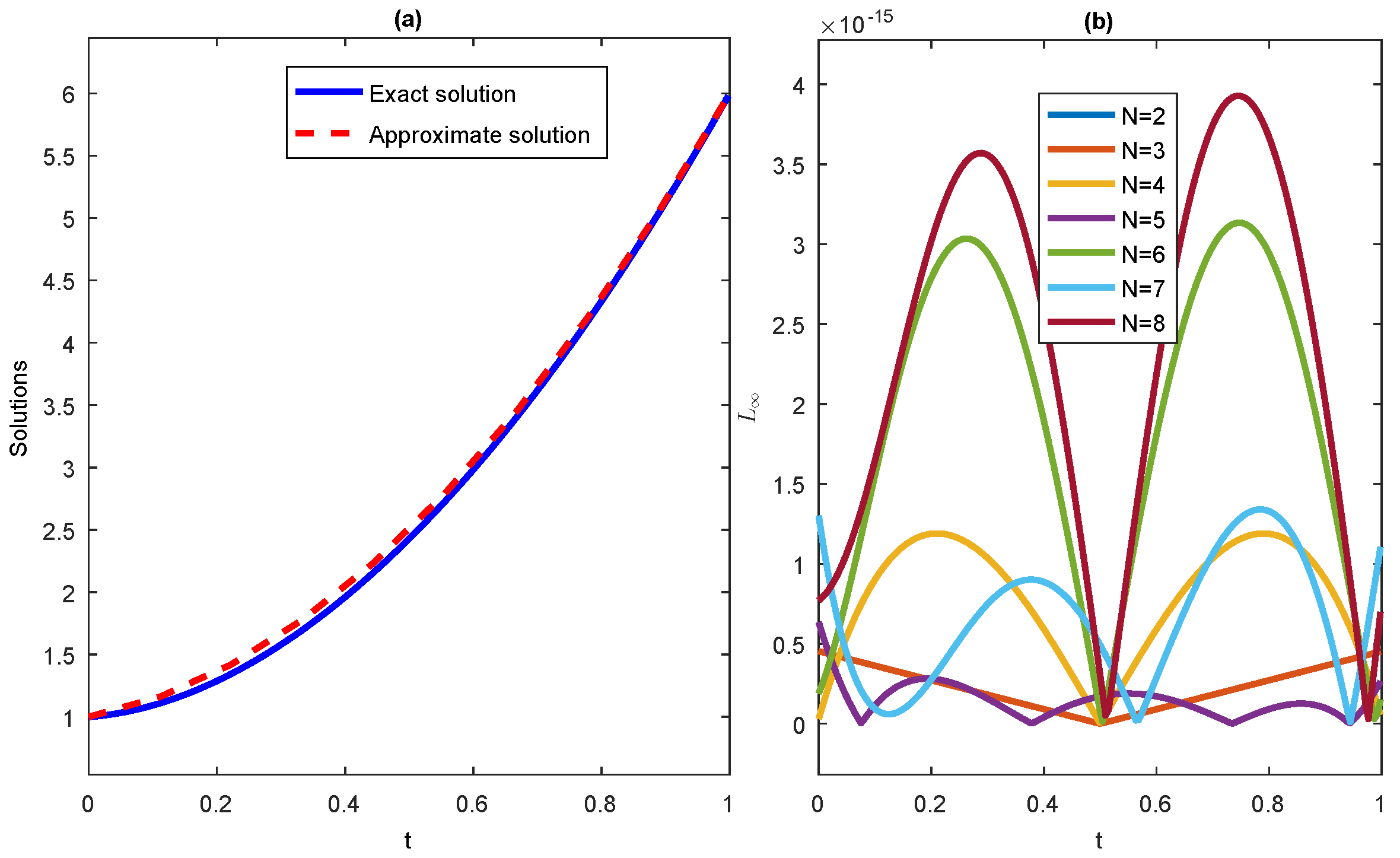
5. Numerical Examples
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rose, B. Fractional Calculas and Its Applications; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Rossikhin, Y.A.; Shitikova, M.V. Applications of fractional calculas to dynomical problem of linear and nonlinear heridatary mechanics of solids. Appl. Mech. Rev. 1997, 50, 15–67. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional calculas: Some basics problems in continuum and statistical mechanics. In Fractals and Fractional Calculas in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: New York, NY, USA, 1997; pp. 291–384. [Google Scholar]
- He, J.H. Some applications of nonlinear fractional differential equations and their approximations. Bull. Sci. Technol. 1999, 15, 86–90. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. Fractional calculas in the transient analysis of viscoelastically damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculas and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Miller, K.S. Fractional differential equations. J. Fract. Calc. Appl. 1993, 3, 49–57. [Google Scholar]
- Agarwal, R.; Belmekki, M.; Benchohra, M. A survey on similar differential equations and inclusions involving Riemann-Liouville fractional derivative. Adv. Differ. Equ. 2009, 10, 857–868. [Google Scholar]
- Kilbas, A.A.; Trujillo, J.J. Differential equation of fractional order, method, results and problems. Appl. Anal. 2002, 81, 435–493. [Google Scholar] [CrossRef]
- Erturk, V.S.; Momani, S. Solving systems of fractional differential equations using differential transform method. J. Comput. Appl. Math. 2008, 215, 142–151. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. Application of variational iteration method to nonlinear differential equations of fractional order. Int. J. Nonlinear Sci. Numer. Simul. 2006, 1, 15–27. [Google Scholar] [CrossRef]
- Abdulaziz, O.; Hashim, I.; Momani, S. Solving systems of fractional differential equations by homotopy-perturbation method. Phys. Lett. A 2008, 372, 451–459. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. A tau approach for solution of the space fractional diffusion equation. Comput. Math. Appl. 2011, 62, 1135–1142. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Mohabbati, M. Numerical solution of fractional telegraph equation via the tau method. Math. Rep. 2015, 17, 155–166. [Google Scholar]
- Nemati, S. Numerical solution of Volterra-Fredholm integral equations using Legendre collocation method. J. Comput. Appl. Math. 2015, 278, 29–36. [Google Scholar] [CrossRef]
- Shah, K.; Khalil, H.; Khan, R.A. A generalized scheme based on shifted Jacobi polynomials for numerical simulation of coupled systems of multi-term fractional-order partial differential equations. LMS J. Comput. Math. 2017, 20, 11–29. [Google Scholar] [CrossRef]
- Shah, K.; Jarad, F.; Abdeljawad, T. Stable numerical results to a class of time-space fractional partial differential equations via spectral method. J. Adv. Res. 2020, 25, 39–48. [Google Scholar] [CrossRef] [PubMed]
- Bhrawy, A.H.; Taha, T.M.; Machado, J.A.T. A review of operational matrices and spectral techniques for fractional calculus. Nonlinear Dyn. 2015, 81, 1023–1052. [Google Scholar] [CrossRef]
- Yousefi, S.A.; Behroozifar, M. Operational matrices of Bernstein polynomials and their applications. Int. J. Syst. Sci. 2010, 41, 709–716. [Google Scholar] [CrossRef]
- Samko, S.G.; Rose, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Soon, C.M.; Coimbra, F.M.; Kobayashi, M.H. The variable viscoelasticity oscillator. Ann. Phys. 2005, 14, 378–389. [Google Scholar] [CrossRef]
- Lin, R.; Liu, F.; Anh, V.; Turner, I. Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation. Appl. Math. Comput. 2009, 212, 435–445. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. Numerical methods for the variable-order fractional advanced-diffusion equation with a nonlinear source term. Numer. Anal. 2009, 47, 1760–1781. [Google Scholar] [CrossRef]
- Chen, C.; Liu, F.; Anh, V.; Turner, I. Numerical schemes with high spatial accuracy for a variable-order anamalous subdiffusion equation. Sci. Comput. 2010, 32, 1740–1760. [Google Scholar]
- Amin, R.; Shah, K.; Ahmad, H.; Ganie, A.H.; Abdel-Aty, A.H.; Botmart, T. Haar wavelet method for solution of variable order linear fractional integro-differential equations. AIMS Math. 2022, 7, 5431–5443. [Google Scholar] [CrossRef]
- Bushnaq, S.; Shah, K.; Tahir, S.; Ansari, K.J.; Sarwar, M.; Abdeljawad, T. Computation of numerical solutions to variable order fractional differential equations by using non-orthogonal basis. AIMS Math. 2022, 7, 10917–10938. [Google Scholar] [CrossRef]
- Keshavarz, E.; Ordokhani, Y.; Razzaghi, M. A numerical solution for fractional optimal control problems via Bernoulli polynomials. J. Vib. Control 2016, 22, 3889–3903. [Google Scholar] [CrossRef]
- Sahu, P.K.; Mallick, B. Approximate solution of fractional order Lane-Emden type differential equation by orthonormal Bernoulli’s polynomials. Int. J. Appl. Comput. Math. 2019, 5, 89. [Google Scholar] [CrossRef]
- Behroozifar, M.; Habibi, N. A numerical approach for solving a class of fractional optimal control problems via operational matrix Bernoulli polynomials. J. Vib. Control 2018, 24, 2494–2511. [Google Scholar] [CrossRef]
- Phang, C.; Toh, Y.T.; Nasrudin, F.S.M. An operational matrix method based on poly-Bernoulli polynomials for solving fractional delay differential equations. Computation 2020, 8, 82. [Google Scholar] [CrossRef]
- Yuzbasi, S. Numerical solutions of fractional Riccati type differential equations by means of the Bernstein polynomials. Comput. Appl. Math. 2013, 219, 6328–6343. [Google Scholar]
- El-Gamel, M.; Adel, W.; El-Azab, M.S. Bernoulli polynomial and the numerical solution of high-order boundary value problems. Math. Nat. Sci. 2019, 4, 45–59. [Google Scholar] [CrossRef]
- Kreyszig, E. Introductory Functional Analysis with Applications; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Nemati, S.; Torres, D.F. Application of bernoulli polynomials for solving variable-order fractional optimal control-affine problems. Axioms 2020, 9, 114. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Stankovic, B. On a differential equation with left and right fractional derivatives. Fract. Calc. Appl. Anal. 2007, 10, 139–150. [Google Scholar] [CrossRef]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 399, 1–77. [Google Scholar] [CrossRef]
- Pandey, R.K.; Singh, O.P.; Baranwal, V.K. An analytic algorithm for the space-time fractional advection-dispersion equation. Comput. Phys. Commun. 2011, 182, 1134–1144. [Google Scholar] [CrossRef]
- Blaszczyk, T.; Bekus, K.; Szajek, K.; Sumelka, W. Approximation and application of the Riesz-Caputo fractional derivative of variable order with fixed memory. Meccanica 2022, 57, 861–870. [Google Scholar] [CrossRef]
- Pitolli, F.; Sorgentone, C.; Pellegrino, E. Approximation of the Riesz-Caputo derivative by cubic splines. Algorithms 2022, 15, 69. [Google Scholar] [CrossRef]
- Almeida, R.; Tavares, D.; Torres, D.F.M. The Variable-Order Fractional Calculus of Variations; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Tohidi, E.; Bhrawy, A.H.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Tohidi, E.; Erfani, K.; Gachpazan, M.; Shateyi, S. A new Tau method for solving nonlinear Lane-Emden type equations via Bernoulli operational matrix of differentiation. J. Appl. Math. 2013, 2013, 276585. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, Z.A.; Ahmad, S.; Zeb, S.; Alrabaiah, H. Bernoulli-Type Spectral Numerical Scheme for Initial and Boundary Value Problems with Variable Order. Fractal Fract. 2023, 7, 392. https://doi.org/10.3390/fractalfract7050392
Khan ZA, Ahmad S, Zeb S, Alrabaiah H. Bernoulli-Type Spectral Numerical Scheme for Initial and Boundary Value Problems with Variable Order. Fractal and Fractional. 2023; 7(5):392. https://doi.org/10.3390/fractalfract7050392
Chicago/Turabian StyleKhan, Zareen A., Sajjad Ahmad, Salman Zeb, and Hussam Alrabaiah. 2023. "Bernoulli-Type Spectral Numerical Scheme for Initial and Boundary Value Problems with Variable Order" Fractal and Fractional 7, no. 5: 392. https://doi.org/10.3390/fractalfract7050392
APA StyleKhan, Z. A., Ahmad, S., Zeb, S., & Alrabaiah, H. (2023). Bernoulli-Type Spectral Numerical Scheme for Initial and Boundary Value Problems with Variable Order. Fractal and Fractional, 7(5), 392. https://doi.org/10.3390/fractalfract7050392







