Application of the Pathway-Type Transform to a New Form of a Fractional Kinetic Equation Involving the Generalized Incomplete Wright Hypergeometric Functions
Abstract
1. Introduction
2. Preliminaries
- (i)
- By setting in Equations (17) and (18) and employing the relation in Equation (6), we have the extended incomplete Gauss hypergeometric function (see [31]):where , andwhere , and .As an immediate consequence of Equations (20) and (21), we have the following decomposition formula:in terms of the generalized hypergeometric function.
- (ii)
- and
3. Statement of Results
4. Illustrative Examples
- (i)
- (ii)
- (iii)
- (iv)
- When we have and , then Equation (38) reduces to a hypergeometric functiongiven by
- (v)
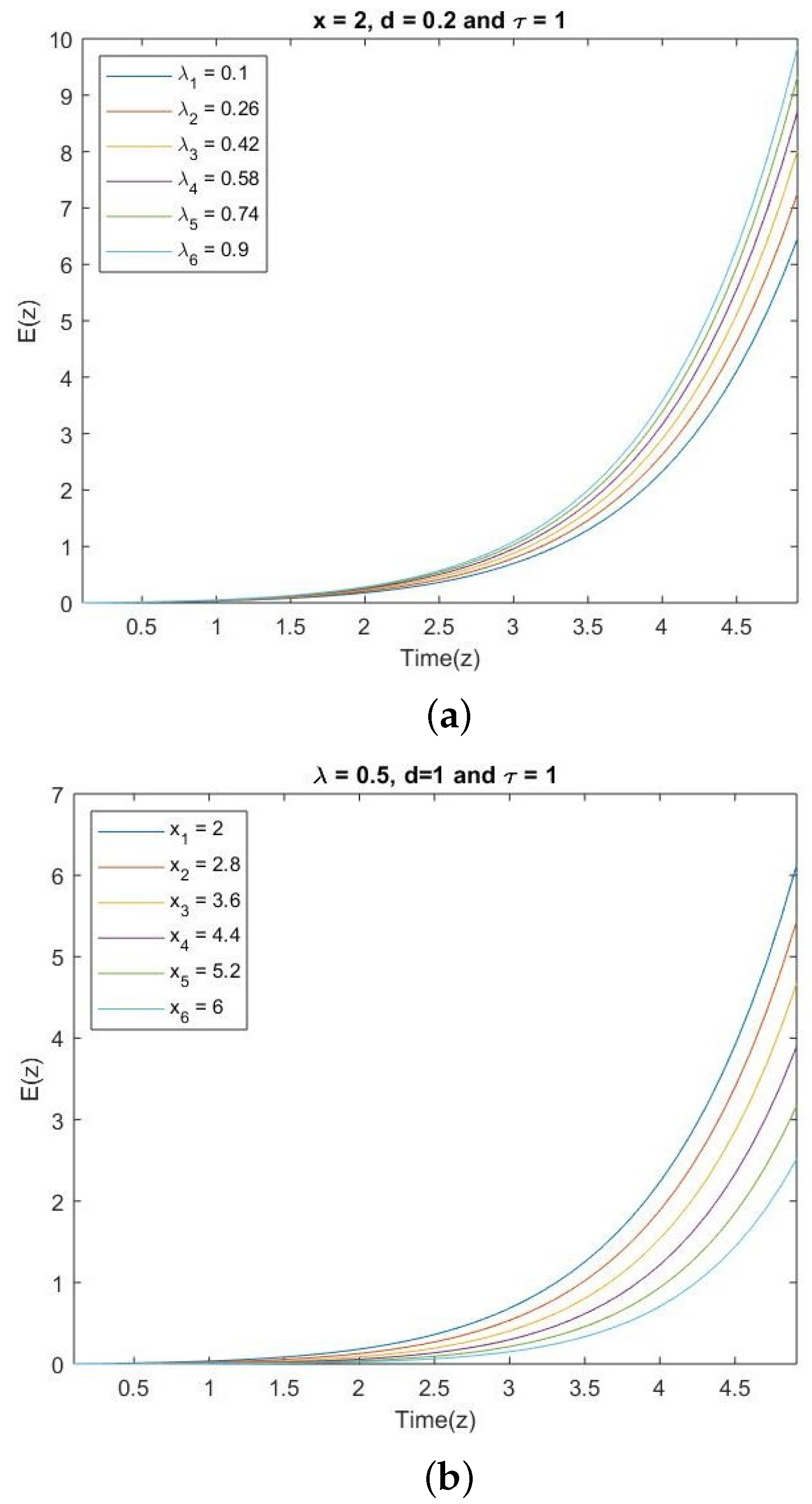
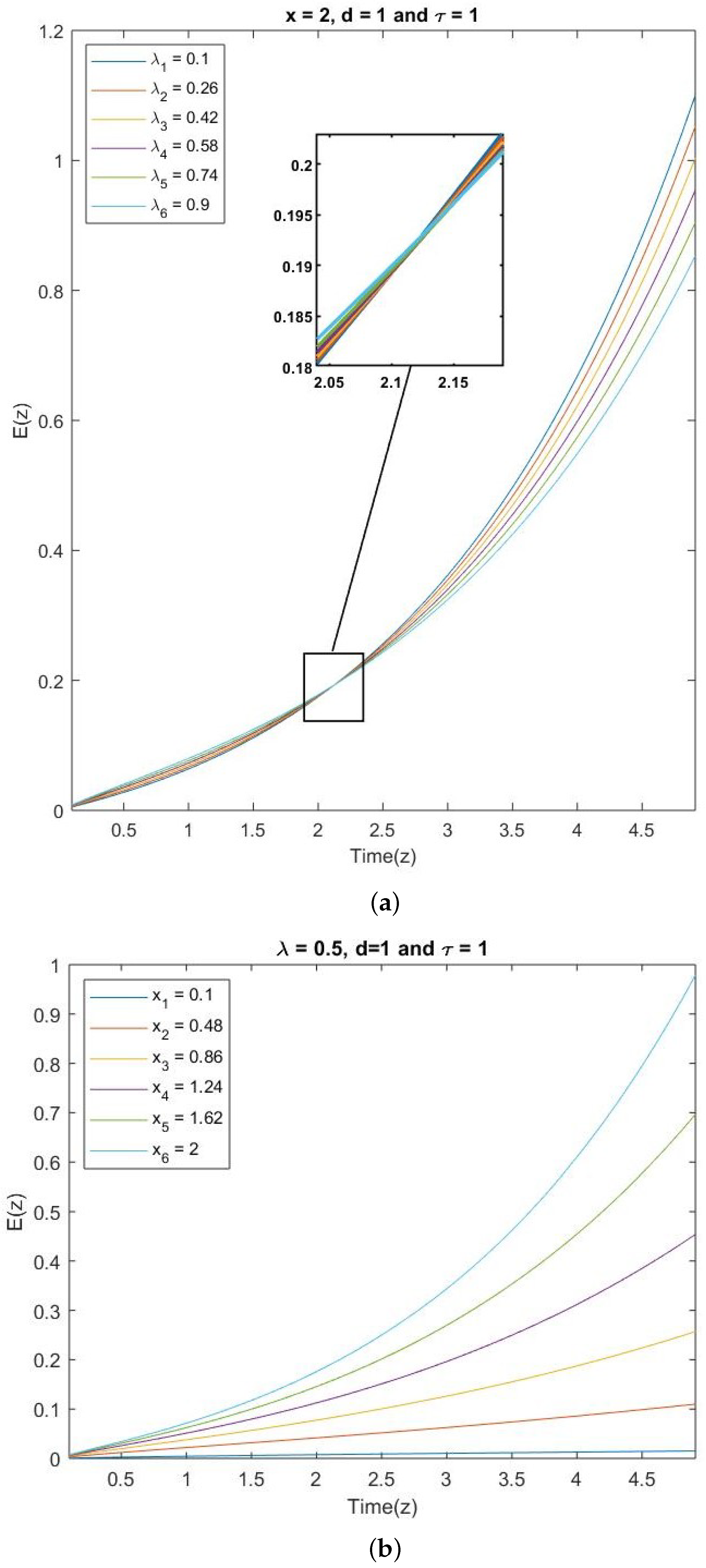
5. Comments on the Graphical Interpretations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbas, S.; Benchohra, M.; Guerekata, G.M.N. Topics in Fractional Differential Equations; Springer: New York, NY, USA, 2012. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2014. [Google Scholar]
- Abbas, M.I.; Ragusa, M.A. Solvability of Langevin equations with two Hadamard fractional derivatives via Mittag-Leffler functions. Appl. Anal. 2020, 101, 3231–3245. [Google Scholar]
- Bakhet, A.; He, F. On the matrix version of extended Struve function and its application on fractional calculus. Filomat 2022, 36, 3381–3392. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Abd-Elhameed, W.M.; Ahmed, H.M. New fractional derivative ex-pression of the shifted third-kind Chebyshev polynomials: Application to a type of non-linear fractional pantograph differential equations. J. Funct. Spaces 2022, 3966135. [Google Scholar]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. On fractional kinetic equations. Astrophys. Space Sci. 2002, 282, 281–287. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. On generalized fractional kinetic equations. Phys. A 2004, 344, 657–664. [Google Scholar]
- Saxena, R.K.; Kalla, S.L. On the solutions of certain fractional kinetic equations. Appl. Math. Comput. 2008, 199, 504–511. [Google Scholar] [CrossRef]
- Chaurasia, V.B.L.; Pandey, S.C. On the new computable solution of the generalized fractional kinetic equations involving the generalized function for the fractional calculus and related functions. Astrophys. Space Sci. 2008, 317, 213–219. [Google Scholar] [CrossRef]
- Kolokoltsov, V.N.; Troeva, M. A new approach to fractional kinetic evolutions. Fractal Fract. 2022, 6, 49. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.H. The fractional kinetic equation and thermonuclear functions. Astrophys. Space Sci. 2000, 327, 53–63. [Google Scholar] [CrossRef]
- Habenom, H.; Oli, A.; Suthar, D.L. (p, q)-Extended Struve function: Fractional integrations and application to fractional kinetic equations. J. Math. 2021, 2021, 5536817. [Google Scholar]
- Sharma, K.P.; Bhargava, A.; Suthar, D.L. Application of the Laplace transform to a new form of fractional kinetic equation involving the composition of the Galue Struve function and the Mittageffler function. Math. Probl. Eng. 2022, 2022, 5668579. [Google Scholar] [CrossRef]
- Khan, O.; Khan, N.; Choi, J.; Nisar, K.S. A type of fractional Kinetic equations associated with the (p, q)-extented τ-hypergeomtric and confluent hypergeomtric functions. Nonlinear Funct. Anal. Appl. 2021, 26, 381–392. [Google Scholar]
- Hidan, M.; Akel, M.; Abd-Elmageed, H.; Abdalla, M. Solution of fractional kinetic equations involving extended (k, t)-Gauss hypergeometric matrix functions. AIMS Math. 2022, 7, 14474–14491. [Google Scholar] [CrossRef]
- Abubakar, U.M. Solutions of fractional kinetic equations using the (p, q; l)-extended τ -Gauss hypergeometric function. J. New Theory 2022, 38, 25–33. [Google Scholar] [CrossRef]
- Purohit, S.D.; Ucar, F. An application of q-Sumudu transform for fractional q-kinetic equation. Turk. J. Math. 2018, 42, 726–734. [Google Scholar] [CrossRef]
- Agarwal, P.; Ntouyas, S.K.; Jain, S.; Chand, M.; Singh, G. Fractional kinetic equations involving generalized k-Bessel function via Sumudu transform. Alex. Eng. J. 2018, 57, 1937–1942. [Google Scholar] [CrossRef]
- Yagci, O.; Sahin, R. Solutions of fractional kinetic equations involving generalized Hurwitz-Lerch Zeta functions using Sumudu transform. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2021, 70, 678–689. [Google Scholar] [CrossRef]
- Akel, M.; Hidan, M.; Boulaaras, S.; Abdalla, M. On the solutions of certain fractional kinetic matrix equations involving Hadamard fractional integrals. AIMS Math. 2022, 7, 15520–15531. [Google Scholar] [CrossRef]
- Ahmed, W.; Salamoon, A.; Pawar, D. Solution of fractional kinetic equation for Hadamard type fractional integral via Mellin transform. Gulf. J. Math. 2022, 12, 15–27. [Google Scholar] [CrossRef]
- Abdalla, M.; Akel, M. Contribution of using Hadamard fractional integral operator via Mellin integral transform for solving certain fractional kinetic matrix equations. Fractal Fract. 2022, 6, 305. [Google Scholar] [CrossRef]
- Kumar, D. Solution of fractional kinetic equation by a class of integral transform of pathway type. J. Math. Phys. 2013, 54, 043509. [Google Scholar] [CrossRef]
- Mathur, G.A.R. Solution of fractional kinetic equations by using integral transform. AIP Conf. Proc. 2020, 2253, 020004. [Google Scholar]
- Dorrego, G.A.; Kumar, D. A generalization of the kinetic equation using the Prabhakar-type operators. Honam Math. J. 2017, 39, 401–416. [Google Scholar]
- Chaudhry, M.A.; Zubair, S.M. On a Class of Incomplete Gamma Functions with Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Virchenko, N.; Kalla, S.L.; Al-Zamel, A. Some results on a generalized hypergeometric function. Integral Transforms Spec. Funct. 2001, 12, 89–100. [Google Scholar] [CrossRef]
- Nisar, K.S.; Rahman, G.; Mubeen, S.; Arshad, M. The incomplete Pochhammer symbols and their application to generalized hypergeometric functions. Int. Bull. Math. Res. 2017, 4, 1–13. [Google Scholar]
- Khan, N.; Usman, T.; Aman, M.; Al-Omari, S.; Araci, S. Computation of certain integral formulas involving generalized Wright function. Adv. Differ. Equ. 2020, 1–10. [Google Scholar] [CrossRef]
- Ghaffar, A.; Saif, A.; Iqbal, M.; Rizwan, M. Two classes of integrals involving extended Wright type generalized hypergeometric function. Commun. Math. Appl. 2019, 10, 599–606. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Chaudhry, M.A.; Agarwal, R.P. The incomplete Pochhammer symbols and their applications to hypergeometric and related functions. Integral Transform. Spec. Funct. 2012, 23, 659–683. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqarni, M.Z.; Bakhet, A.; Abdalla, M. Application of the Pathway-Type Transform to a New Form of a Fractional Kinetic Equation Involving the Generalized Incomplete Wright Hypergeometric Functions. Fractal Fract. 2023, 7, 348. https://doi.org/10.3390/fractalfract7050348
Alqarni MZ, Bakhet A, Abdalla M. Application of the Pathway-Type Transform to a New Form of a Fractional Kinetic Equation Involving the Generalized Incomplete Wright Hypergeometric Functions. Fractal and Fractional. 2023; 7(5):348. https://doi.org/10.3390/fractalfract7050348
Chicago/Turabian StyleAlqarni, Mohammed Z., Ahmed Bakhet, and Mohamed Abdalla. 2023. "Application of the Pathway-Type Transform to a New Form of a Fractional Kinetic Equation Involving the Generalized Incomplete Wright Hypergeometric Functions" Fractal and Fractional 7, no. 5: 348. https://doi.org/10.3390/fractalfract7050348
APA StyleAlqarni, M. Z., Bakhet, A., & Abdalla, M. (2023). Application of the Pathway-Type Transform to a New Form of a Fractional Kinetic Equation Involving the Generalized Incomplete Wright Hypergeometric Functions. Fractal and Fractional, 7(5), 348. https://doi.org/10.3390/fractalfract7050348







