Synchronization in Finite Time of Fractional-Order Complex-Valued Delayed Gene Regulatory Networks
Abstract
1. Introduction
- •
- To analyze the synchronization in finite time for the addressed models, two different controllers are designed to achieve a flexible control of synchronization.
- •
- The presented complex-valued gene regulatory networks are implemented as an entirety form without any decomposition.
- •
- A novel complex-valued sign function is employed to design the adaptive controller to achieve a more efficient control strategy for the problem of synchronization in finite time.
2. Preliminaries
3. System Description
4. Synchronization in Finite Time with a Feedback Controller
5. Synchronization in Finite Time with Adaptive Controller
6. Numerical Examples
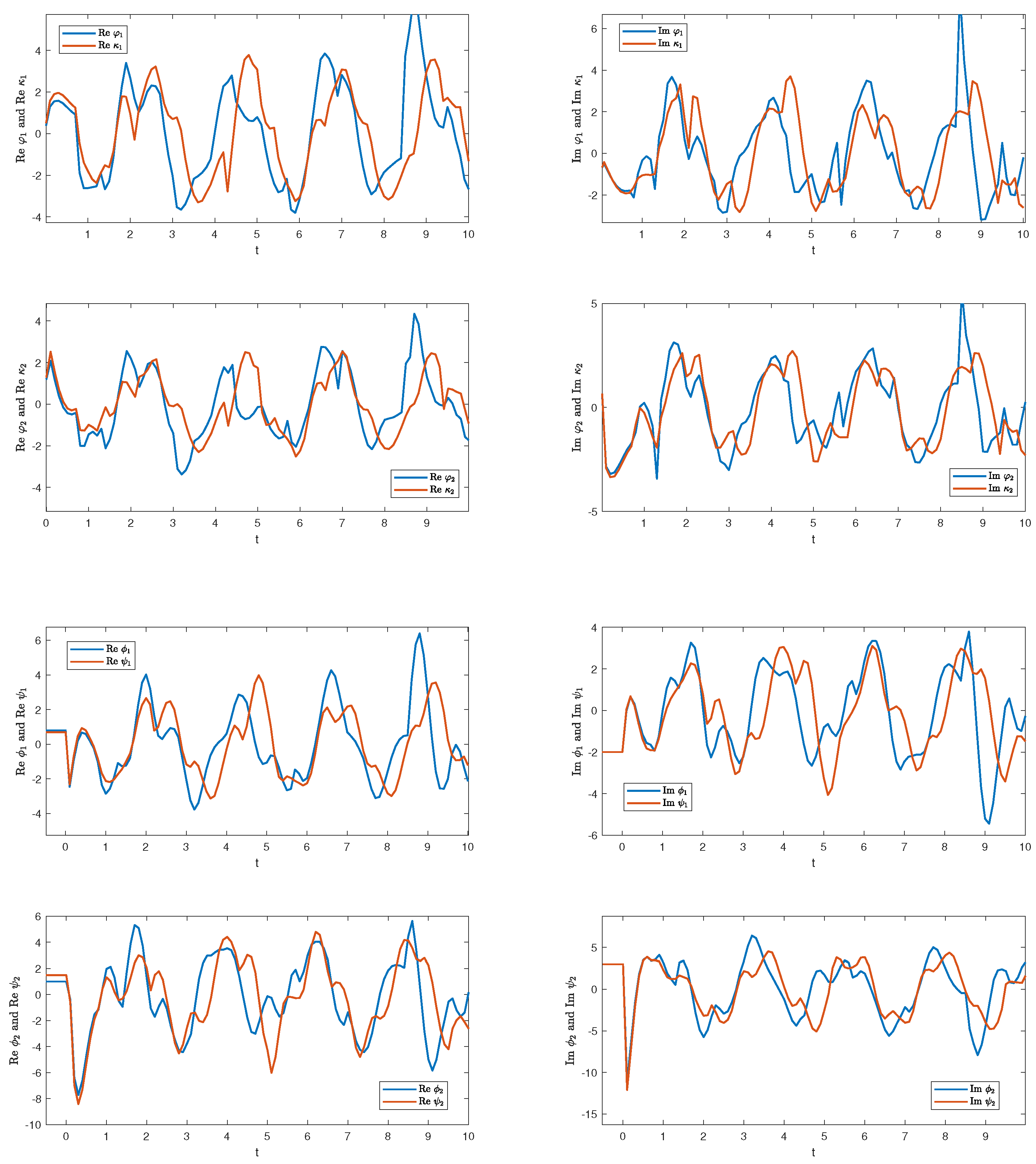
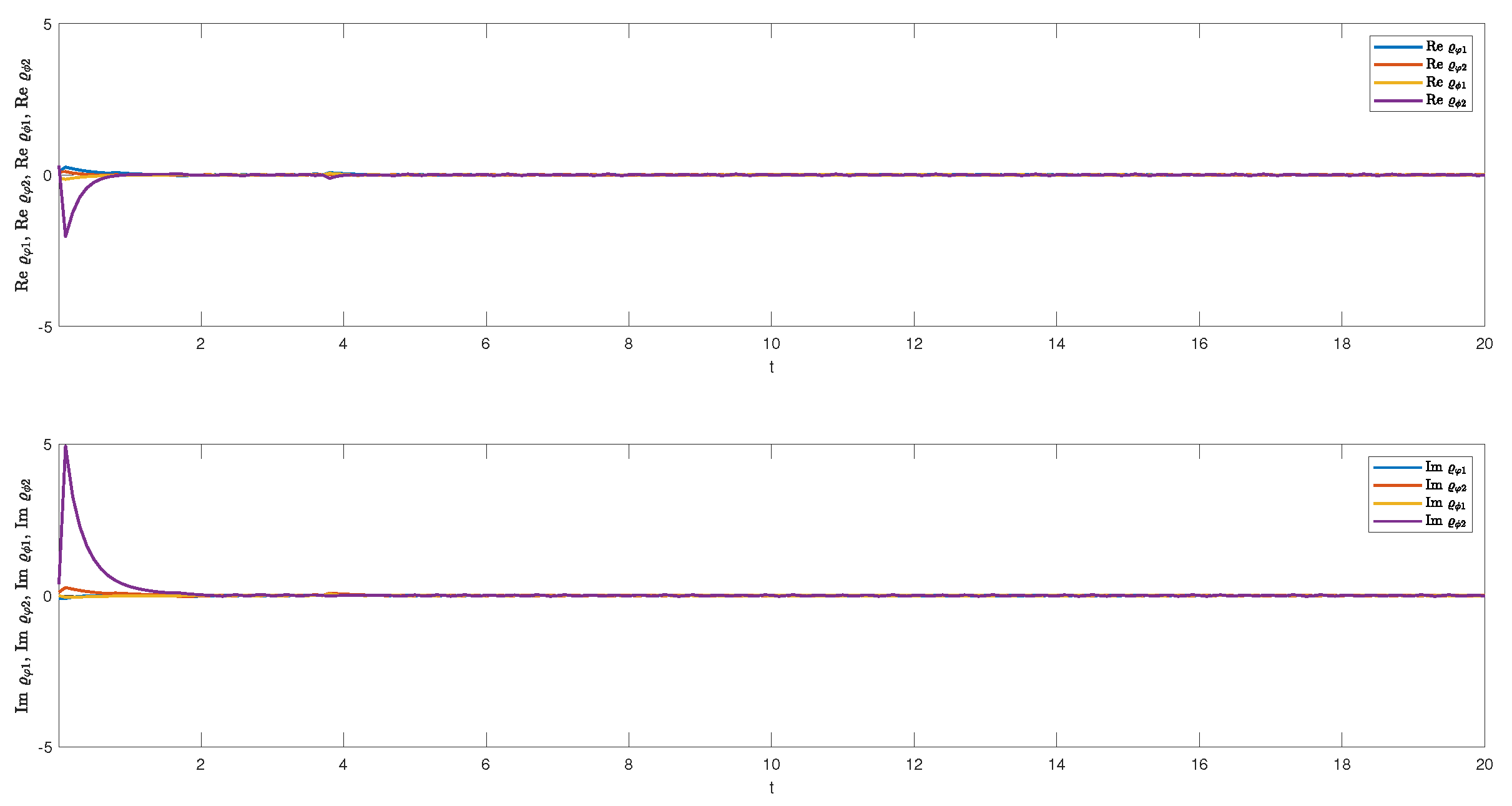
6.1. Synchronization by State Feedback Controller (9)
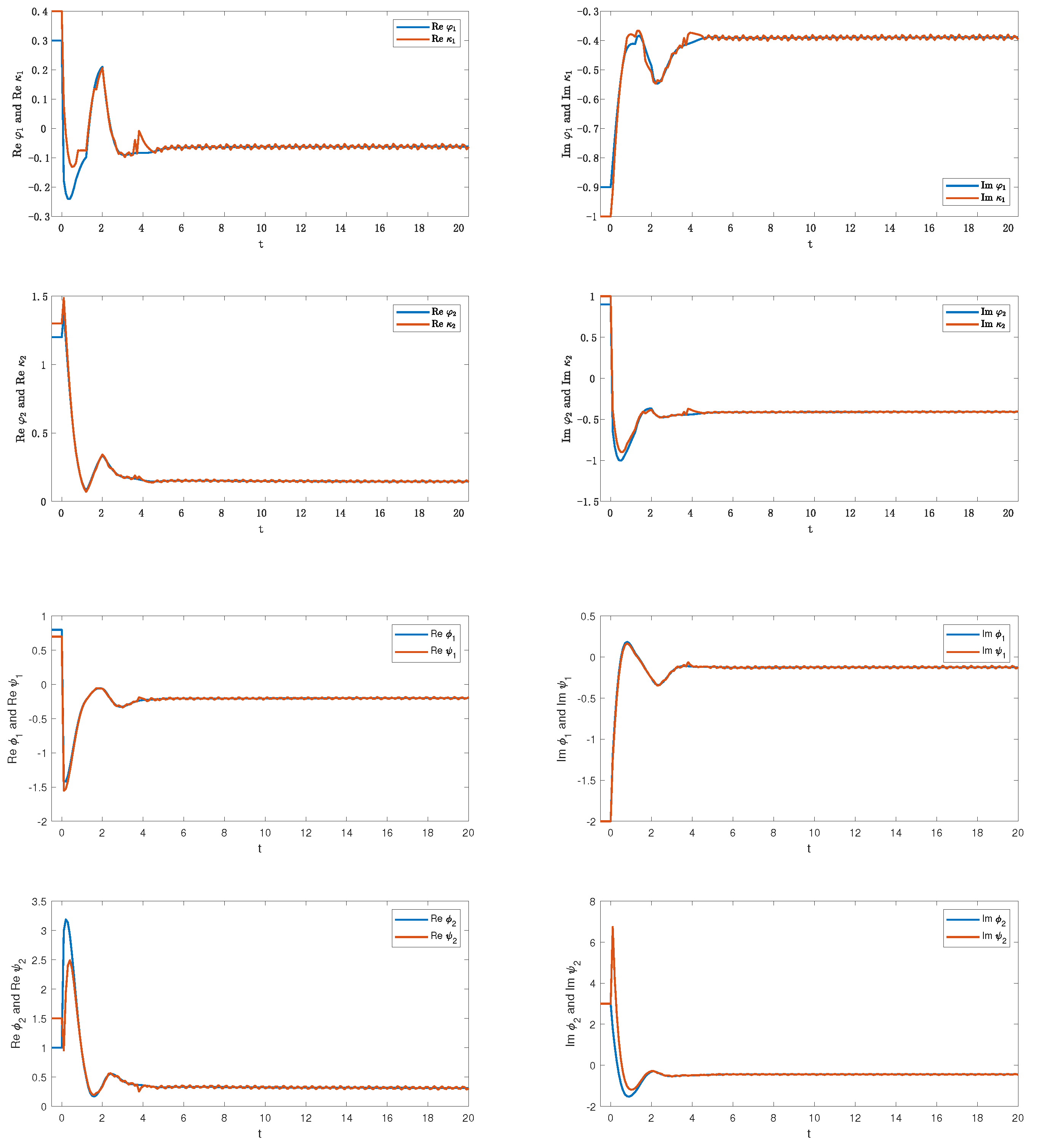
6.2. Synchronization by Adaptive Controller (23)
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Jong, H. Modeling and simulation of genetic regulatory systems: A literature review. J. Comput. Biol. 2002, 9, 67–103. [Google Scholar] [CrossRef]
- Casey, R.; Jong, H.; Gouzé, J.L. Piecewise-linear models of genetic regulatory networks: Equilibria and their stability. J. Math. Biol. 2006, 52, 27–56. [Google Scholar] [CrossRef]
- Cao, Z.; Grima, R. Linear mapping approximation of gene regulatory networks with stochastic dynamics. Nat. Commun. 2018, 9, 1–15. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, S.W.; Guo, W.F.; Wei, Z.G.; Chen, L. Inference of gene regulatory network based on local Bayesian networks. PLoS Comput. Biol. 2016, 12, e1005024. [Google Scholar] [CrossRef]
- Sanchez-Castillo, M.; Blanco, D.; Tienda-Luna, I.M.; Carrion, M.C.; Huang, Y. A Bayesian framework for the inference of gene regulatory networks from time and pseudo-time series data. Bioinformatics 2018, 34, 964–970. [Google Scholar] [CrossRef]
- Tang, W.W.; Dietmann, S.; Irie, N.; Leitch, H.G.; Floros, V.I.; Bradshaw, C.R.; Surani, M.A. A unique gene regulatory network resets the human germline epigenome for development. Cell 2015, 161, 1453–1467. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, L.; Zou, J. Globally asymptotic stability analysis for genetic regulatory networks with mixed delays: An M-matrix-based approach. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 13, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.P.; Wu, C.; Miao, H.; Wu, H. RegNetwork: An integrated database of transcriptional and post-transcriptional regulatory networks in human and mouse. Database 2015, 2015, bav095. [Google Scholar] [CrossRef] [PubMed]
- Shmulevich, I.; Dougherty, E.R.; Kim, S.; Zhang, W. Probabilistic Boolean networks: A rule-based uncertainty model for gene regulatory networks. Bioinformatics 2002, 18, 261–274. [Google Scholar] [CrossRef] [PubMed]
- Karlebach, G.; Shamir, R. Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 2008, 9, 770–780. [Google Scholar] [CrossRef]
- Rao, X.; Chen, X.; Shen, H.; Ma, Q.; Li, G.; Tang, Y.; Dixon, R.A. Gene regulatory networks for lignin biosynthesis in switchgrass (Panicum virgatum). Plant Biotechnol. J. 2019, 17, 580–593. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Jiang, Y.; Peng, L.; Sun, X.; Gan, W.; Zhao, Q.; Tang, H. Inferring gene regulatory networks using the improved Markov blanket discovery algorithm. Interdiscip. Sci. Comput. Life Sci. 2022, 14, 168–181. [Google Scholar] [CrossRef]
- Pu, M.; Chen, J.; Tao, Z.; Miao, L.; Qi, X.; Wang, Y.; Ren, J. Regulatory network of miRNA on its target: Coordination between transcriptional and post-transcriptional regulation of gene expression. Cell. Mol. Life Sci. 2019, 76, 441–451. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, J.; Ai, Z. A novel stability criterion of the time-lag fractional-order gene regulatory network system for stability analysis. Commun. Nonlinear Sci. Numer. Simul. 2019, 66, 96–108. [Google Scholar] [CrossRef]
- Leine, R.I.; Nijmeijer, H. Dynamics and Bifurcations of Non-Smooth Mechanical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Van de Sande, B.; Flerin, C.; Davie, K.; De Waegeneer, M.; Hulselmans, G.; Aibar, S.; Aerts, S. A scalable SCENIC workflow for single-cell gene regulatory network analysis. Nat. Protoc. 2020, 15, 2247–2276. [Google Scholar] [CrossRef] [PubMed]
- Pandiselvi, S.; Raja, R.; Cao, J.; Li, X.; Rajchakit, G. Impulsive discrete-time GRNs with probabilistic time delays, distributed and leakage delays: An asymptotic stability issue. Ima J. Math. Control. Inf. 2019, 36, 79–100. [Google Scholar] [CrossRef]
- Senthilraj, S.; Raja, R.; Zhu, Q.; Samidurai, R.; Zhou, H. Delay-dependent asymptotic stability criteria for genetic regulatory networks with impulsive perturbations. Neurocomputing 2016, 214, 981–990. [Google Scholar] [CrossRef]
- Zang, H.; Zhang, T.; Zhang, Y. Bifurcation analysis of a mathematical model for genetic regulatory network with time delays. Appl. Math. Comput. 2015, 260, 204–226. [Google Scholar] [CrossRef]
- Lei, J.; Shatat, A.S.; Lakys, Y. Fractional Differential Equations in Electronic Information Models. Appl. Math. Nonlinear Sci. 2022, 1–9. [Google Scholar]
- Zhang, D.; Yang, L.; Arbab, A. The Uniqueness of Solutions of Fractional Differential Equations in University Mathematics Teaching Based on the Principle of Compression Mapping. Appl. Math. Nonlinear Sci. 2022, 1–7. [Google Scholar]
- Ding, J. Abnormal Behavior of Fractional Differential Equations in Processing Computer Big Data. Appl. Math. Nonlinear Sci. 2022, 1–9. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Zhang, Y.; Pu, Y.; Zhang, H.; Cong, Y.; Zhou, J. An extended fractional Kalman filter for inferring gene regulatory networks using time-series data. Chemom. Intell. Lab. Syst. 2014, 138, 57–63. [Google Scholar] [CrossRef]
- Wang, L.; Song, Q.; Liu, Y.; Zhao, Z.; Alsaadi, F.E. Finite-time stability analysis of fractional-order complex-valued memristor-based neural networks with both leakage and time-varying delays. Neurocomputing 2017, 245, 86–101. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, W.; Chen, Q.; Chen, M. Non-coding RNAs and their integrated networks. J. Integr. Bioinform. 2019, 16, 20190027. [Google Scholar] [CrossRef]
- Wan, X.; Wang, Z.; Wu, M.; Liu, X. State estimation for discrete time-delayed genetic regulatory networks with stochastic noises under the round-robin protocols. IEEE Trans. Nanobiosci. 2018, 17, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Chen, Y. Fractional order [proportional derivative] controller for a class of fractional order systems. Automatica 2009, 45, 2446–2450. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Zhang, J.; Cheng, F.; Liu, F.; Ding, C. Novel asymptotic stability criterion for fractional-order gene regulation system with time delay. Asian J. Control 2022, 24, 3095–3104. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Xiao, M.; Alsaedi, A.; Hayat, T. Bifurcations in a delayed fractional complex-valued neural network. Appl. Math. Comput. 2017, 292, 210–227. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Wang, Z.H. Stability and Hopf bifurcation of a class of TCP/AQM networks. Nonlinear Anal. Real World Appl. 2010, 11, 1552–1559. [Google Scholar] [CrossRef]
- Guan, Z.H.; Yue, D.; Hu, B.; Li, T.; Liu, F. Cluster synchronization of coupled genetic regulatory networks with delays via aperiodically adaptive intermittent control. IEEE Trans. Nanobiosci. 2017, 16, 585–599. [Google Scholar] [CrossRef]
- Zou, Y.; Su, H.; Tang, R.; Yang, X. Finite-time bipartite synchronization of switched competitive neural networks with time delay via quantized control. ISA Trans. 2022, 125, 156–165. [Google Scholar] [CrossRef]
- Xujun, Y.; Qiankun, S.; Yurong, L.; Zhenjiang, Z. Finite-time stability analysis of fractional-order neural networks with delay. Neurocomputing 2015, 152, 19–26. [Google Scholar]
- Li, M.; Yang, X.; Song, Q.; Chen, X. Robust Asymptotic Stability and Projective Synchronization of Time-Varying Delayed Fractional Neural Networks Under Parametric Uncertainty. Neural Process. Lett. 2022, 54, 4661–4680. [Google Scholar] [CrossRef]
- Du, F.; Lu, J.G. New criterion for finite-time synchronization of fractional order memristor-based neural networks with time delay. Appl. Math. Comput. 2021, 389, 125616. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Cao, J.; Velmurugan, G. Existence and uniform stability analysis of fractional-order complex-valued neural networks with time delays. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 84–97. [Google Scholar] [CrossRef] [PubMed]
- Udhayakumar, K.; Rakkiyappan, R.; Rihan, F.A.; Banerjee, S. Projective multi-synchronization of fractional-order complex-valued coupled multi-stable neural networks with impulsive control. Neurocomputing 2022, 467, 392–405. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Z.; Zhou, T. Global stability analysis of fractional-order gene regulatory networks with time delay. Int. J. Biomath. 2019, 12, 1950067. [Google Scholar] [CrossRef]
- Syed Ali, M.; Narayanan, G.; Orman, Z.; Shekher, V.; Arik, S. Finite time stability analysis of fractional-order complex-valued memristive neural networks with proportional delays. Neural Process. Lett. 2020, 51, 407–426. [Google Scholar] [CrossRef]
- Zheng, B.; Hu, C.; Yu, J.; Jiang, H. Finite-time synchronization of fully complex-valued neural networks with fractional-order. Neurocomputing 2020, 373, 70–80. [Google Scholar] [CrossRef]
- Zeng, J.; Yang, X.; Wang, L.; Chen, X. Robust Asymptotical Stability and Stabilization of Fractional-Order Complex-Valued Neural Networks with Delay. Discret. Dyn. Nat. Soc. 2021, 2021, 5653791. [Google Scholar] [CrossRef]
- Chen, J.; Chen, B.; Zeng, Z. Global asymptotic stability and adaptive ultimate Mittag–Leffler synchronization for a fractional-order complex-valued memristive neural networks with delays. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2519–2535. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Li, W. Adaptive finite-time synchronization control for fractional-order complex-valued dynamical networks with multiple weights. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105239. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Jiang, N.; Liu, X.; Yu, W.; Shen, J. Finite-time stochastic synchronization of genetic regulatory networks. Neurocomputing 2015, 167, 314–321. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Z.; Wang, X.; Sun, F. Stability and synchronization control of fractional-order gene regulatory network system with delay. J. Adv. Comput. Intell. Intell. Inform. 2017, 21, 148–152. [Google Scholar] [CrossRef]
- Qiao, Y.; Yan, H.; Duan, L.; Miao, J. Finite-time synchronization of fractional-order gene regulatory networks with time delay. Neural Netw. 2020, 126, 1–10. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Yang, S.; Yu, J.; Hu, C.; Jiang, H. Quasi-projective synchronization of fractional-order complex-valued recurrent neural networks. Neural Netw. 2018, 104, 104–113. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H. Corrigendum to Projective synchronization for fractional neural networks. Neural Netw. 2015, 67, 152–154. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Shi, L. Finite-time synchronization for competitive neural networks with mixed delays and non-identical perturbations. Neurocomputing 2016, 185, 242–253. [Google Scholar] [CrossRef]
- Baleanu, D.; Sadati, S.J.; Ghaderi, R.; Ranjbar, A.; Jarad, F. Razumikhin stability theorem for fractional systems with delay. Abstr. Appl. Anal. 2010, 2010, 124812. [Google Scholar] [CrossRef]
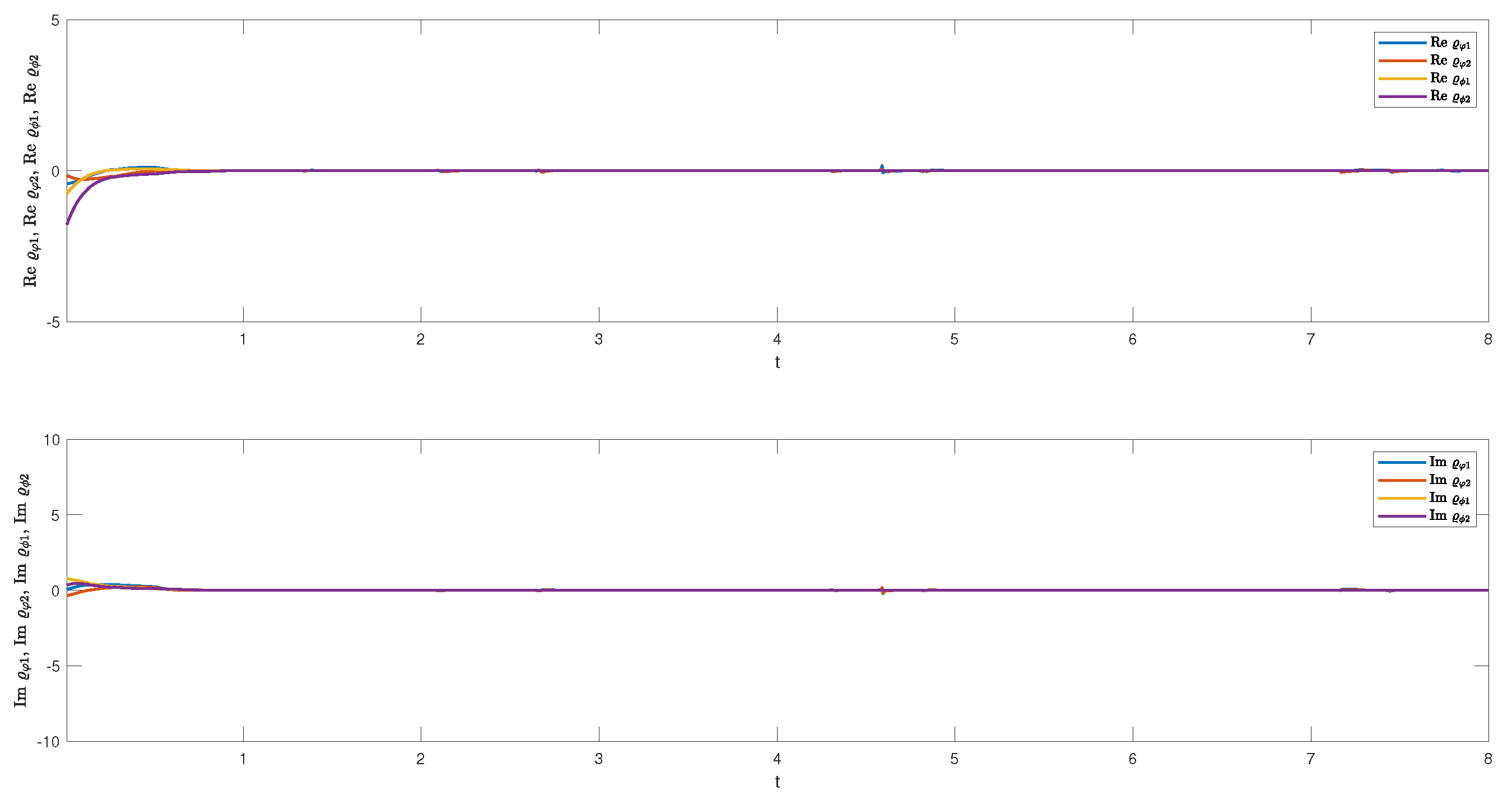
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Yang, X.; Liu, H.; Chen, X. Synchronization in Finite Time of Fractional-Order Complex-Valued Delayed Gene Regulatory Networks. Fractal Fract. 2023, 7, 347. https://doi.org/10.3390/fractalfract7050347
Wang L, Yang X, Liu H, Chen X. Synchronization in Finite Time of Fractional-Order Complex-Valued Delayed Gene Regulatory Networks. Fractal and Fractional. 2023; 7(5):347. https://doi.org/10.3390/fractalfract7050347
Chicago/Turabian StyleWang, Lu, Xujun Yang, Hongjun Liu, and Xiaofeng Chen. 2023. "Synchronization in Finite Time of Fractional-Order Complex-Valued Delayed Gene Regulatory Networks" Fractal and Fractional 7, no. 5: 347. https://doi.org/10.3390/fractalfract7050347
APA StyleWang, L., Yang, X., Liu, H., & Chen, X. (2023). Synchronization in Finite Time of Fractional-Order Complex-Valued Delayed Gene Regulatory Networks. Fractal and Fractional, 7(5), 347. https://doi.org/10.3390/fractalfract7050347