Multistability and Jump in the Harmonically Excited SD Oscillator

Abstract

Coexisting attractors and the consequent jump in a harmonically excited smooth and discontinuous (SD) oscillator with double potential wells are studied in detail herein. The intra-well periodic solutions in the vicinity of the nontrivial equilibria and the inter-well periodic solutions are generated theoretically. Then, their stability and conditions for local bifurcation are discussed. Furthermore, the point mapping method is utilized to depict the fractal basins of attraction of the attractors intuitively. Complex hidden attractors, such as period-3 responses and chaos, are found. It follows that jumps among multiple attractors can be easily triggered by an increase in the excitation level or a small disturbance of the initial condition. The results offer an opportunity for a more comprehensive understanding and better utilization of the multistability characteristics of the SD oscillator.

1. Introduction

Mechanical oscillators play a vital role in many fields, such as engineering [1], lattice dynamics [2], and biology [3]. Due to the changes in geometric configuration, strong irrational nonlinearities occur in many oscillators [4,5,6]. A typical example is the smooth and discontinuous (SD) oscillator proposed by Cao et al. [7,8]. It is geometrically nonlinear, with an irrationally nonlinear restoring force. Whether it is smooth or discontinuous depends on the value of its smoothness parameter. Representing the snap-through truss system, this oscillator has been found to exhibit a large variety and complexity of responses and phenomena [9,10,11], thus receiving much attention in recent years.

Many studies have been conducted to provide a fundamental basis for understanding the dynamics of the SD oscillator. Tian et al. [12] investigated the universal unfolding for codimension-two bifurcation near the equilibria of the SD oscillator, such as pitchfork, Hopf and double Hopf, and double-connected homoclinic and closed-orbit bifurcations. Li et al. [13] obtained periodic solutions of the SD oscillator by applying the four-dimensional averaging method and the complete Jacobian elliptic integrals [13]. On this basis, the stick–slip vibrations and complex equilibrium bifurcations of a self-excited SD oscillator with Coulomb friction were discussed [14]. Santhosh et al. [15] carried out the frequency domain analysis of a harmonically excited SD oscillator semi-analytically and found that saddle-node bifurcation leads to jumping phenomena and symmetry-breaking bifurcations. Chen et al. [16] derived all possible bifurcations of the SD oscillatory system, including degenerate Hopf, homoclinic, double limit cycle, Bautin, and Bogdanov–Takens bifurcations. In terms of the stochastic case, Yue et al. [17] studied the stochastic bifurcations of the SD oscillator with additive and/or multiplicative bounded noises by using the generalized cell mapping method and digraph analysis algorithm. Considering delayed displacement and velocity feedback control, Yang and Cao [18] analyzed the primary resonance and the noise-induced stochastic resonance of a quasi-zero-stiffness SD oscillator via the average method.

In engineering practice, the SD oscillator has been utilized for vibration absorption and vibration energy harvesting. For the former purpose, Hao and Cao [19] employed the SD oscillatory system with a stable-quasi-zero-stiffness characteristic as a vibration isolator. For the latter, Yang et al. [20] proposed an electromagnetic vibration energy harvester based on the SD oscillator and driven by stochastic environmental fluctuation. Zhang et al. [21] applied the SD oscillator in designing an electromagnetic bistable vibration energy harvester with an elastic boundary and experimentally verified its higher probability for inducing favorable inter-well responses than normal energy harvesters.

Up to now, studies on the SD oscillator have shown that multistability is common in this type of oscillatory system. As it is well known, this initial sensitive dynamical behavior is a double-edged sword in engineering applications: it is unwanted for achieving globally stable mechanical vibration but helpful for achieving desired deformations with small energy input. For instance, by making use of the multistability characteristics of some types of energy harvesters, better energy harvesting performance can be achieved due to the absence of the requirement for a constant supply of energy but with a small perturbation of the initial conditions. Therefore, extending the study on the initial conditions for jumps among the multiple responses of the SD oscillator is essential for its practical applications. Currently, research on the initial conditions is still very limited. Most of the discussions on the multistability of this oscillator focus on the mechanism of multistability triggered by system parameters.

Based on the above statement, the goal of this study is to present the mechanism of jump among the coexisting attractors of the SD oscillator analytically and to classify the fractal basins of attraction of the multiple attractors quantitatively. This paper is organized as follows. In Section 2, the unperturbed dynamics of the presented archetypal dynamical model are discussed. In Section 3, the amplitude–frequency characteristics of the steady solutions of the dimensionless system are derived. In Section 4, numerical explorations are performed to verify the validity of the analytical prediction; meanwhile, the basins of attraction of the coexisting attractors are presented. Some conclusions are drawn thereafter.

2. Dynamical Model and Unperturbed Dynamics

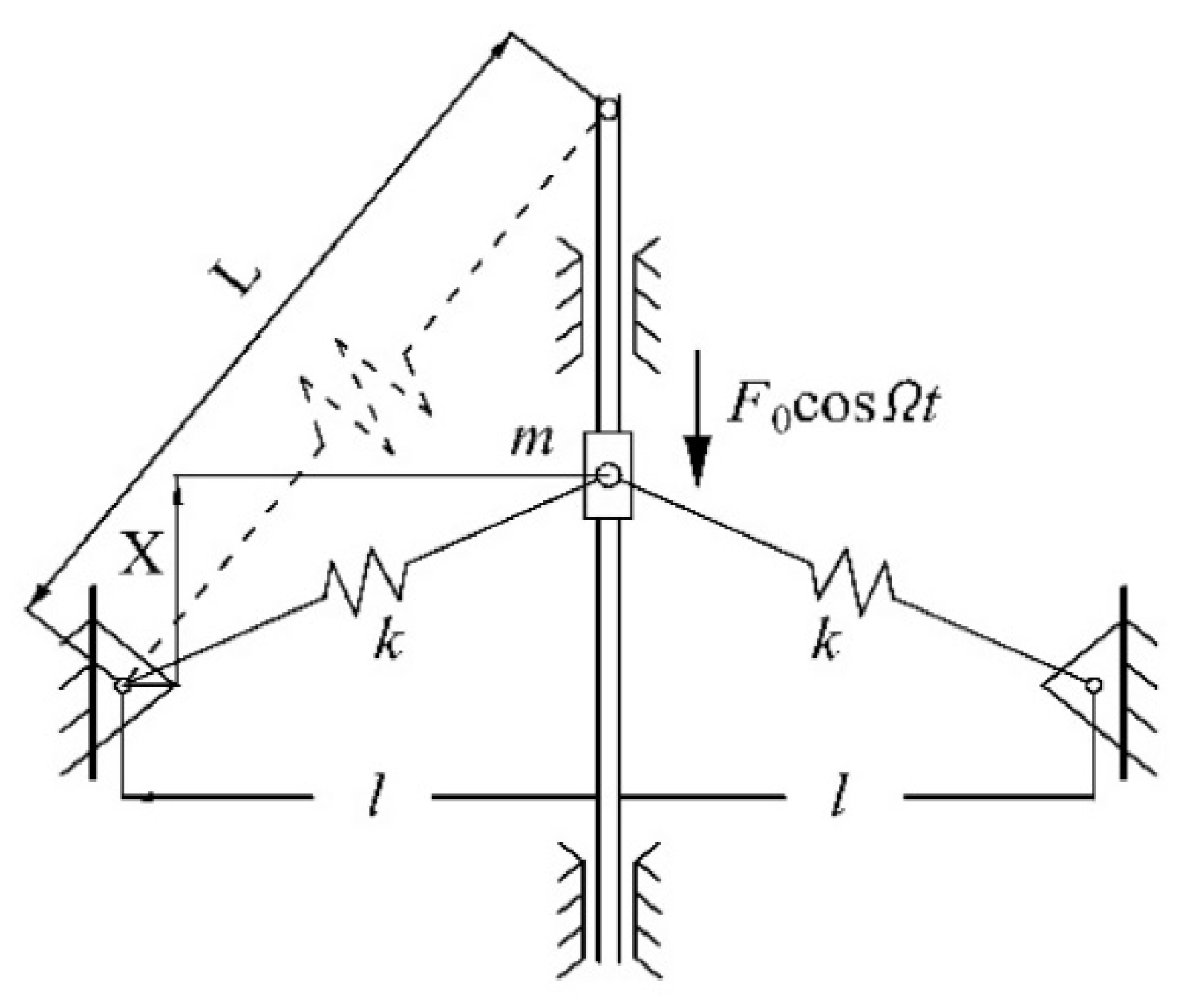
The harmonically excited smooth and discontinuous (SD) oscillator can be represented geometrically as a conventional linear mass–spring–damper system subject to harmonic excitation, as shown in Figure 1. The loaded mass m is attached to two springs pinned to rigid supports on the horizontal plane. It is also subjected to the actions of the harmonic-driven force and the viscous damping force. Since the motion of the mass is in the X direction, applying the equation of motion, we have

$$m\ddot{X}+c\dot{X}+2kX-\frac{2kXL}{\sqrt{X^2+l^2}}=F_0\cos (\mathsf{\Omega }t).$$

(1)

Here, X represents the displacement of the mass, k is the linear stiffness of each spring, L is the unstretched length of each spring, l is the half-distance between the pivots of the inclined springs, and c is the damping coefficient of the viscous damper. F₀ and Ω are the amplitude and frequency of the harmonically excited driven force, respectively. As can be seen in Equation (1), due to the geometric configuration, the resultant of the restoring resistances of the two springs is strongly and irrationally nonlinear even though each spring has a linear stiffness. If we let

$$x=\frac{X}{L},{\omega }_0^2=\frac{2k}{m},\xi =\frac{c}{2m{\omega }_0},T={\omega }_{0}t,\omega =\frac{\mathsf{\Omega }}{{\omega }_0},\alpha =\frac{l}{L},f_0=\frac{F_0}{2kL},$$

(2)

we rewrite system (1) as the following dimensionless system:

$$\dot{x}=y,\dot{y}=-2\xi y-x(1-\frac{1}{\sqrt{x^2+{\alpha }^2}})+f_0\cos \omega T.$$

(3)

System (3) is smooth when $\alpha >0$. When $\alpha =0$, it becomes a discontinuous system given by

$$\dot{x}=y,\dot{y}=-2\xi y-x+\mathrm{sign}(x)+f_0\cos \omega T.$$

(4)

Since the distance l in Figure 1 is positive, we have $\alpha >0$ and a smooth system (3). The unperturbed system of system (3) is

$$\dot{x}=y,\dot{y}=-x+\frac{x}{\sqrt{x^2+{\alpha }^2}}.$$

(5)

Note that the number, position, and stability of its equilibria are determined by the value of the smoothness parameter $\alpha$. For $0<\alpha <1$, there are three equilibria, i.e., a saddle point $O(0,0)$ and two centers $C_{\pm }(\pm x_c,0)$ where $x_c=\sqrt{1-{\alpha }^2}$. For $\alpha \ge 1$, there is only one equilibrium $O(0,0)$. Equation (5) is a Hamilton system with the Hamiltonian $H(x,y)$ and the function of potential energy $V(x)$ in the following form:

$$H(x,y)=\frac{1}{2}{y}^2+\frac{1}{2}{x}^2-\sqrt{x^2+{\alpha }^2}+\alpha ,V(x)=\frac{1}{2}{x}^2-\sqrt{x^2+{\alpha }^2}+\alpha .$$

(6)

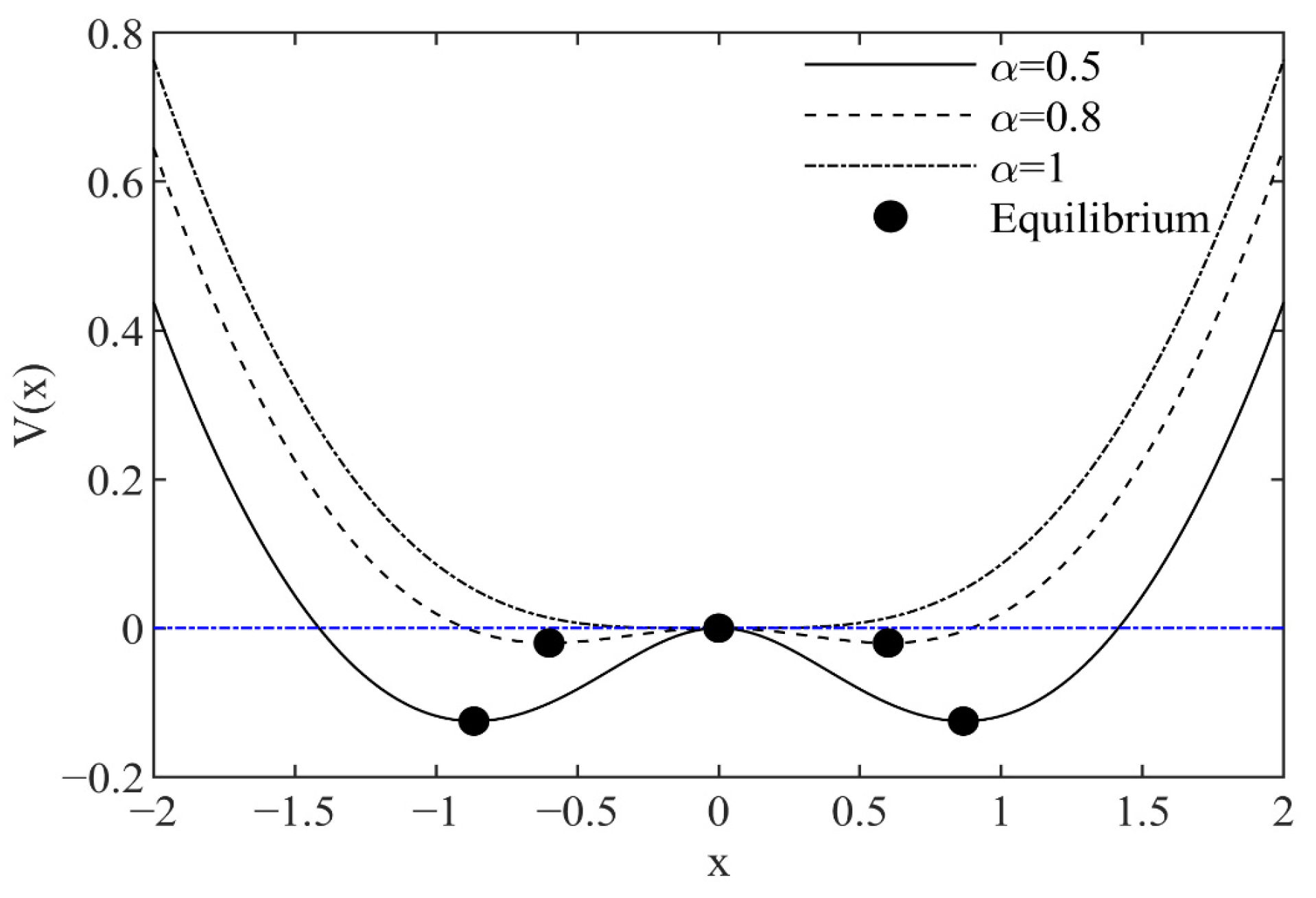
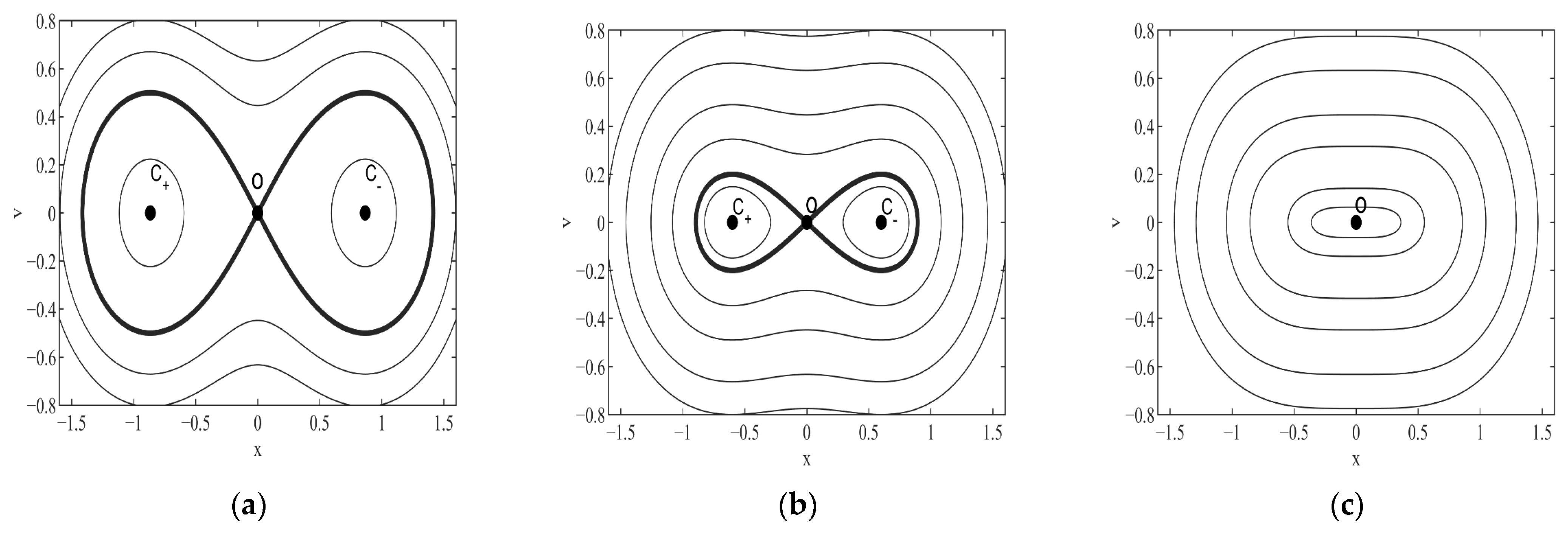
On this basis, the potential function and the phase portraits of the unperturbed system (5) for different values of the smoothness parameter $\alpha$ are depicted in Figure 2 and Figure 3, respectively. The thick curves in Figure 3 show that there are symmetrically double potential wells in the system when $\alpha$ is 0.5 or 0.8. Comparatively, each potential well for $\alpha$ = 0.8 is much smaller than that for $\alpha$ = 0.5. In Figure 3a,b, closed orbits near the non-trivial equilibria $C_{\pm }(\pm x_c,0)$ are within the domains surrounded by homoclinic orbits, while closed orbits near the trivial equilibrium $O(0,0)$ are outside of these domains. At α = 1, there is only one center $O(0,0)$ (see Figure 3c). It follows that the unperturbed system (5) undergoes a subcritical pitchfork bifurcation at $\alpha$ = 1. Since bistability is common in the double-well case [21,22], using the parameters

$$\alpha =0.8,\xi =0.01,$$

(7)

we may observe the interaction among the coexisting attractors of the system (3) with the variation of the excitation parameters.

3. Multiple Responses of the SD Oscillator

3.1. Periodic Responses in the Vicinity of Nontrivial Equilibria

The periodic solutions of the system (3) that perturb from the two nontrivial equilibria $C_{\pm }(\pm x_c,0)$ are intra-well ones within the domains surrounded by homoclinic orbits. Hence, it is convenient for us to apply the method of multiple scales (MMSs) to complete the analytical prediction of these periodic motions. Considering that the excitation amplitude $f_0$ and the damping coefficient $\xi$ are small, we introduce a small parameter ε, thereby satisfying $0<\epsilon \ll 1$ to rescale the parameters of the dimensionless system (3) in the following form:

$$\xi =\epsilon \tilde{\xi },f_0={\epsilon }^2\tilde{f},x=\pm x_c+\widehat{x}.$$

(8)

Equation (3) can be rewritten as

$$\ddot{\widehat{x}}+\widehat{x}\pm x_c=-2\epsilon \tilde{\xi }\dot{\widehat{x}}+{\epsilon }^2\tilde{f}\cos \omega T+\frac{\pm x_c+\widehat{x}}{\sqrt{1+({\widehat{x}}^2\pm 2x_c\widehat{x})}}.$$

(9)

Expanding the fractional terms of the above system as a Taylor series of $\widehat{x}$ in the neighborhood of $C_{\pm }$, and neglecting the higher-order-than-three terms of $\widehat{x}$, yields

$$\ddot{\widehat{x}}+{\widehat{\omega }}^2\widehat{x}=-2\epsilon \tilde{\xi }\dot{\widehat{x}}\mp Q_2{\widehat{x}}^2+Q_3{\widehat{x}}^3+{\epsilon }^2\tilde{f}\cos \omega T$$

(10)

where

$$\widehat{\omega }=x_c,Q_2=\frac{3x_c}{2}(1-x_c^2),Q_3=\frac{1}{2}(5x_c^2-1)(1-x_c^2).$$

(11)

Rescaling the dimensionless excitation frequency $\omega$, the displacement $\widehat{x}$ and time scales of the system (10) are

$$\begin{array}{l}{\omega }^2={\widehat{\omega }}^2+\epsilon \sigma ,\\ \widehat{x}={\displaystyle \sum _{i=0}^n{\epsilon }^i}{\widehat{x}}_i(T_0,T_1,T_2,\cdots ),\\ T_i={\epsilon }^{i}T,\frac{d}{dT}={\displaystyle \sum _{i=0}^n{\epsilon }^i}{D}_i,D_i=\frac{\partial }{\partial T_i},\end{array}$$

(12)

and comparing the coefficients of $\epsilon$, ${\epsilon }^2$, and ${\epsilon }^3$ of the system (10), respectively, we have

$$\epsilon :D_0^2{\widehat{x}}_1+{\omega }^2{\widehat{x}}_1=0,$$

(13)

$${\epsilon }^2:D_0^2{\widehat{x}}_2+{\omega }^2{\widehat{x}}_2=-2D_0{D}_1{\widehat{x}}_1-2\tilde{\xi }{D}_0{\widehat{x}}_1+\sigma {\widehat{x}}_1+\tilde{f}\cos \omega T\mp Q_2{\widehat{x}}_1^2,$$

(14)

and

$${\epsilon }^3:D_0^2{\widehat{x}}_3+{\omega }^2{\widehat{x}}_3=-D_1^2{\widehat{x}}_1-2D_0{D}_2{\widehat{x}}_1-2D_0{D}_1{\widehat{x}}_2-2\tilde{\xi }(D_0{\widehat{x}}_2+D_1{\widehat{x}}_1)+\sigma {\widehat{x}}_2\mp 2Q_2{\widehat{x}}_1{\widehat{x}}_2+Q_3{\widehat{x}}_1^3.$$

(15)

Without loss of generality, we express the periodic solution of Equation (13) as

$${\widehat{x}}_1=A(T_1,T_2)e^{i\omega T_0}+\overline{A}(T_1,T_2)e^{-i\omega T_0},$$

(16)

where

$$A(T_1,T_2)=\frac{a(T_1,T_2)}{2}{e}^{i\phi (T_1,T_2)},$$

(17)

$a(T_1,T_2)$ and $\phi (T_1,T_2)$ represent the amplitude and phase difference of the solution ${\widehat{x}}_1$, respectively. Substituting Equations (16) and (17) into Equation (14), and eliminating the secular terms, yields

$$D_{1}A=-\frac{\tilde{f}i}{4\omega }-\frac{\sigma Ai}{2\omega }-\tilde{\xi }A.$$

(18)

Equation (14) herein becomes

$$D_0^2{\widehat{x}}_2+{\widehat{\omega }}^2{\widehat{x}}_2=\mp Q_2(A^2{e}^{2i\omega T_0}+A\overline{A})+cc$$

(19)

and its solution can be given by

$${\widehat{x}}_2=\pm (\frac{Q_2{A}^2}{3{\omega }^2}{e}^{2i\omega T_0}-\frac{Q_{2}A\overline{A}}{{\omega }^2})+cc.$$

(20)

In a similar manner, by substituting Equations (16), (18), and (20) into Equation (15) and eliminating the secular terms, we obtain

$$D_{2}A=\frac{\tilde{\xi }\tilde{f}}{8{\omega }^2}-\frac{(3A^2\overline{A}{Q}_3+{\tilde{\xi }}^{2}A)i}{2\omega }-\frac{(\sigma \tilde{f}+2{\sigma }^{2}A+\frac{80}{3}{Q}_2^2{A}^2\overline{A})i}{16{\omega }^3}.$$

(21)

Let $\widehat{a}=\epsilon a$. Based on Equations (12), (16), and (20), the periodic solution in the vicinity of the nontrivial equilibria $C_{\pm }$ may be written as

$$x=\pm x_c+\widehat{a}\cos (\omega T+\phi )\pm \frac{Q_2{\widehat{a}}^2}{3{\omega }^2}{\cos }^2(\omega T+\phi )\mp \frac{2Q_{{}_2}{\widehat{a}}^2}{3{\omega }^2}$$

(22)

where $\widehat{a}$ and $\phi$ represent the approximate amplitude and phase angle of the periodic solution, respectively. Considering $\dot{A}\approx D_{0}A+\epsilon D_{1}A+{\epsilon }^2{D}_{2}A$ and Equations (17), (18), and (21), it is, therefore, possible to write the differential equations of $\widehat{a}$ and $\phi$ by using the original dimensionless parameters, namely,

$$\begin{array}{l}\dot{\widehat{a}}=\frac{({\widehat{\omega }}^2-5{\omega }^2)f_0\sin \phi }{8{\omega }^3}+\frac{\xi f_0\cos \phi }{4{\omega }^2}-\xi \widehat{a},\\ \widehat{a}\dot{\phi }=\frac{({\widehat{\omega }}^2-5{\omega }^2)f_0\cos \phi }{8{\omega }^3}-\frac{\xi f_0\sin \phi }{4{\omega }^2}-\frac{\widehat{a}{\xi }^2}{2\omega }+\frac{\widehat{a}({\widehat{\omega }}^2-5{\omega }^2)({\omega }^2-{\widehat{\omega }}^2)}{8{\omega }^3}-\frac{(10Q_2^2+9{\omega }^2{Q}_3)}{24{\omega }^3}{\widehat{a}}^3.\end{array}$$

(23)

Letting the right side of Equation (23) be zero, we can solve the frequency $\omega$ and the amplitude $\widehat{a}$ from the following equation:

$$\begin{array}{l}({\widehat{\omega }}^2-5{\omega }^2)f_0\sin \phi +2\xi f_0\omega \cos \phi =8\xi {\omega }^3\widehat{a},\\ ({\widehat{\omega }}^2-5{\omega }^2)f_0\cos \phi -2\xi f_0\omega \sin \phi =4{\omega }^2{\xi }^2\widehat{a}-({\widehat{\omega }}^2-5{\omega }^2)({\omega }^2-{\widehat{\omega }}^2)\widehat{a}+(\frac{10Q_2^2}{3}+3{\omega }^2{Q}_3){\widehat{a}}^3.\end{array}$$

(24)

Eliminating the triangulation functions of Equation (24) yields

$${({\widehat{\omega }}^2-5{\omega }^2)}^2{f}_0{}^2+4{\xi }^2{f}_0{}^2{\omega }^2=64{\xi }^2{\omega }^6{\widehat{a}}^2+{(4{\omega }^2{\xi }^2+({\widehat{\omega }}^2-5{\omega }^2)({\widehat{\omega }}^2-{\omega }^2)+(\frac{10Q_2^2}{3}+3{\omega }^2{Q}_3){\widehat{a}}^2)}^2{\widehat{a}}^2.$$

(25)

The amplitude $\widehat{a}$ can be determined analytically from the above equation.

Using the Jacobian matrix of Equation (23), we carry out the local stability and bifurcation analysis of the periodic solution. The eigenvalues are computed by the following equation:

$${\lambda }^2+2\xi \lambda +\gamma =0$$

(26)

where

$$\gamma ={\xi }^2+(\frac{{\xi }^2}{2\omega }-\frac{({\widehat{\omega }}^2-5{\omega }^2)({\omega }^2-{\widehat{\omega }}^2)}{8{\omega }^3}+\frac{(10Q_2^2+9{\omega }^2{Q}_3)}{8{\omega }^3}{\widehat{a}}^2)(\frac{{\xi }^2}{2\omega }-\frac{({\widehat{\omega }}^2-5{\omega }^2)({\omega }^2-{\widehat{\omega }}^2)}{8{\omega }^3}+\frac{(10Q_2^2+9{\omega }^2{Q}_3)}{24{\omega }^3}{\widehat{a}}^2).$$

(27)

Since the coefficients $\xi$ and $\gamma$ are real numbers, there is no purely imaginary solution in Equation (26). The stability of the periodic solutions in the neighborhood of $C_{\pm }$ may be changed only if $\lambda$ = 0 in the above equation, namely, $\gamma =0$, implying the occurrence of saddle-node bifurcation.

Based on the above analysis and the symmetry of the periodic responses around the two nontrivial equilibria, the variation in the amplitude of the periodic response with the excitation parameters is illustrated in Figure 4, where the stable and unstable periodic branches are represented by the solid and dashing curves, respectively. The quantitative analysis of the amplitudes of stable periodic responses is carried out via the fourth-order Runge–Kutta approach in the dimensionless system (5) via MATLAB. The time step T is 0.01. As can be seen in Figure 4, the analytical prediction is in good agreement with the numerical results.

The frequency response of the dimensionless system (3) is shown in Figure 4a, where the periodic solution branches for f₀ = 0.001 and f₀ = 0.005 are noticeably different. For f₀ = 0.001, the amplitude of the periodic response changes continuously with the dimensionless excitation frequency ω. In contrast, for f₀ = 0.005, as ω increases, the branches bend to the left and yield multivalued solutions. Apparently, for f₀ = 0.005, when reversely sweeping the frequency ω from 0.8 to 0.4, one can observe a saddle-node bifurcation point, as depicted by the small red circle in Figure 4a, on the left side of which the intra-well periodic response may jump down to the lower stable branch. This implies that, due to the saddle-node bifurcation, when decreasing the value of ω, the dynamics in the neighborhood of each nontrivial equilibrium varies from a single intra-well periodic attractor to bistable periodic attractors. For instance, at ω = 0.54 and ω = 0.55, two values on different sides of the critical value of ω for the saddle-node bifurcation, the numerical results shown in Figure 5a,b are different: for the former, there are two different periodic attractors under different initial velocities; for the latter, there is only one periodic attractor.

Similarly, as can be seen in Figure 4b, there are saddle-node bifurcation points on the branch of ω = 0.5, implying that jumps between bistable periodic branches may be triggered by the increase in the excitation amplitude f₀. As f₀ is increased from 0 to the horizontal abscissa of the left saddle-node bifurcation point, there is only one stable branch. Given f₀ = 0.0032, the numerical results in Figure 5c illustrate that there is only one intra-well periodic attractor in the system (3). As f₀ is further increased, a higher-amplitude stable branch will appear and coexist with the lower-amplitude one, which matches the numerical simulation in Figure 5d. When f₀ exceeds the horizontal abscissa of the right saddle-node bifurcation point, the periodic solution will jump up to the higher-amplitude branch through the saddle-node bifurcation. Instead of bistable periodic attractors, there is only one attractor in the neighborhood of each nontrivial equilibrium.

It follows from Figure 4 that due to the saddle-node bifurcations, jumps between two intra-well periodic attractors in the vicinity of each non-trivial equilibrium may be incurred by varying the excitation amplitude or frequency when f₀ and ω are relatively small.

3.2. Periodic Solution around the Trivial Equilibrium O(0, 0)

To be different from the periodic solutions around the non-trivial equilibria, a periodic solution in the vicinity of the origin O(0, 0) will be outside of the potential wells surrounded by homoclinic orbits. Hence, it will be an inter-well one with a large amplitude. Considering the limitation of the method of multiple scales in approximating periodic solutions in the vicinity of equilibria, it is unsuitable to employ this method for the analysis of the inter-well solution. We herein apply the average method [13,23].

Expressing the inter-well periodic solution by the slowly varying amplitude b and frequency $\omega$, we have

$$x=b\cos (\omega T+\psi ),\dot{x}=-b\omega \sin (\omega T+\psi )$$

(28)

Substituting the above forms of $x$ and $\dot{x}$ into the dimensionless system (3) yields

$$\dot{b}\cos (\omega T+\psi )=b\dot{\psi }\sin (\omega T+\psi ),-\dot{b}\omega \sin (\omega T+\psi )-b\omega \dot{\psi }\cos (\omega T+\psi )=P_1(a,\psi ,T).$$

(29)

Here,

$$P_1(a,\psi ,T)=b{\omega }^2\cos (\omega T+\psi )+2\omega \xi b\sin (\omega T+\psi )-b\cos (\omega T+\psi )(1-\frac{1}{\sqrt{b^2{\cos }^2(\omega T+\psi )+{\alpha }^2}})+f_0\cos \omega T.$$

(30)

Based upon Equations (28)–(30), the slowly varying amplitude and phase angle can be described by the following equation:

$$\dot{b}=-\frac{P_1(a,\psi ,T)}{\omega }\sin (\omega T+\psi ),\dot{\psi }=-\frac{P_1(a,\psi ,T)}{b\omega }\cos (\omega T+\psi ).$$

(31)

Integrating Equation (31) over one period of $[0,\frac{2\pi }{\omega }]$ yields

$$\dot{b}=\frac{-2\xi b\omega -f_0\sin \psi }{2\omega },\dot{\psi }=\frac{-b({\omega }^2-1)-f_0\cos \psi }{2b\omega }+\frac{2{\alpha }^2}{\pi b^2\omega \sqrt{b^2+{\alpha }^2}}{E}_1(\frac{b}{\sqrt{b^2+{\alpha }^2}})-\frac{2\sqrt{b^2+{\alpha }^2}}{\pi b^2\omega }{E}_2(\frac{b}{\sqrt{b^2+{\alpha }^2}}).$$

(32)

Here, the functions $E_1(\frac{b}{\sqrt{b^2+{\alpha }^2}})$ and $E_2(\frac{b}{\sqrt{b^2+{\alpha }^2}})$ are the complete elliptic integrals of the first and second kind, respectively, given by

$$E_1(r)={\displaystyle {\int }_0^{\frac{\pi }{2}}\frac{1}{\sqrt{1-r^2{\sin }^2\theta }}}d\theta ,E_2(r)={\displaystyle {\int }_0^{\frac{\pi }{2}}\sqrt{1-r^2{\sin }^2\theta }}d\theta .$$

(33)

Letting the right side of Equation (32) be zero, we can solve the amplitude of the inter-well periodic solution from $P_2(b,\omega ,\alpha )=0$ where

$$P_2(b,\omega ,\alpha )=4{\xi }^2{\omega }^2{b}^2+{({\omega }^2-1-\frac{4{\alpha }^2}{\pi b^2\sqrt{b^2+{\alpha }^2}}{E}_1(\frac{b}{\sqrt{b^2+{\alpha }^2}})+\frac{4\sqrt{b^2+{\alpha }^2}}{\pi b^2}{E}_2(\frac{b}{\sqrt{b^2+{\alpha }^2}}))}^2{b}^2-f_0{}^2.$$

(34)

Whether the inter-well periodic solution is stable depends on the signs of the real parts of the solutions of the corresponding characteristic equation of the linearized average equation [13]. According to our derivation, the inter-well periodic solution is asymptotically only if its amplitude b is more than the maximum of the horizontal abscissas of the homoclinic orbits and

$$\frac{\partial P_2(b,\omega ,\alpha )}{\partial b}>0,1+\frac{1}{\alpha }{\displaystyle \sum _{n=0}^{+\infty }{(\frac{(2n-1)!!}{(2n)!!})}^2(2n+1){(\frac{b}{\alpha })}^{2n}}>0.$$

(35)

The variation in the inter-well solution branches with the dimensionless excitation is displayed in Figure 6, where the given values of the excitation parameters are the same as those in Figure 4. As can be seen in Figure 6a, under a low excitation amplitude, there is no stable branch. With an increase in the excitation amplitude, given the values of the excitation frequency of $\omega =0.5$ and $\omega =0.6$, there is a stable solution branch (see Figure 6b), which can also be ascribed to saddle-node bifurcation. In Figure 6b, the theoretical prediction perfectly matches the numerical results, thus validating the prediction. It is worth noting that the amplitude of the inter-well response is much greater than that of the intra-well periodic response discussed in the last section. Observing Figure 4b and Figure 6b, it is not difficult for us to find the coexistence of four intra-well periodic attractors around the two nontrivial equilibria and an inter-well periodic attractor for $f_0\ge 0.013$.

4. Attractors and Their Fractal Basins of Attraction

Apart from the variation in the excitation amplitude and frequency, the initial conditions can also lead to jumps among multiple attractors, thus having a significant effect on the dynamical behavior of the SD oscillator. This also suggests the necessity of classifying the basins of attraction (BA) of the attractors, namely the union of initial conditions triggering the same response [1,19]. The point mapping method [24,25] is utilized to depict the BA of the SD oscillatory system (3) on the initial-value plane $-1.5\le x(0)\le 1.5,-1.0\le y(0)\le 1.0$ consisting of $401\times 401$ array of points, which respects the initial conditions. For the same attractor, all initial conditions leading to it are marked in the same color. The sequences of the coexisting attractors and their BA with the variation in the excitation parameters are presented in Figure 7 and Figure 8. There are two columns in each figure: the left and right columns show the phase maps of the coexisting attractors and their BA, respectively. Here, the color to mark each attractor is the same as that of its BA.

Given $f_0=0.005$, the evolution of the responses and their BA with an increase in the dimensionless excitation frequency ω are shown in Figure 7, where $\omega$ varies within the range of [0.2, 0.6]. As shown in Figure 7, there is no inter-well attractor, which is in agreement with the prediction of Figure 6a. For $\omega =0.2$, there are two intra-well attractors around the symmetric nontrivial equilibria $C_{\pm }(\pm x_c,0)$, which are marked in red and black, respectively (see Figure 7a). The neighborhood of each nontrivial equilibrium is single-colored, meaning that the intra-well periodic attractors are locally stable. Comparatively, outside of the neighborhood of $C_{\pm }(\pm x_c,0)$, the BA of the attractors are intermingled, indicating a high probability of a jump between two attractors.

As the value of $\omega$ is increased to 0.45 (see Figure 7c), these intra-well attractors still coexist, and their amplitudes are enlarged. Additionally, two new intra-well attractors with higher amplitudes appear, which can be ascribed to the saddle-node bifurcation depicted in Figure 4a. As shown in Figure 4d, even though the BA boundaries of the two lower-amplitude periodic attractors are fractal, these attractors are still locally stable. In contrast, the BA of the two higher-amplitude attractors, which are marked in yellow and blue, respectively, are too fractal and discrete to be detected, showing that their occurrence probability is pretty low. Thus, they are the so-called rare attractors [26]. Since their BA are not in the vicinity of $C_{\pm }(\pm x_c,0)$, they can also be named as the hidden attractors [27,28].

As $\omega$ is further increased (see Figure 7e–h), the four intra-well attractors still coexist, but their amplitudes are changed: the amplitudes of the smaller intra-well ones become enlarged, while the amplitudes of the bigger ones become smaller. Meanwhile, the BA of the two smaller attractors are eroded by the BA of the bigger ones steadily, as depicted in Figure 7f–h, illustrating an increase in the occurrence probability of the two bigger attractors. During this period, jumps among the four attractors can be triggered easily by a small change in the initial condition.

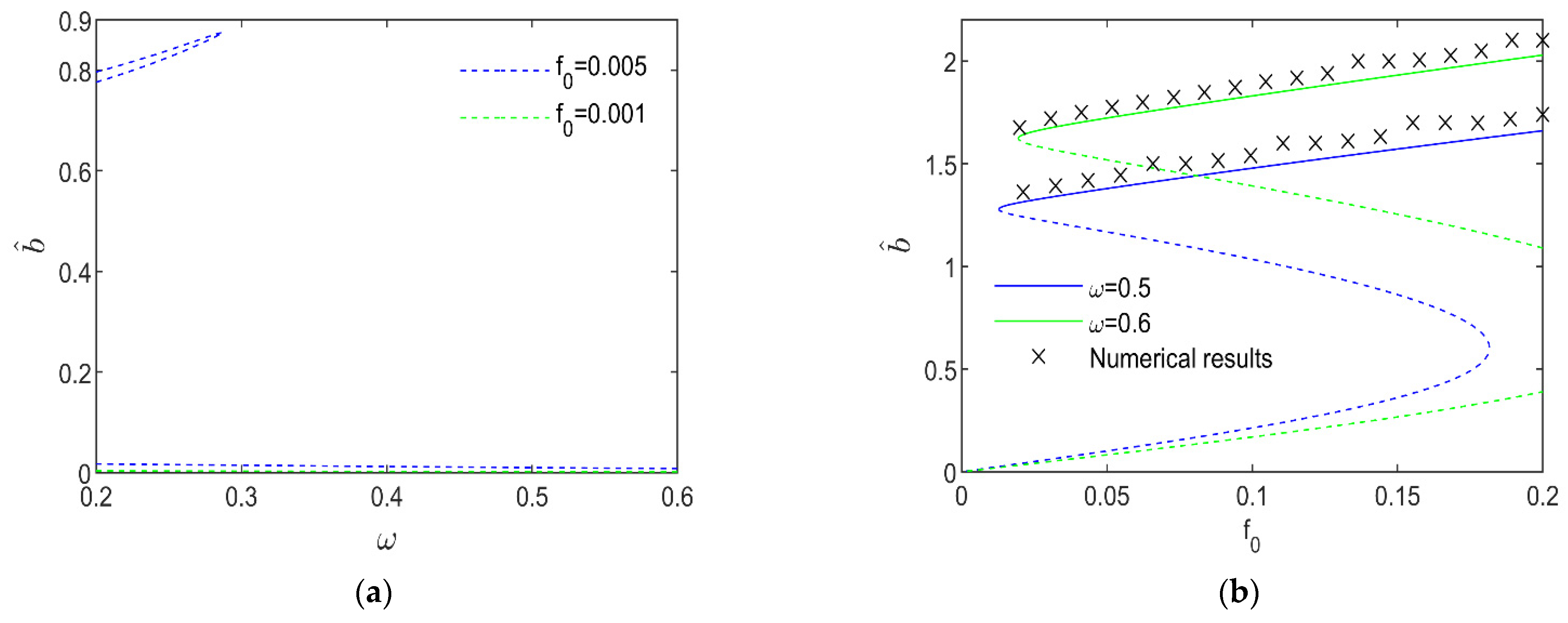
When the value of $\omega$ reaches 0.60 (see Figure 7i,j), the two lower-amplitude attractors vanish, and the higher-amplitude ones are no longer rare or hidden attractors. Figure 6 suggests that with an increase in $\omega$, the higher-amplitude intra-well attractors may replace the lower-amplitudes ones steadily, thus verifying the validity of the analytical results in the last section.

For ω = 0.50, the sequences of the coexisting attractors and the extent of their BA with an increase in the dimensionless excitation amplitude f₀ can be observed in Figure 8, which is more complicated than the evolution in Figure 7.

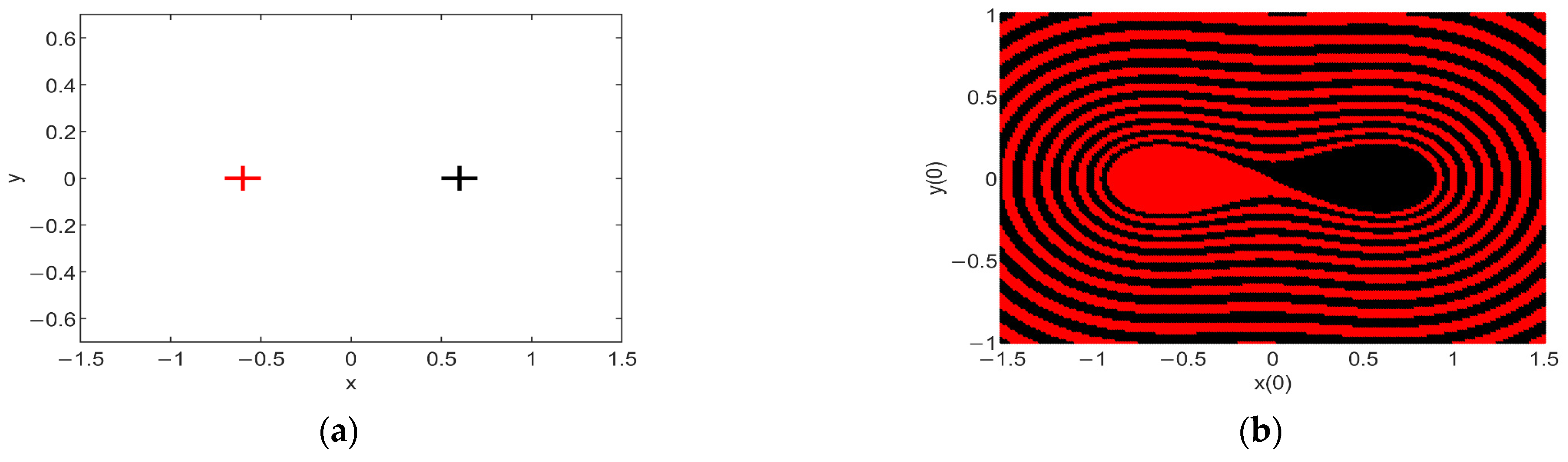
To begin with, for $f_0=0$, there is no excitation in the system (3) and the nontrivial equilibria $C_{\pm }(\pm x_c,0)$ are stable (see Figure 8a). The boundary separating their BA is smooth, as shown in Figure 8b. An initial condition point chosen in the vicinity of $C_{+}(x_c,0)$ or $C_{-}(-x_c,0)$ will surely lead to the corresponding nontrivial equilibrium. Comparatively, a small disturbance of the initial condition in the vicinity of O(0,0) may lead to a jump from one equilibrium attractor to the other.

As $f_0$ increases, the two nontrivial equilibria lose their stability; instead, there are two intra-well periodic attractors around the two equilibria. For instance, for $f_0=0.003$ and $f_0=0$, the BA for the bistable attractors are similar, while those of the corresponding attractors are totally different (see Figure 8a–d).

For $f_0$ = 0.004, two new intra-well periodic attractors appear which amplitudes are higher than the former ones (see the yellow attractor and the blue one in Figure 8e). It follows from Figure 8f that the new attractors are rare and hidden attractors. As $f_0$ further increases from 0.004 to 0.011 (see Figure 8e–j), the BA of these four intra-well attractors are broken into discrete pieces and points.

For $f_0=0.0128$, in addition to these four intra-well periodic attractors, two symmetric intra-well period-3 attractors surrounding $C_{\pm }(\pm x_c,0)$ appear (see the purple and grey phases in Figure 8k). Simultaneously, the BA of the six intra-well attractors are severely fractal (see Figure 8l), demonstrating the high initial-condition sensitivity of the final behavior of the system (3).

As $f_0$ increases to 0.013, besides the six attractors, an inter-well periodic attractor near O(0, 0) appears, as displayed in the light blue phase and the BA in Figure 8m,n, respectively. This agrees perfectly with the prediction in Figure 6b. Since its BA is small and beyond the vicinity of O(0,0), it is also a rare and hidden attractor. It is worth mentioning that the BA of this inter-well attractor has a smooth boundary.

For $f_0$ = 0.014 (see Figure 8o), the period-3 attractors vanish; instead, an inter-well complex attractor traveling around the two nontrivial equilibria appears. Moreover, based on the nature of the BA in Figure 8r, this attractor and the four intra-well attractors are all hidden attractors. As $f_0$ further increases, the BA of the inter-well periodic attractor and the complicated one expands. Since the BA of the latter is discrete and mixed with the BA of the intra-well attractors, a jump among these attractors is easily incurred by a small disturbance of the initial condition. For $f_0$ = 0.15, two intra-well attractors vanish (see Figure 8s), which is in agreement with the prediction in Section 3. In this case, only the BA of the inter-well periodic attractor is continuous with a smooth boundary, showing a higher occurring probability of this attractor.

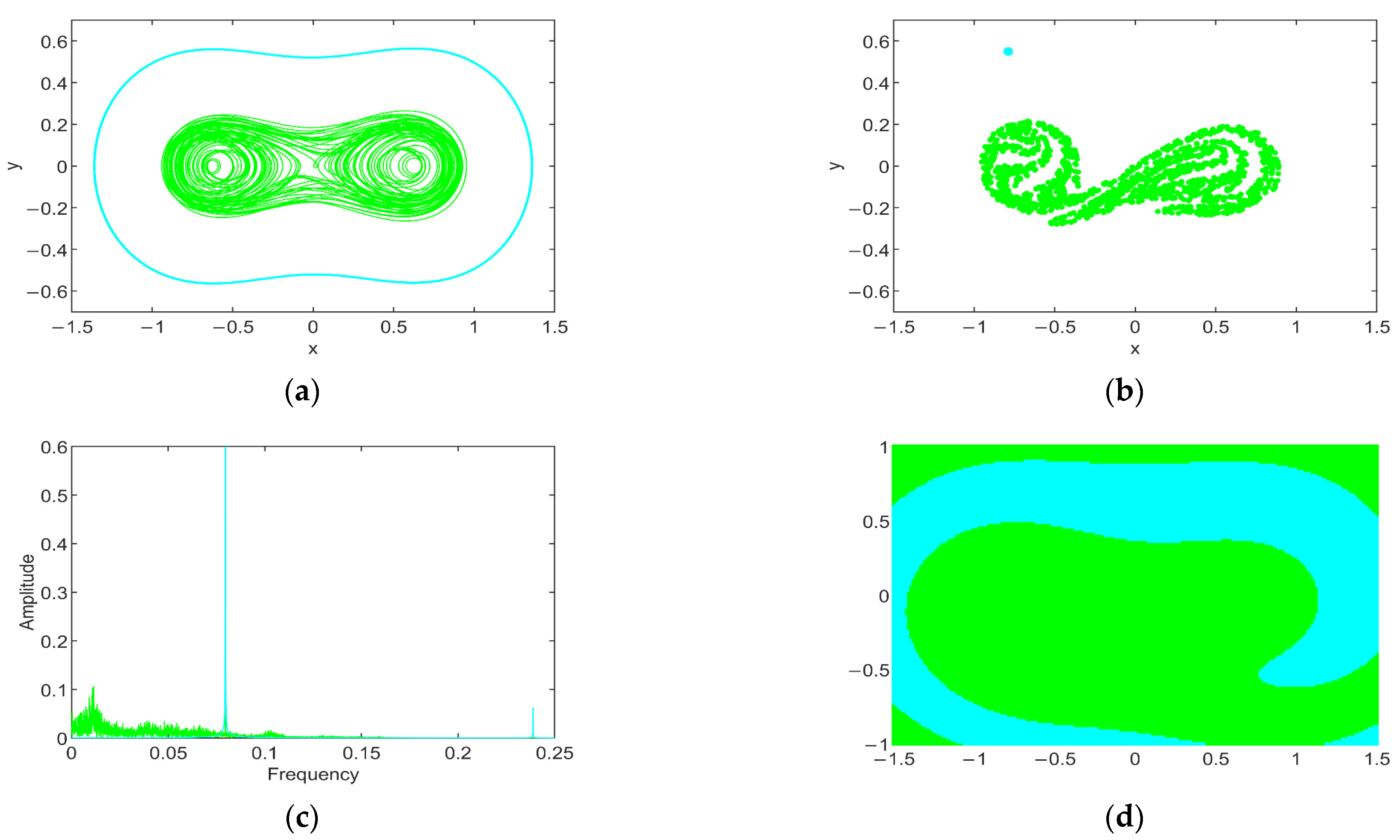
Finally, when $f_0$ reaches 0.02, the intra-well attractors vanish, and only two inter-well attractors coexist in the system (3), i.e., a large-amplitude periodic attractor and a chaotic one, as depicted by the phase map, Poincare map, and frequency spectrum in Figure 9a–c, respectively. Note that the boundary that separates the BA of the chaotic attractor and the large-amplitude periodic attractor is smooth (see Figure 9d).

5. Conclusions and Discussion

In this paper, the multistability and the consequent jump of the harmonically excited SD oscillator were investigated. For the case wherein the nonlinearity of the oscillatory system is continuous, the intra-well periodic responses perturbed from the non-trivial equilibria and the inter-well responses near the trivial equilibrium were predicted, which results are in great agreement with the numerical results.

Given the value of the dimensionless smoothness parameter within the range (0, 1), there are double potential wells in the SD oscillatory system, thus exhibiting multistability. On this basis, we employed two analytical methods, namely, the method of multiple scales and the average method, to present the forms of the intra-well periodic solutions and the inter-well ones, respectively. It was found that, owing to the saddle-node bifurcation of the intra-well periodic solution, jumps between stable intra-well solution branches can be triggered by the excitation-frequency sweep or the increase in the excitation amplitude, leading to bistability in the vicinity of each non-trivial equilibrium. Moreover, the inter-well response can also be induced by increasing the excitation amplitude due to the saddle-node bifurcation of the inter-well solution.

The difference between the two theoretical methods is worth noting. When applying the method of multiple scales, it is not difficult to observe the decay between the analytical results of the intra-well responses and the numerical simulations under a higher excitation amplitude or a much lower excitation frequency. This can be ascribed to the limitation of this method, i.e., the prediction of this method can be quantitatively accurate if the excitation frequency is within a small vicinity of natural frequency and the excitation amplitude is low. Yet, this method is useful, considering its valid qualitative analysis and the convenience of presenting the analytical form of the periodic solutions through it. Comparatively, when utilizing the average method, we can predict more accurate periodic solutions. However, there are complete elliptic integrals in the form of inter-well periodic solutions, implying that the results are semi-analytical.

When increasing the excitation amplitude, we can also observe complex attractors, such as period-3 ones and chaotic ones, coexisting with the periodic attractors. According to the sequences of basins of attraction, with an increase in the excitation parameters, jumps among multiple attractors can be easily incurred by a tiny disturbance of the initial condition. An increase in the excitation frequency or amplitude may break the basins of attraction into discrete pieces and points, thus leading to hidden attractors.

Moreover, for a higher excitation amplitude, bistable inter-well attractors, namely, a chaotic attractor and a large-amplitude periodic attractor, can also be found in the SD oscillatory system. It is worth mentioning that the boundary separating their BA is not fractal but smooth.

Since jumps among multiple attractors could be catastrophic or desirable in practice, the results obtained in this study may provide potential values in the design and applications of oscillatory systems with strong geometric nonlinearities.