The Fractional Analysis of a Nonlinear mKdV Equation with Caputo Operator
Abstract
1. Introduction
2. Preliminaries
3. Analysis of HPTM
4. Analysis of the YTDM
5. Convergence Analysis
6. Applications
- Utilizing the YTDM
- Utilizing the YTDM
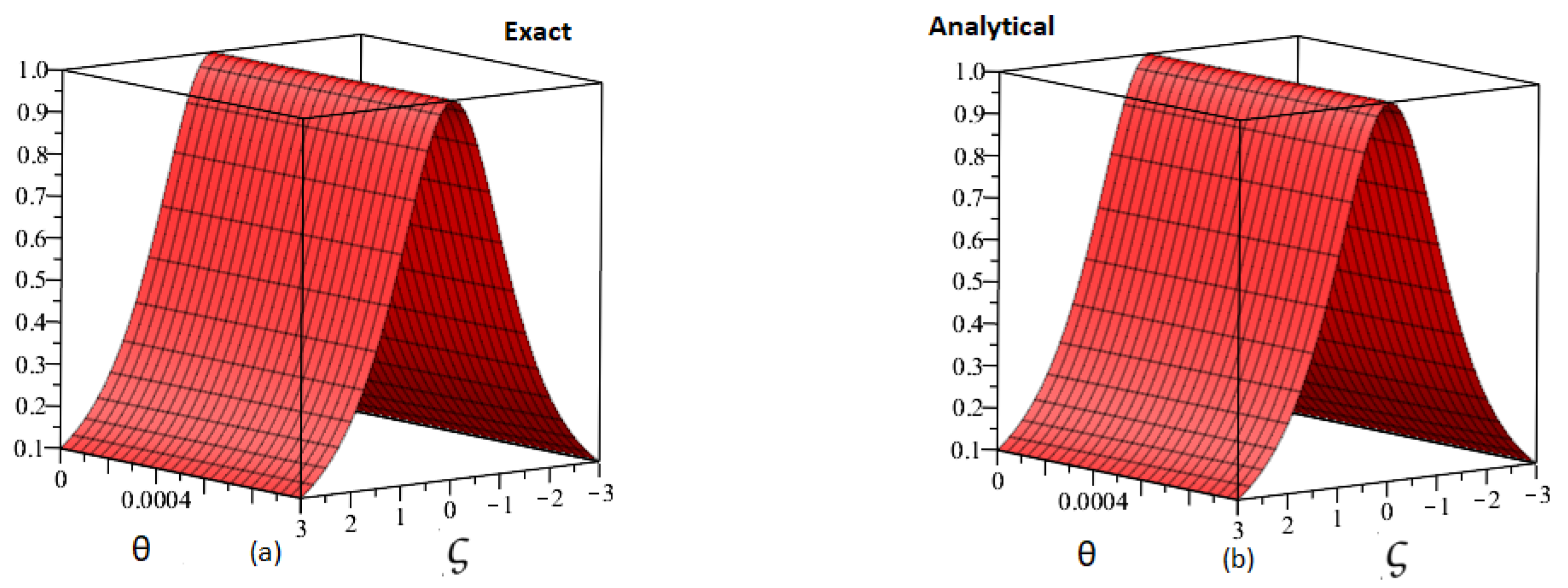
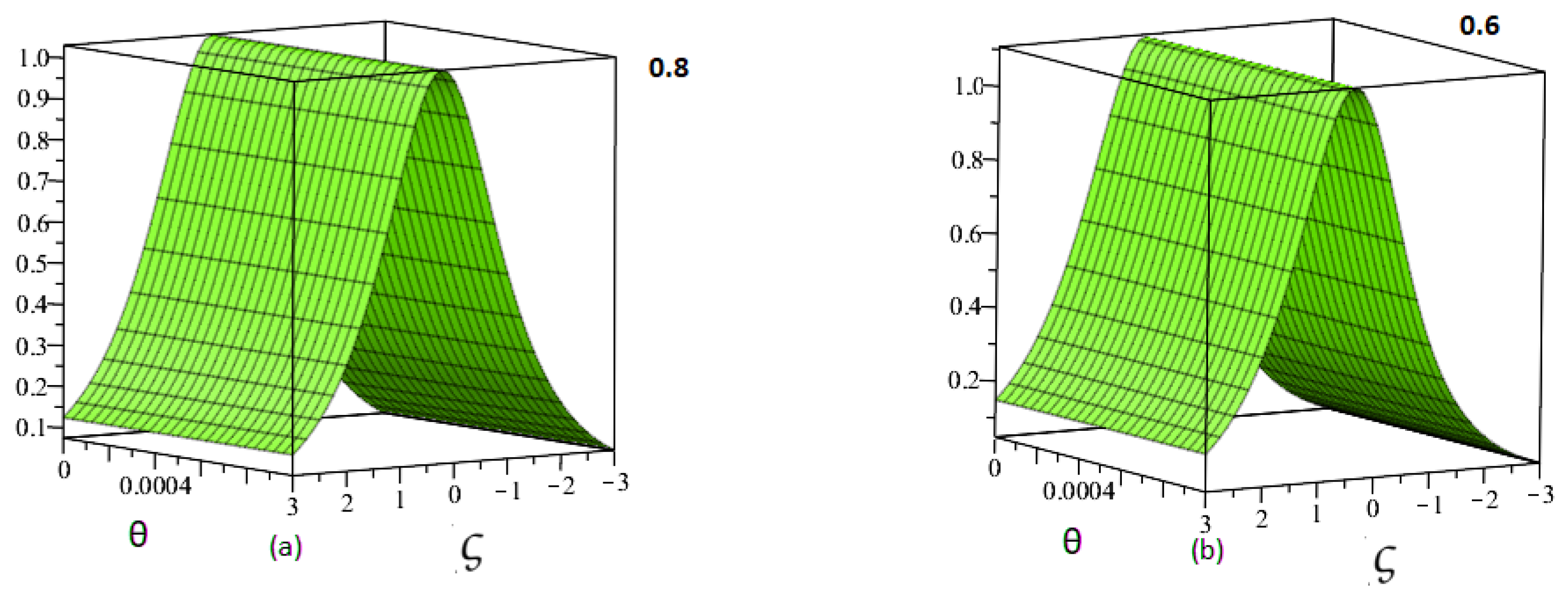
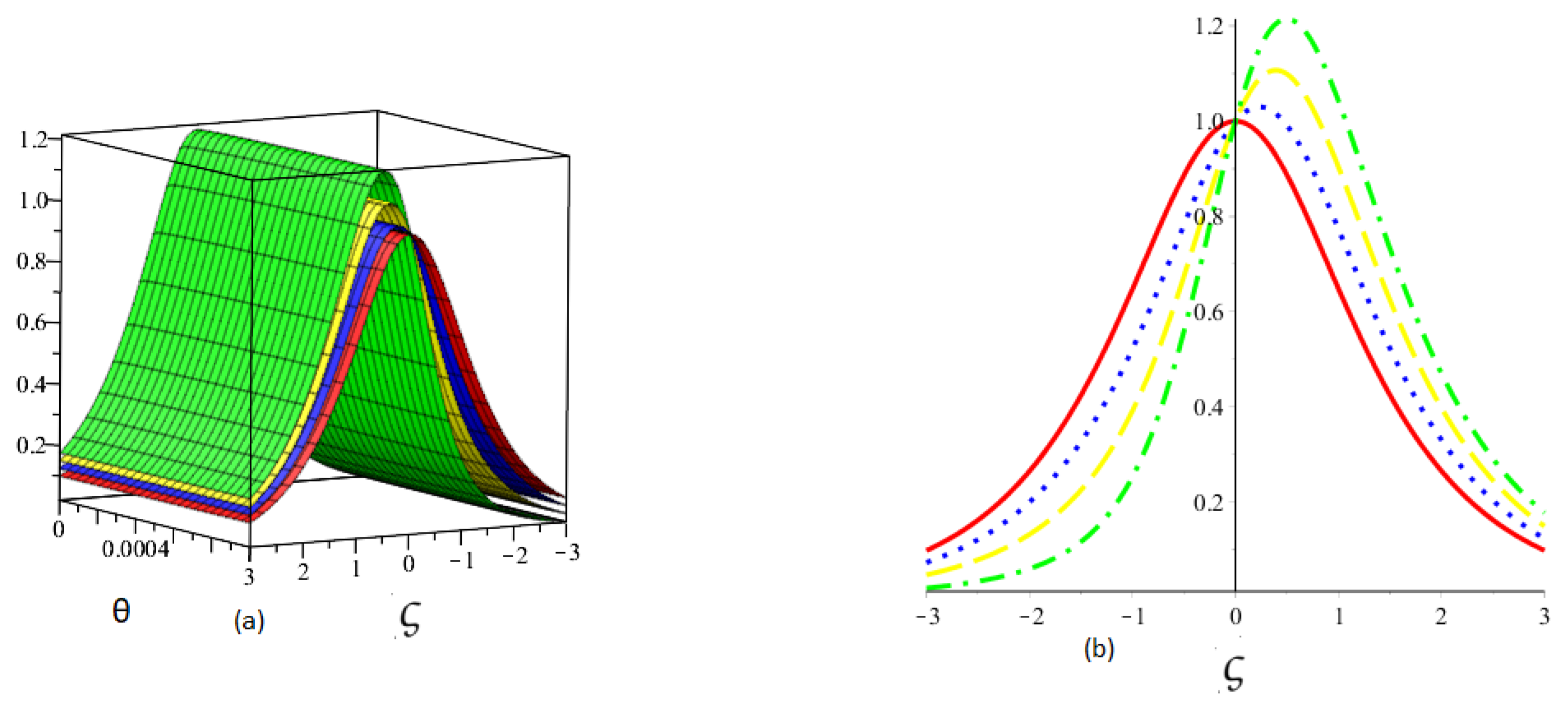
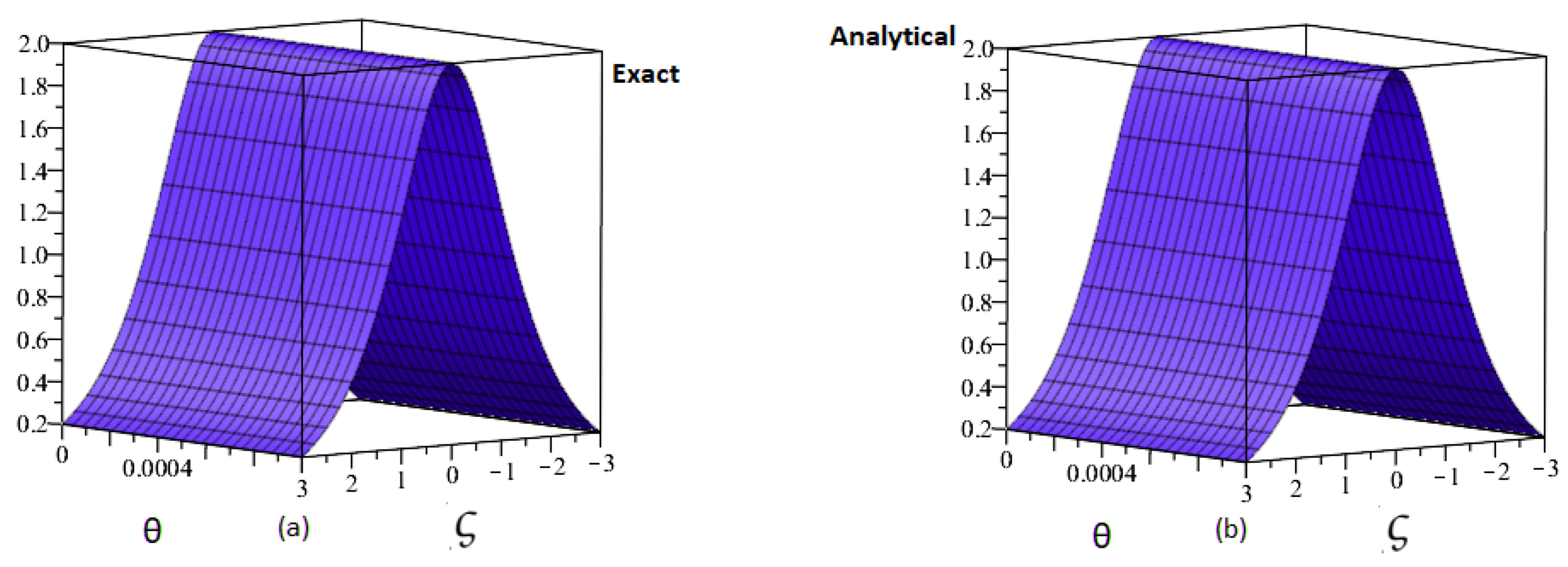
7. Numerical Simulation Studies
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Singh, B.K.; Kumar, P. FRDTM for numerical simulation of multi-dimensional, time-fractional model of Navier-Stokes equation. Ain Shams Eng. J. 2018, 9, 827–834. [Google Scholar] [CrossRef]
- He, J.H. Nonlinear oscillation with fractional derivative and its applications. In Proceedings of the International Conference on Vibrating Engineering, Leuven, Belgium, 16–18 September 1998; Volume 98, pp. 288–291. [Google Scholar]
- Momani, S.; Odibat, Z. Analytical solution of a time-fractional Navier-Stokes equation by Adomian decomposition method. Appl. Math. Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013119. [Google Scholar] [CrossRef]
- Nasrolahpour, H. A note on fractional electrodynamics. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2589–2593. [Google Scholar] [CrossRef]
- Birajdar, G.A. Numerical solution of time fractional Navier-Stokes equation by discrete Adomian decomposition method. Nonlinear Eng. 2014, 3, 21–26. [Google Scholar] [CrossRef]
- Wu, X.; Lai, D.; Lu, H. Generalized synchronization of the fractional-order chaos in weighted complex dynamical networks with nonidentical nodes. Nonlinear Dyn. 2012, 69, 667–683. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D. On the analysis of fractional diabetes model with exponential law. Adv. Differ. Equ. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Chaurasia, V.B.L.; Kumar, D. Solution of the time-fractional Navier-Stokes equation. Gen. Math. Notes 2011, 4, 49–59. [Google Scholar]
- Din, A.; Li, Y.; Khan, F.M.; Khan, Z.U.; Liu, P. On Analysis of fractional order mathematical model of Hepatitis B using Atangana-Baleanu Caputo (ABC) derivative. Fractals 2022, 30, 2240017. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, S.; Farooq, M. A new fractional model for tuberculosis with relapse via Atangana-Baleanu derivative. Chaos Solitons Fractals 2018, 116, 227–238. [Google Scholar] [CrossRef]
- Din, A.; Khan, A.; Zeb, A.; Sidi Ammi, M.R.; Tilioua, M.; Torres, D.F. Hybrid method for simulation of a fractional COVID-19 model with real case application. Axioms 2021, 10, 290. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, S.; Okosun, K.O.; Shah, K. A fractional order pine wilt disease model with Caputo-Fabrizio derivative. Adv. Differ. Equ. 2018, 2018, 1–18. [Google Scholar] [CrossRef]
- Ullah, S.; Altaf Khan, M.; Farooq, M. A new fractional model for the dynamics of the hepatitis B virus using the Caputo-Fabrizio derivative. Eur. Phys. J. Plus 2018, 133, 1–14. [Google Scholar] [CrossRef]
- Xie, Z.; Feng, X.; Chen, X. Partial Least Trimmed Squares Regression. Chemom. Intell. Lab. Syst. 2022, 221, 104486. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Y.; Meng, L.; Chen, X.; Yuan, L.; Cai, Q.; Huang, G. Non-parametric Partial Least Squares-Discriminant Analysis Model Based on Sum of Ranking Difference Algorithm for Tea Grade Identification Using Electronic Tongue Data. Sens. Actuators B Chem. 2020, 311, 127924. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, L.; Yang, L.; Cao, S. Heuristics to Sift Extraneous Factors in Dixon Resultants. J. Symb. Comput. 2022, 112, 105–121. [Google Scholar] [CrossRef]
- Albalawi, W.; El-Tantawy, S.A.; Alkhateeb, Sadah A. The phase shift analysis of the colliding dissipative KdV solitons. J. Ocean. Eng. Sci. 2022, 7, 521–527. [Google Scholar] [CrossRef]
- Douanla, D.V.; Latchio Tiofack, C.G.; Alim, A.; Mohamadou, A.; Alyousef, H.; Ismaeel, S.M.; El-Tantawy, S.A. Dynamics and head-on collisions of multidimensional dust-acoustic shock waves in a self-gravitating magnetized electron depleted dusty plasma. Phys. Fluids 2023, 35, 023103. [Google Scholar] [CrossRef]
- Ali, S.; Shohaib, M.; Masood, W.; Alyousef, H.A.; El-Tantawy, S.A. The attributes of the dust-acoustic solitary and periodic structures in the Saturn’s inner magnetosphere. Phys. Fluids 2023, 35, 023101. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; El-Sherif, L.S.; Bakry, A.M.; Alhejaili, W.; Wazwaz, A.-M. On the analytical approximations to the nonplanar damped Kawahara equation: Cnoidal and solitary waves and their energy. Phys. Fluids 2022, 34, 113103. [Google Scholar] [CrossRef]
- Alharthi, M.R.; Alharbey, R.A.; El-Tantawy, S.A. Novel analytical approximations to the nonplanar Kawahara equation and its plasma applications. Eur. Phys. J. Plus 2022, 37, 1172. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alyousef, H.A.; Alharthi, M.R. Novel approximations to a nonplanar nonlinear Schrödinger equation and modeling nonplanar rogue waves/breathers in a complex plasma. Chaos Solitons Fractals 2022, 163, 112612. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Alharbey, R.A.; Salas Alvaro, H. Novel approximate analytical and numerical cylindrical rogue wave and breathers solutions: An application to electronegative plasma. Chaos Solitons Fractals 2022, 155, 111776. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.; Qiu, T. Fractional Processes and Fractional-Order Signal Processing: Techniques and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Li, X.; Dong, Z.; Wang, L.; Niu, X.; Yamaguchi, H.; Li, D.; Yu, P. A Magnetic Field Coupling Fractional Step Lattice Boltzmann Model for the Complex Interfacial Behavior in Magnetic Multiphase Flows. Appl. Math. Model. 2023, 117, 219–250. [Google Scholar] [CrossRef]
- Longhi, S. Fractional Schrödinger equation in optics. Opt. Lett. 2015, 40, 1117–1120. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022. [Google Scholar] [CrossRef]
- Hilfer, R. Fractional calculus and regular variation in thermodynamics. In Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000; pp. 429–463. [Google Scholar]
- Sun, L.; Hou, J.; Xing, C.; Fang, Z. A Robust Hammerstein-Wiener Model Identification Method for Highly Nonlinear Systems. Processes 2022, 10, 2664. [Google Scholar] [CrossRef]
- Eslami, M.; Fathi Vajargah, B.; Mirzazadeh, M.; Biswas, A. Application of first integral method to fractional partial differential equations. Indian J. Phys. 2014, 88, 177–184. [Google Scholar] [CrossRef]
- Younis, M.; Iftikhar, M. Computational examples of a class of fractional order nonlinear evolution equations using modified extended direct algebraic method. J. Comput. Methods 2015, 15, 359–365. [Google Scholar] [CrossRef]
- Gaber, A.A.; Aljohani, A.F.; Ebaid, A.; Machado, J.T. The generalized Kudryashov method for nonlinear space-time fractional partial differential equations of Burgers type. Nonlinear Dyn. 2019, 95, 361–368. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Liu, K.; Yang, Z.; Wei, W.; Gao, B.; Xin, D.; Sun, C.; Wu, G. Novel Detection Approach for Thermal Defects: Study on Its Feasibility and Application to Vehicle Cables. High Volt. 2022, 1–10. [Google Scholar] [CrossRef]
- El-Wakil, S.A.; Elhanbaly, A.; Abdou, M.A. Adomian decomposition method for solving fractional nonlinear differential equations. Appl. Math. Comput. 2006, 182, 313–324. [Google Scholar] [CrossRef]
- Uddin, M.F.; Hafez, M.G.; Hwang, I.; Park, C. Effect of space fractional parameter on nonlinear ion acoustic shock wave excitation in an unmagnetized relativistic plasma. Front. Phys. 2022, 9, 766. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 19. [Google Scholar] [CrossRef]
- Kashkari, B.S.; El-Tantawy, S.A. Homotopy perturbation method for modeling electrostatic structures in collisional plasmas. Eur. Phys. J. Plus 2021, 136, 121. [Google Scholar] [CrossRef]
- Kashkari, B.S.; El-Tantawy, S.A.; Salas, A.H.; El-Sherif, L.S. Homotopy perturbation method for studying dissipative nonplanar solitons in an electronegative complex plasma. Chaos Solitons Fractals 2020, 130, 109457. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Wang, L.; Ma, Y.; Meng, Z. Haar wavelet method for solving fractional partial differential equations numerically. Appl. Math. Comput. 2014, 227, 66–76. [Google Scholar] [CrossRef]
- Zheng, B.; Wen, C. Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 2008, 21, 194–199. [Google Scholar] [CrossRef]
- Alyobi, S.; Shah, R.; Khan, A.; Shah, N.A.; Nonlaopon, K. Fractional Analysis of Nonlinear Boussinesq Equation under Atangana-Baleanu-Caputo Operator. Symmetry 2022, 14, 2417. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Partial Differential Equations and Solitary Waves Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Masood, W.; Hamid, N.; Ullah, S.; Rahman, A.; Shah, H.A.; Haifa, A.; El-Tantawy, S.A. Formation of acoustic nonlinear structures in non-Maxwellian trapping plasmas. Phys. Fluids 2022, 34, 053113. [Google Scholar] [CrossRef]
- Khattak, M.Y.; Masood, W.; Jahangir, R.; Siddiq, M.; Alyousef, H.A.; El-Tantawy, S.A. Interaction of ion-acoustic solitons for multi-dimensional Zakharov Kuznetsov equation in Van Allen radiation belts. Chaos Solitons Fractals 2022, 161, 112265. [Google Scholar] [CrossRef]
- Douanla1, D.V.; Tiofack, C.G.L.; Alim1, A.M.; Mohamadou, A.; Albalawi, W.; El-Tantawy, S.A.; El-Sherif, L.S. Three-dimensional rogue waves and dust-acoustic dark soliton collisions in degenerate ultradense magnetoplasma in the presence of dust pressure anisotropy. Phys. Fluids 2022, 34, 087105. [Google Scholar] [CrossRef]
- Shohaib, M.; Masood, W.; Siddiq, M.; Alyousef, H.A.; El-Tantawy, S.A. Formation of electrostatic solitary and periodic waves in dusty plasmas in the light of Voyager 1 and 2 spacecraft and Freja satellite observations, Journal of Low Frequency Noise. Vib. Act. Control 2022, 41, 896–909. [Google Scholar]
- Shohaib, M.; Masood, W.; Alyousef, H.A.; Siddiq, M.; El-Tantawy, S.A. Formation and interaction of multi-dimensional electrostatic ion-acoustic solitons in two-electron temperature plasmas. Phys. Fluids 2022, 34, 093107. [Google Scholar] [CrossRef]
- Gürses, M.; Pekcan, A. Nonlocal modified KdV equations and their soliton solutions by Hirota method. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 427–448. [Google Scholar] [CrossRef]
- Alquran, M. Optical bidirectional wave-solutions to new two-mode extension of the coupled KdV-Schrodinger equations. Opt. Quantum Electron. 2021, 53, 588. [Google Scholar] [CrossRef]
- Liu, Z.J.; Adamu, M.Y.; Suleiman, E.; He, J.H. Hybridization of homotopy perturbation method and Laplace transformation for the partial differential equations. Therm. Sci. 2017, 21, 1843–1846. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Fang, J.; Nadeem, M.; Habib, M.; Karim, S.; Wahash, H.A. A New Iterative Method for the Approximate Solution of Klein-Gordon and Sine-Gordon Equations. J. Funct. Spaces 2022, 2022, 9. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. Aims. Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Ghorbani, A. Beyond Adomian polynomials: He polynomials. Chaos Solitons Fractals 2009, 39, 1486–1492. [Google Scholar] [CrossRef]
- Singh, P.; Sharma, D. Convergence and error analysis of series solution of nonlinear partial differential equation. Nonlinear Eng. 2018, 7, 303–308. [Google Scholar] [CrossRef]
- Kumar, M. Numerical solution of singular boundary value problems using advanced Adomian decomposition method. Eng. Comput. 2021, 37, 2853–2863. [Google Scholar]

| (Approx) | (Exact) | |||||
|---|---|---|---|---|---|---|
| 0.2 | 0.986366 | 0.984417 | 0.982469 | 0.980521 | 0.980521 | |
| 0.4 | 0.935975 | 0.932435 | 0.928896 | 0.925358 | 0.925358 | |
| 0.01 | 0.6 | 0.857688 | 0.853125 | 0.848563 | 0.844003 | 0.844003 |
| 0.8 | 0.763194 | 0.758193 | 0.753193 | 0.748196 | 0.748196 | |
| 1 | 0.663457 | 0.658485 | 0.653515 | 0.648547 | 0.648547 | |
| 0.2 | 0.986590 | 0.984630 | 0.982672 | 0.980713 | 0.980713 | |
| 0.4 | 0.936382 | 0.932823 | 0.929265 | 0.925709 | 0.925709 | |
| 0.02 | 0.6 | 0.858213 | 0.853625 | 0.849039 | 0.844456 | 0.844456 |
| 0.8 | 0.763770 | 0.758741 | 0.753715 | 0.748692 | 0.748692 | |
| 1 | 0.664029 | 0.659029 | 0.654034 | 0.649041 | 0.649041 | |
| 0.2 | 0.986811 | 0.984842 | 0.982874 | 0.980904 | 0.980904 | |
| 0.4 | 0.936783 | 0.933206 | 0.929632 | 0.926058 | 0.926058 | |
| 0.03 | 0.6 | 0.858730 | 0.854119 | 0.849512 | 0.844908 | 0.844908 |
| 0.8 | 0.764336 | 0.759283 | 0.754234 | 0.749189 | 0.749189 | |
| 1 | 0.664591 | 0.659568 | 0.654549 | 0.649535 | 0.649535 | |
| 0.2 | 0.987029 | 0.985051 | 0.983076 | 0.981094 | 0.981094 | |
| 0.4 | 0.937180 | 0.985051 | 0.929998 | 0.926407 | 0.926407 | |
| 0.04 | 0.6 | 0.859241 | 0.854611 | 0.849984 | 0.845359 | 0.845359 |
| 0.8 | 0.764896 | 0.759821 | 0.754751 | 0.749685 | 0.749685 | |
| 1 | 0.665149 | 0.660104 | 0.655063 | 0.650029 | 0.650029 | |
| 0.2 | 0.987246 | 0.985260 | 0.983277 | 0.981284 | 0.981284 | |
| 0.4 | 0.937574 | 0.933967 | 0.930364 | 0.926756 | 0.926756 | |
| 0.05 | 0.6 | 0.859749 | 0.855099 | 0.850455 | 0.845811 | 0.845811 |
| 0.8 | 0.765453 | 0.760357 | 0.755267 | 0.750181 | 0.750181 | |
| 1 | 0.665702 | 0.660636 | 0.655576 | 0.650523 | 0.650523 |
| (Approx) | (Exact) | |||||
|---|---|---|---|---|---|---|
| 0.2 | 2.110317 | 2.039013 | 1.974863 | 1.967541 | 1.967541 | |
| 0.4 | 2.093671 | 1.977584 | 1.873145 | 1.861473 | 1.861473 | |
| 0.01 | 0.6 | 1.951520 | 1.825541 | 1.712203 | 1.699649 | 1.699649 |
| 0.8 | 1.727575 | 1.616957 | 1.517440 | 1.506470 | 1.506470 | |
| 1 | 1.474678 | 1.389601 | 1.313060 | 1.304643 | 1.304643 | |
| 0.2 | 2.118130 | 2.046452 | 1.981980 | 1.974024 | 1.974024 | |
| 0.4 | 2.106391 | 1.989695 | 1.884731 | 1.872782 | 1.872782 | |
| 0.02 | 0.6 | 1.965324 | 1.838684 | 1.724776 | 1.712267 | 1.712267 |
| 0.8 | 1.739696 | 1.628498 | 1.528480 | 1.517709 | 1.517709 | |
| 1 | 1.484001 | 1.398477 | 1.321551 | 1.313350 | 1.313350 | |
| 0.2 | 2.125862 | 2.053852 | 1.989092 | 1.980094 | 1.980094 | |
| 0.4 | 2.118979 | 2.001743 | 1.896311 | 1.883925 | 1.883925 | |
| 0.03 | 0.6 | 1.978985 | 1.851759 | 1.737343 | 1.724946 | 1.724946 |
| 0.8 | 1.751690 | 1.639979 | 1.539514 | 1.529116 | 1.529116 | |
| 1 | 1.493226 | 1.407307 | 1.330038 | 1.322232 | 1.322232 | |
| 0.2 | 2.133542 | 2.061228 | 1.996203 | 1.985736 | 1.985736 | |
| 0.4 | 2.131482 | 2.013751 | 1.907887 | 1.894886 | 1.894886 | |
| 0.04 | 0.6 | 1.992553 | 1.864790 | 1.749905 | 1.737675 | 1.737675 |
| 0.8 | 1.763604 | 1.651421 | 1.550545 | 1.540690 | 1.540690 | |
| 1 | 1.502389 | 1.416107 | 1.338522 | 1.331291 | 1.331291 | |
| 0.2 | 2.141182 | 2.068584 | 2.003311 | 1.990940 | 1.990940 | |
| 0.4 | 2.143921 | 2.025728 | 1.919460 | 1.905650 | 1.905650 | |
| 0.05 | 0.6 | 2.006053 | 1.877788 | 1.762464 | 1.750447 | 1.750447 |
| 0.8 | 1.775457 | 1.662833 | 1.561573 | 1.552427 | 1.552427 | |
| 1 | 1.511506 | 1.424885 | 1.347003 | 1.340528 | 1.340528 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alyousef, H.A.; Shah, R.; Shah, N.A.; Chung, J.D.; Ismaeel, S.M.E.; El-Tantawy, S.A. The Fractional Analysis of a Nonlinear mKdV Equation with Caputo Operator. Fractal Fract. 2023, 7, 259. https://doi.org/10.3390/fractalfract7030259
Alyousef HA, Shah R, Shah NA, Chung JD, Ismaeel SME, El-Tantawy SA. The Fractional Analysis of a Nonlinear mKdV Equation with Caputo Operator. Fractal and Fractional. 2023; 7(3):259. https://doi.org/10.3390/fractalfract7030259
Chicago/Turabian StyleAlyousef, Haifa A., Rasool Shah, Nehad Ali Shah, Jae Dong Chung, Sherif M. E. Ismaeel, and Samir A. El-Tantawy. 2023. "The Fractional Analysis of a Nonlinear mKdV Equation with Caputo Operator" Fractal and Fractional 7, no. 3: 259. https://doi.org/10.3390/fractalfract7030259
APA StyleAlyousef, H. A., Shah, R., Shah, N. A., Chung, J. D., Ismaeel, S. M. E., & El-Tantawy, S. A. (2023). The Fractional Analysis of a Nonlinear mKdV Equation with Caputo Operator. Fractal and Fractional, 7(3), 259. https://doi.org/10.3390/fractalfract7030259







