Implementation of Analytical Techniques for the Solution of Nonlinear Fractional Order Sawada–Kotera–Ito Equation
Abstract
1. Introduction
2. Basic Concept
3. Fundamental Concept of HPTM
4. Fundamental Concept of YTDM
5. Application
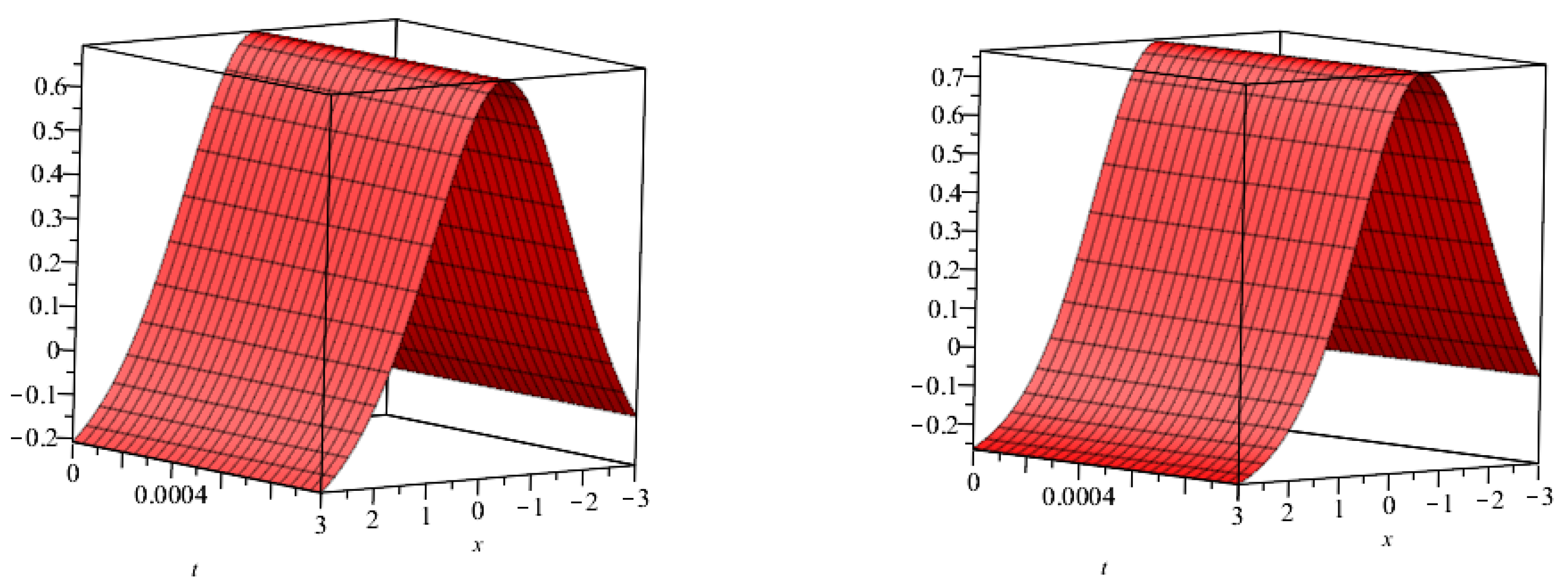
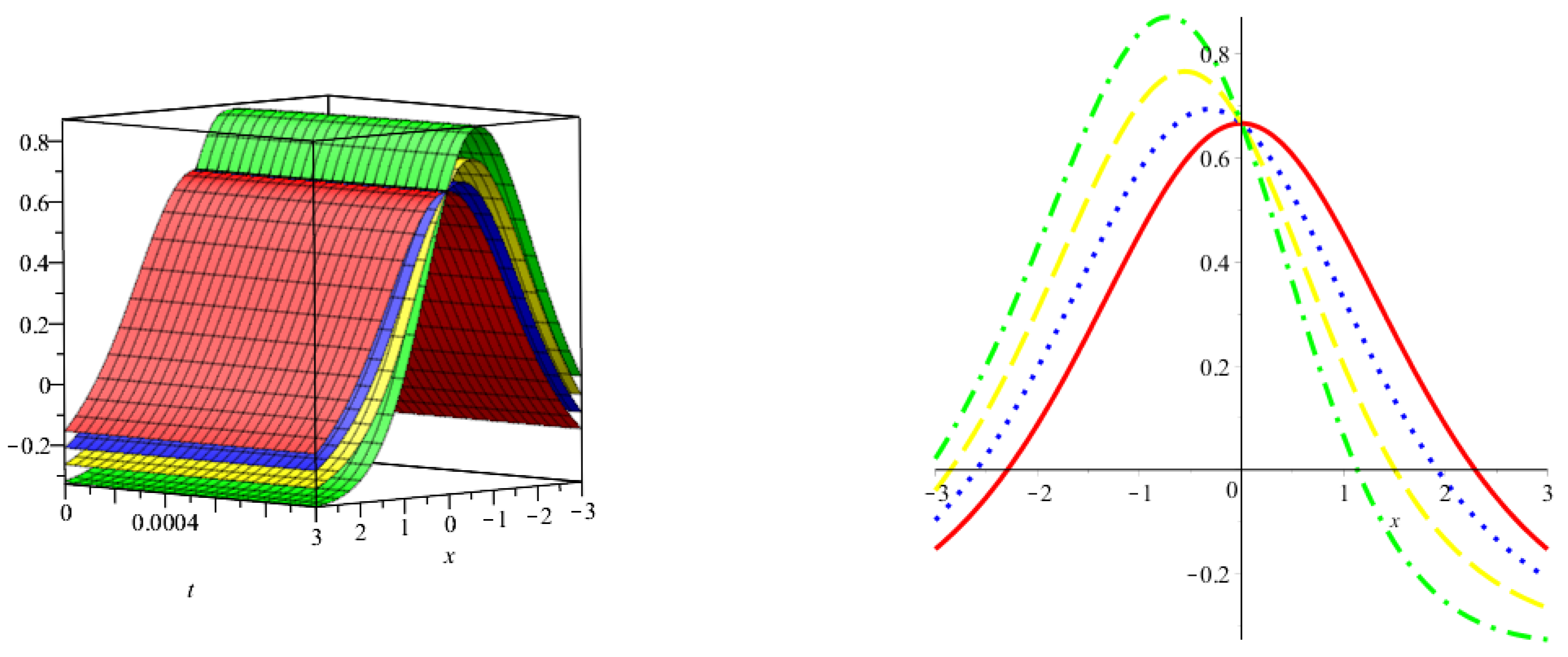
5.1. Example
- Case I: Implementation of HPTM
- Case II: Implementation of YTDM
5.2. Numerical Simulation Studies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riemann, G.F.B. Versuch einer allgemeinen Auffassung der integration und differentiation. In Gesammelte Mathematische Werke; Druck: Leipzig, Germany, 1896. [Google Scholar]
- Caputo, M. Elasticità e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Li, Y.; Liu, F.; Turner, I.W.; Li, T. Time-fractional diffusion equation for signal smoothing. Appl Math Comput. 2018, 326, 108–116. [Google Scholar] [CrossRef]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef]
- Bulut, H.; Sulaiman, T.A.; Baskonus, H.M.; Rezazadeh, H.; Eslami, M.; Mirzazadeh, M. Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation. Optik 2018, 172, 20–27. [Google Scholar] [CrossRef]
- Liu, D.Y.; Gibaru, O.; Perruquetti, W.; Laleg-Kirati, T.M. Fractional order differentiation by integration and error analysis in noisy environment. IEEE Trans. Autom. Control. 2015, 60, 2945–2960. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 2000. [Google Scholar]
- Laroche, E.; Knittel, D. An improved linear fractional model for robustness analysis of a winding system. Control. Eng. Pract. 2005, 13, 659–666. [Google Scholar] [CrossRef]
- Monje, C.; Vinagre, B.; Feliu, V.; Chen, Y. Tuning and auto tuning of fractional order controllers for industry applications. Control. Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef]
- Sabatier, J.; Aoun, M.; Oustaloup, A.; Grgoire, G.; Ragot, F.; Roy, P. Fractional system identification for lead acid battery state of charge estimation. Signal Process. 2006, 86, 2645–2657. [Google Scholar] [CrossRef]
- Vinagre, B.; Monje, C.; Calderon, A.; Suarej, J. Fractional PID controllers for industry application: A brief introduction. J. Vib. Control. 2007, 13, 1419–1430. [Google Scholar] [CrossRef]
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Younis, M.; Iftikhar, M. Computational examples of a class of fractional order nonlinear evolution equations using modified extended direct algebraic method. J. Comput. Methods 2015, 15, 359–365. [Google Scholar] [CrossRef]
- Eslami, M.; Fathi Vajargah, B.; Mirzazadeh, M.; Biswas, A. Application of first integral method to fractional partial differential equations. Indian J. Phys. 2014, 88, 177–184. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Gaber, A.A.; Aljohani, A.F.; Ebaid, A.; Machado, J.T. The generalized Kudryashov method for nonlinear space-time fractional partial differential equations of Burgers type. Nonlinear Dyn. 2019, 95, 361–368. [Google Scholar] [CrossRef]
- El-Wakil, S.A.; Elhanbaly, A.; Abdou, M.A. Adomian decomposition method for solving fractional nonlinear differential equations. Appl. Math. Comput. 2006, 182, 13–324. [Google Scholar] [CrossRef]
- Sarwar, S.; Alkhalaf, S.; Iqbal, S.; Zahid, M.A. A note on optimal homotopy asymptotic method for the solutions of fractional order heat-and wave-like partial differential equations. Comput. Math. Appl. 2015, 70, 942–953. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Uddin, M.F.; Hafez, M.G.; Hwang, I.; Park, C. Effect of Space Fractional Parameter on Nonlinear Ion Acoustic Shock Wave Excitation in an Unmagnetized Relativistic Plasma. Front. Phys. 2022, 9, 766. [Google Scholar] [CrossRef]
- Wang, L.; Ma, Y.; Meng, Z. Haar wavelet method for solving fractional partial differential equations numerically. Appl. Math. Comput. 2014, 227, 66–76. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 2008, 21, 194–199. [Google Scholar] [CrossRef]
- Zheng, B.; Wen, C. Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Alyobi, S.; Shah, R.; Khan, A.; Shah, N.A.; Nonlaopon, K. Fractional Analysis of Nonlinear Boussinesq Equation under Atangana-Baleanu-Caputo Operator. Symmetry 2022, 14, 2417. [Google Scholar] [CrossRef]
- Pomeau, Y.; Ramani, A.; Grammaticos, B. Structural stability of the Korteweg-de Vries solitons under a singular perturbation. Phys. D 1988, 31, 27–134. [Google Scholar] [CrossRef]
- Arora, R.; Sharma, H. Application of HAM to seventh order KdV equations. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 131–138. [Google Scholar] [CrossRef]
- El-Sayed, S.M.; Kaya, D. An application of the ADM to seven-order Sawada-Kotara equations. Appl. Math. Comput. 2004, 157, 93–101. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Jena, S.K.; Sedighi, H.M. On the wave solutions of time-fractional Sawada-Kotera-Ito equation arising in shallow water. Math. Methods Appl Sci. 2021, 44, 583–592. [Google Scholar] [CrossRef]
- Akinyemi, L. q-Homotopy analysis method for solving the seventh-order time-fractional Lax’s Korteweg-de Vries and Sawada-Kotera equations. Comput. Appl. Math. 2019, 38, 191. [Google Scholar] [CrossRef]
- Yaşar, E.; Yildirim, Y.; Khalique, C.M. Lie symmetry analysis, conservation laws and exact solutions of the seventh-order time fractional Sawada-Kotera-Ito equation. Results Phys. 2016, 6, 322–328. [Google Scholar] [CrossRef]
- Al-Shawba, A.A.; Gepreel, K.A.; Abdullah, F.A.; Azmi, A. Abundant closed form solutions of the conformable time fractional Sawada-Kotera-Ito equation using (G’/G)-expansion method. Results Phys. 2018, 9, 337–343. [Google Scholar] [CrossRef]
- Guner, O. New exact solutions for the seventh-order time fractional Sawada-Kotera-Ito equation via various methods. Waves Random Complex Media 2020, 30, 441–457. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local fractional laplace transform and applications. In Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2016; p. 147178. [Google Scholar]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. Aims Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of homotopy technique and perturbation technique for nonlinear problems. Int. J.-Non-Linear Mech. 2003, 35, 743. [Google Scholar]
- Ghorbani, A. Beyond adomian’s polynomials: He polynomials. Chaos Solitons Fractals 2009, 39, 1486–1492. [Google Scholar] [CrossRef]
- Adomian, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]


| x | (Approx) | (Exact) | ||||
|---|---|---|---|---|---|---|
| 0.01 | 0.2 | 0.323702 | 0.323892 | 0.324081 | 0.324269 | 0.324269 |
| 0.4 | 0.316067 | 0.316439 | 0.316809 | 0.317179 | 0.317179 | |
| 0.6 | 0.304051 | 0.304591 | 0.305129 | 0.305666 | 0.305666 | |
| 0.8 | 0.288099 | 0.288788 | 0.289474 | 0.290159 | 0.290159 | |
| 1 | 0.268775 | 0.269588 | 0.270399 | 0.271207 | 0.271207 | |
| 0.02 | 0.2 | 0.323695 | 0.323886 | 0.324076 | 0.324265 | 0.324265 |
| 0.4 | 0.316052 | 0.316427 | 0.316800 | 0.317172 | 0.317172 | |
| 0.6 | 0.304029 | 0.304574 | 0.305116 | 0.305656 | 0.305656 | |
| 0.8 | 0.288072 | 0.288766 | 0.289457 | 0.290145 | 0.290145 | |
| 1 | 0.268742 | 0.269562 | 0.270378 | 0.271191 | 0.271191 | |
| 0.03 | 0.2 | 0.323688 | 0.323880 | 0.324071 | 0.324262 | 0.324262 |
| 0.4 | 0.316038 | 0.316416 | 0.316791 | 0.317164 | 0.317164 | |
| 0.6 | 0.304009 | 0.304558 | 0.305103 | 0.305645 | 0.305645 | |
| 0.8 | 0.288046 | 0.288745 | 0.289440 | 0.290132 | 0.290132 | |
| 1 | 0.268712 | 0.269538 | 0.270358 | 0.271175 | 0.271175 | |
| 0.04 | 0.2 | 0.323681 | 0.323874 | 0.324067 | 0.324258 | 0.324258 |
| 0.4 | 0.316025 | 0.316405 | 0.316782 | 0.317157 | 0.317157 | |
| 0.6 | 0.303990 | 0.304542 | 0.305090 | 0.305634 | 0.305634 | |
| 0.8 | 0.288022 | 0.288725 | 0.289423 | 0.290118 | 0.290118 | |
| 1 | 0.268684 | 0.269514 | 0.270339 | 0.271159 | 0.271159 | |
| 0.05 | 0.2 | 0.323674 | 0.323869 | 0.324062 | 0.324254 | 0.324254 |
| 0.4 | 0.316012 | 0.316394 | 0.316773 | 0.317150 | 0.317150 | |
| 0.6 | 0.303972 | 0.304526 | 0.305077 | 0.305624 | 0.305624 | |
| 0.8 | 0.287999 | 0.288705 | 0.289407 | 0.290104 | 0.290104 | |
| 1 | 0.268656 | 0.269491 | 0.270319 | 0.271143 | 0.271143 |
| x | ||||||
|---|---|---|---|---|---|---|
| 0.01 | 0.2 | 5.6701120000 | 3.7742650000 | 1.8847270000 | 1.4000000000 | 1.4000000000 |
| 0.4 | 1.1121106000 | 7.4026790000 | 3.6966280000 | 1.4000000000 | 1.4000000000 | |
| 0.6 | 1.6151616000 | 1.0751203000 | 5.3687630000 | 1.2000000000 | 1.2000000000 | |
| 0.8 | 2.0593399000 | 1.3707844000 | 6.8452050000 | 1.1000000000 | 1.1000000000 | |
| 1 | 2.4322300000 | 1.6189960000 | 8.0846870000 | 1.0000000000 | 1.0000000000 | |
| 0.02 | 0.2 | 5.7087240000 | 3.7973100000 | 1.8950170000 | 5.7000000000 | 5.7000000000 |
| 0.4 | 1.1196883000 | 7.4479250000 | 3.7168560000 | 5.5000000000 | 5.5000000000 | |
| 0.6 | 1.6261692000 | 1.0816936000 | 5.3981620000 | 4.9000000000 | 4.9000000000 | |
| 0.8 | 2.0733762000 | 1.3791670000 | 6.8827050000 | 4.2000000000 | 4.200000000 | |
| 1 | 2.4488091000 | 1.6288977000 | 8.1289880000 | 3.5000000000 | 3.5000000000 | |
| 0.03 | 0.2 | 5.7415440000 | 3.8172350000 | 1.9040430000 | 1.3000000000 | 1.3000000000 |
| 0.4 | 1.1261329000 | 7.4870780000 | 3.7346340000 | 1.2300000000 | 1.2300000000 | |
| 0.6 | 1.6355328000 | 1.0873838000 | 5.4240200000 | 1.1000000000 | 1.1000000000 | |
| 0.8 | 2.0853172000 | 1.3864244000 | 6.9156990000 | 9.6000000000 | 9.6000000000 | |
| 1 | 2.4629143000 | 1.6374712000 | 8.1679760000 | 7.8000000000 | 7.8000000000 | |
| 0.04 | 0.2 | 5.7708370000 | 3.8352100000 | 1.9122570000 | 2.3200000000 | 2.3200000000 |
| 0.4 | 1.1318886000 | 7.5224370000 | 3.7508470000 | 2.1900000000 | 2.1900000000 | |
| 0.6 | 1.6438970000 | 1.0925244000 | 5.4476190000 | 1.9700000000 | 1.9700000000 | |
| 0.8 | 2.0959854000 | 1.3929824000 | 6.9458240000 | 1.7000000000 | 1.7000000000 | |
| 1 | 2.4755170000 | 1.6452195000 | 8.2035840000 | 1.3800000000 | 1.3800000000 | |
| 0.05 | 0.2 | 5.7976140000 | 3.8517720000 | 1.9198680000 | 3.6100000000 | 3.6100000000 |
| 0.4 | 1.1371537000 | 7.5550530000 | 3.7659070000 | 3.4100000000 | 3.4100000000 | |
| 0.6 | 1.6515506000 | 1.0972681000 | 5.4695580000 | 3.0800000000 | 3.0800000000 | |
| 0.8 | 2.1057483000 | 1.3990351000 | 6.9738420000 | 2.6500000000 | 2.6500000000 | |
| 1 | 2.4870511000 | 1.6523716000 | 8.2367100000 | 2.1700000000 | 2.1700000000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, R.; Mofarreh, F.; Tag, E.M.; Ghamry, N.A. Implementation of Analytical Techniques for the Solution of Nonlinear Fractional Order Sawada–Kotera–Ito Equation. Fractal Fract. 2023, 7, 299. https://doi.org/10.3390/fractalfract7040299
Shah R, Mofarreh F, Tag EM, Ghamry NA. Implementation of Analytical Techniques for the Solution of Nonlinear Fractional Order Sawada–Kotera–Ito Equation. Fractal and Fractional. 2023; 7(4):299. https://doi.org/10.3390/fractalfract7040299
Chicago/Turabian StyleShah, Rasool, Fatemah Mofarreh, ElSayed M. Tag, and Nivin A. Ghamry. 2023. "Implementation of Analytical Techniques for the Solution of Nonlinear Fractional Order Sawada–Kotera–Ito Equation" Fractal and Fractional 7, no. 4: 299. https://doi.org/10.3390/fractalfract7040299
APA StyleShah, R., Mofarreh, F., Tag, E. M., & Ghamry, N. A. (2023). Implementation of Analytical Techniques for the Solution of Nonlinear Fractional Order Sawada–Kotera–Ito Equation. Fractal and Fractional, 7(4), 299. https://doi.org/10.3390/fractalfract7040299






