Dynamical Analysis of Generalized Tumor Model with Caputo Fractional-Order Derivative
Abstract
1. Introduction
2. Advantages of Fractional Epidemic Models
- Improved accuracy: Fractional calculus allows for more accurate modeling of complex systems that cannot be easily described by traditional integer-order differential equations. This leads to more accurate predictions of disease dynamics and better decision making in public health;
- Flexibility: Fractional models can be adapted to fit a variety of data sets, including nonlinear and non-stationary data. This allows for a more flexible and adaptable approach to modeling infectious disease spread;
- Early detection: Fractional models can help detect disease outbreaks earlier than traditional models, which rely on historical data. This allows for more rapid implementation of control measures and containment strategies;
- Capturing long-term memory: Fractional models can account for long-term memory effects, such as the influence of previous outbreaks or social interactions, that may affect the spread of disease. This can lead to a more accurate description of disease dynamics and better prediction of future outbreaks;
- Improving public health policies: Fractional models can be used to evaluate the effectiveness of different public health policies and interventions, such as vaccination programs or social distancing measures. This allows policymakers to make informed decisions based on data and modeling results.
3. Why Caputo Operator?
- By simply replacing with , Re, the famous Riemann–Liouville integral formula is derived from the Cauchy formula for repeated integration; this fractional integral formula is now the foundation for the development of various numerical methods used to solve fractional ordinary and partial differential equations;
- Caputo’s version of classical epidemiological models has been successfully applied in recent works [27,28,29,30], coupled with specifics for the presence of a unique solution and stability analysis. There, numerical simulations were used to show why the Caputo variant is better than the traditional one;
- Recent publications in the field of epidemiology show that traditional models were not able to accurately capture the complicated and chaotic dynamics of the spread of infections. Instead, real data about the epidemic, mostly from reliable sources such as the World Health Organization and empirically published papers, were used to verify and confirm the Caputo versions;
- Furthermore, when we use Caputo’s differential operator to examine the disease’s behavior under different biological parameter values, we obtain a clear picture of the basic reproductive number, which explains the average number of secondary infections produced when an infectious individual enters a completely susceptible class. Consider, for instance, [31,32] and the majority of the references therein.
4. Preliminaries
- 1
- The equilibrium point is locally asymptotically stable if and only if all eigenvalues , of Jacobian matrix satisfy ;
- 2
- The equilibrium point is stable if and only if all eigenvalues , of jacobian matrix satisfy and eigenvalues with = have same algebraic and geometric multiplicity;
- 3
- The equilibrium point is unstable if and only if there exist eigenvalues , for some of Jacobian matrix such that .
5. Existence and Uniqueness of Solutions of Caputo System
- 1.
- , . Where , , and are positive constants;
- 2.
- satisfies the system (4).
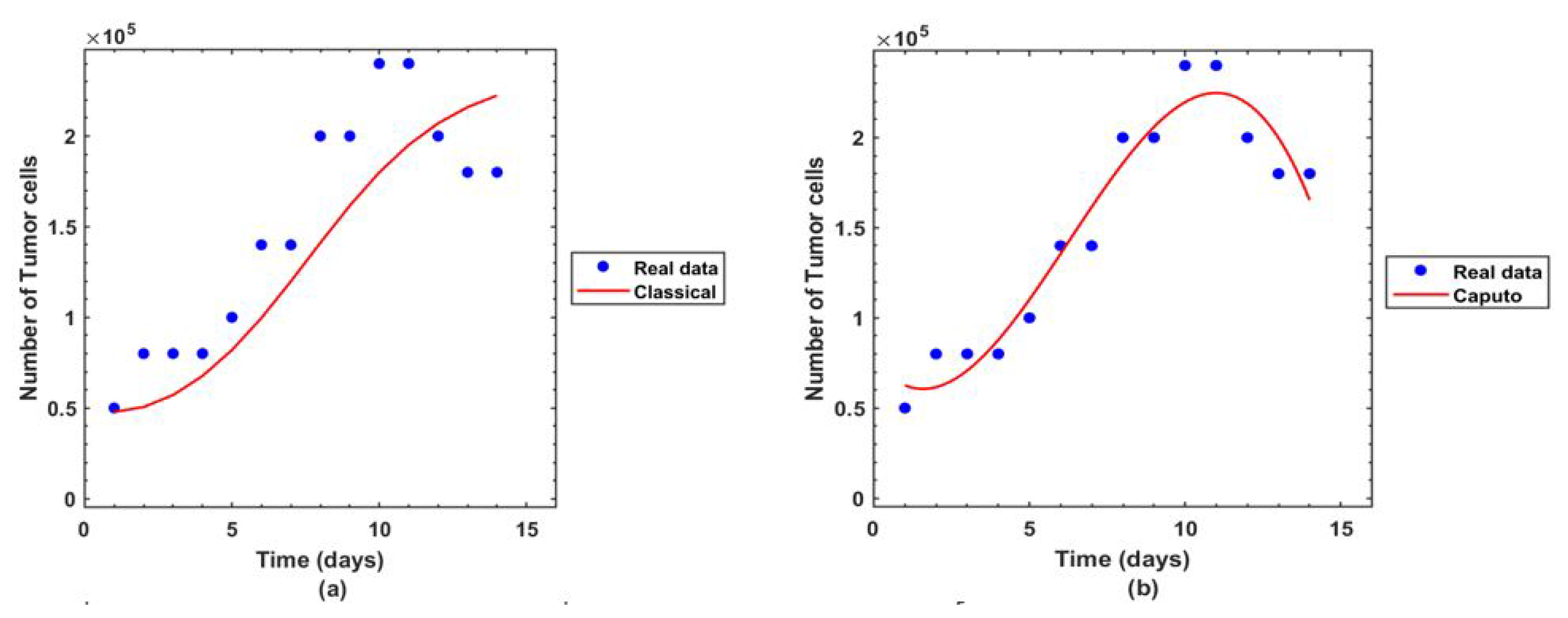
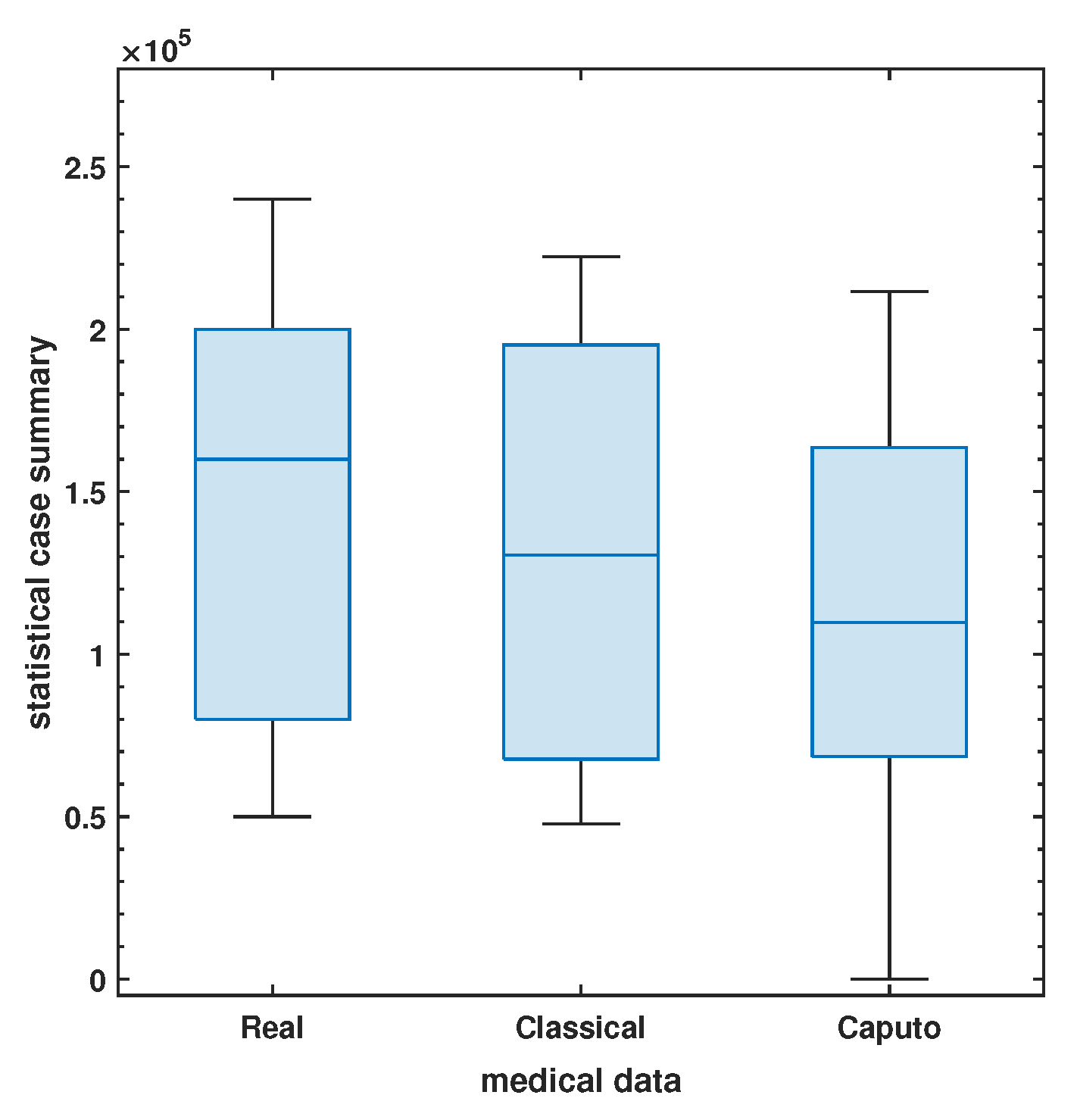
6. Fitting of Biological Parameters with Real Medical Data
7. Dynamical Analysis of Caputo System
7.1. Equilibria of the Caputo System
- i
- , the trivial equilibrium point;
- ii
- , the tumor-dominant equilibrium point;
- iii
- , the positive interior equilibrium point.
7.2. Linearization of Caputo System
7.3. Stability Analysis of Caputo System
- 1.
- and , , ;
- 2.
- and , , , ;
- 3.
- , , , and .
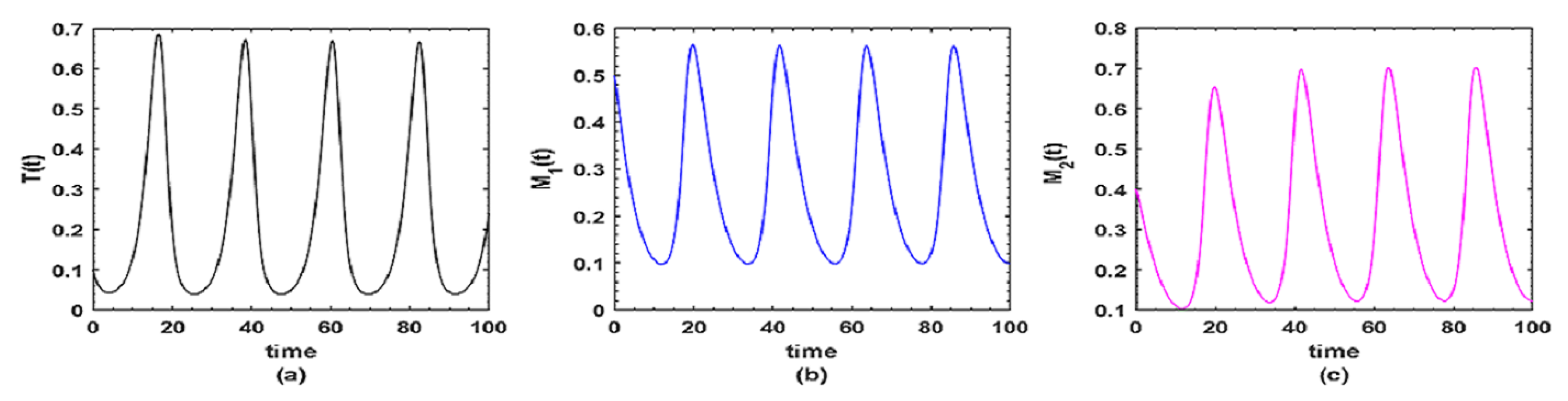
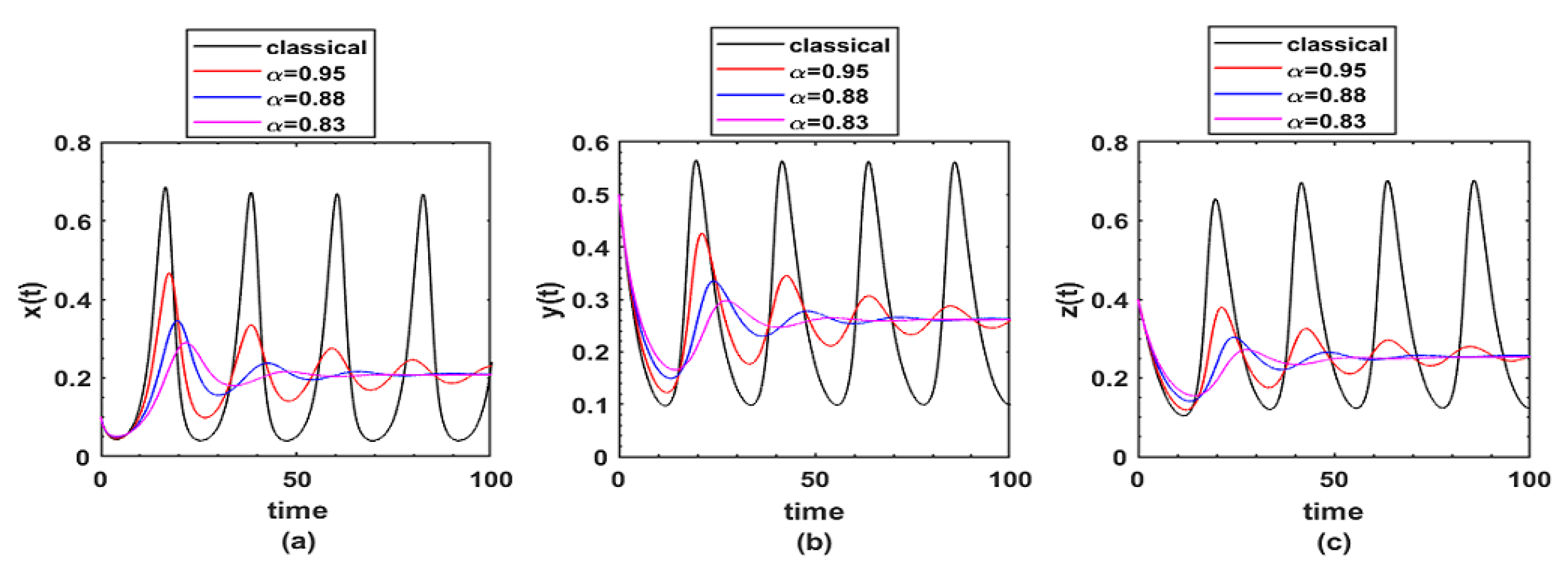
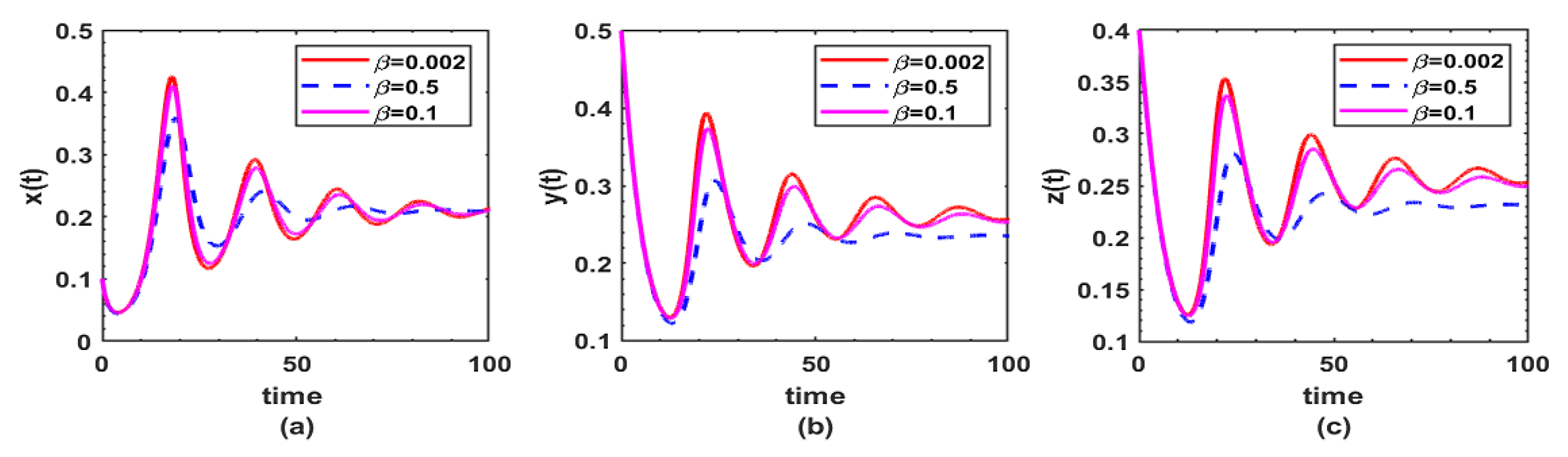
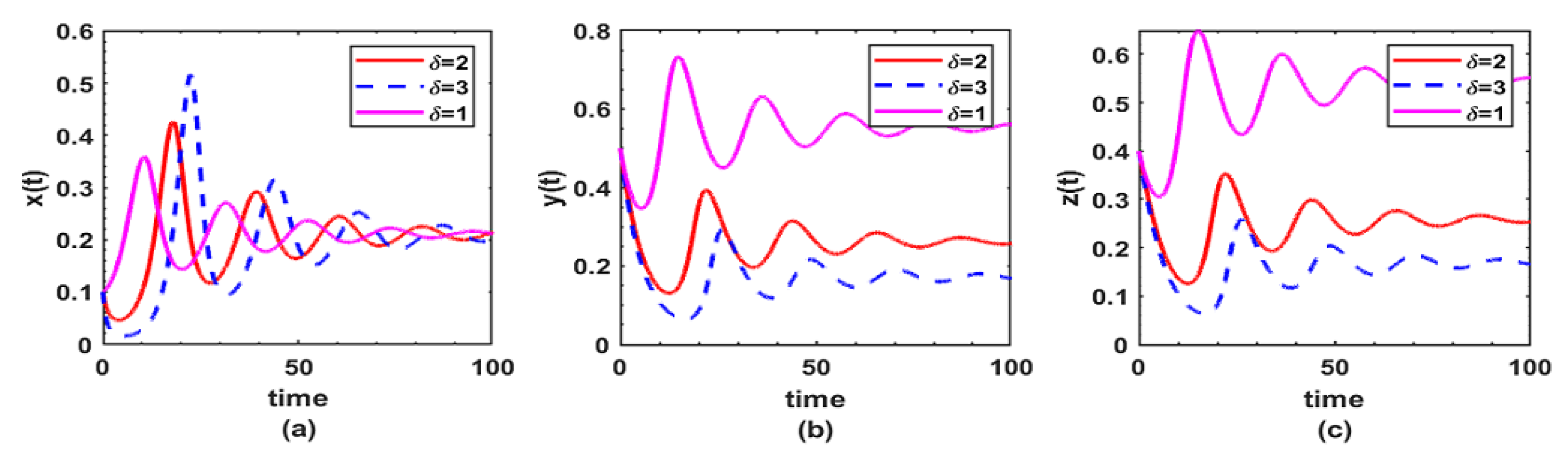
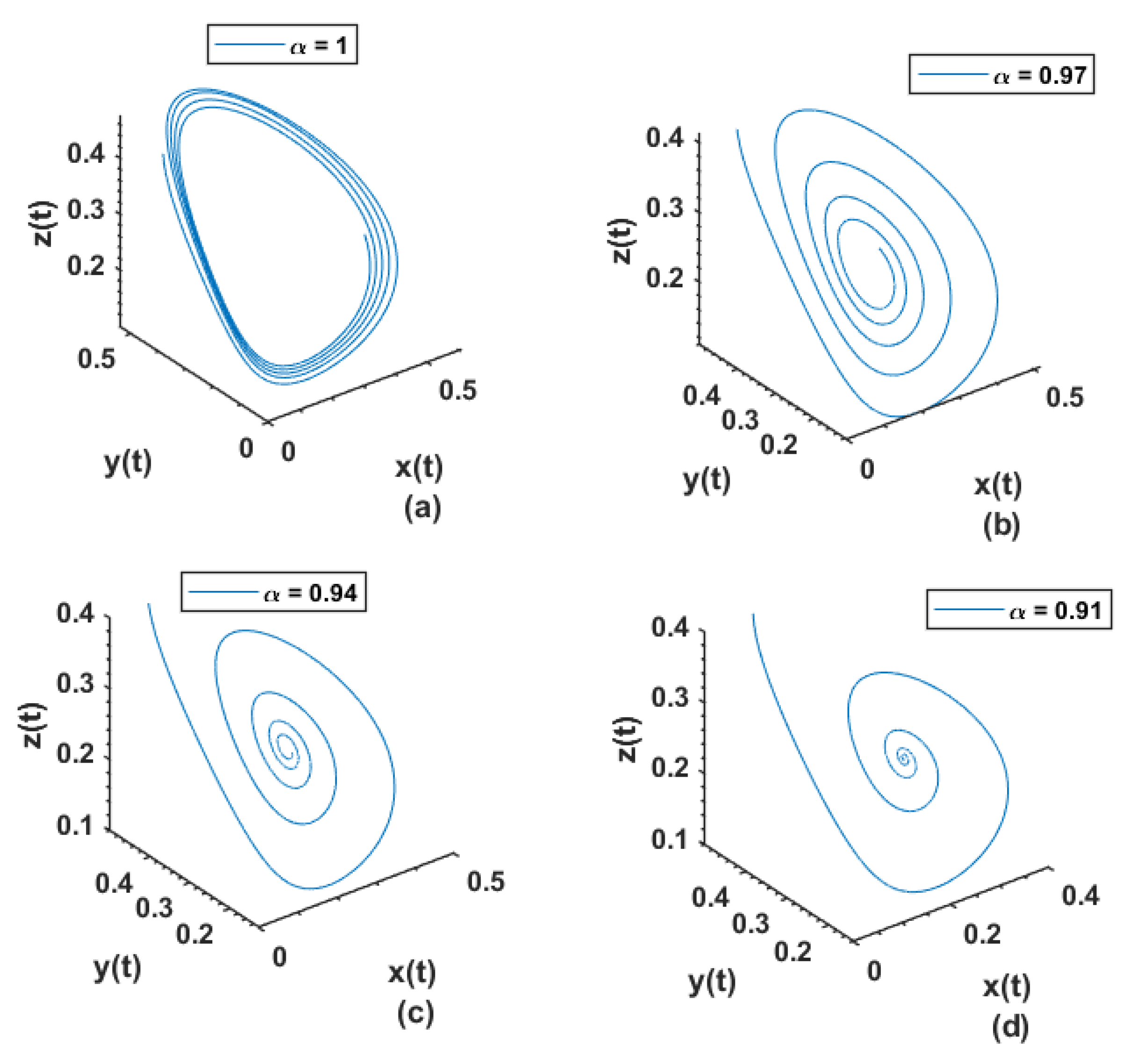
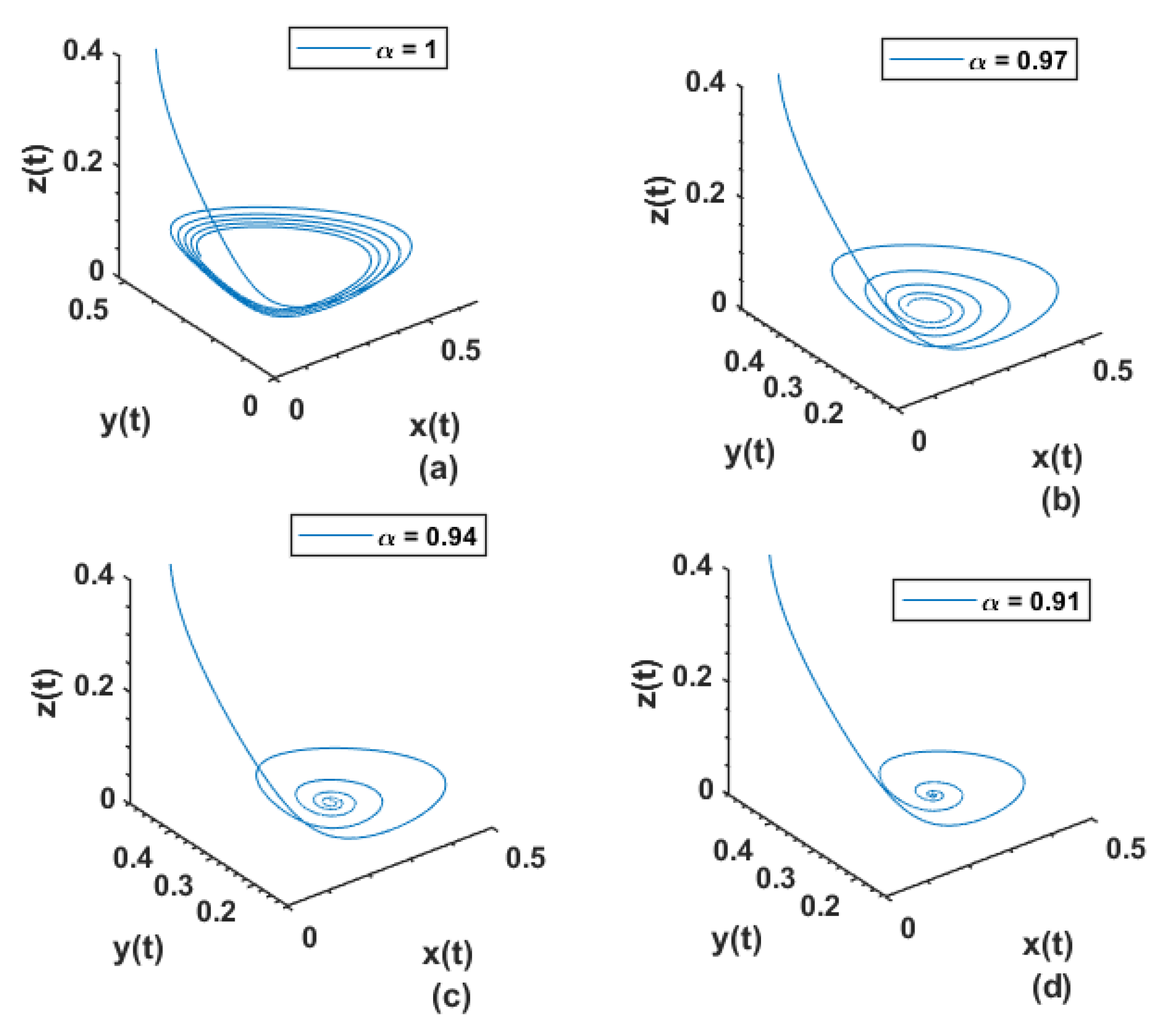
8. Numerical Simulation and Discussion
9. Concluding Remarks with Future Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niu, H.; Chen, Y.; West, B.J. Why Do Big Data and Machine Learning Entail the Fractional Dynamics? Entropy 2021, 23, 297. [Google Scholar] [CrossRef] [PubMed]
- Dunn, G.P.; Old, L.J.; Schreiber, R.D. The three Es of cancer immunoediting. Annu. Rev. Immunol. 2004, 22, 329–360. [Google Scholar] [CrossRef] [PubMed]
- Mantovani, A.; Sozzani, S.; Locati, M.; Allavena, P.; Sica, A. Macrophage polarization: Tumor-associated macrophages as a paradigm for polarized M2 mononuclear phagocytes. Trends. Immunol. 2002, 23, 549–555. [Google Scholar] [CrossRef] [PubMed]
- Sica, A.; Larghi, P.; Mancino, A.; Rubino, L.; Porta, C.; Totaro, M.G.; Rimoldi, M.; Biswas, S.K.; Allavena, P.; Mantovani, A. Macrophage polarization in tumor progression. Semin. Cancer Biol. 2008, 18, 349–355. [Google Scholar] [CrossRef] [PubMed]
- Yaqin, S.; Jicai, H.; Yueping, D.; Yasuhiro, T. Mathematical modelling and bifurcation analysis of pro and anti-tumor macrophages. APM 2020, 2020, 13468. [Google Scholar]
- Allavena, P.; Mantovani, A. Immunology in the clinic review series; focus on cancer: Tumor-associated macrophages: Undisputed stars of the inflammatory tumor microenvironment. Clin. Exp. Immunol. 2012, 167, 195–205. [Google Scholar] [CrossRef]
- Anderson, L.; Jang, S.; Yu, J.L. Qualitative behavior of systems of CD4+ cytokine interactions with treatments. Math. Method Appl. Sci. 2015, 38, 4330–4344. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Amawi, K. A New Approach Using Integral Transform to Solve Cancer Models. Fractal Fract. 2022, 6, 490. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Knott, G.D. modelling tumor regrowth and immunotherapy. Math. Comput. Modell. 2001, 33, 1275–1287. [Google Scholar] [CrossRef]
- Levy, J.A. The importance of the innate immune system in controlling HIV infection and disease. Trends Immunol. 2001, 22, 312–316. [Google Scholar] [CrossRef]
- Banerjee, S.; Sarkar, R.R. Delay-induced model for tumor–immune interaction and control of malignant tumor growth. Biosystems 2008, 91, 268–288. [Google Scholar] [CrossRef]
- Pang, L.; Liu, S.; Liu, F.; Zhang, X.; Tian, T. Mathematical modeling and analysis of tumor-volume variation during radiotherapy. Appl. Math. Model. 2021, 89, 1074–1089. [Google Scholar] [CrossRef]
- Duan, W.L.; Fang, H.; Zeng, C. The stability analysis of tumor-immune responses to chemotherapy system with gaussian white noises. Chaos Solitons Fractals 2019, 127, 96–102. [Google Scholar] [CrossRef]
- Eftimie, R.; Barelle, C. Mathematical investigation of innate immune responses to lung cancer: The role of macrophages with mixed phenotypes. J. Theor. Biol. 2021, 524, 110739. [Google Scholar] [CrossRef]
- Sarmah, D.T.; Bairagi, N.; Chatterjee, S. The interplay between DNA damage and autophagy in lung cancer: A mathematical study. Biosystems 2021, 206, 104443. [Google Scholar] [CrossRef]
- Dong, Y.; Huang, G.; Miyazaki, R.; Takeuchi, Y. Dynamics in a tumor immune system with time delays. Appl. Math. Comput. 2015, 252, 99–113. [Google Scholar] [CrossRef]
- Villasana, M.; Radunskaya, A. A delay differential equation model for tumor growth. J. Math. Biol. 2003, 47, 270–294. [Google Scholar] [CrossRef]
- Gałach, M. Dynamics of the tumor-immune system competition—The effect of time delay. Int. J. Appl. Math. Comput. Sci. 2003, 13, 395–406. [Google Scholar]
- Shen, W.Y.; Chu, Y.M.; ur Rahman, M.; Mahariq, I.; Zeb, A. Mathematical analysis of HBV and HCV co-infection model under nonsingular fractional order derivative. Results Phys. 2021, 28, 104582. [Google Scholar] [CrossRef]
- Chu, Y.M.; Khan, M.F.; Ullah, S.; Shah, S.A.A.; Farooq, M.; bin Mamat, M. Mathematical assessment of a fractional-order vector–host disease model with the Caputo–Fabrizio derivative. Math. Methods Appl. Sci. 2023, 46, 232–247. [Google Scholar] [CrossRef]
- Li, P.; Gao, R.; Xu, C.; Li, Y.; Akgül, A.; Baleanu, D. Dynamics exploration for a fractional-order delayed zooplankton–phytoplankton system. Chaos Solitons Fractals 2023, 166, 112975. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Z.; Ye, H. Optimal control of a fractional-order HIV-immune system with memory. IEEE Trans. Control Syst. Technol. 2012, 20, 763–769. [Google Scholar] [CrossRef]
- Bolton, L.; Cloot, A.H.; Schoombie, S.W.; Slabbert, J.P. A proposed fractional-order gompertz model and its application to tumor growth data. Math. Med. Biol. 2015, 32, 187–207. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, E.; Hashish, A.; Rihan, F.A. On fractional order cancer model. J. Fract. Calc. Appl. Anal. 2012, 3, 1–6. [Google Scholar]
- Rihan, F.A.; Hashish, A.; Al-Maskari, F.; Hussein, M.S.; Ahmed, E.; Riaz, M.B.; Yafia, R. Dynamics of tumor-immune system with fractional-order. J. Tumor Res. 2016, 2, 109. [Google Scholar] [CrossRef]
- Tuan, N.H.; Mohammadi, H.; Rezapour, S. A mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Chaos Solitons Fractals 2020, 140, 110107. [Google Scholar] [CrossRef]
- Ali, A.; Alshammari, F.S.; Islam, S.; Khan, M.A.; Ullah, S. Modeling and analysis of the dynamics of novel coronavirus (COVID-19) with Caputo fractional derivative. Results Phys. 2021, 20, 103669. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ahmad, S.; Ullah, A.; Shah, K.; Alrabaiah, H.; Arfan, M. Mathematical analysis of SIRD model of COVID-19 with Caputo fractional derivative based on real data. Results Phys. 2021, 21, 103772. [Google Scholar] [CrossRef]
- Ahmed, I.; Baba, I.A.; Yusuf, A.; Kumam, P.; Kumam, W. Analysis of Caputo fractional-order model for COVID-19 with lockdown. Adv. Differ. Equ. 2020, 2020, 394. [Google Scholar] [CrossRef]
- Yadav, R.P.; Verma, R. A numerical simulation of fractional order mathematical modeling of COVID-19 disease in case of Wuhan China. Chaos Solitons Fractals 2020, 140, 110124. [Google Scholar] [CrossRef]
- Mohammad, M.; Trounev, A.; Cattani, C. The dynamics of COVID-19 in the UAE based on fractional derivative modeling using Riesz wavelets simulation. Adv. Differ. Equ. 2021, 2021, 115. [Google Scholar] [CrossRef]
- Owen, M.R.; Sherratt, J.A. Modelling the macrophage invasion of tumors: Effects on growth and composition. IMA J. Math. Appl. Med. Biol. 1998, 15, 165–185. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; El-Mesiry, A.E.M.; El-Saka, H.A.A. On the fractional- order logistic equation. Appl. Math. Lett. 2007, 20, 817–823. [Google Scholar] [CrossRef]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin, Germany, 2011. [Google Scholar]
- Baisad, K.; Moonchai, S. Analysis of stability and hopf bifurcation in a fractional gauss-type predator-prey model with allee effect and holling type-III functional response. Adv. Diff. Equ. 2018, 2018, 82. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A. Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Bozkurt, F.; Abdeljawad, T.; Hajji, M.A. Stability analysis of a fractional-order differential equation model of a brain tumor growth depending on the density. Appl. Comput. Math. 2015, 14, 50–62. [Google Scholar]
- Öztürk, I.; Özköse, F. Stability analysis of fractional order mathematical model of tumor-immune system interaction. Chaos Solitons Fractals 2020, 133, 109614. [Google Scholar] [CrossRef]
- Özköse, F.; Yılmaz, S.; Yavuz, M.; Öztürk, İ.; Şenel, M.T.; Bağcı, B.Ş.; Doğan, M.; Önal, Ö. A fractional modeling of tumor–immune system interaction related to Lung cancer with real data. Eur. Phys. J. Plus 2022, 137, 40. [Google Scholar] [CrossRef]
- Solit, D.B.; Garraway, L.A.; Pratilas, C.A.; Sawai, A.; Getz, G.; Basso, A.; Ye, Q.; Lobo, J.M.; She, Y.; Osman, I.; et al. BRAF mutation predicts sensitivity to MEK inhibition. Nature 2006, 439, 358–362. [Google Scholar] [CrossRef]
- da Hora, C.C.; Wurdinger, M.W.S.T.; Tannous, B.A. Patient-derived glioma models: From patients to dish to animals. Cells 2019, 8, 1177. [Google Scholar] [CrossRef] [PubMed]
- Burdall, S.E.; Hanby, A.M.; Lansdown, M.R.; Speirs, V. Breast cancer cell lines: Friend or foe? Breast Cancer Res. 2003, 5, 89. [Google Scholar] [CrossRef] [PubMed]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963. [Google Scholar]
- Mishina, A.P.; Proskuryakov, I.V. Higher Algebra; Nauka: Moscow, Russia, 1965. [Google Scholar]
- Li, C.; Tao, C. On the fractional adams method. Comput. Math. Appl. 2009, 58, 1573–1588. [Google Scholar] [CrossRef]
- Diethelm, K. An algorithm for the numerical solution of differential equations of fractional order. Electron. Trans. Numer. Anal. 1997, 5, 1–6. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approch for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]


| Parameters | Values | Biological Interpretation | Dimensionless Form | Source |
|---|---|---|---|---|
| cells (c) | No. of initial T cells | |||
| cells | No. of initial cells | |||
| cells | No. of initial cells | |||
| a | 0.565/day | Growth rate of T cells | ||
| /cells | Environmental carrying capacity | |||
| 0.2/day (d) | Mortality rate of cells | |||
| 0.2/day (d) | Mortality rate of cells | [33] | ||
| f | /cd | Death rate of T cells by cells | ||
| g | /cd | Death rate of T cells by cells | ||
| /cd | Enabling rate of by T cells | |||
| /cd | Enabling rate of by T cells | |||
| 0.05/day | to conversion rate | |||
| 0.04/day | to conversion rate |
| Parameter | Explanation | (Caputo) | (Classical) | Source |
|---|---|---|---|---|
| Initial T cells | 50,000 | 50,000 | fixed | |
| Initial cells | 2,060,000 | 2,060,000 | fixed | |
| Initial cells | 80,000 | 80,000 | fixed | |
| Fractional order | 7.156 × | 1 | fitted | |
| a | Growth rate of T cells | 0.565 | 0.565 | fixed |
| b | Environmental carrying capacity | 1.15497 × | 3.53497 × | fitted |
| Mortality rate of cells | 0.2 | 0.2 | fixed | |
| Mortality rate of | 0.2 | 0.2 | fixed | |
| f | cells | 3.20516 × | 2.80857 × | fitted |
| Enabling rate of by T | 1 × | 1 × | fixed | |
| Enabling rate of by T cells | 9 × | 9 × | fixed | |
| to conversion rate | 0.05 | 0.05 | fixed | |
| to conversion rate | 0.04 | 0.04 | fixed |
| Parameter | Estimate | Standard Error | t-Statistic | p-Value | Confidence Interval |
|---|---|---|---|---|---|
| 7.156 × | 2.14317 × | 3.2147 | 2.21216 × | {1.2372 × , 7.1729 × } | |
| b | 3.53497 × | 7.08326 × | 4.99061 | 3.14217 × | {1.99166 × , 5.07828 × } |
| f | 2.80857 × | 7.10913 × | 3.95066 | 1.92551 × | {1.25963 × , 4.35752 × } |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padder, A.; Almutairi, L.; Qureshi, S.; Soomro, A.; Afroz, A.; Hincal, E.; Tassaddiq, A. Dynamical Analysis of Generalized Tumor Model with Caputo Fractional-Order Derivative. Fractal Fract. 2023, 7, 258. https://doi.org/10.3390/fractalfract7030258
Padder A, Almutairi L, Qureshi S, Soomro A, Afroz A, Hincal E, Tassaddiq A. Dynamical Analysis of Generalized Tumor Model with Caputo Fractional-Order Derivative. Fractal and Fractional. 2023; 7(3):258. https://doi.org/10.3390/fractalfract7030258
Chicago/Turabian StylePadder, Ausif, Laila Almutairi, Sania Qureshi, Amanullah Soomro, Afroz Afroz, Evren Hincal, and Asifa Tassaddiq. 2023. "Dynamical Analysis of Generalized Tumor Model with Caputo Fractional-Order Derivative" Fractal and Fractional 7, no. 3: 258. https://doi.org/10.3390/fractalfract7030258
APA StylePadder, A., Almutairi, L., Qureshi, S., Soomro, A., Afroz, A., Hincal, E., & Tassaddiq, A. (2023). Dynamical Analysis of Generalized Tumor Model with Caputo Fractional-Order Derivative. Fractal and Fractional, 7(3), 258. https://doi.org/10.3390/fractalfract7030258







