An Application of the Distributed-Order Time- and Space-Fractional Diffusion-Wave Equation for Studying Anomalous Transport in Comb Structures
Abstract
1. Introduction
2. The Structure of the Paper
3. Derivation of the Finite Element Scheme for the Comb Model
3.1. Finite Element Fully Variational Formulation
3.2. Implementation of Finite Element Method with an Unstructured Mesh
| Algorithm 1. Calculate and using finite element method on an unstructured mesh |
|
4. Stability and Convergence
4.1. Stability
4.2. Convergence
5. Numerical Examples
| h | Error | Order | Error | Order | |
|---|---|---|---|---|---|
| 3.1123 × | 5.6929 × | - | 3.7301 × | - | |
| 1.6759 × | 3.0879 × | 0.99 | 1.1009 × | 1.97 | |
| 8.6682 × | 1.5643 × | 1.03 | 2.7245 × | 2.12 | |
| 4.3719 × | 7.5272 × | 1.07 | 6.3251 × | 2.13 | |
| 3.1123 × | 5.6922 × | - | 3.8367 × | - | |
| 1.6759 × | 3.0878 × | 0.99 | 1.1271 × | 1.98 | |
| 8.6682 × | 1.5642 × | 1.03 | 2.8032 × | 2.11 | |
| 4.3719 × | 7.5270 × | 1.07 | 6.5047 × | 2.13 | |
| 3.1123 × | 5.6972 × | - | 3.7652 × | - | |
| 1.6759 × | 3.0889 × | 0.99 | 1.1075 × | 1.97 | |
| 8.6682 × | 1.5645 × | 1.03 | 2.7391 × | 2.12 | |
| 4.3719 × | 7.5275 × | 1.07 | 6.3932 × | 2.13 |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iomin, A.; Méndez, V.; Horsthemke, W. Fractional Dynamics in Comb-Like Structures; World Scientific: Singapore, 2018. [Google Scholar]
- Iomin, A.; Méndez, V. Reaction-subdiffusion front propagation in a comblike model of spiny dendrites. Phys. Rev. E 2013, 88, 012706. [Google Scholar] [CrossRef] [PubMed]
- Iomin, A.; Zaburdaev, V.; Pfohl, T. Reaction front propagation of actin polymerization in a comb-reaction system. Chaos Solitons Fract. 2016, 92, 115–122. [Google Scholar] [CrossRef]
- Méndez, V.; Iomin, A. Comb models for transport along spiny dendrites. In Handbook of Applications of Chaos Theory; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Méndez, V.; Iomin, A. Comb-like models for transport along spiny dendrites. Chaos Solitons Fract. 2013, 53, 46–51. [Google Scholar] [CrossRef]
- Iomin, A. Toy model of fractional transport of cancer cells due to self-entrapping. Phys. Rev. E 2006, 73, 061918. [Google Scholar] [CrossRef] [PubMed]
- Iomin, A. A toy model of fractal glioma development under RF electric field treatment. Eur. Phys. J. E 2012, 35, 42–46. [Google Scholar] [CrossRef]
- Arkhincheev, V.E.; Baskin, E.M. Anomalous diffusion and drift in a comb model of percolation clusters. Zh. Eksp. Teor. Fiz. 1991, 100, 292–300. [Google Scholar]
- Baskin, E.; Iomin, A. Superdiffusion on a Comb Structure. Phys. Rev. Lett. 2004, 93, 120603. [Google Scholar] [CrossRef]
- Christov, C.I.; Jordan, P.M. Heat conduction paradox involving second-sound propagation in moving media. Phys. Rev. Lett. 2015, 94, 154301. [Google Scholar] [CrossRef]
- Compte, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A-Math. Gen. 1997, 30, 7277–7289. [Google Scholar] [CrossRef]
- Iomin, A. Fractional kinetics of glioma treatment by a radio-frequency electric field. Eur. Phys. J. Spec. Top. 2013, 222, 1875–1884. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Q.; Turner, I. Two new implicit numerical methods for the fractional cable equation. J. Comput. Nonlin. Dyn. 2011, 6, 011009. [Google Scholar] [CrossRef]
- Qi, H.T.; Xu, H.Y.; Guo, X.W. The Cattaneo-type time fractional heat conduction equation for laser heating. Comput. Math. Appl. 2013, 66, 824–831. [Google Scholar] [CrossRef]
- Oloniiju, S.D.; Goqo, S.P.; Sibanda, P. A chebyshev spectral method for heat and mass transfer in mhd nanofluid flow with space fractional constitutive model. Front. Heat Mass Transf. 2019, 13, 13–19. [Google Scholar] [CrossRef]
- Eab, C.H.; Lim, S.C. Fractional Langevin equation of distributed order. Phys. Rev. E 2011, 83, 031136. [Google Scholar] [CrossRef]
- Caputo, M. Distributed order differential equations modeling dielectric induction and diffusion. Fract. Calc. Appl. Anal. 2001, 4, 421–442. [Google Scholar]
- Bai, Y.; Wan, S.; Zhang, Y.; Wang, X. Unsteady Falkner-Skan flow of fractional Maxwell fluid towards a stretched wedge with buoyancy effects. Phys. Scripta 2022, 98, 015218. [Google Scholar] [CrossRef]
- Elwakil, S.A.; Zahran, M.A.; Abulwafa, E.M. Fractional (space-time) diffusion equation on comb-like model. Chaos Solitons Fract. 2004, 20, 1113–1120. [Google Scholar] [CrossRef]
- Ervin, V.J.; Roop, J.P. Variational formulation for the stationary fractional advection dispersion equation. Numer. Meth. Part. D. E. 2006, 22, 558–576. [Google Scholar] [CrossRef]
- Bu, W.; Tang, Y.; Yang, J. Galerkin finite element method for two-dimensional Riesz space fractional diffusion equations. J. Comput. Phys. 2014, 276, 26–38. [Google Scholar] [CrossRef]
- Bu, W.; Tang, Y.; Wu, Y.; Yang, J. Finite difference/finite element method for twodimensional space and time fractional Bloch-Torrey equations. J. Comput. Phys. 2015, 293, 264–279. [Google Scholar] [CrossRef]
- Yang, Z.; Yuan, Z.; Nie, Y.; Wang, J.; Zhu, X.; Liu, F. Finite element method for nonlinear Riesz space fractional diffusion equations on irregular domains. J. Comput. Phys. 2017, 330, 863–883. [Google Scholar] [CrossRef]
- Hao, Z.; Park, M.; Lin, G.; Cai, Z. Finite element method for two-sided fractional differential equations with variable coeffificients: Galerkin approach. J. Sci. Comput. 2019, 79, 700–717. [Google Scholar] [CrossRef]
- Wang, H.; Yang, D. Wellposedness of variable-coefficient conservative fractional elliptic differential equations. Siam J. Numer. Anal. 2013, 51, 1088–1107. [Google Scholar] [CrossRef]
- Wang, H.; Yang, D.; Zhu, S. Inhomogeneous Dirichlet boundary-value problems of space-fractional diffusion equations and their finite element approximations. Siam J. Numer. Anal. 2014, 52, 1292–1310. [Google Scholar] [CrossRef]
- Ervin, V.J.; Roop, J.P. Variational solution of fractional advection dispersion equations on bounded domains in Rd. Numer. Methods Partial Differ. Equat. 2007, 23, 256–281. [Google Scholar] [CrossRef]
- Roop, J.P. Variational Solution of the Fractional Advection Dispersion Equation. Ph.D. Thesis, Clemson University, Clemson, SC, USA, 2004. [Google Scholar]
- Moghaddam, B.P.; Machado, J.A.T.; Morgado, M.L. Numerical approach for a class of distributed order time fractional partial differential equations. Appl. Numer. Math. 2019, 136, 152–162. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
- Fan, H.; Zhao, Y.; Wang, F.; Shi, Y.; Tang, Y. A superconvergent nonconforming mixed FEM for multi-term time-fractional mixed diffusion and diffusion-wave equations with variable coefficients. East Asian J. Appl. Math 2021, 11, 63–92. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D flnite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Meth. Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]


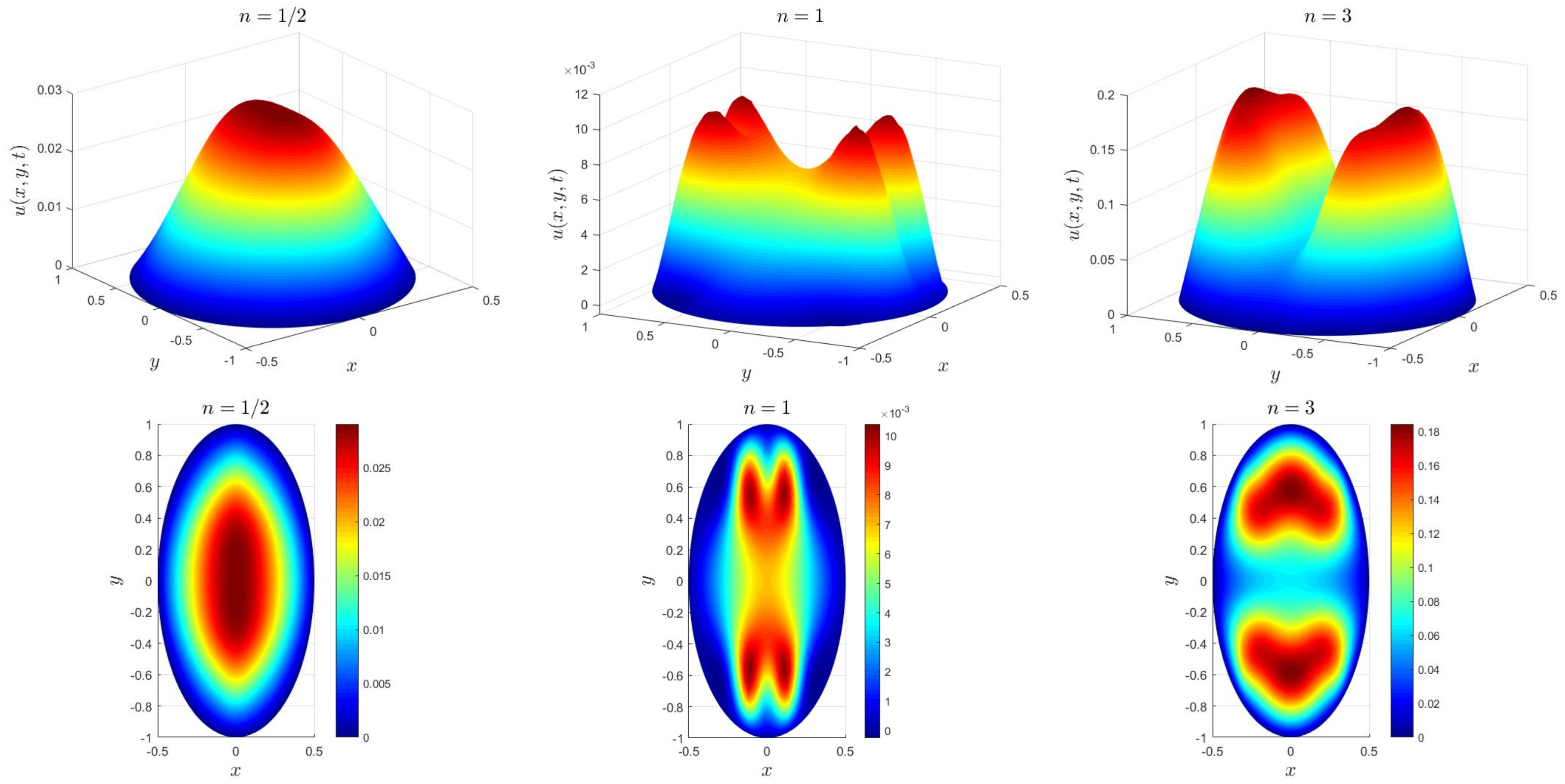
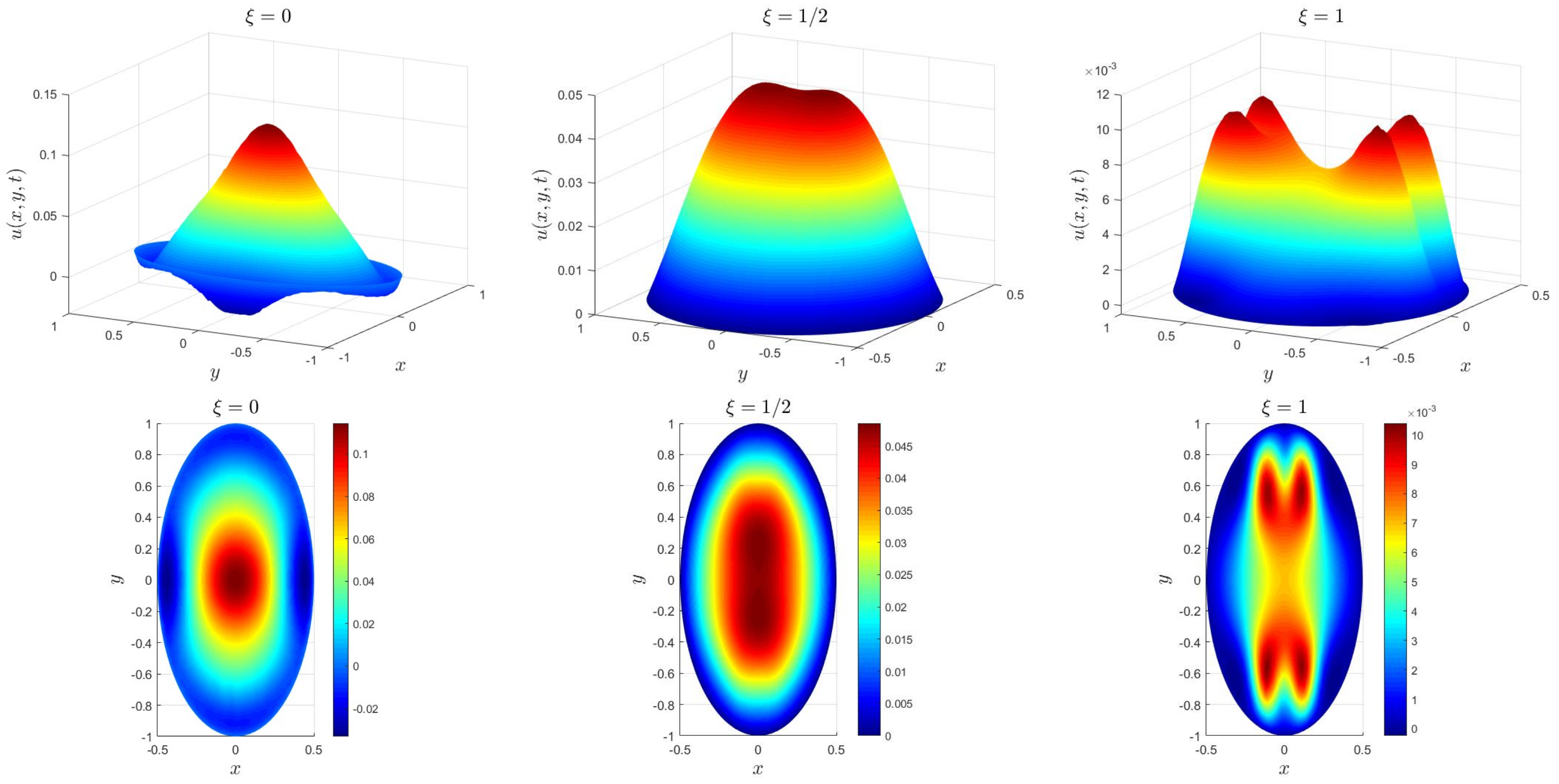
| h | Error | Order | Error | Order | |
|---|---|---|---|---|---|
| 3.0312 × | 1.3401 × | – | 8.9386 × | – | |
| 1.8428 × | 6.7962 × | 1.36 | 2.2350 × | 2.79 | |
| 8.3913 × | 3.4331 × | 0.87 | 5.3636 × | 1.81 | |
| 4.5308 × | 1.6953 × | 1.14 | 1.2951 × | 2.31 | |
| 3.0312 × | 1.3252 × | – | 1.0536 × | – | |
| 1.8428 × | 6.7495 × | 1.36 | 2.5810 × | 2.83 | |
| 8.3913 × | 3.4048 × | 0.87 | 6.3027 × | 1.79 | |
| 4.5308 × | 1.6816 × | 1.14 | 1.5874 × | 2.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhang, S.; Chen, S.; Liu, F.; Feng, L.; Turner, I.; Zheng, L.; Zhu, J. An Application of the Distributed-Order Time- and Space-Fractional Diffusion-Wave Equation for Studying Anomalous Transport in Comb Structures. Fractal Fract. 2023, 7, 239. https://doi.org/10.3390/fractalfract7030239
Liu L, Zhang S, Chen S, Liu F, Feng L, Turner I, Zheng L, Zhu J. An Application of the Distributed-Order Time- and Space-Fractional Diffusion-Wave Equation for Studying Anomalous Transport in Comb Structures. Fractal and Fractional. 2023; 7(3):239. https://doi.org/10.3390/fractalfract7030239
Chicago/Turabian StyleLiu, Lin, Sen Zhang, Siyu Chen, Fawang Liu, Libo Feng, Ian Turner, Liancun Zheng, and Jing Zhu. 2023. "An Application of the Distributed-Order Time- and Space-Fractional Diffusion-Wave Equation for Studying Anomalous Transport in Comb Structures" Fractal and Fractional 7, no. 3: 239. https://doi.org/10.3390/fractalfract7030239
APA StyleLiu, L., Zhang, S., Chen, S., Liu, F., Feng, L., Turner, I., Zheng, L., & Zhu, J. (2023). An Application of the Distributed-Order Time- and Space-Fractional Diffusion-Wave Equation for Studying Anomalous Transport in Comb Structures. Fractal and Fractional, 7(3), 239. https://doi.org/10.3390/fractalfract7030239









