Linearized Crank–Nicolson Scheme for the Two-Dimensional Nonlinear Riesz Space-Fractional Convection–Diffusion Equation
Abstract
1. Introduction
2. Preliminaries
3. CNADI-WSGD Method
- (1)
- To obtain the intermediate solution , we solve a set of equations that define by (19) for every fixed at every mesh point .
- (2)
- To find the numerical solution , we solve a set of equations that define by (20) for each fixed at the points by alternating the spatial direction.
- (3)
- The homogeneous Dirichlet boundary conditions are used as the following:
4. Theoretical Analysis of the CNADI–WSGD Scheme
4.1. Stability of the CNADI–WSGD Approximation
4.2. Convergence of the CNADI–WSGD Approximation
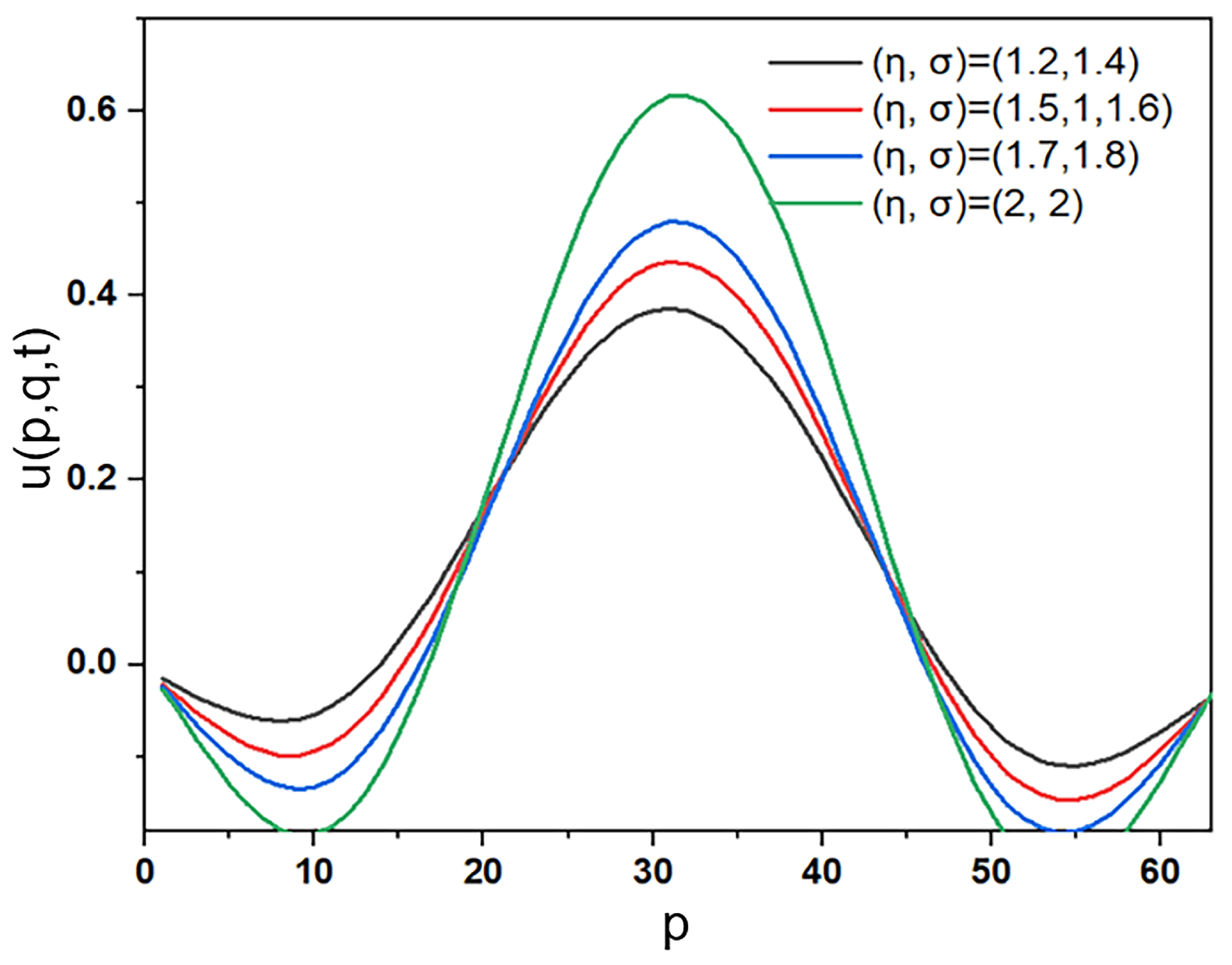
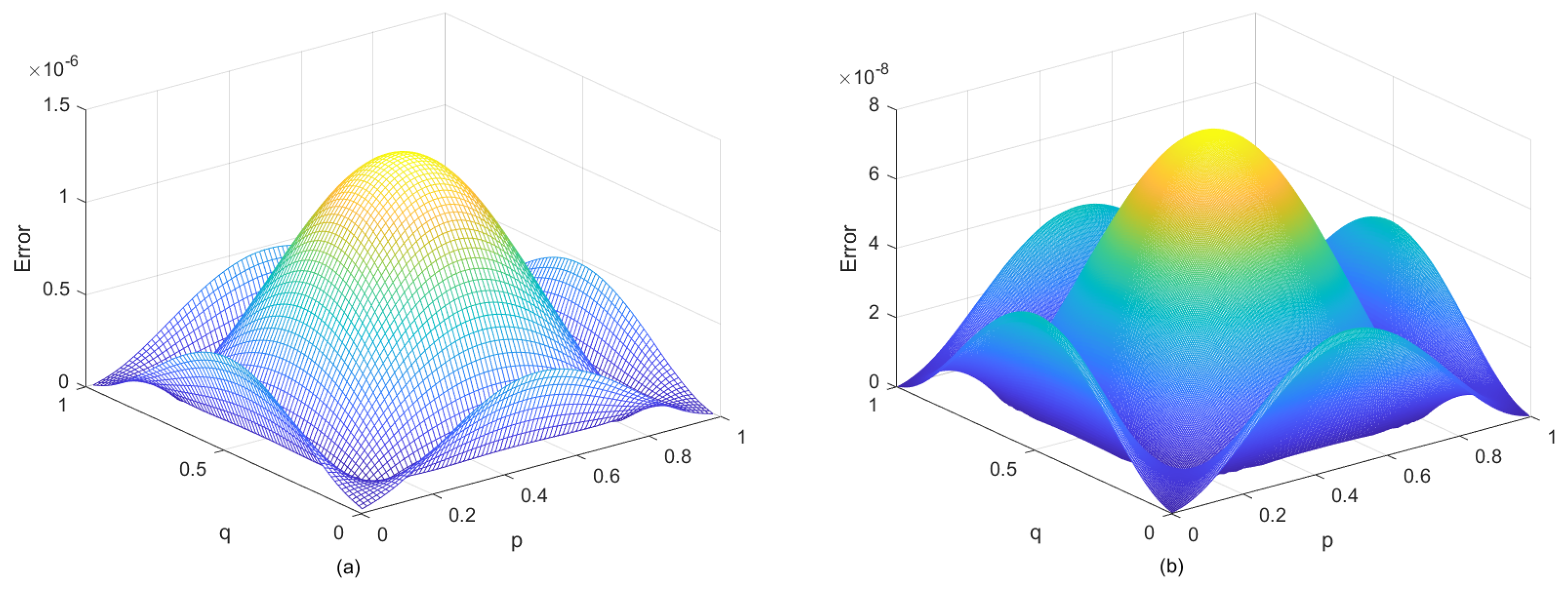
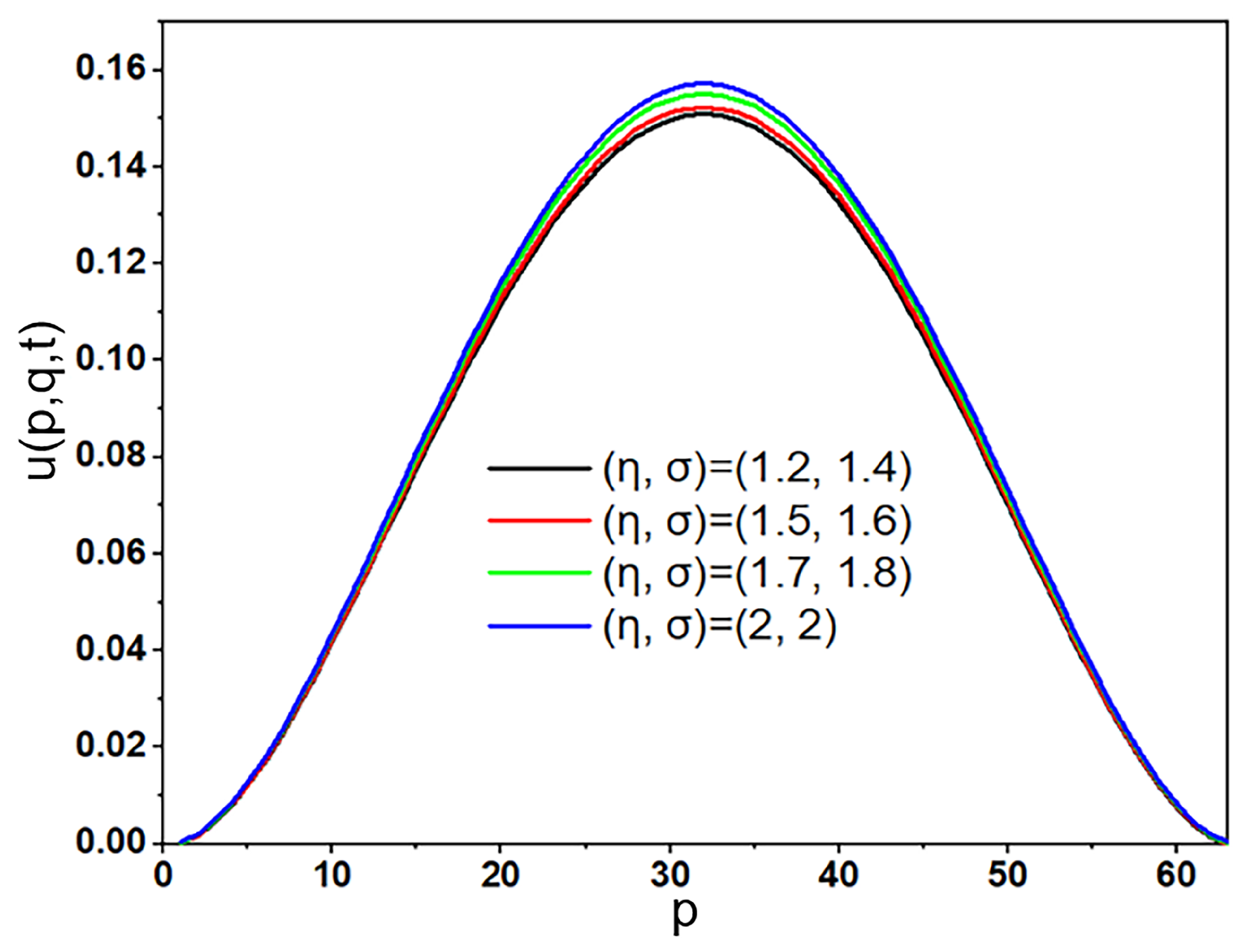
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons Inc.: New York, NY, USA, 1993. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Sheng, H.; Chen, Y.; Qiu, T. Fractional Processes and Fractional-Order Signal Processing: Techniques and Applications; Springer: London, UK, 2011. [Google Scholar]
- Fomin, S.; Chugunov, V.; Hashida, T. Application of fractional differential equations for modeling the anomalous diffusion of contaminant from fracture into porous rock matrix with bordering alteration zone. Transp. Porous Media 2010, 2, 187–205. [Google Scholar] [CrossRef]
- Wang, K.; Wang, H. A fast characteristic finite difference method for fractional advection–diffusion equations. Adv. Water Resour. 2011, 7, 810–816. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 5, 1586–1593. [Google Scholar] [CrossRef]
- Sabatelli, L.; Keating, S.; Dudley, J.; Richmond, P. Waiting time distributions in financial markets. Eur. Phys. J. B 2002, 2, 273–275. [Google Scholar] [CrossRef]
- Basha, M.; Dai, B.; Al-Sadi, W. Existence and stability for a nonlinear coupled p-laplacian system of fractional differential equations. J. Math. 2021, 2021, 6687949. [Google Scholar] [CrossRef]
- Hejazi, H.; Moroney, T.; Liu, F. Stability and convergence of a finite volume method for the space fractional advection–dispersion equation. Comput. Appl. Math. 2014, 255, 684–697. [Google Scholar] [CrossRef]
- Jia, J.; Wang, H. A fast finite volume method for conservative space-fractional diffusion equations in convex domains. J. Comput. Phys. 2016, 310, 63–84. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. A Petrov–Galerkin finite element method for fractional convection-diffusion equations. SIAM J. Numer. Anal. 2016, 1, 481–503. [Google Scholar] [CrossRef]
- Fu, T.; Duan, B.; Zheng, Z. An Effective Finite Element Method with Singularity Reconstruction for Fractional Convection-diffusion Equation. J. Sci. Comput. 2021, 3, 1–18. [Google Scholar] [CrossRef]
- Shen, J.; Stynes, M.; Sun, Z.Z. Two Finite Difference Schemes for Multi-Dimensional Fractional Wave Equations with Weakly Singular Solutions. Comput. Methods Appl. Math. 2021, 4, 913–928. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Finite difference methods for fractional differential equations. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2012, 4, 1230014. [Google Scholar] [CrossRef]
- Anley, E.F.; Zheng, Z. Finite difference approximation method for a space fractional convection–diffusion equation with variable coefficients. Symmetry 2020, 3, 485. [Google Scholar] [CrossRef]
- Huang, J.F.; Nie, N.; Tang, Y. Second order finite difference-spectral method for space fractional diffusion equations. Sci. China Math. 2014, 6, 1303–1317. [Google Scholar] [CrossRef]
- Basha, M.; Anley, E.F.; Dai, B. Numerical Solution for a Nonlinear Time-Space Fractional Convection-Diffusion Equation. J. Comput. Nonlinear Dyn. 2022, 1, 1–22. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Baleanu, D.; Ezz-Eldien, S.S. On shifted Jacobi spectral approximations for solving fractional differential equations. Appl. Math. Comput. 2013, 15, 8042–8056. [Google Scholar] [CrossRef]
- Behroozifar, M.; Ahmadpour, F. A study on spectral methods for linear and nonlinear fractional differential equations. Int. J. Comput. Sci. Math. 2019, 6, 545–556. [Google Scholar] [CrossRef]
- Xu, Q.; Hesthaven, J.S. Discontinuous Galerkin method for fractional convection-diffusion equations. SIAM J. Numer. Anal. 2014, 1, 405–423. [Google Scholar] [CrossRef]
- Mustapha, K. Time-stepping discontinuous Galerkin methods for fractional diffusion problems. Numer. Math. 2015, 3, 497–516. [Google Scholar] [CrossRef]
- Feng, L.B.; Zhuang, P.; Liu, F.; Turner, I.; Li, J. High-order numerical methods for the Riesz space fractional advection-dispersion equations. Comput. Math. Appl. 2016. [Google Scholar] [CrossRef]
- Tian, W.; Deng, W.; Wu, Y. Polynomial spectral collocation method for space fractional advection–diffusion equation. Numer. Methods Partial Differ. Equ. 2015, 2, 514–535. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Baleanu, D. A spectral Legendre–Gauss–Lobatto collocation method for a space-fractional advection diffusion equations with variable coefficients. Rep. Math. Phys. 2013, 2, 219–233. [Google Scholar] [CrossRef]
- Xie, J.; Huang, Q.; Yang, X. Numerical solution of the one-dimensional fractional convection diffusion equations based on Chebyshev operational matrix. SpringerPlus 2016, 5, 1149. [Google Scholar] [CrossRef] [PubMed]
- Borhanifar, A.; Ragusa, M.A.; Valizadehaz, S. High-order numerical method for two-dimensional Riesz space fractional advection-dispersion equation. Discrete Contin. Dyn. Syst. Ser. B 2020, 10, 5495–5508. [Google Scholar]
- Chen, M.; Deng, W. A second-order numerical method for two-dimensional two-sided space fractional convection diffusion equation. Appl. Math. Model. 2014, 13, 3244–3259. [Google Scholar] [CrossRef]
- Chen, M.; Deng, W. Fourth order accurate scheme for the space fractional diffusion equations. SIAM J. Numer. Anal. 2014, 3, 1418–1438. [Google Scholar] [CrossRef]
- Hou, D.; Azaiez, M.; Xu, C. Müntz Spectral Method for Two-Dimensional Space-Fractional Convection-Diffusion Equation. Commun. Comput. Phys. 2019, 26, 1415–1443. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, C.; Brugnano, L. An implicit difference scheme with the KPS preconditioner for two-dimensional time–space fractional convection–diffusion equations. Comput. Math. Appl. 2020, 1, 31–42. [Google Scholar] [CrossRef]
- Bi, Y.; Jiang, Z. The finite volume element method for the two-dimensional space-fractional convection–diffusion equation. Adv. Differ. Equ. 2021, 2021, 379. [Google Scholar] [CrossRef]
- Liu, F.; Chen, S.; Turner, I.; Burrage, K.; Anh, V. Numerical simulation for two-dimensional Riesz space fractional diffusion equations with a nonlinear reaction term. Cent. Eur. J. Phys. 2013, 10, 1221–1232. [Google Scholar] [CrossRef]
- Zeng, F.; Liu, F.; Li, C.; Burrage, K.; Turner, I.; Anh, V. A Crank–Nicolson ADI spectral method for a two-dimensional Riesz space fractional nonlinear reaction-diffusion equation. SIAM J. Numer. Anal. 2014, 6, 2599–2622. [Google Scholar] [CrossRef]
- Zhu, X.; Nie, Y.; Wang, J.; Yuan, Z. A numerical approach for the Riesz space-fractional Fisher’equation in two-dimensions. Int. J. Comput. Math. 2017, 2, 296–315. [Google Scholar] [CrossRef]
- Yang, S. Numerical simulation for the two-dimensional and three-dimensional Riesz space fractional diffusion equations with delay and a nonlinear reaction term. Int. J. Comput. Math. 2019, 10, 1957–1978. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Yverdon-les-Bains, Switzerland, 1993. [Google Scholar]
- Kilbas, A.A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Limited: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Liu, F.; Anh, V.; Turner, I. Numerical solution of the space fractional Fokker–Planck equation. J. Comput. Appl. Math. 2004, 1, 209–219. [Google Scholar] [CrossRef]
- Anley, E.F.; Zheng, Z. Finite Difference Method for Two-Sided Two Dimensional Space Fractional Convection-Diffusion Problem with Source Term. Mathematics 2020, 11, 1878. [Google Scholar] [CrossRef]
- Tian, W.; Zhou, H.; Deng, W. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 2015, 294, 1703–1727. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 1, 80–90. [Google Scholar] [CrossRef]
- Thomas, J.W. Numerical Partial Differential Equations: Finite Difference Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Yu, D.; Tan, H. Numerical Methods of Differential Equations; Science Publisher: Beijing, China, 2003. [Google Scholar]
- Nasrollahzadeh, F.; Hosseini, S.M. An implicit difference-ADI method for the two-dimensional space-time fractional diffusion equation. Iran. J. Math. Sci. Inform. 2016, 2, 71–86. [Google Scholar]

| order | order | CPU(s) | ||||
|---|---|---|---|---|---|---|
| (1.2, 1.8) | 1/4 | - | - | 0.0020 | ||
| 1/8 | 1.7962 | 1.8984 | 0.0059 | |||
| 1/16 | 1.8128 | 2.0041 | 0.0288 | |||
| 1/32 | 2.0094 | 2.0154 | 0.1724 | |||
| 1/64 | 1.9945 | 2.0077 | 0.8077 | |||
| 1/128 | 2.0013 | 2.0006 | 5.8330 | |||
| (1.3, 1.7) | 1/4 | - | - | 0.0022 | ||
| 1/8 | 1.7694 | 1.8583 | 0.0100 | |||
| 1/16 | 1.834 | 1.9669 | 0.0837 | |||
| 1/32 | 1.9703 | 1.985 | 0.1850 | |||
| 1/64 | 1.9805 | 1.9903 | 1.0993 | |||
| 1/128 | 1.9949 | 1.9932 | 8.0243 | |||
| (1.4, 1.6) | 1/4 | - | - | 0.0020 | ||
| 1/8 | 1.7535 | 1.8322 | 0.0066 | |||
| 1/16 | 1.8615 | 1.9434 | 0.0355 | |||
| 1/32 | 1.923 | 1.9669 | 0.1485 | |||
| 1/64 | 1.9806 | 1.9806 | 0.8680 | |||
| 1/128 | 1.991 | 1.989 | 6.9709 |
| CN–ADI | CN–non–ADI | ||||||
|---|---|---|---|---|---|---|---|
| Order | CPU | Order | CPU | ||||
| 1/40 | - | 0.1268 | - | 0.2446 | |||
| 1/80 | 2.0025 | 0.7686 | 2.0025 | 1.3055 | |||
| (1.2,1.8) | 1/160 | 2.0004 | 5.9595 | 2.0004 | 9.8197 | ||
| 1/320 | 1.9994 | 61.1540 | 1.9994 | 72.0935 | |||
| 1/40 | - | 0.1395 | - | 0.2249 | |||
| 1/80 | 1.9939 | 1.1048 | 1.9939 | 1.4776 | |||
| (1.3,1.7) | 1/160 | 1.995 | 7.7145 | 1.995 | 11.2881 | ||
| 1/320 | 1.9978 | 62.0667 | 1.9978 | 82.0642 | |||
| 1/40 | - | 0.1492 | - | 0.2446 | |||
| 1/80 | 1.9829 | 1.0746 | 1.9829 | 1.3055 | |||
| (1.4,1.6) | 1/160 | 1.9938 | 7.7024 | 1.9938 | 9.8197 | ||
| 1/320 | 1.997 | 61.3860 | 1.997 | 72.0935 |
| order | order | CPU(s) | ||||
|---|---|---|---|---|---|---|
| (1.2, 1.8) | 1/4 | - | - | 0.0164 | ||
| 1/8 | 2.0527 | 2.0099 | 0.0076 | |||
| 1/16 | 2.0303 | 2.0295 | 0.0155 | |||
| 1/32 | 2.0308 | 2.0431 | 0.1361 | |||
| 1/64 | 2.0335 | 2.0479 | 0.6257 | |||
| 1/128 | 1.842 | 2.0467 | 3.8980 | |||
| (1.3, 1.7) | 1/4 | - | - | 0.0077 | ||
| 1/8 | 2.0566 | 2.0263 | 0.0077 | |||
| 1/16 | 2.0378 | 2.0394 | 0.0336 | |||
| 1/32 | 2.0429 | 2.0442 | 0.1148 | |||
| 1/64 | 1.9079 | 2.0406 | 0.5898 | |||
| 1/128 | 1.715 | 2.033 | 3.9085 | |||
| (1.4, 1.6) | 1/4 | - | - | 0.0038 | ||
| 1/8 | 2.0599 | 2.0349 | 0.0084 | |||
| 1/16 | 2.0428 | 2.0438 | 0.0367 | |||
| 1/32 | 2.0509 | 2.0419 | 0.1276 | |||
| 1/64 | 1.9846 | 2.0302 | 0.5947 | |||
| 1/128 | 1.7132 | 2.0154 | 3.9343 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basha, M.; Anley, E.F.; Dai, B. Linearized Crank–Nicolson Scheme for the Two-Dimensional Nonlinear Riesz Space-Fractional Convection–Diffusion Equation. Fractal Fract. 2023, 7, 240. https://doi.org/10.3390/fractalfract7030240
Basha M, Anley EF, Dai B. Linearized Crank–Nicolson Scheme for the Two-Dimensional Nonlinear Riesz Space-Fractional Convection–Diffusion Equation. Fractal and Fractional. 2023; 7(3):240. https://doi.org/10.3390/fractalfract7030240
Chicago/Turabian StyleBasha, Merfat, Eyaya Fekadie Anley, and Binxiang Dai. 2023. "Linearized Crank–Nicolson Scheme for the Two-Dimensional Nonlinear Riesz Space-Fractional Convection–Diffusion Equation" Fractal and Fractional 7, no. 3: 240. https://doi.org/10.3390/fractalfract7030240
APA StyleBasha, M., Anley, E. F., & Dai, B. (2023). Linearized Crank–Nicolson Scheme for the Two-Dimensional Nonlinear Riesz Space-Fractional Convection–Diffusion Equation. Fractal and Fractional, 7(3), 240. https://doi.org/10.3390/fractalfract7030240







