Fractional Order Runge–Kutta Methods

Abstract

This paper presents a new class of fractional order Runge–Kutta (FORK) methods for numerically approximating the solution of fractional differential equations (FDEs). We construct explicit and implicit FORK methods for FDEs by using the Caputo generalized Taylor series formula. Due to the dependence of fractional derivatives on a fixed base point, in the proposed method, we had to modify the right-hand side of the given equation in all steps of the FORK methods. Some coefficients for explicit and implicit FORK schemes are presented. The convergence analysis of the proposed method is also discussed. Numerical experiments are presented to clarify the effectiveness and robustness of the method.

1. Introduction

In recent years, the numerical approximation for the solutions of FDEs has attracted increasing attention in many fields of applied sciences and engineering [1,2,3]. It is common for FDEs to be used in formulating many problems in applied mathematics. Developing numerical methods for fractional differential problems is necessary and important because analytic solutions are usually challenging to obtain. Moreover, it is necessary to develop numerical methods that are highly accurate and easy to use.

It is well known that fractional derivatives have different definitions; the most common and important ones in applications are the Riemann–Liouville and Caputo fractional derivatives. Models describing physical phenomena usually prefer the use of the Caputo derivative. One of the reasons is that the Riemann–Liouville derivative needs initial conditions containing the limit values of the Rieman–Liouville fractional derivative at the origin of time. In contrast, the initial conditions for Caputo derivatives are the same as for integer-order differential equations. Therefore, using the Caputo derivative, there is a clear physical interpretation of the prescribed data; see [1,4,5].

Numerous research papers have been published on numerical methods for FDEs. Many researchers considered the trapezoidal method, predictor-corrector method, extrapolation method, and spectral method [6,7,8,9,10,11,12,13,14,15,16]. Some of these methods discretize fractional derivatives directly. As an example, the L1 formula was created by a piecewise linear interpolation approximation for the integrand function on each small interval [17,18]. In [19], the authors applied quadratic interpolation approximation using three points to approximate the Caputo fractional derivative, while in [20], a technique based on the block-by-block approach was presented. This technique became a common method for equations with integral operators. In [21], Caputo fractional differentiation was approximated by a weighted sum of the integer order derivatives of functions. In [22], several numerical algorithms were proposed to approximate the Caputo fractional derivatives by applying higher-order piecewise interpolation polynomials and the Simpson method to design a higher-order algorithm.

These methods are appropriate options if the resulting system of equations, generated from the numerical method, is linear and well-conditioned. However, they present a high computational cost when the problem we are solving is badly conditioned or nonlinear. In light of the above discussion and the analysis of other methods for FDEs, despite many papers on numerical methods for FDEs, there are still insufficient efficient numerical approaches for such equations. Therefore, further studies are still in demand. In this case, step-by-step methods such as the Runge–Kutta method are a good option. They are favored due to their simplicity in both calculation and analysis.

Several authors have used Runge–Kutta methods to solve ordinary, partial differential, and integral equations [23,24,25,26,27,28,29,30]. Lubich and others have done some fundamental works regarding Runge–Kutta methods for Volterra integral equations [28,29,30]. They used the order conditions to derive various Runge–Kutta methods.

One of the efficient implicit Runge–Kutta methods for the numerical approximation of some linear partial differential equations is the Rosenbrock procedure. It is a class of semi-implicit Runge–Kutta methods for the numerical solution of some stiff systems of ODEs. In Osterman and Rochet’s papers [31,32], the authors apply the Rosenbrock methods to solve linear partial differential equations, obtaining a sharp lower bound for the order of convergence. They show that the order of convergence is, in general, fractional. So, for the numerical solution of some fractional linear partial differential equations, we can construct fractional Rosenbrock-type methods, in which a special type of fractional semi-implicit Runge–Kutta method could be considered.

This paper introduces a new class of fractional order Runge–Kutta methods for numerical approximation to the solution of FDEs. Using the Caputo generalized Taylor series formula for the Caputo fractional derivative, we construct explicit and implicit FORK methods comparable to the well-known Runge–Kutta schemes for ordinary differential equations.

The remainder of the paper is organized as follows. In Section 2, we review some definitions and properties of fractional calculus. We propose new explicit and implicit FORK methods for solving FDEs in Section 3 and Section 4. In Section 5, the theoretical analysis of the convergency, stability, and consistency of the proposed methods is presented. Finally, in Section 6, some numerical examples demonstrate the effectiveness of the methods proposed. Also, in Appendix A two Mathematica computer programming codes are given.

2. Preliminaries

This section briefly reviews the definitions of the fractional integral and Caputo fractional derivative and explores some of their properties. A more comprehensive introduction to the fractional derivatives can be found in [1,4,33].

Definition 1.

The Riemann–Liouville fractional integral operator of order $\alpha >0$ for a function $f\left(x\right)\in L_1[a,b]$ with $a\ge 0$ is defined as

$$J_a^{\alpha }f\left(x\right)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_a^x{(x-t)}^{\alpha -1}f\left(t\right)dt,x\in [a,b],J_a^{0}f\left(x\right)=f\left(x\right).$$

where $L_1[a,b]=\left\{f\right|f\mathit{is}a\mathit{measurable}\mathit{function}\mathit{on}[a,b]\mathit{and}{\int }_a^b\left|f\left(x\right)\right|dx<\infty \}, \mathsf{\Gamma }$ is the Gamma function.

Definition 2.

The Caputo fractional derivatives of order $\alpha >0$ of a function $f\left(x\right)\in L_1[a,b]$, with $a\ge 0$, is defined as

$$\begin{array}{cc}\hfill {}_a{}^{c}D_x^{\alpha }f\left(x\right)& =J_a^{n-\alpha }{D}^{n}f\left(x\right)\hfill \\ \hfill & =\left\{\begin{array}{c}\frac{1}{\mathsf{\Gamma }(n-\alpha )}{\int }_a^x{(x-t)}^{n-\alpha -1}{D}^{n}f\left(t\right)dt,n-1<\alpha <n,n\in \mathbb{N},\\ \\ D^{n}f\left(x\right),\begin{array}{cc}& \alpha =n.\end{array}\hfill \end{array}\right.\hfill \end{array}$$

(1)

Theorem 1 

(Generalized Taylor formula for Caputo fractional derivative [34]). Suppose that ${\left({}_a{}^{c}D_t^{\alpha }\right)}^{k}f\left(x\right)\in C(a,b]$ for $k=0,1,\dots ,n+1$, where $0<\alpha ⩽1$, then, $\forall x\in [a,b]$, there exist $\xi \in (a,x)$ such that

$$f\left(x\right)=\sum _{i=0}^n\frac{{(x-a)}^{i\alpha }}{\mathsf{\Gamma }(1+i\alpha )}\left({\left({}_a{}^{c}D_t^{\alpha }\right)}^{i}f\right)\left(a\right)+\frac{{(x-a)}^{(n+1)\alpha }}{\mathsf{\Gamma }(1+(n+1\left)\alpha \right)}\left({\left({}_a{}^{c}D_t^{\alpha }\right)}^{(n+1)}\right)f)\left(\xi \right),$$

(2)

where ${\left({}_a{}^{c}D_t^{\alpha }\right)}^n=\underset{\underset{ntimes}{⏟}}{{}_a{}^{c}D_t^{\alpha }{}_a{}^{c}D_t^{\alpha }\cdots {}_a{}^{c}D_t^{\alpha }}.$

There are also two important functions in fractional calculus. They are a direct generalization of the exponential series, which play essential roles in solving the FDEs and in stability analysis.

Definition 3.

The Mittag–Leffler function is defined as

$$E_{\alpha }\left(x\right)=\sum _{k=0}^{\infty }\frac{x^k}{\mathsf{\Gamma }(1+\alpha k)},\Re \left(\alpha \right)>0,x\in \mathbb{C}.$$

In addition, the two-parameter Mittag–Leffler function is defined by

$$E_{\alpha ,\beta }\left(x\right)=\sum _{k=0}^{\infty }\frac{x^k}{\mathsf{\Gamma }(\beta +\alpha k)},\Re \left(\alpha \right)>0,\beta \in \mathbb{C},x\in \mathbb{C}.$$

We note that $E_{\alpha }\left(x\right)=E_{\alpha ,1}\left(x\right)$ and

$$E_1\left(x\right)=\sum _{k=0}^{\infty }\frac{x^k}{\mathsf{\Gamma }(1+k)}=\sum _{k=0}^{\infty }\frac{x^k}{k!}=exp\left(x\right).$$

3. Fractional Order Runge–Kutta Methods

This section presents a new class of FORK methods for the numerical solutions of FDEs. Consider the following FDE with $0<\alpha \le 1$:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_{t_0}{}^{c}D_t^{\alpha }y\left(t\right)=f(t,y\left(t\right)),t\in [t_0,T],\hfill \\ y\left(t_0\right)=y_0.\hfill \end{array}\right.\end{array}$$

(3)

where $y\left(t\right)\in C[t_0,T]$ and $f(t,y\left(t\right))\in C[t_0,T]\times \mathbb{R}.$ $t_0$ is called the base point of fractional derivative.

We set $t_n=t_0+nh$, $n=0,1,\cdots ,N^m$, where $h=\left(T-t_0\right)/N^m$ is the step size, N is a positive integer (in Section 5, we prove that $m\ge 1/\alpha$). For the existence and uniqueness of the solution of the FDE (3), we consider the following theorem [4].

Theorem 2.

Let $\alpha >0$, $y_0\in \mathbb{R}$, $K>0$ and $T>0$ and also let the function $f:G\to \mathbb{R}$ be continuous and fulfill a Lipschitz condition with respect to the second variable, i.e.,

$$|f(t,y_1)-f(t,y_2)|\le L|y_1-y_2|$$

with some constant $L>0$ independent of $t,y_1$ and $y_2$. Define

$$G=\left\{(t,y):t\in [0,T],|y-y_0|\le K\right\},M=Su{p}_{(t,z)\in G}\left|f(t,z)\right|$$

and

$$T^{*}=\left\{\begin{array}{cc}T,\hfill & M=0,\hfill \\ min\{T,{\left(K\mathsf{\Gamma }\right(\alpha +1)/M)}^{1/\alpha }\},\hfill & else.\hfill \end{array}\right.$$

Then, there exists a unique function $y\in C[0,T^{*}]$ solving the initial-value problem (3).

In the sequel, we assume $f(t,y)$ has continuous partial derivatives with respect to t and y to as high an order as we want.

Now, we introduce an s-stage explicit fractional order Runge–Kutta (EFORK) method for FDEs, which is discussed completely with $s=2$ and $s=3$ stages.

Definition 4.

A family of s-stage EFORK methods is defined as

$$\begin{array}{ccc}& & K_1=h^{\alpha }f(t,y),\hfill \\ & & K_2=h^{\alpha }f(t+c_{2}h,y+a_{21}{K}_1),\hfill \\ & & K_3=h^{\alpha }f(t+c_{3}h,y+a_{31}{K}_1+a_{32}{K}_2),\hfill \\ & & ⋮\hfill \\ & & K_s=h^{\alpha }f(t+c_{s}h,y+a_{s1}{K}_1+a_{s2}{K}_2+\cdots +a_{s,s-1}{K}_{s-1}),\hfill \end{array}$$

(4)

with

$$y_{n+1}=y_n+\sum _{i=1}^s{w}_i{K}_i,$$

(5)

where the unknown coefficients ${\left\{a_{ij}\right\}}_{i=2,j=1}^{s,i-1}$ and the unknown weights ${\left\{c_i\right\}}_{i=2}^s$, ${\left\{w_i\right\}}_{i=1}^s$ has to be determined.

To specify a particular method, one needs to provide ${\left\{a_{ij}\right\}}_{i=2,j=1}^{s,i-1}$ and ${\left\{c_i\right\}}_{i=2}^s$, ${\left\{w_i\right\}}_{i=1}^s$ accordingly. Following Butcher, [23], a method of this type is designated by the following scheme:

$c_2$	$a_{21}$
$c_3$	$a_{31}$	$a_{32}$
⋮	⋮		⋱
$c_s$	$a_{s1}$	$a_{s2}$	⋯	$a_{s,s-1}$
	$w_1$	$w_2$	⋯	$w_{s-1}$	$w_s$

We expand $y_{n+1}$ in (5), in powers of $h^{\alpha }$, such that it agrees with the Taylor series expansion of the solution of the FDE (3) in a specified number of terms (see [35]). According to (2), the generalized Taylor formula for $\alpha \in (0,1]$ with respect to the Caputo fractional derivative of the function $y\left(t\right)$ is defined as follows:

$$\begin{array}{cc}\hfill y\left(t\right)& =y\left(t_0\right)+\frac{{(t-t_0)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{}_{t_0}{}^{c}D_t^{\alpha }y\left(t_0\right)+\frac{{(t-t_0)}^{2\alpha }}{\mathsf{\Gamma }(2\alpha +1)}\left({\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{2}y\right)\left(t_0\right)\hfill \\ \hfill & +\frac{{(t-t_0)}^{3\alpha }}{\mathsf{\Gamma }(3\alpha +1)}\left({\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{3}y\right)\left(t_0\right)+\cdots ,\hfill \end{array}$$

(6)

where using (3),

$${}_{t_0}{}^{c}D_t^{\alpha }y\left(t\right)=f(t,y),{\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{2}y\left(t\right)={}_{t_0}{}^{c}D_t^{\alpha }f(t,y),{\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{3}y\left(t\right)={\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{2}f(t,y),\cdots .$$

(7)

Now, we obtain explicit expressions for (7).

Caputo fractional derivatives of composite function $f(t,y(t\left)\right)$ can be computed by fractional Taylor series:

$$\begin{array}{cc}\hfill f(t,y(t\left)\right)& =f(t_0,y\left(t_0\right))+\frac{{(t-t_0)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{f}_t^{\alpha }(t_0,y\left(t_0\right))+\frac{(y-y_0)}{1!}{f}_y(t_0,y\left(t_0\right))\hfill \\ \hfill & +\frac{{(t-t_0)}^{2\alpha }}{\mathsf{\Gamma }(2\alpha +1)}{f}_{t,t}^{\alpha ,\alpha }(t_0,y\left(t_0\right))+\frac{{(y-y_0)}^2}{2!}{f}_{y,y}(t_0,y\left(t_0\right))\hfill \\ \hfill & +\frac{{(t-t_0)}^{\alpha }(y-y_0)}{\mathsf{\Gamma }(\alpha +1)}{f}_{t,y}^{\alpha ,1}(t_0,y\left(t_0\right))+\frac{{(t-t_0)}^{3\alpha }}{\mathsf{\Gamma }(3\alpha +1)}{f}_{t,t,t}^{\alpha ,\alpha ,\alpha }(t_0,y\left(t_0\right))+\cdots ,\hfill \end{array}$$

(8)

where $f_t^{\alpha }$ is the Caputo fractional derivative of $f(t,y(t\left)\right)$ with respect to t. After inserting $y\left(t\right)-y\left(t_0\right)$ from (6) in (8) and by using the fractional derivative of (8) for $\alpha \in (0,1]$, we have

$$\begin{array}{c}\hfill {}_{t_0}{}^{c}D_t^{\alpha }f(t,y\left(t\right))=f_t^{\alpha }(t_0,y\left(t_0\right))+\left(f(t_0,y\left(t_0\right))+\frac{{(t-t_0)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{}_{t_0}{}^{c}D_t^{\alpha }f(t_0,y\left(t_0\right))+\dots \right)f_y(t_0,y\left(t_0\right))\\ \hfill +\frac{{(t-t_0)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{f}_{t,t}^{\alpha ,\alpha }(t_0,y\left(t_0\right))+\frac{1}{2}\left(\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }{(\alpha +1)}^3}{(t-t_0)}^{\alpha }{f}^2(t_0,y\left(t_0\right))+\dots \right)f_{y,y}(t_0,y\left(t_0\right))\\ \hfill +\left(\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }{(\alpha +1)}^3}{(t-t_0)}^{\alpha }f(t_0,y\left(t_0\right))+\dots \right)f_{t,y}^{\alpha ,1}(t_0,y\left(t_0\right))\\ \hfill +\frac{{(t-t_0)}^{2\alpha }}{\mathsf{\Gamma }(2\alpha +1)}{f}_{t,t,t}^{\alpha ,\alpha ,\alpha }(t_0,y\left(t_0\right))+\cdots ,\end{array}$$

and so

$$\begin{array}{c}\hfill {}_{t_0}{}^{c}D_t^{\alpha }f(t_0,y\left(t_0\right))=f_t^{\alpha }(t_0,y\left(t_0\right))+f(t_0,y\left(t_0\right))f_y(t_0,y\left(t_0\right)).\end{array}$$

(9)

In addition,

$$\begin{array}{c}\hfill {}_{t_0}{}^{c}D_t^{2\alpha }f(t,y\left(t\right))={}_{t_0}{}^{c}D_t^{\alpha }f(t_0,y\left(t_0\right))f_y(t_0,y\left(t_0\right))+f_{t,t}^{\alpha ,\alpha }(t_0,y\left(t_0\right))\\ \hfill +\left(\frac{\mathsf{\Gamma }(2\alpha +1)}{2\mathsf{\Gamma }{(\alpha +1)}^2}{f}^2(t_0,y\left(t_0\right))+\dots \right)f_{y,y}(t_0,y\left(t_0\right))\\ \hfill +\left(\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }{(\alpha +1)}^2}f(t_0,y\left(t_0\right))+\dots \right)f_{t,y}^{\alpha ,1}(t_0,y\left(t_0\right))\\ \hfill +\frac{{(t-t_0)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{f}_{t,t,t}^{\alpha ,\alpha ,\alpha }(t_0,y\left(t_0\right))+\cdots ,\end{array}$$

which yields

$$\begin{array}{cc}\hfill {}_{t_0}{}^{c}D_t^{2\alpha }f(t_0,y\left(t_0\right))& =f_t^{\alpha }(t_0,y\left(t_0\right))f_y(t_0,y\left(t_0\right))+f(t_0,y\left(t_0\right))f_y^2(t_0,y\left(t_0\right))+f_{t,t}^{\alpha ,\alpha }(t_0,y\left(t_0\right))\hfill \\ \hfill & +\frac{1}{2}{f}^2(t_0,y\left(t_0\right))f_{y,y}(t_0,y\left(t_0\right))+f(t_0,y\left(t_0\right))f_{t,y}^{\alpha ,1}(t_0,y\left(t_0\right)).\hfill \end{array}$$

(10)

In a similar manner with (9) and (10), we can obtain the higher fractional derivatives of $f(t,y(t\left)\right)$.

Now, by using (9) and (10), we have

$$\begin{array}{cc}\hfill {}_{t_0}{}^{c}D_t^{\alpha }y\left(t_0\right)& =f(t_0,y_0),\hfill \\ \hfill {\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{2}y\left(t_0\right)& =f_t^{\alpha }(t_0,y_0)+f(t_0,y_0)f_y(t_0,y_0),\hfill \\ \hfill {\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{3}y\left(t_0\right)& =f_t^{\alpha }(t_0,y\left(t_0\right))f_y(t_0,y\left(t_0\right))+f(t_0,y\left(t_0\right))f_y^2(t_0,y\left(t_0\right))+f_{t,t}^{\alpha ,\alpha }(t_0,y\left(t_0\right)\hfill \\ \hfill & +\frac{1}{2}{f}^2(t_0,y\left(t_0\right))f_{y,y}(t_0,y\left(t_0\right))+f(t_0,y\left(t_0\right))f_{t,y}^{\alpha ,1}(t_0,y\left(t_0\right)),\hfill \end{array}$$

(11)

where $f_{t,y}^{\alpha ,i}$, $i=1,2,\cdots ,$ represents the ith integer derivative of the function $f_t^{\alpha }$ with respect to y. As we can see from (6), in Caputo fractional derivatives $\left({\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{k}y\right)\left(t_0\right)$, $k=0,1,2,\cdots$, the argument $t_0$ in $y\left(t_0\right)$ and starting value in ${\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^k$ are the same.

To construct an efficient numerical scheme, we should obtain a similar series with the derivatives evaluated in any other point ($t_n>t_0$), such that the expansion can be constructed independently from the starting point $t_0$. In other words, we need

$$\begin{array}{cc}\hfill y\left(t_{n+1}\right)& =y\left(t_n\right)+\frac{h^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{}_{t_n}{}^{c}D_t^{\alpha }y\left(t_n\right)+\frac{h^{2\alpha }}{\mathsf{\Gamma }(2\alpha +1)}\left({\left({}_{t_n}{}^{c}D_t^{\alpha }\right)}^{2}y\right)\left(t_n\right)\hfill \\ \hfill & +\frac{h^{3\alpha }}{\mathsf{\Gamma }(3\alpha +1)}\left({\left({}_{t_n}{}^{c}D_t^{\alpha }\right)}^{3}y\right)\left(t_n\right)+\cdots ,\hfill \end{array}$$

(12)

and $\left({\left({}_{t_n}{}^{c}D_t^{\alpha }\right)}^{i}y\right)\left(t_n\right),i=1,2,\cdots$. To do so, by using ${}_{t_0}{}^{c}D_t^{\alpha }y\left(t\right)$, we obtain ${}_{t_n}{}^{c}D_t^{\alpha }y\left(t\right)$ for $n=1,2,\cdots ,N^m-1$, as

$$\begin{array}{cc}\hfill {}_{t_n}{}^{c}D_t^{\alpha }y\left(t\right)& ={}_{t_0}{}^{c}D_t^{\alpha }y\left(t\right)-\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_{t_0}^{t_n}{(t-s)}^{-\alpha }Dy\left(s\right)ds\hfill \\ \hfill & ={}_{t_0}{}^{c}D_t^{\alpha }y\left(t\right)-\frac{1}{\mathsf{\Gamma }(1-\alpha )}\sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}{(t-s)}^{-\alpha }Dy\left(s\right)ds.\hfill \end{array}$$

(13)

By using the linear Lagrange interpolation formula for $y\left(s\right)$ in support abscissas $\{t_i,t_{i+1}\}$, we have

$$\begin{array}{cc}\hfill y\left(s\right)& \simeq \frac{(s-t_i)}{(t_{i+1}-t_i)}{y}_{i+1}-\frac{(s-t_{i+1})}{(t_{i+1}-t_i)}{y}_i\hfill \\ \hfill & =\frac{(s-t_i)}{h}{y}_{i+1}-\frac{(s-t_{i+1})}{h}{y}_i,s\in [t_i,t_{i+1}],i=0,1,\dots ,n-1,\hfill \end{array}$$

where, for a sufficiently small h, we have

$$Dy\left(s\right)\simeq \frac{1}{h}(y_{i+1}-y_i),s\in [t_i,t_{i+1}],i=0,1,\dots ,n-1,$$

and

$${\int }_{t_i}^{t_{i+1}}{(t-s)}^{-\alpha }Dy\left(s\right)ds\simeq \frac{(y_{i+1}-y_i)}{h(1-\alpha )}\left[{(t-t_i)}^{1-\alpha }-{(t-t_{i+1})}^{1-\alpha }\right],i=0,1,\cdots ,n-1.$$

From (13) and ${}_{t_0}{}^{c}D_t^{\alpha }y\left(t\right)=f(t,y)$, we have

$${}_{t_n}{}^{c}D_t^{\alpha }y\left(t\right)=f(t,y)-\frac{1}{\mathsf{\Gamma }(1-\alpha )}\sum _{i=0}^{n-1}\frac{(y_{i+1}-y_i)}{h(1-\alpha )}\left[{(t-t_i)}^{1-\alpha }-{(t-t_{i+1})}^{1-\alpha }\right].$$

So we may write

$${}_{t_n}{}^{c}D_t^{\alpha }y\left(t\right)=F_n(t,y),n=0,1,2,\dots .$$

(14)

where $F_0(t,y)=f(t,y)$ and for $n=1,2,3,\cdots ,$ we have

$$F_n(t,y)=f(t,y)-\frac{1}{\mathsf{\Gamma }(2-\alpha )}\sum _{i=0}^{n-1}\frac{y_{i+1}-y_i}{h}\left[{(t-t_i)}^{1-\alpha }-{(t-t_{i+1})}^{1-\alpha }\right].$$

Clearly, $F_n(t,y)$ is continuous and satisfies the Lipschitz condition with respect to the second variable, due to the properties of $f(t,y).$ In what follows, for convenience of notation, we rename $F_n(t,y)$ as $f(t,y)$, i.e., in any initial points $t_n>t_0$, $n=1,2,\dots ,N^m-1$, we consider the right terms of (14) as $f(t_n,y_n)$ instead of $F_n(t_n,y_n)$ in any stages.

Now, to construct FORK methods, we can use the Taylor formula (6) and (11), where ${}_{t_n}{}^{c}D_t^{\alpha }y\left(t\right)$ is defined in (14).

3.1. EFORK Method of Order $2\alpha$

Let us introduce the following EFORK method with two stages:

$$\begin{array}{ccc}& & K_1=h^{\alpha }f(t_n,y_n),\hfill \\ & & K_2=h^{\alpha }f(t_n+c_{2}h,y_n+a_{21}{K}_1),\hfill \\ & & y_{n+1}=y_n+w_1{K}_1+w_2{K}_2,\hfill \end{array}$$

(15)

where coefficients $c_2,a_{21}$ and weights $w_1,w_2$ are chosen to make the approximate value $y_{n+1}$ as close as possible to the exact value $y\left(t_{n+1}\right)$. We expand $K_1$ and $K_2$ about the point $(t_n,y_n)$, where we use the Caputo Taylor formula (12) about point $t_n$ and standard integer-order Taylor formula about $y_n$ as

$$\begin{array}{ccc}& & K_1=h^{\alpha }f(t_n,y_n),\hfill \\ & & K_2=h^{\alpha }f(t_n+c_{2}h,y_n+a_{21}{K}_1)\hfill \\ & & =h^{\alpha }\left[f(t_n,y_n)+\frac{c_2^{\alpha }{h}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{f}_t^{\alpha }+a_{21}{h}^{\alpha }{f}_n{f}_y+\frac{c_2^{2\alpha }{h}^{2\alpha }}{\mathsf{\Gamma }(2\alpha +1)}{f}_{t,t}^{\alpha ,\alpha }+\frac{a_{21}^2{h}^{2\alpha }}{2}{f}_n^2{f}_{y,y}\right.\hfill \\ & & \left.+\frac{c_2^{\alpha }{a}_{21}{h}^{2\alpha }}{\mathsf{\Gamma }(\alpha +1)}{f}_n{f}_{t,y}^{\alpha ,1}+\cdots \right]\hfill \\ & & =h^{\alpha }{f}_n+h^{2\alpha }\left(\frac{c_2^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{f}_t^{\alpha }+a_{21}{f}_n{f}_y\right)\hfill \\ & & +h^{3\alpha }\left(\frac{c_2^{2\alpha }}{\mathsf{\Gamma }(2\alpha +1)}{f}_{t,t}^{\alpha ,\alpha }+\frac{a_{21}^2}{2}{f}_n^2{f}_{y,y}+\frac{c_2^{\alpha }{a}_{21}}{\mathsf{\Gamma }(\alpha +1)}{f}_n{f}_{t,y}^{\alpha ,1}\right)+\cdots .\hfill \end{array}$$

Substituting $K_1$ and $K_2$ in (15), we have

$$\begin{array}{cc}\hfill y_{n+1}& =y_n+(w_1+w_2)h^{\alpha }{f}_n+h^{2\alpha }{w}_2\left(\frac{c_2^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{f}_t^{\alpha }+a_{21}{f}_n{f}_y\right)\hfill \\ \hfill & +w_2{h}^{3\alpha }\left(\frac{c_2^{2\alpha }}{\mathsf{\Gamma }(2\alpha +1)}{f}_{t,t}^{\alpha ,\alpha }+\frac{a_{21}^2}{2}{f}_n^2{f}_{y,y}+\frac{c_2^{\alpha }{a}_{21}}{\mathsf{\Gamma }(\alpha +1)}{f}_n{f}_{t,y}^{\alpha ,1}\right)+\cdots \hfill \end{array}$$

(16)

Comparing (12) with (16) and matching coefficients of powers of $h^{\alpha }$, we obtain three equations:

$$\begin{array}{ccc}& & w_1+w_2=\frac{1}{\mathsf{\Gamma }(\alpha +1)},\hfill \\ & & w_2\frac{c_2^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}=\frac{1}{\mathsf{\Gamma }(2\alpha +1)},\hfill \\ & & w_2{a}_{21}=\frac{1}{\mathsf{\Gamma }(2\alpha +1)}.\hfill \end{array}$$

(17)

From these equations, we see that, if $c_2^{\alpha }$ is chosen arbitrarily (nonzero), then

$$a_{21}=\frac{c_2^{\alpha }}{\mathsf{\Gamma }(\alpha +1)},w_2=\frac{\mathsf{\Gamma }(\alpha +1)}{c_2^{\alpha }\mathsf{\Gamma }(2\alpha +1)},w_1=\frac{1}{\mathsf{\Gamma }(\alpha +1)}-\frac{\mathsf{\Gamma }(\alpha +1)}{c_2^{\alpha }\mathsf{\Gamma }(2\alpha +1)}.$$

(18)

Inserting (17) and (18) in (16) we get

$$\begin{array}{cc}\hfill y_{n+1}& =y_n+\frac{h^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{f}_n+\frac{h^{2\alpha }}{\mathsf{\Gamma }(2\alpha +1)}\left(f_t^{\alpha }+f_n{f}_y\right)\hfill \\ \hfill & +\frac{c_2^{\alpha }{h}^{3\alpha }}{\mathsf{\Gamma }(2\alpha +1)}\left[\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)}{f}_{t,t}^{\alpha ,\alpha }+\frac{1}{2\mathsf{\Gamma }(\alpha +1)}{f}_n^2{f}_{y,y}+\frac{1}{\mathsf{\Gamma }(\alpha +1)}{f}_n{f}_{t,y}^{\alpha ,1}\right]+\cdots .\hfill \end{array}$$

(19)

Subtracting (19) from (12), we obtain the local truncation error $T_n$

$$\begin{array}{cc}\hfill T_n& =y\left(t_{n+1}\right)-y_{n+1}=h^{3\alpha }\left(\frac{1}{\mathsf{\Gamma }(3\alpha +1)}-\frac{c_2^{\alpha }\mathsf{\Gamma }(\alpha +1)}{{\left(\mathsf{\Gamma }(2\alpha +1)\right)}^2}\right)f_{t,t}^{\alpha ,\alpha }\hfill \\ \hfill & +h^{3\alpha }\left(\frac{2}{\mathsf{\Gamma }(3\alpha +1)}-\frac{c_2^{\alpha }}{2\mathsf{\Gamma }(\alpha +1)}\right)f_n^2{f}_{y,y}\hfill \\ \hfill & +h^{3\alpha }\left(\frac{1}{\mathsf{\Gamma }(3\alpha +1)}-\frac{c_2^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}\right)f_n{f}_{t,y}^{\alpha ,1}+\cdots .\hfill \end{array}$$

(20)

We conclude that no choice of the parameter $c_2^{\alpha }$ will make the leading term of $T_n$ vanish for all functions $f(t,y)$. Sometimes, the free parameters are chosen to minimize the sum of the absolute values of the coefficients in $T_n$. Such a choice is called the optimal choice.

$$c_2^{\alpha }=\frac{{\left(\mathsf{\Gamma }(2\alpha +1)\right)}^2}{\mathsf{\Gamma }(3\alpha +1)\mathsf{\Gamma }(\alpha +1)},c_2^{\alpha }=\frac{4\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)},or{c}_2^{\alpha }=\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}.$$

From (20) we have $\frac{T_n}{h^{\alpha }}={\left(h^{\alpha }\right)}^2$. So, we deduce that the 2-stage EFORK method (15) is of order $2\alpha$.

Now, the two-stage EFORK method by listing the coefficients is as follows:

$c_2$	$a_{21}$		,
	$w_1$	$w_2$

,

Choosing $w_1=w_2$ yields

${\left(\frac{2\mathsf{\Gamma }{(\alpha +1)}^2}{\mathsf{\Gamma }(2\alpha +1)}\right)}^{\frac{1}{\alpha }}$	$\frac{2\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)}$		.
	$\frac{1}{2\mathsf{\Gamma }(\alpha +1)}$	$\frac{1}{2\mathsf{\Gamma }(\alpha +1)}$

In addition, the optimal cases of the two-stage EFORK method are

${\left(\frac{{\left(\mathsf{\Gamma }(2\alpha +1)\right)}^2}{\mathsf{\Gamma }(3\alpha +1)\mathsf{\Gamma }(\alpha +1)}\right)}^{\frac{1}{\alpha }}$	$\frac{{\left(\mathsf{\Gamma }(2\alpha +1)\right)}^2}{\mathsf{\Gamma }(3\alpha +1)\mathsf{\Gamma }{(\alpha +1)}^2}$		,
	$\frac{1}{\mathsf{\Gamma }(\alpha +1)}-\frac{\mathsf{\Gamma }(3\alpha +1)\mathsf{\Gamma }{(\alpha +1)}^2}{\mathsf{\Gamma }{(2\alpha +1)}^3}$	$\frac{\mathsf{\Gamma }(3\alpha +1)\mathsf{\Gamma }{(\alpha +1)}^2}{\mathsf{\Gamma }{(2\alpha +1)}^3}$

${\left(\frac{4\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}\right)}^{\frac{1}{\alpha }}$	$\frac{4}{\mathsf{\Gamma }(3\alpha +1)}$		,
	$\frac{1}{\mathsf{\Gamma }(\alpha +1)}-\frac{\mathsf{\Gamma }(3\alpha +1)}{4\mathsf{\Gamma }(2\alpha +1)}$	$\frac{\mathsf{\Gamma }(3\alpha +1)}{4\mathsf{\Gamma }(2\alpha +1)}$

${\left(\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}\right)}^{\frac{1}{\alpha }}$	$\frac{1}{\mathsf{\Gamma }(3\alpha +1)}$		.
	$\frac{1}{\mathsf{\Gamma }(\alpha +1)}-\frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)}$	$\frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)}$

3.2. EFORK Method of Order $3\alpha$

Following (4) and (5), we define a three-stage EFORK method as

$$\begin{array}{ccc}& & K_1=h^{\alpha }f(t_n,y_n),\hfill \\ & & K_2=h^{\alpha }f(t_{+}{c}_{2}h,y_n+a_{21}{K}_1),\hfill \\ & & K_3=h^{\alpha }f(t_n+c_{3}h,y_n+a_{31}{K}_1+a_{32}{K}_2),\hfill \\ & & y_{n+1}=y_n+w_1{K}_1+w_2{K}_2+w_3{K}_3.\hfill \end{array}$$

(21)

where unknown parameters ${\left\{c_i\right\}}_{i=2}^3,{\left\{a_{ij}\right\}}_{i=2,j=1}^{3,i-1}$, and ${\left\{w_i\right\}}_{i=1}^3$ have to be determined accordingly. By using the same procedure as we followed for the two-stage EFORK method, expanding $K_1$, $K_2$ and $K_3$, comparing with (12) and matching coefficients of powers of $h^{\alpha }$, we obtain the following equations:

$$\begin{array}{ccc}\hfill & & w_1+w_2+w_3=\frac{1}{\mathsf{\Gamma }(\alpha +1)},a_{21}=\frac{c_2^{\alpha }}{\mathsf{\Gamma }(\alpha +1)},w_2{c}_2^{2\alpha }+w_3{c}_3^{2\alpha }=\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)},\hfill \\ & & a_{31}+a_{32}=\frac{c_3^{\alpha }}{\mathsf{\Gamma }(\alpha +1)},w_2{c}_2^{\alpha }+w_3{c}_3^{\alpha }=\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)},w_3{a}_{32}{c}_2^{\alpha }=\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}.\hfill \end{array}$$

(22)

Now, we have six equations with eight unknown parameters. According to the Butcher tableau for the three-stage EFORK method, we have

$c_2$	$a_{21}$
$c_3$	$a_{31}$	$a_{32}$
	$w_1$	$w_2$	$w_3$

If $c_2$ and $c_3$ are arbitrarily chosen, we calculate weights ${\left\{w_i\right\}}_{i=1}^3$ and coefficients ${\left\{a_{ij}\right\}}_{i=2,j=1}^{3,i-1}$ from (22) as

${\left(\frac{1}{2\alpha !}\right)}^{\frac{1}{\alpha }}$	$\frac{1}{2{(\alpha !)}^2}$
${\left(\frac{1}{4\alpha !}\right)}^{\frac{1}{\alpha }}$	$\frac{{(\alpha !)}^2\left(2\alpha \right)!+2\left(2\alpha \right){!}^2-\left(3\alpha \right)!}{4{(\alpha !)}^2(2\left(2\alpha \right){!}^2-\left(3\alpha \right)!)}$	$-\frac{\left(2\alpha \right)!}{4\left(2\right(2\alpha )!)-\left(3\alpha \right)!}$
	$\frac{8{(\alpha !)}^2\left(2\alpha \right)!}{\left(3\alpha \right)!}-\frac{6{(\alpha !)}^2}{\left(2\alpha \right)!}+\frac{1}{\alpha !}$	$\frac{2{(\alpha !)}^2(4\left(2\alpha \right){!}^2-\left(3\alpha \right)!)}{\left(2\alpha \right)!\left(3\alpha \right)!}$	$-\frac{8{(\alpha !)}^2(2\left(2\alpha \right){!}^2-\left(3\alpha \right)!)}{\left(2\alpha \right)!\left(3\alpha \right)!}$

As a result, we obtain $\frac{T_n}{h^{\alpha }}={\left(h^{\alpha }\right)}^3$. In a similar procedure to the two and three-stage EFORK methods, we can construct s-stage EFORK methods for $s>3.$

As we can see, to obtain the higher fractional order Runge–Kutta methods, we must consider a method with additional stages. In the next section, we express implicit fractional order Runge–Kutta (IFORK) methods with low stages and high orders.

4. IFORK Methods

We define a s-stage IFORK method by the following equations:

$$K_i=\frac{1}{s}{h}^{\alpha }\sum _{k=1}^{s}f(t_n+c_{ik}h,y_n+\sum _{j=1}^s{a}_{ij}{K}_j),i=1,2,\dots ,s$$

(23)

and

$$y_{n+1}=y_n+\sum _{i=1}^s{w}_i{K}_i,$$

(24)

where

$$\frac{c_{i1}^{\alpha }+c_{i2}^{\alpha }+\dots +c_{is}^{\alpha }}{\alpha !}=s(a_{i1}+a_{i2}+\cdots +a_{is}),i=1,2,\cdots ,s$$

(25)

and the parameters ${\left\{a_{ij}\right\}}_{i,j=1}^{s,s}$, ${\left\{w_i\right\}}_{i=1}^s$ are arbitrary. We state the IFORK method by listing the coefficients as follows:

$c_{11}$	$c_{12}$	⋯	$c_{1s}$	$a_{11}$	$a_{12}$	⋯	$a_{1s}$
$c_{21}$	$c_{22}$	⋯	$c_{2s}$	$a_{21}$	$a_{22}$	⋯	$a_{2s}$
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
$c_{s1}$	$c_{s2}$	⋯	$c_{ss}$	$a_{s1}$	$a_{s2}$	⋯	$a_{ss}$
				$w_1$	$w_2$	⋯	$w_s$

Since the functions $K_i$ are defined by a set of s implicit equations, the derivation of the implicit methods is complicated. Therefore, only the case $s=2$ is investigated.

Consider (23)–(25) with $s=2$ as

$$K_i=\frac{1}{2}{h}^{\alpha }\left[f(t_n+c_{i1}h,y_n+a_{i1}{K}_1+a_{i2}{K}_2)+f(t_n+c_{i2}h,y_n+a_{i1}{K}_1+a_{i2}{K}_2)\right],i=1,2$$

(26)

$$y_{n+1}=y_n+w_1{K}_1+w_2{K}_2$$

(27)

where

$$\frac{c_{i1}^{\alpha }+c_{i2}^{\alpha }}{\alpha !}=2(a_{i1}+a_{i2}),i=1,2.$$

(28)

By using a similar procedure as we followed for the EFORK method, we expand $K_i$ about the point $(t_n,y_n)$, where we apply the Caputo Taylor formula (12) about $t_n$ and standard integer-order Taylor formula about $y_n$.

$$\begin{array}{cc}\hfill K_i& =\frac{1}{2}{h}^{\alpha }[2f_n+\frac{(c_{i1}^{\alpha }+c_{i2}^{\alpha })h^{\alpha }}{\alpha !}{f}_t^{\alpha }+2(a_{i1}{K}_1+a_{i2}{K}_2)f_y+\frac{(c_{i1}^{\alpha }+c_{i2}^{\alpha })h^{2\alpha }}{\left(2\alpha \right)!}{f}_{t,t}^{\alpha ,\alpha }\hfill \\ \hfill & +{(a_{i1}{K}_1+a_{i2}{K}_2)}^2{f}_{y,y}+\frac{(c_{i1}^{\alpha }+c_{i2}^{\alpha })h^{\alpha }}{\alpha !}(a_{i1}{K}_1+a_{i2}{K}_2)f_{t,y}^{\alpha ,1}\hfill \\ \hfill & +\frac{(c_{i1}^{3\alpha }+c_{i2}^{3\alpha })h^{3\alpha }}{\left(3\alpha \right)!}{f}_{t,t,t}^{\alpha ,\alpha ,\alpha }+\frac{(c_{i1}^{2\alpha }+c_{i2}^{2\alpha })h^{2\alpha }}{\left(2\alpha \right)!}(a_{i1}{K}_1+a_{i2}{K}_2)f_{t,t,y}^{\alpha ,\alpha ,1}\hfill \\ \hfill & +\frac{(c_{i1}^{\alpha }+c_{i2}^{\alpha })h^{\alpha }}{\alpha !}\frac{{(a_{i1}{K}_1+a_{i2}{K}_2)}^2}{2}{f}_{t,y,y}^{\alpha ,1,1}+\frac{{(a_{i1}{K}_1+a_{i2}{K}_2)}^3}{3}{f}_{y,y,y}+\cdots ],\hfill \end{array}$$

(29)

where $i=1,2$.

Since Equation (29) are implicit, we cannot obtain the explicit forms for $K_1$ and $K_2$. To determine the explicit form $K_i$, we consider

$$K_i=h^{\alpha }{A}_i+h^{2\alpha }{B}_i+h^{3\alpha }{C}_i+\cdots ,i=1,2$$

(30)

where $A_i$, $B_i$ and $C_i$ are unknowns. Substituting (30) into (29) and matching the coefficients of powers of $h^{\alpha }$, we get

$$\begin{array}{cc}\hfill A_i& =f_n,\hfill \\ \hfill B_i& =\frac{c_{i1}^{\alpha }+c_{i2}^{\alpha }}{2(\alpha !)}[f_t^{\alpha }+f{f}_y]=\frac{c_{i1}^{\alpha }+c_{i2}^{\alpha }}{2(\alpha !)}{D}^{\alpha }f,\hfill \\ \hfill C_i& =\left(a_{i1}\frac{c_{11}^{\alpha }+c_{12}^{\alpha }}{2(\alpha !)}+a_{i2}\frac{c_{21}^{\alpha }+c_{22}^{\alpha }}{2(\alpha !)}\right)f_y{D}^{\alpha }f+\frac{c_{i1}^{2\alpha }+c_{i2}^{2\alpha }}{2\left(2\alpha \right)!}{f}_{t,t}^{\alpha ,\alpha }\hfill \\ \hfill & +\frac{1}{4}{\left(\frac{c_{i1}^{\alpha }+c_{i2}^{\alpha }}{\alpha !}\right)}^2\left(\frac{1}{2}{f}^2{f}_{yy}+f{f}_{t,y}^{\alpha ,1}\right),\hfill \\ \hfill ⋮\end{array}$$

(31)

Inserting (30) and (31) into (27), we have

$$\begin{array}{cc}\hfill y_{n+1}& =y_n+h^{\alpha }\left[w_1{A}_1+w_2{A}_2\right]+h^{2\alpha }\left[w_1{B}_1+w_2{B}_2\right]+h^{3\alpha }\left[w_1{C}_1+w_2{C}_2\right]+\cdots .\hfill \end{array}$$

(32)

Comparing (32) with (12) and equating the coefficient of powers of $h^{\alpha }$, we can get an IFORK method of different orders.

4.1. IFORK Method of Order $2\alpha$

To obtain an IFORK method of order $2\alpha$, we equate the coefficients of $h^{\alpha }$ and $h^{2\alpha }$ in (12) and (32) correspondingly to get

$$\begin{array}{ccc}& & w_1+w_2=\frac{1}{\alpha !},\hfill \\ & & w_1\frac{c_{11}^{\alpha }+c_{12}^{\alpha }}{\alpha !}+w_2\frac{c_{21}^{\alpha }+c_{22}^{\alpha }}{\alpha !}=\frac{2}{\left(2\alpha \right)!},\hfill \end{array}$$

where

$$2(a_{11}+a_{12})=\frac{c_{11}^{\alpha }+c_{12}^{\alpha }}{\alpha !},2(a_{21}+a_{22})=\frac{c_{21}^{\alpha }+c_{22}^{\alpha }}{\alpha !}.$$

There are now six arbitrary parameters to be prescribed. If we neglect $K_2$, i.e., if we choose $a_{21}=a_{22}=a_{12}=0$, $w_2=0$, from the above equations, we find

$$w_1=\frac{1}{\alpha !},c_{11}^{\alpha }+c_{12}^{\alpha }=\frac{2{(\alpha !)}^2}{\left(2\alpha \right)!},a_{11}=\frac{\alpha !}{\left(2\alpha \right)!}.$$

Therefore, a one-stage IFORK method of order $2\alpha$ is obtained as follows:

$$\left\{\begin{array}{c}{K}_1=\frac{1}{2}{h}^{\alpha }\left[f(t_n+c_{11}h,y_n+a_{11}{K}_1)+f(t_n+c_{12}h,y_n+a_{11}{K}_1)\right],\hfill \\ y_{n+1}=y_n+w_1{K}_1.\hfill \end{array}\right.$$

(33)

4.2. IFORK Method of Order $3\alpha$

In addition, we can get an IFORK method of order $3\alpha$ with two stages (26)–(28) when equating the coefficients of $h^{\alpha }$, $h^{2\alpha }$ and $h^{3\alpha }$ in (12) and (32) accordingly. In such case, we obtain the following system of equations:

$$\begin{array}{ccc}& & w_1+w_2=\frac{1}{\alpha !},\hfill \\ & & w_1\frac{c_{11}^{\alpha }+c_{12}^{\alpha }}{\alpha !}+w_2\frac{c_{21}^{\alpha }+c_{22}^{\alpha }}{\alpha !}=\frac{2}{\left(2\alpha \right)!},\hfill \\ & & w_1\left(a_{11}\frac{c_{11}^{\alpha }+c_{12}^{\alpha }}{\alpha !}+a_{12}\frac{c_{21}^{\alpha }+c_{22}^{\alpha }}{\alpha !}\right)+w_2\left(a_{21}\frac{c_{11}^{\alpha }+c_{12}^{\alpha }}{\alpha !}+a_{22}\frac{c_{21}^{\alpha }+c_{22}^{\alpha }}{\alpha !}\right)=\frac{2}{\left(3\alpha \right)!},\hfill \\ & & w_1\frac{c_{11}^{2\alpha }+c_{12}^{2\alpha }}{\left(2\alpha \right)!}+w_2\frac{c_{21}^{2\alpha }+c_{22}^{2\alpha }}{\left(2\alpha \right)!}=\frac{2}{\left(3\alpha \right)!},\hfill \\ & & w_1{\left(\frac{c_{11}^{\alpha }+c_{12}^{\alpha }}{\alpha !}\right)}^2+w_2{\left(\frac{c_{21}^{\alpha }+c_{22}^{\alpha }}{\alpha !}\right)}^2=\frac{8}{\left(3\alpha \right)!},\hfill \end{array}$$

where

$$2(a_{11}+a_{12})=\frac{c_{11}^{\alpha }+c_{12}^{\alpha }}{\alpha !},2(a_{21}+a_{22})=\frac{c_{21}^{\alpha }+c_{22}^{\alpha }}{\alpha !}.$$

The three free parameters can be chosen so that $K_1$ or $K_2$ are explicit. If we want $K_1$ to be explicit, we choose

$$c_{11}=a_{11}=a_{12}=0.$$

Thus, the IFORK method of order $3\alpha$, which is explicit in $K_1$ is given by

$$\left\{\begin{array}{c}{K}_1=\frac{1}{2}{h}^{\alpha }\left[f(t_n,y_n)+f(t_n+c_{12}h,y_n)\right],\hfill \\ K_2=\frac{1}{2}{h}^{\alpha }\left[f(t_n+c_{21}h,y_n+a_{21}{K}_1+a_{22}{K}_2)+f(t_n+c_{22}h,y_n+a_{21}{K}_1+a_{22}{K}_2)\right],\hfill \\ y_{n+1}=y_n+w_1{K}_1+w_2{K}_2.\hfill \end{array}\right.$$

(34)

where the coefficients are given by

$c_{11}$	$c_{12}$	$a_{11}$	$a_{12}$
$c_{21}$	$c_{22}$	$a_{21}$	$a_{22}$	,
		$w_1$	$w_2$

0	0	0	0
${\left(\frac{\left(2\alpha \right)!(2(\alpha !)-\sqrt{2}\sqrt{\left(2\alpha \right)!-2{(\alpha !)}^2})}{\left(3\alpha \right)!}\right)}^{\frac{1}{\alpha }}$	${\left(\frac{\left(2\alpha \right)!(2(\alpha !)+\sqrt{2}\sqrt{\left(2\alpha \right)!-2{(\alpha !)}^2})}{\left(3\alpha \right)!}\right)}^{\frac{1}{\alpha }}$	$\frac{\left(2\alpha \right)!}{\left(3\alpha \right)!}$	$\frac{\left(2\alpha \right)!}{\left(3\alpha \right)!}$
		$\frac{1}{\alpha !}-\frac{\left(3\alpha \right)!}{2\left(2\alpha \right){!}^2}$	$\frac{\left(3\alpha \right)!}{2\left(2\alpha \right){!}^2}$

5. Theoretical Analysis

To ensure that the obtained numerical solution of FORK algorithms approximates the exact solution of FDEs correctly, we first discuss in this section the consistency of the methods and second the convergence analysis of the FORK methods that may impose some additional conditions under which the approximate solution, discussed in Section 3 and Section 4, converges to the exact solution of the problem.

5.1. Consistency

The EFORK and IFORK methods considered before belong to the class of methods that are characterized by the use of $y_n$ on the computation of $y_{n+1}$. This family of one-step methods admits the following representation:

$$\begin{array}{ccc}\hfill & & y_{n+1}=y_n+h^{\alpha }\mathsf{\Phi }(t_n,y_n,y_{n+1},h),n=0,\dots ,N^m-1,\hfill \\ & & y_0=y\left(t_0\right).\hfill \end{array}$$

(35)

where $\mathsf{\Phi }:[t_0,T]\times {\mathbb{R}}^2\times (0,h_0]\to \mathbb{R}$ and for the particular case of the explicit methods we have the representation

$$\begin{array}{ccc}\hfill & & y_{n+1}=y_n+h^{\alpha }\mathsf{\Phi }(t_n,y_n,h),n=0,\dots ,N^m-1,\hfill \\ & & y_0=y\left(t_0\right).\hfill \end{array}$$

(36)

with $\mathsf{\Phi }:[t_0,T]\times \mathbb{R}\times (0,h_0]\to \mathbb{R}$.

We define the truncation error ${\tau }_n$ by

$${\tau }_n=\frac{y_{n+1}-y_n}{h^{\alpha }}-\mathsf{\Phi }(t_n,y_n,y_{n+1},h).$$

(37)

The one-step method (35) and (36) is said to be consistent with Equation (3) if

$$\underset{h\to 0}{lim}{\tau }_n=0,N^m=(T-t_0)/h.$$

Using (12) and (37), we may write

$$\begin{array}{cc}\hfill \underset{h\to 0}{lim}{\tau }_n& {\displaystyle =\underset{h\to 0}{lim}\frac{y_{n+1}-y_n}{h^{\alpha }}-\underset{h\to 0}{lim}\mathsf{\Phi }(t_n,y_n,y_{n+1},h),}\hfill \\ \hfill & =\frac{1}{\mathsf{\Gamma }(\alpha +1)}{}_{t_n}^c{D}_t^{\alpha }y\left(t_n\right)-\underset{h\to 0}{lim}\mathsf{\Phi }(t_n,y\left(t_n\right),y\left(t_{n+1}\right),h),\hfill \\ \hfill & {\displaystyle =\frac{1}{\mathsf{\Gamma }(\alpha +1)}{F}_n(t_n,y\left(t_n\right))-\underset{h\to 0}{lim}\mathsf{\Phi }(t_n,y\left(t_n\right),y(t_n+h),h).}\hfill \end{array}$$

Hence, we may conclude that the proposed one-step IFORK methods are consistent if and only if

$$\mathsf{\Phi }(t,y,y,0)=\frac{1}{\mathsf{\Gamma }(\alpha +1)}{F}_n(t,y),$$

or briefly

$$\mathsf{\Phi }(t,y,y,0)=\frac{1}{\mathsf{\Gamma }(\alpha +1)}f(t,y).$$

Similarly, for explicit methods, we have

$$\mathsf{\Phi }(t,y,0)=\frac{1}{\mathsf{\Gamma }(\alpha +1)}f(t,y).$$

As an example, consider the two-stage EFORK method (15) with (17),

$$y_{n+1}=y_n+h^{\alpha }\left[w_{1}f(t_n,y_n)+w_{2}f(t_n+c_{2}h,y_n+a_{21}{K}_1)\right],$$

where, in comparison to (36), we have

$$\mathsf{\Phi }(t,y,h)=\left[w_{1}f(t,y)+w_{2}f(t+c_{2}h,y+a_{21}{K}_1)\right],$$

Hence, as h tends to 0, it yields

$$\mathsf{\Phi }(t,y,0)=(w_1+w_2)f(t,y),$$

and by using (17), we may write

$$\mathsf{\Phi }(t,y,0)=\frac{1}{\mathsf{\Gamma }(\alpha +1)}f(t,y).$$

Therefore, the two-stage EFORK method (15) is consistent. In addition, the three-stage EFORK method (21) is consistent for

$$\begin{array}{ccc}& & \mathsf{\Phi }(t,y,h)=\left[w_{1}f(t,y)+w_{2}f(t+c_{2}h,y+a_{21}{K}_1)+w_{3}f(t+c_{3}h,y+a_{31}{K}_1+a_{32}{K}_2)\right],\hfill \\ & & \mathsf{\Phi }(t,y,0)=(w_1+w_2+w_3)f(t,y),\hfill \end{array}$$

and so from (22)

$$\mathsf{\Phi }(t,y,0)=\frac{1}{\mathsf{\Gamma }(\alpha +1)}f(t,y).$$

Similarly, we can show the consistency of all proposed FORK methods in Section 3 and Section 4.

5.2. Convergence Analysis

Here, we investigate the convergence behavior of the proposed FORK methods (without loss of generality, we consider only explicit FORK methods). To do so, we express a definition of regularity from [35].

Definition 5.

A one-step method of the form (36)

$$y_{n+1}=y_n+h^{\alpha }\mathsf{\Phi }(t_n,y_n,h),n=0,1,2,\dots ,N^m-1,$$

(38)

is said to be regular if the function $\mathsf{\Phi }(t,y,h)$ is defined and continuous in the domain $t\in [0,T]$, $y\in [0,T^{*}]$ and $h\in [0,h_0]$ ($h_0$ is a positive constant) and if there exists a constant L such that

$$\left|\mathsf{\Phi }\right(t,y,h)-\mathsf{\Phi }(t,z,h\left)\right|\le L|y-z|,$$

for every $t\in [0,T]$, $y,z\in [0,T^{*}]$ and $h\in [0,h_0]$.

To discuss the convergence of the EFORK methods, first, we prove that the given methods in Section 3 are regular. We know from Theorem 2 that $f(t,y)$ satisfies a Lipschitz condition with respect to the second variable. Thus,

$$\begin{array}{cc}\hfill |\mathsf{\Phi }(t_n,y_n,h)-\mathsf{\Phi }(t_n,y_n^{*},h)|& =h^{-\alpha }\left|\sum _{i=1}^s{w}_i{K}_i-\sum _{i=1}^s{w}_i{K}_i^{*}\right|\hfill \\ \hfill & \le h^{-\alpha }\left(w_1|K_1-K_1^{*}|+w_2|K_2-K_2^{*}|+\dots +w_s|K_s-K_s^{*}|\right)\hfill \\ \hfill & \le w_{1}L|y_n-y_n^{*}|+w_{2}L|y_n+a_{21}{K}_1-y_n^{*}-a_{21}{K}_1^{*}|+\dots \hfill \\ \hfill & +w_{s}L|y_n+a_{s1}{K}_1+a_{s2}{K}_2+\dots +a_{ss}{K}_s-y_n^{*}-a_{s1}{K}_1^{*}\hfill \\ \hfill & -a_{s2}{K}_2^{*}-\dots -a_{ss}{K}_s^{*}|\hfill \\ \hfill & \le \dots \le L^{*}|y_n-y_n^{*}|.\hfill \end{array}$$

Therefore, the function $\mathsf{\Phi }$ satisfies a Lipschitz condition in y and it is also continuous; thus, EFORK methods are regular. To establish the convergence behavior, we need the following Lemma from [35].

Lemma 1.

Let ${\omega }_0,{\omega }_1,{\omega }_2,\dots$ be a sequence of real positive numbers that satisfy

$${\omega }_{n+1}\le (1+\zeta ){\omega }_n+\mu ,n=0,1,2\dots$$

where ζ, μ are positive constants. Then,

$${\omega }_n\le e^{n\zeta }{\omega }_0+\left(\frac{e^{n\zeta }-1}{\zeta }\right)\mu ,n=0,1,2,\dots .$$

We now discuss the behavior of the error $e_n=y\left(t_n\right)-y_n$ in EFORK method for the initial-value problem (3).

Theorem 3.

Consider the initial value problem (3) and let $f(t,y(t\left)\right)$ be continuous and satisfy a Lipschitz condition with Lipschitz constant L, and also let ${\left({}_{t_0}{}^{c}D_t^{\alpha }\right)}^{(s+1)}y\left(t\right)$ be continuous for $t\in [t_0,T]$, Then, the given EFORK method in Section 3 is convergent for $m\alpha \ge 1$ if and only if it is consistent.

Proof. 

Let the EFORK method be consistent, and the method can be written in the form

$$y_{n+1}=y_n+h^{\alpha }\mathsf{\Phi }(t_n,y_n,h).$$

(39)

The exact value $y\left(t_n\right)$ will satisfy

$$y\left(t_{n+1}\right)=y\left(t_n\right)+h^{\alpha }\mathsf{\Phi }(t_n,y\left(t_n\right),h)+T_n,$$

(40)

where $T_n$ is the truncation error. By subtracting (39) from (40), we have

$$\begin{array}{cc}\hfill & |e_{n+1}|\le |e_n|+h^{\alpha }|\left(\mathsf{\Phi }(t_n,y\left(t_n\right),h)-\mathsf{\Phi }(t_n,y_n,h)\right)|+|T_n|.\hfill \end{array}$$

Now, from the regularity of the EFORK method, it follows that

$$\begin{array}{cc}\hfill & |e_{n+1}|\le |e_n|+h^{\alpha }L|y\left(t_n\right)-y_n|+|T_n|\le (1+h^{\alpha }L)|e_n|+|T_n|.\hfill \end{array}$$

By using the Lemma 1, we have

$$|e_n|\le {(1+h^{\alpha }L)}^n|e_0|+\left(\frac{e^{n{h}^{\alpha }L}-1}{h^{\alpha }L}\right)\left|T_n\right|,$$

where we assumed that the local truncation error for a sufficiently large n is constant, i.e., $\mathcal{T}=T_n,n=0,1,2,\dots$ In addition, assume that $e_0=0$ and $|T_n|=O\left(h^{p\alpha }\right),p\ge 3$; therefore,

$$\begin{array}{cc}\hfill & |e_n|\le O\left(h^{p\alpha }\right)\left(\frac{e^{n{h}^{\alpha }L}-1}{h^{\alpha }L}\right).\hfill \end{array}$$

In Section 3, we assumed $N^m=\left(T-t_0\right)/h,$ so we have

$$\begin{array}{cc}\hfill & |e_n|\le O\left(h^{(p-1)\alpha }\right)\left(\frac{e^{{(T-t_0)}^{\frac{1}{m}}L{h}^{\alpha -\frac{1}{m}}}-1}{L}\right).\hfill \end{array}$$

Thus, the EFORK methods of Section 3.1 and Section 3.2 are convergent if $\alpha -\frac{1}{m}\ge 0$, i.e $m\alpha \ge 1$. Conversely, let the EFORK method be convergent. It is sufficient that we give a limit of (39) as h tends to 0. Now, the proof of the theorem is complete. □

5.3. Stability Analysis

For the stability analysis of the proposed methods in Section 3 and Section 4, we consider the FDE:

$$\begin{array}{ccc}& & {}_{t_0}{}^{c}D_t^{\alpha }y\left(t\right)=\lambda y\left(t\right),\lambda \in \mathbb{C},0<\alpha \le 1,\hfill \\ & & y\left(t_0\right)=y_0.\hfill \end{array}$$

(41)

According to [1], the exact solution of (41) is $y\left(t\right)=E_{\alpha }\left(\lambda {(t-t_0)}^{\alpha }\right)y_0$. When $Re\left(\lambda \right)<0$, the solution of (41) asymptotically tends to 0 as $t\to \infty$.

We apply the two-stage EFORK method (15) to Equation (41) and obtain

$$\begin{array}{cc}\hfill K_1& =h^{\alpha }f(t_n,y_n)=\lambda h^{\alpha }{y}_n,\hfill \\ \hfill K_2& =h^{\alpha }f(t_n+c_{2}h,y_n+a_{21}{K}_1)=\lambda h^{\alpha }\left(y_n+a_{21}\lambda h^{\alpha }{y}_n\right)\hfill \\ \hfill & =\left[\lambda h^{\alpha }+a_{21}{\left(\lambda h^{\alpha }\right)}^2\right]y_n,\hfill \\ \hfill y_{n+1}& =y_n+w_1{K}_1+w_2{K}_2=y_n+\frac{1}{2\mathsf{\Gamma }(\alpha +1)}\left[2\lambda h^{\alpha }+a_{21}{\left(\lambda h^{\alpha }\right)}^2\right]y_n\hfill \\ \hfill & =\left[1+\frac{\lambda h^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}+\frac{a_{21}{\left(\lambda h^{\alpha }\right)}^2}{2\mathsf{\Gamma }(\alpha +1)}\right]y_n=\left[1+\frac{\lambda h^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}+\frac{c_2^{\alpha }{\left(\lambda h^{\alpha }\right)}^2}{2{\left(\mathsf{\Gamma }(\alpha +1)\right)}^2}\right]y_n\hfill \\ \hfill & =\left[1+\frac{\lambda h^{\alpha }}{\alpha !}+\frac{c_2^{\alpha }{\left(\lambda h^{\alpha }\right)}^2}{2{(\alpha !)}^2}\right]y_n.\hfill \end{array}$$

Therefore, the growth factor for the two-stage EFORK method (15) is [35]

$$E\left(\lambda h^{\alpha }\right)=1+\frac{\lambda h^{\alpha }}{\alpha !}+\frac{c_2^{\alpha }{\left(\lambda h^{\alpha }\right)}^2}{2{(\alpha !)}^2},$$

Now, consider the following definition ([35]):

Definition 6.

A numerical method is called absolutely stable in the sense of Dahlquist if and only if $\left|E\right(\lambda h^{\alpha }\left)\right|\le 1$ when the method is applied with any positive step-size h to the test Equation (41).

The interval of the absolute stability of a numerical method is defined as $[\mathrm{Re}\left(\lambda h^{\alpha }\right),0)$ if and only if $\left|E\right(\lambda h^{\alpha }\left)\right|\le 1$. So, the two-stage method (15) is absolutely stable if

$$|1+\frac{\lambda h^{\alpha }}{\alpha !}+\frac{c_2^{\alpha }{\left(\lambda h^{\alpha }\right)}^2}{2{(\alpha !)}^2}|⩽1.$$

If $\lambda h^{\alpha }<0$, we can find the interval of absolute stability as follows:

$$\frac{-2\alpha !}{c_2^{\alpha }}⩽\lambda h^{\alpha }<0.$$

(42)

According to (42), the interval of absolute stability for the two-stage EFORK method (15) depends on $c_2^{\alpha }$. For instance, if $c_2^{\alpha }=2{(\alpha !)}^2/\left(2\alpha \right)!$, then and so the interval of absolute stability will be

$$\frac{-\left(2\alpha \right)!}{\alpha !}⩽\lambda h^{\alpha }<0.$$

In addition, for $c_2^{\alpha }=\frac{{\left(\mathsf{\Gamma }(2\alpha +1)\right)}^2}{\mathsf{\Gamma }(3\alpha +1)\mathsf{\Gamma }(\alpha +1)}$, we have

$$\frac{-2{(\alpha !)}^2\left(3\alpha \right)!}{{(\left(2\alpha \right)!)}^2}⩽\lambda h^{\alpha }<0.$$

If we choose $c_2^{\alpha }=\frac{4\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}$, we get

$$\frac{-\left(3\alpha \right)!}{2}⩽\lambda h^{\alpha }<0.$$

or, $c_2^{\alpha }=\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}$, we obtain

$$-2\left(3\alpha \right)!⩽\lambda h^{\alpha }<0.$$

The graphs of $E\left(\lambda h^{\alpha }\right)$ for different two-stage EFORK methods are shown in Figure 1 and Figure 2. From these figures, for $(\lambda <0)$, we can find the interval of absolute stability for various $\alpha$.

In addition, we apply the three-stage EFORK method (21) to Equation (41) and get

$$\begin{array}{cc}\hfill y_{n+1}& =\left[1+\frac{\lambda h^{\alpha }}{\alpha !}+\frac{{\left(\lambda h^{\alpha }\right)}^2}{\left(2\alpha \right)!}+\frac{{\left(\lambda h^{\alpha }\right)}^3}{\left(3\alpha \right)!}\right]y_n.\hfill \end{array}$$

Thus, the growth factor for the three-stage EFORK method (21) is

$$E\left(\lambda h^{\alpha }\right)=1+\frac{\lambda h^{\alpha }}{\alpha !}+\frac{{\left(\lambda h^{\alpha }\right)}^2}{\left(2\alpha \right)!}+\frac{{\left(\lambda h^{\alpha }\right)}^3}{\left(3\alpha \right)!}.$$

The three-stage EFORK method is absolutely stable if

$$|1+\frac{\lambda h^{\alpha }}{\alpha !}+\frac{{\left(\lambda h^{\alpha }\right)}^2}{\left(2\alpha \right)!}+\frac{{\left(\lambda h^{\alpha }\right)}^3}{\left(3\alpha \right)!}|⩽1.$$

The graph of $E\left(\lambda h^{\alpha }\right)$ for the three-stage EFORK method (21) is shown in Figure 3. In this figure, we can see the interval of absolute stability for various $\alpha$.

Finally, we apply the IFORK method (33) to Equation (41) and get

$$E\left(\lambda h^{\alpha }\right)=1+\frac{\frac{1}{\alpha !}\lambda h^{\alpha }}{1-\lambda h^{\alpha }\frac{\alpha !}{\left(2\alpha \right)!}},$$

with the interval of absolute stability $(-\infty ,0)$, $\lambda <0$. In a similar manner, we can obtain the interval of absolute stability for IFORK method (34). As we can see, in implicit fractional RK methods, the interval of absolute stability is very large, and they are stable.

6. Numerical Examples

In order to demonstrate the effectiveness and order of accuracy of the proposed methods in Section 3 and Section 4, two examples are considered. All computations have been carried out on a Core i7 PC with Mathematica 13.2 software.

Example 1.

Consider the fractional differential equation

$$\begin{array}{ccc}& & {}_0{}^{c}D_t^{\alpha }y\left(t\right)=-y\left(t\right)+\frac{t^{4-\alpha }}{\mathsf{\Gamma }(5-\alpha )},t\in [0,T],\hfill \\ & & y\left(0\right)=0,\hfill \end{array}$$

such that the exact solution is $y\left(t\right)=t^4{E}_{\alpha ,5}(-t^{\alpha })$. The approximate solutions by the two-stage EFORK method (15), three-stage EFORK method (21), and IFORK methods (33) and (34) are reported in

Table 1. Two-stage method (15) for $T=1$, $m=3$ in Example 1.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/3	1/40	$1.09027\times {10}^{-2}$	$1.1320$
	1/80	$4.97465\times {10}^{-3}$	$1.0013$
	1/160	$2.48509\times {10}^{-3}$	$0.9136$
	1/320	$1.31920\times {10}^{-3}$	$0.8533$
	1/640	$7.30171\times {10}^{-4}$	*

,

Table 2. Two-stage method (15) for $T=1$, $m=2$ in Example 1.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/2	1/40	$2.05503\times {10}^{-3}$	$1.2248$
	1/80	$8.79256\times {10}^{-4}$	$1.1621$
	1/160	$3.92907\times {10}^{-4}$	$1.1171$
	1/320	$1.81137\times {10}^{-4}$	$1.0845$
	1/640	$8.54183\times {10}^{-5}$	*

,

Table 3. Three-stage method (21) for $T=1$, $m=4$ in Example 1.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/4	1/40	$9.94252\times {10}^{-4}$	$0.8437$
	1/80	$5.54011\times {10}^{-4}$	$0.8214$
	1/160	$3.13499\times {10}^{-4}$	$0.8064$
	1/320	$1.79258\times {10}^{-4}$	$0.7958$
	1/640	$1.03255\times {10}^{-4}$	*

,

Table 4. Three-stage method (21) for $T=1$, $m=2$ in Example 1.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/2	1/40	$7.45694\times {10}^{-5}$	$1.5942$
	1/80	$2.46986\times {10}^{-5}$	$1.5789$
	1/160	$8.26771\times {10}^{-6}$	$1.5625$
	1/320	$2.79911\times {10}^{-6}$	$1.5478$
	1/640	$9.57367\times {10}^{-7}$	*

,

Table 5. IFORK methods for $T=1$, $m=2$ in Example 1.

$\mathit{\alpha }$	h	IFORK (33)	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$	IFORK (34)	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/2	1/40	$1.86448\times {10}^{-4}$	$1.0832$	$3.56080\times {10}^{-4}$	$1.7307$
	1/80	$8.79978\times {10}^{-5}$	$1.0492$	$1.07291\times {10}^{-4}$	$1.6666$
	1/160	$4.25221\times {10}^{-5}$	$1.0291$	$3.37953\times {10}^{-5}$	$1.6191$
	1/320	$2.08361\times {10}^{-5}$	$1.0174$	$1.10016\times {10}^{-5}$	$1.5846$
	1/640	$1.02928\times {10}^{-5}$	*	$3.66806\times {10}^{-6}$	*

and

Table 6. IFORK methods for $T=1$, $m=3$ in Example 1.

$\mathit{\alpha }$	h	IFORK (33)	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$	IFORK (34)	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/3	1/40	$3.04275\times {10}^{-4}$	$0.9083$	$5.12337\times {10}^{-3}$	$1.4661$
	1/80	$1.62123\times {10}^{-4}$	$0.8746$	$1.85445\times {10}^{-3}$	$1.3856$
	1/160	$8.84207\times {10}^{-5}$	$0.8482$	$7.09751\times {10}^{-4}$	$1.2940$
	1/320	$4.91160\times {10}^{-5}$	$0.8255$	$2.89458\times {10}^{-4}$	$1.2106$
	1/640	$2.77152\times {10}^{-5}$	*	$1.25070\times {10}^{-4}$	*

(In Appendix A some Mathematica computer programming codes are presented). The computed solutions are compared with the exact solution for different values of h, α, and T. The absolute error in time T is given by

$$E(h,T)=|y\left(t_{N^m}\right)-y_{N^m}|,$$

and the orders of the presented method are computed according to the following relation:

$$Lo{g}_2\frac{E(h,T)}{E(h/2,T)}.$$

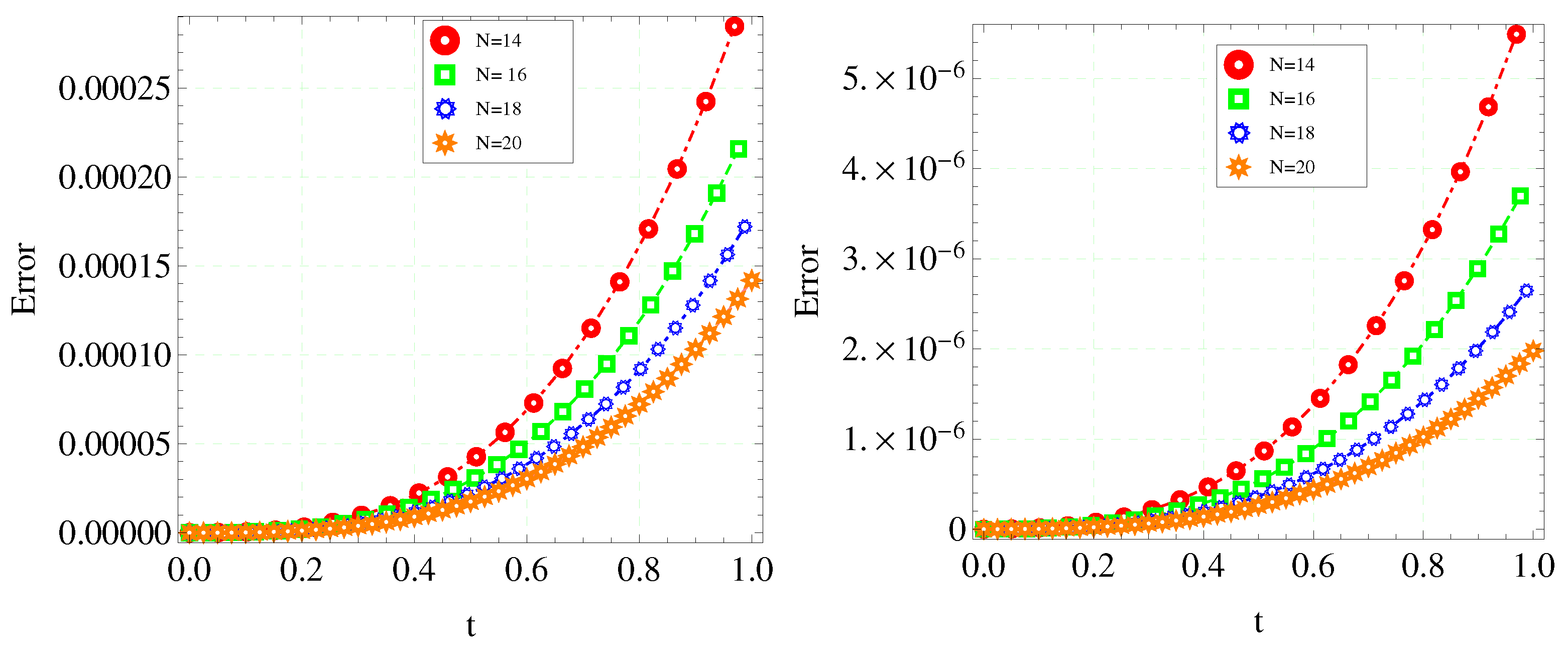
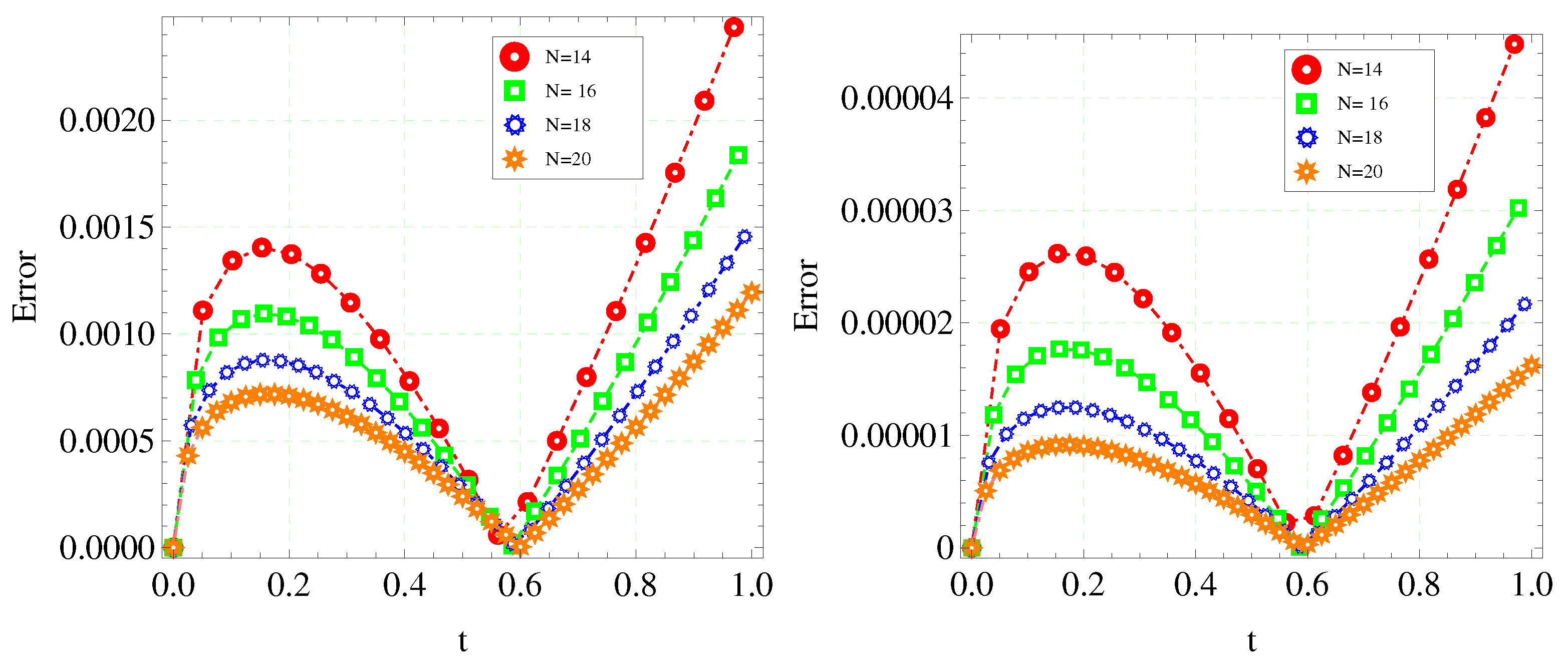
From the Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, we can conclude that the computed orders of truncation errors are in good agreement with the obtained results of Section 3 and Section 4. Figure 4, illustrates the error curves of the two-stage EFORK method (15) and the three-stage EFORK method (21) at $T=1,$ with $\alpha =1/2$, $m=2$ and different values of N.

Example 2.

Consider the following fractional differential equation from [6]:

$$\begin{array}{ccc}& & {}_0{}^{c}D_t^{\alpha }y\left(t\right)=\frac{2}{\mathsf{\Gamma }(3-\alpha )}{t}^{2-\alpha }-\frac{1}{\mathsf{\Gamma }(2-\alpha )}{t}^{1-\alpha }-y\left(t\right)+t^2-t,t\in [0,T],\hfill \\ & & y\left(0\right)=0,\hfill \end{array}$$

with the exact solution $y\left(t\right)=t^2-t$. Again, for different values of h, α, and T, we compared, in

Table 7. Two-stage method (15) for $T=1$, $m=3$ in Example 2.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/3	1/40	$1.00356\times {10}^{-1}$	$1.1075$
	1/80	$4.65748\times {10}^{-2}$	$0.9928$
	1/160	$2.34046\times {10}^{-2}$	$0.9107$
	1/320	$1.24493\times {10}^{-2}$	$0.8523$
	1/640	$6.89556\times {10}^{-3}$	*

,

Table 8. Two-stage method (15) for $T=1$, $m=2$ in Example 2.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/2	1/40	$1.77152\times {10}^{-2}$	$1.2351$
	1/80	$7.52581\times {10}^{-3}$	$1.1738$
	1/160	$3.33574\times {10}^{-3}$	$1.1275$
	1/320	$1.52680\times {10}^{-3}$	$1.0928$
	1/640	$7.15859\times {10}^{-4}$	*

,

Table 9. Three-stage method (21) for $T=1$, $m=4$ in Example 2.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/4	1/40	$9.90939\times {10}^{-3}$	$0.8383$
	1/80	$5.54249\times {10}^{-3}$	$0.8182$
	1/160	$3.14342\times {10}^{-3}$	$0.8047$
	1/320	$1.79955\times {10}^{-3}$	$0.7950$
	1/640	$1.03718\times {10}^{-3}$	*

and

Table 10. Three-stage method (21) for $T=1$, $m=2$ in Example 2.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/2	1/40	$5.79341\times {10}^{-4}$	$1.5592$
	1/80	$1.96590\times {10}^{-4}$	$1.5566$
	1/160	$6.68302\times {10}^{-5}$	$1.5475$
	1/320	$2.28624\times {10}^{-5}$	$1.5374$
	1/640	$7.87606\times {10}^{-6}$	*

, the obtained results by the two-stage EFORK method (15) and the three-stage EFORK method (21) with the exact solution. In

Table 11. IFORK methods for $T=1$, $m=2$ in Example 2.

$\mathit{\alpha }$	h	IFORK (33)	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$	IFORK (34)	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/2	1/40	$1.52888\times {10}^{-3}$	$1.0777$	$2.99223\times {10}^{-3}$	$1.6608$
	1/80	$7.24362\times {10}^{-4}$	$1.0464$	$9.46328\times {10}^{-4}$	$1.6244$
	1/160	$3.50728\times {10}^{-4}$	$1.0279$	$3.06932\times {10}^{-4}$	$1.5943$
	1/320	$1.72002\times {10}^{-4}$	$1.0171$	$1.01649\times {10}^{-4}$	$1.5703$
	1/640	$8.49858\times {10}^{-5}$	*	$3.42297\times {10}^{-5}$	*

and

Table 12. IFORK methods for $T=1$, $m=3$ in Example 2.

$\mathit{\alpha }$	h	IFORK (33)	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$	IFORK (34)	${\mathit{Log}}_2\frac{\mathit{E}(\mathit{h},\mathit{T})}{\mathit{E}(\mathit{h}/2,\mathit{T})}$
1/3	1/40	$2.84493\times {10}^{-3}$	$0.9005$	$4.77620\times {10}^{-2}$	$1.4860$
	1/80	$1.52403\times {10}^{-3}$	$0.8707$	$1.70509\times {10}^{-2}$	$1.3835$
	1/160	$8.33483\times {10}^{-4}$	$0.8463$	$6.53520\times {10}^{-3}$	$1.2859$
	1/320	$4.63592\times {10}^{-4}$	$0.8246$	$2.68020\times {10}^{-3}$	$1.2023$
	1/640	$2.61754\times {10}^{-4}$	*	$1.16478\times {10}^{-3}$	*

, we report the results obtained by the IFORK methods (33) and (34). From Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12, we can conclude that the computed orders are in good agreement with the given results of Section 3 and Section 4.

As we can see, the computational orders for two and three-stage EFORK methods approach $2\alpha$ and $3\alpha$ for $h>0$, respectively. As seen in Tables and Figures, the three-stage EFORK method provides better results than the two-stage EFORK method.

Table 13. $E(h,T)$ for $\alpha =1/2$, $m=2$ and different values of T.

T	2-Stage-Exam.1	3-Stage-Exam.1	2-Stage-Exam.2	3-Stage-Exam.2
0.5	$4.81351\times {10}^{-6}$	$4.20218\times {10}^{-8}$	$9.29068\times {10}^{-5}$	$5.57177\times {10}^{-7}$
1.0	$8.54183\times {10}^{-5}$	$9.57367\times {10}^{-7}$	$3.00335\times {10}^{-3}$	$7.87606\times {10}^{-6}$
1.5	$4.51426\times {10}^{-4}$	$6.00243\times {10}^{-6}$	$2.78127\times {10}^{-3}$	$3.63915\times {10}^{-5}$
2	$1.45778\times {10}^{-3}$	$2.20455\times {10}^{-5}$	$6.26033\times {10}^{-3}$	$9.38735\times {10}^{-5}$
3	$7.50603\times {10}^{-3}$	$1.37070\times {10}^{-4}$	$1.78449\times {10}^{-2}$	$3.26003\times {10}^{-4}$

shows the numerical results for different values of T.

In addition, Table 5, Table 6, Table 11 and Table 12 show that the computational order from relations (33) and (34) of IFORK methods approach $2\alpha$ and $3\alpha$ for $h>0$, respectively.

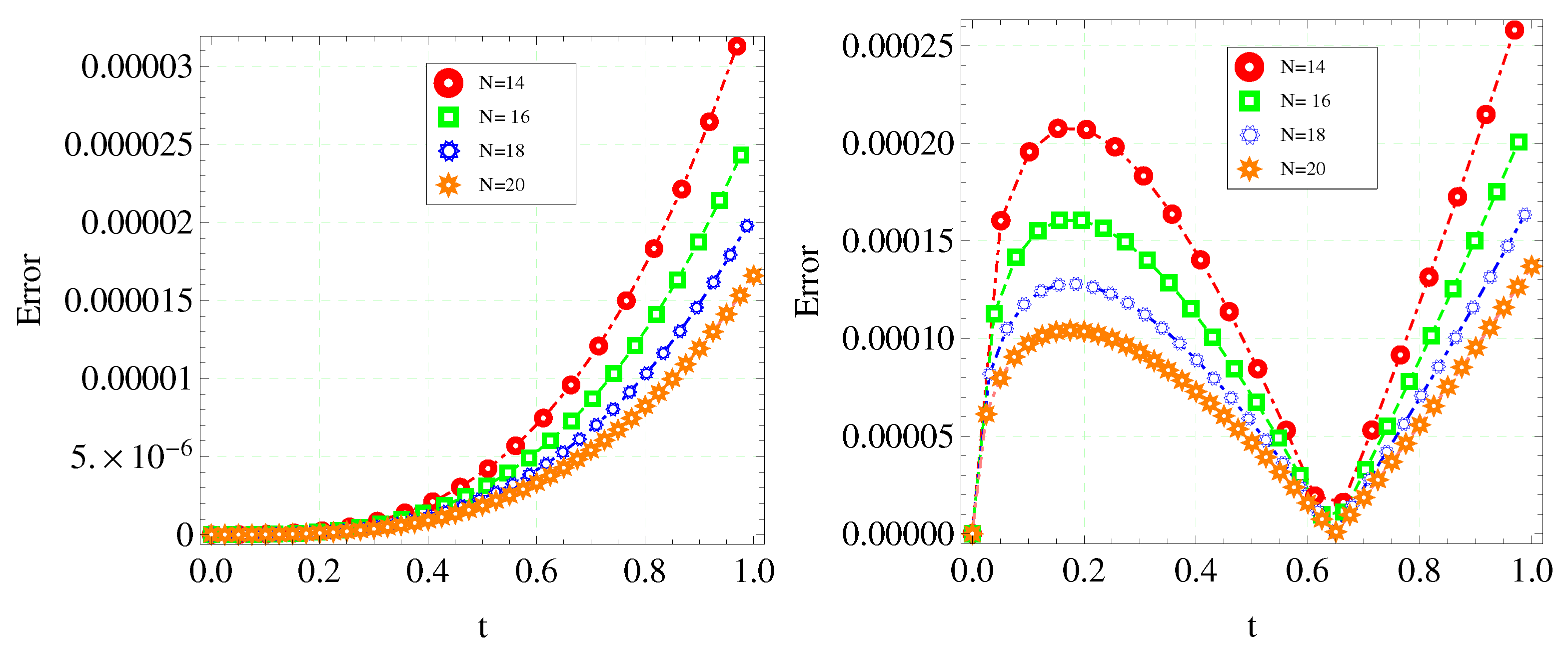
Figure 5, illustrates the numerical results of the two-stage EFORK method (15) and the three-stage EFORK method (21) at $T=1$ for $\alpha =1/2$, $m=2$ and different values of N. Additionally, Figure 6 illustrates the numerical results of the IFORK method (33) for Example 1 and Example 2 at $T=1$ for $\alpha =1/2$, $m=2$ and different values of N.

In addition, the numerical results for the optimal case $c_2^{\alpha }=\frac{{\left(\mathsf{\Gamma }(2\alpha +1)\right)}^2}{\mathsf{\Gamma }(3\alpha +1)\mathsf{\Gamma }(\alpha +1)}$ in the two-stage EFORK method are shown in

Table 14. Optimal two-stage method (15) for $T=1$, $m=2$.

$\mathit{\alpha }$	h	$\mathit{E}(\mathit{h},\mathit{T})$, Example 1	$\mathit{E}(\mathit{h},\mathit{T})$, Example 2
1/2	1/40	$7.35533\times {10}^{-4}$	$6.12299\times {10}^{-3}$
	1/80	$3.55401\times {10}^{-4}$	$2.94885\times {10}^{-3}$
	1/160	$1.72778\times {10}^{-4}$	$1.43060\times {10}^{-3}$
	1/320	$8.45336\times {10}^{-5}$	$6.99024\times {10}^{-4}$
	1/640	$4.15855\times {10}^{-5}$	$3.43589\times {10}^{-4}$

with $\alpha =1/2$ and different values of h.

7. Conclusions

This paper introduces new efficient FORK methods for FDEs based on Caputo generalized Taylor formulas. The proposed methods were examined for consistency, convergence, and stability. The interval of absolute stability of FORK methods has been determined, and implicit fractional order RK methods were shown to be A stable. Some examples were provided to demonstrate the effectiveness of these numerical schemes. We can obtain these results for Riemann–Liouville and Gronwald–Letnikov fractional derivatives accordingly. Recently, a new concept of differentiation called fractal and fractional differentiation was suggested and numerically examined by many researchers [36,37], where the differential operator has two orders: the first is fractional order and the second is the fractal dimension. These differential (integral) operators have not been studied intensively yet. In future work, we will extend the presented method for fractional differential equations with fractal–fractional derivatives.