Abstract
In this study, a fractional nonlinear mixed integro-differential equation (Fr-NMIDE) is presented and has a general discontinuous kernel based on position and time space. Conditions of the existence and uniqueness of the solution is provided through the principal form of the integral equation, based on the Banach fixed point theorem. After applying the properties of a fractional integral, the Fr-NMIDE conformed to the Volterra–Hammerstein integral equation (V-HIE) of the second kind, with a general discontinuous kernel in position with the Hammerstein integral term and a continuous kernel in time to the Volterra term. Then, using a technique of the separating method, we obtained HIE, where its physical coefficients were variable in time. The Toeplitz matrix method (TMM) and its schemes were used to obtain a nonlinear algebraic system by studying the convergence of the system. The Maple 18 program was implemented to present the numerical results, along with corresponding errors.
1. Introduction
As integral equations, integro-differential equations and fractional integro-differential equations (IEs/IDEs/fIDEs) can be used to simulate a wide range of problems in the basic sciences, many scientists have focused their attention on presenting the solutions for these systems. These equations have played a significant role in finding solutions using diverse methods, which is in line with the rapid development in finding the answers to diverse problems originating from the basic sciences. Currently, several studies have concentrated on creating more sophisticated and effective techniques for solving the IEs/IDEs, such as the Rieman–Stieltjes integral conditions [1,2], Lerch polynomials method [3] and Legendre–Chebyshev spectral method [4], along with the numerical observations based on semi-analytical approaches, e.g., Adomian’s decomposition method [5] and HOBW method [6]. The linear/nonlinear equations (IEs/IDEs/ fIDEs) have various uses in fluid mechanics [7], Stokes flow [8], airfoil [9], quantum mechanics [10], integral models [11], mathematical engineering [12], nuclear physics [13] and the theory of laser [14]. The orthogonal polynomials method is considered one of the most significant operators used to solve various scientific problems. Alhazmi [15] used a new technique based on the separation of variables and the orthogonal polynomials method to obtain many spectral relationships based on the mixed integral equation using a generalized potential kernel. Nemati et al. [16] applied the Legendre polynomials scheme for the outcomes of a second-order two-dimensional (2D) Volterra integral model, together with a continuous kernel. Mirzaee and Samadyar [17] discussed the convergence of 2D-orthonormal Bernstein collocation method for solving 2D-mixed Volterra-Fredholm integral equations. Basseem and Alalyani [18] used Chebyshev polynomials to discuss the numerical solution of the quadratic integral equation with a logarithmic kernel. Katani [19] implemented a quadrature scheme for the numerical outcomes of the second kind of Fredholm integral model. Al-Bugami [20] used the Simpson and Trapezoidal schemes to perform numerical representations based on an integral model using 2D surface crack layers. Brezinski and Zalglia [21] used the extrapolation approach to achieve numerical computing results based on the second kind of nonlinear integral model that has a continuous kernel. Baksheesh [22] proposed using the Galerkin scheme to find the approximate results based on the Volterra integral equations of the second kind, which have discontinuous kernels. Alkan and Hatipoglu [23] applied the sinc-collocation method for solving the Volterra-Fredholm IDEs of fractional order. Mosa et al. [24] studied the semi-group scheme to assess uniqueness and existence based on the partial and fractional integro models of heat performance in the Banach space using the Adomian decomposition scheme. Bin Jebreen and Dassios [25] proposed an efficient algorithm to find an approximate solution via the wavelet collocation method for fractional Fredholm integro-differential equations. Akram et al. [26] interpreted the collocation approach to tackle the fractional partial integro-differential equation by employing the extended cubic B-spline Abdelkawy et al. [27] applied the Jacobi–Gauss collocation method after using the Riemann–Liouville fractional integral and derivative fractional to obtain the approximate solution for variable-order fractional integro-differential equations with a weakly singular kernel.
The initial value of the Fr-NMIDE is presented as:
Here, and are the known and unknown continuous functions, respectively, in is the integration domain and . In addition, indicates the constant values of Equation (1) and and v are constants and have physical sense. The kernel , in general, has a singular term. For reference, the essential properties and definitions have been stated using fractional calculus theory.
Definition 1.
For the function , the fractional Riemann–Liouville integral with order is shown as [28]:
The time Abel kernel satisfies the following features: for every continuous function . Integrals
are the continuous time function, i.e.,
In this paper, Section 2 presents the fractional definition to obtain a NMIE. Then, the theorem-based Banach fixed point is discussed to prove the existence and uniqueness of the solution of NMIE. Section 3 presents the convergence of the solution. Section 4 indicates the technique of separation of the variables for the Hammerstein integral model in position and its coefficients. This scheme would help researchers choose the time known function in an easier way, enabling them to choose the necessary time to obtain the required results. Section 5 indicates the convergence analyses of the Hammerstein integral equation. Section 6 shows the Toeplitz matrix scheme to conform the Hammerstein integral model of the nonlinear algebraic system (NAS). The TMM is considered the best numerical method for solving singular integral equations, where the singular terms disappear and we have simple integrals. Section 7 represents the NAS convergence. Section 8 provides the convergence of the error using one of the famous theorems. Section 9 provides the numerical solutions through Maple 18, together with the kernel of the nonlinear integral equation that takes the logarithmic form, the Carleman function and Hilbert kernel. In addition, the corresponding errors are computed.
2. The Solution’s Existence and Uniqueness
The fundamental Caputo fractional integral is used to find the second order NMIE as:
In Equation (2), the free term and the unknown function will be discussed in the same space, , along with the discontinuous kernel . The discontinuous kernel of time , is considered in class , where .
To prove the existence of NMIE (2) based on the unique results, the integral operator form is given below:
The following conditions are presented as:
(i) (i-a) The position kernel satisfies
(i-b) Therefore, the kernel of position and time in satisfies
(ii) The continuous function and its norm is shown as and G is taken as a constant.
(iii) The decreasing function , constant and are used as:
(iii-a) .
(iii-b) .
Theorem 1
(Banach Fixed Point [29]). Consider to be a metric space, where is a null set. Suppose X is complete and is the X contraction, then T contains exactly a single fixed point.
To prove this, K shows the contraction operator on B with integral form presents the unique form of the solution, the general kernel satisfies in (i-b), is the domain of integration, with respect to position and the time .
Theorem 2.
Principal theorem: The NMIE (2) with the use of above conditions and the space takes the form of:
Lemmas (1) and (2) must be proven to satisfy the above theorem.
Lemma 1.
Under conditions (i) to (iii-a), the operator maps the space onto itself:
Proof.
Equation (3) is used to prove
Using (i)–(iii-a) and the inequality of Cauchy–Schwarz, we have:
In the above statement, the operator maps the ball as:
As , therefore . Furthermore, the inequality (5) includes the boundedness operators and . □
Lemma 2.
If (i)–(iii-b) conditions are fulfilled, then operator is a contractive-based Banach space .
Proof.
For and functions using space, Formula (3) becomes:
The conditions (i), (ii) and (iii-b) have been applied to the Cauchy–Schwarz inequality as:
Inequality (7) presents the operator (contraction operator), which shows the continuity in the space. □
3. Convergence of the Solution
Consider the simple iteration , where the two functions are used to satisfy
Consider
where
Taking , the above formula becomes:
and we see
Equation (10) shows the convergent sequence uniformly. Moreover, it provides the convergent solution of the sequence . As is continuous and , is uniformly continuous with an infinite series. This proves the lemma.
4. Separation of Variables Scheme
In the problems of mathematical physics, we find that researchers are interested in finding the unidentified potential function, which is linked to time and position. A variety of methods can be used to obtain the unknown function. One of these methods is time division that turns the mixed integral equation into an algebraic system of integral equations. Researchers apply the separating variable method to solve the mixed integral equation using the coefficients of the space functions. Moreover, these time coefficients are in the form of an integral operator of the Volterra type (Jan [30,31]). This scheme helps researchers to choose the time known function in an easier way, which enables them to choose the necessary time to obtain the required results. The unidentified and known functions and are shown in the separation form as:
where is an unknown function in a position that is to be determined, is the given function in a position and shows the known function in time.
The time function is chosen in the form of a series based on the polynomial constants. This form helps the researcher to categorize the function of time based on the constants as a famous function or time representation in several other forms. It is noted that time series convergence is based on the premise of the experiment time being less than one and the start time is not equal to zero. Assume that
By using the updated form of Equation (13) by using Equation (14), the reader can use the separation of time scheme for the nonlinear mixed integral model in time and position, which leads to a nonlinear integral equation in a position with coefficients linked to t, where . Moreover, Equation (13) represents that the single solution condition on the nonlinear integral equation is an equivalence relationship between position and time, which is given as:
Equation (15) shows the relationship between the position represented in the kernel form (which represents the properties of matter) and the time required for the continuity of these properties, which is known under the condition that there is a single solution. It is noted that at a certain time, an increase that exceeds the standard value of the nucleus may occur, and this leads to instability.
5. Convergence Investigations Based on Nonlinear Integral Model
To check the nonlinear integral model (13) convergence, the solution sequence takes the form:
where and are two distinct arbitrary partial sums of sequence and
where is defined in the Equation (15). Finally, we have
As and for the fixed values, must approach zero. Hence, it is concluded that shows a Cauchy sequence throughout the metric space, which shows the convergent series.
6. Toeplitz Matrix Method (Abdou et al. [32])
Many numerical methods have been used to solve integral equations with continuous or unconnected kernels. In singular integral equations, the best way to solve them is the Toeplitz matrix method (TMM), due to the following reasons: The singular term directly disappears, being transformed into simple integrals that can be solved quickly, and then, forms a linear/nonlinear algebraic system of equations. The degree of convergence in the relative error is less than in the other methods.
There are some methods that give a quick approximation when studying the error, including a circulated preconditioned iterative scheme. Xian et al. [33] considered the conjugate gradient technique with a circulated preconditioned scheme for a linear discretized model. They obtained a matrix whose coefficient kept the structure of a symmetric Toeplitz-plus-tridiagonal. They also studied linear large-scale systems with coefficient matrices based on the non-Hermition Toeplitz and applied a product of a fast Toeplitz matrix-vector through iterative solvers for a linear discretized model (circulant preconditioned method). This numerical scheme provides fast results to reduce computational costs, using to , and storage through to deprived of loss compression, where m is the number of spatial grid nodes.
For TMM, consider , using the nonlinear integral term of as:
The two functions and are
where
and
Equations (18) and (20) are used in , to obtain
The nonlinear integral in Equation (15) shows the NAS of a (2N + 1) system
The matrices show the Toeplitz matrix as:
Equation (23) shows the matrix of two types with a order, including (Toeplitz matrix) and , which shows the zero elements, excluding the first and last columns or rows. The error can be obtained based on the following formula:
7. The Nonlinear Algebraic Toeplitz Matrix System
This section provides the existence based on NAS (22) using the Banach space . The operator form is written as:
where
The following lemma is
Lemma 3.
If the position kernel satisfies the conditions below:
Then,
Proof.
From Equations (18) and (19), we have
Applying the Cauchy–Schwarz inequality and taking the sum from to , the above inequality yields
Based on Equation (27), the function continuity in input , a small constant exists, i.e., . As each value of is bounded, take as:
Similarly, by taking a small value of the constant for Equations (18) and (19), we have
Using (29) and (30), we have
Hence, exists.
To prove the second equation of (28) for , the Cauchy–Schwarz inequality is applied by taking the sum from to
Using and Equation (27), we obtain that as ,
Similarly, from (18) and (19), it is proved that
Finally, we obtain
□
Now, the principal theorem is proven based on the nonlinear algebraic systems.
Theorem 3.
The NAS (22) using the Banach space shows the unique form of the solution, as follows:
where and are constants.
The functions , where for the constants satisfy the following:
where for each integer j.
The below lemmas must be proven for the above theorem.
Lemma 4.
If Equations (34)–(36) are tested, then the operator is defined by using Equation (25), which maps the space onto itself.
Proof.
Suppose U shows all the functions set as in , i.e., is constant and the operator is based on the Banach space:
Using conditions (34) and (35), we have
For each integer j, the above inequality is shown as:
The above inequality (38) represents that the operator maps the U set, where
Hence, have been taken, whereas T and operators are bounded. □
Lemma 5.
Under the conditions (34), (35) and (37), shows a contraction operator in the space
Proof.
For X and Z functions in , Formulas (25) and (26) become:
Using conditions (35) and (37),
The above form indicates that the operator is continuous in space. shows the contraction operator based on . Hence, presents a unique fixed point with specific solutions of the NAS using space. □
8. The Error of the Toeplitz Matrix Method
In any practical use of the TMM, some estimation of the error size is involved. Hence, these two definitions were used to calculate the error of the TMM.
Definition 2.
A local error is used as:
where shows the approximate results of (2).
In the other formula, Equation (40) is used as:
Definition 3.
The TMM shows a convergence of r order in input ; conversely, by taking the large values of exists based on N independently, that is,
Now, we present the theorem, which is provided using NAS, based on Equation (22), which has a unique solution.
Theorem 4.
The error is considered negligible as
Proof.
Since as , then . □
9. Applications
For numerical results and tables, we used Maple 2022.1 software, Version 15, March 2022, Windows, 10, 8 G RAM, 64-bit. In this section, the NMIE of (1) in the following special form was considered
The true result of Equation (44) is .
Example 1
(For logarithmic kernel).
After using (17)–(19) including the famous integral reference as Gradstein et al. [34]:
we have
and
Using (47) and (48), the coefficients of the nonlinear algebraic system (22) are presented as:
In addition,
The formula (50) takes the form:
The linear case can be obtained from Equations (47)–(51) by letting .
Example 2
(For Carleman kernel).
The significance based on the Carleman kernel was shown in the Arutiunian [35] work that presented the plane contact problem using nonlinear plasticity theory as its first calculation. It was reduced through the first-order Fredholm integral model with a Carleman kernel.
After using (17) to (19), we obtain
and
Therefore, the Toeplitz matrix becomes:
The error R is shown as:
Example 3
(Suppose the Hilbert kernel).
The exact output of Equation (57) is .
The integral equation based on the Hilbert kernel, together with the crack problem used in elasticity theory are discussed in [34].
From the above, the results of using the logarithmic function and the effect of time in the first example, as well as the arithmetic error, are described numerically in Table 1 and Figure 1a,b in the nonlinear case () and linear case (). In the second example, the results of using the Carleman function over time periods for the nonlinear and linear cases, as well as the resulting arithmetic error, were derived in Table 2 and Figure 2a,b, respectively. While Table 3 and Figure 3a,b represent the numerical results and arithmetic errors corresponding to the nonlinear and linear cases, respectively, for different values of the coefficient of the Carleman function. In the third example of the Hilbert kernel, the numerical error of the nonlinear case and the linear case has been calculated at in Figure 4a,b, respectively. While for the corresponding results of errors are described in Figure 5a,b.

Table 1.
Solutions of the linear/nonlinear solutions of MIE (44) with a logarithmic kernel, along with the corresponding errors using TMM.
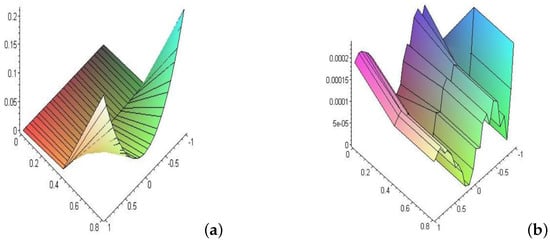
Figure 1.
(a) Shows the corresponding error of NMIE with a logarithmic kernel at different times, whereas (b) illustrates the corresponding error for the linear case at the same times.

Table 2.
Describes the nonlinear and linear cases for MIE (44), with the Carleman kernel, time and .
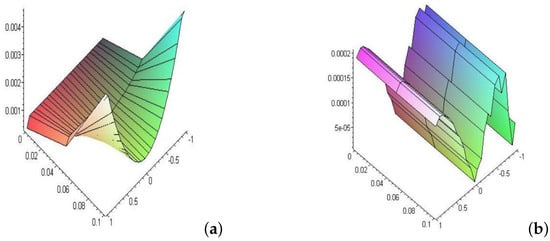
Figure 2.
(a) Shows the error for the nonlinear case at and (b) shows the corresponding error for the linear case at .

Table 3.
Shows the nonlinear and linear cases for Equation (44) for different values of Carleman coefficients at time .
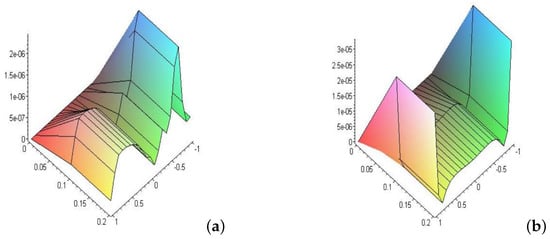
Figure 3.
(a,b) Shows the error of Equation (44) respectively for the nonlinear and linear cases of Carleman coefficients at and .
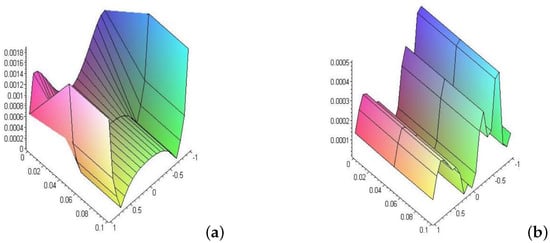
Figure 4.
(a,b) Shows the error of Equation (44) using the Hilbert kernel for the nonlinear and the linear cases at time .
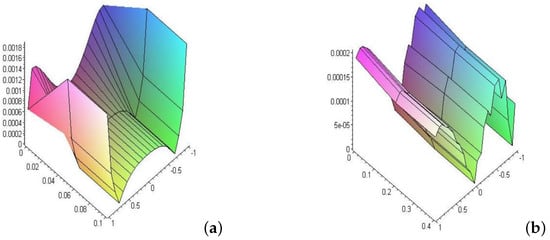
Figure 5.
(a,b) Shows the error of Equation (44) with Hilbert kernel for the nonlinear and the linear cases at time .
10. Conclusions
The following conclusions were drawn:
- 1
- In this paper, the existence of a unique solution is proven using the Banach fixed point theorem. In addition, the reader could use the successive approximate method (Picard method) to arrive at the same conclusion. In the homogeneous case of Equation (1), the successive approximate method fails to prove the existence of a unique solution. For this, we can only use the Banach fixed point theorem.
- 2
- If the two conditions of (i) and (ii) are not satisfied, this means that we have at least one solution. In this case, we would use one of the following theorems: Brouwer fixed point theorem or Schauder fixed point theorem.
- 3
- Using TMM, we have an NAS where the coefficient of the nonlinear term is a function of time. Hence, the existence of a unique solution for the NAS is discussed in the space .
- 4
- The fractional nonlinear mixed integro-differential Equation (1), under certain relations of and v, represents the nonlinear integral equation of the fractional phase-lag termThe delaying or advancing of time reveals the natural phenomena, especially in the presence of thermoelectricity and magnetic media. Some of applications of fractional integro-differential equations are found in physics, chemistry, economics, and biology [12,29]. Equation (59) explains the physical meaning of the fractional equation of time as the first fractional approximation of the time lag equation, and this lag may be before or after real time.
- 5
- 6
- The significance of the logarithmic kernel was approved from its derivatives f with these cases:
- (a)
- Cauchy kernel.
- (b)
- Strong singular kernel
- (c)
- The Carleman function was also established as:where is a continuous function.
- 7
- When the kernel of the equation was in the logarithmic function form , the relative error increased with increasing time. It was also noted that the error in the non-linear case was slightly larger than in the linear case.
- 8
- In Example (2), when the kernel took the Carleman function , we noticed that the behavior of the error when increasing time was the same as that of the logarithmic function. However, by comparison, we found that at small times, the error in the logarithmic function was higher than in the Carleman function. With increasing time, we find that the relative error in the Carleman function is higher than its counterpart in the logarithmic function.
- 9
- In Example (3), the error behavior of the Hilbert kernel was the same as that of the logarithmic form and Carleman function.
11. Future Work
Future work will attempt to solve Equation (1) when the coefficients of the equation are variable. This will lead to solutions for many applications in the sciences related to nonlinear elasticity.
Author Contributions
Supervision, M.A.A.; Project administration, S.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project number: 22UQU4282396DSR01, through the Deanship for Research & Innovation, Ministry of Education in Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors would like to thank the reviewers for their suggestions that helped improve the research. The authors thank the Deanship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number: 22UQU4282396DSR01.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- El-Sayed, A.M.A.; Gamal Ahmed, R. Infinite point and Riemann Stieltjes integral conditions for an integro differential equation. Nonlinear Anal. Model. Control 2019, 24, 733–754. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Gamal Ahmed, R. Solvability of a coupled system of functional integro-differential equations with infinite point and Riemann-Stieltjes integral conditions. Appl. Math. Comput. 2020, 370, 124918. [Google Scholar] [CrossRef]
- Mohamed, D.S. Application of Lerch polynomials to approximate solution of singular Fredholm integral equations with Cauchy kernel. Appl. Math. Inf. Sci. 2022, 16, 565–574. [Google Scholar]
- Hafez, R.M.; Youssri, Y.H. Spectral Legendre-Chebyshev Treatment of 2D linear and nonlinear mixed Volterra-Fredholm integral equation. Math. Sci. Lett. 2020, 9, 37–47. [Google Scholar]
- El-Sayed, S.M.; Abdel-Aziz, M.R. A comparison of Adomian’s decomposition method and wavelet-Galerkin method for solving integro-differential equations. Appl. Math. Comput. 2003, 136, 151–159. [Google Scholar] [CrossRef]
- Ali, M.R.; Mousa, M.M.; Ma, W.-Z. Solution of nonlinear Volterra integral equations with weakly singular kernel by using the HOBW method. Adv. Math. Phys. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Klaseboer, E.; Sun, Q.; Chan, D.Y. Non-singular boundary integral methods for fluid mechanics applications. J. 525 Fluid Mech. 2012, 696, 468–478. [Google Scholar] [CrossRef]
- Ata, K.; Sahin, M. An integral equation approach for the solution of the Stokes flow with Hermite surfaces. Eng. Anal. Bound. Elem. 2018, 96, 14–22. [Google Scholar] [CrossRef]
- Kuzmina, K.; Marchevsky, I. The boundary integral equation solution in vortex methods with the airfoil surface line discretization into curvilinear panels. Proc. Top. Probl. Fluid Mech. 2019, 2019, 131–138. [Google Scholar]
- Lienert, M.; Tumulka, R. A new class of Volterra-type integral equations from relativistic quantum physics. J. Integral Equations Appl. 2019, 31, 535–569. [Google Scholar] [CrossRef]
- Sidorov, D. Integral Dynamical Models: Singularities, Signals and Control; World Scientific: Singapore, 2014. [Google Scholar]
- Abdou, M.A.; Basseem, M. Thermopotential function in position and time for a plate weakened by curvilinear hole. Arch. Appl. Mech. 2022, 92, 867–883. [Google Scholar] [CrossRef]
- Matoog, R.T. Treatments of probability potential function for nuclear integral equation. J. Phys. Math. 2017, 8, 2090-0902. [Google Scholar]
- Gao, J.; Condon, M.; Iserles, A. Spectral computation of highly oscillatory integral equations in laser theory. J. Comput. Phys. 2019, 395, 351–381. [Google Scholar] [CrossRef]
- Alhazmi, S.E.A. New Model for Solving Mixed Integral Equation of the First Kind with Generalized Potential Kernel. J. Math. Res. 2017, 9, 18–29. [Google Scholar] [CrossRef]
- Nemati, S.; Lima, P.M.; Ordokhani, Y. Numerical solution of a class of two-dimensional nonlinear Volterra integral equations using Legendre polynomials. J. Comput. Appl. Math. 2013, 242, 53–69. [Google Scholar] [CrossRef]
- Mirzaee, F.; Samadyar, N. Convergence of 2D-orthonormal Bernstein collocation method for solving 2D-mixed Volterra-Fredholm integral equations. Trans. A. Razmadze Math. Inst. 2018, 172, 631–641. [Google Scholar] [CrossRef]
- Basseem, M.; Alalyani, A. On the Solution of Quadratic Nonlinear Integral Equation with Different Singular Kernels. Math. Probl. Eng. 2020, 2020, 1–7. [Google Scholar] [CrossRef]
- Katani, R. Numerical solution of the Fredholm integral equations with a quadrature method. SeMA J. 2019, 76, 271276. [Google Scholar] [CrossRef]
- Al-Bugami, A.M. Numerical Treating of Mixed Integral Equation Two-Dimensional in Surface Cracks in Finite Layers of Materials. Adv. Math. Phys. 2022, 2022, 1–12. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo-Zaglia, M. Extrapolation methods for the numerical solution of nonlinear Fredholm integral equations. J. Integral Equ. Appl. 2019, 31, 29–57. [Google Scholar] [CrossRef]
- Bakhshayesh, S.J. Discontinuous Galerkin Approximations for Volterra Integral Equations of the First Kind with Convolution Kernel. Indian J. Sci. Technol. 2015, 8, 33. [Google Scholar] [CrossRef]
- Alkan, S.; Hatipoglu, V.F. Approximate solutions of Volterra-Fredholm integro-differential equations of fractional order. Tbil. Math. J. 2017, 10, 1–13. [Google Scholar]
- Mosa, G.A.; Abdou, M.A.; Gawish, F.A.; Abdalla, M.H. On the behavior solutions of fractional and partial integro differential heat equations and its numerical solutions. Math. Slovak 2022, 72, 397–410. [Google Scholar] [CrossRef]
- Jebreen, B.; Dassios, I. On the Wavelet Collocation Method for Solving Fractional Fredholm Integro-Differential Equations. Mathematics 2022, 10, 1272. [Google Scholar] [CrossRef]
- Akram, T.; Ali, Z.; Rabiei, F.; Shah, K.; Kumam, P. A Numerical Study of Nonlinear Fractional Order Partial Integro-Differential Equation with a Weakly Singular Kernel. Fractal Fract. 2021, 5, 85. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Amin, A.Z.M.; Lopes, A.M.; Hashim, I.; Babatin, M.M. Shifted Fractional-Order Jacobi Collocation Method for Solving Variable-Order Fractional Integro-Differential. Fractal Fract. 2021, 6, 19. [Google Scholar] [CrossRef]
- Podlubny, I.; Chechkin, A.; Skovranek, T.; Chen, Y.; Jara, B.M.V. Matrix approach to discrete fractional calculus II: Partial fractional differential equations. J. Comput. Phys. 2009, 228, 3137–3153. [Google Scholar]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley & Sons Inc.: New York, NY, USA, 1978. [Google Scholar]
- Jan, A.R. An asymptotic model for solving mixed integral equation in position and time. J. Math. 2022, 2022, 8063971. [Google Scholar] [CrossRef]
- Jan, A.R. Solution of nonlinear mixed integral equation via collocation method basing on orthogonal polynomials. Heliyen 2022, 8, e1182. [Google Scholar] [CrossRef]
- Abdou, M.A.; El-Borai, M.M.; El-Kojok, M.M. Toeplitz matrix method and nonlinear integral equation of Hammerstein type. J. Comput. Appl. Math. 2009, 223, 765–776. [Google Scholar]
- Gu, X.M.; Huang, T.Z.; Zhao, X.L.; Xu, W.R.; Li, H.B.; Li, L. Circulant preconditioned iterative methods for peridynamic model simulation. Appl. Math. Comput. 2014, 248, 470–479. [Google Scholar] [CrossRef]
- Gradstein, I.S.; Ryzhik, I.M.; Romer, R.H. Tables of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Arutiunian, N.K. Ploskaia kontaktnaia zadacha teorii polzuchesti (The plane contact problem of the theory of creep). J. Appl. Math. Mech. 1959, 23, 1283–1313. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).