Mathematical Modeling of COVID-19 with Vaccination Using Fractional Derivative: A Case Study
Abstract
1. Introduction
2. Model Formulation and Basic Relations to Fractional Calculus
2.1. Model Formulation
2.2. Model Positivity and Boundedness
2.3. Caputo Fractional Order Model
3. Analysis of the Equilibrium Points
3.1. Disease-Free Equilibrium (DFE)
3.2. Basic Reproduction Number
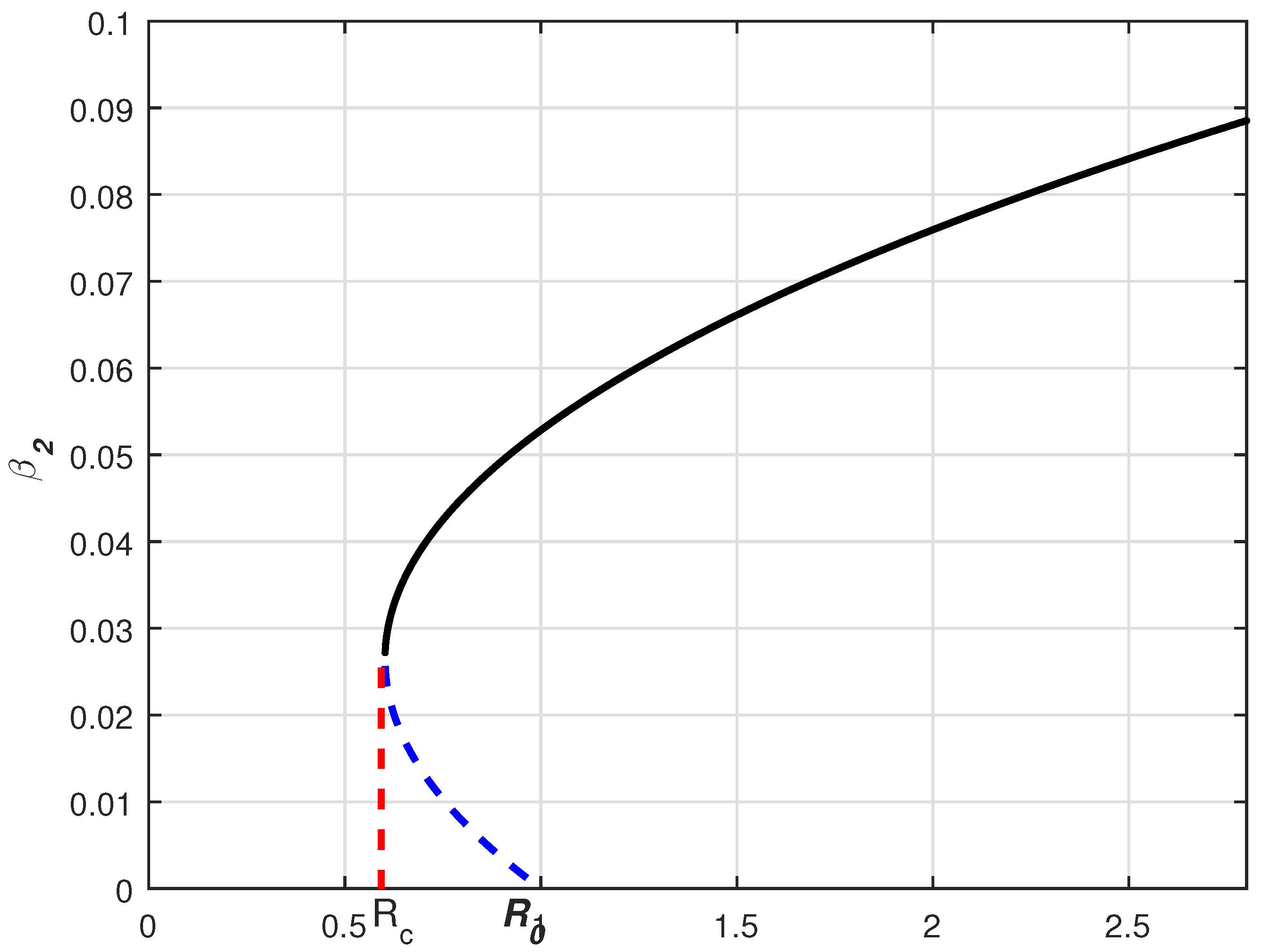
3.3. Endemic Equilibria
- (i)
- a unique endemic equilibrium exists if ,
- (ii)
- a unique endemic equilibrium exists if and ,
- (iii)
- two endemic equilibria exist if , and its related discriminant is positive
- (iv)
- there is no possible equilibria other than the above cases.
4. Stability Analysis
4.1. Global Stability
4.2. Global Stability of Endemic Equilibrium for Special Case (, )
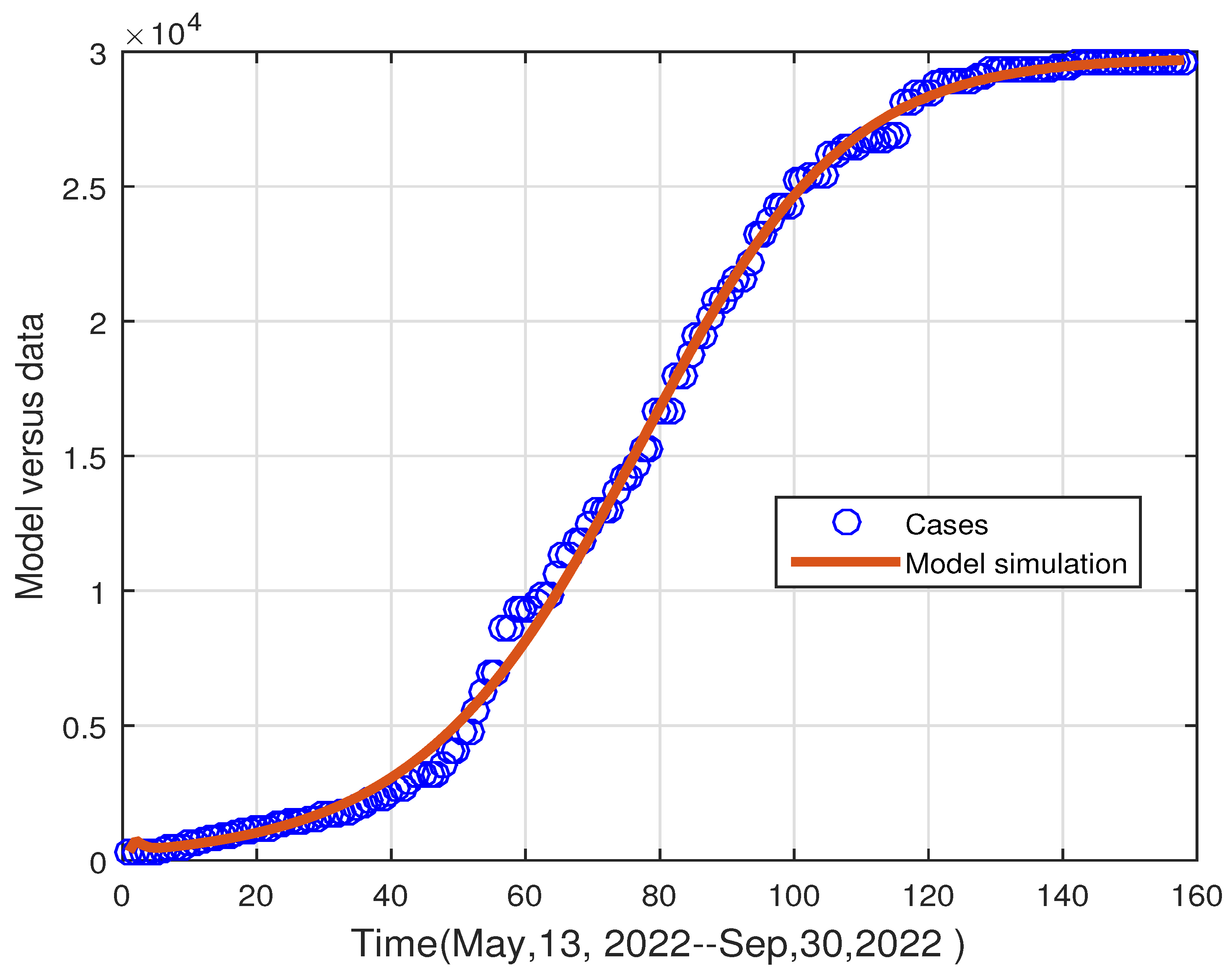
5. Parameter Estimations
6. Numerical Results
6.1. Numerical scheme
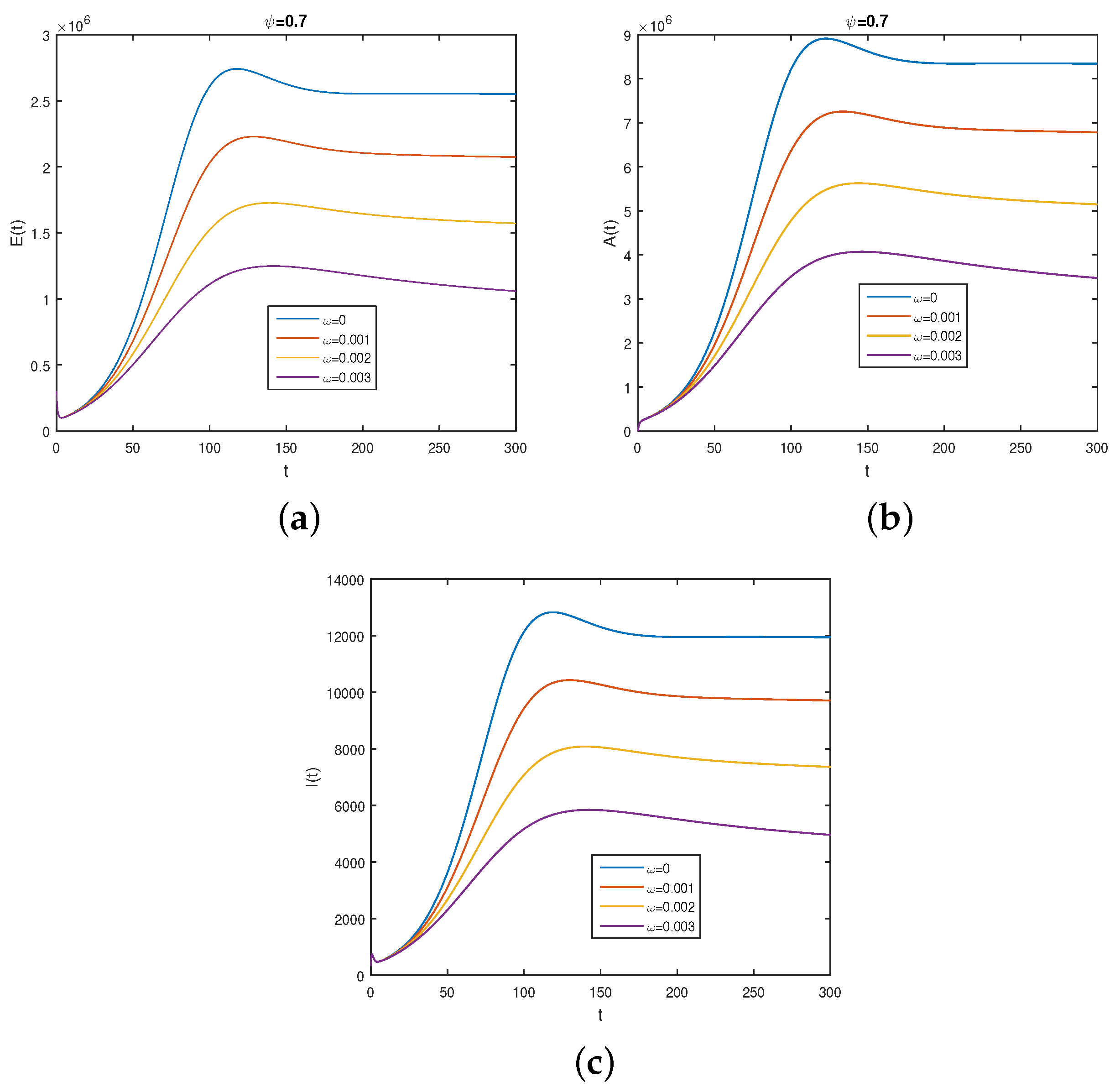
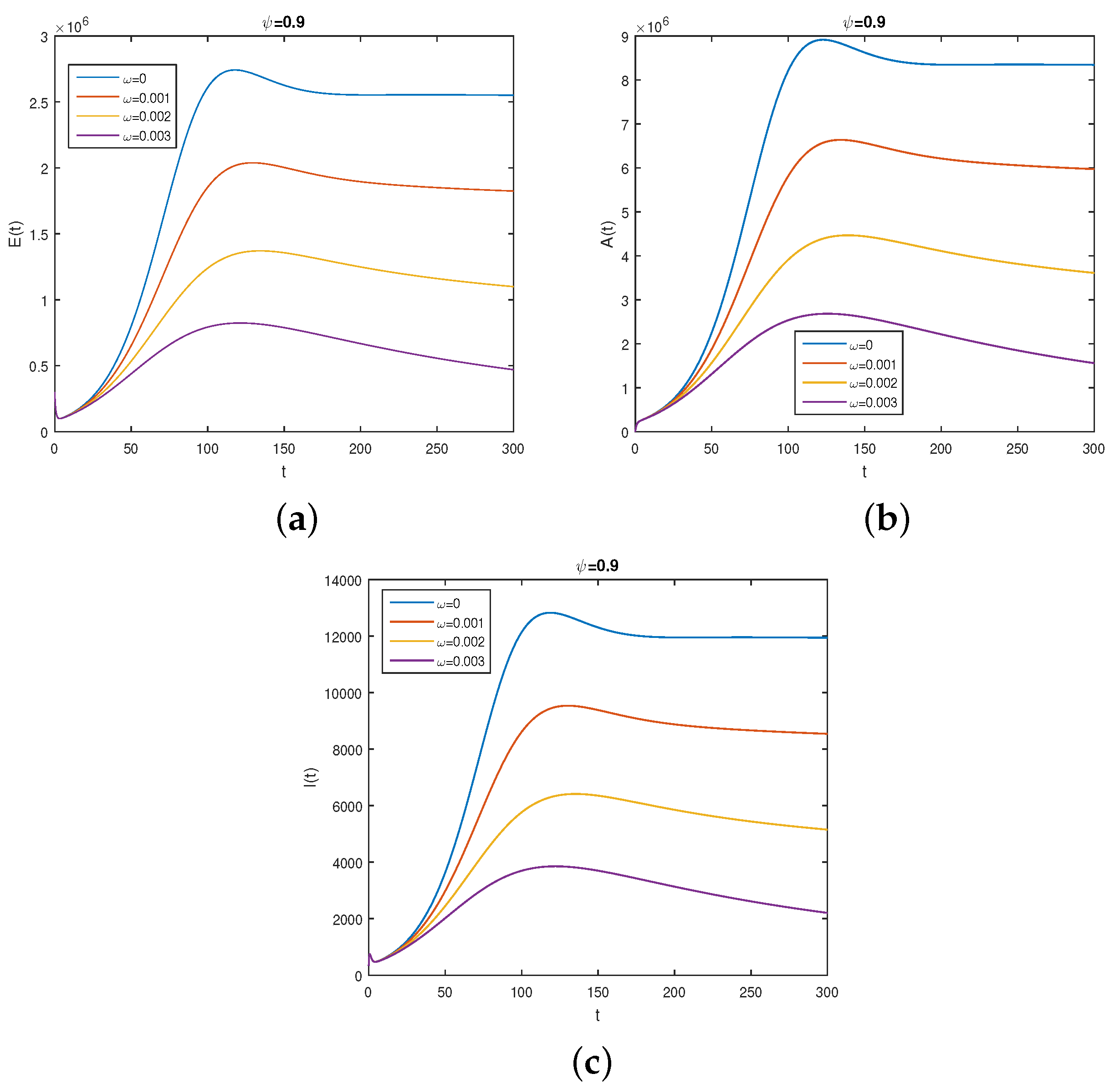
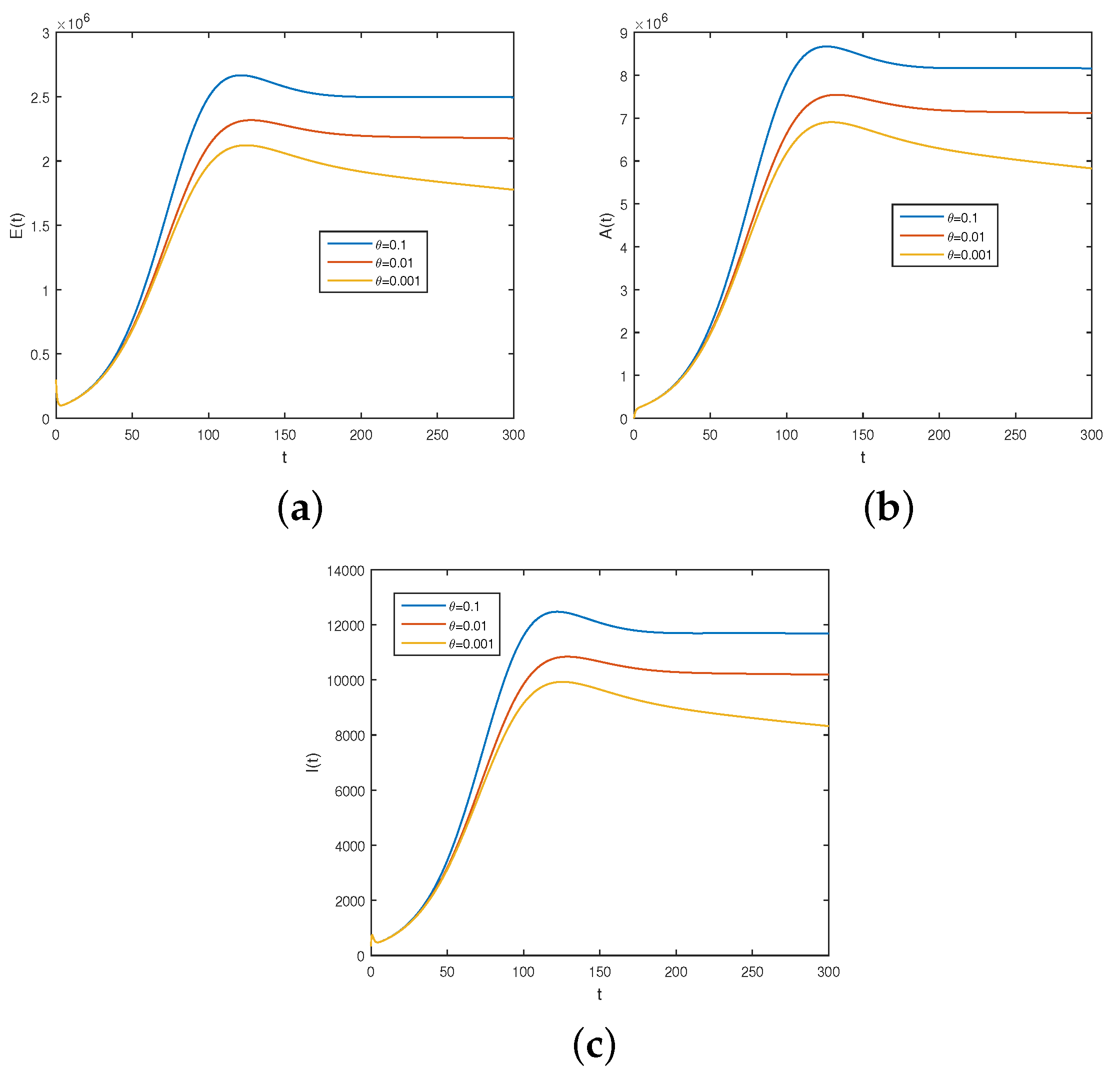
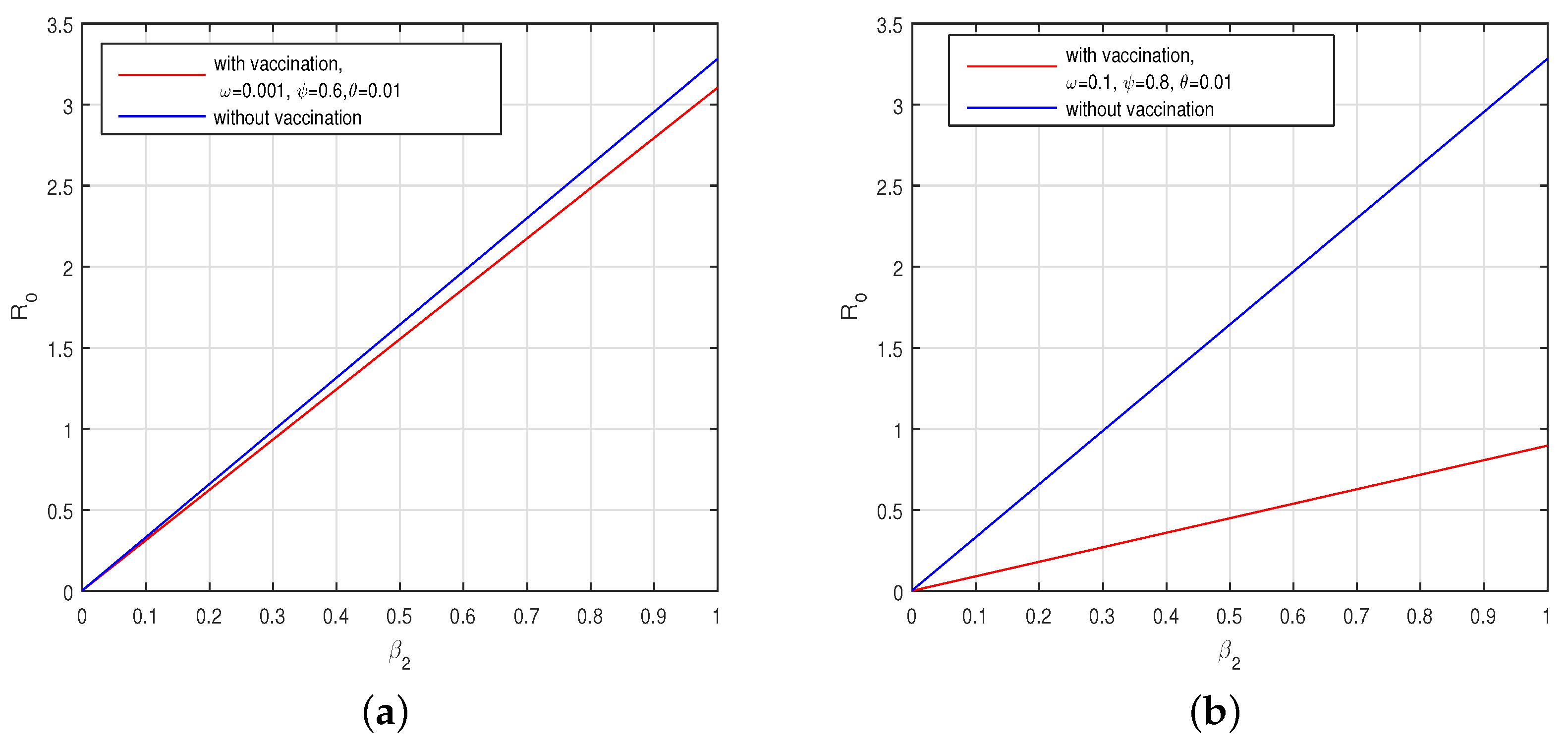
6.2. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World/Countries/Pakistan, Total Coronavirus Cases in Pakistan. Available online: https://www.worldometers.info/coronavirus/country/pakistan/ (accessed on 30 November 2022).
- Khajanchi, S.; Sarkar, K.; Banerjee, S. Modeling the dynamics of COVID-19 pandemic with implementation of intervention strategies. Eur. Phys. J. Plus 2022, 137, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Ullah, M.S.; Higazy, M.; Kabir, K.A. Modeling the epidemic control measures in overcoming COVID-19 outbreaks: A fractional-order derivative approach. Chaos Solitons Fractals 2022, 155, 111636. [Google Scholar] [CrossRef] [PubMed]
- Cioffi, A.; Cioffi, F. COVID-19 vaccine: Risk of inequality and failure of public health strategies. Ethics Med. Public Health 2021, 17, 100653. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Wang, X.; Bao, C.; Ji, Y.; Liu, H.; Meng, Q.; Pan, Q. A multi-regional, hierarchical-tier mathematical model of the spread and control of COVID-19 epidemics from epicentre to adjacent regions. Transbound. Emerg. Dis. 2022, 69, 549–558. [Google Scholar] [CrossRef]
- Deng, J.; Tang, S.; Shu, H. Joint impacts of media, vaccination and treatment on an epidemic Filippov model with application to COVID-19. J. Theor. Biol. 2021, 523, 110698. [Google Scholar] [CrossRef]
- Chen, C.; Chong, N.S. A Filippov model describing the effects of media coverage and quarantine on the spread of human influenza. Math. Biosci. 2018, 296, 98–112. [Google Scholar] [CrossRef]
- Acuña-Zegarra, M.A.; Díaz-Infante, S.; Baca-Carrasco, D.; Olmos-Liceaga, D. COVID-19 optimal vaccination policies: A modeling study on efficacy, natural and vaccine-induced immunity responses. Math. Biosci. 2021, 337, 108614. [Google Scholar] [CrossRef]
- Omame, A.; Umana, R.; Okuonghae, D.; Inyama, S. Mathematical analysis of a two-sex Human Papillomavirus (HPV) model. Int. J. Biomath. 2018, 11, 1850092. [Google Scholar] [CrossRef]
- Elbasha, E.; Podder, C.; Gumel, A. Analyzing the dynamics of an SIRS vaccination model with waning natural and vaccine-induced immunity. Nonlinear Anal. Real World Appl. 2011, 12, 2692–2705. [Google Scholar] [CrossRef]
- Doutor, P.; Rodrigues, P.; Soares, M.d.C.; Chalub, F.A. Optimal vaccination strategies and rational behaviour in seasonal epidemics. J. Math. Biol. 2016, 73, 1437–1465. [Google Scholar] [CrossRef]
- Laarabi, H.; Rachik, M.; El Kahlaoui, O.; Labriji, E. Optimal vaccination strategies of an SIR epidemic model with a saturated treatment. Univers. J. Appl. Math. 2013, 1, 185–191. [Google Scholar] [CrossRef]
- Parsamanesh, M.; Farnoosh, R. On the global stability of the endemic state in an epidemic model with vaccination. Math. Sci. 2018, 12, 313–320. [Google Scholar] [CrossRef]
- Parsamanesh, M.; Erfanian, M.; Mehrshad, S. Stability and bifurcations in a discrete-time epidemic model with vaccination and vital dynamics. BMC Bioinform. 2020, 21, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Liu, H.; Lin, X.; Wei, Y.; Ming, M. Dynamic Analysis of a VSEIR Model with Vaccination Efficacy and Immune Decline. Adv. Math. Phys. 2022, 2022. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A.; Alzahrani, E. The dynamics of COVID-19 with quarantined and isolation. Adv. Differ. Equ. 2020, 2020, 1–22. [Google Scholar] [CrossRef]
- Oud, M.A.A.; Ali, A.; Alrabaiah, H.; Ullah, S.; Khan, M.A.; Islam, S. A fractional order mathematical model for COVID-19 dynamics with quarantine, isolation, and environmental viral load. Adv. Differ. Equ. 2021, 2021, 1–19. [Google Scholar]
- Rihan, F.; Alsakaji, H. Dynamics of a stochastic delay differential model for COVID-19 infection with asymptomatic infected and interacting people: Case study in the UAE. Results Phys. 2021, 28, 104658. [Google Scholar] [CrossRef]
- Anggriani, N.; Ndii, M.Z.; Amelia, R.; Suryaningrat, W.; Pratama, M.A.A. A mathematical COVID-19 model considering asymptomatic and symptomatic classes with waning immunity. Alex. Eng. J. 2022, 61, 113–124. [Google Scholar] [CrossRef]
- Liu, X.; Ullah, S.; Alshehri, A.; Altanji, M. Mathematical assessment of the dynamics of novel coronavirus infection with treatment: A fractional study. Chaos Solitons Fractals 2021, 153, 111534. [Google Scholar] [CrossRef]
- Beigi, A.; Yousefpour, A.; Yasami, A.; Gómez-Aguilar, J.; Bekiros, S.; Jahanshahi, H. Application of reinforcement learning for effective vaccination strategies of coronavirus disease 2019 (COVID-19). Eur. Phys. J. Plus 2021, 136, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Guerra, R.; Flores-Flores, J.P. An algorithm for the robust estimation of the COVID-19 pandemics population by considering undetected individuals. Appl. Math. Comput. 2021, 405, 126273. [Google Scholar] [PubMed]
- Khan, M.A.; Ullah, S.; Kumar, S. A robust study on 2019-nCOV outbreaks through non-singular derivative. Eur. Phys. J. Plus 2021, 136, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Atangana, A. Mathematical modeling and analysis of COVID-19: A study of new variant Omicron. Phys. A Stat. Mech. Its Appl. 2022, 599, 127452. [Google Scholar] [CrossRef]
- Muniyappan, A.; Sundarappan, B.; Manoharan, P.; Hamdi, M.; Raahemifar, K.; Bourouis, S.; Varadarajan, V. Stability and numerical solutions of second wave mathematical modeling on covid-19 and omicron outbreak strategy of pandemic: Analytical and error analysis of approximate series solutions by using hpm. Mathematics 2022, 10, 343. [Google Scholar] [CrossRef]
- Pandey, P.; Gómez-Aguilar, J.; Kaabar, M.K.; Siri, Z.; Abd Allah, A.M. Mathematical modeling of COVID-19 pandemic in India using Caputo-Fabrizio fractional derivative. Comput. Biol. Med. 2022, 145, 105518. [Google Scholar] [CrossRef]
- Zhang, C.; Agarwal, R.P.; Bohner, M.; Li, T. Oscillation of second-order nonlinear neutral dynamic equations with noncanonical operators. Bull. Malays. Math. Sci. Soc. 2015, 38, 761–778. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Q.; Ye, Y.; Qu, B. Using IIR filter in fractional order phase lead compensation PIMR-RC for grid-tied inverters. In IEEE Transactions on Industrial Electronics; IEEE: Piscataway, NJ, USA, 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Areshi, M.; Seadawy, A.R.; Ali, A.; Alharbi, A.F.; Aljohani, A.F. Analytical Solutions of the Predator–Prey Model with Fractional Derivative Order via Applications of Three Modified Mathematical Methods. Fractal Fract. 2023, 7, 128. [Google Scholar] [CrossRef]
- Wu, X.; Wen, S.; Shao, W.; Wang, J. Numerical Investigation of Fractional Step-Down ELS Option. Fractal Fract. 2023, 7, 126. [Google Scholar] [CrossRef]
- He, Y.; Wang, Z. Stability analysis and optimal control of a fractional cholera epidemic model. Fractal Fract. 2022, 6, 157. [Google Scholar] [CrossRef]
- Baba, I.A.; Humphries, U.W.; Rihan, F.A. Role of Vaccines in Controlling the Spread of COVID-19: A Fractional-Order Model. Vaccines 2023, 11, 145. [Google Scholar] [CrossRef] [PubMed]
- Okyere, S.; Ackora-Prah, J. Modeling and analysis of monkeypox disease using fractional derivatives. Results Eng. 2023, 17, 100786. [Google Scholar] [CrossRef] [PubMed]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Pakistan Life Expectancy 1950–2022. Available online: https://www.macrotrends.net/countries/PAK/pakistan/life-expectancy (accessed on 5 November 2022).
- Pakistan Population. Available online: https://www.worldometers.info/world-population%/pakistan-population/ (accessed on 5 November 2022).
- Jajarmi, A.; Baleanu, D. A new fractional analysis on the interaction of HIV with CD4+ T-cells. Chaos Solitons Fractals 2018, 113, 221–229. [Google Scholar] [CrossRef]
- Qureshi, S.; Bonyah, E.; Shaikh, A.A. Classical and contemporary fractional operators for modeling diarrhea transmission dynamics under real statistical data. Phys. A Stat. Mech. Its Appl. 2019, 535, 122496. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]




| Symbol | Definitions | Numeric Value | Ref |
|---|---|---|---|
| Birth rate | Estimated | ||
| Natural mortality rate | [38] | ||
| Contact between healthy and sick people | 0.8983 | Fitted | |
| Contact between healthy and asymptomatic people | 0.3827 | Fitted | |
| Natural immunity loss | 0.3129 | Fitted | |
| Incubation time period | 0.9982 | Fitted | |
| q | The proportion joins class A | 0.9931 | Fitted |
| The proportion joins class I | 0.0069 | Fitted | |
| Recovery rate of asymptomatic people | 0.3028 | Fitted | |
| Recovery of symptomatic people | 0.7926 | Fitted | |
| d | Disease death rate of symptomatic people | 0.6784 | Fitted |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.-C.; DarAssi, M.H.; Alfwzan, W.F.; Khan, M.A.; Alqahtani, A.S.; Alshahrani, S.S.; Muhammad, T. Mathematical Modeling of COVID-19 with Vaccination Using Fractional Derivative: A Case Study. Fractal Fract. 2023, 7, 234. https://doi.org/10.3390/fractalfract7030234
Sun T-C, DarAssi MH, Alfwzan WF, Khan MA, Alqahtani AS, Alshahrani SS, Muhammad T. Mathematical Modeling of COVID-19 with Vaccination Using Fractional Derivative: A Case Study. Fractal and Fractional. 2023; 7(3):234. https://doi.org/10.3390/fractalfract7030234
Chicago/Turabian StyleSun, Tian-Chuan, Mahmoud H. DarAssi, Wafa F. Alfwzan, Muhammad Altaf Khan, Abdulaziz Saad Alqahtani, Saeed S. Alshahrani, and Taseer Muhammad. 2023. "Mathematical Modeling of COVID-19 with Vaccination Using Fractional Derivative: A Case Study" Fractal and Fractional 7, no. 3: 234. https://doi.org/10.3390/fractalfract7030234
APA StyleSun, T.-C., DarAssi, M. H., Alfwzan, W. F., Khan, M. A., Alqahtani, A. S., Alshahrani, S. S., & Muhammad, T. (2023). Mathematical Modeling of COVID-19 with Vaccination Using Fractional Derivative: A Case Study. Fractal and Fractional, 7(3), 234. https://doi.org/10.3390/fractalfract7030234









