Fractional-Order Gas Film Model
Abstract
1. Introduction
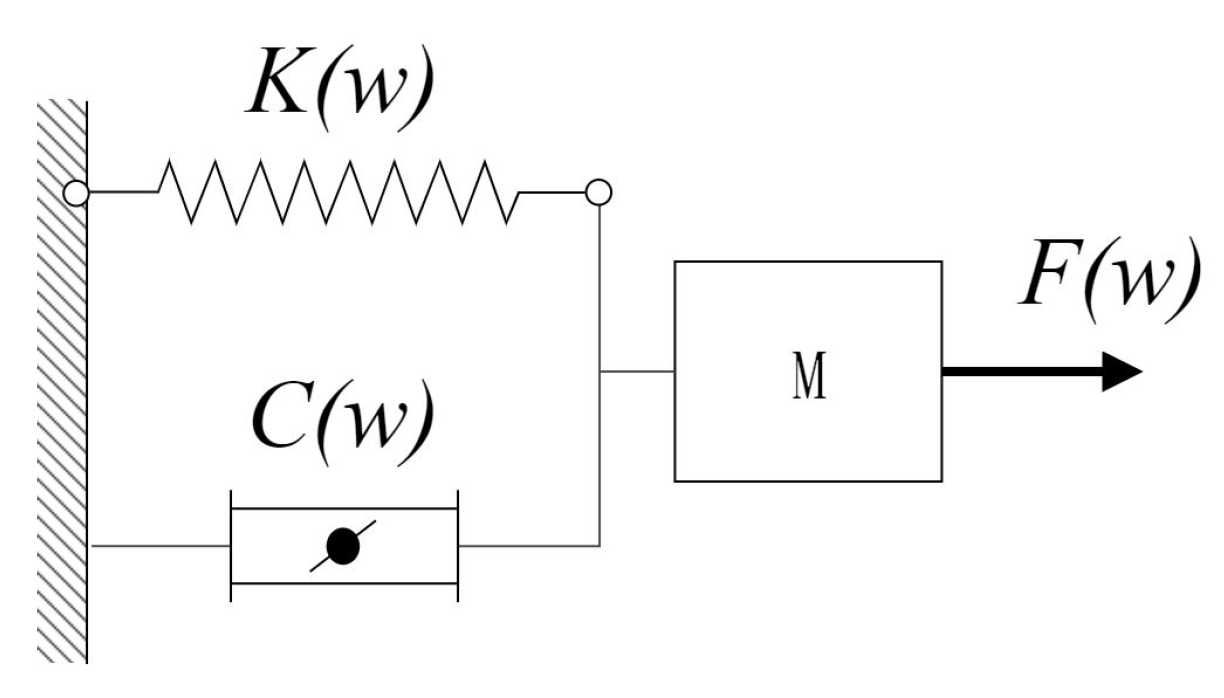
2. Gas Film Dynamic Characteristics
3. Fractional Calculus Definition and Fractional-Order Model
3.1. Fractional Calculus Definition
3.2. Model Component
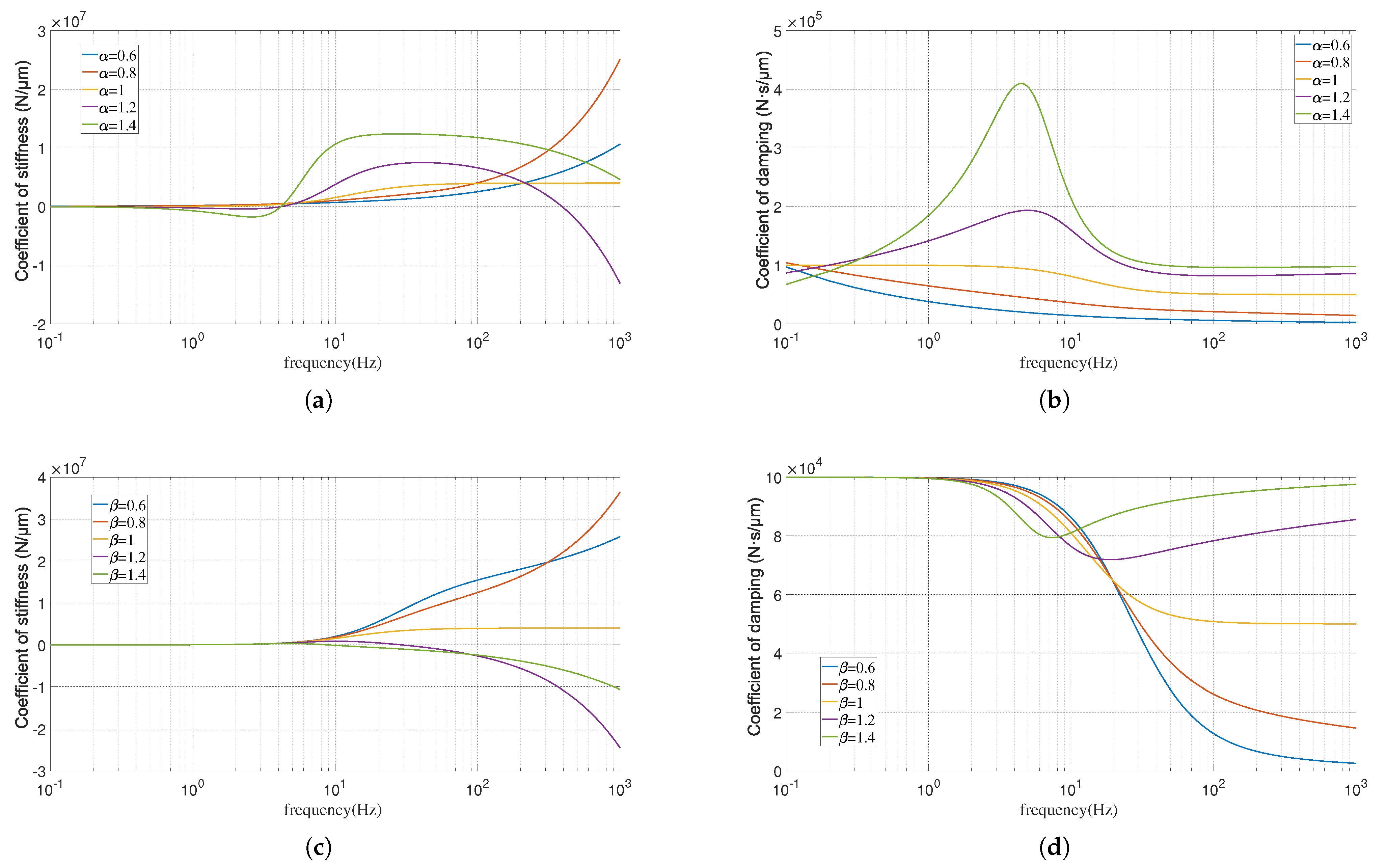
3.3. Fractional-Order Gas Film Models
3.3.1. Fractional-Order Zener Gas Film Model
3.3.2. Fractional-Order Maxwell Gas Film Model
3.3.3. Fractional-Order Three Parameter Gas Film Model
3.3.4. Fractional-Order Burgess Gas Film Model
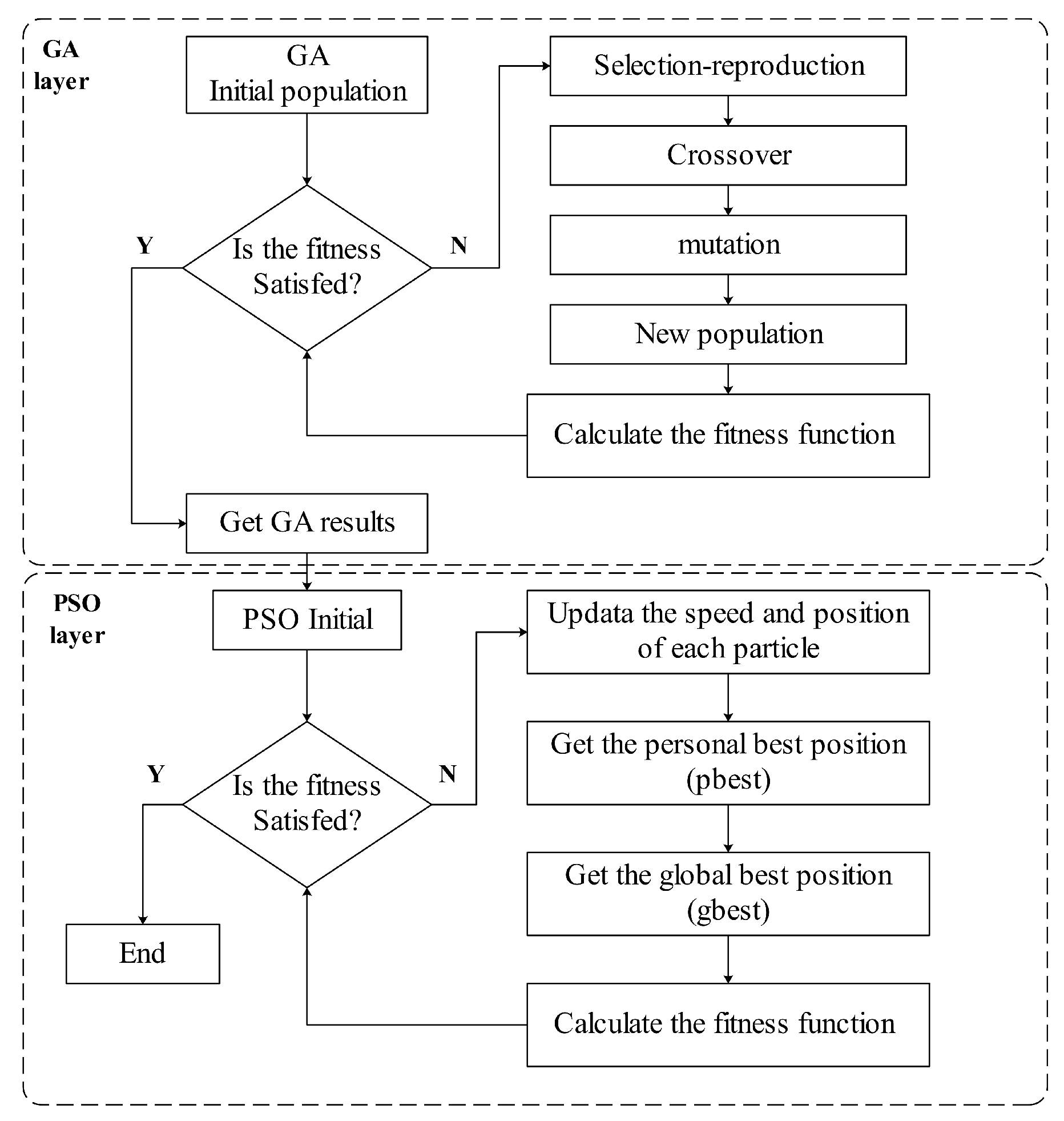
4. Parameter Identification for the FOGF Models
5. Experimental Validation
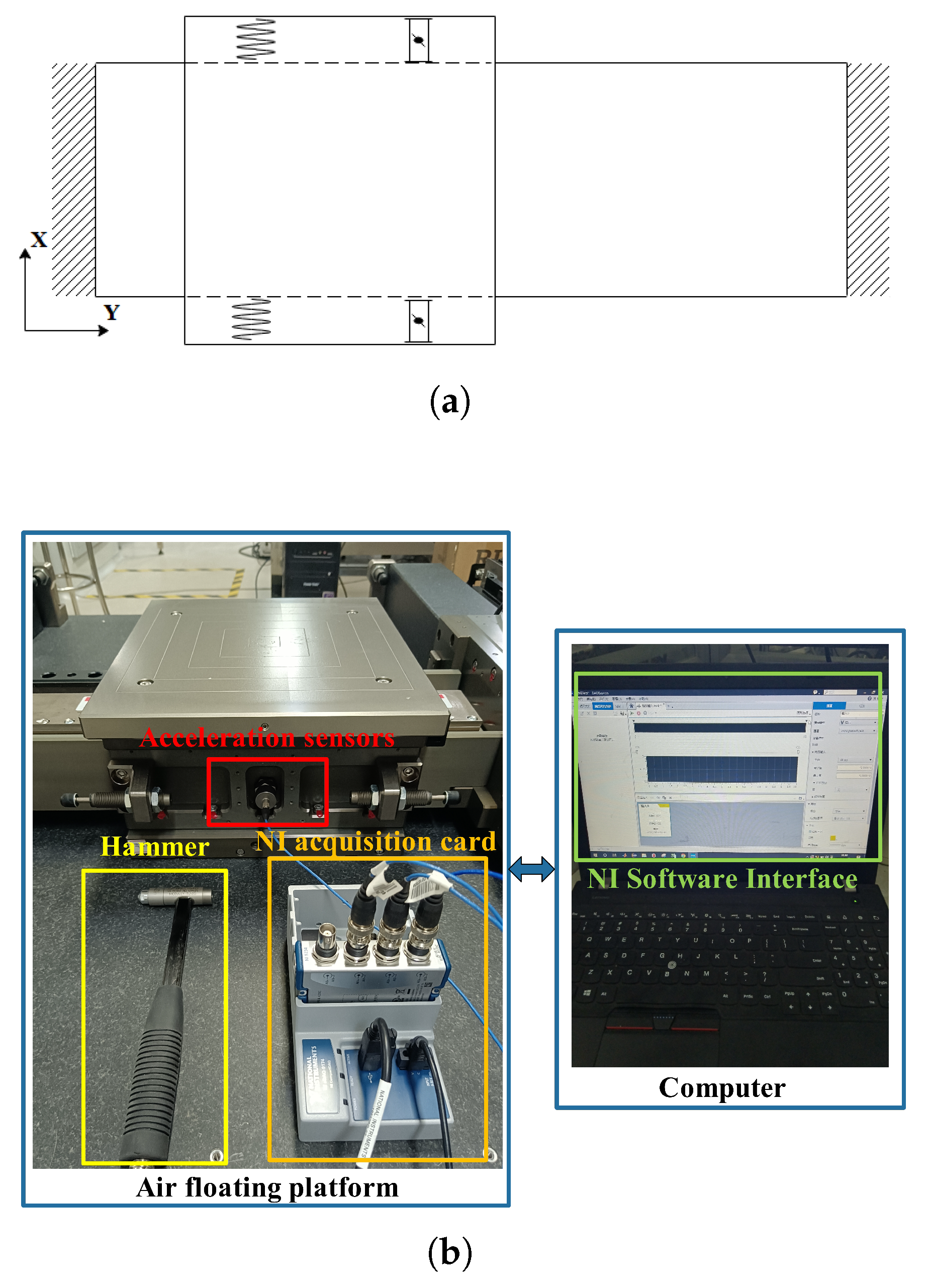
5.1. FOGF Vibration Test System
5.2. Experimental Platform
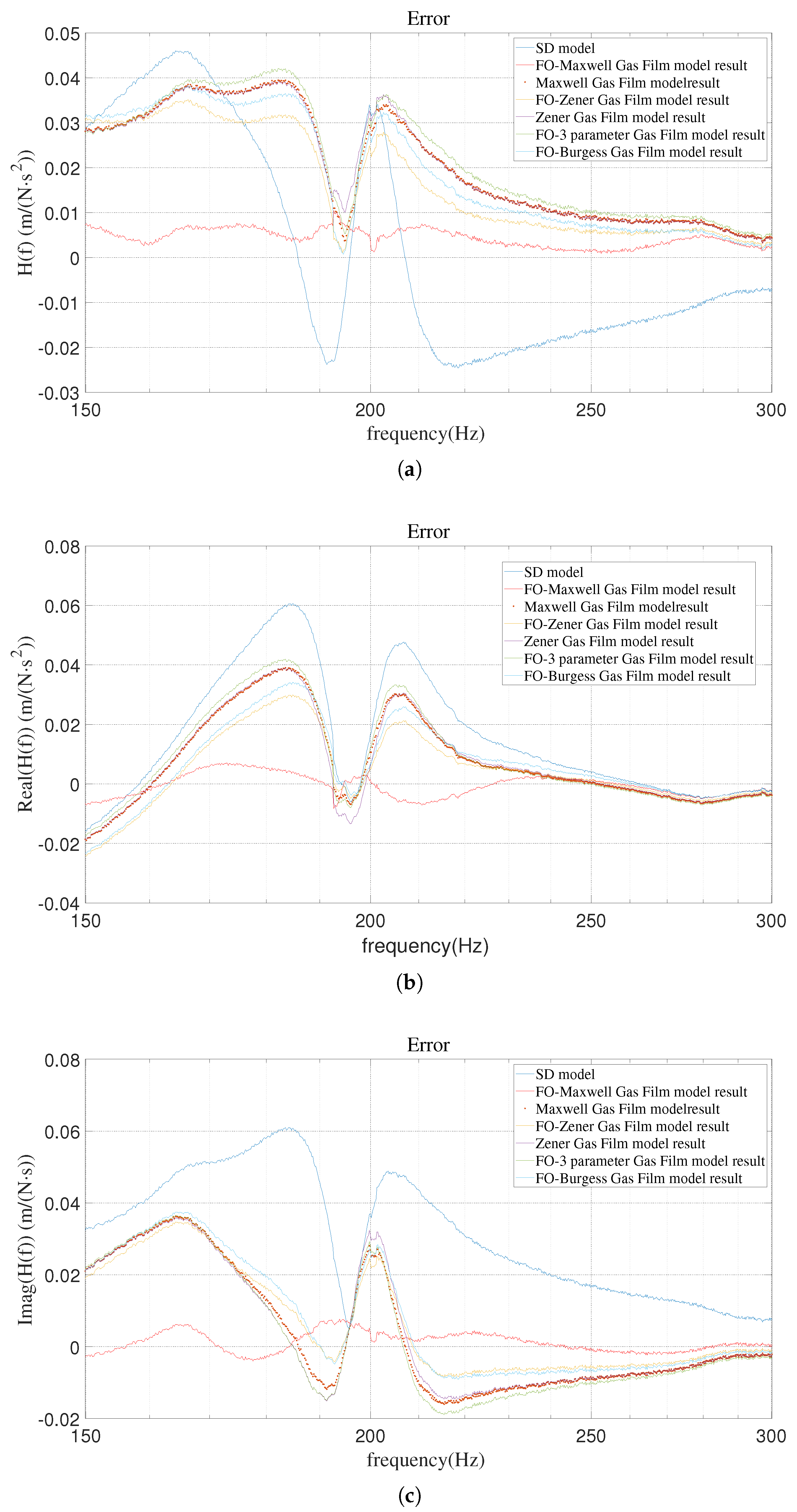
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Powell, J. Design of Aerostatic Bearings; Machinery Pub. Co: Brighton, UK, 1970; pp. 89–99. [Google Scholar]
- Geng, Y.; Wang, Y.; Yan, Y.; Zhao, X. A novel AFM-based 5-axis nanoscale machine tool for fabrication of nanostructures on a micro ball. Rev. Sci. Instruments 2017, 88, 115109. [Google Scholar] [CrossRef]
- Chen, G.; Sun, Y.; Zhang, F.; An, C.; Chen, W.; Su, H. Influence of ultra-precision flycutting spindle error on surface frequency domain error formation. Int. J. Adv. Manuf. Technol. 2017, 88, 3233–3241. [Google Scholar] [CrossRef]
- Krijnen, M.E.; van Ostayen, R.A.; HosseinNia, H. The application of fractional-order control for an air-based contactless actuation system. ISA Trans. 2018, 82, 172–183. [Google Scholar] [CrossRef]
- Bos, E.; Moers, T.; Van Riel, M. Design and verification of an ultra-precision 3D-coordinate measuring machine with parallel drives. Meas. Sci. Technol. 2015, 26, 085904. [Google Scholar] [CrossRef]
- Jayson, E.M.; Murphy, J.; Smith, P.; Talke, F.E. Effects of air bearing stiffness on a hard disk drive subject to shock and vibration. J. Trib. 2003, 125, 343–349. [Google Scholar] [CrossRef]
- Yu, S.; Liu, B.; Hua, W.; Zhou, W. Contact Induced Off-Track Vibrations of Air Bearing-Slider-Suspension System in Hard Disk Drives. Proc. Int. Jt. Tribol. Conf. 2006, 42592, 891–898. [Google Scholar]
- Harrison, W. The Hydrodynamical Theory of Lubrication with Special Reference to Air as a Lubricant; Cambridge University Press: Cambridge, UK, 1913. [Google Scholar]
- Bhat, N.; Kumar, S.; Tan, W.; Narasimhan, R.; Low, T.C. Performance of inherently compensated flat pad aerostatic bearings subject to dynamic perturbation forces. Precis. Eng. 2012, 36, 399–407. [Google Scholar] [CrossRef]
- Charki, A.; Diop, K.; Champmartin, S.; Ambari, A. Numerical simulation and experimental study of thrust air bearings with multiple orifices. Int. J. Mech. Sci. 2013, 72, 28–38. [Google Scholar] [CrossRef]
- Gao, Q.; Qi, L.; Gao, S.; Lu, L.; Song, L.; Zhang, F. A FEM based modeling method for analyzing the static performance of aerostatic thrust bearings considering the fluid-structure interaction. Tribol. Int. 2021, 156, 106849. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Q.; Wang, B.; Zhang, L.; Yang, H.; Peng, Z. Effect of surface waviness on the static performance of aerostatic journal bearings. Tribol. Int. 2016, 103, 394–405. [Google Scholar] [CrossRef]
- Heshmat, H.; Walton, J.F. Starved Hydrodynamic Gas Foil Bearings—Experiment, Micromechanical Phenomenon, and Hypotheses. J. Tribol. 2016, 138, 041703. [Google Scholar] [CrossRef]
- San Andrés, L.; Yang, J.; Devitt, A. On Tilting Pad Carbon–Graphite Porous Journal Bearings: Measurements of Imbalance Response and Comparison to Predictions of Bearing Performance and System Dynamic Response. Tribol. Trans. 2021, 64, 981–995. [Google Scholar] [CrossRef]
- Mallisetty, P.K.; Samanta, P.; Murmu, N. Nonlinear transient analysis of rigid rotor mounted on externally pressurized double-layered porous gas journal bearings accounting velocity slip. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–12. [Google Scholar] [CrossRef]
- Wu, Y.; Deng, M.; Feng, K.; Guan, H.; Cao, Y. Investigations on the nonlinear dynamic characteristics of a rotor supported by porous tilting pad bearings. Nonlinear Dyn. 2020, 100, 2265–2286. [Google Scholar] [CrossRef]
- Durazo-Cardenas, I.; Corbett, J.; Stephenson, D.J. Permeability and dynamic elastic moduli of controlled porosity ultra-precision aerostatic structures. Ceram. Int. 2014, 40, 3041–3051. [Google Scholar] [CrossRef]
- Kang, T.S.; Choi, D.H.; Jeong, T.G. Optimal design of HDD air-lubricated slider bearings for improving dynamic characteristics and operating performance. J. Trib. 2001, 123, 541–547. [Google Scholar] [CrossRef]
- Cui, H.; Wang, Y.; Yue, X.; Huang, M.; Wang, W. Effects of manufacturing errors on the static characteristics of aerostatic journal bearings with porous restrictor. Tribol. Int. 2017, 115, 246–260. [Google Scholar] [CrossRef]
- Chang-Jian, C.W. Chaotic response and bifurcation analysis of a flexible rotor supported by porous and non-porous bearings with nonlinear suspension. Nonlinear Anal. Real World Appl. 2009, 10, 1114–1138. [Google Scholar] [CrossRef]
- Panzera, T.; Rubio, J.; Bowen, C.; Walker, P. Microstructural design of materials for aerostatic bearings. Cem. Concr. Compos. 2008, 30, 649–660. [Google Scholar] [CrossRef]
- Park, D.J.; Kim, C.H.; Jang, G.H.; Lee, Y.B. Theoretical considerations of static and dynamic characteristics of air foil thrust bearing with tilt and slip flow. Tribol. Int. 2008, 41, 282–295. [Google Scholar] [CrossRef]
- Ishibashi, K.; Kondo, A.; Kawada, S.; Miyatake, M.; Yoshimoto, S.; Stolarski, T. Static and dynamic characteristics of a downsized aerostatic circular thrust bearing with a single feed hole. Precis. Eng. 2019, 60, 448–457. [Google Scholar] [CrossRef]
- Maamari, N.; Krebs, A.; Weikert, S.; Wild, H.; Wegener, K. Stability and dynamics of an orifice based aerostatic bearing with a compliant back plate. Tribol. Int. 2019, 138, 279–296. [Google Scholar] [CrossRef]
- Yoshimoto, S.; Kohno, K. Static and dynamic characteristics of aerostatic circular porous thrust bearings (effect of the shape of the air supply area). J. Trib. 2001, 123, 501–508. [Google Scholar] [CrossRef]
- Oiwa, N.; Masuda, M.; Hirayama, T.; Matsuoka, T.; Yabe, H. Deformation and flying height orbit of glass sheets on aerostatic porous bearing guides. Tribol. Int. 2012, 48, 2–7. [Google Scholar] [CrossRef]
- Jia, C.; Pang, H.; Ma, W.; Qiu, M. Analysis of dynamic characteristics and stability prediction of gas bearings. Ind. Lubr. Tribol. 2017, 69, 123–130. [Google Scholar] [CrossRef]
- Fourka, M.; Tian, Y.; Bonis, M. Prediction of the stability of air thrust bearings by numerical, analytical and experimental methods. Wear 1996, 198, 1–6. [Google Scholar] [CrossRef]
- Plante, J.S.; Vogan, J.; El-Aguizy, T.; Slocum, A.H. A design model for circular porous air bearings using the 1D generalized flow method. Precis. Eng. 2005, 29, 336–346. [Google Scholar] [CrossRef]
- Geerts, N. Linear Dynamic Analysis of Rotorsystems with gAs Bearings. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1995. [Google Scholar]
- Sun, Y.; Zeng, L.; Luo, Y.; Li, X. Model Decoupled Synchronization Control Design with Fractional Order Filter for H-Type Air Floating Motion Platform. Entropy 2021, 23, 633. [Google Scholar] [CrossRef]
- Jiang, W.; Jia, W.C.; Liu, S.S.; Hu, Y.T.; Hu, H.P. Roll Vibration Analysis of Planar Aerostatic Bearings through a Distributed Spring Model. In Advanced Materials Research; Trans Tech Publications Ltd.: Bäch, Switzerland, 2012; Volume 346, pp. 332–338. [Google Scholar]
- Arghir, M.; Matta, P. Compressibility effects on the dynamic characteristics of gas lubricated mechanical components. Comptes Rendus Mécanique 2009, 337, 739–747. [Google Scholar] [CrossRef]
- Al-Bender, F. On the modeling of the dynamic characteristics of aerostatic bearing films: From stability analysis to active compensation. Precis. Eng. 2009, 33, 117–126. [Google Scholar] [CrossRef]
- Sahraoui, S.; Zekri, N. On fractional modeling of viscoelastic foams. Mech. Res. Commun. 2019, 96, 62–66. [Google Scholar] [CrossRef]
- Liang, Y.; Guan, P. Improved Maxwell model with structural dashpot for characterization of ultraslow creep in concrete. Constr. Build. Mater. 2022, 329, 127181. [Google Scholar] [CrossRef]
- Hinze, M.; Xiao, S.; Schmidt, A.; Nowak, W. Experimental evaluation and uncertainty quantification for a fractional viscoelastic model of salt concrete. Mech. -Time-Depend. Mater. 2022, 1–24. [Google Scholar] [CrossRef]
- Sánchez, E.; Nájera, A.; Sotomayor, O. Numerical study of the viscoelastic mechanical response of polystyrene in the process of thermoforming through the generalized Maxwell model. Mater. Today Proc. 2022, 49, 107–114. [Google Scholar] [CrossRef]
- Nadzharyan, T.; Kostrov, S.; Stepanov, G.; Kramarenko, E.Y. Fractional rheological models of dynamic mechanical behavior of magnetoactive elastomers in magnetic fields. Polymer 2018, 142, 316–329. [Google Scholar] [CrossRef]
- Alcoutlabi, M.; Martinez-Vega, J. Application of fractional calculus to viscoelastic behavior modeling and to the physical ageing phenomenon in glassy amorphous polymers. Polymer 1998, 39, 6269–6277. [Google Scholar] [CrossRef]
- Zhu, J. Dynamic Characteristics and Nano-Vibration of Aerostatic Bearings; Hua Zhong University of Science and Technology: Wuhan, China, 2014. [Google Scholar]
- Wei, L. Study on Loading Characteristics of Orifice Compensated Aerostatic Thrust Bearing. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2010. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Nabi, K.N.; Abboubakar, H.; Kumar, P. Forecasting of COVID-19 pandemic: From integer derivatives to fractional derivatives. Chaos Solitons Fractals 2020, 141, 110283. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, Y. Finite Element Calculation of the Linear Elasticity Problem for Biomaterials with Fractal Structure. Open Bioinform. J. 2021, 14, 114–122. [Google Scholar] [CrossRef]
- Wu, J.; Wang, L.; Li, L.; Shu, Y.; Yang, L.; Lei, T. Sliding State Analysis of Fractal Rough Interface Based on the Finite Element Method. Materials 2021, 14, 2121. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, Y.; Boretska, I.; Sokolovskyy, I.; Markelov, O.; Storozhuk, O. Application of FEM with Piecewise Mittag-Leffler Functions Basis for the Linear Elasticity Problem in Materials with Fractal Structure. In Proceedings of the 2021 IEEE XVIIth International Conference on the Perspective Technologies and Methods in MEMS Design (MEMSTECH), Polyana (Zakarpattya), Ukraine, 12–16 May 2021; pp. 16–19. [Google Scholar]
- Shymanskyi, V.; Sokolovskyy, Y. Variational Method for Solving the Viscoelastic Deformation Problem in Biomaterials with Fractal Structure. In Proceedings of the IT&I, Kyiv, Ukraine, 1–3 December 2021; pp. 125–134. [Google Scholar]
- Lischke, A.; Zayernouri, M.; Zhang, Z. Spectral and spectral element methods for fractional advection–diffusion–reaction equations. Handb. Fract. Calc. Appl. Numer. Methods 2019, 3, 157–183. [Google Scholar]
- Shah, F.A.; Abass, R.; Debnath, L. Numerical solution of fractional differential equations using Haar wavelet operational matrix method. Int. J. Appl. Comput. Math. 2017, 3, 2423–2445. [Google Scholar] [CrossRef]
- Li, X. Numerical solution of fractional differential equations using cubic B-spline wavelet collocation method. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3934–3946. [Google Scholar] [CrossRef]
- Torge, M.; Bottlender, R.; Strauß, A.; Möller, H. Numerische klassifikation psychopathologischer daten mittels der logistischen Regression. Eur. Psychiatry 1998, 13, 321s. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Oustaloup, A.; Moreau, X.; Nouillant, M. The CRONE suspension. Control Eng. Pract. 1996, 4, 1101–1108. [Google Scholar] [CrossRef]
- Chen, B.; Li, C.; Wilson, B.; Huang, Y. Fractional modeling and analysis of coupled MR damping system. IEEE/CAA J. Autom. Sin. 2016, 3, 288–294. [Google Scholar]
- Premalatha, K.; Natarajan, A. Hybrid PSO and GA for global maximization. Int. J. Open Probl. Compt. Math 2009, 2, 597–608. [Google Scholar]
- He, P.; Fang, Q.; Jin, H.; Ji, Y.; Gong, Z.; Dong, J. Coordinated design of PSS and STATCOM-POD based on the GA-PSO algorithm to improve the stability of wind-PV-thermal-bundled power system. Int. J. Electr. Power Energy Syst. 2022, 141, 108208. [Google Scholar] [CrossRef]
- Kumar, M.; Husain, D.; Upreti, N.; Gupta, D. Genetic Algorithm: Review and Application. 2010. Available online: https://ssrn.com/abstract=3529843 (accessed on 16 June 2022).
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- De Oca, M.A.M.; Stutzle, T.; Birattari, M.; Dorigo, M. Frankenstein’s PSO: A composite particle swarm optimization algorithm. IEEE Trans. Evol. Comput. 2009, 13, 1120–1132. [Google Scholar] [CrossRef]
- Siewert, T.A.; Manahan, M.; McCowan, C.N.; Holt, J.; Marsh, F.; Ruth, E. The history and importance of impact testing. ASTM Spec. Tech. Publ. 2000, 1380, 3–16. [Google Scholar]
- Ali, N.; García, J. Experimental studies on the dynamic characteristics of rolling element bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 659–666. [Google Scholar] [CrossRef]
- Lin, T.R.; Farag, N.H.; Pan, J. Evaluation of frequency dependent rubber mount stiffness and damping by impact test. Appl. Acoust. 2005, 66, 829–844. [Google Scholar] [CrossRef]
- Tang, Z.; Pillay, P.; Omekanda, A.M. Vibration prediction in switched reluctance motors with transfer function identification from shaker and force hammer tests. IEEE Trans. Ind. Appl. 2003, 39, 978–985. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, C.; Wang, Z.; Mao, K. Study on dynamic characteristics of the disc spring system in vibration screen. Shock Vib. 2020, 2020, 3518037. [Google Scholar] [CrossRef]
- Dou, Y.; Wang, P.; Ding, W.; Wang, S.; Wei, K. Effect of viscoelastic-plastic dynamic properties of rail pads on curved rail dynamic characteristics based on the modified SEM–SM hybrid method. Veh. Syst. Dyn. 2022, 1–25. [Google Scholar] [CrossRef]

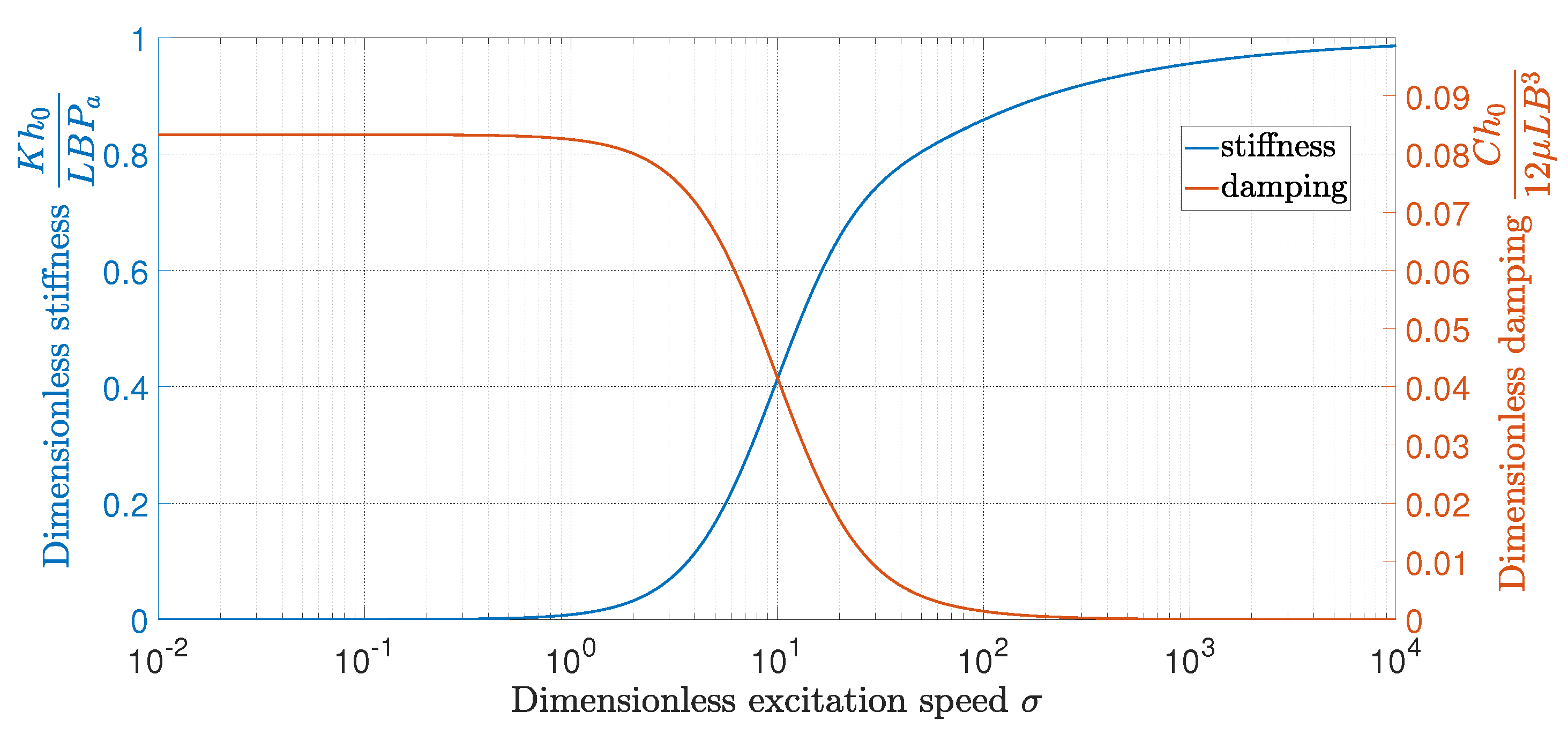

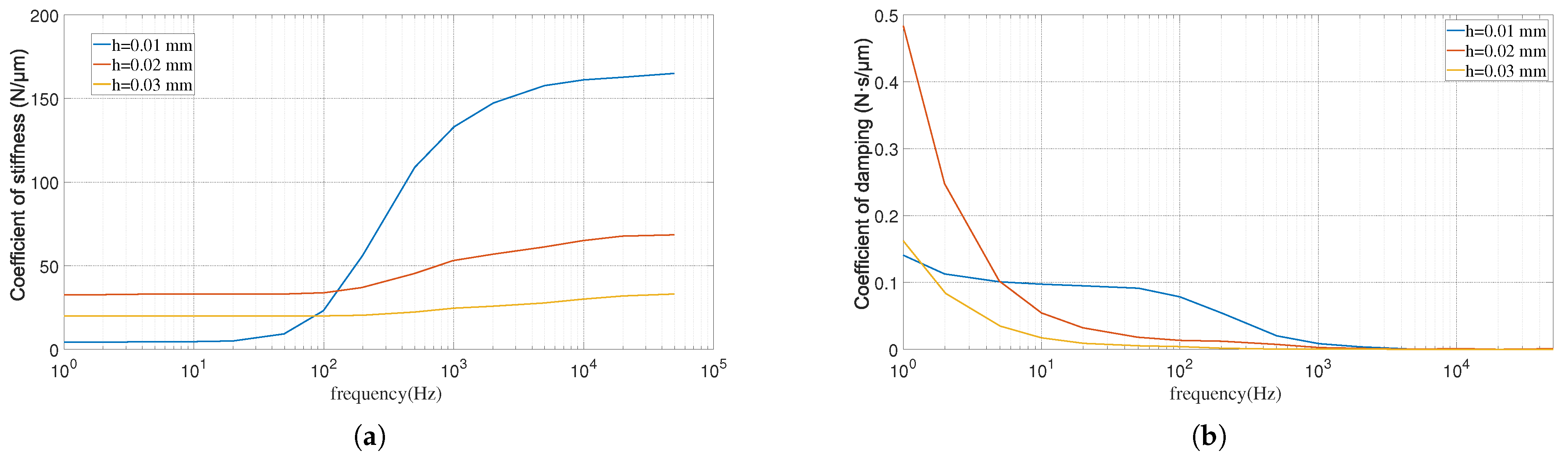
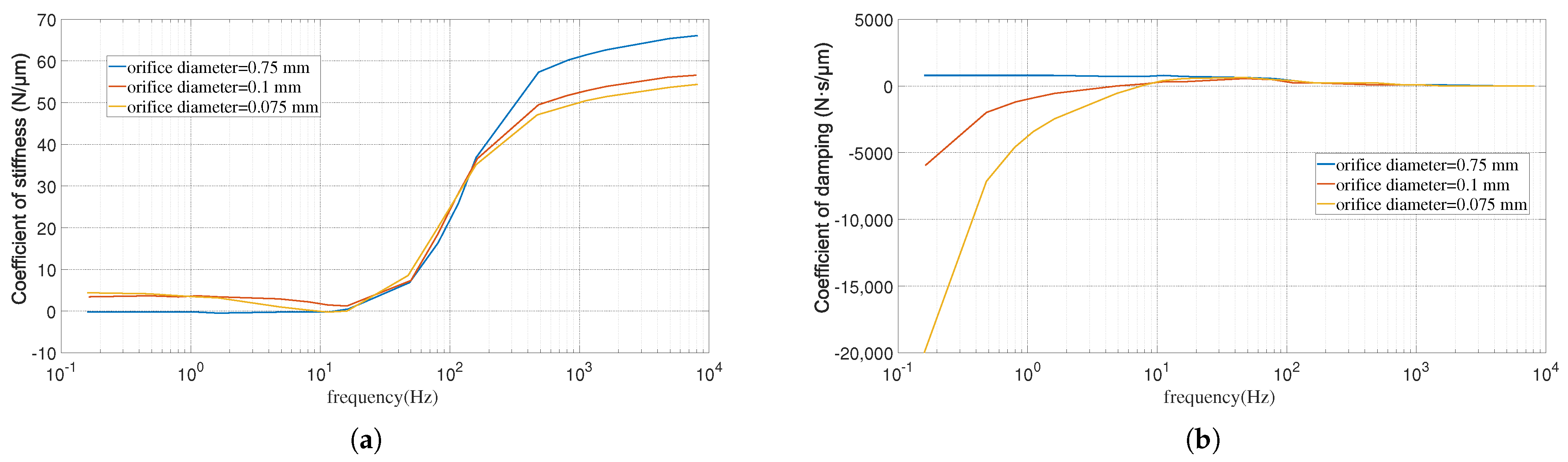




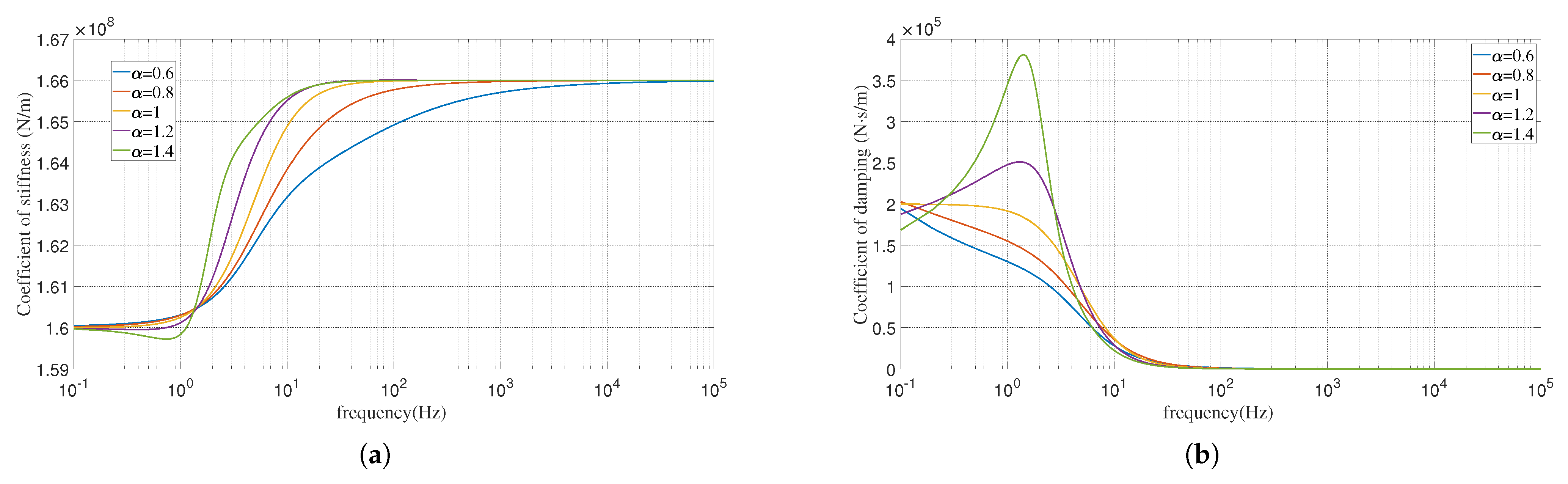




| Model | Parameter Numbers | Identification Results (units: N/m, N·s/m) |
|---|---|---|
| SD model | 2 | , |
| FOZGF model | 4 | , , , |
| Zener model | 3 | , , |
| FOMGF model | 7 | , , , , , , |
| Maxwell model | 5 | , , , , |
| FOTGF model | 5 | , , , , |
| FOBGF model | 6 | , , , , , |
| TGF model | 3 | , , |
| BGF model | 4 | , , , , |
| Model | RMS | E | Peak Error | |
|---|---|---|---|---|
| SD model [31,32] | 0.0016643 | 0.00% | 0.06095 | 0.00% |
| FOZGF model | 0.00092817 | 44.23% | 0.03514 | 42.34% |
| Zener model [33,41] | 0.0011119 | 33.19% | 0.0392 | 35.70% |
| FOMGF model | 0.00022979 | 86.19% | 0.01041 | 82.91% |
| Maxwell model | 0.0011131 | 33.12% | 0.03948 | 35.22% |
| FOTGF model | 0.0011844 | 28.83% | 0.04209 | 31% |
| FOBGF model | 0.0010477 | 37.05% | 0.03826 | 37.23% |
| TGF model | 0.0078358 | −370.8% | 0.3560 | −484.09% |
| BGF model | 0.0082992 | −398.6% | 0.3717 | −509.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Luo, Y.; Han, B. Fractional-Order Gas Film Model. Fractal Fract. 2022, 6, 561. https://doi.org/10.3390/fractalfract6100561
Tang X, Luo Y, Han B. Fractional-Order Gas Film Model. Fractal and Fractional. 2022; 6(10):561. https://doi.org/10.3390/fractalfract6100561
Chicago/Turabian StyleTang, Xu, Ying Luo, and Bin Han. 2022. "Fractional-Order Gas Film Model" Fractal and Fractional 6, no. 10: 561. https://doi.org/10.3390/fractalfract6100561
APA StyleTang, X., Luo, Y., & Han, B. (2022). Fractional-Order Gas Film Model. Fractal and Fractional, 6(10), 561. https://doi.org/10.3390/fractalfract6100561








