G-Fractional Diffusion on Bounded Domains in
Abstract
1. Introduction
2. G-Fractional Diffusion in Bounded Domains
3. First-Passage Times
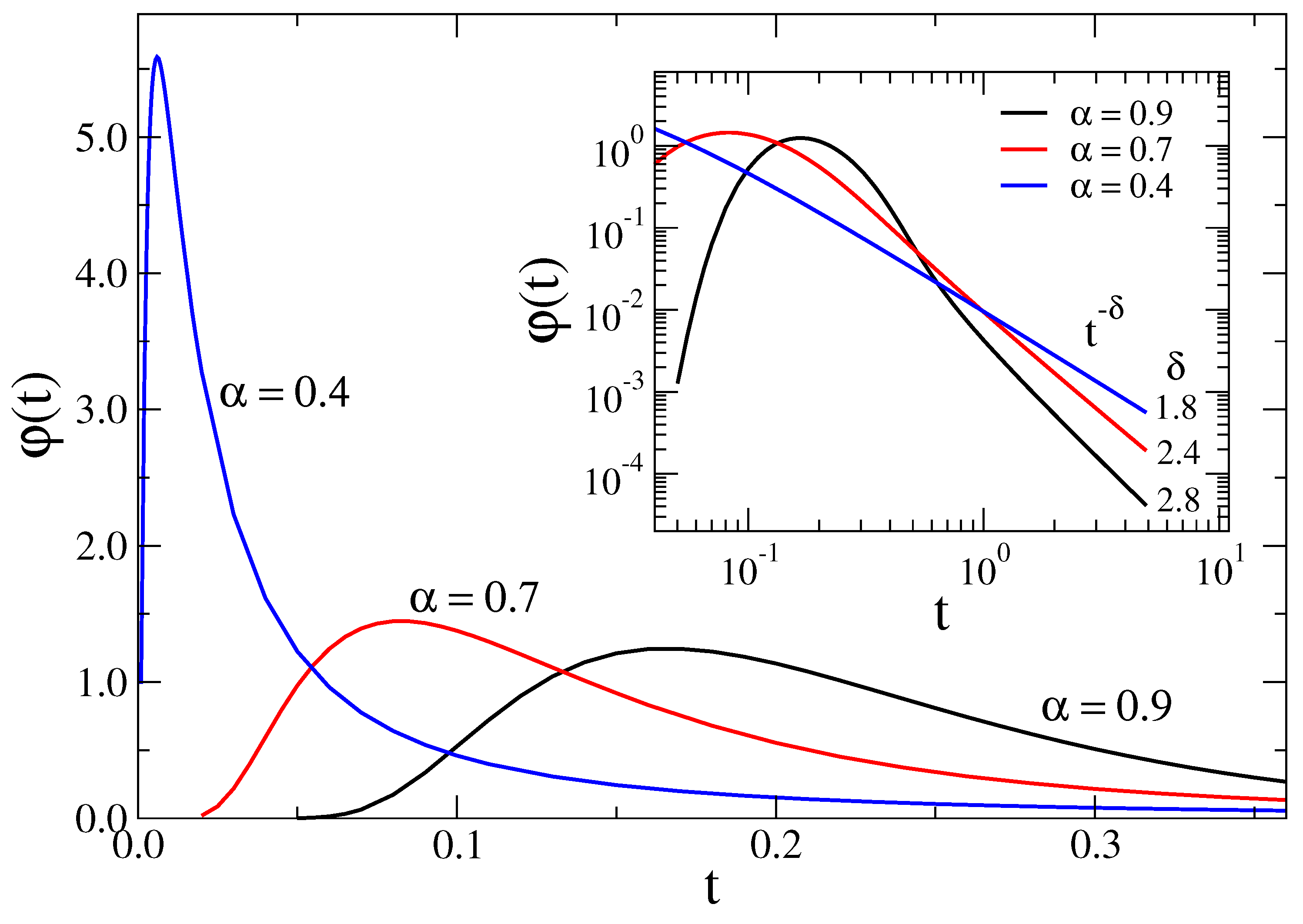
4. Rectangular Domains
5. The Fractional Dodson Diffusion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks: From Tools to Applications; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Kosztołowicz, T.; Dutkiewicz, A. Composite subdiffusion equation that describes transient subdiffusion. Phys. Rev. E 2022, 106, 044119. [Google Scholar] [CrossRef] [PubMed]
- Kosztołowicz, T.; Dutkiewicz, A. Subdiffusion equation with Caputo fractional derivative with respect to another function. Phys. Rev. E 2021, 104, 014118. [Google Scholar] [CrossRef] [PubMed]
- Kosztołowicz, T.; Dutkiewicz, A. Stochastic interpretation of g-subdiffusion process. Phys. Rev. E 2021, 104, L042101. [Google Scholar] [CrossRef] [PubMed]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Angelani, L.; Garra, R. g-fractional diffusion models in bounded domains. Phys. Rev. E 2023, 107, 014127. [Google Scholar] [CrossRef] [PubMed]
- Pskhu, A.V. Green Function of the First Boundary-Value Problem for the Fractional Diffusion-Wave Equation in a Multidimensional Rectangular Domain. J. Math. Sci. 2022, 260, 325–334. [Google Scholar] [CrossRef]
- Garra, R.; Giusti, A.; Mainardi, F. The fractional Dodson diffusion equation: A new approach. Ric. Mat. 2018, 67, 899–909. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications, 2nd ed.; Springer: Berlin, Germany, 2020. [Google Scholar]
- Grebenkov, D.S.; Nguyen, B.-T. Geometrical Structure of Laplacian Eigenfunctions. SIAM Rev. 2013, 55, 601–667. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Nane, E.; Vellaisamy, P. Fractional Cauchy problems on bounded domains. Ann. Probab. 2009, 37, 979–1007. [Google Scholar] [CrossRef]
- Nane, E. Fractional Cauchy problems on bounded domains: Survey of recent results. In Fractional Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2012; pp. 185–198. [Google Scholar]
- Dodson, M.H. Closure temperature in cooling geochronological and petrological systems. Contrib. Mineral. Petrol. 1973, 40, 259–274. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Angelani, L. Run-and-tumble particles, telegrapher’s equation and absorption problems with partially reflecting boundaries. J. Phys. A Math. Theor. 2015, 48, 495003. [Google Scholar] [CrossRef]
- Angelani, L.; Garra, R. On fractional Cattaneo equation with partially reflecting boundaries. J. Phys. A Math. Theor. 2020, 53, 085204. [Google Scholar] [CrossRef]
- Bressloff, P.C. Encounter-based model of a run-and-tumble particle. J. Stat. Mech. 2022, 2022, 113206. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angelani, L.; Garra, R.
G-Fractional Diffusion on Bounded Domains in
Angelani L, Garra R.
G-Fractional Diffusion on Bounded Domains in
Angelani, Luca, and Roberto Garra.
2023. "G-Fractional Diffusion on Bounded Domains in
Angelani, L., & Garra, R.
(2023). G-Fractional Diffusion on Bounded Domains in





