Nonexistence of Finite-Time Stable Equilibria in a Class of Nonlinear Integral Equations
Abstract
1. Introduction
2. Preliminaries
2.1. Generalized Operators
- .
- .
- .
- .
2.2. Generalized Systems
3. Main Results
4. Examples
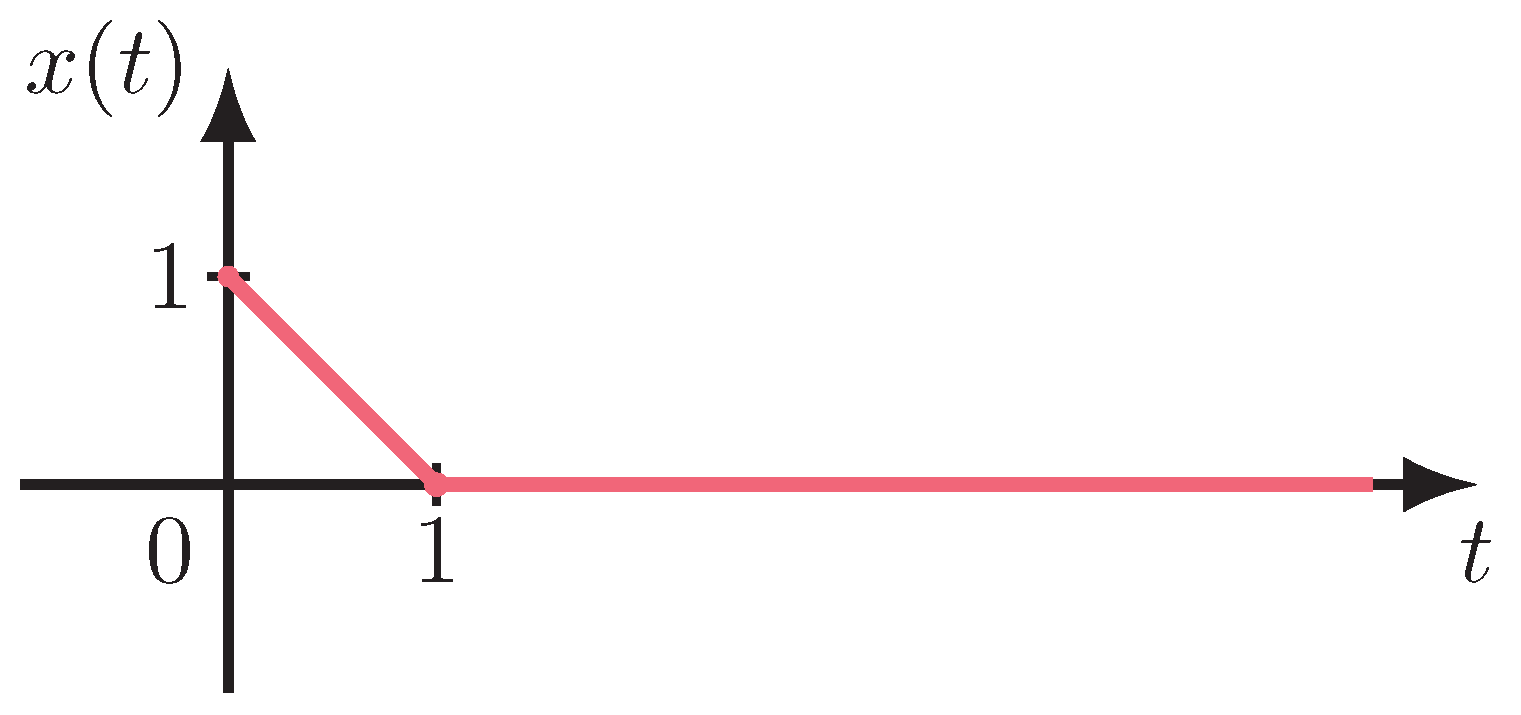
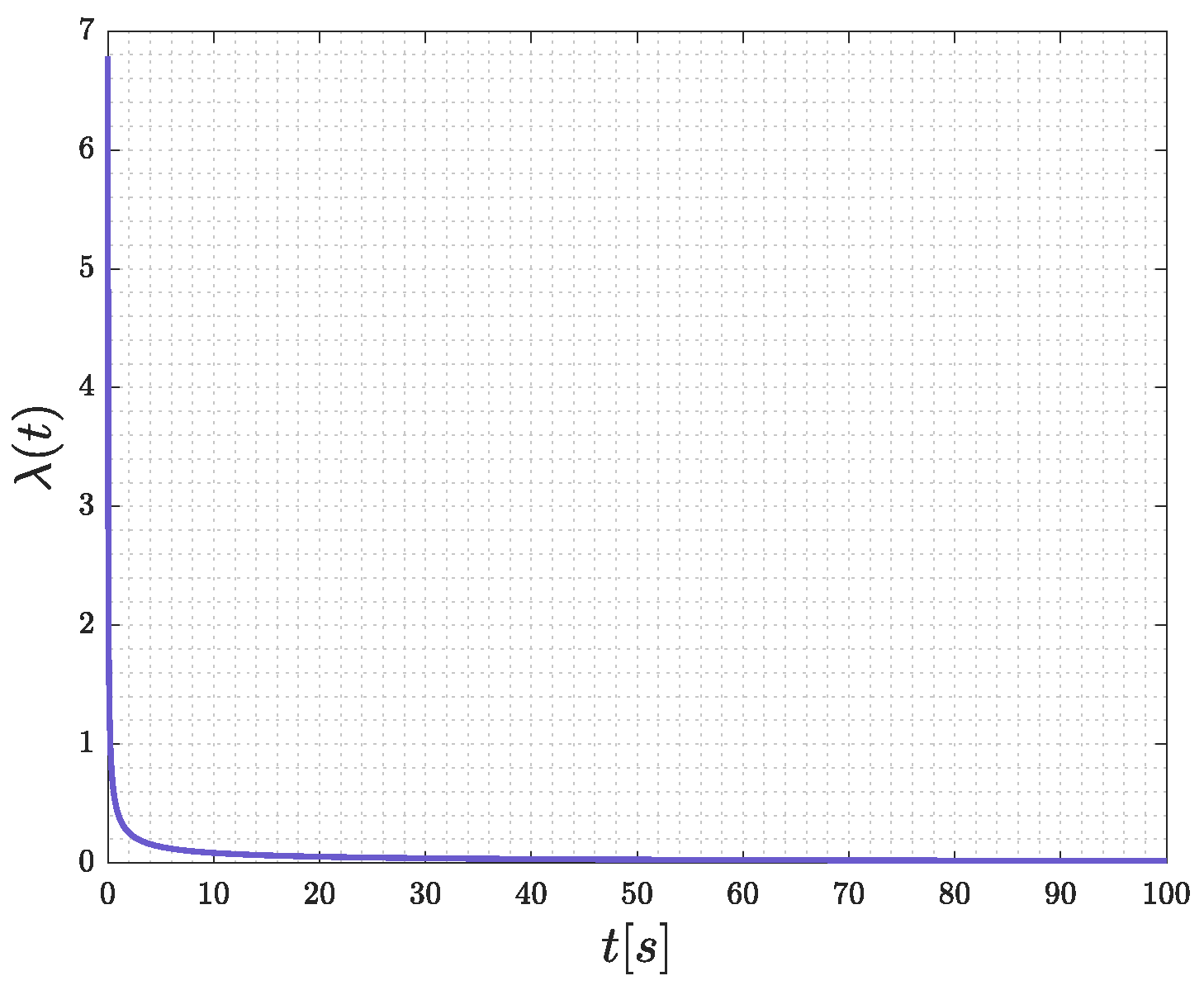
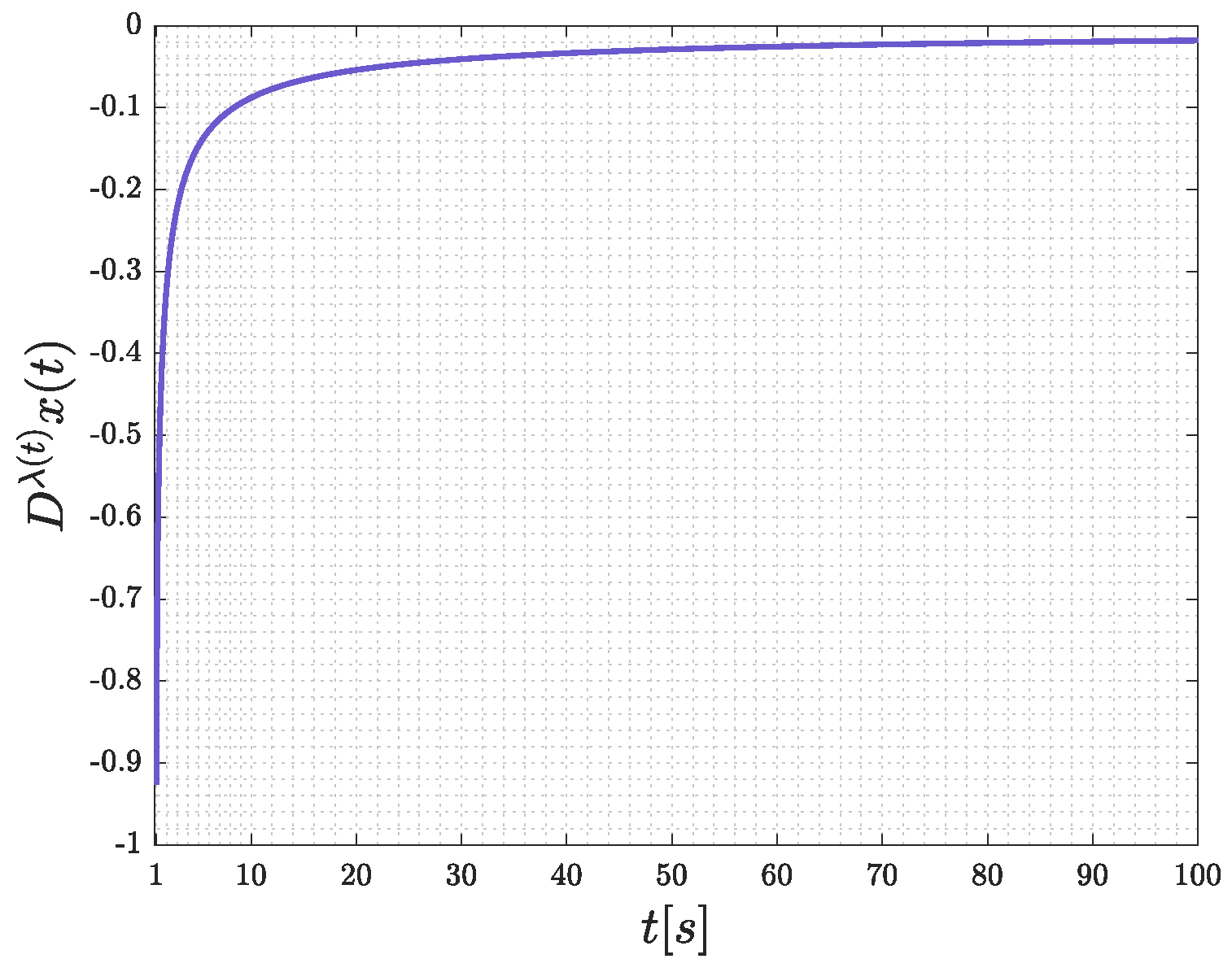
4.1. Fractional-Order Systems with General Analytic Kernels
4.2. Distributed-Order System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Almeida, R.; Tavares, D.; Torres, D.F. The Variable-Order Fractional Calculus of Variations; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Garrappa, R.; Giusti, A.; Mainardi, F. Variable-order fractional calculus: A change of perspective. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105904. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. The kernel of the distributed order fractional derivatives with an application to complex materials. Fractal Fract. 2017, 1, 13. [Google Scholar] [CrossRef]
- Jiao, Z.; Chen, Y.Q.; Podlubny, I. Distributed Order Dynamic Systems, Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Li, Y.; Chen, Y.Q. Theory and implementation of weighted distributed order integrator. In Proceedings of the 2012 IEEE/ASME 8th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications, Suzhou, China, 8–10 July 2012; pp. 119–124. [Google Scholar]
- Zhou, F.; Zhao, Y.; Li, Y.; Chen, Y.Q. Design, implementation and application of distributed order PI control. ISA Trans. 2013, 52, 429–437. [Google Scholar] [CrossRef]
- Li, Y.; Sheng, H.; Chen, Y.Q. On distributed order integrator/differentiator. Signal Process. 2011, 91, 1079–1084. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Caputo, M.; Fabrizio, M. On the notion of fractional derivative and applications to the hysteresis phenomena. Meccanica 2017, 52, 3043–3052. [Google Scholar] [CrossRef]
- Saad, K.M.; Atangana, A.; Baleanu, D. New fractional derivatives with non-singular kernel applied to the Burgers equation. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 063109. [Google Scholar] [CrossRef]
- Garrappa, R.; Kaslik, E. Stability of fractional-order systems with Prabhakar derivatives. Nonlinear Dyn. 2020, 102, 567–578. [Google Scholar] [CrossRef]
- Subashini, R.; Jothimani, K.; Nisar, K.S.; Ravichandran, C. New results on nonlocal functional integro-differential equations via Hilfer fractional derivative. Alex. Eng. J. 2020, 59, 2891–2899. [Google Scholar] [CrossRef]
- Oliveira, D.; de Oliveira, E.C. Hilfer–Katugampola fractional derivatives. Comput. Appl. Math. 2018, 37, 3672–3690. [Google Scholar] [CrossRef]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, Ž. Hilfer–Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef]
- Luchko, Y.; Trujillo, J. Caputo-type modification of the Erdélyi-Kober fractional derivative. Fract. Calc. Appl. Anal. 2007, 10, 249–267. [Google Scholar]
- Sonine, N. Sur la généralisation d’une formule d’Abel. Acta Math. 1884, 4, 171–176. [Google Scholar] [CrossRef]
- Kochubei, A.N. General fractional calculus, evolution equations, and renewal processes. Integral Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Luchko, Y. Operational calculus for the general fractional derivative and its applications. Fract. Calc. Appl. Anal. 2021, 24, 338–375. [Google Scholar] [CrossRef]
- Luchko, Y. General fractional integrals and derivatives with the Sonine kernels. Mathematics 2021, 9, 594. [Google Scholar] [CrossRef]
- Luchko, Y. General fractional integrals and derivatives of arbitrary order. Symmetry 2021, 13, 755. [Google Scholar] [CrossRef]
- Hanyga, A. A comment on a controversial issue: A generalized fractional derivative cannot have a regular kernel. Fract. Calc. Appl. Anal. 2020, 23, 211–223. [Google Scholar] [CrossRef]
- Garrappa, R.; Giusti, A. A computational approach to exponential-type variable-order fractional differential equations. arXiv 2023, arXiv:2303.06653. [Google Scholar]
- Muñoz-Vázquez, A.J.; Fernández-Anaya, G.; Martínez-Fuentes, O. Stability analysis of a class of integral equations with not necessarily differentiable solutions. J. Comput. Appl. Math. 2021, 398, 113702. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Martínez-Fuentes, O.; Fernández-Anaya, G. Generalized PI control for robust stabilization of dynamical systems. Math. Comput. Simul. 2022, 202, 22–35. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, P.; Yang, X.J.; Feng, Y.; Liu, J. A new fractional derivative model for the anomalous diffusion problem. Therm. Sci. 2019, 23, 1005–1011. [Google Scholar] [CrossRef]
- Shen, J.; Lam, J. Non-existence of finite-time stable equilibria in fractional-order nonlinear systems. Automatica 2014, 50, 547–551. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Sánchez-Orta, A.; Parra-Vega, V. A general result on non-existence of finite-time stable equilibria in fractional-order systems. J. Frankl. Inst. 2019, 356, 268–275. [Google Scholar] [CrossRef]
- Wu, Y.; Gao, Y.; Li, W. Finite-time synchronization of switched neural networks with state-dependent switching via intermittent control. Neurocomputing 2020, 384, 325–334. [Google Scholar] [CrossRef]
- Sidorov, D. Existence and blow-up of Kantorovich principal continuous solutions of nonlinear integral equations. Differ. Equ. 2014, 50, 1217–1224. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Fernandez, A.; Özarslan, M.A.; Baleanu, D. On fractional calculus with general analytic kernels. Appl. Math. Comput. 2019, 354, 248–265. [Google Scholar] [CrossRef]
- Artin, E. The Gamma Function; Courier Dover Publications: Mineola, NY, USA, 2015. [Google Scholar]
- Martínez-Fuentes, O.; Meléndez-Vázquez, F.; Fernández-Anaya, G.; Gómez-Aguilar, J.F. Analysis of fractional-order nonlinear dynamic systems with general analytic kernels: Lyapunov stability and inequalities. Mathematics 2021, 9, 2084. [Google Scholar] [CrossRef]
- Seaborn, J.B. Hypergeometric Functions and Their Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 8. [Google Scholar]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag-Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag–Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 314–329. [Google Scholar] [CrossRef]
- Giusti, A. General fractional calculus and Prabhakar’s theory. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz-Vázquez, A.J.; Martinez-Fuentes, O.; Fernández-Anaya, G. Nonexistence of Finite-Time Stable Equilibria in a Class of Nonlinear Integral Equations. Fractal Fract. 2023, 7, 320. https://doi.org/10.3390/fractalfract7040320
Muñoz-Vázquez AJ, Martinez-Fuentes O, Fernández-Anaya G. Nonexistence of Finite-Time Stable Equilibria in a Class of Nonlinear Integral Equations. Fractal and Fractional. 2023; 7(4):320. https://doi.org/10.3390/fractalfract7040320
Chicago/Turabian StyleMuñoz-Vázquez, Aldo Jonathan, Oscar Martinez-Fuentes, and Guillermo Fernández-Anaya. 2023. "Nonexistence of Finite-Time Stable Equilibria in a Class of Nonlinear Integral Equations" Fractal and Fractional 7, no. 4: 320. https://doi.org/10.3390/fractalfract7040320
APA StyleMuñoz-Vázquez, A. J., Martinez-Fuentes, O., & Fernández-Anaya, G. (2023). Nonexistence of Finite-Time Stable Equilibria in a Class of Nonlinear Integral Equations. Fractal and Fractional, 7(4), 320. https://doi.org/10.3390/fractalfract7040320









