Abstract
This paper applies a recently proposed numerical algorithm to discuss the deflection of viscoelastic micro-beams in the time domain with direct access. A nonlinear-fractional order model for viscoelastic micro-beams is constructed. Before solving the governing equations, the operator matrices of shifted Chebyshev polynomials are derived first. Shifted Chebyshev polynomials are used to approximate the deflection function, and the nonlinear fractional order governing equation is expressed in the form of operator matrices. Next, the collocation method is used to discretize the equations into the form of algebraic equations for solution. It simplifies the calculation. MATLAB software was used to program this algorithm to simulate the numerical solution of the deflection. The effectiveness and accuracy of the algorithm are verified by the numerical example. Finally, numerical simulations are carried out on the viscoelastic micro-beams. It is found that the viscous damping coefficient is inversely proportional to the deflection, and the length scale parameter of the micro-beam is also inversely proportional to the deflection. In addition, the stress and strain of micro-beam, the change of deflection under different simple harmonic loads, and potential energy of micro-beam are discussed. The results of the study fully demonstrated that the shifted Chebyshev polynomial algorithm is effective for the numerical simulations of viscoelastic micro-beams.
1. Introduction
Fractional calculus is the definition of arbitrary order differential and integral. It is unified with integer order calculus and is the extension of integer order calculus. Integer order calculus has been generally accepted as a mathematical tool to describe theories of classical physics and related subjects. However, when doing research on some complex systems and complex phenomena, the description of these systems by classical integer order calculus equations will encounter some problems. For example, it is necessary to construct nonlinear equations, introduce some empirical parameters and assumptions, construct new models, etc. Based on the above reasons, people urgently hope to have an available mathematical tool and basic principles to model these complex systems. Fractional differential equations are well suited to characterize materials and processes with memory and genetic properties [1,2,3,4,5,6]. It has the advantages of simple modeling, clear physical meaning of parameters, and accurate description for the description of complex systems. Therefore, fractional calculus is known as one of the important tools for mathematical modeling of complex mechanics and physical processes [7,8,9,10]. Nowadays, inspired by many physical phenomena, scholars worldwide have made more and more contributions in different fields by applying fractional-order constitutive relations and fractional-order systems containing fractional-order derivatives and integrals [11,12,13], and these new models are superior to the traditional integer-order ones. Fractal methods are widely used in the modeling of deformation–relaxation processes. Among them, viscoelastic materials are very closely coupled with fractional-order differential and fractional-order integral operators. Viscoelastic materials have four major characteristics, which are relaxation, creep, preconditioning, and hysteresis, and the traditional integer-order vibration equations cannot accurately describe the viscoelastic material properties. However, the fractional order derivative model has fewer parameters and a better fitting effect. Hendy et al. [14] proposed a unified new model for the thermal viscoelasticity theory of fractional heat transfer. Bonfanti et al. [15] proposed that fractional calculus is a promising tool for accurately describing the rheological properties of soft materials and provided an easy-to-understand fractional viscoelastic model description.
Researchers pay more and more attention to the combination of viscoelastic properties and fractional constitutive models. They have established that the fractional-order constitutive model can better describe the viscoelastic behavior, so a series of related studies have been conducted on it. Lewandowski [16], for example, used the fractional constitutive model of the beam to study the nonlinear vibration behavior of the beam under simple harmonic loading. Duan et al. [17] considered relaxation, creep, dissipation, and hysteresis resulting from a six-parameter fractional constitutive model and its particular cases. Usuki [18] investigated the effect of viscoelastic fractional order through drawing of the phase and group rate curves on beams with solid round cross-sectional sections. Catania [19] analyzed the vibration of fractional-order nonuniform beams using the finite element method. The rheological model used is a combination of the fractional Zener model and fractional standard linear solid model. Xu [20] discretized the beam according to the discontinuous characteristic position of the beam during vibration analysis, and then calculated the vibration extent of the beam from the spreading, transfer, and reflection matrices associated with the beam.
The viscoelastic control equations established using the fractional order constitutive model are not easily solved analytically [21]. Therefore, for ideal results, researchers mostly use the discussion of numerical solutions to make approximations. Approaches to the solution of fractional order governing equations also include the Galerkin method [22], the finite element method [23], the finite difference method [24], and the Laplace transform [25]. However, the limitation of these methods is that they cannot be solved directly in the time domain and require complex transformation processes. In other words, a Laplace transform of the frequency domain solution is required to obtain the time domain solution. The complexity of Laplace transform and inverse transform makes the fractional order equations difficult to answer efficiently [26]. The variational iterative method is an influential method for solving some linear and nonlinear problems. Birol et al. [27] studied the basic idea of the variational iterative method and its convergence, and used the variational iterative method to solve some fractional order differential equations. The Adomian decomposition method was used by Duan et al. [28] to solve fractional order differential equations. Muhammad Abbas et al. [29] used cubic B-spline functions to solve third-order time fractional differential equations. In addition, polynomial algorithms also work well when solving approximations to fractional order systems, such as Legendre wavelet method [30], Legendre polynomials method, Bernstein polynomials method [31], Chebyshev wavelet method [32], etc. The method approximates the unknown function with polynomials, uses the properties of fractional order differentiation to infer the matrices of differential operators of the polynomials, in addition to combining the idea of operator matrices to turn it into a problem of solving a system of the algebraic equations.
In recent years, microstructure-scale experiments confirm the existence of size effects on the mechanical properties of microstructures. Traditional mechanical theories do not contain any scale-associated parameters in their constitutive relations, and are not able to relate and explain the phenomenon of dimensional effects on mechanical properties. Therefore, the research on microstructures in the engineering field is gradually increasing. For example, in [33], the size-dependent buckling of variable-thickness FG-CNTRC microplates under inhomogeneous biaxial compression was investigated using third-order shear deformation theory (TSDT) and modified couple stress theory (MCST) combined with the total potential energy principle. In [34], a general PD beam-shell model based on microbeam bonding is proposed. The bond deformation is obtained directly by interpolation method, the micropotential energy of the bond is established, and the micromodulus of the beam-shell model is solved spontaneously.
Micro-beams are one of the most diffusible microstructures and have been analyzed by many researchers. The vibration amplitude of functionally graded (FGM) microbeams has been studied in detail by Al-Basyouni et al. [35]. Farokhi et al. [36] discussed the free vibration theory of crystalline microbeams and solved the equations of motion of PQC microbeams using modified coupled stress theory (MCST) and differential quadrature method (DQM). Zhang et al. [37] have numerically researched the modal properties of a microperforated sandwich beam having a corrugated square honeycomb hybrid core using the finite element method. It can be seen that research on microstructures is gradually increasing in the engineering field.
The chapter distribution is shown below. In this paper, Section 2 introduces the fractional order calculus definition and properties, and establishes the dimensionless fractional order constitutive equations for viscoelastic micro-beams. Section 3 presents the relevant properties of shifted Chebyshev polynomials and computes integer-order and fractional-order differential operator matrices. A number of examples of this algorithm are presented in Section 4. The stress, strain, deflection, and potential energy of viscoelastic micro-beams were obtained in Section 5. The practical application of the algorithm in the study of viscoelastic materials is demonstrated. Section 6 concludes the paper.
2. Pre-Requisite Knowledge
In this section, the fractional order calculus is defined and its properties are described in detail for easier understanding of the applications that follow [38]. Combining the theoretical knowledge of viscoelastic materials, a governing equation for a viscoelastic micro-beam is derived and established using a fractional order model.
2.1. Definition and Related Properties of Fractional Order Calculus
From the existing literature [21], it is clear that the fractional order calculus has several different ways of definition, including the Riemann–Liouville definition [39], the Caputo definition, and the Grünwald–Letnikov definition [40]. This paper applies the Caputo definition of a fractional order differential operator [39].
Definition 1.
The order derivative of Caputo may be expressed by the following equation:
where is a continuous differentiable function of order q on . When , is a Caputo fractional order derivative operator. is Gamma function, .
From Definition 1, the fractional order derivative of a polynomial can be introduced as the following equation:
The fractional order derivative of Caputo has the following properties.
The result of finding the fractional order derivative of Caputo for a constant is zero: , where C is a constant.
The Caputo fractional order derivative satisfies the linearity property [41]: , where .
Definition 2.
Supposing that is a continuous and integrable function on , , we have [21]:
From Definition 2, the fractional order integration of a polynomial can be introduced as the following equation:
Definition 3.
If and along with all its derivatives are continuous in , under this condition, the Leibniz rule for fractional differentiation takes the form [21]:
2.2. Establishment of Viscoelastic Micro-Beams Constitutive Equations
In this part, we will discuss the motion equations for viscoelastic micro-beams. The motion equations are obtained from the Euler–Bernoulli beam theory and the Modified Coupled Stress Theory. For the convenience of the derivation, we will ignore the effects of rotational inertia and shear stress.
The cross section of viscoelastic micro-beams is denoted by A, the density by , and the modulus of elasticity by E. The viscoelastic micro-beam studied in this paper is a beam structure with both ends fixed, which is illustrated in Figure 1.
Figure 1.
Bending deformation of viscoelastic micro-beams under simple harmonic load .
The kinetic (T) and potential () energies for viscoelastic micro-beams can be obtained using Modified Couple Stress Theory (MCST) [22]:
where represents the transverse deflection, t represents the time, x represents the axial coordinate, V represents the occupied area volume, represents the stress tensor, represents the strain tensor, m represents the deviation part of the couple stress tensor, and represents the symmetric curvature tensor.
Through the von Kármán stress–strain relationship, the strain expression for the nonlinear Euler–Bernoulli beam can be written as:
where z represents the vertical coordinate.
Furthermore, the relationship between the symmetric curvature tensor and the rotation vector might usefully be described in [42]:
where u is the displacement vector.
By means of Equation (8), the elements of are obtained as:
using Equation (9) to find the coupled stress tensor as , where the components are found to be:
is the shear modulus of elasticity, and L is the length scale parameter.
From Equations (6), (7), (9), and (10), the potential energy for the viscoelastic micro-beam can be obtained by calculating [22] as:
For a viscoelastic micro-beam affected by an external loads f, the amount of change in virtual work carried out with an applied load and the amount of change in virtual work carried out with non-conservative viscous damping loads, considering the viscous damping factor, are [22,43]:
From Hamilton’s principle, it is obtained that [22,43]:
The kinetic energy expressions of Equation (6) and Equations (11) and (12) are brought into Equation (13) to obtain the equations of motion governing for a nonlinear viscoelastic micro-beam as:
In studying the properties of viscoelastic micro-beams, we will invoke the fractional Kelvin–Voigt model. For obtaining a fractional order constitutive equation, the moduli of elasticity E and shear modulus are modified to [22]:
where denotes the viscoelastic coefficient, and denotes the order of the fractional order derivative (, integer order at ). Thus, Equation (14) can be rewritten as:
Next, the calculations are simplified by replacing the physical quantities involved in the above with suitable variables by means of dimensionless methods [22]:
where h is the height of the micro-beam. Replacing the dimensionless parameters into the equation, the following fractional order viscoelastic constitutive equation can be obtained:
In the above equation, the overbar has been removed from the symbol for simplicity, where the boundary conditions of the equation are:
and the initial conditions are:
3. Shift Chebyshev Polynomial Numerical Algorithm
In the literature reviewed, we can find that there are many ways to solve the governing equations of fractional viscoelastic micro-beams, such as using the finite difference method (FDM) and the finite element method (FEM) to solve at the same time. In addition, the FDM method is required to be discretized in the time domain, and the FEM method is required to discretize in space. Alternatively, Laplace transform and inverse transform can be used to solve the problem. These methods are more complicated, and it is not easy to directly solve the deflection changes of viscoelastic material micro-beams at different times and different positions in the time domain [44]. Using the algorithm proposed in this paper to solve the fractional differential equation only needs to apply the least squares method and the MATLAB program, and the program takes about 20 s to run, which is simple and fast, and has a good accuracy rate.
The shifted Chebyshev polynomial algorithm can be better applied to the solution of fractional differential equations. Therefore, the properties are described in detail in this section for the shifted Chebyshev polynomials. In addition, the viscoelastic micro-beam governing equation with operator matrix form is derived.
3.1. Correlation Properties of Shifted Chebyshev Polynomials
Chebyshev polynomials satisfy the recurrence relation [45,46,47]:
where , , , , …
For the Shifted Chebyshev polynomials, the interval of the independent variable s becomes , in which L is a non-negative real number. According to the shifted Chebyshev polynomials, a new independent variable u is introduced such that . Therefore, the recurrence relation of the new independent variable u with respect to the shifted Chebyshev polynomials is obtained as:
where , .
On the interval , the general formula for the shift Chebyshev based polynomials has been written as [48]:
where , . The shifted Chebyshev polynomials with weighted orthogonality are in the closed range . The orthogonality relation is satisfied by:
where .
Thus, the vector consisting of the shifted Chebyshev polynomials is:
Let , and let be the coefficient matrix of the shifted Chebyshev polynomials. Then,
where . Clearly, is a full rank invertible matrix.
3.2. Functional Approximation of
Let be a differentiable and square integrable function on the closed interval . Then, the approximate form of with respect to the shifted Chebyshev polynomials can be expressed as:
where , is the shifted Chebyshev polynomials coefficient. can be approximated by the first terms as:
where , is the matrix consisting of shifted Chebyshev polynomials. The form of is shown below:
Similarly, for any continuous two-dimensional function , is a continuous integrable function on this interval. It can be written in the form of a truncated sequence as follows:
where , is to replace the independent variable x in with t.
3.3. Differential Operator Matrices on the Basis of Shifted Chebyshev Polynomials
3.3.1. Integer-Order Differential Operator Matrices
Definition 4.
There exists a matrix satisfying condition . Then, is said to be a matrix of a first order differential operator based on shifted Chebyshev polynomials.
From Equation (26), the derivative of the first-order differential operator of can be calculated as:
where H is a square matrix of order . that is .
From , we have:
Therefore,
That is, . is the matrix of a first-order differential operator based on shifted Chebyshev polynomials of with respect to x.
Similarly, we can proceed to define the second order differential operator matrices.
Definition 5.
There exists a matrix satisfying the condition . Then, is said to be a matrix of a second order differential operator based on shifted Chebyshev polynomials:
where is the matrix of a second-order differential operator based on shifted Chebyshev polynomials of with respect to x.
Thus, the m-order differential operator matrix based on the shifted Chebyshev polynomials can be derived:
That is, , .
In summary, it is obtained that:
where is the matrix of a first-order differential operator based on shifted Chebyshev polynomials for with respect to t.
3.3.2. Fractional Order Differential Operator Matrices
Definition 6.
There exists a matrix satisfying condition ; then, is said to be a matrix of a differential operator of order α based on the shifted Chebyshev polynomials.
From Equation (26), the derivative of the -order differential operator of can be calculated as:
where , that is, ,
Thus, , is the matrix of fractional order differential operator based on shifted Chebyshev polynomials for with respect to t.
In summary, it is obtained that:
3.3.3. Handling of Nonlinear Terms
According to Definition 2 and Definition 3, the nonlinear terms of the governing Equation (18) can be dealt with as follows:
where
Note in Formula (46) that, because for , the infinite sum can be cut; just take the first n terms.
3.4. Algebraic Equation Form of the Viscoelastic Micro-Beam
Using Equations (37)–(46), Equation (18) is discretized into the following form:
The boundary conditions are: .
The initial conditions are: .
The algorithm is based on the collocation method, which converts the fractional differential equation into a set of algebraic equations, solves the coefficient matrix U, uses the least squares method and MATLAB software to calculate, and substitutes the result into Equation (31) to obtain the numerical solution of the fractional differential equation. Through the introduction of the shifted Chebyshev polynomial algorithm in Section 3, we can summarize the steps required to use the algorithm as follows:
- First, approximate the function: ;
- Integer-order fractional-order differential operators are derived;
- Substituting the operator matrix into Equation (18) converts the initial equation into an algebraic equation;
- Next, it is necessary to use the collocation method to discretize the variables; take the nodes to discretize the variables into
- Finally, the system of algebraic equations is solved using the method of least squares.
4. Convergence Analysis and Numerical Example
4.1. Convergence Analysis
This section will introduce the uniform convergence of shifted Chebyshev polynomials.
Theorem 1.
Assume that the function is times continuously differentiable, i.e., and . If is the best approximation to from Y, the mean error bound can be expressed as:
where
Proof.
Let the Taylor expansion of be ; then,
In addition, because is the best approximation to from Y. Therefore,
The upper bound on can be obtained by taking the square root. □
4.2. Numerical Example
The accuracy of the shifted Chebyshev polynomial algorithm will be illustrated by a numerical example. The following equation is a dimensionless equation, and the coefficients in the equation can be any value in the interval range without practical significance. The specific equation is given in below (See Appendix A for detailed calculation procedure):
The boundary conditions and initial conditions are written as follows:
. Where , , .
The analytical solution of Equation (49) can be found as:
When , Equation (49) is solved by the shifted Chebyshev polynomial algorithm. The numerical solution is found by using a MATLAB program and matching point method. is the numerical solution, and is the absolute error:
In Figure 2a–c are the analytical solution, numerical solution, and absolute error of Equation (49), respectively. By observing Figure 2c, it can be found that the change trend of the absolute error is: viewed from the x-axis, it is symmetrically distributed. From the perspective of the t-axis, the absolute error fluctuates less and is relatively stable in the range of and increases sharply at . However, from a macro point of view, the absolute error is small. It can be seen in Figure 2c that the maximum magnitude of error is , and the minimum magnitude is . Therefore, the shifted Chebyshev polynomial algorithm has a relatively high accuracy and can effectively solve such fractional order differential equations. This is then used to solve the problem for the governing equations of viscoelastic micro-beams.
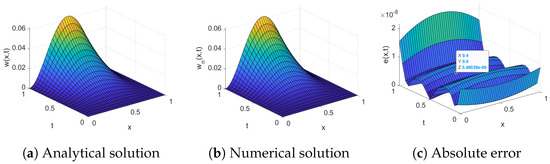
Figure 2.
Numerical example results.
Table 1, Table 2, Table 3 and Table 4 list the absolute errors between the numerical solution and the analytical solution when the derivative , , , and , respectively. When , the series of absolute errors are and ; when , the series of absolute errors are and , and when , the series of absolute errors are and . We can see that, when calculating the fractional derivative equation, the fitting effect of the numerical solution is better. By observing Table 4, when (first order derivative), the absolute error is relatively large, and the fitting effect is not ideal.

Table 1.
Absolute error of each point when .

Table 2.
Absolute error of each point when .

Table 3.
Absolute error of each point when .

Table 4.
Absolute error of each point when .
By comparing the absolute errors of solutions of fractional differential equations and integer order differential equations, for equations of this type, the numerical solutions obtained by fractional order differential equations have a better fitting effect than integer order differential equations.
5. Numerical Simulation
This section presents numerical simulations of the nonlinear viscoelastic micro-beam governing equation. All of the following studies will be based on the parameter values provided in Table 5. The MATLAB program for solving the fractional order differential equation of the same form as Equation (49) has been constructed in Section 4. Now, it is necessary to substitute the material parameters listed in Table 5 into the MATLAB program to find the numerical solution of the deflection first, i.e., the solution of Equation (49). After that, they are solved separately according to the relationship between deflection and stress, strain, and potential energy. The program only needs to run for about 20 s, which is fast and easy to solve. In addition, the solved deflection solution is fully consistent with the actual situation of the micro-beam, where the deflection occurs at the boundary conditions, and initial conditions are zero, and the most obvious deflection occurs at the middle of the micro-beam.

Table 5.
Values of the parameters.
5.1. Effect of Viscous Damping Coefficient on Deflection of the Micro-Beam
Figure 3 shows the effect of different viscous damping coefficients on the deflection of the micro-beam. Because the effect of the viscous damping coefficient on the deflection is not very obvious intuitively, we apply a simple harmonic load () with a frequency of to reach the resonant frequency of the micro-beam (through multiple experiments, it is determined that the resonance frequency is between 1.69–1.71), so that the amplitude reaches the maximum value. In this way, the observation effect will be more intuitive and clear. The deflection change of the micro-beam is symmetrical from the middle position of the micro-beam. In other words, under the action of simple harmonic load, the deflection is the most obvious in the middle of the micro-beam, and the closer to the fixed points at both ends, the smaller the deflection. By observing Figure 3, it can be found that: when the viscous damping coefficient , the maximum deflection is ; when the viscous damping coefficient , the maximum deflection is ; when the viscous damping coefficient , the maximum deflection is . It can be found that the smaller the viscous damping coefficient, the greater the deflection of the micro-beam. This is consistent with the properties of viscoelastic damping. The larger the damping coefficient, the stronger the ability to resist the deformation of the material, resulting in smaller deflection. This is also consistent with the conclusion obtained in [49], that is, as the viscous damping coefficient increases, the amplitude of the longitudinal impedance decreases.
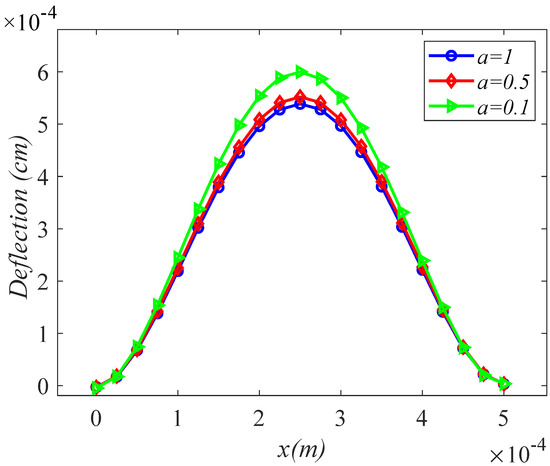
Figure 3.
Effect of different viscous damping coefficients on deflection of the micro-beam.
5.2. Effect of Length Scale Parameters on Deflection of the Micro-Beam
In this section, different micro-beams with length scale parameters are analyzed as research objects, and the applied load is . Figure 4 shows the deflection variation of the micro-beam with five length scale parameters in the middle position. By observing Figure 4, it can be found that, as time goes on, the deflection increases. The micro-beam with the smallest length scale parameter () has the largest deflection, and the deflection reaches at . When the micro-beam length scale parameter is 192, the deflection is the smallest. In addition, the deflection is at . Under the same load, the deflection of the micro-beam decreases with the increase of the length scale parameters at the same time. It can be predicted that the stiffness of the structure increases as the length scale parameter increases. This is compared with the deflection of micro-beams under different length scale parameters shown in [50], and the conclusion is found to be consistent.
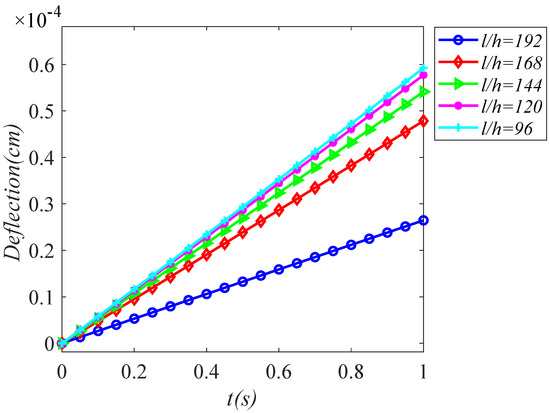
Figure 4.
Deflection of micro-beams of different length scale parameters.
5.3. Effect of Different Simple Harmonic Loads on the Deflection of the Micro-Beam
The effect of different simple harmonic loads on the deflection of the micro-beam is investigated with a viscous damping coefficient of . Since the use of simple harmonic forces is more frequent in practical engineering, we therefore mainly study the deflection variation of micro-beam when in is constant, primary, secondary, and tertiary functions, respectively, and .
The four plots in Figure 5 show the deflection on the micro-beam at the moment of time for the four cases where in the simple harmonic load is constant (Figure 5a), primary function (Figure 5b), secondary function (Figure 5c), and tertiary function (Figure 5d), respectively. From the four graphs, it can be found that the deflection of the micro-beam increases as angular frequency increases, when takes the same value. We can guess that = 0.75–1.25 is a stage that gradually tends to the resonance frequency. The rule at this stage is that the deflection increases with frequency. This is consistent with the reality. Moreover, this is also in line with the deflection curve of the Euler–Bernoulli beam [51,52], which shows that the analysis of the micro-beam deflection in this article is correct. Under the load in Figure 5d, at t = 0.5 s, the deflection produced by and is very close. Under the load in Figure 5c, the deflection produced when and is quite different. There is a maximum difference of in the middle of the beam. This provides a new idea for the future research on simple harmonic loads, which is beneficial to expanding the idea of solving practical engineering problems.
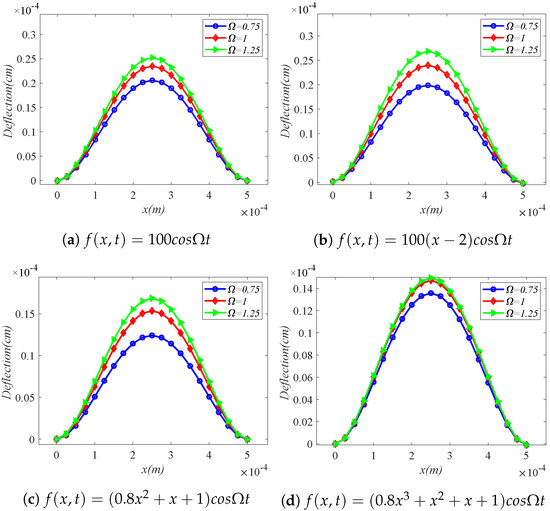
Figure 5.
Deflection of the micro-beam under different simple harmonic loads.
5.4. Stress and Strain of the Micro-Beam
From the stress–strain relationship equation:
Stress and strain are positively related. Figure 6a,b show the variation of strain and stress of the micro-beam at different locations at different times under the simple harmonic load . Through the three-dimensional graph, it can be clearly seen that the trend of stress and strain is consistent, showing a positive relationship. Under the simple harmonic load, the stress is symmetrical at in the middle of the micro-beam. At , the stress and strain of the micro-beam are zero at any position, which conforms to the initial condition of the governing equation of the viscoelastic micro-beam. As the loading time increases, the force resisting the deformation of the micro-beam also increases. The stress and strain values of the micro-beam are the smallest at the middle position, and the stress and strain gradually increase when approaching the two ends. The stress reaches the maximum at and , which are and , respectively. This shows that the micro-beam has the weakest ability to resist deformation in the middle position, and the closer to the end point, the stronger the ability to resist deformation. This is consistent with the theory of Euler–Bernoulli beams with both ends fixed. It is shown that the shifted Chebyshev polynomial algorithm is capable of solving the stress and strain problems in viscoelastic materials.
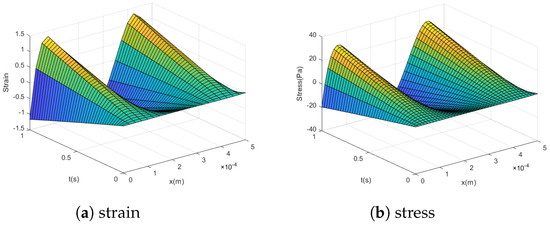
Figure 6.
Stress and strain in the viscoelastic micro-beam under .
5.5. Potential Energy Change of the Micro-Beam
The previous sections compare the physical quantities of viscous damping coefficient, length scale parameters, micro-beam deflection, and strain with the conclusions in other papers. It can be verified that the algorithm proposed in this paper is effective for the numerical simulation of viscoelastic micro-beams. Therefore, in this section, we will numerically simulate the potential energy of micro-beams to provide more reference data for the study of viscoelastic materials.
The variation of potential energy for the viscoelastic micro-beam subjected to the simple harmonic load will be studied in this section. The potential energy here is the energy generated by the elastic deformation of the micro-beam. The relationship between potential energy and deflection can be found from Equation (11). According to the algorithm proposed in this paper, the deflection occurred by the micro-beam is found. Then, the potential energy generated by the micro-beam during the motion is found. The three-dimensional relationship diagram can be obtained as shown in Figure 7.
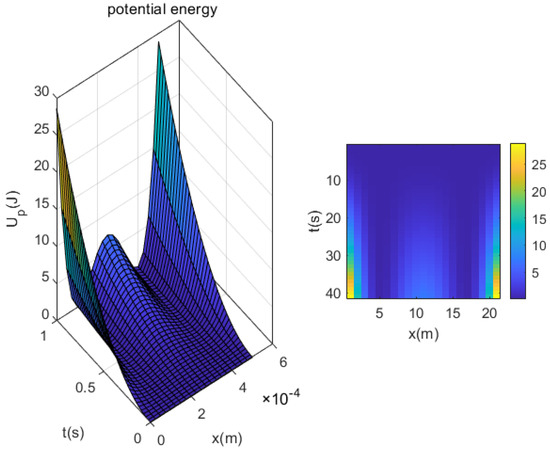
Figure 7.
Potential energy change of the viscoelastic micro-beam.
Figure 7 shows the potential energy values generated by the micro-beam at different times and at different positions under the simple harmonic load . By looking at the three-dimensional diagram on the left and the planar diagram on the right, we can see that the generated potential energy is symmetrical with respect to the micro-beam . The generated potential energy decreases and then increases from the middle of the micro-beam towards the two end points. The maximum potential energy can reach . The potential energy in the middle position is . The position with the smallest potential energy is at and . The potential energy starts to increase sharply about from the ends of the micro-beam. The potential energy generated increases with the time of application of the simple harmonic load.
See Table A1 for explanations of professional terms.
6. Conclusions
In this paper, a numerical algorithm for solving nonlinear-fractional order differential equations is proposed. The features of the algorithm are mainly reflected in the following three aspects. First, the algorithm can directly find the numerical solution of the unknown function in the time domain, and only needs to substitute the operator matrix form of the fractional order differential equation into the Matlab program, which is easier to operate. Secondly, the numerical solution of the fractional order differential equation is solved with high accuracy using this algorithm. This can be verified in the numerical example, where the error between the analytical and numerical solutions is of the order of . In addition, the numerical simulations of micro-beams in viscoelastic materials is investigated in this paper, and the following conclusions are obtained. This has important practical implications for the study of viscoelastic materials:
- The constitutive equations of the nonlinear-fractional-order viscoelastic micro-beam are first established and dimensionless. The numerical examples are used to demonstrate the effectiveness and accuracy of the algorithm;
- Through numerical analysis, it is found that viscous damping has the effect of resisting deformation. The larger the viscous damping coefficient, the stronger the ability to resist deformation;
- The algorithm is used to compare the deflection of micro-beams under different length scale parameters. It can be found that the deflection of the microbeam is inversely proportional to the length scale parameter;
- The deflection changes of the viscoelastic micro-beam were obtained using this algorithm. The effect of different simple harmonic loads on the deflection variation of the micro-beam was studied. It can be found that, when the frequency of the simple harmonic load approaches the first resonance region, the deflection will increase as the frequency increases. It is also consistent with the actual situation;
- Using this algorithm, we calculated the stress and strain of the micro-beam. The calculated stress and strain conform to the properties of viscoelastic materials, and the two are also proportional. The reliability of the algorithm is verified;
- Using this algorithm, the change in potential energy of a viscoelastic micro-beam under the simple harmonic load was calculated. It is found that the value of the potential energy of the micro-beam is symmetrically distributed in the middle of the micro-beam, with the potential energy decreasing and then increasing. The potential energy increases sharply at the two end points of the micro-beam.
This paper provides a research direction for the research of fractional viscoelastic constitutive model and dynamic analysis of viscoelastic materials. In the future, further research can be carried out on this basis. The research directions are as follows:
- The parameters in the paper are all selected from the references, and experiments can be carried out in the future to use the experimental data for kinetic analysis;
- In the future, the algorithm in this paper can be used to compare the fitting effects of different fractional models to the same viscoelastic material micro-beam;
- In the future, more complex viscoelastic materials can be numerically simulated using variable fractional orders.
Author Contributions
Writing—original draft, A.Y., Q.Z., J.Q., Y.C. (Yuhuan Cui) and Y.C. (Yiming Chen). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52074126) and the Hebei Provincial Natural Science Foundation of China (E2022209110).
Data Availability Statement
No data was used for the research described in the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
From Formula (51), we know that:
Substituting Equations (A1)–(A7) into the left side of the equal sign in Equation (49), Equation (49) becomes:
It can be obtained that Equation (A8) is equal to Equation (50).
In addition, for boundary conditions:
The initial conditions are as follows:
Appendix B

Table A1.
Nomenclature.
Table A1.
Nomenclature.
| Symbol | Explanation |
|---|---|
| Caputo fractional order derivative operator | |
| fractional integration | |
| A | cross-sectional area |
| density | |
| E | modulus of elasticity |
| T | kinetic energy |
| potential energy | |
| t | time |
| x | position |
| V | occupied area volume |
| stress | |
| strain | |
| m | deviation part of the couple stress tensor |
| symmetric curvature tensor | |
| z | vertical coordinate |
| rotation vector | |
| shear modulus of elasticity | |
| L | length scale parameter |
| I | Moment of inertia |
| a | Viscous damping coefficient |
| viscoelastic coefficient | |
| h | height |
| ,, | Family of shifted Chebyshev polynomials |
| Chebyshev polynomials | |
| Shifted Chebyshev polynomials | |
| Coefficient matrix | |
| Integer order operator matrix | |
| fractional operator matrix | |
| analytical solution | |
| numerical solution | |
| absolute error | |
| load | |
| frequency |
References
- Antil, H.; Brown, T.S.; Khatri, R.; Onwunta, A.; Verma, D.; Warma, M. Optimal Control, Numerics, and Applications of Fractional PDEs. arXiv 2021, arXiv:2106.13289. [Google Scholar]
- Sheikh, N.A.; Chuan Ching, D.L.; Khan, I.; Ahmad, A.; Ammad, S. Concrete Based Jeffrey Nanofluid Containing Zinc Oxide Nanostructures: Application in Cement Industry. Symmetry 2020, 12, 1037. [Google Scholar] [CrossRef]
- Alcoutlabi, M.; Martinez-Vega, J.J. Application of fractional calculus to viscoelastic behavior modelling and to the physical ageing phenomenon in glassy amorphous polymers. Polymer 1998, 39, 6269–6277. [Google Scholar] [CrossRef]
- Sun, H.G.; Yong, Z.; Baleanu, D.; Wen, C.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Song, Y.; Shateyi, S. Inverse Multiquadric Function to Price Financial Options under the Fractional Black—Scholes Model. Fractal Fract. 2022, 6, 599. [Google Scholar] [CrossRef]
- Rexma Sherine, V.; Chellamani, P.; Ismail, R.; Avinash, N.; Britto Antony Xavier, G. Estimating the Spread of Generalized Compartmental Model of Monkeypox Virus Using a Fuzzy Fractional Laplace Transform Method. Symmetry 2022, 14, 2545. [Google Scholar] [CrossRef]
- Enelund, M.; Lesieutre, G.A. Time domain modeling of damping using anelastic displacement fields and fractional calculus. Int. J. Solids Struct. 1999, 36, 4447–4472. [Google Scholar] [CrossRef]
- Tarasov, V.E. Generalized Memory: Fractional Calculus Approach. Fractal Fract. 2018, 2, 23. [Google Scholar] [CrossRef]
- Zguaid, K.; Alaoui, F.; Boutoulout, A. Regional observability for linear time fractional systems. Math. Comput. Simul. 2021, 185, 77–87. [Google Scholar] [CrossRef]
- Cb, A.; Th, A.; Ypl, B.; Ga, C.; Msod, E.; Hj, F.; Aaa, G. Analytical solutions of fractional wave equation with memory effect using the fractional derivative with exponential kernel. Results Phys. 2021, 25, 104196. [Google Scholar]
- Shen, L.J. Fractional derivative models for viscoelastic materials at finite deformations. Int. J. Solids Struct. 2019, 190, 226–237. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Pilipovic, S. Zener Model with General Fractional Calculus: Thermodynamical Restrictions. Fractal Fract. 2022, 6, 617. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z. Numerical simulation of fractional evolution model arising in viscoelastic mechanics. Appl. Numer. Math. 2021, 169, 303–320. [Google Scholar] [CrossRef]
- Hendy, M.H.; Amin, M.M.; Ezzat, M.A. Two-dimensional problem for thermoviscoelastic materials with fractional order heat transfer. J. Therm. Stress 2019, 42, 1298–1315. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020. [Google Scholar] [CrossRef]
- Lewandowski, R.; Wielentejczyk, P. Nonlinear vibration of viscoelastic beams described using fractional order derivatives. J. Sound Vib. 2017, 399, 228–243. [Google Scholar] [CrossRef]
- Duan, J.S.; Hu, D.C.; Chen, Y.Q. Simultaneous Characterization of Relaxation, Creep, Dissipation, and Hysteresis by Fractional-Order Constitutive Models. Fractal Fract. 2021, 5, 36. [Google Scholar] [CrossRef]
- Usuki, T.; Suzuki, T. Dispersion curves for a viscoelastic Timoshenko beam with fractional derivatives. J. Sound Vib. 2012, 331, 605–621. [Google Scholar] [CrossRef]
- Catania, G.; Fasana, A.; Sorrentino, S. Finite element analysis of vibrating non-homogeneous beams with fractional derivative viscoelastic models. IFAC Proc. Vol. 2006, 39, 280–285. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Tai, Y.; Xu, X.; Chen, N. Vibration analysis of complex fractional viscoelastic beam structures by the wave method. Int. J. Mech. Sci. 2019, 167, 105204. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. In Proceedings of the Mathematics in Science and Engineering, San Diego, CA, USA, 15 January 1999. [Google Scholar]
- Loghman, E.; Bakhtiari-Nejad, F.; Ali, K.E.; Abbaszadeh, M.; Amabili, M. Nonlinear vibration of fractional viscoelastic micro-beams. Int. J. Non-Linear Mech. 2021, 137, 103811. [Google Scholar] [CrossRef]
- Cao, J.; Wang, Z.; Wang, Z. A Uniform Accuracy High-Order Finite Difference and FEM for Optimal Problem Governed by Time-Fractional Diffusion Equation. Fractal Fract. 2022, 6, 475. [Google Scholar] [CrossRef]
- Loghman, E.; Kamali, A.; Bakhtiari-Nejad, F.; Abbaszadeh, M. Nonlinear free and forced vibrations of fractional modeled viscoelastic FGM micro-beam. Appl. Math. Model. 2021, 92, 297–314. [Google Scholar] [CrossRef]
- Attia, M.A.; Melaibari, A.; Shanab, R.A.; Eltaher, M.A. Dynamic Analysis of Sigmoid Bidirectional FG Microbeams under Moving Load and Thermal Load: Analytical Laplace Solution. Mathematics 2022, 10, 4797. [Google Scholar] [CrossRef]
- Eltayeb, H.; Kılıçman, A.; Bachar, I. On the Application of Multi-Dimensional Laplace Decomposition Method for Solving Singular Fractional Pseudo-Hyperbolic Equations. Fractal Fract. 2022, 6, 690. [Google Scholar] [CrossRef]
- Birol; Bayram, M. Analytical approximate solution of time-fractional Fornberg—Whitham equation by the fractional variational iteration method. Alex. Eng. J. 2014, 53, 911–915. [Google Scholar]
- Duan, J.S.; Chaolu, T.; Rach, R.; Lu, L. The Adomian decomposition method with convergence acceleration techniques for nonlinear fractional differential equations. Comput. Math. Appl. 2013, 66, 728–736. [Google Scholar] [CrossRef]
- Abbas, M.; Bibi, A.; Alzaidi, A.S.M.; Nazir, T.; Majeed, A.; Akram, G. Numerical Solutions of Third-Order Time-Fractional Differential Equations Using Cubic B-Spline Functions. Fractal Fract. 2022, 6, 528. [Google Scholar] [CrossRef]
- Chen, Y.M.; Wei, Y.Q.; Liu, D.Y.; Yu, H. Numerical solution for a class of nonlinear variable order fractional differential equations with Legendre wavelets. Appl. Math. Lett. 2015, 46, 83–88. [Google Scholar] [CrossRef]
- Jin, S.; Xie, J.; Qu, J.; Chen, Y. A Numerical Method for Simulating Viscoelastic Plates Based on Fractional Order Model. Fractal Fract. 2022, 6, 150. [Google Scholar] [CrossRef]
- Chen, Y.; Han, X.; Liu, L. Numerical Solution for a Class of Linear System of Fractional Differential Equations by the HaarWavelet Method and the Convergence Analysis. Comput. Model. Eng. Sci. 2014, 97, 391–405. [Google Scholar]
- Roodgar Saffari, P.; Sher, W.; Thongchom, C. Size Dependent Buckling Analysis of a FG-CNTRC Microplate of Variable Thickness under Non-Uniform Biaxial Compression. Buildings 2022, 12, 2238. [Google Scholar] [CrossRef]
- Shen, G.; Xia, Y.; Hu, P.; Zheng, G. Construction of peridynamic beam and shell models on the basis of the micro-beam bond obtained via interpolation method. Eur. J. Mech. A Solids 2021, 86, 104174. [Google Scholar] [CrossRef]
- Al-Basyouni, K.S.; Tounsi, A.; Mahmoud, S.R. Size dependent bending and vibration analysis of functionally graded micro beams based on modified couple stress theory and neutral surface position. Compos. Struct. 2015, 125, 621–630. [Google Scholar] [CrossRef]
- Ysla, B.; Tx, A. Free vibration of the one-dimensional piezoelectric quasicrystal microbeams based on modified couple stress theory. Appl. Math. Model. 2021, 96, 733–750. [Google Scholar]
- Zhang, Z.J.; Zhang, Q.C.; Li, F.C.; Yang, J.W.; Liu, J.W.; Liu, Z.Y.; Jin, F. Modal characteristics of micro-perforated sandwich beams with square honeycomb-corrugation hybrid cores: A mixed experimental-numerical study. THin-Walled Struct. 2019, 137, 185–196. [Google Scholar] [CrossRef]
- Shishkina, E.; Sitnik, S. Basics of fractional calculus and fractional order differential equations—ScienceDirect. Transmutations, Singular and Fractional Differential Equations with Applications to Mathematical Physics; Academic Press: Cambridge, MA, USA, 2020; pp. 53–84. [Google Scholar]
- Rossikhin, Y.A.; Shitikova, M.V. On fallacies in the decision between the Caputo and Riemann–Liouville fractional derivatives for the analysis of the dynamic response of a nonlinear viscoelastic oscillator. Mech. Res. Commun. 2012, 45, 22–27. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Tp, A.; Atd, B. Numerical solution method for multi-term variable order fractional differential equations by shifted Chebyshev polynomials of the third kind. Alex. Eng. J. 2021, 61, 5145–5153. [Google Scholar]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int. J. Eng. Sci. 2013, 68, 11–23. [Google Scholar] [CrossRef]
- LeonardMeirovitch. Fundamentals of Vibrations; Waveland Pr Inc.: Long Grove, IL, USA, 2010. [Google Scholar]
- Zhang, Y.C.; Jun-Zheng, W.U.; Zhang, C.Y.; Zhang, N.H. Free Vibration of a Viscoelastic-Elastic Laminated Microcantilever Beam. Chin. Q. Mech. 2017. [Google Scholar] [CrossRef]
- Karunakar, P.; Chakraverty, S. Shifted Chebyshev polynomials based solution of partial differential equations. Sn Appl. Sci. 2019, 1, 285. [Google Scholar] [CrossRef]
- Akrami, M.H.; Atabakzadeh, M.H.; Erjaee, G.H. The operational matrix of fractional integration for shifted Legendre polynomials. Iran. J. Sci. Technol. Trans. Sci. 2013, 37, 439–444. [Google Scholar]
- Atabakzadeh, M.H.; Akrami, M.H.; Erjaee, G.H. Chebyshev operational matrix method for solving multi-order fractional ordinary differential equations. Appl. Math. Model. 2013, 37, 8903–8911. [Google Scholar] [CrossRef]
- Zhao, F.; Huang, Q.; Xie, J.; Li, Y.; Ma, L.; Wang, J. Chebyshev polynomials approach for numerically solving system of two-dimensional fractional PDEs and convergence analysis. Appl. Math. Comput. 2017, 313, 321–330. [Google Scholar] [CrossRef]
- Meng, K.; Cui, C.; Liang, Z.; Li, H.; Pei, H. An Analytical Solution for Longitudinal Impedance of a Large-Diameter Floating Pile in Soil with Radial Heterogeneity and Viscous-Type Damping. Appl. Sci. 2020, 10, 4906. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. Nonlinear forced vibration of functionally graded Timoshenko microbeams with thermal effect and parametric excitation. Int. J. Mech. Sci. 2019, 155, 405–416. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Y.; Cheng, G.; Barrière, T. Numerical analysis of fractional partial differential equations applied to polymeric visco-elastic Euler–Bernoulli beam under quasi-static loads. Chaos Solitons Fractals 2020, 140, 110255. [Google Scholar] [CrossRef]
- Samayoa, D.; Kryvko, A.; Velázquez, G.; Mollinedo, H. Fractal Continuum Calculus of Functions on Euler–Bernoulli Beam. Fractal Fract. 2022, 6, 552. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).