An Advanced Fractional Order Method for Temperature Control
Abstract
:1. Introduction
2. Modeling with EnergyPlus
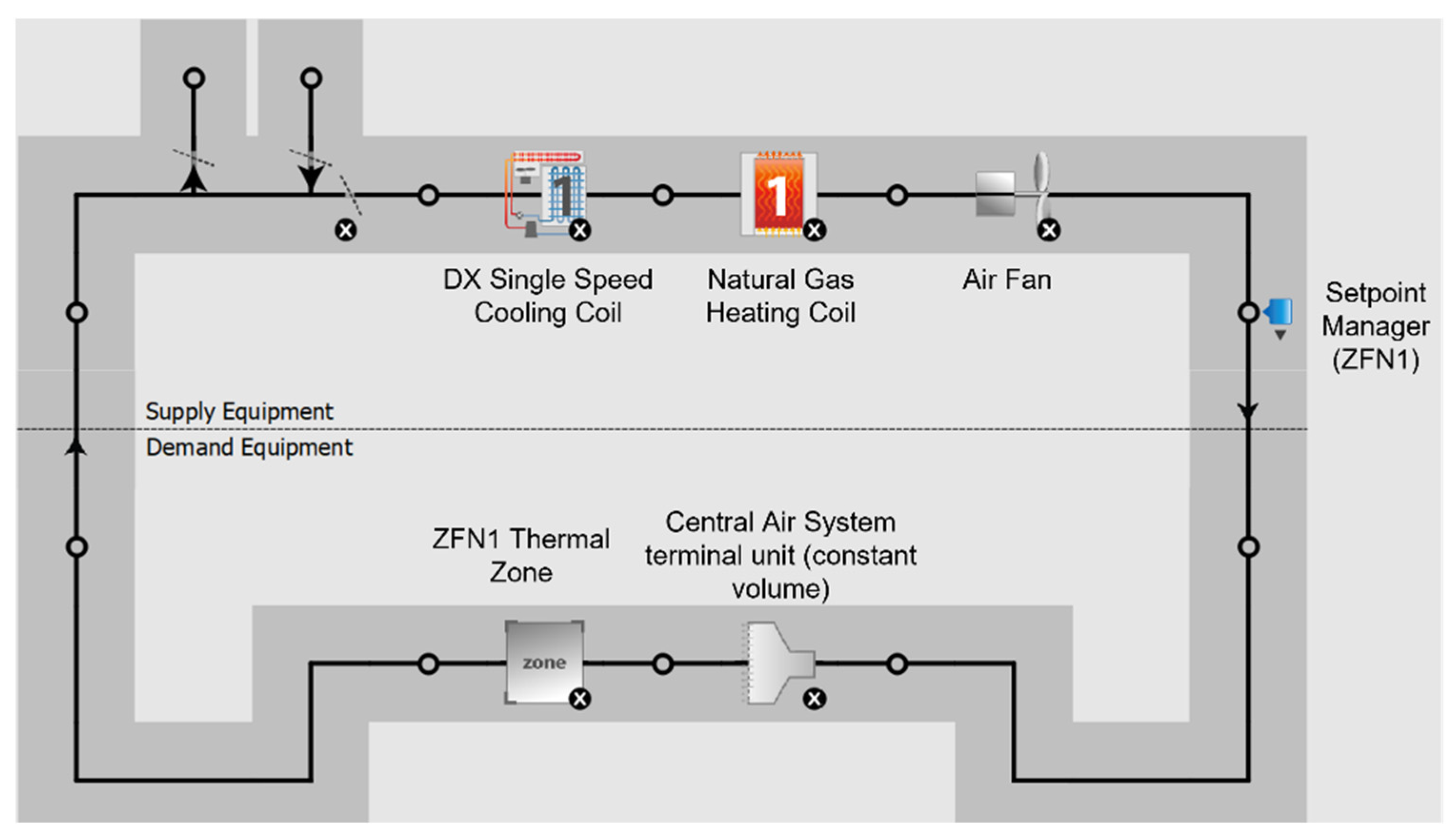
2.1. Building Description and Materials
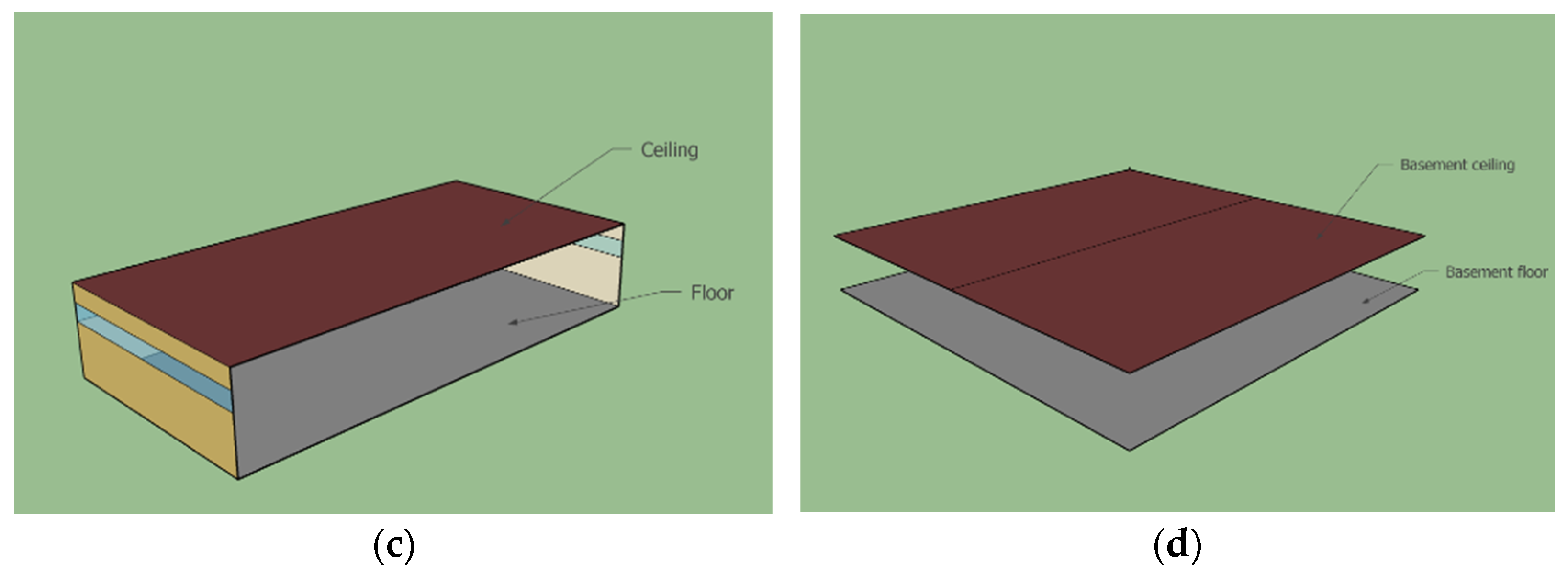
2.2. EnergyPlus Model
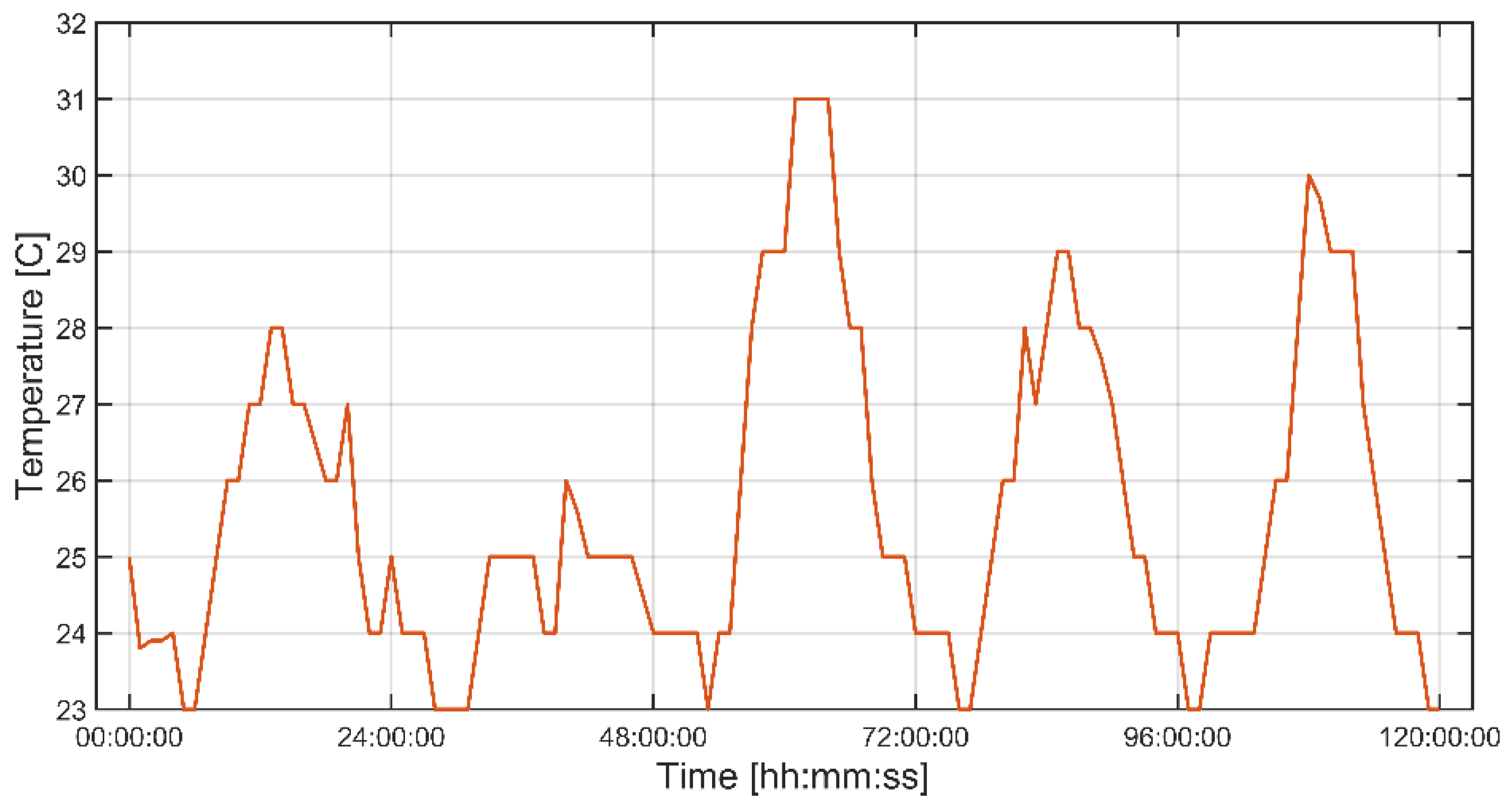
2.3. Meteorological Data
2.4. System Identification
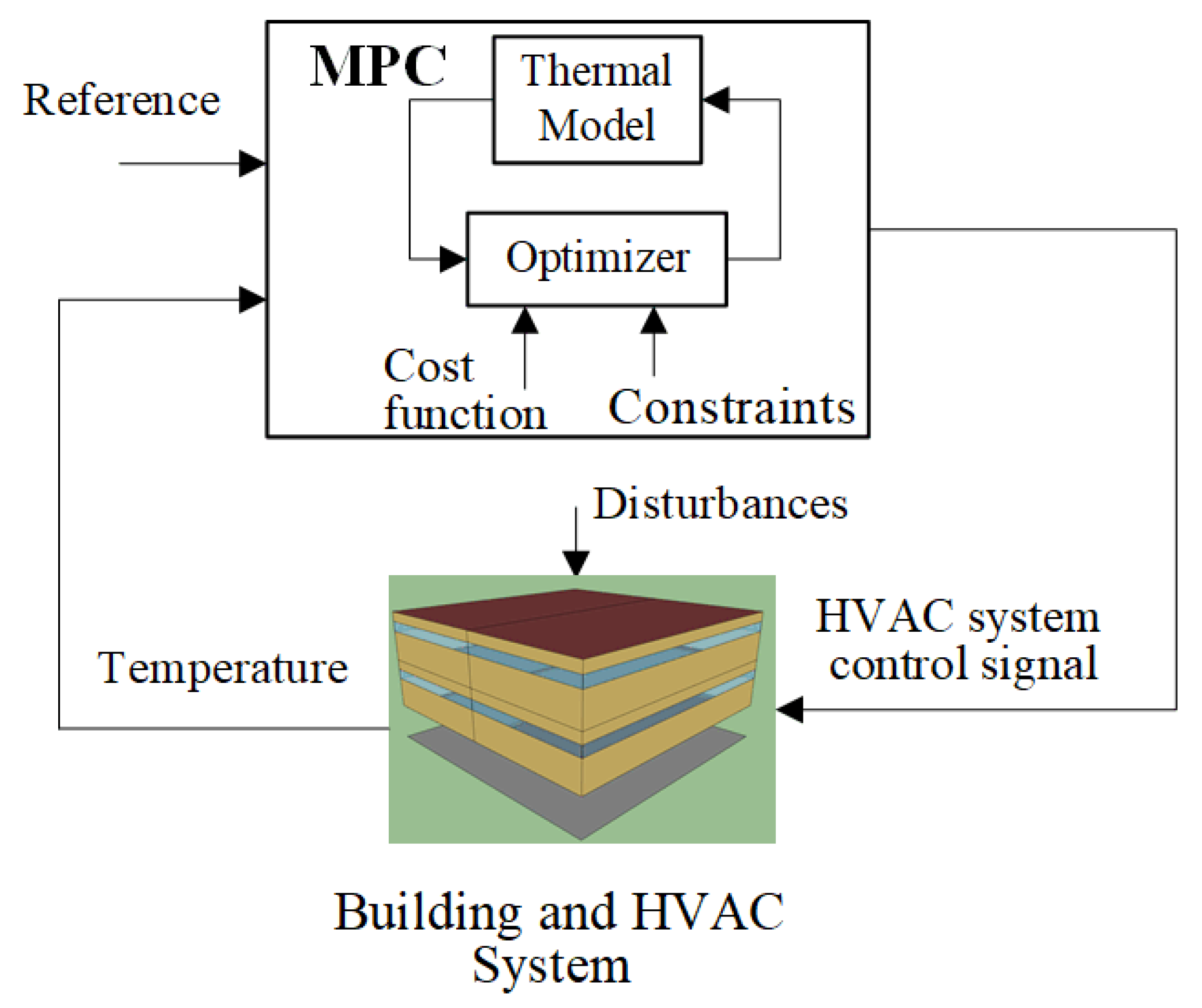
3. Control Strategy
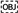 is the optimized future control actions. Based on these future input effects, the predicted system outputs can be defined as:
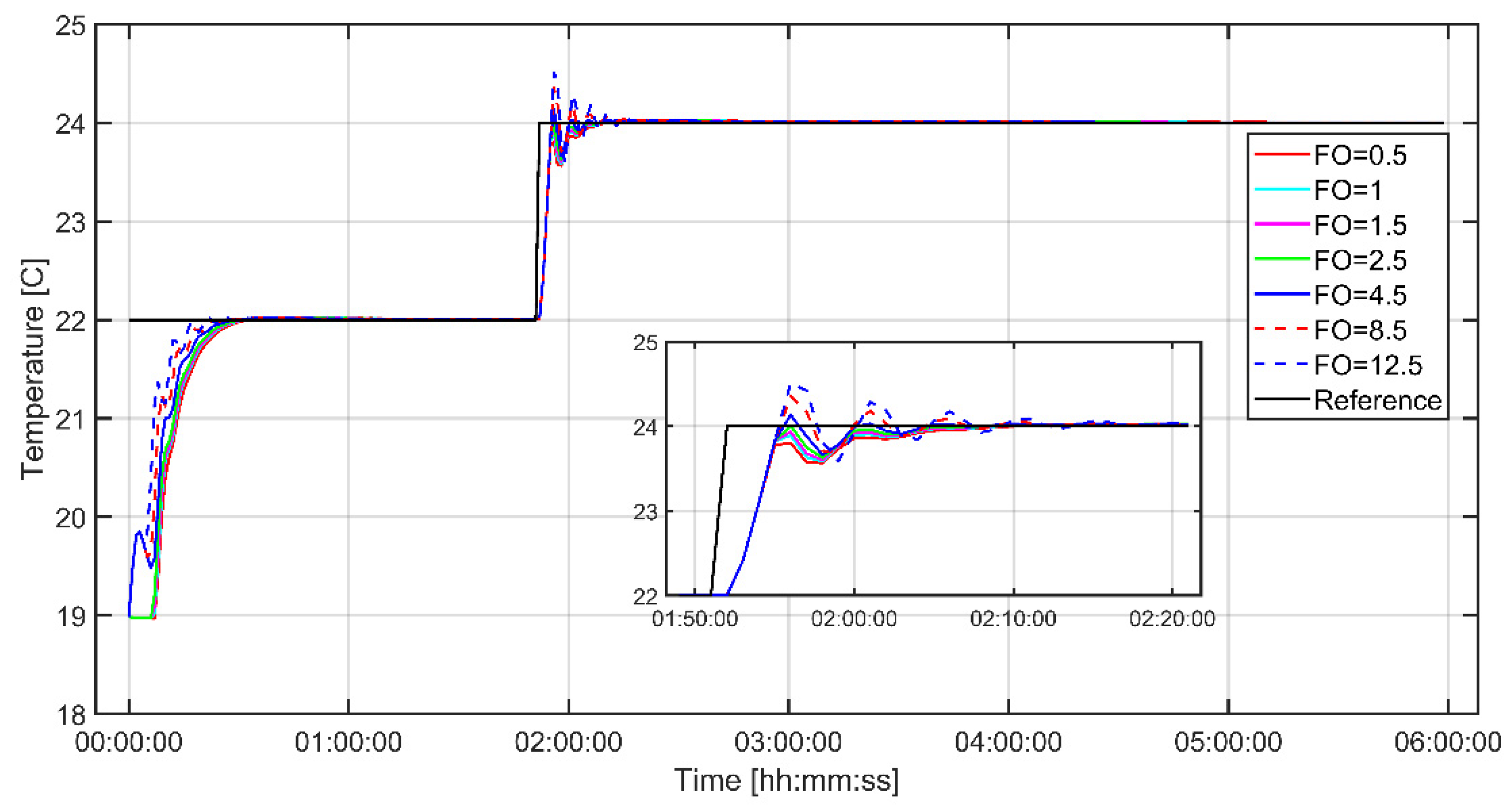
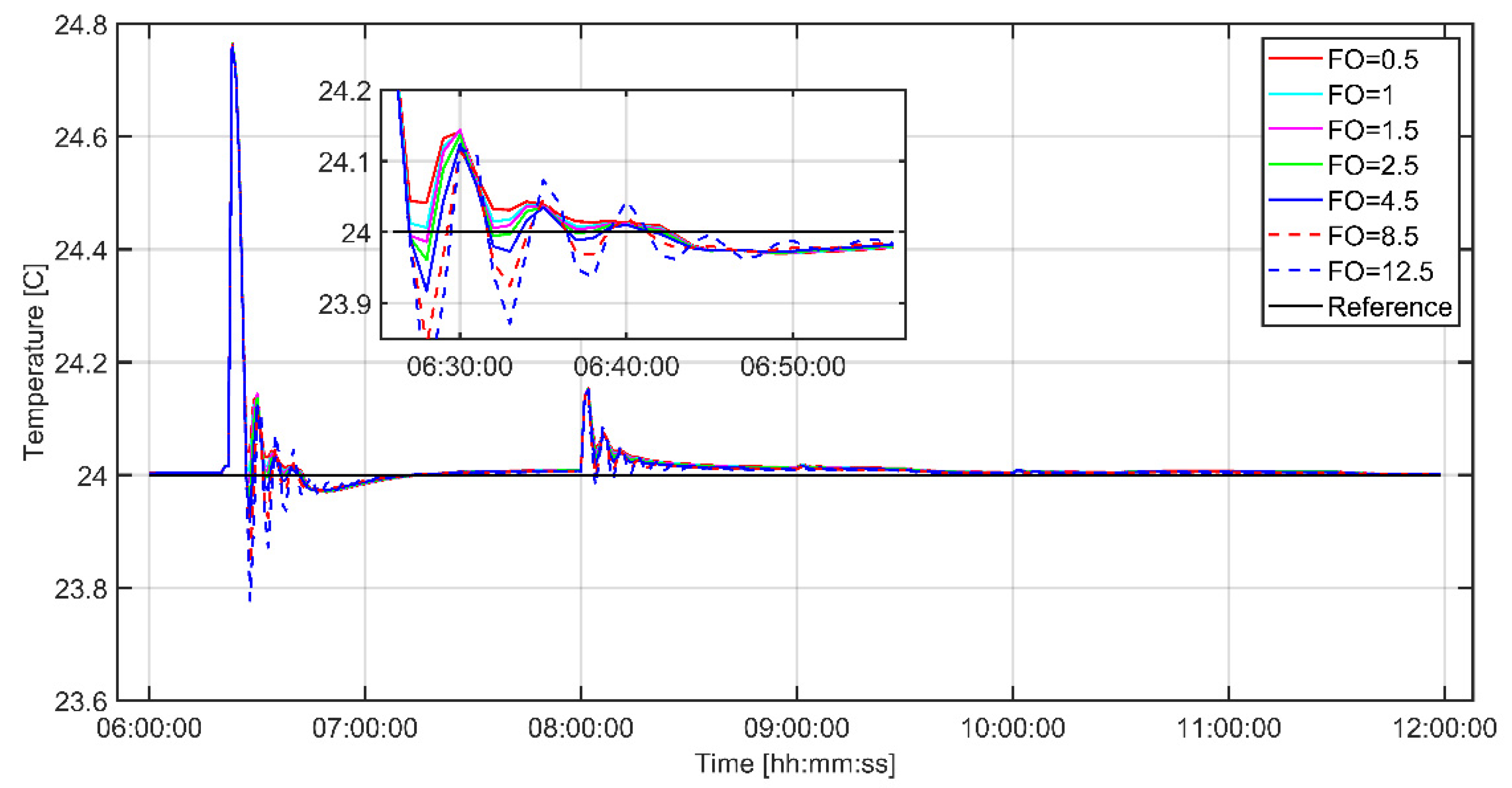
is the optimized future control actions. Based on these future input effects, the predicted system outputs can be defined as:4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- González-Torres, M.; Pérez-Lombard, L.; Coronel, J.F.; Maestre, I.R.; Yan, D. A review on buildings energy information: Trends, end-uses, fuels and drivers. Energy Rep. 2022, 8, 626–637. [Google Scholar] [CrossRef]
- 2019 Global Status Report for Buildings and Construction Sector. Available online: https://www.unep.org/resources/publication/2019-global-status-report-buildings-and-construction-sector (accessed on 29 July 2022).
- Sources of Greenhouse Gas Emissions. Available online: https://www.epa.gov/ghgemissions/sources-greenhouse-gas-emissions#commercial-and-residential (accessed on 29 July 2022).
- Royapoor, M.; Antony, A.; Roskilly, T. A review of building climate and plant controls, and a survey of industry perspectives. Energy Build. 2018, 158, 453–465. [Google Scholar] [CrossRef]
- Ma, Y.; Borrelli, F.; Hencey, B.; Coffey, B.; Bengea, S.; Haves, P. Model predictive control for the operation of building cooling systems. IEEE Trans. Control. Syst. Technol. 2012, 20, 796–803. [Google Scholar]
- Kathirgamanathan, A.; De Rosa, M.; Mangina, E.; Finn, D.P. Data-driven predictive control for unlocking building energy flexibility: A review. Renew. Sustain. Energy Rev. 2021, 135, 110120. [Google Scholar] [CrossRef]
- Carlet, P.G.; Favato, A.; Bolognani, S.; Dörfler, F. Data-driven continuous-set predictive current control for synchronous motor drives. IEEE Trans. Power Electron. 2022, 37, 6637–6646. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Y.; Zhang, L. Disturbance-deadbeat inductance observer-based current predictive control for surface-mounted permanent magnet synchronous motors drives. IET Power Electron. 2020, 13, 1172–1180. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, Y.; Fan, M.; Ji, A.; Xiao, Y.; Zhang, X.; Zhang, W.; Garcia, C.; Vasquez, S.; Rodriguez, J. An improved implicit model predictive current control with continuous control set for PMSM drives. IEEE Trans. Transp. Electrif. 2022, 8, 2444–2455. [Google Scholar] [CrossRef]
- Abu-Ali, M.; Berkel, F.; Manderla, M.; Reimann, S.; Kennel, R.; Abdelrahem, M. Deep learning-based long-horizon MPC: Robust, high performing and computationally efficient control for PMSM drives. IEEE Trans. Power Electron. 2022, 37, 12486–12501. [Google Scholar] [CrossRef]
- Zhao, S.; Cajo, R.; De Keyser, R.; Ionescu, C.M. The potential of fractional order distributed MPC applied to steam/water loop in large scale ships. Processes 2020, 8, 451. [Google Scholar] [CrossRef]
- Zhao, S.; Cajo, R.; De Keyser, R.; Liu, S.; Ionescu, C.M. Nonlinear predictive control applied to steam/water loop in large scale ships. IFAC Pap. 2019, 52, 868–873. [Google Scholar] [CrossRef]
- Cheng, C.; Peng, C.; Zhang, T. Fuzzy k-means cluster based generalized predictive control of ultra supercritical power plant. IEEE Trans. Ind. Inform. 2021, 17, 4575–4583. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Cantoni, F.; Oliveri, A.; Procopio, R.; Rosini, A.; Invernizzi, M.; Storace, M. An MPC-based approach for emergency control ensuring transient stability in power grids with steam plants. IEEE Trans. Ind. Electron. 2019, 66, 5412–5422. [Google Scholar] [CrossRef]
- Yang, S.; Wan, M.P.; Chen, W.; Ng, B.F.; Dubey, S. Experiment study of machine-learning-based approximate model predictive control for energy-efficient building control. Appl. Energy 2021, 288, 116648. [Google Scholar] [CrossRef]
- Yang, S.; Wan, M.P.; Chen, W.; Ng, B.F.; Dubey, S. Model predictive control with adaptive machine-learning-based model for building energy efficiency and comfort optimization. Appl. Energy 2020, 271, 115147. [Google Scholar] [CrossRef]
- Rout, R.; Subudhi, B. Design of line-of-sight guidance law and a constrained optimal controller for an autonomous underwater vehicle. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 416–420. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Karras, G.C.; Marantos, P.; Kyriakopoulos, K.J. A robust predictive control approach for underwater robotic vehicles. IEEE Trans. Control Syst. Technol. 2020, 28, 2352–2363. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar]
- Taheri, S.; Hosseini, P.; Razban, A. Model predictive control of heating, ventilation, and air conditioning (HVAC) systems: A state-of-the-art review. J. Build. Eng. 2022, 60, 105067. [Google Scholar] [CrossRef]
- Dastjerdi, A.A.; Vinagre, B.M.; Chen, Y.; HosseinNia, S.H. Linear fractional order controllers; A survey in the frequency domain. Annu. Rev. Control 2019, 47, 51–70. [Google Scholar] [CrossRef]
- Moreles, M.; Lainez, R. Mathematical modelling of fractional order circuit elements and bioimpedance applications. Commun. Nonlinear Sci. Numer. Simul. 2017, 46, 81–88. [Google Scholar] [CrossRef]
- Zheng, W.; Huang, R.; Luo, Y.; Chen, Y.; Wang, X.; Chen, Y. A look-up table based fractional order composite controller synthesis method for the pmsm speed servo system. Fractal Fract. 2022, 6, 47. [Google Scholar] [CrossRef]
- Cajo, R.; Mac, T.T.; Plaza, D.; Copot, C.; De Keyser, R.; Ionescu, C. A survey on fractional order control techniques for unmanned aerial and ground vehicles. IEEE Access 2019, 7, 66864–66878. [Google Scholar] [CrossRef]
- Hashemizadeh, E.; Ebrahimzadeh, A.; Physica, A. An efficient numerical scheme to solve fractional diffusion-wave and fractional Klein-Gordon equations in fluid mechanics. Stat. Mech. Its Appl. 2018, 503, 1189–1203. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Liu, J.; Ma, C.; Yan, H. Characteristic analysis of the fractional-order hyperchaotic complex system and its image encryption application. Signal Process. 2020, 169, 107373. [Google Scholar] [CrossRef]
- Sohail, A.; Beg, O.; Li, Z.; Celik, S. Physics of fractional imaging in biomedicine. Prog. Biophys. Mol. Biol. 2018, 140, 13–20. [Google Scholar] [CrossRef]
- Ivanescu, M.; Dumitrache, I.; Popescu, N.; Popescu, D. Fractional order model identification of a person with Parkinson’s disease for wheelchair control. Fractal Fract. 2023, 7, 23. [Google Scholar] [CrossRef]
- Huang, C.; Wang, J.; Chen, X.; Cao, J. Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw. 2021, 141, 344–354. [Google Scholar] [CrossRef]
- Huang, C.; Liu, H.; Shi, X.; Chen, X.; Xiao, M.; Wang, Z.; Cao, J. Bifurcations in a fractional-order neural network with multiple leakage delays. Neural Netw. 2020, 131, 115–126. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Gao, R.; Xu, C.; Shang, Y. New exploration on bifurcation in fractional-order genetic regulatory networks incorporating both type delays. Eur. Phys. J. Plus 2022, 137, 598. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Review of modeling methods for HVAC systems. Appl. Therm. Eng. 2014, 67, 507–519. [Google Scholar] [CrossRef]
- Zhan, S.; Chong, A. Data requirements and performance evaluation of model predictive control in buildings: A modeling perspective. Renew. Sustain. Energy Rev. 2021, 142, 110835. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.; Do, S.; Mago, P.J.; Lee, K.H.; Cho, H. Energy Modeling and Model Predictive Control for HVAC in Buildings: A Review of Current Research Trends. Energies 2022, 15, 7231. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Gray-box modeling and validation of residential HVAC system for control system design. Appl. Energy 2015, 137, 134–150. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- Klein, S.A.; Beckman, W.A.; Mitchell, J.W.; Duffie, J.A.; Duffie, N.A.; Freeman, T.L.; Mitchell, J.C.; Braun, J.E.; Evans, B.L.; Kummer, J.P.; et al. TRNSYS 17: A Transient System Simulation Program, Solar Energy Laboratory; University of Wisconsin: Madison, WI, USA, 2010. [Google Scholar]
- Ferrarini, L.; Fathi, E.; Disegna, S.; Rastegarpour, S. Energy consumption models for residential buildings: A case study. In Proceedings of the 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, 10–13 September 2019. [Google Scholar]
- Široký, J.; Oldewurtel, F.; Cigler, J.; Prívara, S. Experimental analysis of model predictive control for an energy efficient building heating system. Appl. Energy 2011, 88, 3079–3087. [Google Scholar] [CrossRef]
- Martinčević, A.; Vašak, M. Constrained Kalman filter for identification of semiphysical building thermal models. IEEE Trans. Control Syst. Technol. 2020, 28, 2697–2704. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, S.; Cajo, R.; Ren, W.; Li, B. Power tracking control of marine boiler-turbine system based on fractional order model predictive control algorithm. J. Mar. Sci. Eng. 2022, 10, 1307. [Google Scholar] [CrossRef]
- dostaji4/EnergyPlus-Co-Simulation-Toolbox. Available online: https://github.com/dostaji4/EnergyPlus-co-simulation-toolbox (accessed on 5 May 2022).
- ASHRAE Handbook. Available online: https://www.ashrae.org/technical-resources/ashrae-handbook (accessed on 1 September 2022).
- Climate.OneBuilding.Org. Available online: https://climate.onebuilding.org/papers/EnergyPlus_Weather_File_Format.pdf (accessed on 5 May 2022).
- Ebrahimpour, A. New Software for Generation of Typical Meteorological Year. In Proceedings of the World Renewable Energy Congress, Linköping, Sweden, 8–13 May 2011. [Google Scholar]
- Ljung, L. System Identification Toolbox for Use With Matlab, 6th ed.; The Math-Works: Natick, MA, USA, 2003. [Google Scholar]
- De Keyser, R. Model based predictive control for linear systems. In Control Systems, Robotics and Automation, Advanced Control Systems V; Unbehauen, H., Ed.; EOLSS Publishers/UNESCO: Oxford, UK, 2003; Volume XI, pp. 24–58. [Google Scholar]
- De Keyser, R.; Ionescu, C.M. The disturbance model in model based predictive control. In Proceedings of the 2003 IEEE Conference on Control Applications, 2003 (CCA 2003), Istanbul, Turkey, 25 June 2003. [Google Scholar]
- Fernandez, E.; Ipanaque, W.; Cajo, R.; De Keyser, R. Classical and advanced control methods applied to an anaerobic digestion reactor model. In Proceedings of the 2019 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaiso, Chile, 13–27 November 2019. [Google Scholar]
- Romero, M.; de Madrid, A.P.; Vinagre, B.M. Arbitrary real-order cost functions for signals and systems. Signal Process. 2011, 91, 372–378. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P.S. Generalized predictive control—Part I. The basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]


| Parameters | Nu | Np | Ts | N1 |
|---|---|---|---|---|
| Values | 1 | 30 | 60 s | 1 |
| Index | FO (0.5) | FO (1) | FO (1.5) | FO (2) | FO (2.5) | FO (3) | FO (4) | FO (4.5) |
|---|---|---|---|---|---|---|---|---|
| IAE | 9.0898 | 8.5755 | 8.3136 | 8.1064 | 7.9328 | 7.8286 | 7.7099 | 7.6835 |
| ISU | 32.9162 | 33.8012 | 34.4025 | 34.9530 | 35.5080 | 36.0807 | 37.2308 | 37.8603 |
| RIAE | 0.9434 | 1 | 1.0315 | 1.0579 | 1.0810 | 1.0954 | 1.1123 | 1.1161 |
| RISU | 1.0269 | 1 | 0.9825 | 0.9670 | 0.9519 | 0.9368 | 0.9079 | 0.8928 |
| Index | FO (5) | FO (6) | FO (7) | FO (8) | FO (8.5) | FO (9) | FO (10) | FO (12.5) |
|---|---|---|---|---|---|---|---|---|
| IAE | 7.6667 | 7.6849 | 7.7938 | 8.0320 | 8.1662 | 8.3047 | 8.6038 | 9.1152 |
| ISU | 38.5106 | 39.8635 | 41.2617 | 42.7213 | 43.4871 | 44.2778 | 45.9401 | 50.1256 |
| RIAE | 1.1185 | 1.1159 | 1.1003 | 1.0677 | 1.0501 | 1.0326 | 0.9967 | 0.9408 |
| RISU | 0.8777 | 0.8479 | 0.8192 | 0.7912 | 0.7773 | 0.7634 | 0.7358 | 0.6743 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cajo, R.; Zhao, S.; Birs, I.; Espinoza, V.; Fernández, E.; Plaza, D.; Salcan-Reyes, G. An Advanced Fractional Order Method for Temperature Control. Fractal Fract. 2023, 7, 172. https://doi.org/10.3390/fractalfract7020172
Cajo R, Zhao S, Birs I, Espinoza V, Fernández E, Plaza D, Salcan-Reyes G. An Advanced Fractional Order Method for Temperature Control. Fractal and Fractional. 2023; 7(2):172. https://doi.org/10.3390/fractalfract7020172
Chicago/Turabian StyleCajo, Ricardo, Shiquan Zhao, Isabela Birs, Víctor Espinoza, Edson Fernández, Douglas Plaza, and Gabriela Salcan-Reyes. 2023. "An Advanced Fractional Order Method for Temperature Control" Fractal and Fractional 7, no. 2: 172. https://doi.org/10.3390/fractalfract7020172
APA StyleCajo, R., Zhao, S., Birs, I., Espinoza, V., Fernández, E., Plaza, D., & Salcan-Reyes, G. (2023). An Advanced Fractional Order Method for Temperature Control. Fractal and Fractional, 7(2), 172. https://doi.org/10.3390/fractalfract7020172









