Fourth-Order Numerical Solutions for a Fuzzy Time-Fractional Convection–Diffusion Equation under Caputo Generalized Hukuhara Derivative
Abstract
1. Introduction
2. Preliminaries and Fundamental Definitions
- is upper semi-continuous on ,
- is fuzzy convex,
- is normal,
- Closure ofis compact,
- 5.
- and thatis-differentiable at if
- 6.
- 7.
- (
- 8.
- (
3. High-Order Compact Finite Difference Method in Fuzzy Environment
4. Time Fractional Convection–Diffusion Equation in Fuzzy Environment
5. The Fuzzy Fourth-Order Compact Implicit Scheme Method for the Solution of FTFCDE
6. The Fuzzy Fourth-Order FTCS Method for the Solution of FTFCDE
7. The Truncation Error Analysis
8. Stability Analysis
- 9.
- 10.
9. Numerical Experiments
10. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Taneco-Hernández, M.A. Analytical solution of the time fractional diffusion equation and fractional convection-diffusion equation. Rev. Mex. Física 2019, 65, 82–88. [Google Scholar]
- Qiao, Y.; Zhai, S.; Feng, X. RBF-FD method for the high dimensional time fractional convection-diffusion equation. Int. Commun. Heat Mass Transf. 2017, 89, 230–240. [Google Scholar] [CrossRef]
- Chang, A.; Sun, H.; Zheng, C.; Lu, B.; Lu, C.; Ma, R.; Zhang, Y. A time fractional convection–diffusion equation to model gas transport through heterogeneous soil and gas reservoirs. Phys. A Stat. Mech. Its Appl. 2018, 502, 356–369. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Yang, B. An approximation scheme for the time fractional convection–diffusion equation. Appl. Math. Comput. 2018, 335, 305–312. [Google Scholar] [CrossRef]
- Zureigat, H.; Ismail, A.I.; Sathasivam, S. Numerical solutions of fuzzy fractional diffusion equations by an implicit finite difference scheme. Neural Comput. Appl. 2019, 31, 4085–4094. [Google Scholar] [CrossRef]
- Zhang, Y. A finite difference method for fractional partial differential equation. Appl. Math. Comput. 2009, 215, 524–529. [Google Scholar] [CrossRef]
- Zhai, S.; Feng, X.; He, Y. An unconditionally stable compact ADI method for three-dimensional time-fractional convection–diffusion equation. J. Comput. Phys. 2014, 269, 138–155. [Google Scholar] [CrossRef]
- Zhong, G.; Yi, M.; Huang, J. Numerical method for solving fractional convection diffusion equations with time-space variable coefficients. IAENG Int. J. Appl. Math. 2018, 48, 62–66. [Google Scholar]
- Gao, G.H.; Sun, H.W. Three-point combined compact alternating direction implicit difference schemes for two-dimensional time-fractional advection-diffusion equations. Commun. Comput. Phys. 2015, 17, 487–509. [Google Scholar] [CrossRef][Green Version]
- Fazio, R.; Jannelli, A.; Agreste, S. A finite difference method on non-uniform meshes for time-fractional advection–diffusion equations with a source term. Appl. Sci. 2018, 8, 960. [Google Scholar] [CrossRef]
- Sweilam, N.H.; El-Sakout, D.M.; Muttardi, M.M. Compact finite difference method to numerically solving a stochastic fractional advection-diffusion equation. Adv. Differ. Equ. 2020, 2020, 189. [Google Scholar] [CrossRef]
- Li, L.; Jiang, Z.; Yin, Z. Compact finite-difference method for 2D time-fractional convection–diffusion equation of groundwater pollution problems. Comput. Appl. Math. 2020, 39, 142. [Google Scholar] [CrossRef]
- Senol, M.; Atpinar, S.; Zararsiz, Z.; Salahshour, S.; Ahmadian, A. Approximate solution of time-fractional fuzzy partial differential equations. Comput. Appl. Math. 2019, 38, 18. [Google Scholar] [CrossRef]
- Shah, K.; Seadawy, A.R.; Arfan, M. Evaluation of one dimensional fuzzy fractional partial differential equations. Alex. Eng. J. 2020, 59, 3347–3353. [Google Scholar] [CrossRef]
- Zureigat, H.; Ismail, A.I.; Sathasivam, S. Numerical solutions of fuzzy time fractional advection-diffusion equations in double parametric form of fuzzy number. Math. Methods Appl. Sci. 2021, 44, 7956–7968. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Armand, A.; Gouyandeh, Z. Fuzzy fractional differential equations under generalized fuzzy Caputo derivative. J. Intell. Fuzzy Syst. 2014, 26, 1481–1490. [Google Scholar] [CrossRef]
- Salahshour, S.; Allahviranloo, T.; Abbasbandy, S. Solving fuzzy fractional differential equations by fuzzy Laplace transforms. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1372–1381. [Google Scholar] [CrossRef]
- Stefanini, L.; Bede, B. Generalized Hukuhara differentiability of interval-valued functions and interval differential equations. Nonlinear Anal. Theory Methods Appl. 2009, 71, 1311–1328. [Google Scholar] [CrossRef]
- Bede, B.; Stefanini, L. Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst. 2013, 230, 119–141. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F. Implicit difference approximation for the time fractional diffusion equation. J. Appl. Math. Comput. 2006, 22, 87–99. [Google Scholar] [CrossRef]
- Das, A.K.; Roy, T.K. Exact solution of some linear fuzzy fractional differential equation using Laplace transform method. Glob. J. Pure Appl. Math 2017, 13, 5427–5435. [Google Scholar]
- Karatay, I.; Bayramoglu, S.R. High-order compact difference scheme for the numerical solution of time fractional heat equations. Sci. World J. 2014, 2014, 642989. [Google Scholar] [CrossRef] [PubMed]
- Johnsen, S.G.; Pääkkönen, T.M.; Andersson, S.; Johansen, S.T.; Wittgens, B. On the wall boundary conditions for species-specific mass conservation equations in mathematical modelling of direct precipitation fouling from supersaturated, multi-component fluid mixtures. arXiv 2017, arXiv:1703.01448. [Google Scholar]
- Arshad, M.; Hassan, A. A numerical study on the hybrid nanofluid flow between a permeable rotating system. Eur. Phys. J. Plus 2022, 137, 1126. [Google Scholar] [CrossRef]
- Hassan, A.; Hussain, A.; Arshad, M.; Karamti, H.; Awrejcewicz, J.; Alharbi, F.M.; Galal, A.M. Computational investigation of magneto-hydrodynamic flow of newtonian fluid behavior over obstacles placed in rectangular cavity. Alex. Eng. J. 2022. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Hassan, A.; Karamti, H.; Wroblewski, P.; Khan, I.; Galal, A.M. Scrutinization of Slip Due to Lateral Velocity on the Dynamics of Engine Oil Conveying Cupric and Alumina Nanoparticles Subject to Coriolis Force. Math. Probl. Eng. 2022, 2022, 2526951. [Google Scholar] [CrossRef]
- İbiş, B.; Bayram, M. Approximate solution of time-fractional advection-dispersion equation via fractional variational iteration method. Sci. World J. 2014, 2014, 769713. [Google Scholar] [CrossRef]
- Ding, H.F.; Zhang, Y.X. Notes on Implicit finite difference approximation for time fractional diffusion equations [Comput. Math. Appl. 56 (2008) 1138–1145]. Comput. Math. Appl. 2011, 61, 2924–2928. [Google Scholar] [CrossRef][Green Version]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burrage, K. Stability and convergence of the difference methods for the space–time fractional advection–diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Li, D.; Sun, W.; Wu, C. A novel numerical approach to time-fractional parabolic equations with nonsmooth solutions. Numer. Math. Theory Methods Appl. 2021, 14, 355–376. [Google Scholar]
- Qin, H.; Li, D.; Zhang, Z. A novel scheme to capture the initial dramatic evolutions of nonlinear subdiffusion equations. J. Sci. Comput. 2021, 89, 65. [Google Scholar] [CrossRef]
- Zhang, Z. Finite element superconvergence on Shishkin mesh for 2-D convection-diffusion problems. Math. Comput. 2003, 72, 1147–1177. [Google Scholar] [CrossRef]
- Allen, E.J.; Novosel, S.J.; Zhang, Z. Finite element and difference approximation of some linear stochastic partial differential equations. Stoch. Int. J. Probab. Stoch. Process. 1998, 64, 117–142. [Google Scholar] [CrossRef]
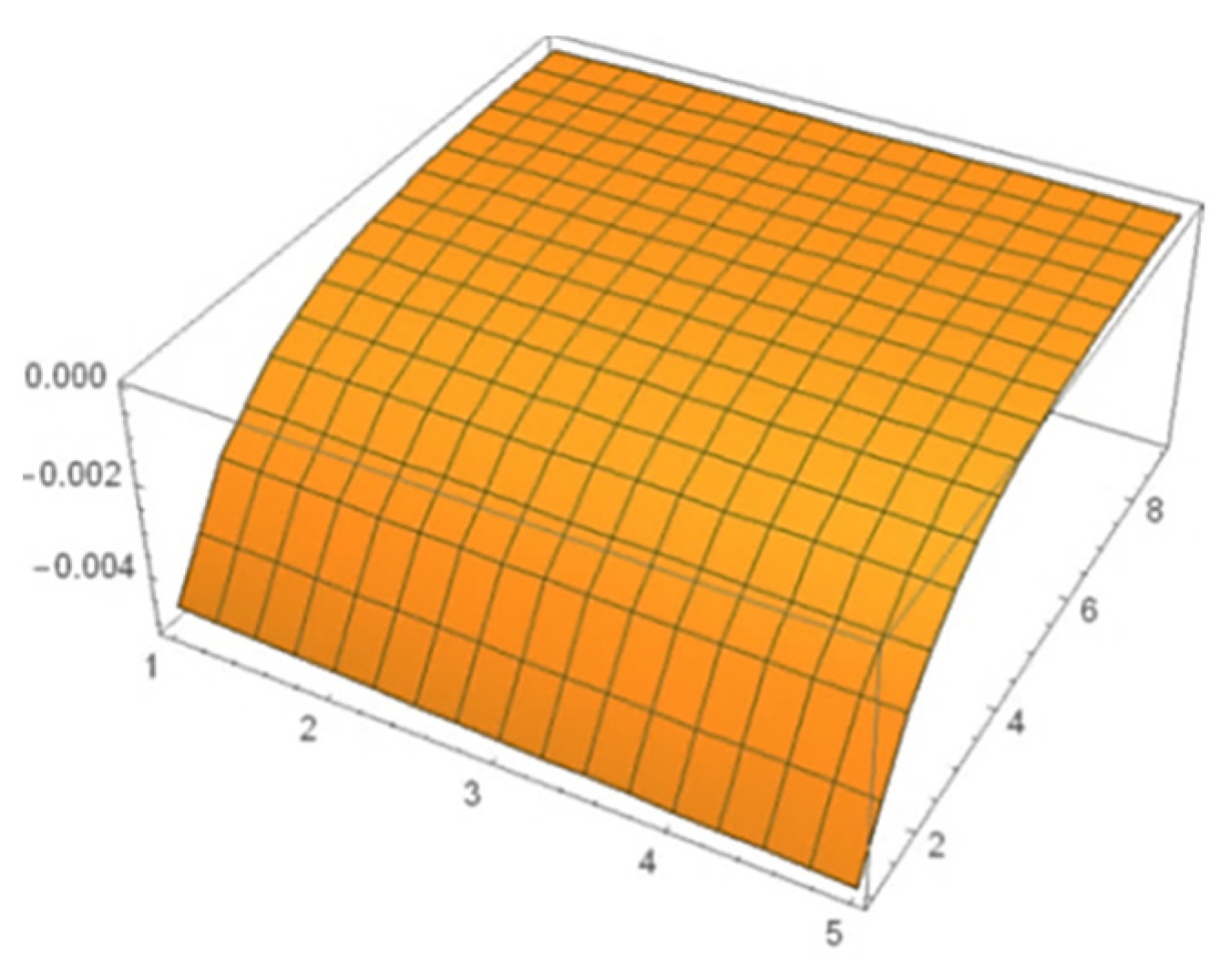
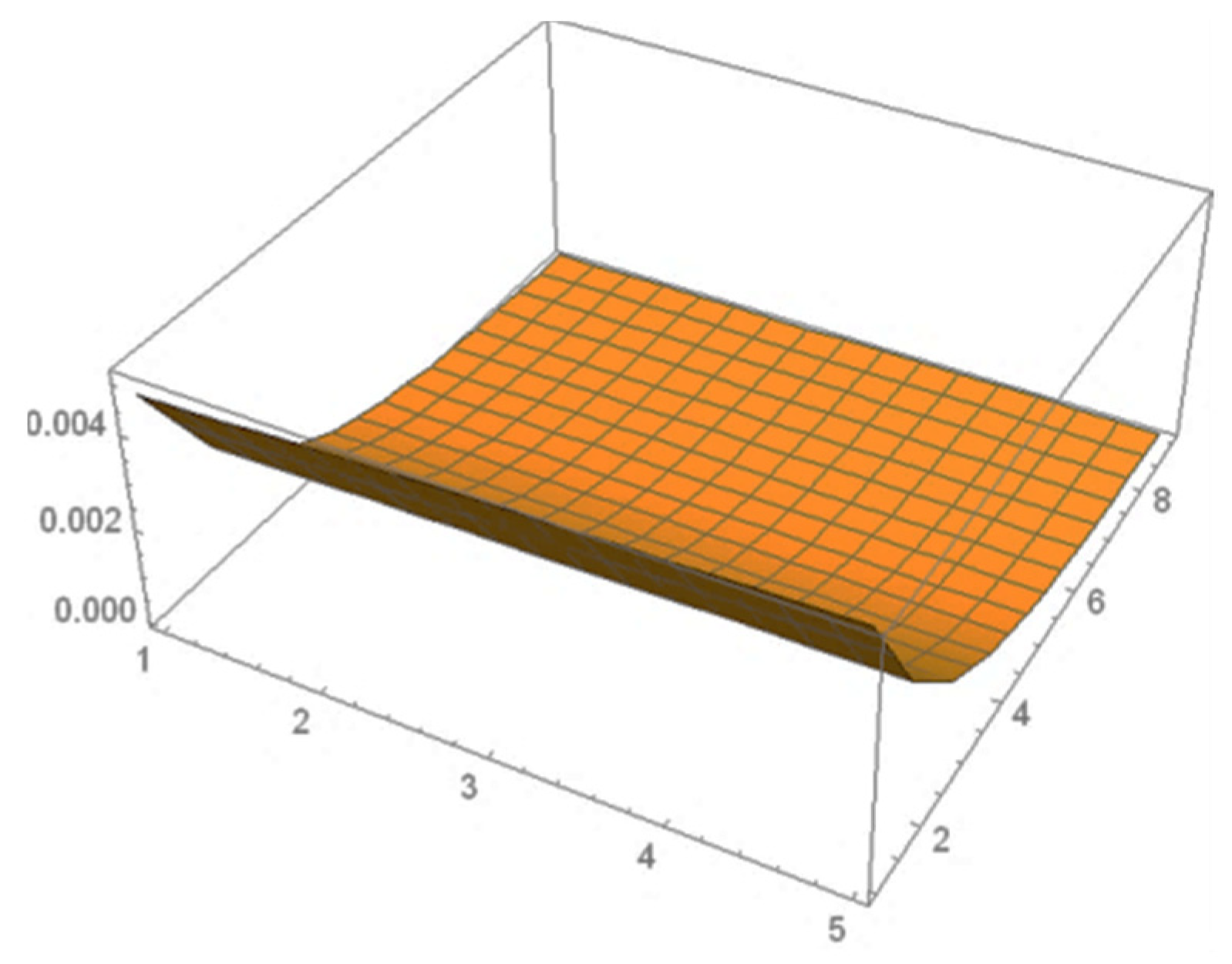
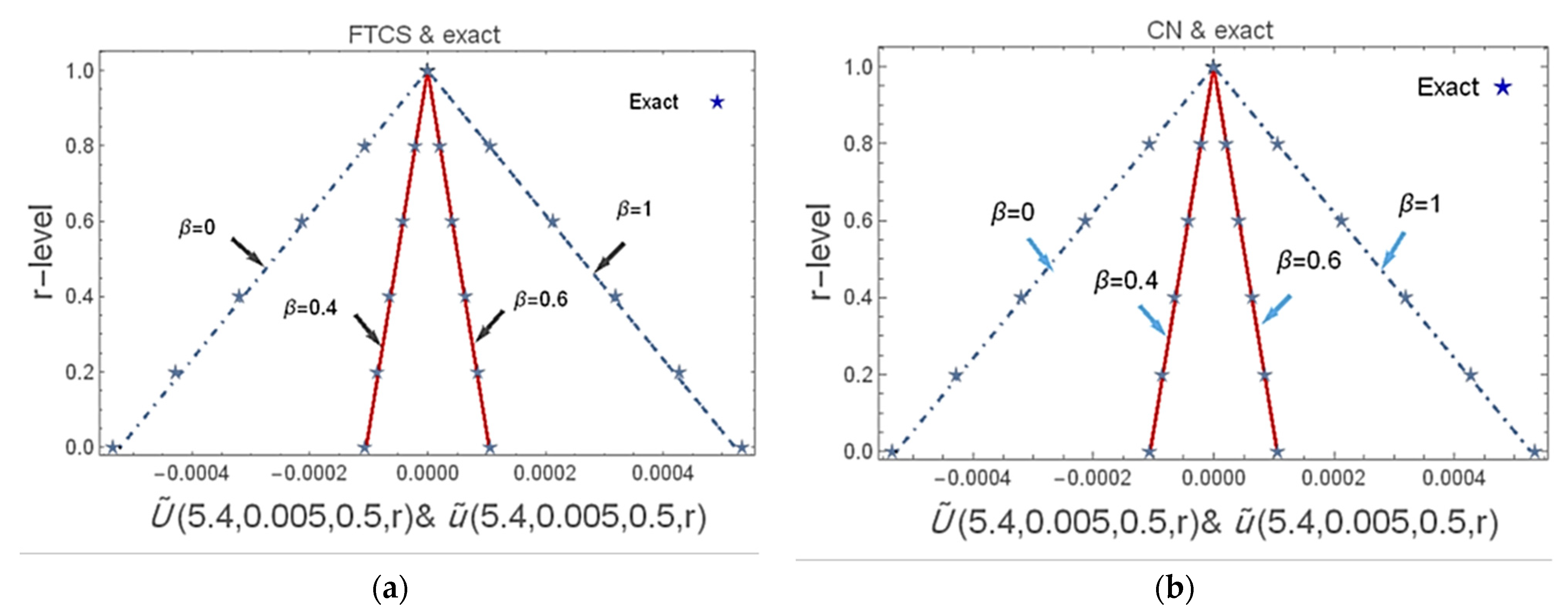
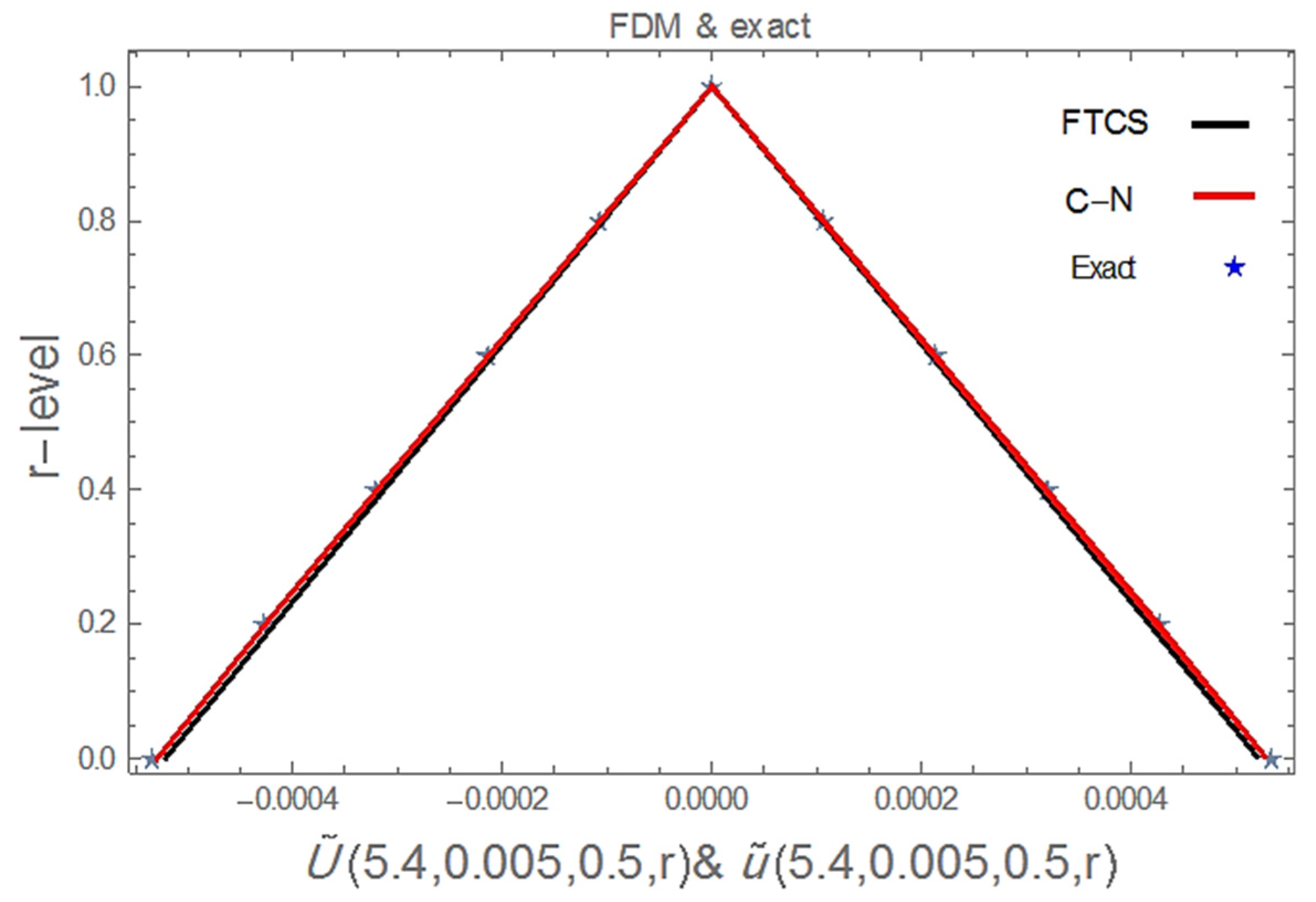

| Fourth Order Compact FTCS | Fourth Order Compact Implicit Scheme | ||||
|---|---|---|---|---|---|
| Lower Solution When | |||||
| 0 | 0 | 0 | 0 | ||
| Upper Solution When | 0 | ||||
| 0.2 | |||||
| 0.4 | |||||
| 0.6 | |||||
| 0.8 | |||||
| 1 | 0 | 0 | 0 | 0 | |
| Fourth-Order Compact FTCS | Fourth-Order Compact Implicit Scheme | ||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ||
| 0 | |||||
| 0.2 | |||||
| 0.4 | |||||
| 0.6 | |||||
| 0.8 | |||||
| 1 | 0 | 0 | 0 | 0 | |
| Second-Order Classical Implicit Scheme | Fourth-Order Compact Implicit Scheme | ||||
|---|---|---|---|---|---|
| Lower Solution When | |||||
| 0 | 0 | 0 | 0 | ||
| Upper Solution When | 0 | ||||
| 0.2 | |||||
| 0.4 | |||||
| 0.6 | |||||
| 0.8 | |||||
| 1 | 0 | 0 | 0 | 0 | |
| Second-Order Classical Implicit Scheme | Fourth-Order Compact Implicit Scheme | ||||
|---|---|---|---|---|---|
| Lower Solution When | |||||
| 0 | 0 | 0 | 0 | ||
| Upper Solution When | 0 | ||||
| 0.2 | |||||
| 0.4 | |||||
| 0.6 | |||||
| 0.8 | |||||
| 1 | 0 | 0 | 0 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zureigat, H.; Al-Smadi, M.; Al-Khateeb, A.; Al-Omari, S.; Alhazmi, S.E. Fourth-Order Numerical Solutions for a Fuzzy Time-Fractional Convection–Diffusion Equation under Caputo Generalized Hukuhara Derivative. Fractal Fract. 2023, 7, 47. https://doi.org/10.3390/fractalfract7010047
Zureigat H, Al-Smadi M, Al-Khateeb A, Al-Omari S, Alhazmi SE. Fourth-Order Numerical Solutions for a Fuzzy Time-Fractional Convection–Diffusion Equation under Caputo Generalized Hukuhara Derivative. Fractal and Fractional. 2023; 7(1):47. https://doi.org/10.3390/fractalfract7010047
Chicago/Turabian StyleZureigat, Hamzeh, Mohammed Al-Smadi, Areen Al-Khateeb, Shrideh Al-Omari, and Sharifah E. Alhazmi. 2023. "Fourth-Order Numerical Solutions for a Fuzzy Time-Fractional Convection–Diffusion Equation under Caputo Generalized Hukuhara Derivative" Fractal and Fractional 7, no. 1: 47. https://doi.org/10.3390/fractalfract7010047
APA StyleZureigat, H., Al-Smadi, M., Al-Khateeb, A., Al-Omari, S., & Alhazmi, S. E. (2023). Fourth-Order Numerical Solutions for a Fuzzy Time-Fractional Convection–Diffusion Equation under Caputo Generalized Hukuhara Derivative. Fractal and Fractional, 7(1), 47. https://doi.org/10.3390/fractalfract7010047









