Abstract
In this paper, we study the stability and Hopf bifurcation of a class of six-neuron fractional BAM neural networks with multiple delays. Firstly, the model is transformed into a fractional neural network model with two nonidentical delays by using variable substitution. Then, by assigning a value to one of the time delays and selecting the remaining time delays as parameters, the critical value of Hopf bifurcation for different time delays is calculated. The study shows that when the time lag exceeds its critical value, the equilibrium point of the system will lose its stability and generate Hopf bifurcation. Finally, the correctness of theoretical analysis is verified by simulation.
1. Introduction
Artificial neural networks (ANNs), also referred to as neural networks (NNs), is a distributed parallel information processing algorithm mathematical model that imitates the behavior characteristics of biological neural networks. Because of its strong adaptability, high fault tolerance, fast computing speed, and other capabilities, it has important applications in many fields, such as pattern recognition, image processing, intelligent signal sensing analysis, target tracking, and identification. In references [1,2] Hopfield proposed single-layer and layered feedback neural networks, respectively. After that, a large number of scholars and researchers further studied Hopfield’s method, thus forming the research upsurge of artificial neural networks in recent years. Associative memory network is an important branch of neural networks which obtains the original pattern by simulating human brain and storing sample patterns with the weight of neural networks and performing large-scale parallel computation. Among all kinds of associative memory network models, the bidirectional associative memory (BAM) neural network proposed by B. Kosko [3] in 1988 is the most widely used. The BAM neural network is a kind of feedback system with bidirectional stability, which has the characteristics of large-scale parallel data processing and strong self-organization. Research on the BAM neural network has been one of the hot topics in recent years. Song studied the stability and bifurcation problems of a class of BAM neural networks with three neurons in the literature [4]. Cao [5] gave a sufficient criterion for the stability and Hopf bifurcation generation of a class of BAM neural networks with four neurons. In reference [6], Gopalsamy put forward the meaning of leakage delay of BAM neural networks. Cheng [7] presented a class of three-layer neural networks, and discussed the direction of generating Hopf bifurcation and the stability of bifurcation periodic solution.
Fractional calculus originated in 1695, almost at the same time as classical calculus, and has a history of more than 300 years. However, due to the limitations of technology and environment, fractional calculus was only discussed and studied in the pure mathematics field at first. After 1974, the theory and application of fractional calculus developed rapidly, and it was applied in biological systems, control systems, chaos and turbulence, electrochemistry, viscoelastic mechanics, and many other fields. Matignon [8] and Deng [9] both studied the stability of finite dimensional fractional order systems and give a method to judge stability of fractional order linear systems. Li proposed the definition of Mittag–Leffler stability in the literature [10], and further proposed the definition of generalized Mittag–Leffler stability [11], which enriched the stability theory of fractional calculus. Huang discussed the bifurcation control problem for a class of predator–prey systems with incommensurate fractional order delays [12]. Compared with the integer differential system, the fractional differential dynamic model can more accurately describe some non-classical phenomena in natural science and engineering applications, but the current fractional calculus theory is not perfect and in many aspects needs in-depth research, such as bifurcation direction. Fractional calculus still has broad development prospects and will have important research significance in the future.
Time delays exist in mechanical, physical, biological, and economic system models. The existence of a time delay, on the one hand, will destroy the dynamic performance of the system and make the system unstable. On the other hand, in some control systems, people can make the system reach the ideal state by changing the time delay. The use of time delays can better solve practical problems, so the study of dynamic behavior of all kinds of systems with time delays has important theoretical research significance and practical application value. In recent years, because the fractional order delay differential equation can describe the dynamic behavior of the system more accurately and has better control of the system, more and more scholars have become committed to studying the dynamic behavior of the fractional order BAM neural network model with multiple delays. Xu discussed the global existence of periodic solutions of BAM neural networks with six neurons in document [13]. In reference [14], the stability and Hopf bifurcation direction of integer order BAM neural networks with different distribution of six neurons are discussed, respectively. Then, in references [15,16,17], for the fractional BAM neural network with six neurons, a sufficient criterion for the stability of the model solution and bifurcation generation are given. In [18,19], Huang studied the stability and bifurcation problems of integer order BAM neural networks with 6 and () neurons, respectively, and discussed the fractional order BAM neural networks with four neurons in [20,21], and gave the sufficient conditions for the stability of system solutions and Hopf bifurcation generation. The model in the literature [18] is as follows.
where represents the connection weight between the neuron of I-layer and the neuron of J-layer. is the decay rates of internal neurons, are activation functions, represents the transmission delay between I-layer neurons and J-layer neurons. See reference [18] for parameter details.
In this paper, the stability of fractional BAM neural networks with multiple delays is discussed. Different from the model established in reference [18], the model established in this paper introduces a fractional derivative and assumes that is more suitable for practical application. Similar to the method of reference [20], this paper also converts the multi-delay model into double-delay model, but the number of neurons is increased in this paper when establishing the model, which increases the complexity of the model in some respects.
Compared with the integer order BAM neural network with multiple delays ([22,23]), the dynamic behavior of the network will become more complex due to the existence of the fractional order. The description of the dynamic behavior of the system will depend on the flexible application of the fractional derivative knowledge and the stability and bifurcation theory of the fractional system.
It is worth noting that previous studies generally studied the stability and bifurcation of fractional order systems with the same order. In this paper, six different fractional orders are considered in the modeling process. With the increase of dimension of neural networks and different fractional orders, then the characteristic equation of model will become a more complex higher-order transcendental equation. It will be challenging to analyze the distribution of the roots of the characteristic equation of the model.
This article is organized as follows. In Section 2, the definition of the Caputo fractional derivative and some lemmas are given. In Section 3, sufficient conditions for asymptotic stability of equilibrium point and Hopf bifurcation generation of the system (3) are obtained by a linearizing system (3) and we analyze its characteristic equation with time delay as a parameter. The two delays in system (4) are discussed as parameters, respectively. In Section 4, two examples are given to verify the correctness of the theoretical results. Finally, the main conclusions are given in Section 5.
2. Preliminaries
The commonly used fractional derivatives are the Riemann–Liouville derivative, the Caputo derivative, and the Grunwald–Letnikov derivative. Considering that the Caputo derivative makes it easier to select a initial value, this paper adopts a Caputo-type fractional derivative to calculate. In order to obtain the main results of this paper, the following definitions and lemmas are given.
Definition 1.
Caputo fractional derivative [24] is defined as
where is the Gamma function.
The Laplace transform of the fractional derivative of Caputo is
If , then .
Lemma 1
([9]). Consider the following fractional linear system with multiple state variables.
where . The characteristic equation of the system (2) is as follows.
If all the real parts of the roots of equation are negative, then the zero solution of system (2) is Lyapunov globally asymptotically stable.
Based on the above discussion, this paper improves system (1) and establishes the following fractional order BAM neural network model with multiple delays.
In the above model, is the Caputo fractional derivative and .
Now, let us do the following transformation
Then the equivalent form of the system (3) can be obtained, that is,
In order to carry out the follow-up work smoothly, the following hypothesis is given.
Hypothesis 1 (H1).
.
3. Local Stability of Equilibrium Point and Existence of Hopf Bifurcation
From (H1), we know that the zero point of the system (4) is its equilibrium point. The linearized form of system (4) is obtained as follows.
where It is easy to find its characteristic equation
where
where
3.1. The Hopf Bifurcation of a System (3) with Time Delay as Parameter
When , Equation (6) is equal to
Suppose is a pure imaginary root of Equation (7), and represents the real and imaginary parts of , respectively. There are
In order to carry out the follow-up work smoothly, the following hypothesis is given.
Hypothesis 2 (H2).
The Equation (10) has at least one positive real root.
Let represent all positive real roots of Equation (10). The bifurcation point of Equation (7) at is obtained from Equation (9), and its expression is as follows.
Lemma 2.
Proof.
When , Equation (6) becomes
Let be a pure imaginary root of Equation (12), and use to represent the real and imaginary parts of , respectively. There are
Then the following two equations can be obtained by the transformation derivation of the Equation (13).
and
where
□
In order to carry out the follow-up work smoothly, the following hypothesis is given.
Hypothesis 3 (H3).
Let Equation (14) exist m positive real roots, denoted as , and then we can use Equation (15) to obtain
Let , and is the value corresponding to . Then Equation (10) has at least one pair of pure imaginary roots. The proof ends.
Next we consider the stability of system (4) at equilibrium. For the smooth follow-up work, we propose the following assumptions.
Hypothesis 4 (H4).
. (See below for the meanings of and .)
Lemma 3.
Proof.
When , Equation (6) is equal to
Now mark , where and () are mutual prime positive integers, and M is the least common multiple of . Let , then Equation (17) become unary n-degree polynomial about s, and . According to the fundamental theorem of algebra, this equation has n complex roots. For convenience, expressed as . Then, we obtain from (H4). Therefore, all the roots of Equation (17) satisfy .
From Lemma 1, the system (6) is asymptotically stable at if (H4) is satisfied. The proof ends.
□
Hypothesis 5 (H5).
(See below for the meanings of and )
Lemma 4.
If (H5) is satisfied, the transversality condition is valid.
Proof.
Let be the root of Equation (6) near that satisfies and now find the transversal condition. Let us take the derivative of (6) with respect to , and obtain
where is the first derivative of with respect to . Simplify the above equation to obtain
where
Let us define the real numbers and as follows.
that is, and represent the real and imaginary parts of and at (), respectively.
The following equation can be obtained by assuming (H5).
The transversal condition is satisfied. The proof ends.
□
To sum up, from Lemmas 2–4, the following theorem can be obtained.
Theorem 1.
If (H1)–(H5) hold, then we can obtain the following conclusion for system (3).
- (1)
- If , then when , the zero equilibrium point of the fractional order system is asymptotically stable.
- (2)
- If , then when , the zero equilibrium point of fractional order system loses stability and produces Hopf bifurcation.
3.2. The Hopf Bifurcation of a System (3) with Time Delay as Parameter
When , the Equation (6) becomes
Assume that is a pure virtual root Equation (20), and use to represent the real and imaginary parts of , respectively. There are
Hypothesis 6 (H6).
Without loss of generality, if all positive real roots of Equation (23) are expressed as , then the bifurcation point of Equation (20) at can be deduced from Equation (22). Namely,
Lemma 5.
Proof.
When , Equation (6) can be written as
Let is a pure imaginary root of the Equation (25), and use to represent the real and imaginary parts of , respectively. Then we can obtain
□
Hypothesis 7(H7).
Let Equation (27) have n positive real roots, denoted as , and from Equation (28) we can easily obtain
We have , where is the value corresponding to . At least one pair of pure imaginary roots exists in Equation (25). The proof ends.
Hypothesis 8 (H8).
(See below for the meanings of and ).
Lemma 6.
If (H8) is satisfied, then the transversality condition is true.
Proof.
Let be the root of Equation (6) near that satisfies , and then find the transversal condition. If take the derivative of Equation (6) with respect to , we obtain
where is the first derivative of with respect to . The following formula is obtained by simplifying the above formula.
and
The real numbers and are defined as follows.
that is, and represent the real and imaginary parts of and at , respectively.
Then the following formula can be easily obtained from (H8),
The transversal condition is satisfied. The proof ends.
□
In summary, from Lemma 3, Lemma 5, and Lemma 6, we can obtain Theorem 2 as follows.
Theorem 2.
If the (H1),(H4) and (H6)–(H8) hold, then we can obtain the following conclusion for the system (3).
- (1)
- If , then when , the zero equilibrium point of the fractional order system is asymptotically stable.
- (2)
- If , then when , the zero equilibrium point of fractional order system loses stability and produces Hopf bifurcation.
4. Numerical Examples
In this section, we will give two numerical examples to support the theoretical results. Example 1 and Example 2 verify the validity and correctness of Theorem (1) and Theorem (2) respectively. It is obvious that the system (3) is equivalent to the system (4) and the system (3) form.
4.1. Example 1
Take Consider the following system
It is clear that the system (32) has an equilibrium point (0, 0, 0, 0, 0, 0). is obtained by numerical calculation. Take , which is . Then we have , and . That is, the (H1)–(H5) are satisfied. When taking , that is, , the Figure 1 can be obtained through Matlab simulation. It is obvious that the zero equilibrium point of the system (32) is locally asymptotically stable. And take , , it can be seen from Figure 2 that the zero-equilibrium point of the system loses its stability and produces Hopf bifurcation.
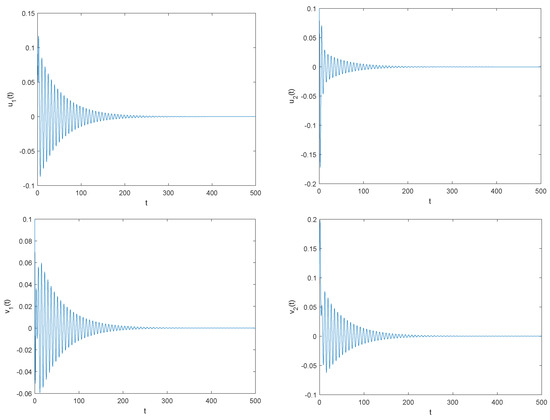
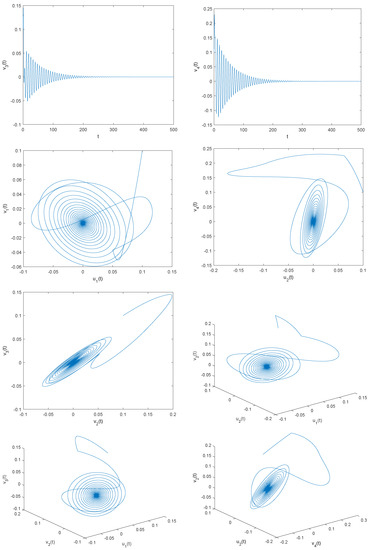
Figure 1.
When , the zero equilibrium of the system (32) is asymptotically stable.


Figure 2.
When , the zero equilibrium of the system (21) loses stability and produces Hopf bifurcation.
4.2. Example 2
Take Consider the following system
It is clear that the system (33) has an equilibrium point (0,0,0,0,0,0). is obtained by numerical calculation. Take , which is . We have , and . That is, (H1), (H4), and (H6)–(H8) are satisfied. When taking , that is, , the Figure 3 can be obtained through Matlab simulation. It is obvious that the zero equilibrium point of the system (33) is locally asymptotically stable. And take , , it can be seen from Figure 4 that the zero-equilibrium point of the system loses its stability and produces Hopf bifurcation.
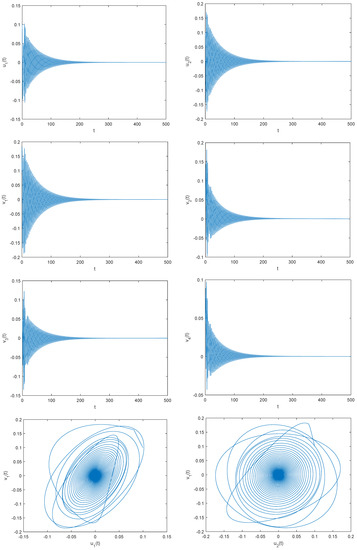

Figure 3.
When , the zero equilibrium of the system (33) is asymptotically stable.
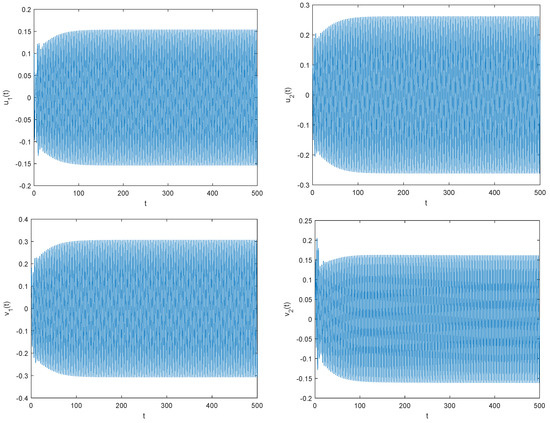

Figure 4.
When , the zero equilibrium of the system (33) loses its stability and produces Hopf bifurcation.
In [25,26], the unified program code can easily be edited for the numerical simulation. However, because there are six different fractional orders in this model, it is difficult to write Matlab code. Accordingly, we mainly use the Simulink tool in Matlab software to draw phase diagram and trajectory diagram of the model, which has achieved good results.
5. Conclusions
In this paper, we study the dynamic behavior of a class of fractional order simplified BAM neural networks with multiple delays.Firstly, the system with four delays is transformed into a system with two delays. Then, by fixing one delay () and taking the other delay () as a bifurcation parameter, the dynamic behavior of the fractional order system with two delays is analyzed, and sufficient conditions for the local stability of the zero solution and Hopf bifurcation are obtained. Through analysis, it is found that the fractional order delay system remains stable when the time delay is small, while when the time delay exceeds the critical value , the zero solution of the nonlinear fractional order system will lose stability and produce Hopf bifurcation. Finally, two simulation examples are given to illustrate the effectiveness and feasibility of the main results. The fractional BAM neural network model with six neurons studied in this paper is relatively simple, and there are still many problems to be studied, such as the study of bifurcation control and the establishment of higher dimensional neural network model, which need to be further discussed.
Author Contributions
Conceptualization, B.L., M.L., C.X. and H.C.; Formal analysis, B.L. and M.L.; Investigation, B.L., M.L. and C.X.; Methodology, B.L., M.L. and C.X.; Software, B.L. and W.L.; Supervision, B.L.; Validation, M.L.; Visualization, B.L. and W.L.; Writing—original draft, B.L.; Writing—review & editing, B.L., M.L., C.X., H.C. and W.L. All authors have read and agreed to the published version of the manuscript.
Funding
Supported partly by the National Natural Science Foundation of China (12261015), Hunan Natural Science Foundation (2020JJ4516), Hunan Provincial Key Foundation of Education Department (17A181), Hunan Provincial Postgraduate Research and Innovation Project (CX20220980).
Data Availability Statement
In this study there is no data used.
Conflicts of Interest
The authors declare that there are no competing interest regarding the publication of the present paper.
References
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [PubMed]
- Kosko, B. Bidirectional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18, 49–60. [Google Scholar] [CrossRef]
- Song, Y.L.; Han, M.A.; Wei, J.J. Stability and Hopf bifurcation analysis on a simplified BAM neural network with delays. Phys. Nonlinear Phenom. 2005, 200, 185–204. [Google Scholar] [CrossRef]
- Yu, W.W.; Cao, J.D. Stability and Hopf bifurcation analysis on a four-neuron BAM neural network with time delays. Phys. Lett. A 2006, 351, 64–78. [Google Scholar] [CrossRef]
- Gopalsamy, K. Leakage delays in BAM. J. Math. Anal. Appl. 2007, 325, 1117–1132. [Google Scholar] [CrossRef]
- Cheng, Z.S.; Li, D.H.; Cao, J.D. Stability and Hopf bifurcation of a three-layer neural network model with delays. Neurocomputing 2016, 175, 355–370. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Deng, W.H.; Li, C.P.; Lu, J.H. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 2009, 59, 1810–1821. [Google Scholar] [CrossRef]
- Huang, C.D.; Cao, J.D.; Xiao, M.; Alsaadi, F.E. Controlling bifurcation in a delayed fractional predator–prey system with incommensurate orders. Appl. Math. Comput. 2017, 293, 293–310. [Google Scholar] [CrossRef]
- Xu, C.J.; He, X.F.; Li, P.L. Global existence of periodic solutions in a six-neuron BAM neural network model with discrete delays. Neurocomputing 2011, 74, 3257–3267. [Google Scholar] [CrossRef]
- Xu, C.J.; Tang, X.H.; Liao, M.X. Stability and bifurcation analysis of a six-neuron BAM neural network model with discrete delays. Neurocomputing 2011, 74, 689–707. [Google Scholar] [CrossRef]
- Xu, C.J.; Liao, M.X.; Li, P.L.; Liu, Z. Bifurcation Properties for Fractional Order Delayed BAM Neural Networks. Cogn. Comput. 2021, 13, 322–356. [Google Scholar] [CrossRef]
- Xu, C.J.; Liu, Z.X.; Yao, L.Y.; Aouiti, C. Further exploration on bifurcation of fractional-order six-neuron bi-directional associative memory neural networks with multi-delays. Appl. Math. Comput. 2021, 410, 126458. [Google Scholar] [CrossRef]
- Xu, C.J.; Liu, Z.X.; Liao, M.X.; Xiao, Q.; Yuan, S. Fractional-order bidirectional associate memory (BAM) neural networks with multiple delays: The case of Hopf bifurcation. Math. Comput. Simul. 2021, 182, 471–494. [Google Scholar] [CrossRef]
- Huang, C.D.; Li, N.; Cao, J.D.; Hayat, T. Dynamical analysis of a delayed six-neuron BAM network. Complexity 2016, 21, 9–28. [Google Scholar] [CrossRef]
- Huang, C.D.; Cao, J.D.; Alofi, A.; AI-Mazrooei, A.; Elaiw, A.M. Dynamics and control in an (n + 2)-neuron BAM network with multiple delays. Nonlinear Dyn. 2017, 1, 313–336. [Google Scholar] [CrossRef]
- Huang, C.D.; Wang, J.; Chen, X.P.; Cao, J. Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw. Off. J. Int. Neural Netw. Soc. 2021, 141, 344–354. [Google Scholar] [CrossRef]
- Huang, C.D.; Liu, H.; Chen, Y.F.; Song, F. Dynamics of a fractional-order BAM neural network with leakage delay and communication delay. Fractals 2021, 29, 2150073. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Thoiyab, N.M.; Zhu, Q.X.; Cao, J.D.; Muruganantham, P. New global asymptotic robust stability of dynamical delayed neural networks via intervalized interconnection matrices. IEEE Trans. Cybern. 2022, 52, 11794–11804. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.B.; Wang, Y.; Gunasekaran, N.; Vadivel, R. Almost Sure Consensus of Multi-Agent Systems: An Intermittent Noise. IEEE Trans. Circuits Syst. Express Briefs 2022, 69, 2897–2901. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Wang, T.S.; Wang, Y.; Cheng, Z.S. Stability and Hopf Bifurcation Analysis of a General Tri-diagonal BAM Neural Network with Delays. Neural Process. Lett. 2021, 53, 4571–4592. [Google Scholar] [CrossRef]
- Xiao, M.; Zheng, W.X.; Cao, J.D. Hopf Bifurcation of an (n + 1)-Neuron Bidirectional Associative Memory Neural Network Model with Delays. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 118–132. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).