Neutral-Type and Mixed Delays in Fractional-Order Neural Networks: Asymptotic Stability Analysis

Abstract

The lack of a conventional Lyapunov theory for fractional-order (FO) systems makes it difficult to study the dynamics of fractional-order neural networks (FONNs). Instead, the existing literature derives necessary conditions for various dynamic properties of FONNs using Halanay-type lemmas. However, when these lemmas are used, the results are frequently more conservative than those produced for integer-order neural networks (NNs). In order to provide sufficient criteria that are less conservative than those found in other research, a novel application of the Halanay-type lemma is made within this study. Thus, for extremely general FONNs containing neutral-type, time-varying, and distributed delays, sufficient conditions presented by way of linear matrix inequalities (LMIs) and algebraic inequalities are achieved. For the FO scenario, a model this broad and including so many different kinds of delays is developed for the first time. Additionally, a novel form of Lyapunov-like function is built, which results in less stringent algebraic inequalities. One of the first times in the setting of FONNs, the free-weighting matrix method is also used to further lower the conservativeness of the obtained conditions. Based on different Lyapunov-type functions, three theorems are developed regarding the asymptotic stability of the proposed networks. Three numerical simulations are used to demonstrate the theoretical developments.

1. Introduction

Several methods for determining the differentiation and integration operators of real or complex orders are examined in fractional calculus. Although fractional calculus was developed a long time ago, problems in physics and engineering have only recently been satisfactorily solved using it. Engineers and scientists in recent years have therefore come to understand that the fractional derivative may be utilized to better define several phenomena. Differential equations of the fractional order have been proved to be more effective at describing a wide variety of systems in interdisciplinary fields such as physics, heat transfer, mechanics, acoustics, electromagnetics, chemistry, biology, economy, and finance.

The infinite memory property has been proved for FO systems. Given this, an NN model would be significantly enhanced by the addition of a fractional derivative or integral, which represent the memory term. As a result, in [1], FONNs were developed. Stability and synchronization properties of different types for this sort of networks have been researched since then: asymptotic [2,3,4,5,6,7], Mittag–Leffler [8,9,10,11,12,13], or finite-time [14,15,16,17,18,19,20,21,22], and other dynamic properties, such as dissipativity [23,24,25], etc.

Time delays are present when NNs are implemented in electronics, because of the amplifiers’ limited speed of switching. The NNs might become unstable and chaotic as a result of these time delays. As a consequence, time delays are required in NN models. Time-delay NNs have grown into their own field of study, with hundreds of papers published each year. New and improved models are constantly being created. FONNs with time delays are unquestionably a good example of a model which has come to the attention of researchers lately. Therefore, in our FONN model, we add bounded time-varying delays. FONNs frequently include time-varying delays, most recently in [20,21,26,27,28,29,30,31,32,33].

We also incorporate continuously distributed delays in our model, because dispersion propagation delays can arise as a result of a distribution of conduction velocities throughout an NN implementation path. In [20,34,35,36,37], distributed delays were incorporated into FONN models.

It is also thought that past derivative knowledge affects the current state in neutral-type systems. These models are better at capturing the characteristics of brain response processes that take place in everyday life. The presence of the neutral-type delays complicates the analysis of these systems as opposed to traditional models with time-delay. Vibration masses connected to an elastic bar, population dynamics, and automatic control all require neutral-type time delays. Neutral delays may develop once NNs are implemented in VLSI circuits, which motivates greater study of NNs with such delays. Neutral-type delays have hardly been employed with FONNs. Among the papers using delays of this type are [21,38,39].

We create a highly generic FONN model which incorporates all the delays indicated before—neutral-type, time-varying, and distributed delays—by taking into consideration everything mentioned above. According to our best knowledge, this type of broad model has never before been established in the literature.

The fact that the sign does not change for the fractional derivative of a function does not always indicate its monotonicity, which is why the traditional Lyapunov theory is sadly unavailable for FO systems. As a result, several lemmas have to be used by the academic community to examine the dynamic properties of FONNs. The most popular and often used lemmas among the available options are those of Halanay-type. They generate far more conservative sufficient conditions for certain dynamics of FONNs than those typically derived for integer-order NNs as a result of how they are used. The conservativeness of the resulting conditions stems from the fact that, for FONNs with delay, there is no theorem of Lyapunov–Krasovskii-type, which suggests that the Lyapunov-type functions which may be constructed for them are substantially more constrained than those used for integer-order NNs. In this work, an unique application of the lemma of Halanay-type is made in order to build sufficient criteria with less conservatism for the proposed generic model, which are provided as LMIs and algebraic inequalities.

Thus, three different and generic functions of Lyapunov-type are formulated, one of which is applied here for the first time in the setting of delayed FONNs, to our awareness. Starting from these functions, three theorems formulate sufficient conditions given as LMIs and as algebraic inequalities, which ensure the unique equilibrium point’s asymptotic stability for the introduced model. One numerical example illustrates each of the three theorems.

The following are the key findings of this study: (1) neutral-type, time-varying, and distributed delays are incorporated in the proposed FONN model; (2) three theorems based on different functions of Lyapunov-type build sufficient conditions in the form of algebraic inequalities and LMIs, respectively, for the unique equilibrium point’s asymptotic stability for the presented model; (3) one of the formulated Lyapunov-like functions is put forward for the first time, in the setting of FONNs, in this paper; (4) to moreover decrease the conservatism of the established criteria, the free-weighting matrix method is used, when it comes to FONNs, one of the first times; (5) the methods employed are sufficiently generic to be used for the investigation of different dynamical properties of FONNs, and may also be applied to models with fewer kinds of delays.

The remaining portions of the study are organized as follows: the three theorems stated in Section 3 are proved using the lemmas and assumptions introduced in Section 2, which also introduces some fundamental terminology relevant to fractional calculus. Section 4 provides the three illustrative numerical simulations for the theorems. The article’s final observations are developed in Section 5.

Notations: $A<0$—matrix A is negative definite; ${\lambda }_{min}\left(P\right)$—smallest eigenvalue of matrix P; $A^T$—transpose of matrix A; $\left|\right|·\left|\right|$—$L_2$ norm; $|·|$—$L_1$ norm; ${\mathbb{R}}^{+}$—positive real numbers; $\mathbb{R}$—real numbers.

2. Preliminaries

The discussion of fractional calculus will begin with a few basic definitions.

Definition 1 

([40]). “The fractional integral of order α for an integrable function $x:[t_0,\infty )\to \mathbb{R}$ is defined as:

$$I_{t_0}^{\alpha }x\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_{t_0}^t{(t-s)}^{\alpha -1}x\left(s\right)ds,$$

where $t\ge t_0$, $\alpha >0$, and $\Gamma (·)$ is the gamma function, defined by:

$$\Gamma \left(\tau \right)={\int }_0^{\infty }{t}^{\tau -1}{e}^{-t}dt,$$

for $\mathrm{Re}\left(\tau \right)>0$, where $\mathrm{Re}(·)$ represents the real part.”

Definition 2 

([40]). “The fractional Caputo derivative of order α for a function $x\in {\mathcal{C}}^n([t_0,\infty ),\mathbb{R})$ is defined by:

$$D_{t_0}^{\alpha }x\left(t\right)=\frac{1}{\Gamma (n-\alpha )}{\int }_{t_0}^t\frac{x^{\left(n\right)}\left(s\right)}{{(t-s)}^{\alpha -n+1}}ds,$$

where $t\ge t_0$ and n is a positive integer, with $n-1<\alpha <n$. Moreover, when $0<\alpha <1$, we have that:

$$D_{t_0}^{\alpha }x\left(t\right)=\frac{1}{\Gamma (1-\alpha )}{\int }_{t_0}^t\frac{\dot{x}\left(s\right)}{{(t-s)}^{\alpha }}ds.”$$

The FONN system is defined as:

$$D_0^{\alpha }{x}_i\left(t\right)=-c_i{x}_i\left(t\right)+\sum _{j=1}^N{a}_{ij}{f}_j\left(x_j\left(t\right)\right)+\sum _{j=1}^N{b}_{ij}{f}_j\left(x_j(t-\kappa \left(t\right))\right)+\sum _{j=1}^N{g}_{ij}{\int }_{t-\eta }^t{f}_j\left(x_j\left(s\right)\right)ds+h_i{D}_{-\theta }^{\alpha }{x}_i(t-\theta )+I_i,$$

(1)

$\forall i=1,\dots ,N$, and $c_i\in {\mathbb{R}}^{+}$—self-feedback weight; $h_i\in \mathbb{R}$—neutral-type weight; $\theta \in {\mathbb{R}}^{+}$—neutral-type delay; $a_{ij}\in \mathbb{R}$—weight without time delay; $b_{ij}\in \mathbb{R}$—weight with time delay; $\kappa :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$—time-varying delays; $g_{ij}\in \mathbb{R}$—distributed delay weight; $\eta \in {\mathbb{R}}^{+}$—distributed delay; $x_i\left(t\right)\in \mathbb{R}$—state at t; $\forall t>0$, $f_j:\mathbb{R}\to \mathbb{R}$—nonlinear activation functions; $\forall j=1,\dots ,N$; $I_i\in \mathbb{R}$—external input.

We assume that the time-varying delays $\kappa :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ are in $\mathcal{C}({\mathbb{R}}^{+},{\mathbb{R}}^{+})$, and that there is a $\kappa >0$ which satisfies $\kappa \left(t\right)<\kappa$, $\forall t>0$. We also define $\omega :=max\{\kappa ,\eta ,\theta \}$.

For system (1), we formulate the initial conditions as:

$$x_i\left(t\right)={\zeta }_i\left(t\right),\forall t\in [-\omega ,0],$$

and ${\zeta }_i\in \mathcal{C}([-\omega ,0],\mathbb{R})$, $\forall i=1,\dots ,N$. For each $\zeta \in \mathcal{C}([-\omega ,0],{\mathbb{R}}^N)$, its norm is given by $\left|\right|\zeta \left|\right|={\sum }_{i=1}^N{sup}_{t\in [-\omega ,0]}\left|{\zeta }_i\left(t\right)\right|.$

We make the assumption that NNs (1) possess a unique equilibrium point, designated in what follows as ${\mathbf{x}}^{*}=(x_1^{*},\dots ,x_N^{*})$.

By denoting ${\chi }_i\left(t\right)=x_i\left(t\right)-x_i^{*}$, $\forall t>0$, $\forall i=1,\dots ,N$, system (1) has the following expression:

$$D_0^{\alpha }{\chi }_i\left(t\right)=-c_i{\chi }_i\left(t\right)+\sum _{j=1}^N{a}_{ij}{\overline{f}}_j\left({\chi }_j\left(t\right)\right)+\sum _{j=1}^N{b}_{ij}{\overline{f}}_j\left({\chi }_j(t-\kappa \left(t\right))\right)+\sum _{j=1}^N{g}_{ij}{\int }_{t-\eta }^t{\overline{f}}_j\left({\chi }_j\left(s\right)\right)ds+h_i{D}_{-\theta }^{\alpha }{\chi }_i(t-\theta ),$$

(2)

$\forall i=1,\dots ,N$, and ${\overline{f}}_j\left({\chi }_j\left(t\right)\right)=f_j({\chi }_j\left(t\right)+x_j^{*})-f_j\left(x_j^{*}\right)$, $\forall t>0$, $\forall j=1,\dots ,N$.

For system (2), $\forall i=1,\dots ,N$, its initial conditions are:

$${\chi }_i\left(t\right)={\psi }_i\left(t\right)={\zeta }_i\left(t\right)-x_i^{*},\forall t\in [-\omega ,0],$$

and ${\psi }_i\in \mathcal{C}([-\omega ,0],\mathbb{R})$.

System (2) can be cast in terms of matrices as:

$$D_0^{\alpha }\chi \left(t\right)=-C\chi \left(t\right)+A\overline{f}\left(\chi \left(t\right)\right)+B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)+G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds+H{D}_{-\theta }^{\alpha }\chi (t-\theta ).$$

(3)

We will make the following supposition on the activation functions:

Assumption 1 

([21]). “The activation functions $f_j$, $\forall j=1,\dots ,N$, satisfy, $\forall x,x^{\prime }\in \mathbb{R}$, the following Lipschitz conditions:

$$|f_j\left(x\right)-f_j\left(x^{\prime }\right)|\le l_j|x-x^{\prime }|,$$

where $l_j>0$, $\forall j=1,\dots ,N$, are the Lipschitz constants. We also denote $L:=\mathrm{diag}(l_1,\dots ,l_N)$.”

The following lemmas will also be employed in our proofs:

Lemma 1 

([41]). “If $x\in {\mathcal{C}}^1([t_0,\infty ),{\mathbb{R}}^N)$ and $P\in {\mathbb{R}}^{N\times N}$ is a positive definite matrix, then

$$D_{t_0}^{\alpha }\left(x^T\left(t\right)Px\left(t\right)\right)\le x^T\left(t\right)P{D}_{t_0}^{\alpha }x\left(t\right)+D_{t_0}^{\alpha }x\left(t\right){}^{T}Px\left(t\right),\forall t\ge t_0,$$

where $0<\alpha <1$.”

Lemma 2 

([35]). “Let $V:[t_0-\rho ,\infty )\to {\mathbb{R}}^{+}$ be bounded on $[t_0-\rho ,t_0]$ and continuous on $[t_0,\infty )$. If there exist ϕ, $v_h$, $\forall h=1,\dots ,m$, such that

$$D_{t_0}^{\alpha }V\left(t\right)\le -\varphi V\left(t\right)+\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega ),$$

where $0<\alpha <1$, $v_h>0$, $\varphi >{\sum }_{h=1}^m{v}_h$, $\rho =max\{{\rho }_1,\dots ,{\rho }_m\}$, then ${lim}_{t\to \infty }V\left(t\right)=0$.”

Lemma 3 

([42]). “For any vectors $X,Y\in {\mathbb{R}}^N$ and any positive definite matrix $Q\in {\mathbb{R}}^{N\times N}$, the following inequality holds:

$$X^{T}Y+Y^{T}X\le X^{T}QX+Y^T{Q}^{-1}Y."$$

Lemma 4 

([43]). “If $x\in {\mathcal{C}}^1([t_0,\infty ),{\mathbb{R}}^N)$ and $P\in {\mathbb{R}}^{N\times N}$ is a positive definite matrix, then

$$D_{t_0}^{\alpha }{\left(\right|x\left(t\right)|}^{T}P\left|x\left(t\right)\right|)\le {\left|x\left(t\right)\right|}^{T}P\mathrm{sign}\left(x\left(t\right)\right)\odot D_{t_0}^{\alpha }x\left(t\right)+D_{t_0}^{\alpha }x{\left(t\right)}^T\odot \mathrm{sign}{\left(x\left(t\right)\right)}^{T}P\left|x\left(t\right)\right|,\forall t\ge t_0,$$

where $0<\alpha <1$, and ⊙ represents the Hadamard product.”

Remark 1. 

The product of Hadamard-type is used to condense the phrasing of the inequality in Lemma 4. It is defined, for two same-dimensional matrices or vectors, as their element-wise product.

Lemma 5 

([44]). “If $x\in {\mathcal{C}}^1([t_0,\infty ),\mathbb{R})$ and $p\ge 1$, then

$$D_{t_0}^{\alpha }{\left|x\left(t\right)\right|}^p\le p{\left|x\left(t\right)\right|}^{p-1}\mathrm{sign}\left(x\left(t\right)\right)D_{t_0}^{\alpha }x\left(t\right),\forall t\ge t_0,$$

where $0<\alpha <1$.”

Lemma 6 

(Young’s inequality). Let $u>0$, $v>0$, $r>1$, $s>1$ and $\frac{1}{r}+\frac{1}{s}=1$, then the inequality

$$uv\le \frac{1}{r}{u}^r+\frac{1}{s}{v}^s,$$

holds, with equality if $u^r=v^s$.

3. Main Results

Note: $0<\alpha <1$ is used in the remaining parts of the paper.

Theorem 1. 

In the setting of Assumption 1, the equilibrium point of system (1) is asymptotically stable if there are positive definite (PD) matrix P, diagonal PD matrices $R_1$, $R_2$, any matrices $N_1$, $N_2$, $N_3$, $N_4$, $N_5$, $N_6$, and positive numbers ϕ, $v_1$, $v_2$, $v_3$, such that $\varphi >v_1+v_2+v_3$, and the subsequent LMI is true:

$$\Omega <0,$$

(4)

where

${\Omega }_{1,1}=-PC-CP+(2+\varphi )P+L^T{R}_{1}L-N_{2}C-C{N}_2^T,$${\Omega }_{1,2}=-C^T{N}_1^T-N_2,$${\Omega }_{1,6}=PA+N_{2}A+C{N}_3^T,$

${\Omega }_{1,7}=PB+N_{2}B+C{N}_4^T,$${\Omega }_{1,8}=N_{2}G+C^T{N}_5^T,$${\Omega }_{1,9}=N_{2}H+C^T{N}_6^T,$${\Omega }_{2,2}=-N_1-N^T,$

${\Omega }_{2,6}=N_{1}A+N_3^T,$${\Omega }_{2,7}=N_{1}B+N_4^T,$${\Omega }_{2,8}=N_{1}G+N_5^T,$${\Omega }_{2,9}=N_{1}H+N_6^T,$${\Omega }_{3,3}=L^T{R}_{2}L-v_{2}P,$

${\Omega }_{4,4}=-v_{3}P,$${\Omega }_{5,5}=-v_{4}P,$${\Omega }_{6,6}=-R_1-N_{3}A-A^T{N}_3^T,$${\Omega }_{6,7}=-N_{3}B-A^T{N}_4^T,$${\Omega }_{6,8}=-N_{3}G-A^T{N}_5^T,$

${\Omega }_{6,9}=-N_{3}H-A^T{N}_6^T,$${\Omega }_{7,7}=-R_2-N_{4}B-B^T{N}_4^T,$${\Omega }_{7,8}=-N_{4}G-B^T{N}_5^T,$${\Omega }_{7,9}=-N_{4}H-B^T{N}_6^T,$

${\Omega }_{8,8}=G^{T}PG-N_{5}G-G^T{N}_5^T,$${\Omega }_{8,9}=-N_{5}H-G^T{N}_6^T,$${\Omega }_{9,9}=H^{T}PH-N_{6}H-H{N}_6^T.$

Proof. 

The subsequent function is firstly defined:

$$V\left(t\right)={\chi }^T\left(t\right)P\chi \left(t\right).$$

By calculating, along the trajectories of system (1), the derivative of FO for the above-defined function, and employing Lemma 1, we obtain:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )$$

$$\begin{array}{cc}\le & D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-v_{1}V(t-\kappa \left(t\right))-v_{2}V(t-\eta )-v_{3}V(t-\theta )\hfill \\ \le & {\chi }^T\left(t\right)P{D}_0^{\alpha }\chi \left(t\right)+D_0^{\alpha }\chi {\left(t\right)}^{T}P\chi \left(t\right)+\varphi {\chi }^T\left(t\right)P\chi \left(t\right)-v_1{\chi }^T(t-\kappa \left(t\right))P\chi (t-\kappa \left(t\right))\hfill \\ & -v_2{\chi }^T(t-\eta )P\chi (t-\eta )-v_3{\chi }^T(t-\theta )P\chi (t-\theta )\hfill \\ =& {\chi }^T\left(t\right)P\left[-C\chi \left(t\right)+A\overline{f}\left(\chi \left(t\right)\right)+B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)+G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds+H{D}_{-\theta }^{\alpha }\chi (t-\theta )\right]\hfill \\ & +{\left[-C\chi \left(t\right)+A\overline{f}\left(\chi \left(t\right)\right)+B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)+G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds+H{D}_{-\theta }^{\alpha }\chi (t-\theta )\right]}^{T}P\chi \left(t\right)\hfill \\ & +\varphi {\chi }^T\left(t\right)P\chi \left(t\right)-v_1{\chi }^T(t-\kappa \left(t\right))P\chi (t-\kappa \left(t\right))-v_2{\chi }^T(t-\eta )P\chi (t-\eta )-v_3{\chi }^T(t-\theta )P\chi (t-\theta )\hfill \\ =& -{\chi }^T\left(t\right)PC\chi \left(t\right)+{\chi }^T\left(t\right)PA\overline{f}\left(\chi \left(t\right)\right)+{\chi }^T\left(t\right)PB\overline{f}\left(\chi (t-\kappa \left(t\right))\right)+{\chi }^T\left(t\right)PG{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\hfill \\ & +{\chi }^T\left(t\right)PH{D}_{-\theta }^{\alpha }\chi (t-\theta )-{\chi }^T\left(t\right)CP\chi \left(t\right)+\overline{f}{\left(\chi \left(t\right)\right)}^T{A}^{T}P\chi \left(t\right)+\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{B}^{T}P\chi \left(t\right)\hfill \\ & +{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{G}^{T}P\chi \left(t\right)+D_{-\theta }^{\alpha }\chi {(t-\theta )}^{T}HP\chi \left(t\right)+\varphi {\chi }^T\left(t\right)P\chi \left(t\right)\hfill \\ & -v_1{\chi }^T(t-\kappa \left(t\right))P\chi (t-\kappa \left(t\right))-v_2{\chi }^T(t-\eta )P\chi (t-\eta )-v_3{\chi }^T(t-\theta )P\chi (t-\theta ).\hfill \end{array}$$

(5)

From Assumption 1, we deduce the existence of PD diagonal matrices $R_1$ and $R_2$ which satisfy:

$$0\le {\chi }^T\left(t\right)L^T{R}_{1}L\chi \left(t\right)-\overline{f}{\left(\chi \left(t\right)\right)}^T{R}_1\overline{f}\left(\chi \left(t\right)\right),$$

(6)

$$0\le {\chi }^T(t-\kappa \left(t\right))L^T{R}_{2}L\chi (t-\kappa \left(t\right))-\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{R}_2\overline{f}\left(\chi (t-\kappa \left(t\right))\right).$$

(7)

Using Lemma 3, in which $Q=P^{-1}$, we have that:

$${\chi }^T\left(t\right)PG{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds+{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{G}^{T}P\chi \left(t\right)$$

$$\le {\chi }^T\left(t\right)P{P}^{-1}P\chi \left(t\right)+{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{G}^{T}PG\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right),$$

(8)

$${\chi }^T\left(t\right)PH{D}_{-\theta }^{\alpha }\chi (t-\theta )+D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{H}^{T}P\chi \left(t\right)$$

$$\le {\chi }^T\left(t\right)P{P}^{-1}P\chi \left(t\right)+D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{H}^{T}PH{D}_{-\theta }^{\alpha }\chi (t-\theta ).$$

(9)

Now, using (6)–(9) together with (5), we obtain that:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )$$

$$\begin{array}{ccc}& \le & -{\chi }^T\left(t\right)PC\chi \left(t\right)-{\chi }^T\left(t\right)CP\chi \left(t\right)+{\chi }^T\left(t\right)PA\overline{f}\left(\chi \left(t\right)\right)+\overline{f}{\left(\chi \left(t\right)\right)}^T{A}^{T}P\chi \left(t\right)\hfill \\ & & +{\chi }^T\left(t\right)PB\overline{f}\left(\chi (t-\kappa \left(t\right))\right)+\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{B}^{T}P\chi \left(t\right)+{\chi }^T\left(t\right)P\chi \left(t\right)\hfill \\ & & +{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{G}^{T}PG\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)+{\chi }^T\left(t\right)P\chi \left(t\right)\hfill \\ & & +D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{H}^{T}PH{D}_{-\theta }^{\alpha }\chi (t-\theta )+{\chi }^T\left(t\right)L^T{R}_{1}L\chi \left(t\right)-\overline{f}{\left(\chi \left(t\right)\right)}^T{R}_1\overline{f}\left(\chi \left(t\right)\right)\hfill \\ & & +{\chi }^T(t-\kappa \left(t\right))L^T{R}_{2}L\chi (t-\kappa \left(t\right))-\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{R}_2\overline{f}\left(\chi (t-\kappa \left(t\right))\right)\hfill \\ & & +\varphi {\chi }^T\left(t\right)P\chi \left(t\right)-v_1{\chi }^T(t-\kappa \left(t\right))P\chi (t-\kappa \left(t\right))-v_2{\chi }^T(t-\eta )P\chi (t-\eta )\hfill \\ & & -v_3{\chi }^T(t-\theta )P\chi (t-\theta ).\hfill \\ \hfill \end{array}$$

(10)

For any matrices $N_1$, $N_2$, $N_3$, $N_4$, $N_5$, $N_6$, the following equality holds:

$$\begin{array}{ccc}\hfill 0& =& \left[D_0^{\alpha }\chi {\left(t\right)}^T{N}_1+{\chi }^T\left(t\right)N_2-\overline{f}{\left(\chi \left(t\right)\right)}^T{N}_3-\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{N}_4-{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{N}_5\right.\hfill \\ & & \left.-D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{N}_6\right]\times \left[-D_0^{\alpha }\chi \left(t\right)-C\chi \left(t\right)+A\overline{f}\left(\chi \left(t\right)\right)+B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)+G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right.\hfill \\ & & \left.+H{D}_{-\theta }^{\alpha }\chi (t-\theta )\right]\hfill \\ & =& -D_0^{\alpha }\chi {\left(t\right)}^T{N}_1{D}_0^{\alpha }\chi \left(t\right)-D_0^{\alpha }\chi {\left(t\right)}^T{N}_{1}C\chi \left(t\right)+D_0^{\alpha }\chi {\left(t\right)}^T{N}_{1}A\overline{f}\left(\chi \left(t\right)\right)+D_0^{\alpha }\chi {\left(t\right)}^T{N}_{1}B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)\hfill \\ & & +D_0^{\alpha }\chi {\left(t\right)}^T{N}_{1}G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds+D_0^{\alpha }\chi {\left(t\right)}^T{N}_{1}H{D}_{-\theta }^{\alpha }\chi (t-\theta )\hfill \\ & & -{\chi }^T\left(t\right)N_2{D}_0^{\alpha }\chi \left(t\right)-{\chi }^T\left(t\right)N_{2}C\chi \left(t\right)+{\chi }^T\left(t\right)N_{2}A\overline{f}\left(\chi \left(t\right)\right)\hfill \\ & & +{\chi }^T\left(t\right)N_{2}B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)+{\chi }^T\left(t\right)N_{2}G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds+{\chi }^T\left(t\right)N_{2}H{D}_{-\theta }^{\alpha }\chi (t-\theta )\hfill \\ & & +\overline{f}{\left(\chi \left(t\right)\right)}^T{N}_3{D}_0^{\alpha }\chi \left(t\right)+\overline{f}{\left(\chi \left(t\right)\right)}^T{N}_{3}C\chi \left(t\right)-\overline{f}{\left(\chi \left(t\right)\right)}^T{N}_{3}A\overline{f}\left(\chi \left(t\right)\right)-\overline{f}{\left(\chi \left(t\right)\right)}^T{N}_{3}B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)\hfill \\ & & -\overline{f}{\left(\chi \left(t\right)\right)}^T{N}_{3}G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds-\overline{f}{\left(\chi \left(t\right)\right)}^T{N}_{3}H{D}_{-\theta }^{\alpha }\chi (t-\theta )\hfill \\ & & +\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{N}_4{D}_0^{\alpha }\chi \left(t\right)+\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{N}_{4}C\chi \left(t\right)-\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{N}_{4}A\overline{f}\left(\chi \left(t\right)\right)\hfill \\ & & -\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{N}_{4}B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)-\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{N}_{4}G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\hfill \\ & & -\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T{N}_{4}H{D}_{-\theta }^{\alpha }\chi (t-\theta )\hfill \\ & & +{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{N}_5{D}_0^{\alpha }\chi \left(t\right)+{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{N}_{5}C\chi \left(t\right)-{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{N}_{5}A\overline{f}\left(\chi \left(t\right)\right)\hfill \\ & & -{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{N}_{5}B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)-{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{N}_{5}G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\hfill \\ & & -{\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T{N}_{5}H{D}_{-\theta }^{\alpha }\chi (t-\theta )\hfill \\ & & +D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{N}_6{D}_0^{\alpha }\chi \left(t\right)+D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{N}_{6}C\chi \left(t\right)-D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{N}_{6}A\overline{f}\left(\chi \left(t\right)\right)\hfill \\ & & -D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{N}_{6}B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)-D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{N}_{6}G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\hfill \\ & & -D_{-\theta }^{\alpha }\chi {(t-\theta )}^T{N}_{6}H{D}_{-\theta }^{\alpha }\chi (t-\theta ).\hfill \\ \hfill \end{array}$$

(11)

Taking the transpose of (11), and summing the original and transpose identities to (10), we have:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )\le {\xi }^T\left(t\right)\Omega \xi \left(t\right),$$

where $\Omega$ is defined in (4), and

$$\begin{array}{ccc}\hfill \xi \left(t\right)& =& \left[\begin{array}{cccccc}{\chi }^T\left(t\right)& D_0^{\alpha }\chi {\left(t\right)}^T& {\chi }^T(t-\kappa \left(t\right))& {\chi }^T(t-\eta )& {\chi }^T(t-\theta )& \overline{f}{\left(\chi \left(t\right)\right)}^T\end{array}\right.\hfill \\ & & {\left.\begin{array}{ccc}\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)}^T& {\left({\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds\right)}^T& D_{-\theta }^{\alpha }\chi {(t-\theta )}^T\end{array}\right]}^T.\hfill \end{array}$$

Because, by (4), $\Omega <0$, we obtain that:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )\le 0.$$

If we apply Lemma 2, the deduction that ${lim}_{t\to \infty }V\left(t\right)=0$ can be made. Because ${\lambda }_{min}\left(P\right)$${\left|\right|\chi \left(t\right)\left|\right|}^2\le {\chi }^T\left(t\right)P\chi \left(t\right)=V\left(t\right)$, we obtain the asymptotic stability of the equilibrium point of system (1), which ends the demonstration of the theorem. □

The system (1) is taken into account for the following theorem without any neutral-type delays, leaving it with solely mixed delays.

Theorem 2. 

In the setting of Assumption 1, the equilibrium point of system (1) is asymptotically stable if there are positive numbers ${\omega }_i$, $i=1,\dots ,N$, positive numbers ϕ, $v_1$, $v_2$, such that $\varphi >v_1+v_2$, positive number $r>1$, and the following inequalities hold:

$$\begin{array}{ccc}\hfill -c_i{\omega }_{i}r+{\omega }_i(r-1){\displaystyle \sum _{j=1}^N}|a_{ij}|l_j+l_i{\displaystyle \sum _{j=1}^N}|a_{ji}|{\omega }_j+{\omega }_i(r-1){\displaystyle \sum _{j=1}^N}|b_{ij}|l_j+{\omega }_i(r-1){\displaystyle \sum _{j=1}^N}\left|g_{ij}\right|l_j\eta +\varphi {\omega }_i& <& 0,\hfill \\ \hfill l_i{\displaystyle \sum _{j=1}^N}\left|b_{ji}\right|{\omega }_j-v_1{\omega }_i& <& 0,\hfill \\ \hfill l_i{\displaystyle \sum _{j=1}^N}\left|g_{ji}\right|{\omega }_j\eta -v_2{\omega }_i& <& 0,\hfill \\ \hfill \end{array}$$

(12)

$\forall i=1,\dots ,N$.

Proof. 

The subsequent function is firstly defined:

$$V\left(t\right)=\sum _{i=1}^N{\omega }_i{\left|{\chi }_i\left(t\right)\right|}^r.$$

By calculating, along the trajectories of system (1), the derivative of FO for the above-defined function, and employing Lemma 5 and Assumption 1, we obtain:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )$$

$$\begin{array}{ccc}& \le & D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-v_{1}V(t-\kappa \left(t\right))-v_2{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}V(t+\omega )\hfill \\ & \le & {\displaystyle \sum _{i=1}^N}\left({\omega }_{i}r|{\chi }_i{\left(t\right)|}^{r-1}\mathrm{sign}\left({\chi }_i\left(t\right)\right)D_0^{\alpha }{\chi }_i\left(t\right)+\varphi {\omega }_i|{\chi }_i{\left(t\right)|}^r-v_1{\omega }_i|{\chi }_i(t-\kappa \left(t\right)){|}^r-v_2{\omega }_i{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}{\left|{\chi }_i(t+\omega )\right|}^r\right)\hfill \\ & =& {\displaystyle \sum _{i=1}^N}\left({\omega }_{i}r{\left|{\chi }_i\left(t\right)\right|}^{r-1}\mathrm{sign}\left({\chi }_i\left(t\right)\right)\left[-c_i{\chi }_i\left(t\right)+{\displaystyle \sum _{j=1}^N}{a}_{ij}{\overline{f}}_j\left({\chi }_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^N}{b}_{ij}{\overline{f}}_j\left({\chi }_j(t-\kappa \left(t\right))\right)\right.\right.\hfill \\ & & \left.\left.+{\displaystyle \sum _{j=1}^N}{g}_{ij}{\int }_{t-\eta }^t{\overline{f}}_j\left({\chi }_j\left(s\right)\right)ds\right]+\varphi {\omega }_i|{\chi }_i{\left(t\right)|}^r-v_1{\omega }_i|{\chi }_i{(t-\kappa \left(t\right))|}^r-v_2{\omega }_i{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}{\left|{\chi }_i(t+\omega )\right|}^r\right)\hfill \\ & \le & {\displaystyle \sum _{i=1}^N}\left(-c_i{\omega }_{i}r|{\chi }_i{\left(t\right)|}^r+{\omega }_{i}r|{\chi }_i{\left(t\right)|}^{r-1}{\displaystyle \sum _{j=1}^N}|a_{ij}|l_j|{\chi }_j\left(t\right)|+{\omega }_{i}r|{\chi }_i{\left(t\right)|}^{r-1}{\displaystyle \sum _{j=1}^N}|b_{ij}|l_j\left|{\chi }_j(t-\kappa \left(t\right))\right|\right.\hfill \\ & & \left.+{\omega }_{i}r|{\chi }_i{\left(t\right)|}^{r-1}{\displaystyle \sum _{j=1}^N}|g_{ij}|l_j{\int }_{t-\eta }^t|{\chi }_j\left(s\right)|ds+\varphi {\omega }_i|{\chi }_i{\left(t\right)|}^r-v_1{\omega }_i|{\chi }_i{(t-\kappa \left(t\right))|}^r-v_2{\omega }_i{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}{\left|{\chi }_i(t+\omega )\right|}^r\right)\hfill \\ & \le & {\displaystyle \sum _{i=1}^N}\left(-c_i{\omega }_{i}r|{\chi }_i{\left(t\right)|}^r+{\omega }_{i}r{\displaystyle \sum _{j=1}^N}|a_{ij}|l_j|{\chi }_i{\left(t\right)|}^{r-1}|{\chi }_j\left(t\right)|+{\omega }_{i}r{\displaystyle \sum _{j=1}^N}|b_{ij}|l_j|{\chi }_i{\left(t\right)|}^{r-1}\left|{\chi }_j(t-\kappa \left(t\right))\right|\right.\hfill \\ & & +{\omega }_{i}r{\displaystyle \sum _{j=1}^N}|g_{ij}|l_j\eta |{\chi }_i{\left(t\right)|}^{r-1}{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}|{\chi }_j(t+\omega )|+\varphi {\omega }_i|{\chi }_i{\left(t\right)|}^r-v_1{\omega }_i{\left|{\chi }_i(t-\kappa \left(t\right))\right|}^r\hfill \\ & & \left.-v_2{\omega }_i{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}{\left|{\chi }_i(t+\omega )\right|}^r\right).\hfill \\ \hfill \end{array}$$

(13)

By applying Lemma 6, we have that:

$$|{\chi }_i{\left(t\right)|}^{r-1}|{\chi }_j\left(t\right)|\le \frac{r-1}{r}|{\chi }_i{\left(t\right)|}^r+\frac{1}{r}{\left|{\chi }_j\left(t\right)\right|}^r,$$

$$|{\chi }_i{\left(t\right)|}^{r-1}|{\chi }_j(t-\kappa \left(t\right))|\le \frac{r-1}{r}|{\chi }_i{\left(t\right)|}^r+\frac{1}{r}{\left|{\chi }_j(t-\kappa \left(t\right))\right|}^r,$$

$$|{\chi }_i{\left(t\right)|}^{r-1}{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}|{\chi }_j(t+\omega )|\le \frac{r-1}{r}|{\chi }_i{\left(t\right)|}^r+\frac{1}{r}{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}{\left|{\chi }_j(t+\omega )\right|}^r,$$

$\forall i,j=1,\dots ,N$, $\forall t>0$.

Now, (13) becomes:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-{\displaystyle \sum _{h=1}^m}{v}_h{\displaystyle \underset{-{\rho }_h\le \omega \le 0}{sup}}V(t+\omega )$$

$$\begin{array}{ccc}& \le & {\displaystyle \sum _{i=1}^N}\left(-c_i{\omega }_{i}r|{\chi }_i{\left(t\right)|}^r+{\omega }_{i}r{\displaystyle \sum _{j=1}^N}\left|a_{ij}\right|l_j\left[\frac{r-1}{r}|{\chi }_i{\left(t\right)|}^r+\frac{1}{r}{\left|{\chi }_j\left(t\right)\right|}^r\right]\right.\hfill \\ & & +{\omega }_{i}r{\displaystyle \sum _{j=1}^N}\left|b_{ij}\right|l_j\left[\frac{r-1}{r}|{\chi }_i{\left(t\right)|}^r+\frac{1}{r}{\left|{\chi }_j(t-\kappa \left(t\right))\right|}^r\right]\hfill \\ & & +{\omega }_{i}r{\displaystyle \sum _{j=1}^N}\left|g_{ij}\right|l_j\eta \left[\frac{r-1}{r}|{\chi }_i{\left(t\right)|}^r+\frac{1}{r}{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}{\left|{\chi }_j(t+\omega )\right|}^r\right]\hfill \\ & & \left.+\varphi {\omega }_i|{\chi }_i{\left(t\right)|}^r-v_1{\omega }_i|{\chi }_i{(t-\kappa \left(t\right))|}^r-v_2{\omega }_i{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}{\left|{\chi }_i(t+\omega )\right|}^r\right)\hfill \\ & =& {\displaystyle \sum _{i=1}^N}\left[-c_i{\omega }_{i}r+{\omega }_i(r-1)\sum _{j=1}^N|a_{ij}|l_j+l_i{\displaystyle \sum _{j=1}^N}|a_{ji}|{\omega }_j+{\omega }_i(r-1){\displaystyle \sum _{j=1}^N}|b_{ij}|l_j+{\omega }_i(r-1){\displaystyle \sum _{j=1}^N}\left|g_{ij}\right|l_j\eta \right.\hfill \\ & & \left.+\varphi {\omega }_i\right]|{\chi }_i{\left(t\right)|}^r+\left[l_i{\displaystyle \sum _{j=1}^N}\left|b_{ji}\right|{\omega }_j-v_1{\omega }_i\right]|{\chi }_i{(t-\kappa \left(t\right))|}^r+\left[l_i{\displaystyle \sum _{j=1}^N}\left|g_{ji}\right|{\omega }_j\eta -v_2{\omega }_i\right]{\displaystyle \underset{-\eta \le \omega \le 0}{sup}}{\left|{\chi }_i(t+\omega )\right|}^r].\hfill \end{array}$$

Taking relations (12) into account, we obtain that:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-{\displaystyle \sum _{h=1}^m}{v}_h{\displaystyle \underset{-{\rho }_h\le \omega \le 0}{sup}}V(t+\omega )\le 0.$$

If we apply Lemma 2, the deduction that ${lim}_{t\to \infty }V\left(t\right)=0$ can be made. Because $\left({min}_i{\omega }_i\right)$ ${\sum }_{i=1}^N|{\chi }_i{\left(t\right)|}^r\le {\sum }_{i=1}^N{\omega }_i{\left|{\chi }_i\left(t\right)\right|}^r=V\left(t\right)$, we obtain the asymptotic stability of the equilibrium point of system (1), which ends the demonstration of the theorem. □

The system (1) is taken into account for the following theorem with no distributed nor neutral-type delays, leaving the system with just time-varying delays.

Theorem 3. 

In the setting of Assumption 1, the equilibrium point of system (1) is asymptotically stable if there are PD matrix P, diagonal PD matrices $R_1$, $R_2$, and positive numbers ϕ, $v_1$, such that $\varphi >v_1$, and the following LMI holds:

$$\Omega <0,$$

(14)

where

${\Omega }_{1,1}=-PC-CP+\varphi P+L^T{R}_{1}L,$${\Omega }_{1,3}=P\left|A\right|,$${\Omega }_{1,4}=P\left|B\right|,$${\Omega }_{2,2}=L^T{R}_{2}L-v_{1}P,$${\Omega }_{3,3}=-R_1,$${\Omega }_{4,4}=-R_2.$

Proof. 

The subsequent function is firstly defined:

$$V\left(t\right)={\left|\chi \left(t\right)\right|}^{T}P\left|\chi \left(t\right)\right|.$$

By calculating, along the trajectories of system (1), the derivative of FO for the above-defined function, and employing Lemma 4, we obtain:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )$$

$$\begin{array}{ccc}& \le & D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-v_{1}V(t-\kappa \left(t\right))\hfill \\ & \le & {\left|\chi \left(t\right)\right|}^{T}P\mathrm{sign}\left(\chi \left(t\right)\right)\odot D_0^{\alpha }\chi \left(t\right)+D_0^{\alpha }\chi {\left(t\right)}^T\odot \mathrm{sign}{\left(\chi \left(t\right)\right)}^{T}P\left|\chi \left(t\right)\right|\hfill \\ & & +{\varphi \left|\chi \left(t\right)\right|}^{T}P\left|\chi \left(t\right)\right|-v_1{\left|\chi (t-\kappa \left(t\right))\right|}^{T}P\left|\chi (t-\kappa \left(t\right))\right|\hfill \\ & =& {\left|\chi \left(t\right)\right|}^{T}P\mathrm{sign}\left(\chi \left(t\right)\right)\odot \left[-C\chi \left(t\right)+A\overline{f}\left(\chi \left(t\right)\right)+B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)\right]\hfill \\ & & +{\left[-C\chi \left(t\right)+A\overline{f}\left(\chi \left(t\right)\right)+B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)\right]}^T\odot \mathrm{sign}{\left(\chi \left(t\right)\right)}^{T}P\left|\chi \left(t\right)\right|\hfill \\ & & +{\varphi \left|\chi \left(t\right)\right|}^{T}P\left|\chi \left(t\right)\right|-v_1{\left|\chi (t-\kappa \left(t\right))\right|}^{T}P\left|\chi (t-\kappa \left(t\right))\right|\hfill \\ & \le & -{\left|\chi \left(t\right)\right|}^{T}PC\left|\chi \left(t\right)\right|+{\left|\chi \left(t\right)\right|}^{T}P\left|A\right||\overline{f}{\left(\chi \left(t\right)\right)|+|\chi \left(t\right)|}^{T}P\left|B\right||\overline{f}\left(\chi (t-\kappa \left(t\right))\right)|\hfill \\ & & -{\left|\chi \left(t\right)\right|}^{T}CP\left|\chi \left(t\right)\right|+|\overline{f}{\left(\chi \left(t\right)\right)|}^T{\left|A\right|}^{T}P\left|\chi \left(t\right)\right|\hfill \\ & & +|\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)|}^T{\left|B\right|}^{T}P\left|\chi \left(t\right)\right|\hfill \\ & & +{\varphi \left|\chi \left(t\right)\right|}^{T}P\left|\chi \left(t\right)\right|-v_1{\left|\chi (t-\kappa \left(t\right))\right|}^{T}P\left|\chi (t-\kappa \left(t\right))\right|.\hfill \\ \hfill \end{array}$$

(15)

From Assumption 1, we deduce the existence of PD diagonal matrices $R_1$ and $R_2$ which satisfy:

$$0\le {\left|\chi \left(t\right)\right|}^T{L}^T{R}_{1}L\left|\chi \left(t\right)\right|-|\overline{f}{\left(\chi \left(t\right)\right)|}^T{R}_1\left|\overline{f}\left(\chi \left(t\right)\right)\right|,$$

(16)

$$0\le {\left|\chi (t-\kappa \left(t\right))\right|}^T{L}^T{R}_{2}L\left|\chi (t-\kappa \left(t\right))\right|-|\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)|}^T{R}_2\left|\overline{f}\left(\chi (t-\kappa \left(t\right))\right)\right|.$$

(17)

Now, using (16) and (17) together with (15), we obtain that:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )$$

$$\begin{array}{ccc}& \le & -{\left|\chi \left(t\right)\right|}^{T}PC\left|\chi \left(t\right)\right|-{\left|\chi \left(t\right)\right|}^{T}CP\left|\chi \left(t\right)\right|+{\left|\chi \left(t\right)\right|}^{T}P\left|A\right||\overline{f}\left(\chi \left(t\right)\right)|+|\overline{f}{\left(\chi \left(t\right)\right)|}^T{\left|A\right|}^{T}P\left|\chi \left(t\right)\right|\hfill \\ & & +{\left|\chi \left(t\right)\right|}^{T}P\left|B\right||\overline{f}\left(\chi (t-\kappa \left(t\right))\right)|+|\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)|}^T{\left|B\right|}^{T}P\left|\chi \left(t\right)\right|\hfill \\ & & +{\left|\chi \left(t\right)\right|}^T{L}^T{R}_{1}L\left|\chi \left(t\right)\right|-|\overline{f}{\left(\chi \left(t\right)\right)|}^T{R}_1\left|\overline{f}\left(\chi \left(t\right)\right)\right|\hfill \\ & & +{\left|\chi (t-\kappa \left(t\right))\right|}^T{L}^T{R}_{2}L\left|\chi (t-\kappa \left(t\right))\right|-|\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)|}^T{R}_2\left|\overline{f}\left(\chi (t-\kappa \left(t\right))\right)\right|\hfill \\ & & +{\varphi \left|\chi \left(t\right)\right|}^{T}P\left|\chi \left(t\right)\right|-v_1{\left|\chi (t-\kappa \left(t\right))\right|}^{T}P\left|\chi (t-\kappa \left(t\right))\right|.\hfill \\ \hfill \end{array}$$

(18)

Relation (18) can now be recast in the following form:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )\le {\xi }^T\left(t\right)\Omega \xi \left(t\right),$$

where $\Omega$ is defined in (14), and

$$\xi \left(t\right)={\left[\begin{array}{cccc}{\left|\chi \left(t\right)\right|}^T& {\left|\chi (t-\kappa \left(t\right))\right|}^T& |\overline{f}{\left(\chi \left(t\right)\right)|}^T& |\overline{f}{\left(\chi (t-\kappa \left(t\right))\right)|}^T\end{array}\right]}^T.$$

Because, by (14), $\Omega <0$, we obtain the following:

$$D_0^{\alpha }V\left(t\right)+\varphi V\left(t\right)-\sum _{h=1}^m{v}_h\underset{-{\rho }_h\le \omega \le 0}{sup}V(t+\omega )\le 0.$$

By applying Lemma 2, we deduce that ${lim}_{t\to \infty }V\left(t\right)=0$. Because ${\lambda }_{min}{\left(P\right)\left|\right|\chi \left(t\right)\left|\right|}^2\le {\left|\chi \left(t\right)\right|}^{T}P\left|\chi \left(t\right)\right|=V\left(t\right)$, we obtain that the equilibrium point of system (1) is asymptotically stable, which concludes the theorem’s demonstration. □

4. Numerical Examples

In this section, numerical simulations will be provided in order to illustrate each of Theorems 1–3.

For all the examples, the fractional order is taken to be $\alpha =0.75$.

Example 1. 

For the first example, consider the FONN with neutral-type delay and mixed delays given by:

$$D_0^{\alpha }x\left(t\right)=-Cx\left(t\right)+A\overline{f}\left(x\left(t\right)\right)+B\overline{f}\left(x(t-\kappa \left(t\right))\right)+G{\int }_{t-\eta }^t\overline{f}\left(x\left(s\right)\right)ds+H{D}_{-\theta }^{\alpha }x(t-\theta )+I,$$

(19)

where

$$C=\left[\begin{array}{cc}3& 0\\ 0& 4\end{array}\right],A=\left[\begin{array}{cc}0.1& 0.2\\ 0.2& -0.1\end{array}\right],B=\left[\begin{array}{cc}0.1& 0.1\\ -0.1& 0.1\end{array}\right],G=\left[\begin{array}{cc}-0.01& 0.01\\ -0.01& -0.01\end{array}\right],$$

$$H=\left[\begin{array}{cc}0.01& 0\\ 0& 0.02\end{array}\right],f_j\left(x\right)=\frac{1}{25}\frac{1}{1+e^{-x}},\forall j=1,2,\forall x\in \mathbb{R},$$

and $\theta =0.07$, $\kappa \left(t\right)=0.1|sint|$, and $\eta =0.05$. Thus, $\kappa =0.1$ and $\omega =max\{\kappa ,\eta ,\theta \}=0.1$. We can clearly see from their definitions that the activation functions satisfy the Lipschitz condition in Assumption 1, and $L=\left[\begin{array}{cc}0.01& 0\\ 0& 0.01\end{array}\right]$. If we denote by ${\mathbf{x}}^{*}=(x_1^{*},x_2^{*})$ the unique equilibrium of system (19) and by ${\chi }_i\left(t\right)=x_i\left(t\right)-x_i^{*}$, $\forall t>0$, $\forall i=1,2$, system (19) is transformed as:

$$D_0^{\alpha }\chi \left(t\right)=-C\chi \left(t\right)+A\overline{f}\left(\chi \left(t\right)\right)+B\overline{f}\left(\chi (t-\kappa \left(t\right))\right)+G{\int }_{t-\eta }^t\overline{f}\left(\chi \left(s\right)\right)ds+H{D}_{-\theta }^{\alpha }\chi (t-\theta ),$$

(20)

where ${\overline{f}}_j\left({\chi }_j\left(t\right)\right)=f_j({\chi }_j\left(t\right)+x_j^{*})-f_j\left(x_j^{*}\right)$, $\forall t>0$, $\forall j=1,2$. It can be verified that the conditions of Theorem 1 hold for $\varphi =0.1$, $v_1=v_2=v_3=v_4=0.02$, $R_1=\mathrm{diag}(1.0185,1.0236)$, $R_2=\mathrm{diag}(1.0079,1.0079)$ (in order not to clutter the article, we do not provide the values for the other matrices). This means that, based on Theorem 1, the unique equilibrium point of system (19) is asymptotically stable.

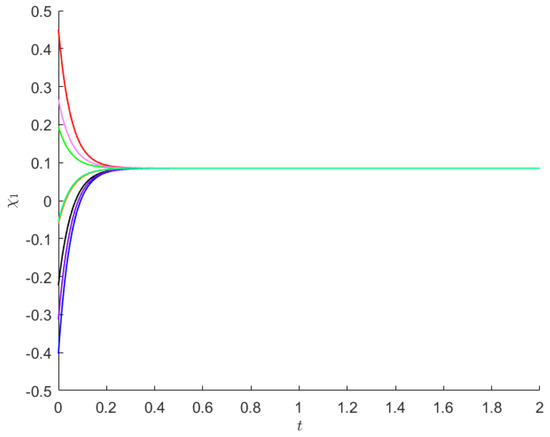
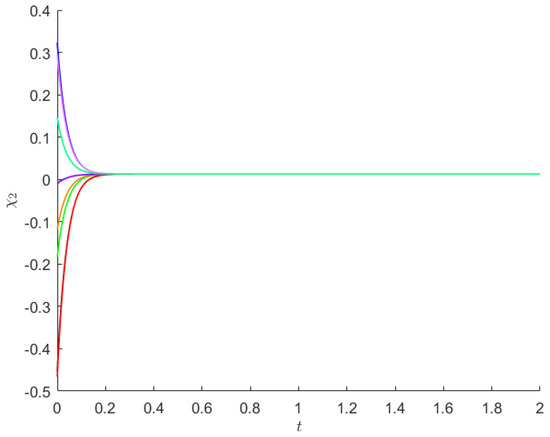
Starting from 8 initial points, the state trajectories of ${\chi }_1$ and ${\chi }_2$ of system (19) are presented in Figure 1 and Figure 2.

Example 2. 

The second example uses the same system (19), but does not include a neutral-type delay. The parameters are as follows:

$$C=\left[\begin{array}{cc}0.7& 0\\ 0& 0.8\end{array}\right],A=\left[\begin{array}{cc}0.01& -0.01\\ 0.02& -0.01\end{array}\right],B=\left[\begin{array}{cc}-0.02& 0.01\\ 0.01& 0.02\end{array}\right],G=\left[\begin{array}{cc}0.01& -0.01\\ 0.02& -0.01\end{array}\right],$$

$$f_j\left(x\right)=\frac{1}{1+e^{-x}},\forall j=1,2,\forall x\in \mathbb{R},$$

and $\kappa \left(t\right)=0.1|cost|$, and $\eta =0.05$. Thus, $\kappa =0.1$, and $\omega =max\{\kappa ,\eta \}=0.1$. Again, the activation functions satisfy Assumption 1, and $L=\left[\begin{array}{cc}0.25& 0\\ 0& 0.25\end{array}\right]$. If $r=1.5$, ${\omega }_1={\omega }_2=1$, $\varphi =0.5$, $v_1=v_2=0.125$, it is simple to confirm that the requirements of Theorem 2 are met. Thus, Theorem 2 allows us to infer the asymptotic stability of the unique equilibrium of system (19), with the parameters given above.

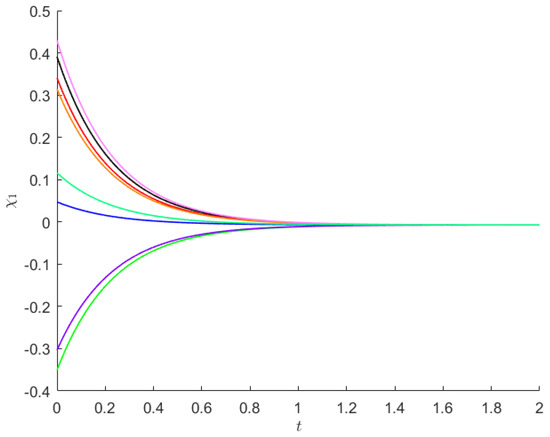
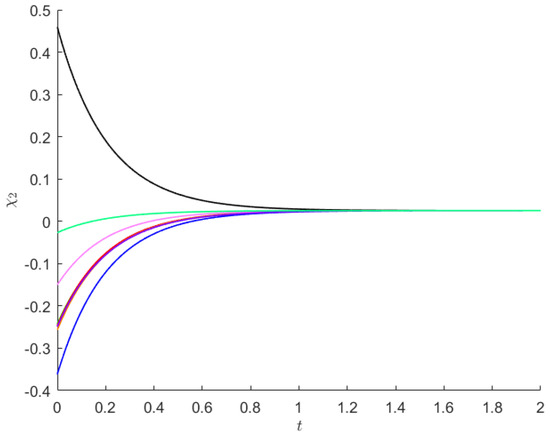
Starting from 8 initial points, the state trajectories of ${\chi }_1$ and ${\chi }_2$ of system (19) are presented in Figure 3 and Figure 4.

Example 3. 

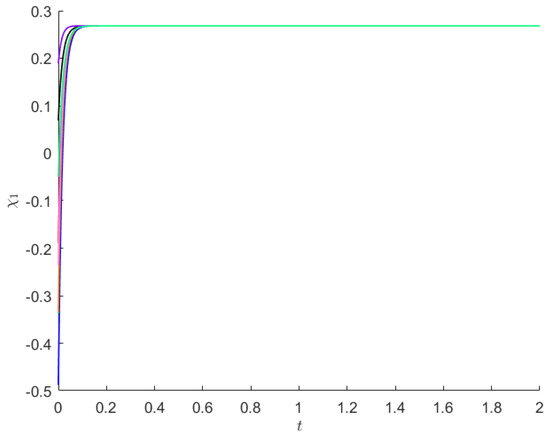
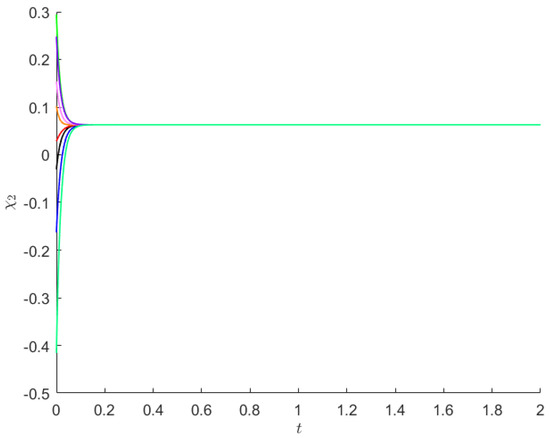
The last example uses the same system (19) only with time-varying delays. Its parameters are:

$$C=\left[\begin{array}{cc}10& 0\\ 0& 9\end{array}\right],A=\left[\begin{array}{cc}1& 2\\ 2& -1\end{array}\right],B=\left[\begin{array}{cc}1& 1\\ -1& 1\end{array}\right],$$

$$f_j\left(x\right)=\frac{1}{25}\frac{1}{1+e^{-x}},\forall j=1,2,\forall x\in \mathbb{R},$$

and $\kappa \left(t\right)=0.2|cost|$. Now, $\kappa =0.2$, and $\omega =\kappa =0.2$. The activation functions satisfy Assumption 1, and we have that $L=\left[\begin{array}{cc}0.01& 0\\ 0& 0.01\end{array}\right]$. The requirements of Theorem 3 are met for $\varphi =0.001$, $v_1=0.0005$, $P=\left[\begin{array}{cc}0.1636& -0.0013\\ -0.0013& 0.1765\end{array}\right]$, $R_1=\mathrm{diag}(1.0293,1.0327)$, $R_2=\mathrm{diag}(0.7572,0.7872)$, which means that the unique equilibrium point of system (19) having the above parameters is asymptotically stable.

Starting from 8 initial points, the state trajectories of ${\chi }_1$ and ${\chi }_2$ of system (19) are presented in Figure 5 and Figure 6.

5. Conclusions

The asymptotic stability of FONNs with neutral-type, time-varying, and distributed delays was deduced using three sufficient conditions, which were described in terms of algebraic inequalities and LMIs. To our knowledge, this is the first time that a broad model of this kind has been put forward. The delayed FONNs configuration saw the introduction of a brand-new sort of function of Lyapunov-type, and this is one of the first instances the free-weighting matrix method has been applied to this kind of network. The conservatism of the derived criteria is greatly reduced by both of these contributions. The innovative approach in which the lemma of Halanay-type is used for FO systems also helps to reduce conservatism. Each of the three theorems was illustrated by means of a numerical example.

The techniques presented in this study are broad, and may be utilized to deduce sufficient conditions for the asymptotic stability of NN models with impulsive effects, Markov jump parameters, or reaction–diffusion terms, and also to address other dynamic properties, such as synchronization, dissipativity, or passivity. These developments constitute promising future work endeavors.