Abstract
In this paper, we study the numerical solution of fractional Jaulent–Miodek equations with the help of two modified methods: coupled fractional variational iteration transformation technique and the Adomian decomposition transformation technique. The Jaulent–Miodek equation has applications in several related fields of physics, including control theory of dynamical systems, anomalous transport, image and signal processing, financial modelings, nanotechnology, viscoelasticity, nanoprecipitate growth in solid solutions, random walk, modeling for shape memory polymers, condensed matter physics, fluid mechanics, optics and plasma physics. The results are presented as a series of quickly converging solutions. Analytical solutions have been performed in absolute error to confirm the proposed methodologies are trustworthy and accurate. The generated solutions are visually illustrated to guarantee the validity and applicability of the taken into consideration algorithm. The study’s findings show that, compared to alternative analytical approaches for analyzing fractional non-linear coupled Jaulent–Miodek equations, the Adomian decomposition transform method and the variational iteration transform method are computationally very efficient and accurate.
1. Introduction
In recent years, fractional differential equations have risen to prominence due to their proved usefulness in a number of seemingly unrelated scientific and engineering fields. For example, the nonlinear oscillations of an earthquake can be characterized by a fractional derivative, and the fractional derivative of the traffic fluid dynamics model can solve the insufficiency resulting from the assumption of continuous traffic flows [1,2]. Numerous chemical processes, mathematical biology, engineering, and scientific problems [3,4,5,6] are also modeled with fractional differential problems. Nonlinear partial differential equations (NPDEs) characterize a variety of physical, biological, and chemical phenomena. Current research focuses on developing precise traveling wave solutions for such equations. Exact solution replies help scientists understand the complicated physical phenomena and dynamical processes portrayed by NPDEs [7,8,9]. In the past four decades, numerous important methodologies for attaining accurate solutions to NPDEs have been proposed [10,11]. The Jaulent–Miodek equation was developed in 1979 by Jaulent and Miodek as an application to energy-dependent potentials [12,13]. The JM equation first came into existence in several related fields of physics, including classical dynamics [14], condensed material physics [15], optics [16], and fluid mechanics [17]. The goal of this study is to investigate the numerical results of the following difficult and anomalous physical model,
With initial conditions
where is the arbitrary constant and . Numerous writers have looked at the system of nonlinear JM equation in the past using various methods, including the Sumudu transformation homotopy perturbation technique (STHPM) [18], Hermite Wavelets and OHAM [19], Invariant subspace technique [20], and many others [21,22,23]. On the other hand, new methods for explaining nonlinear differential systems with fractional orders have been discovered throughout the past three decades, along with novel computer algorithms and symbolic programming. Fundamental significance is attached to the nonlinear fractional differential equations analytical and numerical solutions. Since nonlinear fractional differential equations are used to mathematically model most complex processes to solve both linear and nonlinear differential equations, Keskin and Oturance [24] devised the Reduced Differential Transform Method (RDTM) in 2009 [25].
2. Basic Preliminaries
In this section, we give some definitions of fractional calculus used in our present work.
Definition 1.
The derivative of order fractional in Caputo sense is defined as
Definition 2.
For a function , the Yang transform is denoted by or and is defined as
and inverse transform is as
Laplace–Yang duality Property:
If the Laplace Transform of the function is , then
Substitute in the integral on right-hand side we get
We get,
Additionally, from the above equations, we get
Definition 3.
The Yang transformation in terms of fractional-order derivative is as
Definition 4.
The Yang transform in terms of nth derivative is as
3. The Methodology of Adomian Decomposition Transform Method
In this section, the Adomian decomposition transform method solution system for fractional partial differential fractional equations.
with initial conditions
where the Caputo fractional derivative of order , , and , are linear and non-linear functions, respectively, and , are source operators.
The Yang transformation is applied to Equation (8), we have
Using the Yang transform differentiation property, we get
ADTM defines the result of infinite series and ,
Adomian polynomials decomposition of nonlinear terms of and are described as
All forms of nonlinearity the Adomian polynomials can be represented as
Putting Equations (12) and (14) into Equation (11), gives
Using the inverse Yang transform of Equation (15), we get
we define the following terms,
the general for , is given by
4. The Producer of Yang Variational Iteration Method
In this section explain the Yang variational iteration method the solution of FPDEs.
with initial conditions
where is the Caputo fractional derivative of order , , and , are linear and non-linear functions, respectively, and , are source operators.
The Yang transformation is applied to Equation (18),
Using the differentiation property Yang transform, we get
The procedure iteration method is define as
A Lagrange multiplier as
the inverse Yang transformation , the iteration method Equation (22) can be given as
the initial iteration can be find as
5. Implementation of Techniques
Problem 1.


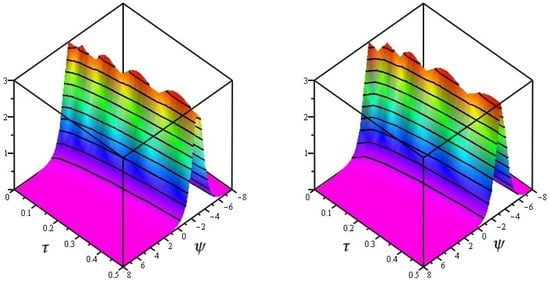
Consider the fractional-order non-linear Jaulent–Miodek equation is given as
With initial conditions
Taking Yang transform of (26),
Using inverse Yang transformation, we get
Applying the Adomian procedure, we have
The nonlinear terms find with the help of Adomain polynomials
For
for
for
The ADTM solution is
The approximate solution by VITM
Apply the iteration technique, we have
where
For
The exact solution of Equation (8) at ,
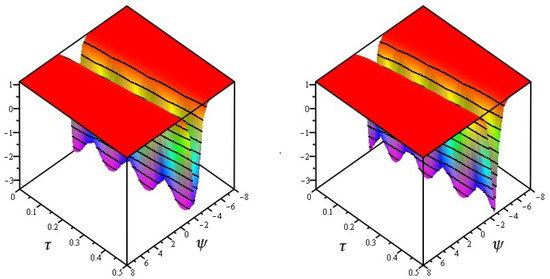
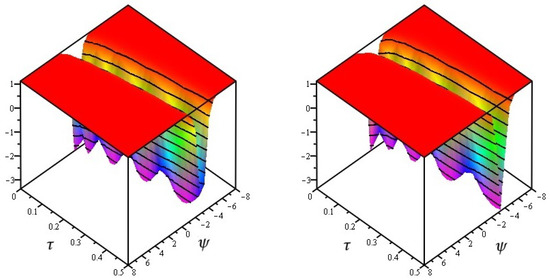
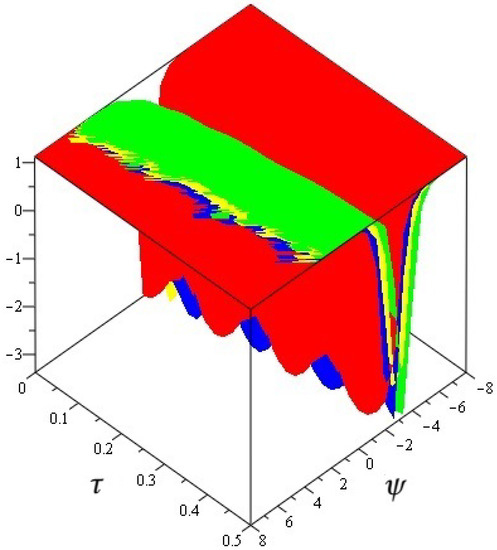
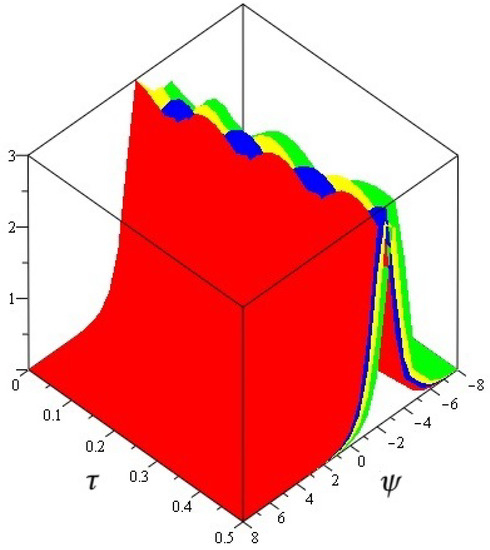
Figure 1, exact and analytical solution of at and and Figure 2, analytical solutions of at and . Figure 3, the different fractional-order of ϖ of . In Table 1 and Table 2 the different fractional-order of ℘ of and of Problem 1.

Figure 1.
Exact and analytical solution of at and .

Figure 2.
The analytical solutions of at and .

Figure 3.
The different fractional-order of of .

Table 1.
The different fractional-order of ℘ at of of Problem 1.

Table 2.
The different fractional-order of ℘ at Problem 1.
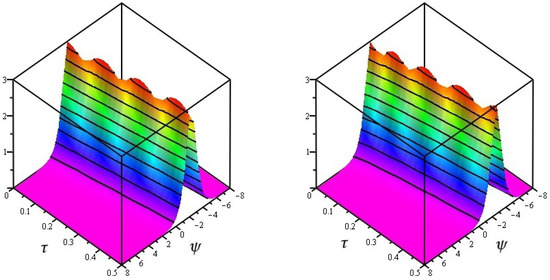
Figure 4, exact and analytical solution of at and and Figure 5, the analytical solutions of at and . Figure 6, the different fractional-order of ϖ of .

Figure 4.
Exact and analytical solution of at and .

Figure 5.
The analytical solutions of at and .

Figure 6.
The different fractional-order of of .
6. Conclusions
In this paper, we have successfully applied two modified methods to investigate the numerical results of fractional system Jaulent–Miodek equations connected with energy dependent Schrodinger potential. Accord between the obtained numerical solution by ADTM and VITM with exact results appears very appreciable by way of illustrative solutions. The suggested algorithms are simple to implement, efficient for achieving the solutions of nonlinear coupled JM equations of fractional order. In addition, both the ADTM and the VITM yield convergent series solutions with easily determinable components without using perturbation, linearization, or limiting assumptions. We can draw a final conclusion that the suggested methods are extremely analytical and more reliable, and that they can be used to analyze nonlinear issues that develop in complicated processes.
Author Contributions
Methodology, S.A. and M.M.A.-S.; Software, S.A.; Validation, R.S.; Investigation, M.M.A.-S. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded by Deputy for Research & Innovation, Ministry of Education through Initiative of Institutional Funding at University of Ha’il-Saudi Arabia through project number IFP-22 020.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Said, L.A.; Radwan, A.G.; Madian, A.H.; Soliman, A.M. Three fractional-order-capacitors-based oscillators with controllable phase and frequency. J. Circuits Syst. Comput. 2017, 26, 1750160. [Google Scholar] [CrossRef]
- Said, L.A.; Madian, A.H.; Radwan, A.G.; Soliman, A.M. Fractional order oscillator with independent control of phase and frequency. In 2014 2nd International Conference on Electronic Design (ICED). In Proceedings of the 2014 2nd International Conference on Electronic Design (ICED), Penang, Malaysia, 19–21 August 2014; pp. 224–229. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Sabatier, J.A.T.M.J.; Agrawal, O.P.; Machado, J.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007; p. 9. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Method; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Debnath, L. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 54, 3413–3442. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Alshehry, A.S.; Nonlaopon, K.; Shah, R.; Ababneh, O.Y. Fractional view analysis of delay differential equations via numerical method. AIMS Math. 2022, 7, 20510–20523. [Google Scholar] [CrossRef]
- Mukhtar, S.; Shah, R.; Noor, S. The Numerical Investigation of a Fractional-Order Multi-Dimensional Model of Navier-Stokes Equation via Novel Techniques. Symmetry 2022, 14, 1102. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Alshehry, A.S.; Nonlaopon, K.; Shah, R.; Ababneh, O.Y. Approximate analytical solution of time-fractional vibration equation via reliable numerical algorithm. AIMS Math. 2022, 7, 19739–19757. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Kai, Y.; Chen, S.; Zhang, K.; Yin, Z. Exact solutions and dynamic properties of a nonlinear fourth-order time-fractional partial differential equation. Waves Random Complex Media 2022, 1–12. [Google Scholar] [CrossRef]
- Jaulent, M.; Miodek, I. Nonlinear evolution equations associated with energy-dependent Schrodinger potentials. Lett. Math. Phys. 1976, 1, 243–250. [Google Scholar] [CrossRef]
- Jaulent, M. Inverse scattering problems in absorbing media. J. Math. Phys. 1976, 17, 1351–1360. [Google Scholar] [CrossRef]
- Hong, T.; Wang, Y.Z.; Huo, Y.S. Bogoliubov quasiparticles carried by dark solitonic excitations in non-uniform Bose-Einstein condensates. Chin. Phys. Lett. 1998, 15, 550–552. [Google Scholar] [CrossRef]
- Ma, W.X.; Li, C.X.; He, J. A second Wronskian formulation of the Boussinesq equation. Nonlinear Anal. Theory Methods Appl. 2009, 70, 4245–4258. [Google Scholar] [CrossRef]
- Jie-Fang, Z. Multiple soliton solutions of the dispersive long-wave equations. Chin. Phys. Lett. 1999, 16, 4. [Google Scholar]
- Das, G.C.; Sarma, J.; Uberoi, C. Explosion of a soliton in a multicomponent plasma. Phys. Plasmas 1997, 4, 2095–2100. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. Nonlinear Fractional Jaulent-Miodek and Whitham-Broer-Kaup Equations within Sumudu Transform. Abstr. Appl. Anal. 2013, 2013, 160681. [Google Scholar] [CrossRef]
- Gupta, A.K.; Ray, S.S. An investigation with Hermite Wavelets for accurate solution of fractional Jaulent-Miodek equation associated with energy-dependent Schrodinger potential. Appl. Math. Comput. 2015, 270, 458–471. [Google Scholar] [CrossRef]
- Majlesi, A.; Ghehsareha, H.R.; Zaghian, A. On the fractional Jaulent-Miodek equation associated with energy-dependent Schrodinger potential: Lie symmetry reductions, explicit exact solutions and conservation laws. Eur. Phys. J. Plus 2015, 132, 1–13. [Google Scholar] [CrossRef]
- Yildirim, A.; Kelleci, A. Numerical simulation of the Jaulent-Miode equation by He’s homotopy perturbation method. World Appl. Sci. J. 2009, 7, 84–89. [Google Scholar]
- He, J.H.; Zhang, L.N. Generalized solitary solution and compacton-like solution of the Jaulent- Miodek equations using the Exp-function method. Phys. Lett. A 2008, 372, 1044–1047. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Domairry, G.; Dinarvand, S. The homotopy analysis method for explicit analytical solutions of Jaulent-Miodek equations. Numer. Meth. Partial Differ. Equ. 2009, 25, 430–439. [Google Scholar] [CrossRef]
- Keskin, Y.; Oturanc, G. Reduced differential transform method for partial differential equations. Int. J. Nonlienar Sci. Numer. Simul. 2009, 10, 741–749. [Google Scholar] [CrossRef]
- Saravanan, A.; Magesh, N. An efficient computational technique for solving the Fokker-Planck equation with space and time fractional derivatives. J. King Saud Univ.-Sci. 2016, 28, 160–166. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).