Higher-Order Dispersive and Nonlinearity Modulations on the Propagating Optical Solitary Breather and Super Huge Waves
Abstract
1. Introduction
2. Optical Solitary Solution
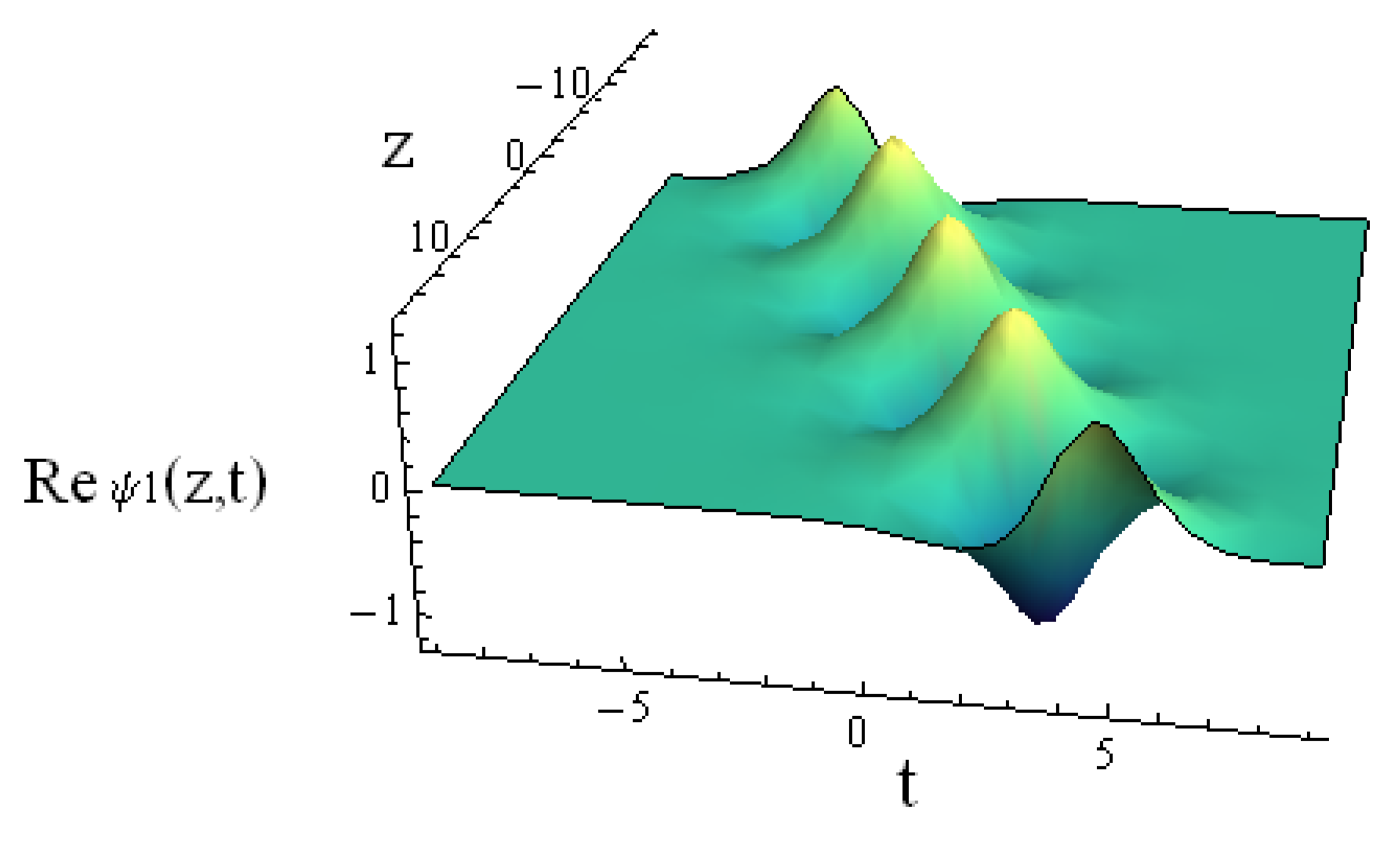
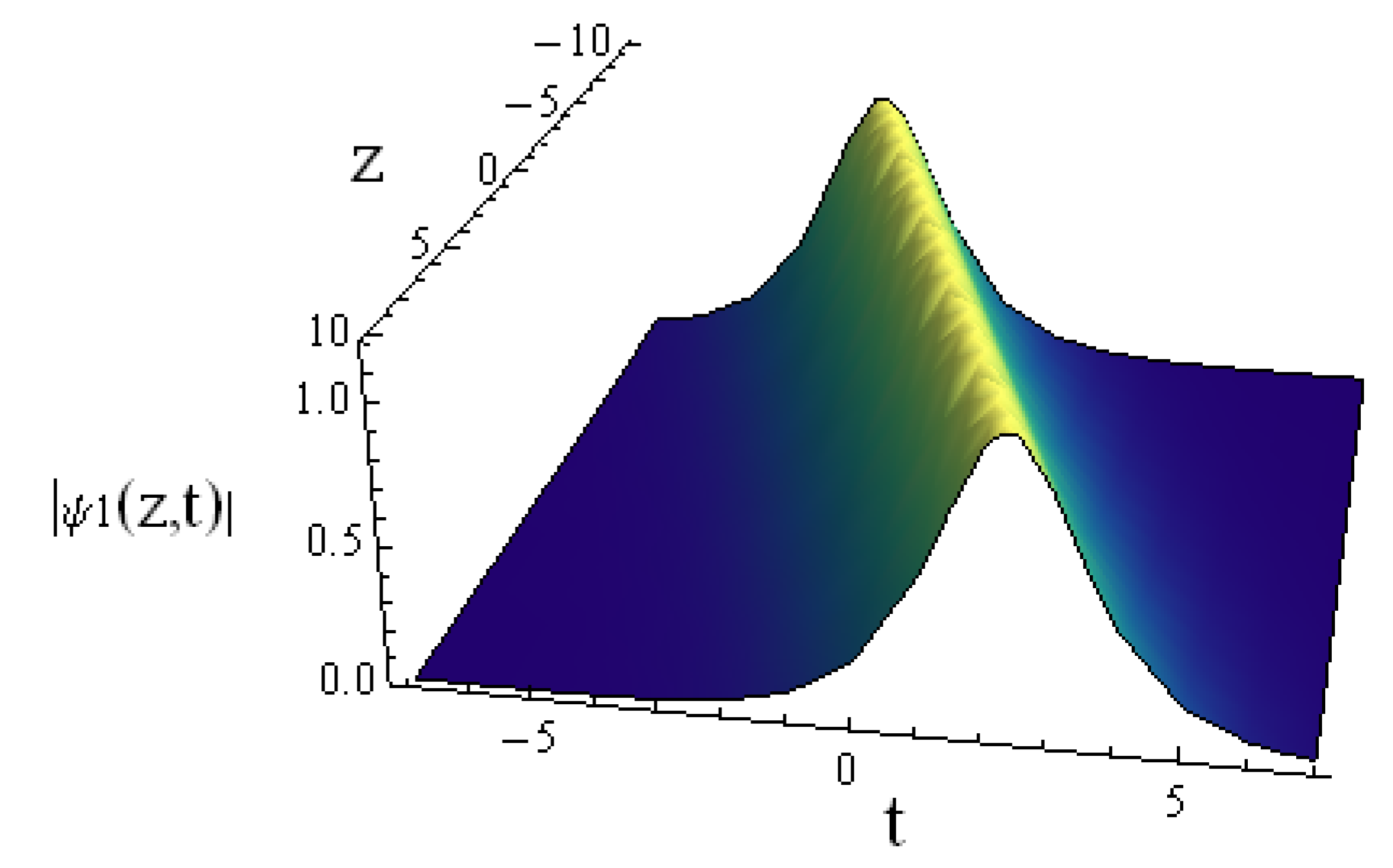
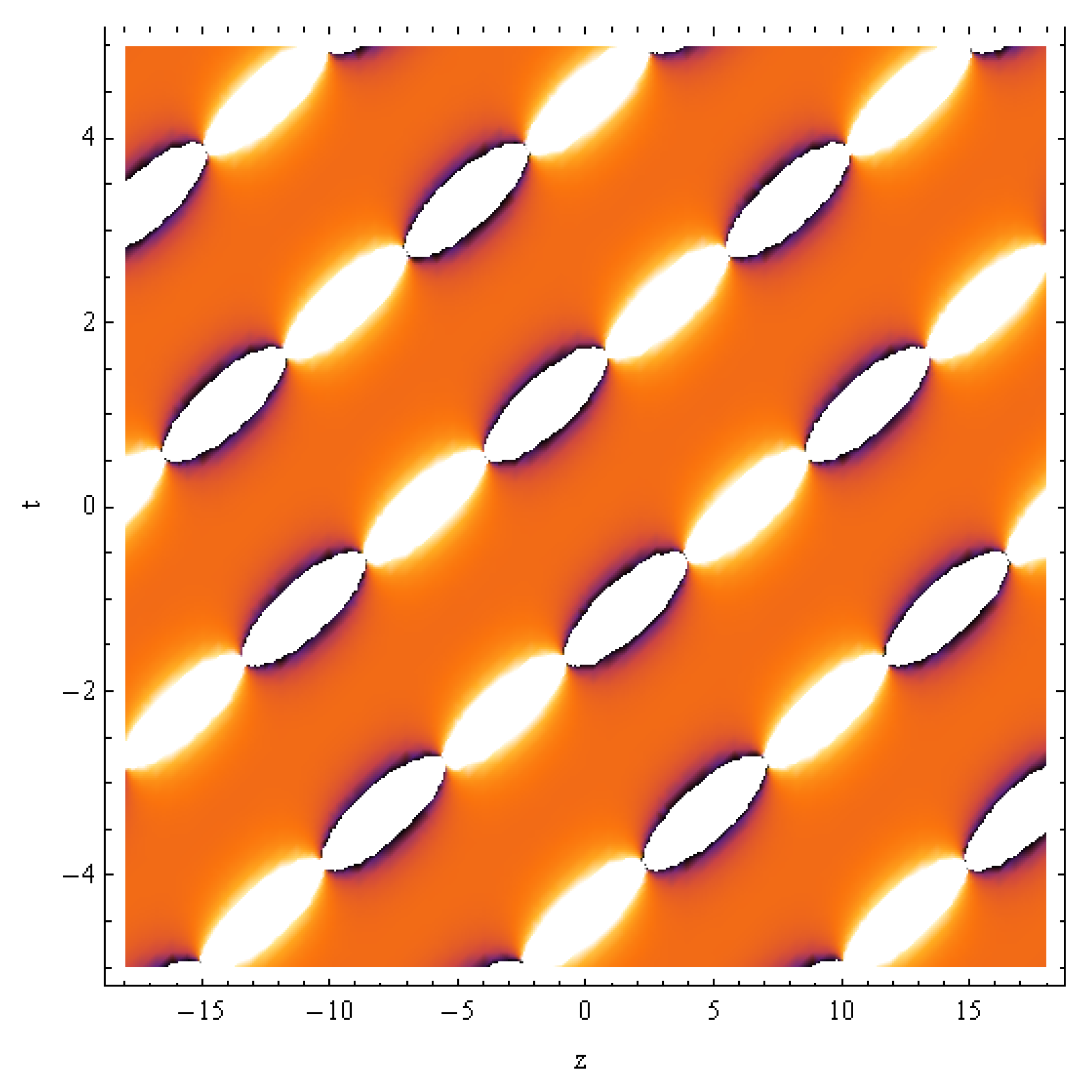
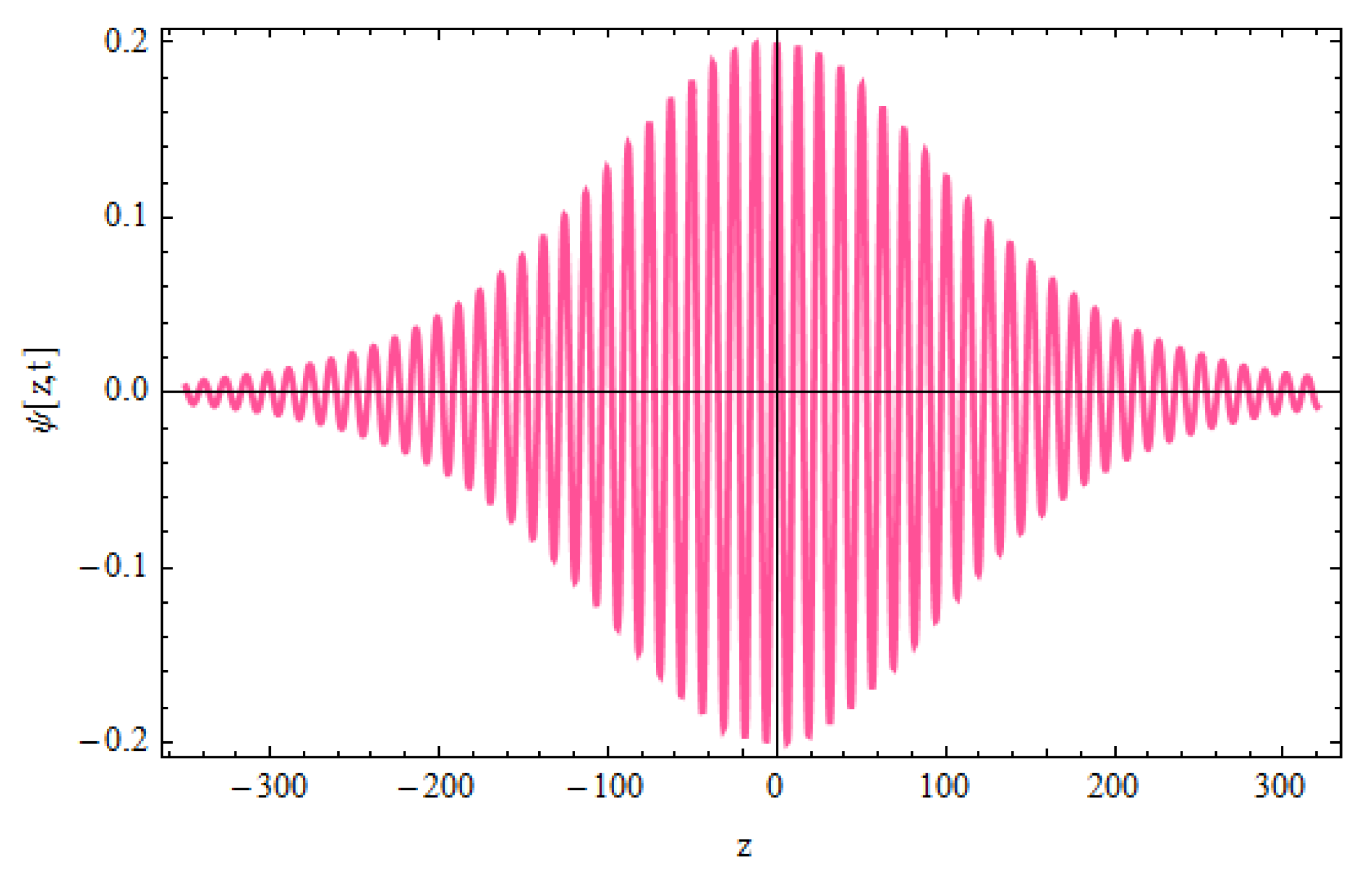
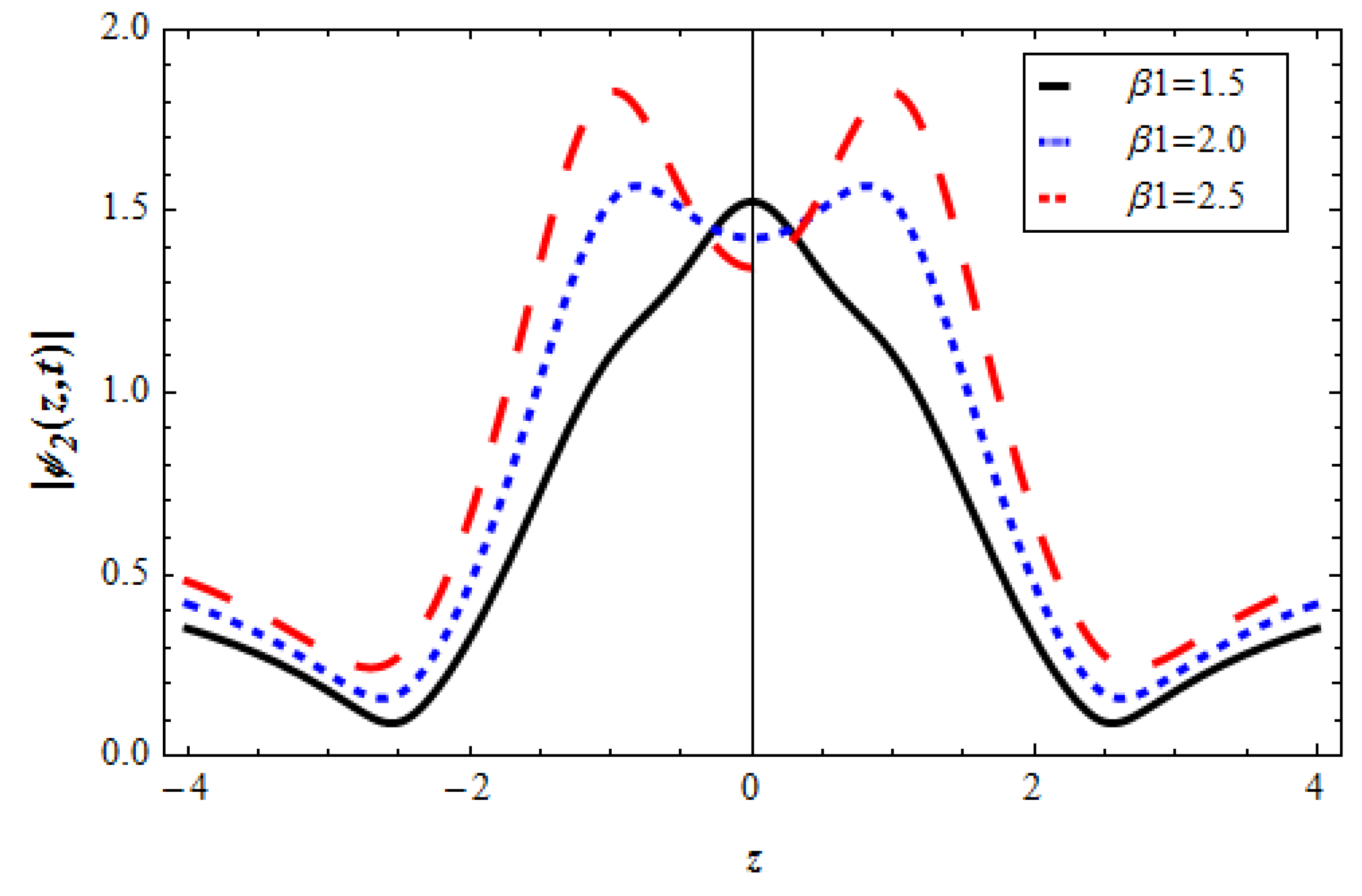
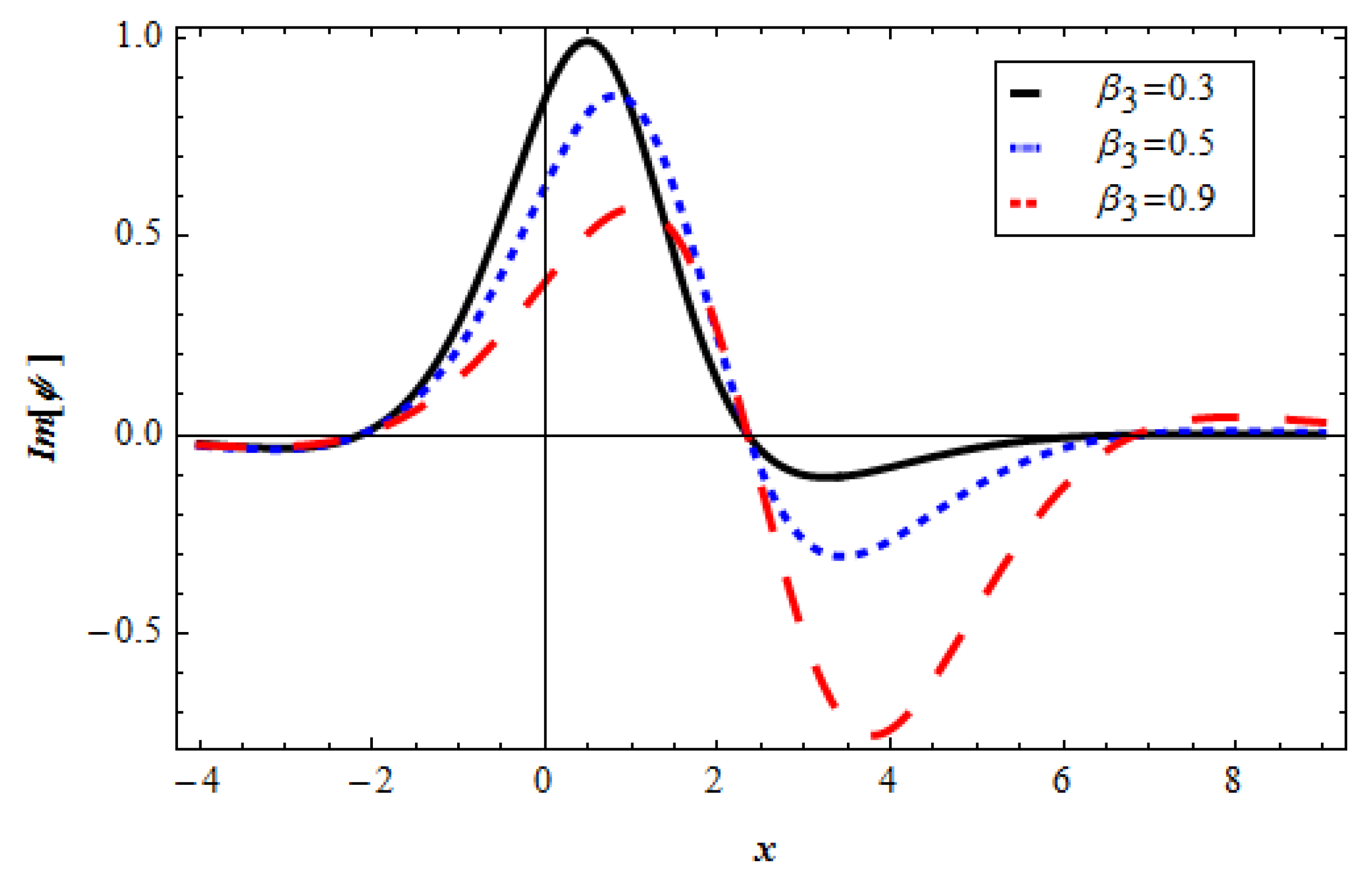
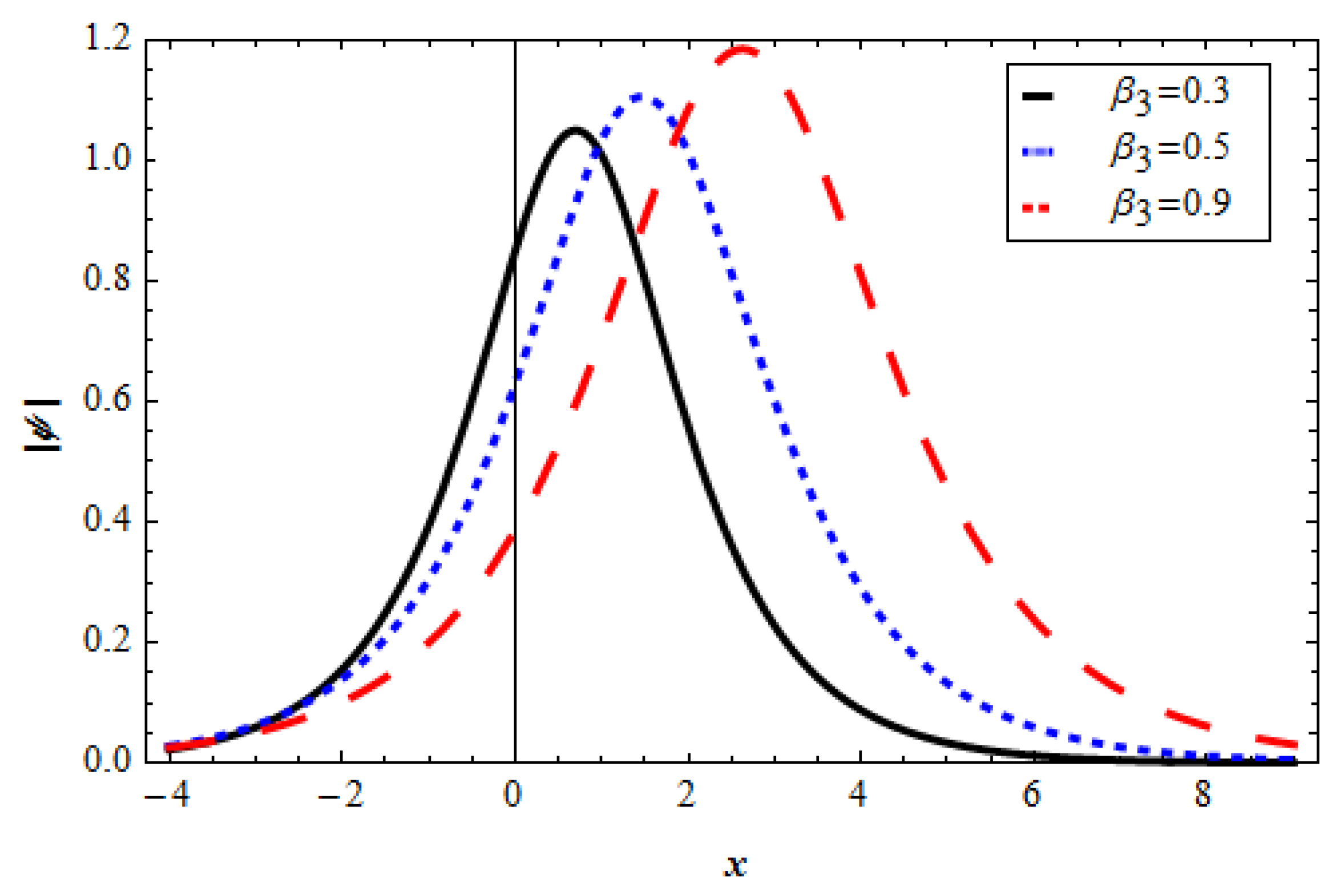
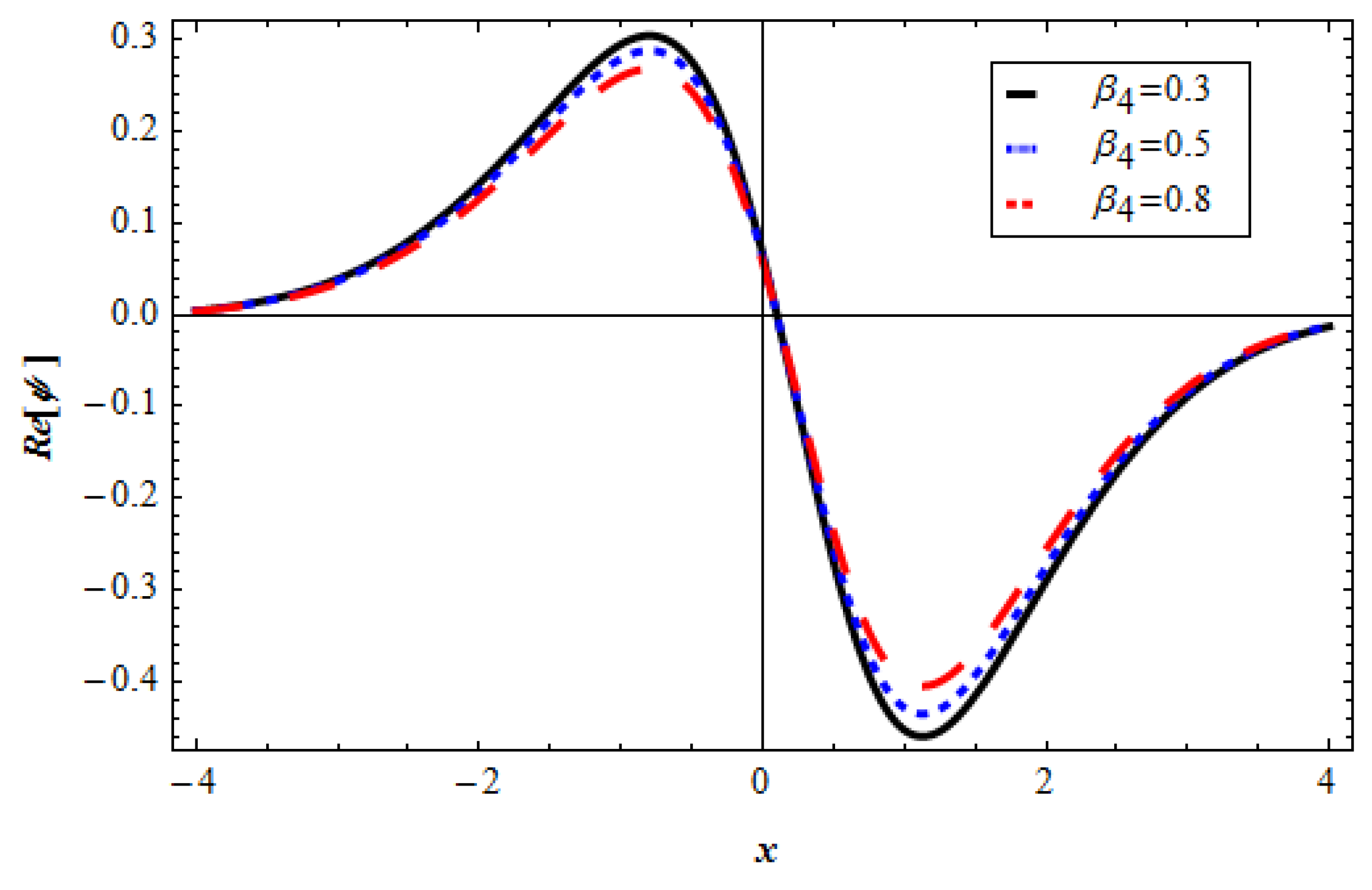
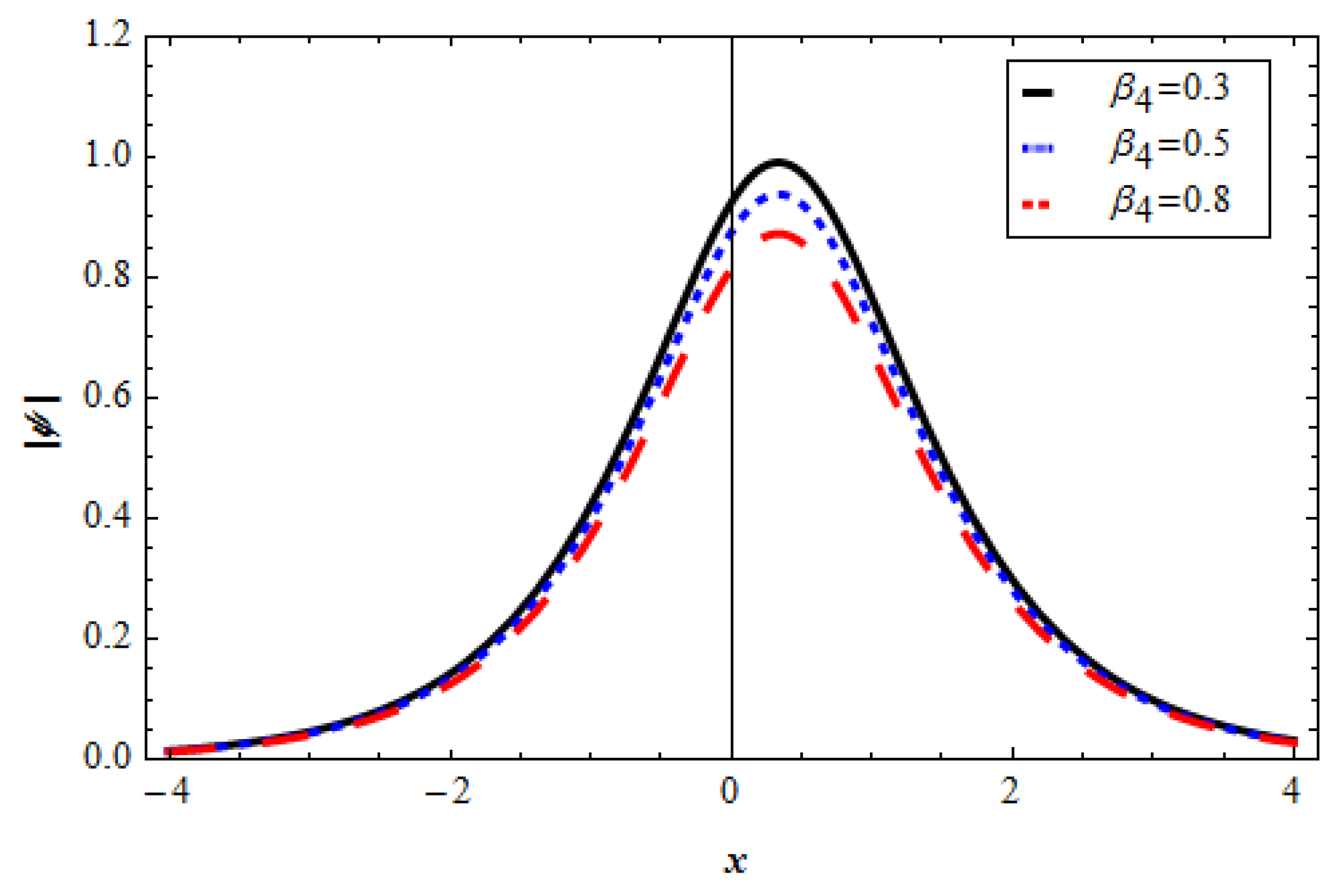
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biondini, G.; El, G.A.; Hoefer, M.A.; Miller, P.D. Dispersive hydrodynamics: Preface. Physica D 2016, 333, 1–5. [Google Scholar] [CrossRef]
- Chang, J.J.; Engels, P.; Hoefer, M.A. Formation of dispersive shock waves by merging and splitting Bose-Einstein condensates. Phys. Rev. Lett. 2008, 101, 170404. [Google Scholar] [CrossRef] [PubMed]
- Dutton, Z.; Budde, M.; Slowe, C.; Hau, L.V. Observation of quantum shock waves created with ultra-vompressed slow light pulses in a Bose-Einstein condensate. Science 2001, 293, 663–668. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic: San Francisco, CA, USA, 1995. [Google Scholar]
- Triki, H.; Bensalem, C.; Biswas, A.; Khan, S.; Zhou, Q.; Adesanya, S.; Moshokoa, S.P.; Belic, M. Self-similar optical solitons with continuous-wave background in a quadratic-cubic non-centrosymmetric waveguide. Opt. Commun. 2019, 437, 392–398. [Google Scholar] [CrossRef]
- Nakkeeran, K. Bright and dark optical solitons in fiber media with higher-order effects. Chaos Solitons Fractals 2002, 13, 673–679. [Google Scholar] [CrossRef]
- Guan, W.Y.; Li, B.Q. New observation on the breather for a generalized nonlinear Schrödinger system with two higher-order dispersion operators in inhomogeneous optical fiber. Optik 2019, 181, 853–861. [Google Scholar] [CrossRef]
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Li, B.Q.; Ma, Y.L. Periodic and N-kink-like optical solitons for a generalized Schrödinger equation with variable coefficients in an inhomogeneous fiber system. Optik 2019, 179, 854–860. [Google Scholar] [CrossRef]
- Alharbi, Y.F.; Abdelrahman, M.A.E.; Sohaly, M.A.; Inc, M. Stochastic treatment of the solutions for the resonant nonlinear Schrödinger equation with spatio-temporal dispersions and inter-modal using beta distribution. Eur. Phys. J. Plus 2020, 135, 368. [Google Scholar] [CrossRef]
- Abdelwahed, H.G.; El-Shewy, E.K.; Abdelrahman, M.A.E.; Alsarhana, A.F. On the physical nonlinear (n+1)-dimensional Schrödinger equation applications. Results Phys. 2021, 21, 103798. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Abdelrahman, M.A.E.; Abdo, N.F. On the nonlinear new wave solutions in unstable dispersive environments. Phys. Scripta 2020, 95, 045220. [Google Scholar] [CrossRef]
- Abdelwahed, H.G.; Abdelrahman, M.A.E.; Alghanim, S.; Abdo, N.F. Higher-order Kerr nonlinear and dispersion effects on fiber optics. Results Phys. 2021, 26, 104268. [Google Scholar] [CrossRef]
- Chen, J.; Pelinovsky, D.E.; Upsal, J. Modulational instability of periodic standing waves in the derivative NLS equation. J. Nonlinear Sci. 2021, 31, 58. [Google Scholar] [CrossRef]
- McDonald, G.D.; Kuhn, C.C.N.; Hardman, K.S.; Bennetts, S.; Everitt, P.J.; Altin, P.A.; Debs, J.E.; Close, J.D.; Robins, N.P. Bright solitonic matter-wave interferometer. Phys. Rev. Lett. 2014, 113, 013002. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.L. Nth-order rogue wave solutions for a variable coefficient Schrödinger equation in inhomogeneous optical fibers. Optik 2022, 251, 168103. [Google Scholar] [CrossRef]
- Li, B.Q.; Ma, Y.L. Interaction properties between rogue wave and breathers to the manakov system arising from stationary self-focusing electromagnetic systems. Chaos Solitons Fractals 2022, 156, 111832. [Google Scholar] [CrossRef]
- Husakou, A.V.; Herrmann, J. Supercontinuum generation of higher-order solitons by fission in photonic crystal fibers. Phys. Rev. Lett. 2001, 87, 203901. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Bhadra, S.K.; Agrawal, G.P. Perturbation of higher-order solitons by fourth-order dispersion in optical fibers. Opt. Commun. 2009, 282, 3798–3803. [Google Scholar] [CrossRef]
- Liu, C. Exact solutions for the higher-order nonlinear Schrödinger equation in nonlinear optical fibres. Chaos Solitons Fractals 2005, 23, 949–955. [Google Scholar] [CrossRef]
- Tamilthiruvalluvar, R.; Wamba, E.; Subramaniyan, S.; Porsezian, K. Impact of higher-order nonlinearity on modulational instability in two-component Bose-Einstein condensates. Phys. Rev. E 2019, 99, 032202. [Google Scholar] [CrossRef]
- Alharbi, Y.F.; Sohaly, M.A.; Abdelrahman, M.A.E. Fundamental solutions to the stochastic perturbed nonlinear Schrödinger’s equation via gamma distribution. Results Phys. 2021, 25, 104249. [Google Scholar] [CrossRef]
- Alkhidhr, H.A.; Abdelwahed, H.G.; Alghanim, M.A.E.A.S. Some solutions for a stochastic NLSE in the unstable and higher order dispersive environments. Results Phys. 2022, 34, 105242. [Google Scholar] [CrossRef]
- Ma, Y.L. Interaction and energy transition between the breather and rogue wave for a generalized nonlinear Schrödinger system with two higher-order dispersion operators in optical fibers. Nonlinear Dyn. 2019, 97, 95–105. [Google Scholar] [CrossRef]
- Li, B.Q. Phase transitions of breather of a nonlinear Schrödinger equation in inhomogeneous optical fiber system. Optik 2020, 217, 164670. [Google Scholar] [CrossRef]
- Li, B.Q.; Ma, Y.L. Extended generalized Darboux transformation to hybrid rogue wave and breather solutions for a nonlinear Schrödinger equation. Appl. Math. Comput. 2020, 386, 125469. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Whitham, G.B. On the propagation of weak shock waves. J. Fluid Mech. 1956, 1, 290–318. [Google Scholar] [CrossRef]
- Musher, S.L.; Rubenchik, A.M.; Zakharov, V.E. Weak Langmuir turbulence. Phys. Rep. 1995, 252, 178–274. [Google Scholar] [CrossRef]
- XGao, Y.; Guo, Y.J.; Shan, W.R. Optical waves/modes in a multicomponent inhomogeneous optical fiber via a three-coupled variable-coefficient nonlinear Schrödinger system. Appl. Math. Lett. 2021, 120, 107161. [Google Scholar]
- Li, B.Q.; Ma, Y.L. N-order rogue waves and their novel colliding dynamics for a transient stimulated Raman scattering system arising from nonlinear optics. Nonlinear Dyn. 2020, 101, 2449–2461. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guoa, Y.J.; Shanb, W.R. Looking at an open sea via a generalized (2+1)-dimensional dispersive long-wave system for the shallow water: Scaling transformations, hetero-Bäcklund transformations, bilinear forms and N solitons. Eur. Phys. J. Plus 2021, 136, 893. [Google Scholar] [CrossRef]
- Stepanyants, Y.A.; Zakharov, D.V.; Zakharov, V.E. Lump interactions with plane solitons. Radiophys Quantum El 2022, 64, 665–680. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Zakharov, V.E. Soliton turbulence in approximate and exact models for deep water waves. Fluids 2020, 5, 67. [Google Scholar] [CrossRef]
- Dyachenko, S.A.; Nabelek, P.; Zakharov, D.V.; Zakharov, V.E. Primitive solutions of the Korteweg–de Vries equation. Theor Math Phys. 2020, 202, 334–343. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, D.S. Exotic wave patterns in Riemann problem of the high-order Jaulent-Miodek equation: Whitham modulation theory. Stud. Appl. Math. 2022, 149, 588–630. [Google Scholar] [CrossRef]
- Cheemaa, N.; Younis, M. New and more exact traveling wave solutions to integrable (2+1)-dimensional Maccari system. Nonlinear Dyn. 2016, 83, 1395–1401. [Google Scholar] [CrossRef]
- Alomair, R.A.; Hassan, S.Z.; Abdelrahman, M.A.E. A new structure of solutions to the coupled nonlinear Maccari’s systems in plasma physics. AIMS Math. 2022, 7, 8588–8606. [Google Scholar] [CrossRef]
- Kourakis, I.; Shukla, P.K. Exact theory for localized envelope modulated electrostatic wavepackets in space and dusty plasmas. Nonlinear Process. Geophys. 2005, 12, 407–423. [Google Scholar] [CrossRef]
- Noman, A.A.; Islam, M.K.; Hassan, M.; Banik, S.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Dust-ion-acoustic rogue waves in a dusty plasma having super-thermal electrons. Gases 2021, 1, 106–116. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 2009, 80, 026601. [Google Scholar] [CrossRef] [PubMed]






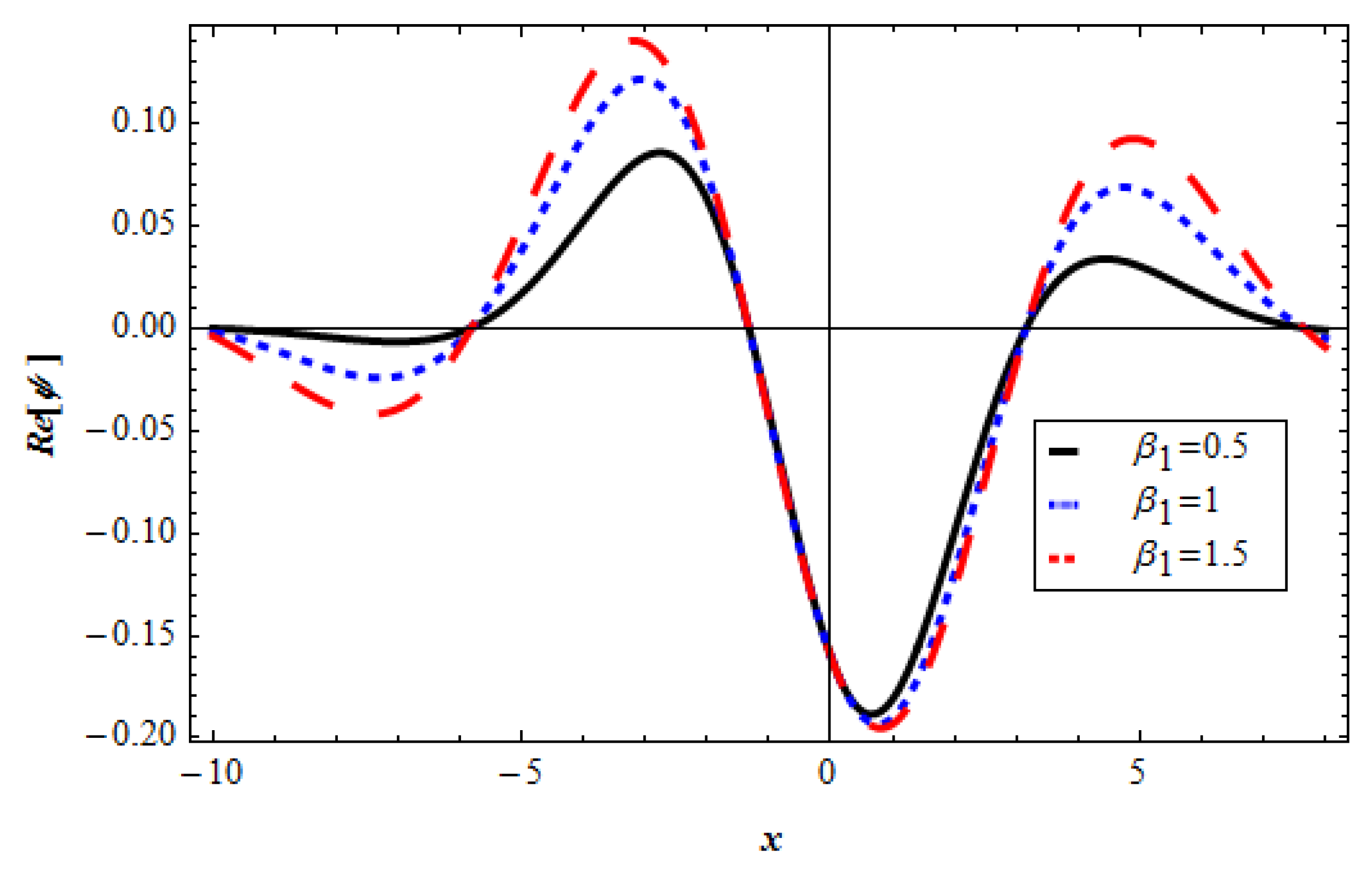
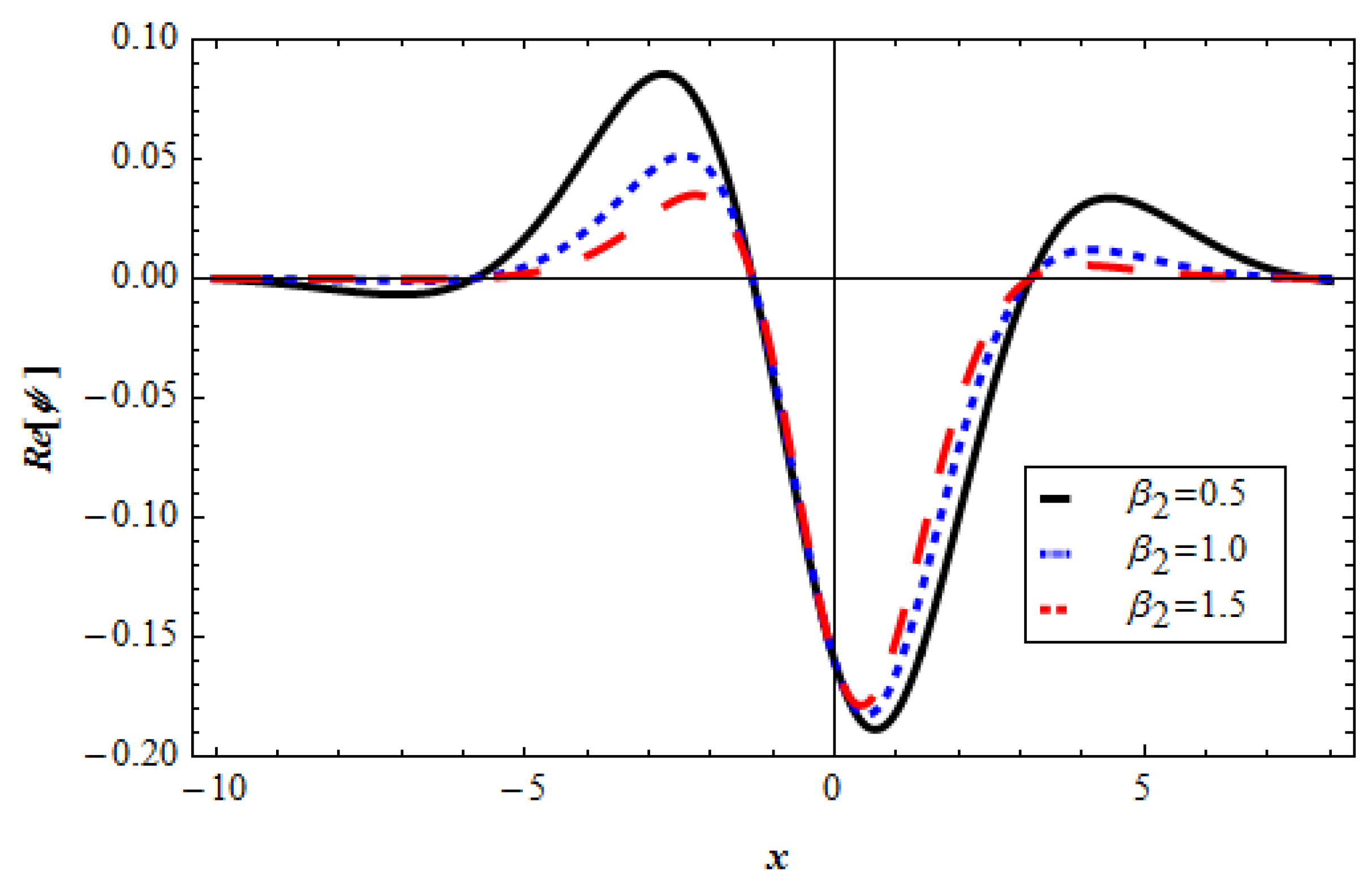

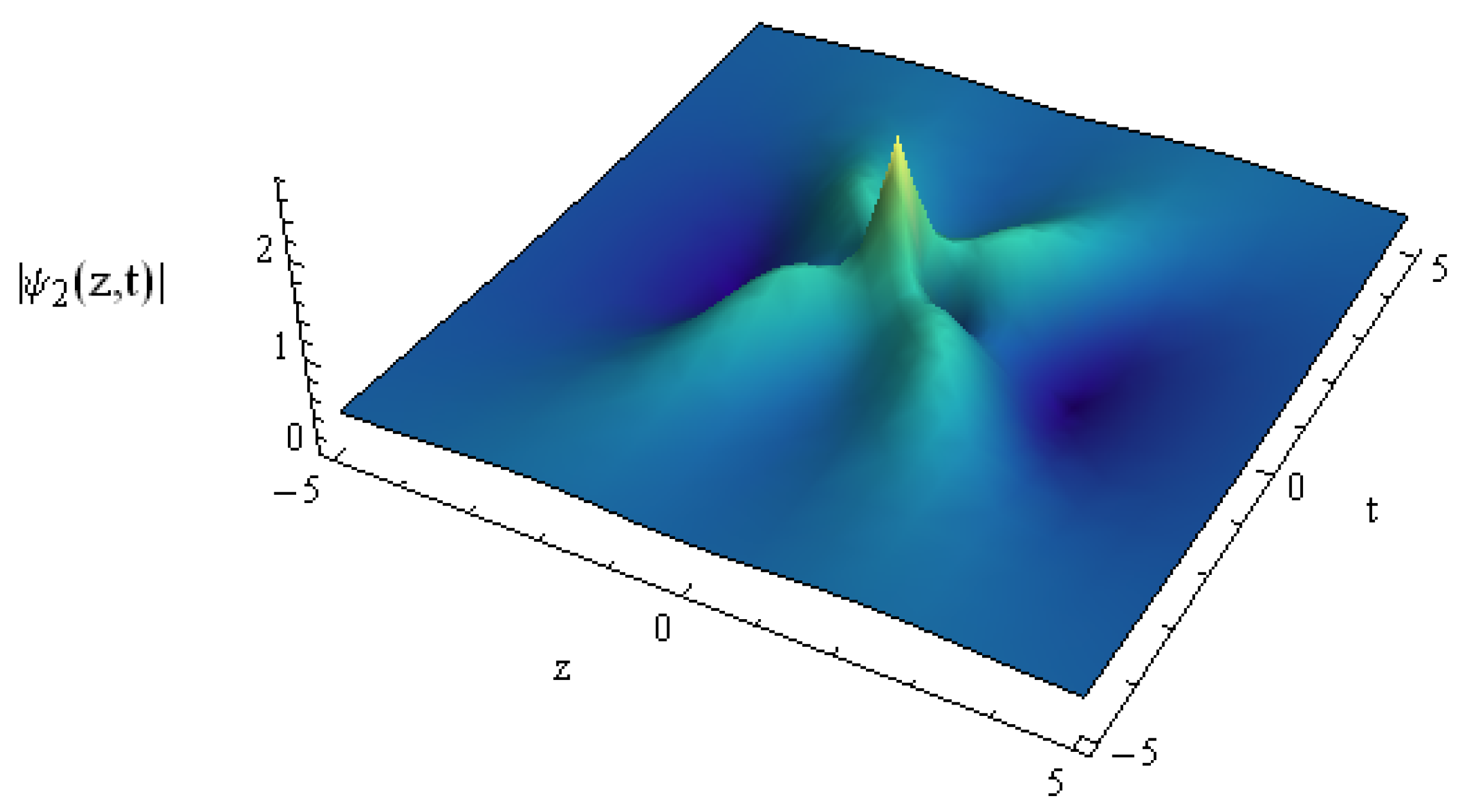
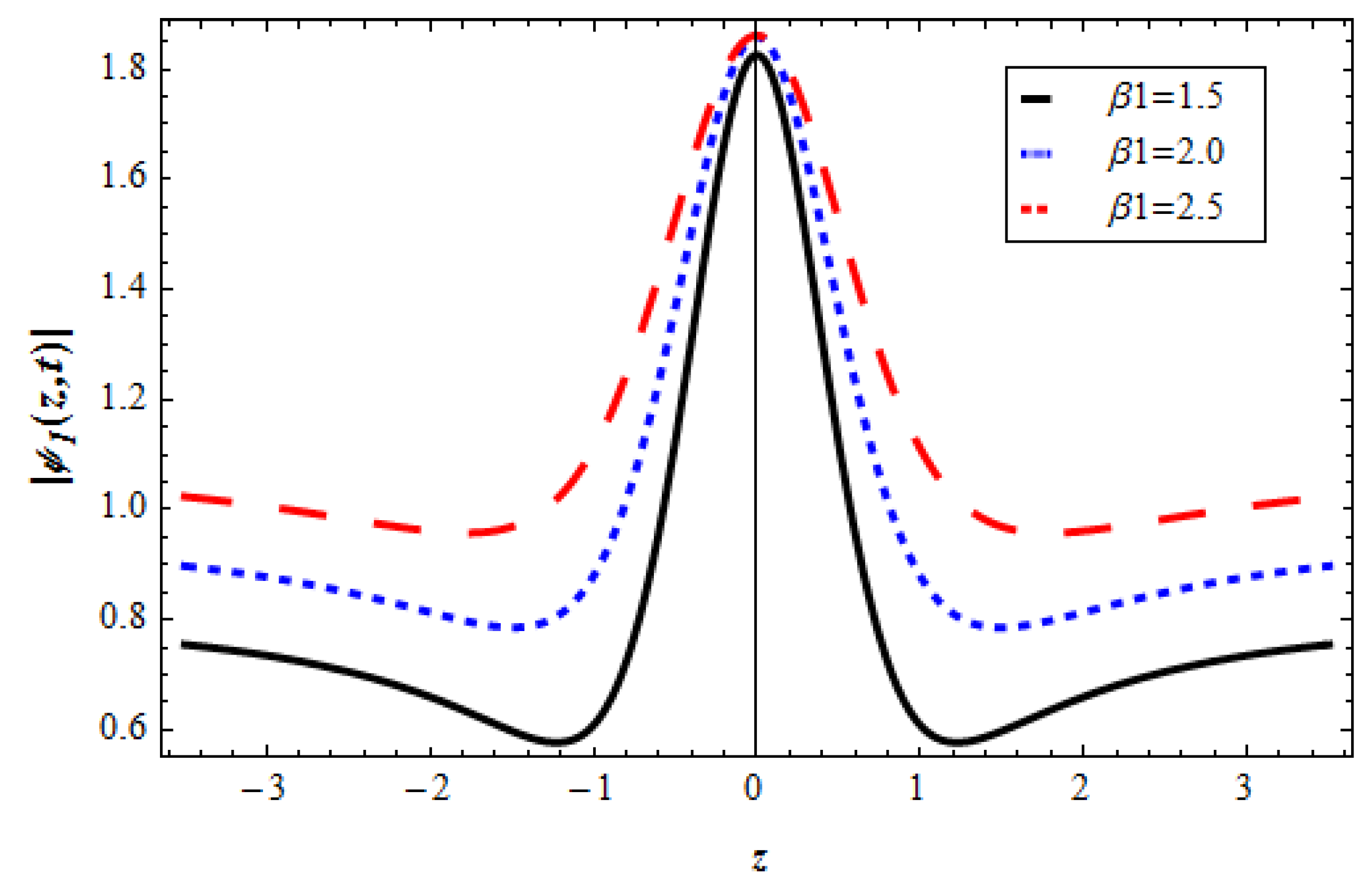
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelwahed, H.G.; Alsarhana, A.F.; El-Shewy, E.K.; Abdelrahman, M.A.E. Higher-Order Dispersive and Nonlinearity Modulations on the Propagating Optical Solitary Breather and Super Huge Waves. Fractal Fract. 2023, 7, 127. https://doi.org/10.3390/fractalfract7020127
Abdelwahed HG, Alsarhana AF, El-Shewy EK, Abdelrahman MAE. Higher-Order Dispersive and Nonlinearity Modulations on the Propagating Optical Solitary Breather and Super Huge Waves. Fractal and Fractional. 2023; 7(2):127. https://doi.org/10.3390/fractalfract7020127
Chicago/Turabian StyleAbdelwahed, H. G., A. F. Alsarhana, E. K. El-Shewy, and Mahmoud A. E. Abdelrahman. 2023. "Higher-Order Dispersive and Nonlinearity Modulations on the Propagating Optical Solitary Breather and Super Huge Waves" Fractal and Fractional 7, no. 2: 127. https://doi.org/10.3390/fractalfract7020127
APA StyleAbdelwahed, H. G., Alsarhana, A. F., El-Shewy, E. K., & Abdelrahman, M. A. E. (2023). Higher-Order Dispersive and Nonlinearity Modulations on the Propagating Optical Solitary Breather and Super Huge Waves. Fractal and Fractional, 7(2), 127. https://doi.org/10.3390/fractalfract7020127









